Open Access Article
Open Access ArticleData-efficient fine-tuning of foundational models for first-principles quality sublimation enthalpies
Harveen Kaura,
Flaviano Della Pia a,
Ilyes Batatia
a,
Ilyes Batatia b,
Xavier R. Advincula
b,
Xavier R. Advincula ac,
Benjamin X. Shi
ac,
Benjamin X. Shi a,
Jinggang Lan
a,
Jinggang Lan de,
Gábor Csányi
de,
Gábor Csányi b,
Angelos Michaelides
b,
Angelos Michaelides a and
Venkat Kapil
a and
Venkat Kapil *afg
*afg
aYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: v.kapil@ucl.ac.uk
bEngineering Laboratory, University of Cambridge, Cambridge, CB2 1PZ, UK
cCavendish Laboratory, Department of Physics, University of Cambridge, Cambridge, CB3 0HE, UK
dDepartment of Chemistry, New York University, New York, NY 10003, USA
eSimons Center for Computational Physical Chemistry at New York University, New York, New York 10003, USA
fDepartment of Physics and Astronomy, University College, London WC1E 6BT, UK
gThomas Young Centre and London Centre for Nanotechnology, London WC1E 6BT, UK. E-mail: v.kapil@ucl.ac.uk
First published on 9th August 2024
Abstract
Calculating sublimation enthalpies of molecular crystal polymorphs is relevant to a wide range of technological applications. However, predicting these quantities at first-principles accuracy – even with the aid of machine learning potentials – is a challenge that requires sub-kJ mol−1 accuracy in the potential energy surface and finite-temperature sampling. We present an accurate and data-efficient protocol for training machine learning interatomic potentials by fine-tuning the foundational MACE-MP-0 model and showcase its capabilities on sublimation enthalpies and physical properties of ice polymorphs. Our approach requires only a few tens of training structures to achieve sub-kJ mol−1 accuracy in the sublimation enthalpies and sub-1% error in densities at finite temperature and pressure. Exploiting this data efficiency, we perform preliminary NPT simulations of hexagonal ice at the random phase approximation level and demonstrate a good agreement with experiments. Our results show promise for finite-temperature modelling of molecular crystals with the accuracy of correlated electronic structure theory methods.
1 Introduction
Molecular crystals form an essential class of materials with technological applications in industries such as pharmaceuticals,1 electronics,2 and agriculture.3 Often, molecular crystals exhibit competing polymorphs, i.e., multiple metastable crystalline phases with very similar stability (for instance, relative free energies can be within ≈1 kJ mol−1 error).4 While the most common experimental probe of the polymorph stability is the sublimation enthalpy, recent work shows discrepancies across calorimetry literature for prototypical molecular crystals beyond 1 kcal mol−1 (ref. 5) ≈ 4.2 kJ mol−1. Hence, there is a need for an independent estimation of sublimation enthalpies using first-principles methods.Although possible in theory, predicting sublimation enthalpies with first principles methods is challenging due to the need for high accuracy. Reliable predictions require a tolerance of nearly 4.2 kJ mol−1 for absolute sublimation enthalpies and a tighter tolerance of less than 1 kJ mol−1 for relative sublimation enthalpies.4 As shown by Zen et al.,6 predicting absolute sublimation enthalpies of common molecular solids, such as ice, ammonia, carbon dioxide and aromatic hydrocarbons, consistently to 1 kcal mol−1 requires computationally demanding “correlated” electronic structure techniques. These techniques include quantum fixed-node Diffusion Monte Carlo,7 periodic coupled cluster8 or random phase approximation (RPA) with singles excitations.9,10 Similarly, achieving correct relative stabilities, accurate to 1 kJ mol−1, of prototypical polymorphs of oxalic acid, glycine, paracetamol, and benzene requires statistical mechanics incorporating dynamical disorder via thermal effects,11,12 thermal expansion,13 and anharmonic quantum nuclear motion.11–13
Unfortunately, the computational cost associated with correlated electronic structure theory6 or rigorous quantum statistical mechanics,14 individually or in tandem, remains high. Hence, sublimation enthalpies are commonly approximated inexpensively with dispersion-corrected density functional theory (DFT) for a static geometry optimized lattice at zero kelvin.15 As a consequence of their static description, these enthalpies are compared indirectly with experiments requiring a careful extrapolation of measured enthalpies to a static lattice at zero kelvin.16 Unfortunately, this is typically associated with an error-prone ad hoc subtraction of zero-point energy corrections calculated using DFT.17 Furthermore, considering the inherent uncertainties in measured sublimation enthalpies,5 there is a need for relative stabilities that can be unambiguously compared with experiments at their respective thermodynamic conditions.13
In this context, machine learning potentials (MLPs)18–22 provide an avenue for first-principles-accuracy modelling of molecular crystals at finite temperature. MLPs have been used as computationally inexpensive surrogates for first-principles potential energy surfaces (PES) for ranking putative polymorphs in increasing order of lattice energies.23–25 MLPs have also facilitated finite-temperature modelling of polymorphs of simple compounds like hydrogen26 and water,27,28 with converged system sizes and simulation times. More recently, Kapil and Engel13 developed an MLP-based framework for predicting polymorph relative stabilities for paradigmatic molecular crystals containing up to four chemical species, such as benzene, glycine, and succinic acid. While their approach enables rigorous predictions of relative and absolute stabilities at finite temperatures, it presents a number of limitations arising from those of conventional MLPs. These include a >kJ mol−1 error in out-of-distribution prediction, the need for large volumes of training data (>1000 structures per compound), and declining accuracy and data efficiency with an increasing number of chemical species. These deficiencies make finite-temperature stability calculations for generic molecular compounds costly and prohibitive when using chemically-accurate electronic structure theory.6
In this work, we present an accurate and data-efficient MLP-based approach for finite-temperature modelling and sublimation enthalpy prediction of given polymorphs of a compound. Using ice polymorphs as a test bed, we show that using the multi atomic cluster expansion (MACE) architecture22 supplemented with fine-tuned training of the foundational MACE-MP-0 model is sufficient to reach sub-kJ mol−1 accuracy with as few as 50 training structures. In Section 2, we discuss the shortcomings of conventional MLPs and the capabilities of the newer methods with a focus on MACE and MACE-MP-0, followed by the details of our protocol, including the dataset generation, training and validation steps. In Section 3, we apply our approach to crystalline ice – a prototypical system exhibiting a high degree of polymorphism with good quality experimental data on densities and sublimation enthalpies.16 We demonstrate the accuracy and generality of our approach on the excellent agreement of finite-temperature density and sublimation enthalpies of ice polymorphs directly against the DFT level. Finally, we explore simulations of ice polymorphs directly at the RPA level by training on a few tens of periodic total energy and force calculations. While the results of RPA simulations are sensitive to the orbitals used to expand the independent particle response function,29,30 using hybrid-functional orbitals yields a good description of the density of ice. In Section 4, we discuss the limitations of this work and future efforts for direct finite-temperature simulations for characterizing molecular crystal polymorphs at the accuracy of correlated electronic structure.
2 Theory and methods
2.1 Brief review of machine learning models
MLPs typically represent the total energy of a system as a sum of atomic energies. Standard models of the atomic energy of a central atom first preprocess the relative atomic positions of all atoms up to a cutoff into so-called “atomic representations”.31,32 Subsequently, the representations are used as inputs to a regression model,31,32 such as a Gaussian process,19 and artificial18 or deep neural networks,33 trained on total energy of the system and its gradients such as atomic forces and stress tensors.34,35 Typically, these representations are n-body correlation functions (defined for every n-tuple of atom types and typically truncated at n = 2 or 3) of relative atomic positions which encode rotational, permutational, and inversion invariances.20,36Standard architectures, such as the Behler–Parrinello neural network (BPNN) framework,35 Gaussian Approximation Potential,19 SchNet,37 DeepMD,33 and Moment Tensor Potential,38 can be constructed by mixing and matching various flavours of two- or three-body atomic representations and regression models. Despite their success, standard models have two main limitations. First, the truncation of body order leads to the incompleteness of the atomic representations, limiting their accuracy and smoothness.39 The accuracy can be systematically improved, but including higher body order representations involves a much higher computational cost and labour.38,40,41 Second, the number of representations scales combinatorially with the number of chemical species as n-body representations are defined for every n-tuple of atomic species. Hence, for a given accuracy cutoff, standard MLPs exhibit an exponentially increasing cost with an increasing number of chemical species. Similarly, for a fixed cost, these models have a steeply worsening accuracy with increasing chemical species.
Newer MLPs such as NequIP,21 MACE,22 and PET,42 implemented as Euclidean graph neural networks,43 address these issues by incorporating (near) complete atomic representations.20 In addition, they exploit a learnable latent chemical space21,44,45 for smoothly interpolating or extrapolating representations across chemical species at 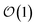 cost without compromising accuracy.46 Specifically, in the MACE architecture, the initial node representations of the graph neural network are based on the atomic cluster expansion20 up to a selected body order (typically n = 4). MACE systematically constructs higher body-order representations in terms of the output of the previous layer and an equivariant and high body-order message passing scheme.45 Hence, increasing the number of layers or body order of the message passing enables learning correlation functions of arbitrary order. However, thanks to its message passing scheme, MACE can efficiently construct high body-order representations with a simple architecture (e.g., the default parameters of MACE with just two layers give access to a body order of 13).47 Finally, embedding chemical information in a learnable latent space,48 MACE displays an
cost without compromising accuracy.46 Specifically, in the MACE architecture, the initial node representations of the graph neural network are based on the atomic cluster expansion20 up to a selected body order (typically n = 4). MACE systematically constructs higher body-order representations in terms of the output of the previous layer and an equivariant and high body-order message passing scheme.45 Hence, increasing the number of layers or body order of the message passing enables learning correlation functions of arbitrary order. However, thanks to its message passing scheme, MACE can efficiently construct high body-order representations with a simple architecture (e.g., the default parameters of MACE with just two layers give access to a body order of 13).47 Finally, embedding chemical information in a learnable latent space,48 MACE displays an  computational cost with the number of chemical species.
computational cost with the number of chemical species.
Exploiting these capabilities for datasets with a large number of elements, Batatia et al.49 have recently developed a so-called MACE-MP-0 foundational MLP model trained on a diverse Materials Project dataset. Specifically, MACE-MP-0 is trained on the MPTrj dataset, comprising 1.5 million small periodic unit cells of inorganic (molecular) crystals with elements across the periodic table. The training set includes total energies, forces and stress tensors estimated at the PBE(+U) level. Trained for elements across the periodic table, the MACE-MP-0 model is capable of out-of-the-box usage for general materials with qualitative (and sometimes quantitative) PBE accuracy. Other classes of foundational MLPs exist, such as CHGNET50 and M3GNet,51 based on materials project datasets and the ALIGNN-FF50 based on the JARVIS-DFT dataset. Unlike MACE-MP-0, these models are based on three-body atomic representations.
While MACE-MP-0’s accuracy is insufficient for studying molecular crystal polymorphs, its parameters may provide a starting point for training system-specific models at a different level of theory. Considering that the pre-trained n-body atomic representations are valid for generic materials, using the MACE-MP-0 parameters as a starting point for fine-tuning may require less data and computational time compared to training a new model from scratch.
2.2 Details of our framework
(1) Dataset Sampling. We perform a short first-principles molecular dynamics (MD) simulation in the NPT ensemble. To ensure this step is inexpensive, we select a generalized gradient approximation (GGA) DFT level of theory and coarsely converged electronic structure parameters and simulation lengths up to 5 ps.
(2) Dataset generation. We randomly select 500 structures to perform total energy, force, and stress calculations with tightly converged parameters. We collect total energies, forces and stress tensors as target properties, thereby generating a dataset of 500 structures, energy and its gradients. The validation set includes 100 randomly selected structures. The remaining structures are split into training sets of increasing sizes with 50, 100, 160, 200, 320 and 400 structures. The larger sets include structures from the smaller ones.
(3) Model development and validation. We train two types of models for each training set – a MACE model trained from scratch and a MACE model fine-tuned from MACE-MP-0 in which we use the initial parameters from the foundational models as a starting point. We compare learning curves by plotting the root mean square errors (RMSEs) of the total energies and the atomic force components, thereby identifying the training set sizes and the training methods that deliver sub-kJ mol−1 accuracy.
(4) Model testing against DFT. We perform an additional out-of-distribution test in the NPT ensemble sampled by the MLPs and compare it against the DFT ensemble. We study the convergence of the average potential energy and density from NPT simulations as a function of the size of the training set. We obtain a converged DFT reference for the average potential energy and density by performing DFT single point energy calculations on 100 uniformly stridden configurations. We use the difference between MACE and DFT energies to estimate the averages at DFT level using statistical reweighting. We identify the training set sizes that deliver good accuracy against the DFT reference ensemble.
The models from step 4 can be used for production simulations in the NPT ensemble with larger simulation sizes and long simulation times. The same procedure is used for training the model at the RPA level, replacing DFT with RPA level total energy and force calculations.
Systems and thermodynamic conditions. We validate our pipeline on the densities and sublimation enthalpies of ice polymorphs Ih, II, VI and VIII at 100 K and 1 bar. We use simulation cells with 128 molecules for ice Ih, 96 molecules for ice II and 80 molecules for ice VI and VIII. These simulation cells ensure lattice parameters greater than 10 Å. We employ the revPBE functional with (zero-damping) D3 dispersion correct due to its good performance against diffusion Monte Carlo for ice phases.52
Dataset Sampling. We use the CP2K code53 for efficient sampling of the dataset via ab initio molecular dynamics simulations. The electronic structure is described using Kohn–Sham density functional theory with a plane-wave basis set truncated at an energy cutoff of 500 Rydberg, TZV2P-GTH basis sets,54 GTH-PBE pseudopotentials,55 and Γ-point sampling of the Brillouin zone. The simulations are carried out in the NPT ensemble using an isotropic cell at a constant pressure of 1 bar and 100 K.
Dataset generation. We use the VASP code56–58 to perform single-point energy calculations at revPBE-D3 level with SCF parameters from ref. 52. Our over-conservative parameters allow us to minimize the amount of noise in our training set. We used hard PAW (PBE) pseudopotentials59,60 with an energy cutoff of 1000 eV, Γ-point with supercells lattice parameters exceeding 10 Å, and a dense FFT grid (PREC = high).
We also perform total energy and force calculations at the RPA level. We use the EXX + RPA@PBE0(ADMM) approach, which computes exact exchange (EXX) and the RPA correlation energy based on PBE0 orbitals estimated within the auxiliary density matrix method (ADMM).61 We employ the sparse tensor-based nuclear gradients of RPA62 as implemented in CP2K. All calculations use the triple-zeta cc-TZ and RI_TZ basis sets alongside GTH-PBE0 pseudopotentials. The Hartree–Fock exchange contribution to the SCF and the Z-vector equation is calculated within the ADMM approximation.
Model training (from scratch). We use two MACE layers, with a spherical expansion of up to lmax = 3, and 4-body messages in each layer (correlation order 3). We use a self-connection for both layers, a 128-channel dimension for tensor decomposition and a radial cutoff of 6 Å. We expand the interatomic distances into 8 Bessel functions multiplied by a smooth polynomial cutoff function to construct radial features, which in turn fed into a fully connected feed-forward neural network with three hidden layers of 64 hidden units and SiLU non-linearities. A maximal message equivariance of L = 2 is applied. The irreducible representations of the messages have alternating parity (in e3nn notation, 128x0e + 128x1o + 128x2e). The version of software used to perform the from-scratch training corresponds to the 0c9ff32b4c4bf50a02b07931c65b3325b4bb64ee commit of the GitHub repository https://github.com/ACEsuit/mace with CUDA 11.7.
Model training (fine-tuned from MACE-MP-0). We fine-tune the large MACE-MP-0 (ref. 49) model by continuing training from the last checkpoint and, therefore, using the same hyperparameters. A self-connection is used only at the first layer. The remaining parameters are the same as the model trained from scratch. A development version of the fine-tuning code was used with CUDA 12.1, which has been merged into the MACE 0.3.4 release.
Model testing. We use the i-PI code63 to perform NPT MD simulations using an ASE64 as a client for calculating MACE total energy, forces and stress. We perform 50 ps long simulations employing a timestep of 0.5 fs. We use the fully flexible Martyna–Tuckerman–Tobias–Klein65 barostat implementation with a relaxation time of 1 ps. For efficient sampling, we use an optimally damped generalized Langevin equation thermostat for the system and the lattice degrees of freedom.66 We sample positions, potential energies, and densities every 100 MD steps.
3 Results and discussion
3.1 Performance on validation set
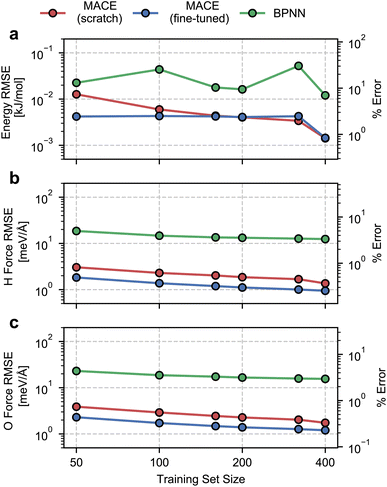
We begin by evaluating the accuracy and data efficiency of the MACE architecture and the “from scratch” and “fine-tuned” training protocols. We perform this test on the ice Ih phase and check whether the MACE models deliver sub-kJ mol−1 accuracy on the validation set.As shown in Fig. 1, we report RMSEs of the energy per molecule and the force components on H and O atoms as a function of the size of the training set. A MACE model trained from scratch reports an energy RMSE of nearly 0.01 kJ mol−1 with the smallest training set comprising 50 structures. On an absolute scale, this error is extremely low. However, it corresponds to 10% of the mean energy variation in the validation set, which is nearly the per atom standard deviation of the potential energy at 100 K. With 400 structures, i.e., the entire dataset, we report an energy RMSE of around 0.001 kJ mol−1. This error corresponds to around 1% of the validation set standard deviation.
We next study the effect of fine-tuning the parameters of the MACE-MP-0 model, which implies starting the training from the last checkpoint of the foundational model. As seen in Fig. 1(a), fine-tuning improves the accuracy of the models, compared to training from scratch, for small datasets containing fewer than 160 structures. With just 50 training structures, a fine-tuned MACE model reports an energy RMSE that corresponds to around 2% of the validation set standard deviation. For training set sizes, beyond 160 structures we see nearly identical performance of the from-scratch and fine-tuned models on the energy RMSE.
The RMSEs of the force components on H and O atoms paint a similar picture. The from-scratch MACE models report a small RMSE of nearly 2 meV Å−1 with just 50 structures, nearly 1% of the validation set standard deviation, with a systematic reduction in error with increasing training data. On the other hand, fine-tuning the MACE-MP-0 model results improved accuracy and data efficiency with nearly 1 meV Å−1 RMSE with 50 structures and sub meV Å−1 RMSE with over 200 structures. We observe improvements in force RMSEs across the full range of training set sizes.
To contextualize these RMSEs, we also report RMSEs obtained with a standard 2- or 3-body atomic-representation-based model. We select the BPNN35 architecture which has been widely used for simulating the bulk,67 interfacial68 and confined phases of water.69 We observe nearly order-of-magnitude higher energy and force RMSEs with the BPNN scheme, with indications of saturating errors with 400 training structures. Although on an absolute scale, the BPNN model reports small energy RMSE, it corresponds to saturation at around 10% relative error. The saturation in the RMSEs is likely due to a ceiling on learning capacity due to incomplete atomic representations. We note the much higher data efficiency of the MACE models, which exhibit a higher accuracy even with an order of magnitude and fewer training data.
3.2 Performance at finite temperature and pressure
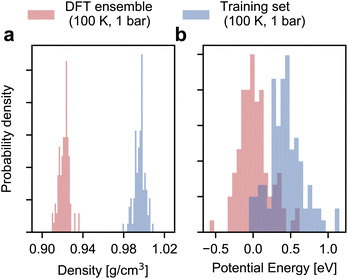
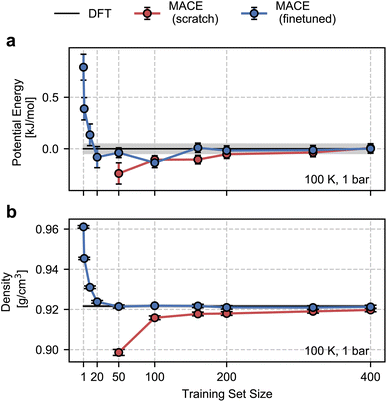
As shown in Fig. 2, the configurational ensemble used to generate the training and validation datasets deviates significantly in energy and volume distributions from that of revPBE-D3 with converged electronic structure parameters. The configurations used for training correspond to denser structures, with shorter interatomic distances and, consequently, higher potential energies compared to the DFT ensemble. Hence, the RMSEs in Fig. 1 only reflect the quality of regression in the training ensemble.To assess model performance at finite thermodynamic conditions, we perform fully flexible NPT simulations at 100 K and 1 bar for each model. We found the BPNN NPT simulations to be unstable due to overfitting on the training ensemble, hence we only present results for the MACE models. We report the thermodynamic average of the potential energy and the density as a function of the size of the training set in Fig. 3. Exploiting MACE’s high fidelity, we perform statistical reweighting to calculate the DFT reference of the average potential energy and the density. For this purpose, we use the trajectory sampled by the fine-tuned MACE trained on 100 structures. The DFT references allow us to test MLPs against their DFT in their thermodynamic ensembles directly.
As shown in Fig. 3, the from-scratch MACE models generalize well to the true thermodynamic ensemble displaying sub-kJ mol−1 error for the average potential energy at 100 K and 1 bar. Despite these small errors, we note that the from-scratch MACE thermodynamic averages deviate from the DFT reference at 50 structures, yielding a statistically significant agreement for models trained with more than 200 structures. These small errors lead to significant disagreements in the density (a quantity that is much harder to converge compared to energy or forces as per empirical evidence70). We require training on 400 structures to converge the density to the DFT reference within statistical error.
With the fine-tuned models, we observe a remarkable performance against the DFT ensemble. Even for the smallest training set comprising 50 structures, we observe a quantitative agreement in the density and the average energy. Inspired by this result, we trained new fine-tuned models with 1, 2, 10, and 20 structures and studied their performance on density and the average energy in the NPT ensemble. With just 10 structures, the properties obtained with the fine-tuned models are within 1% (0.09 g cm−3) of the DFT density and 0.5 kJ mol−1 of the DFT energy. These tests suggest the potential of our approach for finite-temperature modelling of molecular polymorphs with a few tens of training structures. This is a marked improvement over our previous work in ref. 13, which required over a few hundred or thousands of structures and differential learning for stable NPT simulations.
3.3 DFT-level sublimation enthalpies and physical properties of ice polymorphs
The fine-tuned MACE model only requires up to a hundred training structures for ice Ih for first-principles-quality NPT simulations. We next check if the observed data-efficiency for ice Ih is valid for other polymorphs. For this purpose, we predict the sublimation enthalpy and density of ice II, VI, and VIII at finite thermodynamic conditions and check agreement with the DFT ensemble.For each polymorph, we train a fine-tuned MACE model on 100 structures and perform NPT simulations at 100 K and 1 bar to estimate the density and the average potential energy. To estimate the sublimation enthalpy, we further train a fine-tuned MACE model on 200 structures of a water molecule providing a gas phase reference enthalpy at 100 K and 1 bar. The training set was developed in the same way as for the ice polymorphs with initial NVT sampling using CP2K at revPBE-D3 level and converged DFT calculations on randomly sampled structures using VASP. Finally, for an apples-to-apples comparison, we compare with DFT-level densities and sublimation enthalpies calculated using statistical reweighting.
As shown in Table 1, the densities and sublimation enthalpies estimated with MACE at 100 K and 1 bar agree remarkably with the reference DFT estimations up to the statistical error. In most cases, the discrepancies between MACE and DFT are within the 1σ statistical error of DFT estimations. In all the cases, the agreement for the sublimation enthalpy and the density are within 0.5 kJ mol−1 and 1% respectively. These results demonstrate the data efficiency and generalizability of the fine-tuned MACE models to the full NPT ensemble of energy and volume despite being trained on a skewed ensemble.
| Polymorph | Density [g cm−3] | Sublimation enthalpy [kJ mol−1] | ||||
|---|---|---|---|---|---|---|
| MACE | DFT | % Error | MACE | DFT | Error | |
| Ih | 0.922 ± 0.001 | 0.922 ± 0.001 | 0.012 ± 0.161 | −58.208 ± 0.089 | −58.214 ± 0.089 | 0.006 ± 0.126 |
| II | 1.200 ± 0.002 | 1.190 ± 0.009 | 0.896 ± 0.764 | −57.055 ± 0.091 | −56.814 ± 0.145 | 0.241 ± 0.0172 |
| VI | 1.329 ± 0.001 | 1.330 ± 0.006 | 0.083 ± 0.461 | −55.225 ± 0.091 | −55.215 ± 0.114 | 0.010 ± 0.146 |
| VIII | 1.569 ± 0.001 | 1.565 ± 0.003 | 0.262 ± 0.196 | −56.063 ± 0.107 | −55.719 ± 0.143 | 0.349 ± 0.179 |
3.4 Random phase approximation level physical properties of ice Ih in the NPT ensemble
The sub-kJ mol−1 accuracy of the fine-tuned MACE models at finite thermodynamic conditions suggests that they are capable of learning at the accuracy of correlated electronic structure theory levels for relative and absolute sublimation enthalpies. In addition, the low data requirement of the fine-tuned MACE models makes them practically viable for training on small datasets generated at computationally demanding correlated electronic structure theory level.To explore this possibility, we consider modelling the properties of ice Ih at the RPA level. We consider this approach, as there exists an efficient implementation in CP2K.62,71 Additionally, there exist tests for zero Kelvin calculations on ice Ih with both Gaussian Type Orbitals in CP2K, which compare well with those using plane waves in VASP.29 It is to be noted that the RPA correlation energy estimated with PBE orbitals leads to underbinding and, thus, an underprediction of the density, while Hartree–Fock orbitals lead to overbinding and, thus, an overprediction of the density.29 Following the suggestion of Macher et al.,29 we used hybrid functional orbitals from PBE0 estimated with the ADMM approximation, which we refer to as EXX + RPA@PBE0(ADMM). For brevity, we will refer to this level of theory as RPA level unless stated otherwise. We trained a fine-tuned MACE model at this level for ice Ih using 75 periodic total energy and force calculations.
We found that training at the RPA level was more challenging than at the DFT level. Our training set resulted in an energy mean absolute error (MAE) of 0.03 kJ mol−1 and a force MAE of 24.8 meV Å−1, which is significantly higher than the energy MACE of 0.001 meV per atom and force 1 meV Å−1 MAE on the DFT training set. This is due to the noise in the forces resulting from the ADMM approximation, which reduces the computational cost associated with RPA-level calculations. ADMM also leads to a spurious offset in the total energy, which doesn’t allow us to estimate sublimation energies but, fortunately, doesn’t significantly affect structural properties.30 A full study of water at the RPA level with comprehensive convergence tests without the auxiliary density matrix method will be presented elsewhere.
Despite the noisy training set, we were able to report stable NPT simulations at RPA level at 100 K and 1 bar, as shown in Fig. 4. However, due to the high cost of single-point calculations, we were unable to perform statistical reweighting for direct validation. Nonetheless, the accuracy afforded by our simulation allowed us to compare meaningfully with experiments.
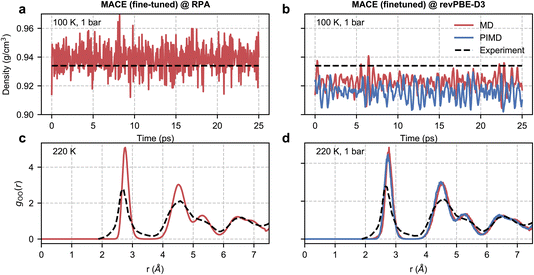 | ||
| Fig. 4 RPA-level simulations of ice Ih. Panel (a) shows the time series of the density of ice Ih from a classical NPT simulation at 100 K and 1 bar with a MACE model trained at EXX + RPA@PBE0(ADMM) level. Panel (b) shows the same quantity but with classical and path-integral NPT simulations using the MACE model trained at the revPBE-D3 level. The black dashed lines correspond to the experimental density72 at 100 K and 1 bar. Panel (c) shows the oxygen–oxygen pair correlation function of ice Ih at 220 K estimated from an RPA level MACE NVT simulation. Panel (d) reports the same quantity but with classical and path-integral NPT simulations at 220 K and 1 bar using the MACE model trained at the revPBE-D3 level. The black lines correspond to the experimental pair correlation function73 measured at 220 K and 1 bar. | ||
We first study the density of ice at 100 K, which is 0.934 g cm−3 as observed in experiments.72 Macher et al.’s29 calculations show that the exact exchange and RPA correlation using (delocalized) PBE orbitals lead to an underpredicted density of around 0.910 g cm−3, while using exact exchange computed using (localized) Hartree–Fock orbitals and RPA correlation using PBE orbitals overestimates the density to around 0.955 g cm−3. Consistent with these results, our RPA calculations based on exact exchange and correlation using PBE0(ADMM) orbitals result in a density of 0.939 g cm−3, which is only marginally higher than the experimental density. Our RPA results also show an improvement over revPBE-D3 density of 0.922 g cm−3. The missing quantum nuclear effects in our RPA-level simulations explain the remaining (small) discrepancy between the NPT and experimental densities. We were unable to confirm this directly as our path integral simulations were not stable. However, we were able to confirm that the instability of the simulations is linked to the noisy forces by performing path integral simulations using our revPBE-D3 level fine-tuned model. As can be seen in Fig. 4(b), we report stable simulations with quantum nuclear effects despite not training on configurations generated using path integral simulations. Quantum nuclear effects marginally reduce the density of ice Ih, nearly to the same extent as the overestimation of the classical density estimated at RPA level compared to experiments.
Finally, with access to stable trajectories, we compared the structure of ice Ih with radiation total scattering experiments at 220 K (ref. 73) by calculating the oxygen–oxygen pair correlation function. Although our potential is trained on configurations corresponding to a 100 K and 1 bar ensemble, our models can generalize to higher temperatures. Unfortunately, due to the noisy RPA-level forces, as diagnosed by stable classical and path-integral simulations in the revPBE-D3 NPT ensemble at 220 K in Fig. 4(d), we report unstable simulations in the NPT ensemble at 220 K and 1 bar. On the other hand, we can perform stable simulations in the NVT ensemble at 220 K and compare the predicted pair correlation function with the experiment in Fig. 4(c). We report an overall good agreement with the experimental pair correlation function and with the revPBE-D3, modulo the over-structuring of the first and second peaks. Although quantum nuclear motion at 220 K is expected to broaden the first and second peaks but not sufficiently enough to explain the extent of static disorder in experiments. The non-zero probability in the 3–4 Å range could arise from defect migration at the grain boundaries in the power sample. Alternatively, the disagreement for short distances (or large reciprocal space vectors) could be an artefact of the empirical potential structure refinement74 used to analyze experimental data.
4 Conclusions
In summary, we explore the accuracy, extrapolation power, and data efficiency of the MACE architecture for predictive finite-temperature sublimation enthalpies of ice polymorphs. In doing so, we present a simple workflow for first-principles quality studies of a polymorph of a molecular compound at a given temperature and pressure. First, we perform a short GGA level first principles NPT MD simulation with coarse convergence parameters. Second, we randomly sample configurations and perform single-point total energy, force, and stress calculations with converged parameters to determine the appropriate choice of electronic structure theory. Third, we fit MACE MLPs and perform simulations in the NPT ensemble to calculate the density and the average potential energy. To estimate the sublimation enthalpy, we follow the same steps for the gas phase molecule. Finally, as an optional step, we perform DFT calculations on the NPT sampled configurations to estimate DFT-level thermodynamic quantities using statistical reweighting for direct testing.Training a MACE model by finetuning the parameters of the pre-trained MACE-MP-0 model, as opposed to training it from scratch, results in improved accuracy and data efficiency. Only 50 to 100 training structures sampled for a given T, P condition are needed to achieve sub-kJ mol−1 and sub 1% agreement on the average energy and density, respectively, against the reference DFT NPT ensemble. Exploiting the accuracy and low data requirement of our approach, we develop an RPA-quality machine learning model for simulating ice Ih in the NPT ensemble. Our RPA simulations demonstrate an overall good agreement with the experimental density and pair-correlation functions and an improvement beyond DFT. At the same time, the noise in RPA training forces compromises the MLP’s data efficiency and robustness compared to the DFT level. Our work highlights the importance of tightly converged electronic structure theory training data, particularly at correlated levels.
We conclude by discussing some limitations that need to be addressed to make our approach applicable to more complex molecular crystals, such as the CSP blind test candidates.75 For instance, our initial data generation step, which uses first-principles MD, took around 24 hours on 8 nodes of an Intel Xeon E5-2690 v3 @ 2.60 GHz (12 cores). However, this step could prove expensive for larger or more complex molecular crystals. Hence, future work will explore less expensive sampling protocols, ranging from MD using the MACE-MP-0 model or a random structure search sampling.76 Second, our approach could require a significantly large volume of training data for systems with a large number of polymorphs, as we generate training data and models separately for each polymorph. Hence, we will study the data efficiency associated with pooling training configurations to develop a single model for all polymorphs. Finally, our approach currently doesn’t include quantum nuclear effects in sublimation enthalpies, which could prove important for obtaining quantitative agreement with experiments. With these developments, we foresee predictive sublimation enthalpy and physical property predictions for molecular crystals at the accuracy of correlated electronic structure and path integral molecular dynamics.
Data availability
The data and scripts that support the findings of this study are openly available in https://github.com/venkatkapil24/fine-tuning-MLPs-ice-polymorphs.Conflicts of interest
GC has equity interest in Symmetric Group LLP that licenses force fields commercially and also in Ångström AI.Acknowledgements
We thank Kit Joll, Keith Buttler, Sander Vandenhaute, and Michele Ceriotti for insightful discussions and their comments on the manuscript. V. K. acknowledges support from the Ernest Oppenheimer Early Career Fellowship and the Sydney Harvey Junior Research Fellowship, Churchill College, University of Cambridge and University College London’s startup funds. J. L. thanks the Simons Foundation Postdoctoral Fellowship. A. M. and X. R. A. acknowledge support from the European Union under the “n-AQUA” European Research Council project (Grant No. 101071937). I. B. was supported by the Harding Distinguished Postgraduate Scholarship. B. X. S. acknowledges support from the EPSRC Doctoral Training Partnership (EP/T517847/1). We are grateful for computational support from the Swiss National Supercomputing Centre under projects s1209 and s1288, the UK national high-performance computing service, ARCHER2, for which access was obtained via the UKCP consortium and the EPSRC grant ref EP/P022561/1, and the Cambridge Service for Data Driven Discovery (CSD3).Notes and references
- J. Bernstein, Nat. Mater., 2005, 4, 427–428 CrossRef CAS PubMed.
- S. R. Forrest, Nature, 2004, 428, 911–918 CrossRef CAS PubMed.
- J. Yang, C. T. Hu, X. Zhu, Q. Zhu, M. D. Ward and B. Kahr, Angew. Chem., 2017, 129, 10299–10303 CrossRef.
- S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- F. Della Pia, A. Zen, D. Alfè and A. Michaelides, Phys. Rev. Lett., 2024, 133, 046401 CrossRef PubMed.
- A. Zen, J. G. Brandenburg, J. Klimeš, A. Tkatchenko, D. Alfè and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1724–1729 CrossRef CAS PubMed.
- W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Rev. Mod. Phys., 2001, 73, 33–83 CrossRef CAS.
- G. H. Booth, A. Grüneis, G. Kresse and A. Alavi, Nature, 2013, 493, 365–370 CrossRef CAS PubMed.
- J. Klimeš, J. Chem. Phys., 2016, 145, 094506 CrossRef PubMed.
- X. Ren, A. Tkatchenko, P. Rinke and M. Scheffler, Phys. Rev. Lett., 2011, 106, 153003 CrossRef PubMed.
- M. Rossi, P. Gasparotto and M. Ceriotti, Phys. Rev. Lett., 2016, 117, 115702 CrossRef PubMed.
- V. Kapil, E. Engel, M. Rossi and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 5845–5857 CrossRef CAS PubMed.
- V. Kapil and E. A. Engel, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2111769119 CrossRef CAS PubMed.
- T. E. Markland and M. Ceriotti, Nat. Rev. Chem, 2018, 2, 0109 CrossRef CAS.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- E. Whalley, J. Chem. Phys., 1984, 81, 4087–4092 CrossRef CAS.
- G. A. Dolgonos, J. Hoja and A. D. Boese, Phys. Chem. Chem. Phys., 2019, 21, 24333–24344 RSC.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Advances in Neural Information Processing Systems, 2022, vol. 35, pp. 11423–11436 Search PubMed.
- V. L. Deringer, D. M. Proserpio, G. Csányi and C. J. Pickard, Faraday Discuss., 2018, 211, 45–59 RSC.
- S. Wengert, G. Csányi, K. Reuter and J. T. Margraf, Chem. Sci., 2021, 12, 4536–4546 RSC.
- P. W. V. Butler, R. Hafizi and G. Day, Machine Learned Potentials by Active Learning from Organic Crystal Structure Prediction Landscapes, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-97rmb.
- B. Cheng, G. Mazzola, C. J. Pickard and M. Ceriotti, Nature, 2020, 585, 217–220 CrossRef CAS PubMed.
- B. Cheng, M. Bethkenhagen, C. J. Pickard and S. Hamel, Nat. Phys., 2021, 17, 1228–1232 Search PubMed.
- L. Zhang, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2021, 126, 236001 CrossRef CAS PubMed.
- M. Macher, J. Klimeš, C. Franchini and G. Kresse, J. Chem. Phys., 2014, 140, 084502 CrossRef CAS PubMed.
- M. Del Ben, J. Hutter and J. VandeVondele, J. Chem. Phys., 2015, 143, 054506 CrossRef PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- M. J. Willatt, F. Musil and M. Ceriotti, J. Chem. Phys., 2019, 150, 154110 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- S. N. Pozdnyakov, M. J. Willatt, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2020, 125, 166001 CrossRef CAS PubMed.
- J. Nigam, S. Pozdnyakov and M. Ceriotti, J. Chem. Phys., 2020, 153, 121101 CrossRef CAS PubMed.
- F. Bigi, S. N. Pozdnyakov and M. Ceriotti, Wigner kernels: body-ordered equivariant machine learning without a basis, arXiv, 2023, preprint, arXiv:2303.04124, DOI:10.48550/arXiv.2303.04124.
- S. N. Pozdnyakov and M. Ceriotti, Smooth, exact rotational symmetrization for deep learning on point clouds, arXiv, 2024, preprint, arXiv:2305.19302, DOI:10.48550/arXiv.2305.19302.
- M. Geiger and T. Smidt, e3nn: Euclidean Neural Networks, arXiv, 2022, Preprint, arXiv:2207.09453, DOI:10.48550/arXiv.2207.09453.
- M. J. Willatt, F. Musil and M. Ceriotti, Phys. Chem. Chem. Phys., 2018, 20, 29661–29668 RSC.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Advances in Neural Information Processing Systems, 2022, vol. 35, p. 11423 Search PubMed.
- N. Lopanitsyna, G. Fraux, M. A. Springer, S. De and M. Ceriotti, Phys. Rev. Mater., 2023, 7, 045802 CrossRef CAS.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, J. Chem. Phys., 2023, 159, 044118 CrossRef PubMed.
- J. P. Darby, D. P. Kovács, I. Batatia, M. A. Caro, G. L. Hart, C. Ortner and G. Csányi, Phys. Rev. Lett., 2023, 131, 028001 CrossRef CAS PubMed.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, F. Berger, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. Della Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, F. Falcioni, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, P. Grigorev, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, J. R. Kermode, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O’Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, B. X. Shi, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, T. D. Swinburne, J. Tilly, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, A foundation model for atomistic materials chemistry, arXiv, 2024, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096.
- K. Choudhary, B. DeCost, L. Major, K. Butler, J. Thiyagalingam and F. Tavazza, Digital Discovery, 2023, 2, 346–355 RSC.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- F. Della Pia, A. Zen, D. Alfè and A. Michaelides, J. Chem. Phys., 2022, 157, 134701 CrossRef CAS PubMed.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- A. Bussy, O. Schütt and J. Hutter, J. Chem. Phys., 2023, 158, 164109 CrossRef CAS PubMed.
- V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Cheng, A. Cuzzocrea, R. H. Meißner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kühne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. Van Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214–223 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157 CrossRef CAS.
- M. Ceriotti, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2009, 102, 020601 CrossRef PubMed.
- B. Cheng, E. A. Engel, J. Behler, C. Dellago and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1110–1115 CrossRef CAS PubMed.
- V. Kapil, D. P. Kovacs, G. Csányi and A. Michaelides, Faraday Discuss., 2024, 249, 50–68 RSC.
- V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512–516 CrossRef CAS PubMed.
- I.-B. Magdău, D. J. Arismendi-Arrieta, H. E. Smith, C. P. Grey, K. Hermansson and G. Csányi, npj Comput. Mater., 2023, 9, 146 CrossRef.
- M. Del Ben, M. Schönherr, J. Hutter and J. VandeVondele, J. Phys. Chem. Lett., 2013, 4, 3753–3759 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 86th edn, 2005 Search PubMed.
- A. K. Soper, Water and ice structure in the range 220–365 K from radiation total scattering experiments, arXiv, 2014, preprint, arXiv:1411.1322, DOI:10.48550/arXiv.1411.1322.
- D. T. Bowron, Pure Appl. Chem., 2008, 80, 1211–1227 CrossRef CAS.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2024 |