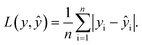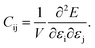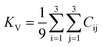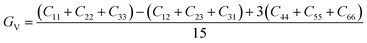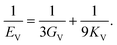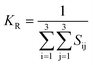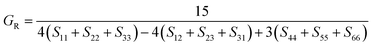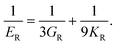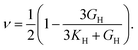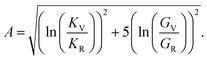Open Access Article
Open Access ArticleKnowledge distillation of neural network potential for molecular crystals†
Takuya Taniguchi *
*
Center for Data Science, Waseda University, 1-6-1 Nishiwaseda, Shinjuku-ku, Tokyo 169-8050, Japan. E-mail: takuya.taniguchi@aoni.waseda.jp
First published on 18th July 2024
Abstract
Organic molecular crystals exhibit various functions due to their diverse molecular structures and arrangements. Computational approaches are necessary to explore novel molecular crystals from the material space, but quantum chemical calculations are costly and time-consuming. Neural network potentials (NNPs), trained on vast amounts of data, have recently gained attention for their ability to perform energy calculations with accuracy comparable to quantum chemical methods at high speed. However, NNPs trained on datasets primarily consisting of inorganic crystals, such as the Materials Project, may introduce bias when applied to organic molecular crystals. This study investigates the strategies to improve the accuracy of a pre-trained NNP for organic molecular crystals by distilling knowledge from a teacher model. The most effective knowledge transfer was achieved when fine-tuning using only soft targets, i.e., the teacher model's inference values. As the ratio of hard target loss increased, the efficiency of knowledge transfer decreased, leading to overfitting. As a proof of concept, the NNP created through knowledge distillation was used to predict elastic properties, resulting in improved accuracy compared to the pre-trained model.
Introduction
Organic molecular crystals are materials where molecules form a crystal by arranging themselves in a periodic manner. They are important for applications in optoelectronics and pharmaceuticals.1–3 The physical and chemical properties of these crystals largely depend on the intra- and intermolecular interactions, exhibiting diverse structures and functions even with slight differences in molecular structure.4 Elucidating the diverse properties of molecular crystals through experiments is time-consuming work. Therefore, it is crucial to efficiently screen materials using computational approaches.5–8 Quantum chemical methods such as density functional theory (DFT) are powerful tools to calculate the physicochemical properties of molecular crystals, but incur significant computational costs to accurately model these interactions.9,10 To address the limitation of DFT, neural network potentials (NNPs) have been gaining attention in recent years.11–18 NNPs, by learning from a vast amount of computational data, can estimate potential energy with high accuracy comparable to DFT, while requiring two to three orders of magnitude less computational time. This enables extensive simulations that were hard with traditional computational methods.To construct a NNP with high predictive accuracy, the quality and quantity of training data are crucial. The Materials Project, commonly used for training NNPs, is a computational database focused mainly on inorganic crystals.19 Almost all universal NNPs are trained on trajectory datasets based on data from the Materials Project.11–18 Since data on organic molecular crystals are very limited in the Materials Project, it has been reported that a universal NNP, the Crystal Hamiltonian Graph Network (CHGNet),18 tended to overestimate the unit cell volume of molecular crystals with an average error of around 20% after structure relaxation.20 In contrast, a NNP trained with molecular crystals, the PreFerred Potential (PFP),15 is found to have a smaller error of unit cell volume of around 2–3%.20
In molecular crystals, machine learning potentials have also been constructed and used for materials discovery.21–25 In many cases, trajectory data from a single or limited type of molecular crystal are used for learning, with the aim of improving the efficiency of crystal structure prediction (CSP) or molecular dynamics (MD) for specific crystals. Although the types of elements are more limited compared to inorganic materials, it is important to construct machine learning potentials with high generalization performance for organic molecular crystals as well.
Recent universal NNPs are based on the architecture of graph neural networks (GNNs). GNNs are the functions to predict properties treating molecules and crystals as graph data.26,27 It is generally known that predictive models with a larger number of layers and parameters tend to achieve higher accuracy. On the other hand, models with a large number of parameters require more computational resources for training and inference, so there is motivation to use lightweight models with fewer parameters for practical purposes.28 Moreover, models that are open for use are more convenient for customization and it is easier to interpret output results compared to closed models.
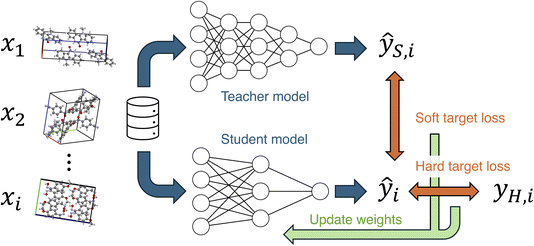
Knowledge distillation is known as an efficient method for transferring knowledge from a more accurate model to another.29,30 The knowledge distillation is often used with the intention of creating lightweight models, but it can also be utilized to enhance the customizability of models.31 In knowledge distillation, the output of the teacher model is used as knowledge to be learned by the student model (Fig. 1). The teacher's output is used as a soft target, and a soft target loss is employed during training in addition to a hard target loss. The sum of the soft and hard target losses becomes the loss function to be minimized, and the weights of the student model are updated. This approach is expected to achieve higher accuracy compared to training without knowledge distillation. In the field of materials chemistry, the effectiveness of knowledge distillation has been reported for biomolecules and inorganic materials,32,33 but it remains unclear for organic molecular crystals. If the knowledge distillation is effective for molecular crystals, a knowledge transferred model will enable accurate MD simulations and material screening with low computational costs, contributing to the development of novel molecular crystals.
This work addresses the research question of how the knowledge distillation of NNP improves the structure optimization of organic molecular crystals. The NNP trained on the Materials Project, CHGNet, is additionally trained with molecular crystal data. The methods of tuning the pre-trained CHGNet were compared, and the effectiveness of knowledge distillation from a teacher model was verified. The differences in learning efficiency were investigated by changing the ratio of hard target loss for soft target loss. This study clarified the significance of using the soft target of the teacher model when adapting the knowledge of molecular crystals to NNP. Then, the knowledge transferred model was used to predict the elastic properties as the proof of concept. The differences from other NNPs of molecular crystals is that this work investigates the effect of additional learning on the NNP trained solely by inorganic crystals, to understand the learning behavior of the neural network. Since knowledge distillation was found to efficiently promote learning, this finding may lead to practical strategies for modifying or repurposing NNPs to fit other material domains, leading to the design and screening of functional molecular crystals.
Results and discussion
Evaluation of pretrained NNPs
CHGNet is the NNP trained by a trajectory dataset of the Materials Project (named MPtrj dataset).18 This dataset consists of 1.58 million structures of 0.15 million compounds. The MPtrj dataset is primarily composed of inorganic crystal structures (Fig. 2a). Organic molecular crystals constitute only 1.8% of the total, representing a small proportion in the dataset. Using the relative frequency density of the distribution, the difference in potential energy of inorganic and organic crystals becomes evident (Fig. 2b). The mean energy of inorganic crystals is −6.21 eV per atom, exhibiting a distribution with a larger absolute value compared to that of organic crystals. Furthermore, organic molecular crystals exhibit a narrower distribution width, which can be attributed to their structures with limited types of elements compared to inorganic crystals.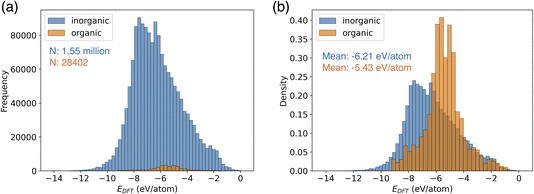 | ||
| Fig. 2 Data distribution of potential energy in the MPtrj dataset. (a) The histogram of organic and inorganic crystal structures. (b) The relative frequency density of the histogram. | ||
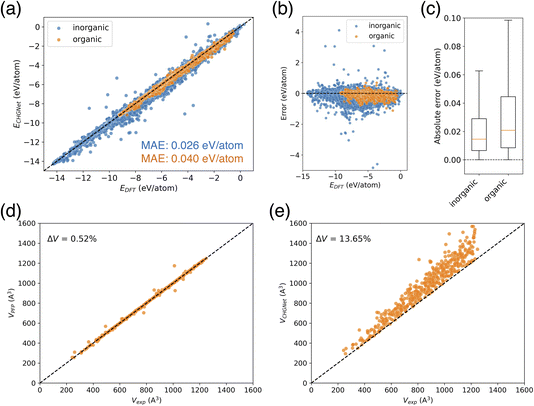
When calculating the energies of this training dataset using the pre-trained CHGNet model, the mean absolute error (MAE) of the potential energy for inorganic crystals was 0.026 eV per atom, while the MAE for organic crystals was 0.040 eV per atom (Fig. 3a). Despite the greater diversity of elements in inorganic crystals, their MAE was smaller than that of organic crystals. The high performance can be explained by the fact that inorganic crystal structures account for 98.2% of the dataset, ensuring an adequate amount of training data. While some inorganic crystals show large differences between their predicted and actual values (Fig. 3b), only a tiny portion (0.09%) of the inorganic crystal data has an absolute error exceeding 0.5 eV per atom. In fact, over 60% of the data points have an absolute error below 0.02 eV per atom (Fig. 3c). On the other hand, organic crystal structures constitute only 1.8% of the dataset, suggesting that there is still room for additional training. Although there is no data point with large error like those observed in inorganic crystals, only 49% of the organic crystal data has an absolute error smaller than 0.02 eV per atom, indicating a larger error distribution than inorganic crystals (Fig. 3c). Furthermore, while no positive or negative slope bias was observed in the error distribution, the predicted values tend to be slightly underestimated (Fig. 3b).
Next, we performed a validation of the pretrained NNPs, PFP, and CHGNet. The validation dataset consists of organic crystals randomly sampled from the Crystallographic Open Database (COD), and the cell volume reproducibility after structural relaxation was evaluated. The COD dataset contains diverse molecules (Fig. S1†), and was not used in the pretraining of either PFP or CHGNet. For NNPs, it is important to appropriately describe the potential energy surface. Since the cell volume is related to the stable structure corresponding to the minimum point on the potential surface, a high reproducibility of cell volume suggests that the potential function can adequately describe the stable structure. As it is a convenient way to check the validity of the potential function, we used cell volume reproducibility for the initial evaluation.
The results showed that for the COD validation dataset, the percentage error of cell volume was 0.52% for pretrained PFP, but 13.65% for the pretrained CHGNet (Fig. 3d and e). PFP reproduced the volume with small errors for most structures, whereas CHGNet overestimated the cell volume for all structures. As the volume of the input structure increases, the plots show greater dispersion and larger errors. The findings that PFP demonstrates good cell volume reproducibility and CHGNet overestimates the cell volume in organic crystals, align with a previous report;20 despite using older model versions (PFP v4.0.0 and CHGNet v0.2.0), the updated pretrained models yielded comparable results to those reported in the previous paper.
Knowledge distillation of NNP
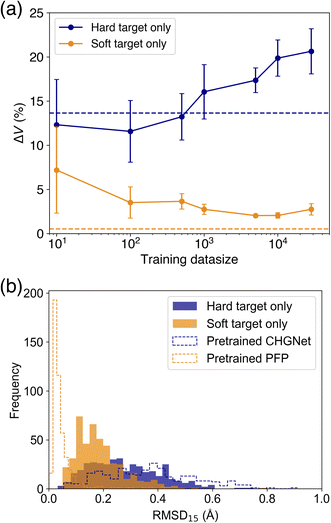
As it was found that PFP performs well in reproducing the cell volume of organic molecular crystals, we compare the effect of knowledge transfer from PFP to CHGNet to investigate the learning efficiency of adapting an NNP trained on the Materials Project to the domain of organic molecular crystals. As shown in Fig. 1, knowledge distillation uses a loss function with a soft target to update the weights of the neural network. In this case, the hard target is the DFT-calculated energy and forces from the MPtrj dataset, and the soft target is the energy and forces inferred by PFP. The loss function is calculated by adding the energy and force losses for both hard and soft targets, weighted by their respective loss ratios (see Experimental section). To investigate how the loss ratios influence the learning efficiency, we examine the relationship between the hard target loss ratios (rH,E and rH,F) and the metric, while keeping the soft target loss ratios (rS,E and rS,F) constant.Before training with soft targets, we conducted additional training using only hard targets. The results show that when the number of training data (Ntrain) ranged from 10 to 500, the volume reproducibility became better than that of the pre-trained model (Fig. 4a). However, when Ntrain exceeded 1000, the volume reproducibility became worse depending on the amount of data. Although the standard deviation was large, the average volume reproducibility was best at Ntrain = 100.
When using soft targets for knowledge transfer, the best model was that trained by a soft target only without a hard target (Table 1). The best volume reproducibility was achieved at Ntrain = 5000 (Fig. 4). The knowledge distillation reduced the error by 11% from the pretrained one. The error bars became smaller depending on Ntrain up to 5000. When the number of data was increased further, the volume reproducibility deteriorated slightly, and the error bars became larger. In addition to the cell volume, the structural similarity between experimental and optimized structures was evaluated based on root mean square deviation of 15 molecules (RMSD15).34 The knowledge distilled model afforded better RMSD15 than the model trained on a hard target only and the pretrained CHGNet, while the pretrained PFP was the best on the RMSD15 metric (Fig. 4b). This result is consistent with the reproducibility of cell volume. Since the reproducibility of cell volume is positively correlated with RMSD15 (Fig. S2†), the reproducibility of cell volume was used for evaluating the cases using both hard and soft targets.
| rH,E | rH,F | ΔV (%) | Optimal Ntrain |
|---|---|---|---|
| 0 | 0 | 2.03 (0.09) | 5000 |
| 0.1 | 0.1 | 2.49 (0.61) | 1000 |
| 0.5 | 2.46 (0.50) | 1000 | |
| 1 | 2.14 (0.37) | 5000 | |
| 2 | 2.44 (0.76) | 100 | |
| 10 | 2.27 (0.19) | 500 | |
| 0.5 | 0.1 | 2.75 (0.97) | 500 |
| 0.5 | 2.65 (1.08) | 500 | |
| 1 | 2.38 (0.39) | 1000 | |
| 2 | 2.23 (0.26) | 500 | |
| 10 | 2.66 (0.51) | 500 | |
| 1 | 0.1 | 4.51 (2.56) | 500 |
| 0.5 | 4.67 (2.67) | 500 | |
| 1 | 4.64 (2.03) | 1000 | |
| 2 | 4.95 (1.93) | 500 | |
| 10 | 6.19 (1.69) | 500 | |
| 2 | 0.1 | 8.20 (4.02) | 100 |
| 0.5 | 8.77 (3.25) | 100 | |
| 1 | 8.77 (3.56) | 100 | |
| 2 | 7.35 (2.93) | 100 | |
| 10 | 8.02 (2.59) | 100 | |
| 10 | 0.1 | 7.29 (4.89) | 100 |
| 0.5 | 8.34 (6.36) | 10 | |
| 1 | 8.45 (5.73) | 100 | |
| 2 | 8.19 (3.46) | 100 | |
| 10 | 9.28 (3.70) | 100 |
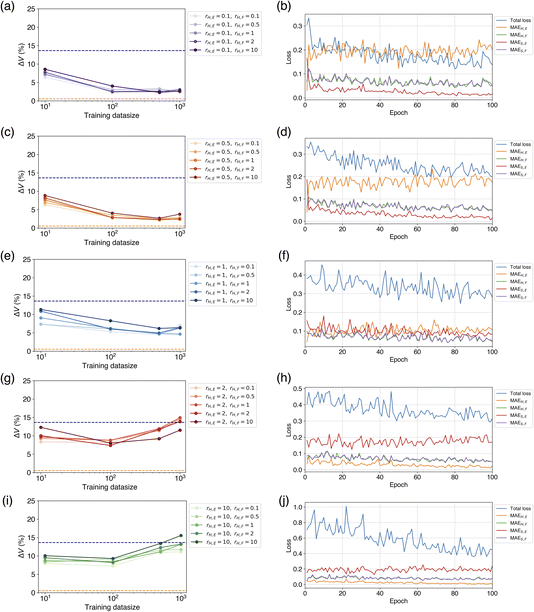
When using both hard and soft targets for learning, we investigated the efficiency by varying the loss ratios rH,E and rH,F, of the hard targets. At rH,E = 0.1 and 0.5, the percentage error of volume reproducibility was 2–3%, which was slightly worse than the model finetuned on a soft target only (Table 1). The best results were achieved at Ntrain of 500 or more, in most cases. The force loss ratio rH,F did not affect the metric. The next best result was obtained at rH,E = 1, and the percentage error of volume reproducibility was 4–6% at Ntrain = 500 or 1000. The results at rH,E = 2 and 10 were much worse to be 8–9% at Ntrain = 10 or 100 in most cases.
The dependence of rH,E and rH,F on ΔV and optimal Ntrain was visualized by colored scatter plots (Fig. 5). It is evident that a smaller rH,E leads to an improved volume reproducibility, while rH,F has minimal influence on this metric (Fig. 5a). Furthermore, a smaller rH,E tends to increase the optimal Ntrain, a trend that is unaffected by rH,F (Fig. 5b). The results obtained from learning with soft targets alone are consistent with these observations. These findings suggest that a smaller rH,E allows for a greater transfer of knowledge from the teacher model, resulting in a CHGNet model that effectively mimics the properties of the teacher model, PFP. Conversely, a larger rH,E hinders the transfer of knowledge from the teacher model, causing the model's behavior to resemble that of learning with hard targets only. As the hard targets are contained in the MPtrj dataset, which is used for pre-training, the re-learning of a subset of the data (in this case, organic crystals) is likely to induce overfitting.
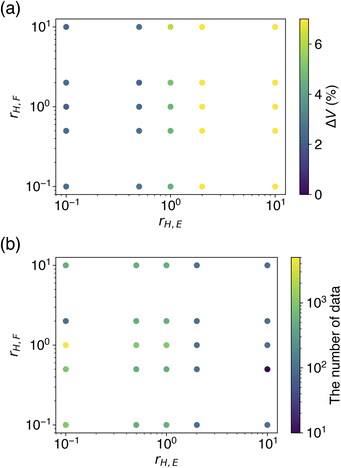 | ||
| Fig. 5 Evaluation of how different hard target loss ratios affect the performance metrics. (a) The cell volume reproducibility. (b) The number of training data that yielded the result. | ||
To investigate the reason for these learning results, we compared the loss behavior during the learning process. Fig. 6 shows the ΔV for each combination of rH,E and rH,F within the range of the number of training data up to 1000, and the changes of the loss curves when rH,F = 1 at Ntrain = 1000. When rH,E = 0.1, which yielded the best volume reproducibility, a crossover between MAEH,E and MAES,E occurred early in the learning process (Fig. 6a and b). At the beginning of learning, MAEH,E is smaller than MAES,E, but after the first epoch of learning, MAEH,E is larger than MAES,E. This suggests that a switch to the characteristics of the teacher model occurred. As the number of epochs increased, MAES,E continued to decrease while MAEH,E did not decrease. This indicates that the model was approaching the behavior of the teacher model. Unlike the loss change of the energy, there was no significant difference of force loss between the soft and hard targets, and both decreased as the number of epochs progressed synchronously (Fig. 6b). This loss transition is consistent with the fact that ΔV did not depend on rH,F. It has been confirmed that MAEH,F and MAES,F exhibit similar behaviors even when rH,F is not equal to 1. When rH,E = 0.5, a crossover was also observed in the energy loss, exhibiting similar behavior to the case of rH,E = 0.1 (Fig. 6d).
When rH,E = 1, there was no crossover between MAEH,E and MAES,E in the early stages of learning, but their values became almost the same (Fig. 6f). At this point, it can be considered that the properties of the pretrained CHGNet and the teacher model were in a state of competition. As the number of epochs increased, MAES,E became gradually smaller than MAEH,E, suggesting that the tuned model's property approached that of the teacher model slightly. Consequently, the metric ΔV is relatively close to those of the cases where rH,E = 0.1 and 0.5. There was also no significant difference of force losses between the soft and hard targets.
When rH,E = 2 and 10, neither a crossover between MAEH,E and MAES,E nor a phenomenon where MAEH,E and MAES,E become comparable was observed; MAEH,E was consistently smaller than MAES,E (Fig. 6h and j). MAES,E hardly decreased from the beginning of learning, while MAEH,E continued to decrease. This behavior suggests that the student model is not only unable to sufficiently obtain knowledge from the teacher model but also prone to overfitting. Consequently, the tuned model was similar to the model learned by only hard targets. As Ntrain increases, the model is likely to result in overfitting or yield worse metrics compared to the pretrained model.
Summarizing the behavior of these learning processes, the following can be said. When rH,E < rS,E, the loss for the soft target energy decreases significantly, and knowledge transfer succeeds. When rH,E = rS,E, the losses for the hard and soft target energies become similar and compete, leading to medium transfer of knowledge. When rH,E > rS,E, the loss for the soft target energy does not decrease at all, and the loss difference between soft hard targets widens. If the loss for the soft target energy does not decrease, knowledge transfer fails. In all cases, the force losses for both the soft and hard targets decrease synchronously. Therefore, the contribution of the loss for energy should be greater than that of the loss for forces in the knowledge transfer of NNP.
Proof of concept using elastic properties
Since the tuned NNP using knowledge distillation should be more applicable to organic crystals than the pretrained CHGNet, this NNP was used to predict the elastic moduli of organic molecular crystals as a proof of concept. Elastic moduli are fundamental properties that affect material flexibility and drug compressibility.35 Various elastic moduli, such as Young's modulus and the bulk modulus, can be calculated from a 6 × 6 symmetric matrix with up to 21 independent components. However, due to the difficulty of measurement, the number of organic crystals for which the elastic constant matrix has been experimentally measured is very limited, around 100 compounds.36 Therefore, computational screening is desirable, but DFT calculation has a high computational cost, making NNP an effective alternative.The elasticity dataset, reported in the literature,20,36 was used for comparison. This dataset contains 44 small molecules with molecular weights up to 440 g mol−1 (Fig. S1†). Moreover, they have diverse molecular structures, with many molecules having π-conjugated systems or hydrogen bonding properties (Fig. S3†). Most of their crystal structures and elastic constant matrices were measured at room temperature. When calculating the elastic moduli of structures optimized by NNP, the predicted values correspond to those of thermodynamically stable (0 K) structures, which may lead to discrepancies with experimental elastic moduli measured at finite temperatures.
The accuracy of elastic constant predictions at 0 K can vary significantly depending on the material system. While many inorganic crystals show relatively small temperature dependence, softer molecular crystals can exhibit substantial changes in elastic properties with temperature. For instance, experimental data for naphthalene shows that its stiffness constants change by about 70% from room temperature to low temperature.37–39 Furthermore, computational studies on molecular organic crystals have demonstrated that changes in bulk and shear moduli between 0 K and high temperature can typically be 40–50%.40 These significant temperature-induced changes in elastic properties highlight the limitations of relying solely on 0 K predictions for such materials. In this proof of concept, we calculate the elastic moduli of optimized structures to assess how much the CHGNet improves when trained on a small portion of organic crystals, while recognizing the limitations of our 0 K approach for molecular systems.
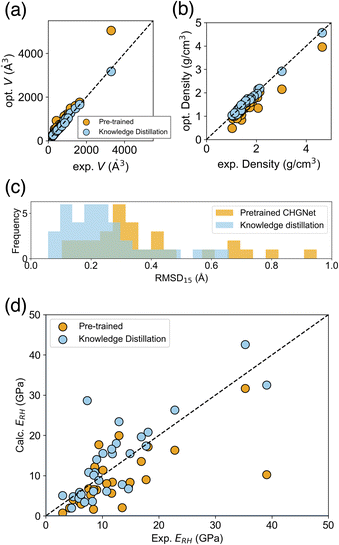
The reproducibility of cell volume and density on this dataset after the structure relaxation, improved from MAE = 18.0 to 3.3% for cell volume, and MAE = 0.22 to 0.05 g cm−3 for density, using knowledge distillation (Fig. 7a and b). Other cell parameters are shown in ESI Fig. 4 and 5.† The structural similarity RMSD15 between experimental and relaxed structures was also evaluated, and the knowledge distilled model was better than the pretrained CHGNet (Fig. 7c), consistent with the previous evaluation on the COD dataset.
On the MAEs of predicted elastic moduli, the knowledge transferred CHGNet comprehensively outperformed the pretrained one, and showed performance close to the teacher model PFP (Table 2). For example, the Young's modulus ERH, which is the average property by Reuss and Hill schemes, is reported to be a better approximation of the experimental Young's modulus.35 The MAE of ERH calculated by the knowledge transferred model was 4.01 GPa, which is smaller than that of the pretrained model (5.44 GPa). The observed–predicted plot of ERH using the knowledge distillation indicated superior predictions as well, with smaller errors for most of the data (Fig. 7d). The superiority of the knowledge transferred model over the pretrained one holds true for the Young's and shear moduli E, G of all averaging schemes (Table 2). The mean model, which assumes that there is no relationship between the input structure and output, provides reference metrics. The knowledge transferred model also demonstrates superiority over these reference metrics.
| Mean model | PFP | Pretrained CHGNet | Knowledge distillation | |
|---|---|---|---|---|
| a E: Young's modulus, K: bulk modulus, G: shear modulus, v: Poisson's ratio, A: anisotropy, and the subscript is the averaging method. | ||||
| EV (GPa) | 5.72 | 4.51 | 4.80 | 4.58 |
| ER (GPa) | 4.82 | 3.58 | 5.73 | 4.29 |
| EH (GPa) | 5.03 | 3.81 | 5.15 | 4.02 |
| ERH (GPa) | 4.88 | 3.55 | 5.44 | 4.01 |
| KV (GPa) | 4.10 | 5.32 | 3.31 | 4.44 |
| KR (GPa) | 3.10 | 5.18 | 4.54 | 3.80 |
| KH (GPa) | 3.56 | 5.25 | 3.87 | 3.90 |
| KRH (GPa) | 3.32 | 5.22 | 4.19 | 3.72 |
| GV (GPa) | 2.36 | 1.75 | 1.98 | 1.78 |
| GR (GPa) | 2.00 | 1.32 | 2.57 | 1.81 |
| GH (GPa) | 2.09 | 1.44 | 2.10 | 1.62 |
| GRH (GPa) | 2.02 | 1.32 | 2.33 | 1.67 |
| v | 0.04 | 0.05 | 0.11 | 0.05 |
| A | 0.68 | 0.58 | 1.37 | 0.68 |
For bulk modulus K, none of the models surpassed the mean model. However, among the NNPs, the knowledge transferred model performed the best. Since the teacher model tends to overestimate bulk moduli, while the pretrained CHGNet tends to underestimate them, the knowledge transferred model likely achieved the lowest MAE for bulk moduli by cancelling out the errors of both models. Among several averaging schemes, the Voigt scheme afforded better metrics for the pretrained model. This should be because the Voigt average tends to overestimate the elastic modulus and may work to reduce the inherent bias of the pretrained CHGNet. The observed–predicted plots of all properties are presented in ESI Fig. 6 and 7.†
Finally, we consider that our 0 K predictions may overestimate the elastic constants for the organic molecular crystals in our study. While it has been suggested that 0 K predictions can sometimes reproduce experimental moduli, this assumption may not hold for all systems, particularly for softer molecular crystals. Future work should incorporate temperature effects, either through temperature-dependent MD simulations or by applying appropriate correction factors based on experimental data or more advanced computational methods.
Conclusions
This study demonstrates that knowledge distillation is an effective technique for improving the performance of models in predicting the properties of organic molecular crystals. The student model, which learned the knowledge of the teacher model PFP, improved its volume reproducibility to an accuracy close to that of the teacher model. The student model's properties became similar to the teacher model when only soft targets were used. As the ratio of hard target loss in the loss function increased, it became more difficult to transfer knowledge from the teacher model. Furthermore, when the loss ratio for energy between hard and soft targets was rH,E < rS,E, a crossover of MAEH,E and MAES,E occurred early in the learning process. This behavior was inferred to be crucial for approximating the teacher model. Unlike the behavior of energy loss, the force loss exhibited almost identical behavior for both soft and hard targets. The difference in force loss ratios rH,F and rS,F did not affect the learning process. As a proof of concept, the knowledge transferred model was used to predict elastic properties, resulting in improved prediction errors compared to the pretrained model. This work will inspire the creation of viable tactics for modifying or adapting NNPs to be compatible with other material sectors. Recently, techniques for merging neural networks to create better models have been advancing. Combining knowledge transferred lightweight NNPs may offer the possibility of developing the generalization performance of NNPs.Experimental
Preparation of training dataset
The training data for CHGNet (MPtrj) was downloaded from the Figshare repository.41 This dataset contains 1.58 million structural data points of 0.15 million compounds and the results of DFT calculations. Among these, structures composed solely of H, C, N, O, P, S, F, Cl, Br, and I were considered organic crystals. Structures meeting all of the following criteria were regarded as complex crystals: (1) containing two or more elements from H, C, N, O, P, S, F, Cl, Br, and I; (2) containing at least one element other than H, C, N, O, P, S, F, Cl, Br, and I; and (3) having 80% or more of the total atoms composed of H, C, N, O, P, S, F, Cl, Br, and I. All other crystals were considered inorganic crystals. For the hard target, the energies and forces of the organic crystals in MPtrj were used. For the soft target, the energies and forces obtained from single-point calculations using Preferred Potential (PFP) v5.0.0, provided by the cloud service Matlantis, were used for the same structural data.Loss function in knowledge distillation
In the training for knowledge distillation, the summation of the MAE of energy and force of hard and soft targets is used to be minimized. The MAE is defined asThe loss function is a weighted sum as follows:
L = rH,EL(EH,Ê) + rH,FL(FH,![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif) ) + rS,EL(ÊS,Ê) + rS,FL( ) + rS,EL(ÊS,Ê) + rS,FL(![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif) S, S,![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif) ). ). |
![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif) are outputs of CHGNet (v0.3.0) as student model, ÊS and
are outputs of CHGNet (v0.3.0) as student model, ÊS and ![[F with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0046_0302.gif) S are outputs of PFP (v5.0.0) as the soft target, and EH and FH are DFT calculated results in the MPtrj dataset as the hard target. The letters, rH,E, rH,F, rS,E, and rS,F, are the loss ratios for hard and soft targets of energy and force, respectively. For training using only the hard target, rH,E = rH,F = 1 and rS,E = rS,F = 0 were used. For training using only the soft target, rH,E = rH,F = 0 and rS,E = rS,F = 1 were used. When using both hard and soft targets, the loss ratios for the soft target were fixed to be rS,E = rS,F = 1, and the loss ratios for the hard target were varied between 0.1 and 10. In all trainings, the weights of the pre-trained CHGNet, except for the multilayer perceptron (MLP), were fixed, and only the weights of the MLP were tuned. The training was conducted with epochs of 100, learning rate of 0.01 and batch size of 32, using an Ubuntu 20.04 computer (CPU memory: 128 GB) equipped with a single GPU (NVIDIA RTX 6000 Ada).
S are outputs of PFP (v5.0.0) as the soft target, and EH and FH are DFT calculated results in the MPtrj dataset as the hard target. The letters, rH,E, rH,F, rS,E, and rS,F, are the loss ratios for hard and soft targets of energy and force, respectively. For training using only the hard target, rH,E = rH,F = 1 and rS,E = rS,F = 0 were used. For training using only the soft target, rH,E = rH,F = 0 and rS,E = rS,F = 1 were used. When using both hard and soft targets, the loss ratios for the soft target were fixed to be rS,E = rS,F = 1, and the loss ratios for the hard target were varied between 0.1 and 10. In all trainings, the weights of the pre-trained CHGNet, except for the multilayer perceptron (MLP), were fixed, and only the weights of the MLP were tuned. The training was conducted with epochs of 100, learning rate of 0.01 and batch size of 32, using an Ubuntu 20.04 computer (CPU memory: 128 GB) equipped with a single GPU (NVIDIA RTX 6000 Ada).
The evaluation of the additionally trained CHGNet was performed using organic crystal structures randomly downloaded from the Crystallographic Open Database, COD (n = 477). For structural optimization with NNPs, the experimental data from COD was used as the initial structure, and the optimization, including cell parameters, was carried out using the Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) method until the forces acting on the atoms were below 0.03 eV Å−1.42
Calculation of elastic properties by NNP
The dataset of experimental elastic constant matrices (named elasticity dataset) was originally reported by Spackman et al.,36 and then modified to address the issue of missing hydrogen atoms.20 Each cif file was processed as Atoms object using ASE library, and then structure relaxation was performed using LBFGS method, with a maximum of 2000 iterations and a residual force threshold at 0.03 eV Å−1. The elastic constants can be derived from the strain second derivatives of the crystal energy as follows,Once the elastic constants tensor is obtained, averaged elastic properties were calculated. In the Voigt scheme, the bulk modulus (KV) and shear modulus (GV) were calculated from the stiffness matrix components, Cij. In the Reuss scheme, the average values, KR and GR, are derived from the inverse of the stiffness matrix, known as the compliance matrix, Sij. The Poisson's ratio (ν) and Young's modulus (E) are deduced from K and G. The Hill scheme is the arithmetic mean of the Reuss and Voigt averages. The arithmetic mean of the Reuss and Hill schemes was also used for better approximation of experimental values. For some crystals, the elastic moduli can be negative due to the relative magnitudes of the matrix components. We excluded such crystals from the evaluation. The calculation of each elastic modulus is summarized as follows.
For K, G, and E, Voigt average yields the following formulae,
Reuss average yields the following formulae
Hill average is the arithmetic mean of Voigt and Reuss values.
Poisson's ratio (ν) is given by
Anisotropy (A) is given by
Data availability
The code for executing the workflow of the paper can be found at https://github.com/takuyhaa/chgnet-KD. The identifiers of COD data are also found at the github. The MPtrj dataset, used for the pretrained CHGNet, is reported at https://doi.org/10.6084/m9.figshare.23713842.v2. The Elasticity dataset of organic molecular crystals is first reported at https://doi.org/10.1002/anie.202110716, and then modified at https://doi.org/10.1039/D3CE01263H.Author contributions
This research was conducted by T. T., who is responsible for all the following roles: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, validation, visualization, writing – original draft, and writing – review & editing.Conflicts of interest
The author received joint research funding from ENEOS corporation and licensed Matlantis for using the PFP model from the Preferred Computational Chemistry, Inc.; a joint venture of the Preferred Networks, Inc. and ENEOS corporation.Acknowledgements
This study was financially supported by JSPS Grant-in-Aid (22K14747 and 24K17748), the Waseda University Grant for Special Research Projects (2022C-313, 2023C-292, 2023R-050, 2024C-297), JST ACT-X (JPMJAX23DD), and ENEOS Corporation.References
- J. A. Bhatt, D. Bahl, K. Morris, L. L. Stevens and R. V. Haware, Eur. J. Pharm. Biopharm., 2020, 153, 23–35 CrossRef CAS.
- T. Taniguchi, H. Sugiyama, H. Uekusa, M. Shiro, T. Asahi and H. Koshima, Nat. Commun., 2018, 9, 538 CrossRef PubMed.
- S. Hayashi, F. Ishiwari, T. Fukushima, S. Mikage, Y. Imamura, M. Tashiro and M. Katouda, Angew. Chem., Int. Ed., 2020, 59, 16195–16201 CrossRef CAS PubMed.
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford University, Oxford, 2020, vol. 30 Search PubMed.
- D. Takagi, K. Ishizaki, T. Asahi and T. Taniguchi, Digital Discovery, 2023, 2, 1126–1133 RSC.
- J. Hoja, H. Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio Jr. and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- S. Wengert, G. Csányi, K. Reuter and J. T. Margraf, Chem. Sci., 2021, 12, 4536–4546 RSC.
- J. Yang, S. De, J. E. Campbell, S. Li, M. Ceriotti and G. M. Day, Chem. Mater., 2018, 30, 4361–4371 CrossRef CAS.
- A. M. Reilly, et al., Acta Crystallogr., 2016, 72, 439–459 CAS.
- L. M. LeBlanc, J. A. Weatherby, A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Theory Comput., 2018, 14, 5715–5724 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- S. Takamoto, S. Izumi and J. Li, Comput. Mater. Sci., 2022, 207, 111280 CrossRef CAS.
- S. Takamoto, C. Shinagawa and D. Motoki, et al., Nat. Commun., 2022, 13, 2991 CrossRef CAS.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185 CrossRef.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- A. Jain, S. P. Ong and G. Hautier, et al., APL Mater., 2013, 1, 011002 CrossRef.
- T. Taniguchi, CrystEngComm, 2024, 26, 631–638 RSC.
- V. Kapil and E. A. Engel, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2111769119 CrossRef CAS PubMed.
- K. Ni, F. Pan and Y. Zhu, Adv. Funct. Mater., 2022, 32, 2203894 CrossRef CAS.
- S. Wengert, G. Csányi, K. Reuter and J. T. Margraf, J. Chem. Theory Comput., 2022, 18, 4586–4593 CrossRef CAS PubMed.
- P. W. Butler, R. Hafizi and G. M. Day, J. Phys. Chem. A, 2024, 128, 945–957 CrossRef CAS.
- S. Hattori and Q. Zhu, arXiv, 2024, preprint, arXiv:2404.11587, DOI:10.48550/arXiv.2404.11587.
- T. Taniguchi, M. Hosokawa and T. Asahi, ACS Omega, 2023, 8, 39481–39489 CrossRef CAS PubMed.
- Z. Dong, J. Feng, Y. Ji and Y. Li, J. Phys. Chem. A, 2023, 127, 5921–5929 CrossRef CAS PubMed.
- V. Gupta, K. Choudhary, B. DeCost, F. Tavazza, C. Campbell, W. K. Liao, A. Choudhary and A. Agrawal, npj Comput. Mater., 2024, 10, 1 CrossRef CAS.
- G. Hinton, O. Vinyals and J. Dean, arXiv, 2015, preprint, arXiv:1503.02531, DOI:10.48550/arXiv.1503.02531.
- J. Gou, B. Yu, S. J. Maybank and D. Tao, Int. J. Comput. Vision, 2021, 129, 1789–1819 CrossRef.
- L. Zhang, L. Shen, L. Ding, D. Tao and L. Y. Duan, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022, pp. 10174–10183 Search PubMed.
- K. Das, B. Samanta, P. Goyal, S. C. Lee, S. Bhattacharjee and N. Ganguly, AAAI, 2023, 37, 7323–7331 CrossRef.
- W. Hu, B. Liu, J. Gomes, M. Zitnik, P. Liang, V. Pande and J. Leskovec, arXiv, 2019, preprint, arXiv:1905.12265, DOI:10.48550/arXiv.1905.12265.
- J. A. Chisholm and W. D. S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231 CrossRef.
- V. Mazel, V. Busignies, H. Diarra and P. Tchoreloff, J. Pharm. Sci., 2012, 101, 2220–2228 CrossRef CAS PubMed.
- P. R. Spackman, A. Grosjean, S. P. Thomas, D. P. Karothu, P. Naumov and M. A. Spackman, Angew. Chem., Int. Ed., 2022, 61, e202110716 CrossRef CAS PubMed.
- G. K. Afanasieva and R. M. Myasnikova, Kristallografiya, 1970, 15, 189 Search PubMed.
- K. V. Mirskaya, I. E. Kozlova and V. F. Bereznitskaya, Phys. Status Solidi B, 1974, 62, 291–294 CrossRef CAS.
- K. S. Alexandrov, G. S. Belikova, A. P. Ryzhenkov, V. R. Teslenko and A. I. Kitaigorodskii, Kristallografiya, 1963, 8, 221 Search PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- B. Deng, Materials Project Trajectory (MPtrj) Dataset, 2023, DOI:10.6084/m9.figshare.23713842.v2.
- R. Fletcher, Practical Methods of Optimization, Wiley, New York, 1980, vol. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00090k |
| This journal is © The Royal Society of Chemistry 2024 |