Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mapping inorganic crystal chemical space
Hyunsoo
Park
 a,
Anthony
Onwuli
a,
Anthony
Onwuli
 a,
Keith T.
Butler
a,
Keith T.
Butler
 b and
Aron
Walsh
b and
Aron
Walsh
 *a
*a
aDepartment of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bDepartment of Chemistry, University College London, London WC1H OAJ, UK
First published on 16th April 2024
Abstract
The combination of elements from the Periodic Table defines a vast chemical space. Only a small fraction of these combinations yields materials that occur naturally or are accessible synthetically. Here, we enumerate binary, ternary, and quaternary element and species combinations to produce an extensive library of over 1010 stoichiometric inorganic compositions. The unique combinations are vectorised using compositional embedding vectors drawn from a variety of published machine-learning models. Dimensionality-reduction techniques are employed to present a two-dimensional representation of inorganic crystal chemical space, which is labelled according to whether the combinations pass standard chemical filters and if they appear in known materials databases.
Introduction
The fundamental building blocks of materials are the chemical elements of the Periodic Table. Depending on the choice of elements and the interactions between them, the resulting material may be stable or unstable; crystalline or amorphous; insulating or conducting. The principles connecting the chemical composition, crystal structure, and physical properties of materials remain a subject of long-standing interest1,2 and ongoing study.Materials informatics has emerged as an important subject at the interface of traditional materials science and data science.3 It uses informatics techniques to understand, design, and discover materials. The underlying materials data may be drawn from experimental investigations (e.g., crystal-structure databases populated from X-ray or neutron diffraction measurements) or from computer simulations (e.g., structure–property databases based on density functional theory calculations).
In this study, we consider the cartography of inorganic crystal chemical space. Specifically, we address the combination of 2–4 elements to form stoichiometric inorganic compounds. This builds upon our earlier work4 by featurising each chemical composition using embedding vectors from machine-learning models and labelling the entries to probe the distribution of known and unknown materials. The resulting hyperspace is reduced to two dimensions to produce visual representations that show hints of the innate separation between allowed and forbidden compounds.
Chemical enumeration
As the number of chemical components increases, there is a combinatorial explosion in the number of possible compounds. We previously reported the code Semiconducting Materials from Analogy and Chemical Theory (SMACT) to enable rapid screening over such large configurational spaces.5 This was inspired by early work on the exploration of new semiconducting materials based on electron-counting principles.6 The Python library features element and species classes, with integrated iteration tools and adjustable chemical filters.We can make the combinatorial space of multi-component compounds more tractable by introducing chemical constraints. We choose to work with the first 103 elements of the Periodic Table (from H to Lr). This pool of atomic building blocks is expanded into 421 species when the accessible oxidation states are considered. For instance, Fe(II) and Fe(III) are both formed from the element Fe, but exhibit distinct physicochemical properties, such as the black pigment Fe(II)O and the red antiferromagnet Fe(III)2O3.
We consider the set of binary (AwBx), ternary (AwBxCy) and quaternary (AwBxCyDz) combinations where the stoichiometric factors w, x, y, z <  . This approach yields a total number of 225
. This approach yields a total number of 225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879 unique compounds for binary combinations, 77
879 unique compounds for binary combinations, 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637
637![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 for ternary combinations, and 16
589 for ternary combinations, and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902
902![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534
534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 for quaternary combinations. We ensure that combinations with equivalent stoichiometry, such as MgO and Mg2O2, are excluded from our analysis.
325 for quaternary combinations. We ensure that combinations with equivalent stoichiometry, such as MgO and Mg2O2, are excluded from our analysis.
We apply established chemical filters to distinguish between plausible (“allowed”) and implausible (“forbidden”) inorganic stoichiometries. The first filter is charge-neutrality, based on the sum of the formal charge (q) of each species:
| wqA + xqB + yqC + zqD = 0 | (1) |
This chemical filter can be framed equivalently in terms of electron counting or valency, which is common in the study of semiconductors.6,7 The filter applies to a broad range of inorganic materials, particularly those classified as being formed from ionic and covalent interatomic interactions, where the charge-neutrality principle holds. However, it may not be suitable for describing metallic alloys (e.g., Cu1−xZnx), intermetallic compounds (e.g., Ni3Al), and non-stoichiometric compounds (e.g., YBa2Cu3O7−δ), as these materials often involve different chemical bonding and variable compositions with electron-counting rules that go beyond the scope of simple charge-neutrality considerations. Special consideration would also be required for mixed-valence compounds, where a single element appears in the same compound with multiple oxidation states. For example, the binary compound magnetite, Fe3O4, contains an equal number of Fe(II) and Fe(III) ions, and thus would be described as a ternary compound by SMACT based on its three distinct constituent species.
A second filter is the electronegativity balance, which requires that the most electronegative ion has the most negative charge in the compound. Using the Pauling electronegativity scale,8χanion − χcation > 0. For example, the pnictide semiconductor GaSb is allowed by this filter (χanion(Sb) − χcation(Ga) = 0.24), and the oxide catalyst Sb2O3 is also allowed, where Sb is the cation (χanion(O) − χcation(Sb) = 1.39). This filter helps distinguish between allowed and forbidden inorganic stoichiometries based on electronegativity considerations, ensuring that the composition contains sensible combinations of species.
Each chemical composition can be assigned a label {‘allowed’, ‘forbidden’} according to whether it passes these chemical filters for inorganic compounds. They can also be labelled as {‘known’, ‘unknown’} according to the presence of that composition in the Materials Project (MP)9 database. The entries considered here were retrieved via the MP API (v2023.11.1) using an anonymised formula notation (e.g., AB2), ensuring a consistent approach to formula representation. We can then categorise each enumerated composition according to its combination of labels: standard {‘allowed’, ‘known’}; missing {‘allowed’, ‘unknown’}; interesting {‘forbidden’, ‘known’}; and unlikely {‘forbidden’, ‘unknown’}.
Examples of chemical compositions generated from the screening procedure are given in Table 1. The metal oxide examples include binary (Zn–O), ternary (Li–Zn–O), and quaternary (Li–Zn–Sn–O) systems. Seven compounds, ZnO, ZnO2, LiZnO2, Li6ZnO4, Li2ZnSn3O8, LiZn4SnO8, and LiZn4Sn4O8, are present in the MP database within our stoichiometry limits. In the binary system, Zn(II)O and Zn(II)O2 are classified as standard, given that Zn can exhibit an oxidation state of +2 with electronegativity 1.65, and oxygen has oxidation states of −2 (oxide) and −1 (peroxide) with an electronegativity of 3.44. Interestingly, Zn2O passes the chemical filter with the less common +1 oxidation state of Zn (often associated with the presence of Zn–Zn bonds) but is not found in the MP database, so it is identified as missing. In the ternary Li–Zn–O system, LiZnO2 and Li6ZnO4 are standard materials, while various missing and unlikely compounds are identified. The quaternary Li–Zn–Sn–O system features two interesting materials, LiZn4SnO8 and LiZn4Sn4O8, distinct from the binary and ternary systems that lack such cases. However, both interesting cases are found to be thermodynamically metastable in MP and decompose exothermically to standard compounds, such as ZnO, Li2SnO3, and Li2ZnSn3O8.
| Standard | Missing | Interesting | Unlikely | |
|---|---|---|---|---|
| Chemical filter | Allowed | Allowed | Forbidden | Forbidden |
| Materials Project | Known | Unknown | Known | Unknown |
| Binary (Zn–O) | ZnO | Zn2O | — | ZnO3 |
| ZnO2 | — | |||
| Ternary (Li–Zn–O) | LiZnO2 | LiZnO | — | LiZnO4 |
| Li6ZnO4 | — | — | ||
| Quaternary (Li–Zn–Sn–O) | Li2ZnSn3O8 | LiZnSnO2 | LiZn4SnO8 | LiZnSnO |
| — | LiZn4Sn4O8 | — |
Inorganic crystal chemical space
Summary statistics for the binary, ternary and quaternary chemical compounds generated are given in Table 2. Among binary, ternary, quaternary compounds, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464, 10
464, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779
779![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441, and 2
441, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909
909![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434
434![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982 compounds respectively passed the chemical filter. Within the MP database, there are 9981 binary, 36
982 compounds respectively passed the chemical filter. Within the MP database, there are 9981 binary, 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 ternary, and 17
866 ternary, and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 quaternary compounds identified. For binary compounds, with a total of 225
417 quaternary compounds identified. For binary compounds, with a total of 225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879 unique combinations, 3627 (1.6%) are standard, 9837 (4.4%) are missing, 6354 (2.8%) are interesting, and the vast majority, 206
879 unique combinations, 3627 (1.6%) are standard, 9837 (4.4%) are missing, 6354 (2.8%) are interesting, and the vast majority, 206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 (91.2%), are deemed unlikely to be formed. Even for the simple case of combining two components, the compositional space is sparsely populated.
061 (91.2%), are deemed unlikely to be formed. Even for the simple case of combining two components, the compositional space is sparsely populated.
| Unique combinations | Standard | Missing | Interesting | Unlikely | |
|---|---|---|---|---|---|
| Chemical filter | — | Allowed | Allowed | Forbidden | Forbidden |
| Materials Project | — | Known | Unknown | Known | Unknown |
| Binary (AwBx) | 225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879 879 |
3627 (1.6%) | 9837 (4.4%) | 6354 (2.8%) | 206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 (91.2%) 061 (91.2%) |
| Ternary (AwBxCy) | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 637![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 (0.03%) 713 (0.03%) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754 754![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728 (13.9%) 728 (13.9%) |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 (0.01%) 153 (0.01%) |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 845![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995 (86.1%) 995 (86.1%) |
| Quaternary (AwBxCyDz) | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902 902![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534 534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 (0.00%) 455 (0.00%) |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909 909![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 (17.2%) 527 (17.2%) |
962 (0.00%) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993 993![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381 (82.8%) 381 (82.8%) |
This pattern is more extreme in ternary compounds, where only 0.03% are standard, and the number of interesting compounds is negligible. The quaternary compounds continue this trend, with a rounded total of 0.00% being standard or interesting, and 82.8% falling into the unlikely category. Significantly, the data reveals an increase in missing compounds from the MP database across the complexity spectrum: 4.4% in binary, 13.9% in ternary, and 17.2% in quaternary. This escalation may suggest that as the complexity of the compounds grows, the probability of their synthesis or the identification of novel stable crystal materials decreases. Concurrently, the potential for discovering new crystalline materials increases, as evidenced by the larger missing category in higher-order compounds. The statistics hint at unexplored territories in materials science, particularly for ternary and quaternary compounds.
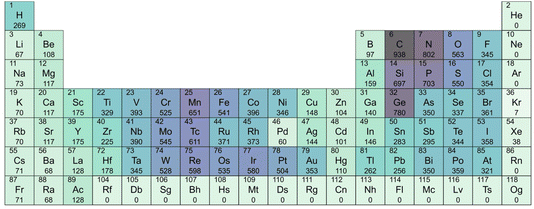
A Periodic Table including the elements that commonly appear in binary compounds allowable by the chemical filters is shown in Fig. 1. Elements with a greater number of oxidation states (accessible species) are more abundant. Among the non-metallic elements, carbon (C), nitrogen (N), oxygen (O), silicon (Si), phosphorus (P), sulfur (S), chlorine (Cl), and germanium (Ge) are notable for their multiple accessible oxidation states. This enables them to participate in a diverse range of chemical compositions while maintaining charge neutrality. The same is true for transition metals such as chromium (Cr), manganese (Mn) and iron (Fe). Furthermore, elements with high electronegativity values, such as fluorine (F) and oxygen (O), are also favoured by the filters. F, with an electronegativity of 3.44, and O, with 3.98, despite having only one and two negative oxidation states, respectively, are likely to pass the SMACT filters as stable anions. In summary, elements with either many oxidation states or high electronegativity are favourable for forming more inorganic compounds.
Materials embedding vectors
An integer representation of elements, in terms of atomic number, is straightforward and intuitive for human chemists to learn. However, machine-learning models benefit from the descriptive power of a higher dimensional representation, often in the form of continuous element vectors, Vi. To effectively represent elements, several types of element embedding have been developed. The Magpie10 representation, for instance, incorporates diverse element properties, such as atomic weight, electronegativity, and melting temperature. Oliynyk11 embedding comprises chemical descriptor vectors, derived from properties of elements. Mat2vec,12 utilising natural language processing (NLP) techniques, learned material representations from an extensive text corpus, capturing the context and relationships of different materials as mentioned in the scientific literature. This method effectively leverages unstructured textual data to enhance understanding of material properties. Skipatom13 learned representations by predicting the surrounding atomic environment of a target atom based on structural information. It emphasizes capturing the local chemical environments and their impact on material properties. Megnet16 (ref. 14) utilises graph neural networks, where the embedding is based on graph attributes that include whole graph information. This method employs the weights of the neural networks to predict the formation energy of crystalline materials, treating the atomic structure of materials as a graph with detailed node and edge representations. We employ the Python package ElementEmbeddings15 to compile the various embeddings.To make compositional embeddings from element embeddings for compounds, a weighted sum of the constituent element embeddings is performed, i.e.,
| VComposition = (wVA + xVB + yVC + zVD)/(w + x + y + z) | (2) |
This step is implemented as the CompositionalEmbedding function in the ElementEmbeddings package.
Dimensionality reduction
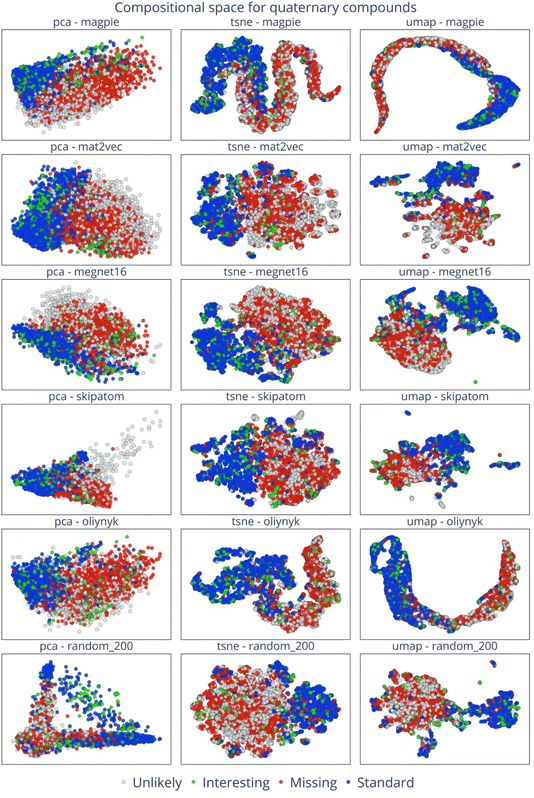
To systematically map the inorganic crystalline chemical space in two dimensions, we utilise three primary dimensionality-reduction techniques. These are Principal Component Analysis (PCA)16 and t-distributed Stochastic Neighbour Embedding (t-SNE),17 both implemented using the sklearn library,18 as well as Uniform Manifold Approximation and Projection (UMAP),19 which is implemented using the UMAP Python library.We consider five distinct element embeddings: Magpie, Mat2vec, Megnet16, Skipatom, and Oliynyk. A random embedding of 200 dimensions is used to act as a control with no embedded chemical information, while still providing a unique representation for each element. The dimensionality of the embedding vectors is 22, 200, 16, 44 and 200 for Magpie, Mat2vec, Megnet16, Oliynyk, and Skipatom, respectively. For a comprehensive analysis, 3000 data points were randomly selected for each of the four categories: standard, missing, interesting, and unlikely. These data points are transformed into two-dimensional vectors using the specified dimensionality-reduction methods. The resulting embeddings are visually represented for binary, ternary, and quaternary compounds in Fig. 2–4, respectively.
For binary compounds, the distribution patterns of embedding vectors reveal distinct characteristics across different element embeddings. Vectors derived from Mat2vec, Skipatom, and Random element embeddings exhibit a dispersed distribution across the reduced space. In contrast, the embeddings generated using Magpie and Oliynyk show a more concentrated, clustered configuration. Fig. 5 captures this phenomenon, presenting the reduced embedding vectors for binary compounds, consistent with those in Fig. 2, but classified into distinct categories according to types of chemical compounds based on the anion present, such as pnictides, halides, chalcogenides, and oxides. Notably, the observed clustering patterns with the Mat2vec, Skipatom, and Random embeddings indicate a pronounced tendency for these vectors to group according to specific types. For instance, the oxide binary compounds (marked as green points) form isolated clusters. Such a tendency suggests that atom types play a significant role in the construction of compositional embeddings, which are derived from a weighted sum of individual element embeddings. On the other hand, the Magpie and Oliynyk embeddings, formulated based on a variety of atomic properties, indicate the presence of influential atomistic characteristics that extend beyond merely the types of atom species.
The analysis of the PCA plots of Mat2vec, Oliynyk, and Megnet16 in Fig. 2 exhibits a separation of interesting from standard and missing compositions. This segregation indicates that interesting compounds, which are known stable materials yet excluded by chemical filters, possess unique and distinct characteristics that set them apart from other categories. This is expected, as large families of metallic alloys and intermetallic compounds fall into this category. For ternary systems, a similar trend is observed, where standard materials demarcate themselves from those interesting and missing. This is particularly evident in the Mat2vec, Megnet16, and Oliynyk embeddings in Fig. 3. It is worth highlighting that the standard and missing materials have a separate distribution in the quaternary space of Fig. 4. It hints that navigating missing materials could unveil unexplored regions of the chemical space, potentially leading to the discovery of synthesisable materials with unique properties and applications. Indeed, the high fraction of empty space that exists for multi-component compounds has recently been exploited in a large-scale computational screening study that identified 2.2 million plausible inorganic crystals20 and offers a fertile playground for generative machine-learning models.21–24
Overall, the degree of clustering across categories escalates from binary to quaternary systems with the increasing order of complexity and chemical diversity inherent in higher-order compounds. With the transition to quaternary compounds, the distinct characteristics of each class become more salient. It is worth highlighting that the dimension reduction, resulting from the unsupervised learning algorithms, demonstrates cohesive clustering that corresponds to our classification with a striking clustering of the standard and missing compositions.
Conclusions
We have explored the vast expanse of inorganic crystal space, encompassing an array of 1010 compounds that span binary, ternary, and quaternary compounds. While the uncharted space may be considered infinite, we tame it by introducing chemical constraints in the form of filters and limits on stoichiometric combinations. We label the resulting entries as standard, missing, interesting and unlikely, according to whether they pass these filters and if they are present in the Materials Project database. This separates the proportion of discovered compounds that conform to standard chemical rules to form stable inorganic solids. Furthermore, we have visualised the inorganic crystal chemical space through the lens of these two filters, revealing that higher-order compounds exhibit pronounced distinctive characteristics. It hints that navigating complex spaces could unlock materials with novel properties in unexplored regions, offering new avenues for scientific exploration. The study thus serves as a foundational reference for future endeavours in data-driven materials discovery, emphasising the potential of unknown regions within the chemical space.Data availability
This study used several open-access tools, including the SMACT (https://github.com/WMD-group/SMACT) and ElementEmbeddings (https://github.com/WMD-group/ElementEmbeddings) packages. The associated scripts (or notebooks) to generate the plots in this paper are available in the SMACT examples directory. Interactive plots for binary combinations can be generated using CrystalSpace (https://github.com/WMD-group/CrystalSpace).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Daniel W. Davies for fruitful discussions and past contributions to the SMACT package. This work was supported by EPSRC project EP/X037754/1. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1).References
- L. Pauling, The Principles Determining the Structure of Complex Ionic Crystals, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS.
- W. H. Bragg and W. L. Bragg, The reflection of X-rays by crystals, Proc. R. Soc. London, Ser. A, 1997, 88, 428–438 Search PubMed.
- K. Rajan, Materials informatics, Mater. Today, 2005, 8, 38–45 CrossRef CAS.
- D. W. Davies, K. T. Butler, A. J. Jackson, A. Morris, J. M. Frost, J. M. Skelton and A. Walsh, Computational Screening of All Stoichiometric Inorganic Materials, Chem, 2016, 1, 617–627 CAS.
- D. W. Davies, K. T. Butler, A. J. Jackson, J. M. Skelton, K. Morita and A. Walsh, SMACT: Semiconducting Materials by Analogy and Chemical Theory, J. Open Source Softw., 2019, 4, 1361 CrossRef.
- B. R. Pamplin, A systematic method of deriving new semiconducting compounds by structural analogy, J. Phys. Chem. Solids, 1964, 25, 675–684 CrossRef CAS.
- C. H. L. Goodman, The prediction of semiconducting properties in inorganic compounds, J. Phys. Chem. Solids, 1958, 6, 305–314 CrossRef.
- L. Pauling, The Nature of the Chemical Bond IV, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, High-Throughput Machine-Learning-Driven Synthesis of Full-Heusler Compounds, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Unsupervised word embeddings capture latent knowledge from materials science literature, Nature, 2019, 571, 95–98 CrossRef CAS PubMed.
- L. M. Antunes, R. Grau-Crespo and K. T. Butler, Distributed representations of atoms and materials for machine learning, npj Comput. Mater., 2022, 8, 44 CrossRef.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- A. Onwuli, A. V. Hegde, K. V. T. Nguyen, K. T. Butler and A. Walsh, Element similarity in high-dimensional materials representations, Digital Discovery, 2023, 2, 1558–1564 RSC.
- S. Wold, K. Esbensen and P. Geladi, Principal component analysis, Chemom. Intell. Lab. Syst., 1987, 2, 37–52 CrossRef CAS.
- L. van der Maaten and G. Hinton, Visualizing Data using t-SNE, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2018, 12, 2825 Search PubMed.
- L. McInnes, J. Healy, N. Saul and L. Großberger, UMAP: Uniform Manifold Approximation and Projection, J. Open Source Softw., 2018, 3, 861 CrossRef.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Inverse Design of Solid-State Materials via a Continuous Representation, Matter, 2019, 1, 1370–1384 CrossRef.
- M. Alverson, S. Baird, R. Murdock, Ho (Enoch) Sin-Hang, J. Johnson and T. Sparks, Generative adversarial networks and diffusion models in material discovery, Digital Discovery, 2024, 3, 62–80 RSC.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal diffusion variational autoencoder for periodic material generation, arXiv, 2022, preprint, arXiv:2110.06197 DOI:10.48550/arXiv.2110.06197.
- C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, S. Shysheya, J. Crabbé, L. Sun, J. Smith, R. Tomioka and T. Xie, MatterGen: a generative model for inorganic materials design, arXiv, 2023, preprint, arXiv:2312.03687, DOI:10.48550/arXiv.2312.03687.
| This journal is © The Royal Society of Chemistry 2025 |