Open Access Article
Open Access ArticlePerformance of machine learning for ozone modeling in Southern California during the COVID-19 shutdown†
Khanh
Do
 ab,
Arash Kashfi
Yeganeh
ab,
Ziqi
Gao
c and
Cesunica E.
Ivey
ab,
Arash Kashfi
Yeganeh
ab,
Ziqi
Gao
c and
Cesunica E.
Ivey
 *bd
*bd
aDepartment of Chemical and Environmental Engineering, University of California Riverside, Riverside, CA, USA. E-mail: iveyc@berkeley.edu
bCenter for Environmental Research and Technology, Riverside, CA, USA
cDepartment of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA, USA
dNow at Department of Civil and Environmental Engineering, University of California, Berkeley, Berkeley, CA, USA
First published on 29th March 2024
Abstract
We combine machine learning (ML) and geospatial interpolations to create two-dimensional high-resolution ozone concentration fields over the South Coast Air Basin (SoCAB) for the entire year of 2020. The interpolated ozone concentration fields were constructed using 15 building sites whose daily trends were predicted by random forest regression. Spatially interpolated ozone concentrations were evaluated at 12 sites that were independent from the machine learning sites and historical data to find the most suitable prediction method for SoCAB. Ordinary kriging interpolation had the best performance overall for 2020. The model is best at interpolating ozone concentrations inside the sampling region (bounded by the building sites), with R2 ranging from 0.56 to 0.85 for those sites. All interpolation methods poorly predicted and underestimated ozone concentrations for Crestline during summer, indicating that the site has a distribution of ozone concentrations that is independent from all other sites. Therefore, historical data from coastal and inland sites should not be used to predict ozone in Crestline using data-driven spatial interpolation approaches. The study demonstrates the utility of ML and geospatial techniques for evaluating air pollution levels during anomalous periods. Both ML and the Community Multiscale Air Quality model do not fully capture the irregularities caused by emission reductions during the COVID-19 lockdown period (March–May) in the SoCAB. Including 2020 training data in the ML model training improves the model's performance and its potential to predict future abnormalities in air quality.
Environmental significanceIn the spring of 2020, shifts in emissions and subsequent air pollution levels associated with COVID-19 lockdown measures were significantly different compared with any previous period in the Anthropocene. We investigate the utility of deterministic and machine learning models in capturing the observed anomalies in ozone concentrations across the South Coast Air Basin, a region with spatially heterogeneous formation of secondary pollutants. The directionality of model biases before, during, and after the lockdown period gives insight into the NOX and VOC limited characteristics of locations across the Basin, which guides future emissions reduction strategies. |
1. Introduction
In the atmosphere, the non-linear relationship between nitrogen oxides (NOX), volatile organic compounds (VOCs), and ozone is complex. In the United States, the COVID-19 pandemic and the ensuing shutdown presented an unintentionally optimal period to observe, revise, and improve our existing air quality models and observe the sensitivity of the NOX–VOC–ozone relationship in real time. In California, the pandemic shutdown began on March 16, 2020, when significantly reduced traffic volume was observed. In Los Angeles and Ventura Counties, there was approximately a 30% decrease in vehicle miles traveled (VMT) on weekdays and up to a 40% decrease on weekends in 2020.1 This unusual event temporarily changed the conventional distribution of primary and secondary air pollutants in the South Coast Air Basin (SoCAB). Since NOx and VOC emissions declined with the reduction in traffic flow,2 we expected significant changes in ozone concentrations in Southern California. Several studies were published regarding the pandemic that investigated the effects of the COVID-19 shutdown on air pollutants. For instance, Jiang et al., used WRF-Chem to simulate the major air pollutants before lockdown and during lockdown and found an increase in ozone in urban areas due to emission reductions during the lockdown.2 The COVID-19 shutdown also provided an estimation of the impacts of future large-scale emission reduction strategies on ozone concentrations in SoCAB.3Of particular interest is the exploration of possible differences in ozone prediction performance of different modeling approaches during periods of significant emissions and meteorological anomalies. The Community Multiscale Air Quality (CMAQ) modeling system, developed by the U.S. Environmental Protection Agency (EPA), is widely-used for multi-day air quality simulations to estimate air pollutant concentrations with prescribed emissions and meteorology inputs (Ooka et al., 2011; Rao et al., 1996; Wong et al., 2012).4–6 From the model outputs, scientists and regulators can better predict the interactions between future emissions, meteorology, and air pollutants to strengthen recommendations for emissions control programs. Chemical transport models (CTMs), such as CMAQ, are based on first principles equations and are initiated with interpolated observation data, hence avoiding most obstacles introduced by data missingness in observations. Machine learning (ML) as an alternative modeling approach has attracted more attention from air quality researchers. Although ML and CTMs have a similar goal to accurately predict air pollution, ML heavily depends on the quality and quantity of historical data. In contrast with CTMs, which produce larger scale, spatially resolved outputs, ML only provides accurate predictions strictly at trained locations when used for ambient air quality applications.
As most ML approaches depend heavily on observational data, we introduce spatial interpolation as a central procedure for increased comparability with the CMAQ data. Also, the relative sparseness of monitoring stations and the locality of air pollutants have been shown to misrepresent spatially-varying air quality over a large area.7 Spatial interpolation methods (e.g., nearest neighbors, linear or polynomial interpolation, continuous natural neighbor interpolation, etc.) have proven useful for overcoming these limitations.8 Yu et al. evaluated 14 unique spatial modeling methods for eight air pollutants in Atlanta, Georgia for developing spatiotemporal air pollutant concentrations fields.9 Wong et al., assessed four spatial interpolation methods (spatial averaging, nearest neighbor, inverse distance weighting (IDW), and kriging) to estimate ozone and PM10 concentrations.10 In California, the South Coast Air Quality Management District (SCAQMD) operates 38 air monitoring stations in Southern California over an area of approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743 square miles, including SoCAB, portions of the Salton Sea Air Basin, and Mojave Desert Air Basin, with an average of 283 square miles per monitoring station.11,12 Therefore, spatial interpolation is expected to enhance the observational analyses that follow.
743 square miles, including SoCAB, portions of the Salton Sea Air Basin, and Mojave Desert Air Basin, with an average of 283 square miles per monitoring station.11,12 Therefore, spatial interpolation is expected to enhance the observational analyses that follow.
This paper focuses on the performance of deterministic and ML models under rapid changes in emissions and meteorological conditions, specifically during the COVID-19 lockdown period in March through May of 2020. We compare three spatial interpolation techniques to the CMAQ model and evaluate biases related to COVID-19 lockdown anomalies. Furthermore, we aim to answer the question of whether there were other periods with emissions changes similar to the COVID-19 lockdown period within the past few decades and how those changes impacted the behavior of ozone in different regions of Southern California.
2. Study area and datasets
This study targeted the Southern California region, including Los Angeles, Orange, Riverside, and San Bernardino counties. The region has been historically challenged with poor air quality, with especially higher ozone concentrations than the rest of the United States. The coastal areas tend to have higher relative humidity (RH) and lower temperatures than inland Southern California. Since the turn of the century, SoCAB has been designated as a nonattainment area for the 1997 8 hour ozone standard (80 ppb), with design values for ozone well above the 2015 standard of 70 ppb (Fig. 1). In 2019, the maximum daily 8 hour average (MDA8) ozone concentration in SoCAB was 108 ppb at the design value location with a classification of “extreme” (Redlands, California).13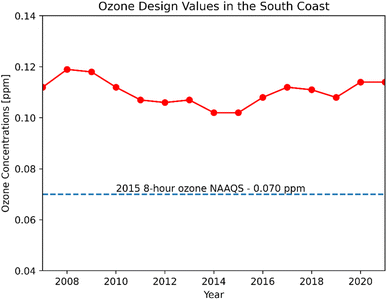 | ||
| Fig. 1 Ozone design values for the South Coast Air Basin from 2006 to 2020 (https://www.epa.gov/air-trends/air-quality-design-values). | ||
2.1 Model input data
The input meteorological data for the CMAQ simulation were generated using the Weather Research and Forecasting (WRF) model. WRF was initiated using initial and boundary condition meteorology data from the North American Mesoscale (NAM) Forecast System integrated with high-resolution sea surface temperature (SST) from the Group for High Resolution Sea Surface Temperature. We used the WRF Objective Analysis program to improve the meteorological simulation, and this step blends observed surface and upper air observations with the background WRF fields. The surface and upper air observations were sourced from NCEP ADP Global Surface Observational Weather Data (ds461) and NCEP ADP Global Upper Air Observational Weather Data (ds351) via the National Center for Atmospheric Research's Research Data Archive, respectively.14We re-projected gridded 4 km emissions from 2019 for the year 2020 using a two-step adjustment to account for changes due to the COVID-19 lockdown.15 In the first step, a linear projection factor (eqn (1)) was applied to 2019 gridded emissions based on SCAQMD basin-wide, total annual emissions spanning from 2012 to 2034, where the District's future projections began in the year 2020. The correction factor was calculated for seven air pollutant groups (total organic gases, reactive organic gases, CO, NOX, SOX, NH3, PM).
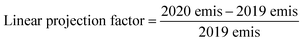 | (1) |
The second step accounted for traffic reductions due to the COVID-19 lockdown, and reductions were highest from March to May 2020, then slowly but not fully rebounding to pre-lockdown levels toward the end of 2020.1 SCAQMD basin-wide projections understandably did not reflect the decrease in mobile source emissions due to unforeseen traffic reductions. Moreover, weekly traffic metrics in 2020 were acquired for the total flow, flow change, and speed change at 2991 locations in Southern California.16 Since the traffic data were not evenly distributed over the study domain, we used k-nearest neighbors (k-NN) to obtain the traffic data for grid cells (locations) that had no more than five reported data points (k value ≤ 5). For the grid cells with more than five reported data points, we normalized traffic volume and then averaged the normalized data.
2.2 Machine learning inputs
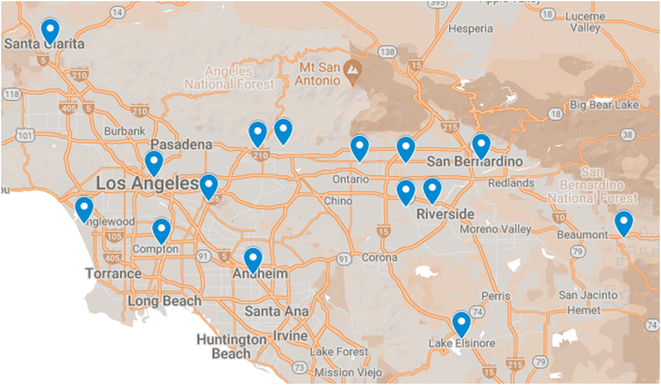
We used two air quality features (NO2 and NO) and four meteorological features (temperature, relative humidity, wind speed, and wind direction) from 15 air monitoring sites in SoCAB (Fig. 2). Hourly meteorological and air quality data used for ML training and validation were obtained from the Air Quality System (AQS) Data Mart (https://aqs.epa.gov/aqsweb/airdata/download_files.html#Raw, last access Jan 19, 2023). We checked the data to ensure that hourly data were available for all training features. If there was a missing data point for one of the features, we removed the invalid hour and all corresponding features. The date range of the model training data was 2009–2010 and 2016–2019 for all 15 sites (Fig. 2). The period from 2011–2015 was not included in our models due to the limited availability of wind direction and wind speed at the sites. We used 2020 data for model testing and evaluation (Table 1).| Ground Monitoring Locations | Anaheim, Azusa, Banning, Compton, Fontana, Glendora, Lake Elsinore, Los Angeles International Airport (LAX), LA North Main Street, Mira Loma, Rubidoux, San Gabriel, Santa Clarita, San Bernardino, Upland |
| Features | NO2, NO, temperature, relative humidity, wind speed, wind direction |
| Label | Ozone |
| Data sources | EPA AQS data mart, CARB air quality and meteorological information system (AQMIS) |
| Training years | 2009, 2010, 2016, 2017, 2018, 2019 |
| Evaluation year | 2020 |
3. Methods
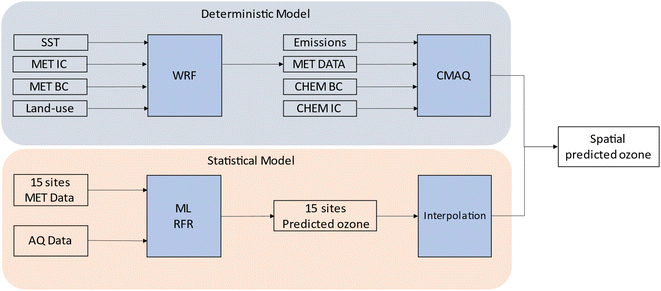
We carried out a parallel approach using both ML and CMAQ to predict 2-D ozone concentrations as shown in Fig. 4. The deterministic model (top panel) utilized WRF and CMAQ to simulate ozone concentrations based on the emissions and meteorological inputs described above. In contrast, the ML model (bottom panel) relied on observational meteorology and air quality data to predict ozone concentrations. ML and CMAQ models were evaluated with observational data to assess their performance, especially in response to the irregular emissions patterns of 2020. Additionally, predictions from ML and interpolation were explored to examine the NOx and VOC limited regimes in Southern California, providing insights into how the models perform in different regions.3.1 CMAQ modeling
In this study, we compared the performance of both CMAQ and ML with spatial interpolations of ozone concentrations in SoCAB for the year 2020.17,18 The CMAQ simulation covered three distinct periods to study the impact of COVID-19 lockdown on air pollutant concentrations: pre-lockdown (Jan 1st to Mar 15th), lockdown (Mar 16th to May 15th), and post-lockdown (after May 16th) periods. Meteorological modeling was carried out using the Weather Research and Forecasting (WRF) model version 3.9 with 4 km horizontal grid spacing, 11 vertical layers for the finest domain (10 layers near the surface), and 156 × 102 grid cells (Fig. 3). There were two parent domains with coarser horizontal grid spacing (36 km and 12 km for domain 1 and domain 2, respectively). WRF configurations were optimized for SoCAB, and they included the use of United States Geological Survey (USGS) land use, thermal diffusion surface physics, and Yonsei University planetary boundary layer scheme (Hong et al., 2006; Huang et al., 2014).17,18 The CMAQ simulation used the modified 2020 emissions and previously described WRF simulations as inputs. The choice of chemical mechanism was SAPRC07tc_ae6_aq, i.e., SAPRC07tc photochemical mechanism, aerosol module 6, and aqueous chemistry (Byun & Schere, 2006; Carter, 2010).19,20 | ||
| Fig. 3 The third and inner-most domain (red boundary) with 4 km horizontal grid spacing covered the entire SCAQMD region (thick black lines). | ||
3.2 Machine learning
In a preceding study, we tested multiple ML algorithms to obtain a better method that resulted in the highest prediction accuracy for ozone concentrations in the SoCAB. Those included neural network, support vector machine, k-nearest neighbors, and random forest.21 Here, we selected random forest regression (RFR), as RFR is the most suitable ML algorithm for predicting ozone concentrations in SoCAB. We also conducted a 10-fold cross-validation over the training data to fine tune the training RFR model in the previous study.21The random forest (RF) algorithm is a supervised learning method employing a tree-based ensemble approach. Each decision tree is derived from training data and represents a subset of the training data. In our model, we have a vector x with n features, denoted as x = (xi, …, xn)T. The goal is to find a function f(x) for predicting ozone concentrations. RF is a collection of decision trees consisting of J trees that are split into j branches from hi, …, hj. The learning function computes the average of all decision trees, expressed as 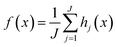 . RF is a combination of multiple decision trees trained on an independent collection of input variables. To reduce the model bias, RFR selects a random subset of features from the input features for each tree, and the output of RFR is the average result from all the decision trees (Rodriguez-Galiano et al., 2015; Zhang & Ma, 2012).22,23
. RF is a combination of multiple decision trees trained on an independent collection of input variables. To reduce the model bias, RFR selects a random subset of features from the input features for each tree, and the output of RFR is the average result from all the decision trees (Rodriguez-Galiano et al., 2015; Zhang & Ma, 2012).22,23
In this study, we selected six training features to predict ozone concentrations, which included two air quality features (NO and NO2) and four meteorological features (temperature, relative humidity, wind speed, and wind direction). The two air quality features are directly related to ozone formation in the troposphere. Ozone undergoes the photolytic cycle during the day and is removed by NOx during nighttime.24–26 The four meteorological features were well studied in our previous work and were shown as the most important features to capture the variability in annual ozone, especially in SoCAB.27–29
We used the scikit-learn 0.22 library supported by the Python programming language to train our RFR model. Again, the input features are NO2, NO, temperature, relative humidity, wind speed, and wind direction, and the label is ozone. We tuned the algorithm by varying the number of decision trees, the depth of the tree, sample split, and the sample leaf to obtain the best prediction accuracy. We used the same model tuning approached described in Do et al. (2023) (Table 2).21
| Hyperparameter | Description |
|---|---|
| n_estimators = 16 | The number of trees in the forest |
| max_features = ‘auto’ | The number of features to consider when looking for the best split |
| max_depth = none | The maximum depth of the tree |
| min_samples_split = 5 | The minimum number of samples required to split an internal node |
| min_samples_leaf = 30 | The minimum number of samples required to be at a leaf node |
| min_weight_fraction_leaf = 0 | The minimum weighted fraction of the sum total of weights required to be at a leaf node |
| max_leaf_nodes = none | Best nodes are defined as relative reduction in impurity |
3.3 Spatial interpolation
To generate a 2-D ozone concentration map, we first ran the RFR model to obtain the ozone concentrations at each air monitoring location (15 sites), which served as the model building sites. In other words, we applied a pointwise ML algorithm to predict ozone concentrations at each trained location. Next, we spatially interpolated the output over the target Southern California region. We applied three different spatial interpolation methods (ordinary kriging, inverse distance weighting (IDW), and bicubic interpolation) and comparatively evaluated the performance of each method. Each interpolation approach is described below.Ordinary kriging was applied to interpolate ozone concentration at 10 km resolution over the study area. Generally, kriging predicts the values for unknown locations by performing a series of linear combinations of values at known locations. Eqn (2) expresses the generic form of the estimator to predict the optimum value Z* of an unknown location by combining the known values Zi with their weights λi.30 We can write the variance σ2 as an optimization problem (eqn (3)) that can be solved using the Lagrange multiplier μ (eqn (4)).
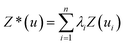 | (2) |
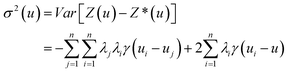 | (3) |
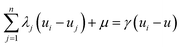 | (4) |
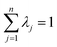 | (5) |
Bicubic interpolation is another method for interpolating data points on a 2-D grid. The interpolated surface can be written in terms of two variables (eqn (6)). The polynomial p consists of sixteen coefficients aij that are solved with sixteen boundary conditions (i.e., (x = 0, y = 0), (x = 1,y = 0), (x = 0,y = 1), (x = 1,y = 1)) and its derivatives with respect to x, y, and xy.32
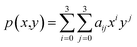 | (6) |
The IDW interpolation method accounts for the distances between the interpolated points and the measured locations. The assumption for IDW is that points close to each other are more alike and have more significant influence than those farther apart. Thus, the nearest measured values have greater weights assigned. Eqn (7) shows that the predicted value Z(x) is inversely proportional to the distance between the measured and interpolated points d(x,xi).
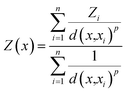 | (7) |
4. Model evaluation
Fig. 5 shows a snapshot of the ozone concentrations over the interpolation region at 4:00 PM on June 22, 2020 (the highest ozone episode of the day), using ordinary kriging. The colored dots with a white border are the actual values at the evaluation sites, and those without a white border are the RFR predicted values for training sites. The model successfully reconstructed the spatial trends in the region, where the lowest ozone levels were in the southwest (coastal) and the highest were in the east (inland), and there was good agreement with the actual ozone concentrations. Fig. S2 and S3† show the heatmap for bicubic and IDW interpolation for the same timestamp. Although all interpolation methods predicted the lowest ozone concentrations in the Southwest, the highest ozone concentrations were predicted in the Northeast of the study region for bicubic and in the North for IDW. The concentration gradient increased from south to north for bicubic and IDW, but from west to east for ordinary kriging.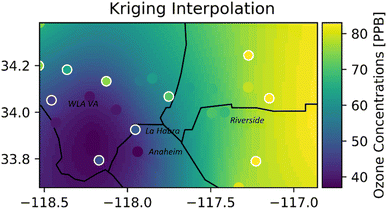 | ||
| Fig. 5 Hourly ozone heatmap (16:00 on June 22, 2020) using ordinary kriging. The dots with white borders are the evaluation sites, and dots without borders are the training sites. | ||
The performance of the models was evaluated based on commonly used statistical metrics: mean bias (MB), correlation coefficient, root mean square error, and R2 (equations listed in ESI†). The models were evaluated based on data from 27 air monitoring stations in SoCAB, of which 15 sites were used to evaluate the training sites, and the other 12 sites were used to evaluate the performance of the three interpolation methods at non-training sites. Tables 3 and 4 highlight R2 for daily average ozone for the bicubic, IDW, and ordinary kriging interpolations, as well as R2 for the CMAQ comparison. We used the entire year to evaluate the interpolation methods, but we only used the five highest ozone months from May to September for the CMAQ evaluation.
| Sites | Bicubic R2 | IDW R2 | Ordinary kriging R2 | CMAQ R2 |
|---|---|---|---|---|
| Anaheim | 0.66 | 0.67 | 0.74 | 0.41 |
| Azusa | 0.52 | 0.64 | 0.77 | 0.59 |
| Banning | 0.17 | 0.46 | 0.73 | 0.26 |
| Compton | 0.65 | 0.67 | 0.77 | 0.48 |
| Fontana | 0.88 | 0.89 | 0.87 | 0.59 |
| Glendora | 0.46 | 0.53 | 0.72 | 0.52 |
| Lake Elsinore | 0.52 | 0.70 | 0.79 | 0.56 |
| LA North Main ST | 0.36 | 0.67 | 0.78 | 0.48 |
| LAX | 0.31 | 0.48 | 0.65 | 0.25 |
| Mira Loma | 0.56 | 0.71 | 0.86 | 0.67 |
| Rubidoux | 0.46 | 0.65 | 0.86 | 0.68 |
| San Bernardino | 0.68 | 0.85 | 0.86 | 0.67 |
| San Gabriel | 0.53 | 0.77 | 0.81 | 0.62 |
| Santa Clarita | 0.27 | 0.72 | 0.84 | 0.61 |
| Upland | 0.76 | 0.80 | 0.86 | 0.61 |
| Sites | Bicubic R2 | IDW R2 | Ordinary kriging R2 | CMAQ R2 |
|---|---|---|---|---|
| Crestline | 0.35 | 0.42 | 0.42 | 0.23 |
| La Habra | 0.75 | 0.80 | 0.77 | 0.44 |
| Long Beach | 0.46 | 0.60 | 0.56 | 0.30 |
| Mission Viejo | 0.15 | 0.36 | 0.49 | 0.39 |
| North Hollywood | 0.67 | 0.67 | 0.79 | 0.59 |
| Pasadena | 0.55 | 0.71 | 0.78 | 0.57 |
| Perris | 0.55 | 0.72 | 0.80 | 0.56 |
| Pomona | 0.71 | 0.83 | 0.84 | 0.68 |
| Redlands | 0.60 | 0.74 | 0.71 | 0.57 |
| Reseda | 0.63 | 0.63 | 0.71 | 0.01 |
| West LA | 0.29 | 0.56 | 0.60 | 0.28 |
| Winchester | 0.37 | 0.40 | 0.39 | 0.45 |
The bicubic R2 indicates the poorest performance of the three interpolation methods. IDW showed a significant improvement compared to bicubic interpolation. Since IDW accounts for the distances between the interpolation points and the data points, farther data points have less influence on the interpolation points. Ordinary kriging resulted in the best interpolation method because the method not only accounts for the distance between building points and interpolated data by assigning larger weight λi to the near neighbors, but it also considers the variability of data by considering the variance of input data, σ2.34
ML with interpolation gave a poor performance for Crestline and Winchester locations. Crestline is located in the mountains and to the northeast of SoCAB, which is elevated terrain associated with upper air and a different air mass at times. Crestline ozone was not well-correlated with coastal or inland sites. Thus, interpolated Crestline ozone based on coastal or inland data points will likely yield poor results. The Winchester air monitoring site is located near the Skinner Reservoir (Fig. S1†), far away from other data points (Lake Elsinore and Banning). Low R2 for Winchester can be explained by the influence of the lake and local meteorology and air quality. The ordinary kriging model performed well for locations bounded by data points with R2 above 0.56. However, poor interpolation results occurred for peripheral locations in SoCAB (Crestline, Mission Viejo, and Winchester). LAX ozone levels were not well correlated with meteorology, and training the ML model with fewer meteorological features did not affect the performance of the LAX location. Overall, model performance increased from the West to the East, with better prediction for inland sites.
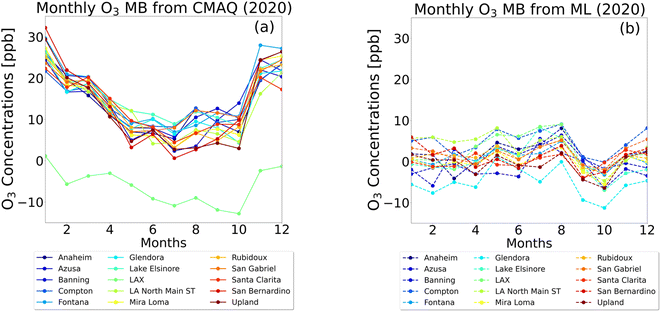
The distribution of the monthly mean bias (MB) for ordinary kriging interpolation centered around zero with the range between +9 ppb for Compton (August) and −11 ppb for Glendora (October). Eleven building sites have a net positive monthly MB, and four have a net negative monthly MB (Fig. 6). The results from the CMAQ simulation overestimated the ozone levels. CMAQ's best performance was from May to October when the MBs were the smallest. CMAQ underestimates the ozone concentrations at the LAX location, due to the site's proximity to the Pacific Ocean, colder model temperatures, and potential discrepancies in aviation emissions. In general, ozone concentrations in the SoCAB are highest during the summer and lowest in the winter, corresponding with the temperature. Although the CMAQ simulation captures diurnal variation, the seasonal variation is not as well-represented (Fig. S4, S5, S7, and S11†). Lower performing CMAQ results could come from uncertainties in emissions estimates. CMAQ generally overestimated ozone concentrations because the simulated nighttime ozone concentrations were higher than those observed, potentially due to underestimated nighttime NOx emissions.15 In other words, there was not enough NOx emitted in the model during the daytime for ozone formation and at night for ozone removal.35,36
Training features can be varied to study the sensitivity to modeled ozone response. For example, we can perturb the temperature, RH, or emissions values and examine the ozone levels corresponding to the change in the features. However, because the formation of ozone results from a complex combination of chemical reactions, resulting impacts are nonlinear and interdependent. Therefore, when using ML to test for sensitivity to a feature, one should consider feature dependencies. For example, in testing temperature impacts on ozone concentration, we must consider both how temperature impacts photolysis rates (NO2 degradation) as well as simultaneous correlations/anticorrelation with other meteorological variables, such as RH or wind speed.
Although the interpolation R2 values for the 15 building sites are high, the accuracies of the 12 evaluation sites are somewhat lower than those reported in other studies. In our previous work, where we employed RFR to predict O3 levels in Fontana, we achieved an R2 of 0.86. Additionally, Lyu et al. utilized the RFR method to predict ozone concentrations in the Beijing–Tianjin–Hebei region, achieving a monthly R2 of 0.93 (Lyu et al., 2022).37 Two factors contribute to the performance of the evaluation sites in our approach. First, the estimation of O3 concentrations in evaluation sites relied on historical data from neighboring building sites. However, the building sites are not evenly distributed in Southern California, and the performance of the interpolating locations is inversely proportional to the distance of the building sites. Second, O3 levels are more locally influenced in SoCAB, and the relationship between NOx and VOC is not strictly linear. Therefore, the estimation from interpolation might not fully capture this locality. We also note that the choice of averaging period will impact R2, such that comparison of daily vs. monthly values will lead to discrepancies that favor a longer averaging period.
5. Discussion
The reduction in traffic volumes during the lockdown from March to May led to a decrease in observed CO and NOX.3,16 As a result, we expected an overall reduction in ozone levels over the SoCAB region. The average diurnal ozone concentrations before the lockdown (Jan–Feb) in 2020 were noticeably greater than the average from 2016–2019 for all 15 building sites. Fig. 7 shows the averaged diurnal profiles of three 2020 periods for inland sites, Lake Elsinore and Fontana: pre-lockdown (a and d), lockdown (b and e), and post-lockdown (c and f) periods. Before the lockdown, the 2020 ozone concentrations (red line) in Lake Elsinore and Fontana exceeded the four-year average (blue line), indicating a recent worsening of ozone trends in Southern California. The ML model with the interpolation method (black line) successfully predicted this ozone trend before the lockdown. During the lockdown, observed ozone levels in 2020 significantly decreased in Lake Elsinore, dropping below the four-year average. After the lockdown, ozone levels in 2020 rebounded but remained lower than the pre-lockdown period. The ML model effectively captured these ozone trends throughout the three periods of 2020 for the Lake Elsinore site. In contrast, ozone levels in Fontana did not decrease significantly below the four-year average during the lockdown and remained high afterward. It is important to note that Lake Elsinore is located in a remote area surrounded by trees. During the lockdown, Lake Elsinore showed a drop in ozone concentrations, indicating that the location is in a NOx limited atmosphere, where fluctuations in NOx have a significant impact on ozone levels. On the other hand, Fontana is an urban site, and the ozone levels did not exhibit significant improvement during the lockdown, suggesting that Fontana is located in a VOC limited atmosphere.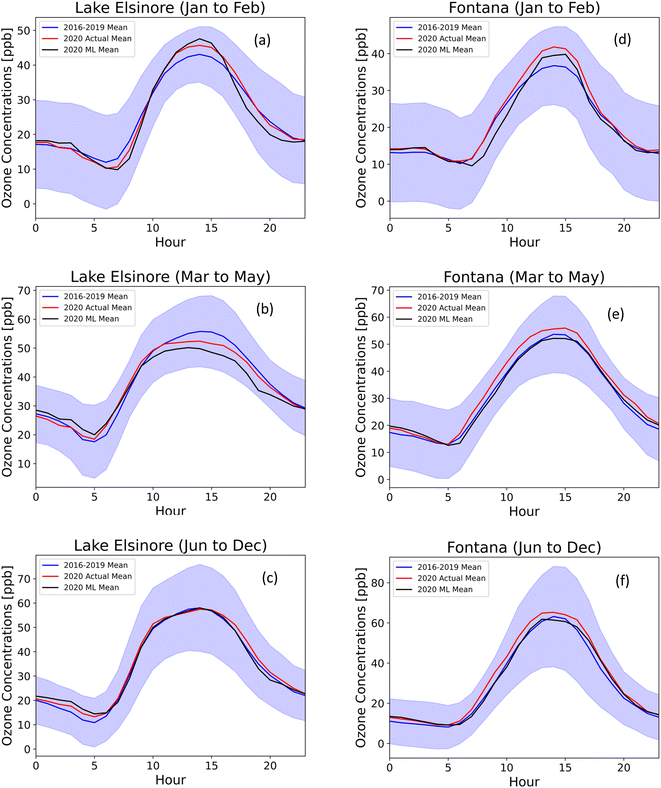 | ||
| Fig. 7 Averaged diurnal profiles of 2016–2019 (blue), actual 2020 (red), and ML predicted 2020 (black) ozone concentrations (ppb) at Lake Elsinore (a–c) and Fontana (d–f) for three different periods: (a and d) pre-lockdown (Jan to Feb), (b and e) lockdown (Mar to May), and (c and f) post-lockdown (after May). The shaded area is the standard deviation of the 2016–2019 measurements. Additional sites are provided in the ESI.† | ||
Post-lockdown differences compared to the four-year average were not significant across the 15 sites. The RFR model captured ozone trends throughout 2020, although slightly lower during lockdown and despite the observed reduction in NOx, suggesting that meteorological features would play an important role in predicting ozone levels during anomalous episodes in addition to air quality features. Actual and modeled discrepancies also indicate anomalous ozone behavior during lockdown. For instance, several sites in the SoCAB showed an increase in ozone levels based on the diurnal profile implying that the urban locations in the SoCAB were in VOC limited regimes, where there was NOx reduction-initiated ozone enhancement.38
The diurnal NOx concentrations at all sites in Southern California exhibit a consistent pattern, in which both pre-lockdown and post-lockdown NOx levels were significantly higher than during the lockdown period. In Fig. S13,† the diurnal changes in NOx levels are illustrated for pre-lockdown (blue), lockdown (orange), and post-lockdown (green) between the 2020 NOx and the average from 2016–2019. Positive values before the lockdown suggest an increase in NOx levels in 2020 compared to the historical average of 2016–2019. However, during the lockdown, the differences are negative, indicating a significant decrease in 2020 NOx levels compared to the historical data due to a substantial decrease in traffic and anthropogenic activities.
We computed the diurnal differences between 2020 O3 and historical O3 (average from 2016 to 2019) for both actual 2020 O3 and ML 2020 O3 (Fig. S17 and S18†) to show the trends in O3 concentrations for the pre-lockdown, lockdown, and post-lockdown periods. During the lockdown (orange line), the Lake Elsinore site exhibits negative changes of −4 ppb at 15:00, the peak O3 concentration time of the day. However, in the early morning, the O3 changes turn positive (∼3 ppb), attributed to the reduced NOX titration. Post-lockdown (green line) shows mostly positive differences, indicating an increase in O3 concentrations due to rising emissions and transition to summertime. In Fontana, O3 trends do not show significant differences across the three periods. Notably, during peak O3 hours (13:00–16:00), O3 levels are more than 3 ppb higher compared to historical values, suggesting that the reduction in emissions has an inverse effect on O3 concentrations. It's worth noting that the ML model successfully predicted O3 trends in Lake Elsinore for all three periods. However, the ML model failed to predict the behavior of O3 in Fontana, as it estimated a decrease in O3 during the lockdown. The summary of the machine learning method and its performance across different regimes in the SoCAB is illustrated in Fig. 8.
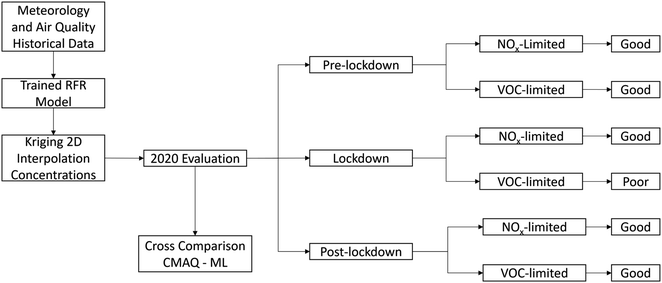 | ||
| Fig. 8 Flow chart of the ML model to summarize the ML method and the evaluation results in the South Coast Air Basin. | ||
To illustrate the variations in NOx corresponding to changes in O3 for three periods (pre-lockdown, lockdown, and post-lockdown), we calculated the O3 sensitivity using the ratio of differences in O3 and NOx between 2020 and historical data, as shown in eqn (8).
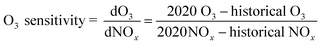 | (8) |
In the VOC limited regimes, we forecast the sensitivity of O3 to be minimal regarding the changes in NOx. This is evident for areas with substantial NOx emissions, such as Azusa, Fontana, and Upland (Fig. 9), where the sensitivities of O3 (dO3/dNOx) during the lockdown are minimal. Conversely, in NOx limited regimes, we expect to observe a reduction in O3 corresponding to the decrease in emissions. Therefore, the sensitivities of O3 in NOx limited regimes are maximized during the lockdown, as illustrated in Fig. 9 for Lake Elsinore and Banning. At hour 14:00, O3 concentrations in Lake Elsinore decreased more than 12 ppb per 1 ppb reduction in NOx.
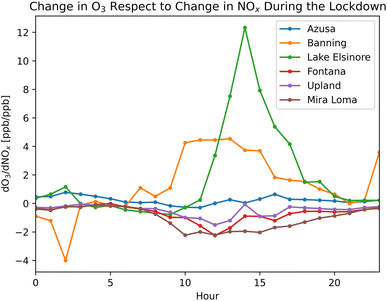 | ||
| Fig. 9 O3 sensitivity for six locations in Southern California during the lockdown period reflecting the change in O3 with respect to the change in NOx between 2020 data and historical data. | ||
The ML model with interpolation successfully predicted O3 trends by utilizing four meteorological parameters and two observed ozone precursors (listed in Table 1). It is important to note that O3 exhibits strong relationships with meteorology, NOx, and VOCs. Due to data availability, VOC data were omitted from the training set. The current ML model has some weaknesses for testing the sensitivity of O3 to anomalous precursor levels and meteorology. Our ML model performs well in predicting O3 levels where the test data resembles the training data. However, the model struggles to give accurate predictions when the test data significantly differs from the training sets. For instance, during the lockdown, the model failed to predict the O3 concentrations in the VOC limited regimes. This suggests that relying on ML models to predict future scenarios may be unreliable under new regimes. Considering additional features, such as VOCs in the training sets, may enhance the model's ability to predict accurately when extrapolating beyond the feature space. To our understanding, there are no ML models known for effective extrapolation of the training data to provide reliable predictions.
6. Conclusion
This study highlights the advantages of spatial interpolation methods for ozone predictions during anomalous environmental events. With modern processor architectures (e.g., AMD Zen 3 or Intel Alder Lake), training the RFR model and performing high-resolution interpolation over the SoCAB region for one prediction year took less than five minutes of walltime with a 16-core processor. In contrast, CMAQ walltime was 16 days for a year-long simulation for the SoCAB region. Further, ozone modeling for 2020 was challenging because of unforeseen emissions conditions from March to September, during which traffic volume significantly decreased (up to 40% reduction in some locations). We hypothesized that mid-2020 ozone levels would decrease semi-proportionally due to the decline in traffic volume. However, the changes in ozone levels in the SoCAB were small in magnitude, but directionally the changes were informative for future emissions reductions planning (increased ozone indicates VOC limitations).Ordinary kriging interpolation using ML building provided daily data, addressed data missingness, and captured 2020 ozone trends with low bias despite the sudden change in emissions. The ML model with the interpolation method successfully captured ozone trends throughout three periods in 2020, particularly in locations operating under a NOx limited regime, such as Lake Elsinore. However, it faced challenges in predicting ozone levels during the lockdown period in areas characterized by a VOC limited regime, like Fontana. ML inherently relies on patterns learned from historical data to make predictions, especially for inputs that resemble past occurrences. In this study, the ML model struggled to make accurate predictions for VOC limited regime, suggesting that events akin to the COVID-19 lockdown had not been encountered in the past. Unfortunately, due to the unavailability of speciated VOC data, we didn't incorporate them as a training feature in the model. Since ozone formation exhibits a non-linear correlation with both NOx and VOC, the inclusion of speciated VOC data would likely enhance the model's accuracy, especially for regions with a VOC limited atmosphere. Our ML model provides regulators with valuable insights into NOx and VOC limited regimes across the Southern California domain, enabling policymakers to devise more effective emission reduction strategies and improve air quality at hyperlocal scales.
Data and source codes
All training and evaluating air quality and meteorology data are available at https://aqs.epa.gov/aqsweb/airdata/download_files.html#Raw. Weekly traffic observations in Southern California and emissions are available upon request. Source codes for ML and interpolation were uploaded to GitHub: https://github.com/kdo037/Machine-Learning-with-Spatial-Interpolation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This paper was prepared as a result of work sponsored, paid for in part by, the South Coast Air Quality Management District (SCAQMD). The opinions, findings, conclusions, and recommendations are those of the authors and do not necessarily represent the views of SCAQMD. We acknowledge Graduate Assistant in Areas of Need (GAANN) support from the University of California, Riverside Chemical and Environmental Department. The authors thank the South Coast Air Quality Management District for providing emissions data and Dwaraknath Ravichandran and Prof. Shams Tanvir, who provided 2020 traffic data for emission correction. The authors acknowledge partial support from the University of California Institute for Transportation Studies for work conducted for this manuscript. The authors thank Prof. Armistead G. Russell and Dr Charles L. Blanchard for their guidance on this work.References
- Caltrans, Caltrans PeMS [Internet], 2023, available from: https://dot.ca.gov/programs/traffic-operations/census/mvmt.
- Z. Jiang, H. Shi, B. Zhao, Y. Gu, Y. Zhu and K. Miyazaki, et al., Modeling the impact of COVID-19 on air quality in southern California: implications for future control policies, Atmos. Chem. Phys., 2021, 21(11), 8693–8708 CrossRef CAS , available from: https://acp.copernicus.org/articles/21/8693/2021/.
- C. Ivey, Z. Gao, K. Do, A. Kashfi Yeganeh, A. Russell, C. L. Blanchard, et al., Impacts of the 2020 COVID-19 Shutdown Measures on Ozone Production in the Los Angeles Basin, Chemistry, 2020, available from: https://chemrxiv.org/articles/preprint/Impacts_of_the_2020_COVID-19_Shutdown_Measures_on_Ozone_Production_in_the_Los_Angeles_Basin/12805367/1 Search PubMed.
- R. Ooka, M. Khiem, H. Hayami, H. Yoshikado, H. Huang and Y. Kawamoto, Influence of meteorological conditions on summer ozone levels in the central Kanto area of Japan, Procedia Environ. Sci., 2011, 4, 138–150 CrossRef CAS.
- J. B. Flaum, S. T. Rao and I. G. Zurbenko, Moderating the Influence of Meteorological Conditions on Ambient Ozone Concentrations. Journal of the Air & Waste Management Association, J. Air Waste Manage. Assoc., 1996, 46(1), 35–46 CrossRef CAS PubMed.
- D. C. Wong, J. Pleim, R. Mathur, F. Binkowski, T. Otte and R. Gilliam, et al., WRF-CMAQ two-way coupled system with aerosol feedback: software development and preliminary results, Geosci. Model Dev., 2012, 5(2), 299–312 CrossRef.
- J. S. Apte, K. P. Messier, S. Gani, M. Brauer, T. W. Kirchstetter and M. M. Lunden, et al., High-Resolution Air Pollution Mapping with Google Street View Cars: Exploiting Big Data, Environ. Sci. Technol., 2017, 51(12), 6999–7008 CrossRef CAS PubMed.
- J. Joseph, H. O. Sharif, T. Sunil and H. Alamgir, Application of validation data for assessing spatial interpolation methods for 8-h ozone or other sparsely monitored constituents, Environ. Pollut., 2013, 178, 411–418 CrossRef CAS PubMed.
- H. Yu, A. Russell, J. Mulholland, T. Odman, Y. Hu and H. H. Chang, et al., Cross-comparison and evaluation of air pollution field estimation methods, Atmos. Environ., 2018, 179, 49–60 CrossRef CAS.
- D. W. Wong, L. Yuan and S. A. Perlin, Comparison of spatial interpolation methods for the estimation of air quality data, J. Exposure Anal. Environ. Epidemiol., 2004, 14, 404–415 CrossRef CAS PubMed.
- M. Miyasato, L. Tisopulos, J. Low, R. Bermudez and B. Vlasich, Annual Air Quality Monitoring Network Plan, 2016, pp. 1–28, available from: http://www.aqmd.gov/docs/default-source/clean-air-plans/air-quality-monitoring-network-plan/annual-air-quality-monitoring-network-plan.pdf Search PubMed.
- South Coast Air Quality Management District, Final 2016 Air Quality Management Plan, 2017 Search PubMed.
- California Air Resources Board, Trends Summary, 2023, available from: https://www.arb.ca.gov/adam/trends/trends1.php Search PubMed.
- W. Wang, C. Bruyere, M. Duda, J. Dudhia, D. Gill, M. Kavulich, et al., WRF Version 3.9 User's Guide, 2017, available from: https://www2.mmm.ucar.edu/wrf/users/docs/user_guide_V3/user_guide_V3.9/ARWUsersGuideV3.9.pdf Search PubMed.
- Z. Zhu, K. Do, C. E. Ivey and D. Collins, Assessing CMAQ Model Discrepancies in Vertical Ozone Profiles in a Heavily-Polluted Air Basin using UAV Measurements, Environ. Sci.: Atmos., 2023, in review Search PubMed.
- S. Tanvir, D. Ravichandran, C. Ivey, M. Barth and K. Boriboonsomsin, Traffic, Air Quality, and Environmental Justice in the South Coast Air Basin During California's COVID-19 Shutdown, in Pandemic in the Metropolis, ed. Loukaitou-Sideris A., Bayen A. M., Circella G. and Jayakrishnan R., Springer International Publishing, Cham, 2023, pp. 131–148, available from: https://link.springer.com/10.1007/978-3-031-00148-2_9 Search PubMed.
- S. Y. Hong, Y. Noh and J. Dudhia, A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes, Mon. Weather Rev., 2006, 134(9), 2318–2341 CrossRef.
- M. Huang, B. Huang and A. H. Huang, Implementation of 5-layer thermal diffusion scheme in weather research and forecasting model with Intel Many Integrated Cores, in, High-Performance Computing in Remote Sensing IV, ed. B. Huang, S. López and Z. Wu, Amsterdam, Netherlands, 2014, p. 924709 Search PubMed.
- D. Byun and K. L. Schere, Review of the Governing Equations, Computational Algorithms, and Other Components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Applied Mechanics Reviews, Appl. Mech. Rev., 2006, 59(2), 51–77 CrossRef.
- W. P. L. Carter, Development of the SAPRC-07 chemical mechanism, Atmos. Environ., 2010, 44(40), 5324–5335 CrossRef CAS.
- K. Do, M. Manasi, A. Kashfi Yeganeh, Z. Gao, C. L. Blanchard and C. E. Ivey, A Machine Learning Approach to Quantify the Impact of Meteorology on Tropospheric Ozone in the Inland Empire, CA, Environ. Sci.: Atmos., 2023, 3, 1159–1173 CAS.
- V. Rodriguez-Galiano, M. Sanchez-Castillo, M. Chica-Olmo and M. Chica-Rivas, Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines, Ore Geol. Rev., 2015, 71, 804–818 CrossRef.
- Ensemble Machine Learning, ed. C. Zhang and Y. Ma, Springer, New York, 2012, p. 329 Search PubMed.
- W. H. Brune, Introduction to Atmospheric Chemistry: Daniel J. Jacob; Princeton University Press, Princeton, NJ, 1999, 266pp., ISBN 0-691-00185-5, Atmos. Environ., 2001, 35(9), 1715 CrossRef CAS , available from: https://linkinghub.elsevier.com/retrieve/pii/S1352231000004325.
- S. C. Liu, D. Kley, M. McFarland, J. D. Mahlman and H. Levy, On the origin of tropospheric ozone, J. Geophys. Res., 1980, 85, 7546–7552 CrossRef CAS.
- J. F. Trousdell, D. Caputi, J. Smoot, S. A. Conley and I. C. Faloona, Photochemical production of ozone and emissions of NOx and CH4 in the San Joaquin Valley, Atmos. Chem. Phys., 2019, 19, 10697–10716 CrossRef CAS.
- L. Camalier, W. Cox and P. Dolwick, The effects of meteorology on ozone in urban areas and their use in assessing ozone trends, Atmos. Environ., 2007, 41(33), 7127–7137 CrossRef CAS , available from: https://www.sciencedirect.com/science/article/pii/S1352231007004165.
- Z. Gao, C. E. Ivey, C. L. Blanchard, K. Do, S. M. Lee and A. G. Russell, Separating emissions and meteorological impacts on peak ozone concentrations in Southern California using generalized additive modeling, Environ. Pollut., 2022, 307, 119503 CrossRef CAS PubMed , available from: https://linkinghub.elsevier.com/retrieve/pii/S0269749122007175.
- D. Jaffe, Role of Meteorology, Emissions and Smoke on Ozone in the South Coast Air Basin, Final Project Report for CRC Project A-118, Coordinating Research Council, Alpharetta, GA, 2020, available from: http://crcao.org/wp-content/uploads/2020/01/CRCProject-A-118-Final-Report_Jan2020.pdf Search PubMed.
- M. A. Oliver and R. Webster, Kriging: A method of interpolation for geographical information systems, Int. J. Geogr. Inf. Syst., 1990, 4(3), 313–332 CrossRef.
- J. K. Yamamoto, An alternative measure of the reliability of ordinary kriging estimates, Math. Geol., 2000, 32(4), 489–509 CrossRef.
- M. C. Seiler and F. A. Seiler, Numerical Recipes in C: The Art of Scientific Computing, Risk Anal., 1989, 9(3), 415–416 CrossRef.
- P. M. Bartier and C. P. Keller, Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW), Comput. Geosci., 1996, 22(7), 795–799 CrossRef CAS , available from:https://linkinghub.elsevier.com/retrieve/pii/0098300496000210.
- Z. Kebaili Bargaoui and A. Chebbi, Comparison of two kriging interpolation methods applied to spatiotemporal rainfall, J. Hydrol., 2009, 365(1–2), 56–73 CrossRef , available from: https://linkinghub.elsevier.com/retrieve/pii/S0022169408005726.
- N. R. Awang and N. A. Ramli, Preliminary Study of Ground Level Ozone Nighttime Removal Process in an Urban Area, Journal of Tropical Resources and Sustainable Science, 2017, 5(2), 83–88 Search PubMed.
- S. S. Brown, J. E. Dibb, H. Stark, M. Aldener, M. Vozella and S. Whitlow, et al., Nighttime removal of NOx in the summer marine boundary layer, Geophys. Res. Lett., 2004, 31(7), 2004GL019412 CrossRef.
- Y. Lyu, Q. Ju, F Lv, J. Feng, X. Pang and X. Li, Spatiotemporal variations of air pollutants and ozone prediction using machine learning algorithms in the Beijing-Tianjin-Hebei region from 2014 to 2021, Environ. Pollut., 2022, 306, 119420 CrossRef PubMed.
- H. A. Parker, S. Hasheminassab, J. D. Crounse, C. M. Roehl and P. O. Wennberg, Impacts of Traffic Reductions Associated With COVID-19 on Southern California Air Quality, Geophys. Res. Lett., 2020, 47(23), e2020GL090164 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ea00159h |
| This journal is © The Royal Society of Chemistry 2024 |