Investigating the influence of oriented external electric fields on modulating spin-transition temperatures in Fe(II) SCO complexes: a theoretical perspective†
Rupesh Kumar
Tiwari
 ,
Rajdeep
Paul
,
Rajdeep
Paul
 and
Gopalan
Rajaraman
and
Gopalan
Rajaraman
 *
*
Department of Chemistry, Indian Institute of Technology, Powai, Mumbai, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 12th August 2024
Abstract
Spin-crossover complexes, valued for their bistability, are extensively studied due to their numerous potential applications. A primary challenge in this molecular class is to identify effective methods to adjust the spin-transition temperature, which frequently falls outside the desired temperature range. This typically necessitates intricate chemical design and synthesis or the use of stimuli such as light or pressure, each introducing its own set of challenges for integrating these molecules into end-user applications. In this work, we aim to address this challenge using an oriented external electric field (OEEF) as one stimulus to modulate the spin-transition temperatures. For this purpose, we have employed both periodic and non-periodic calculations on three well-characterised Fe(II) SCO complexes, namely [Fe(phen)2(NCS)2] (1, phen = 1,10-phenanthroline), [Fe(bt)2(NCS)2] (2, bt = 2,2′-bi-2-thiazoline) and [Fe(py)2phen(NCS)2] (3, py = pyridine) possessing a similar structural motif of {FeN4N′2}. To begin with, DFT calculations employing the TPSSh functional were performed on complexes 1 to 3, and the estimated low-spin (LS) and high-spin (HS) gaps are 24.6, 15.3 and 15.4 kJ mol−1, and these are in the range expected for Fe(II) SCO complexes. In the next step, an OEEF was applied in the molecule along the pseudo-C2 axis that bisects two coordinated –NCS groups. Application of an OEEF was found to increase the Fe-ligand bond length and found to affect the spin-transition at the particular applied OEEF. While the HS state of 1 becomes the ground state at an applied field of 0.514 V Å−1, the LS state lies at a higher energy of 1.3 kJ mol−1. Similarly, complexes 2 and 3 also show the HS ground state at an applied field of 0.514 V Å−1, where the LS state stays at higher energies of 6.13 and 11.62 kJ mol−1, respectively. It is found that the overall change in enthalpy (ΔHHL) and entropy (ΔSHL) for the spin transition in the presence of OEEFs decreases upon increasing the strength of the applied field. The computed spin-transition temperature (T1/2) using DFT was found to be in close agreement with the experimentally reported values. It is estimated that on increasing the strength of the applied electric field, the T1/2 increases significantly. While the DFT computed T1/2 values for the optimised geometry of 1, 2 and 3 were found to be 134.6 K, 159.9 K and 111.4 K respectively, at the applied field of 0.6425 V Å−1T1/2 increases up to 187.3 K, 211.0 K and 184.4 K respectively, unveiling an hitherto unknown strategy to tune the T1/2 values. A limited benchmarking was performed with five additional exchange–correlation functionals: PBE, BLYP, B3LYP*, B3LYP, and PBE0. These functionals were found to be unsuitable for predicting the correct SCO behaviour for complex 2, and their behaviour under various electric fields did not improve. This emphasises the importance of choosing the correct functional at zero OEEF prior to testing them under various electric fields. Furthermore, calculations were performed with complex 1 adsorbed on the Au(111) surface. The formation of an Au–S bond during adsorption significantly stabilises the low-spin (LS) state, hindering the observation of spin-crossover (SCO) behaviour. Nonetheless, the application of an OEEF reduces this gap and brings the T1/2 value closer to the desired temperature. This offers a novel post-fabrication strategy for attaining SCO properties at the interface.
Introduction
Spin-crossover complexes (SCO) are a class of transition metal compounds characterised by their ability to switch between two distinct spin states: low spin (LS) and high spin (HS). This bistability is a key feature of SCO, allowing for manipulation through external stimuli like temperature, light, and magnetic fields. The transition between these spin states can have significant effects on the properties and behaviour of SCO compounds, making them promising candidates for various applications such as molecular switches, sensors, and data storage devices. The ability to control the spin state of these complexes offers exciting opportunities for the development of novel materials with tailored magnetic and electronic properties.1–7 The spin state switching of SCO molecules involves changes in various properties such as geometrical, optical, mechanical, magnetic and electric properties. Among others, the Fe(II) SCO molecules with an octahedral ligand field are found to be most common, where at lower temperatures they have a diamagnetic S = 0 spin state while at higher temperatures they occupy the paramagnetic HS state (S = 2), thanks to a smaller difference between the pairing energy and the crystal field splitting.8–11 The bistable nature of SCO molecules makes them prominent candidates for memory storage devices12–14 and room-temperature molecular spintronic devices.15–18 The existence of room-temperature magnetic moment in these molecules could also be exploited for molecular transistor-based quantum information devices.19–21 The technological applications of the SCO complex would require the immobilisation of the system by fabricating it on the surface.22–25 However as demonstrated in the majority of the cases, the SCO properties observed both in the solid state and in solution are not transferable on the surfaces.26 This is correlated with the nature of the surface, with metallic surfaces particularly prone to the loss of SCO properties while other surfaces such as MoS2/boron-nitride are shown to retain the properties in the examples studied.16,27,28 Recently, Sánchez-de-Armas and colleagues investigated the deposition of [Fe(phen)2(NCS)2] molecules on Au(111), Cu(111), and Ag(111) surfaces. Their findings suggest that this deposition process leads to larger energy differences between the high-spin (HS) and low-spin (LS) states (ΔEHL), thereby reducing the probability of the spin transition occurring.26 Another hurdle with the applications of SCO systems in electronic/spintronic devices is in choosing the source of external stimuli which induce the spin-crossover properties. Temperature/light as external stimuli are not always the preferred source as they cannot realize the controlled transition, and the full conversion from LS to HS states is challenging to achieve. Other stimuli generally employed, such as pressure, have practical implementation difficulties.29We have recently shown that an electric field can be employed to modulate the magnetic properties of lanthanide-based single-molecule magnets (SMMs) wherein if an oriented external electric field (OEEF) is applied along a particular bond, the strength of metal–ligand bonding can be manipulated. As the difference in energy between HS and LS complexes in the SCO system stems primarily from the metal–ligand bonding, we envisage that an OEEF can be a useful stimulus to affect the LS to HS transition.30 There are several advantages in employing an OEEF over the existing stimuli such as (i) a controlled and precise spin transition as electric fields/pulses can be delivered in short temporal space,31 (ii) a faster spin transition compared to thermal activation,32 (iii) requirement of lower energy inputs compared to thermal methods, (iv) greater compatibility with solid-state electronic devices33 and (v) facilitating the miniaturisation of electronic devices.34 In this regard, the work of Bousseksou and co-workers gains attention as they have shown recently that the application of an unidirectional electric field of 40 kV cm−1 (4.0 × 10−4 V Å−1) in [Fe(Htrz)2(trz)](BF4) within the thermal hysteresis region leads to a spin transition from the metastable HS to stable LS state.35 The applications of external electric fields have also been explored in other fields, such as in enhancing the magnetisation reversal barrier of SMMs,36–38 C–H bond activation,39 CO2 reduction,40 Diels–Alder reactions41 (Scheme 1a), spin-electric coupling,42etc. Previously, Medforth and co-workers have shown that the magnetic properties of manganese porphine alter upon adsorption on the Au(111) surface; however, this can be partially reversed by applying an electric potential.43
 | ||
| Scheme 1 (a) A schematic representation of the Diels–Alder reaction in the presence of a bias voltage from Coote and co-workers;74 (b) optimised structure of 1@Au(111) along the direction of the OEEF applied. Colour code: Au, golden; S, pale yellow; N, blue; C, grey. Hydrogen atoms are omitted for clarity. The green arrow shows the direction of the electric field. Fig. 1a reproduced from ref. 74 with permission from Springer Nature, copyright 2016. | ||
Despite such experimental precedents, how the metal–ligand bonding and hence the LS and HS gap vary with respect to the OEEF is not understood. More importantly, as this can be delivered on the surface once the molecules are deposited, it offers a rare opportunity to modulate molecules that do not exhibit SCO on the surfaces. With this in mind, our goal here is to perform a computational study of the SCO properties of [Fe(phen)2(NCS)2]44 (1, phen = 1,10-phenanthroline), [Fe(bt)2(NCS)2]45 (2, bt = 2,2′-bi-2-thiazoline) and [Fe(py)2phen(NCS)2]46 (3, py = pyridine) in the presence of OEEFs. We then went one step further and studied the adsorption of 1 on the Au(111) surface and explored the role of an OEEF at the molecule–surface interface (Scheme 1b). Particularly, we aim to answer the following intriguing questions: (i) is it possible to tune the spin-transition temperature using an OEEF? (ii) how do various thermodynamic parameters such as ΔH and ΔS behave in controlling the SCO in the presence of an OEEF? (iii) Is an OEEF a viable post-fabrication stimulus for tuning the spin-transition temperatures of molecules adsorbed on the Au(111) surface?
Computational methodology
Non-periodic density functional theory (DFT) calculations were performed using the Gaussian 09 suite of programs (Revision D.01).47 The geometries of all stationary points were relaxed with no restriction using the unrestricted TPSSh hybrid functional and def2SVP basis set unless otherwise mentioned.48 The choice of the methodology employed is based on the previous literature and benchmarking for similar molecules.49–52 To augment this further, we have also performed limited benchmarking of the functional in the presence of an electric field employing PBE,53 BLYP,54 B3LYP*,55,56 B3LYP,57 and PBE058 functionals with a varying percent of HF exchange (refs). Third-order dispersion corrections were implemented throughout the calculations to account for the non-covalent interactions.59Vibrational frequency calculations were performed to characterise the nature of all stationary points and to evaluate several energy corrections such as zero-point energy (ZPE), change in enthalpy (ΔH) and change in entropy (ΔS). The effect of solvation has been incorporated by employing the PCM solvation model60 using methanol as the solvent. The effect of the electric field has been incorporated in the calculations using the keyword “Field = M ± N” keyword available in the Gaussian suite. The electric field is applied along the Z-direction (FZ), i.e. along the line bisecting the S–S distance and crossing the iron atom (see Fig. 1a, b and c). The strength of the electric field has been varied between −0.01× and +25 × 10−4 au (−0.5140 V Å−1 to +0.5140 V Å−1) with a step size of 0.025 au (0.1285 V Å−1, note: 1 au = 51.4 V Å−1).
The adsorption behaviour of a single molecule on Au(111) surfaces was investigated through periodic DFT calculations utilising the Vienna ab initio simulation package (VASP) code.61–63 These calculations employed the Generalized Gradient Approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)64 exchange–correlation functional and projector-augmented wave (PAW)65 potentials. To describe the localised 3d orbitals of Fe, an effective Hubbard term (Ueff) of 1.7 eV was incorporated using Dudarev's approach.66 The used value, 1.7 eV, is consistent with Ueff values employed in previous calculations for the same SCO complex.67 When employing plane-wave basis sets, the DFT+U method emerges as a feasible substitute for computationally demanding hybrid approaches like the TPSSh functional. Extensive studies have demonstrated its efficacy in achieving a favourable balance between LS and HS states for SCO complexes involving both Fe(II) and Fe(III) metal centres.16,67,68 Valence electrons are described using a plane-wave basis set with a cut-off of 500 eV, and the Γ-point of the Brillouin zone is used.69 The optimised bulk parameters for the Au(111) unit cell are a = b = c = 2.94 Å. The Au (111) supercell consists of a three-layer slab made of a 6 × 6-unit cell (17.63 × 17.63 Å) with a 25 Å vacuum along the z direction to avoid the interaction between the cells (see Scheme 1b).
The Au atoms of the two lowest layers are kept fixed during optimisation, while atoms of the upper layer are relaxed. Electronic relaxation is carried out until the total energy change between two consecutive steps falls below 10−6 eV, while ionic relaxation continues until the Hellmann–Feynman forces drop below 0.025 eV Å−1. van der Waals interactions are incorporated using the Tkatchenko–Scheffler method.70 For every adsorption configuration, we optimise two distinct magnetic states: one with S = 0, LS and the other with S = 2, HS. The adsorption energies (Eads) are computed as Eads = Eads_molecule − (Eslab + Emolecule). The energies of the slab (Eslab) and the isolated molecule (Emolecule) are determined through geometry optimisation calculations utilising the same supercell as the adsorbed molecule. This approach minimises numerical inaccuracies. Hence, negative adsorption energies signify bound states. The OEEFs were applied along the Z-direction of the slab (similar to the pristine molecule) as developed by Neugebauer and Scheffler using the set of keywords EFIELD, IDIPOL and LDIPOL as implemented in the VASP suite.71 Here, EFILD describes the amount of the electric field applied in V Å−1, while IDIPOL suggests the direction of the applied electric field. LDIPOL = .TRUE. sets the dipole correction onto the potential to avoid the interactions between the periodically repeated images.72
Results and discussion
DFT optimised geometries and SCO properties of complexes 1, 2 and 3 in the absence/presence of OEEFs
To start with, we have performed non-periodic DFT optimisation of pristine molecules 1, 2 and 3 at the TPSSh/def2SVP level in the Gaussian suite in both LS and HS states (see Fig. 1a, b and c).49–51 The optimised geometrical parameters were in agreement with the X-ray structures (see Tables S1–S6†). As expected, an increase in Fe–N bond length of ∼0.2 Å was noted, as we move from LS to HS geometry. The d-orbital-based crystal field splitting Δ(t2g–eg) for the LS geometry in 1, 2 and 3 was found to be 4.14 eV, 3.90 eV and 4.15 eV, respectively (Table S7†). Similarly, in the HS geometry the gap was noted to be 1.18 eV, 1.40 eV and 1.08 eV, respectively. The crystal field suggests a stronger crystal field splitting in the LS due to stronger and shorter Fe–N bonds (see Fig. S1E–S6†). The ΔEHL gap of 35 kJ mol−1, 27 kJ mol−1 and 27 kJ mol−1 was found for complexes 1–3, respectively. This is relatively larger than the enthalpy of the bulk structure (Tables S8–S10†) reported from experiments and this could be associated with the methodology employed/the lack of solid-state effects in our calculations. The zero-point-energy (ZPE) correction to the electronic energy yields ΔEHL gaps of 24.6 kJ mol−1, 15.3 kJ mol−1 and 15.4 kJ mol−1 for 1–3, respectively. It is clear from this gap that ZPE correction favours the HS state by an average energy of 10.9 (11.7, 11.3) kJ mol−1 for 1 (2 and 3). The computed ΔHHL (ΔSHL) values for 1, 2 and 3 were found to be 5.2 kJ mol−1, 6.1 kJ mol−1, and 4.9 kJ mol−1 (86.3 J mol−1 K−1, 83.9 J mol−1 K−1, and 96.1 J mol−1 K−1) respectively. The computed ΔSHL values were found to be significantly overestimated compared to experiments, but the ΔHHL values are in reasonable agreement with experiments along with the predicted trend. The overestimation of the entropy corrections obtained from computed vibrations is one of the known problems of the DFT, irrespective of the nature of the exchange–correlation functionals52,73 (see Table 1).| ΔEHL + ZPE (kJ mol−1) | ΔSHL (J K−1 mol−1) | ΔSexpHL (J K−1 mol−1) | ΔHHL (kJ mol−1) | ΔHexpHL (kJ mol−1) | |
|---|---|---|---|---|---|
| 1 | 24.6 | 86.3 | 48.8 ± 0.7 | 5.2 | 8.6 ± 0.1 |
| 2 | 15.3 | 83.9 | 54.5 ± 4.0 | 6.1 | 9.6 ± 0.7 |
| 3 | 15.4 | 96.1 | 37.0 ± 5.0 | 4.9 | 3.7 ± 0.5 |
The Eigen-value plot for complexes 1–3, both in the HS and LS states, as depicted in Fig. S1–S6,† unveils intriguing insights into the ΔEHL gap. Specifically, a larger gap is observed for complex 1, while a similar gap is found for complexes 2 and 3, which is attributed to variations in the ligand field. Despite all three molecules having two –SCN ligands, differences arise due to the nature of the donor atoms. In complex 1, the phen ligand's nitrogen atom exerts a stronger ligand field, leading to the destabilisation of both the dx2−y2 and dz2 orbitals, resulting in a larger ΔEHL gap. Conversely, in complex 2, the bt ligand acts as a weaker donor, stabilising both orbitals but with a greater stabilisation observed for dx2−y2, causing a splitting of degeneracy. In complex 3, despite the presence of one phen ligand, the pyridinic nitrogen donation and associated bite angles lead to a weaker ligand field, with dx2−y2 being more stabilised than dz2. Consequently, both complexes 2 and 3 exhibit relatively smaller ΔEHL gaps compared to complex 1.
In the next step, we attempt to apply the OEEF on complexes 1–3. While various orientations are possible for applying the OEEF in 1–3, given the fact that all three molecules have two –NCS groups, on surfaces such as Au(111), the sulphur atom is expected to bind. Keeping this in mind, the experimental set-up that would deliver the OEEF similar to the one demonstrated in the work of Coote and co-workers74 in the cycloaddition reaction would involve the pseudo-C2 axis that passes between two –NCS groups. We have chosen this direction for the free molecule as well so that a direct comparison with the applied electric field can be made once the molecules are adsorbed on the Au(111) surface as described in the later part of the work.
An OEEF was applied along the line between the NCS group crossing through the Fe atom (+Z-direction, see Fig. 1a). It is found that in the presence of an electric field, Fe–N1 and Fe–N2 bond lengths increase significantly. The Fe–N1 and Fe–N2 bond lengths increase from ∼1.9 Å to ∼2.0 Å in all three complexes at an applied electric field of 0.025 au (0.1285 V Å−1 see Tables S1–S6†) for the LS state (see Fig. 2a).
When 0.6425 V Å−1 electric field is applied on LS geometries of 1–3, an average increase of 0.1 Å in the Fe–N bond length was noticed. The increase in the Fe–N bond length of 0.1 Å suggests that a spin transition is expected to occur at this applied electric field, as earlier experimental studies suggest a ballpark figure of ∼0.1–0.2 Å for the LS to HS transition for this type of complex (see Fig. 2b). To probe the SCO phenomenon induced by an electric field, the HS–LS energy gap was computed, which suggests that in complex 1, the HS state becomes a ground state at an applied electric field of 0.6425 V Å−1 (0.0125 au), while the LS state lies at 1.23 kJ mol−1 higher in energy. Similarly, complexes 2 and 3 also exhibit the HS state as a ground state at an applied electric field of 0.6425 V Å−1 and 0.5140 V Å−1 (0.0125 and 0.010 au) with the LS state staying at 9.54 and 0.51 kJ mol−1 higher in energy respectively (see Tables S8–S10†). The crystal field splitting also alters significantly due to the applied electric field. The t2g–eg gap of the LS state for 1, 2 and 3 decreases up to 3.95 eV, 3.71 eV, and 3.95 eV, respectively, at an applied field of 0.6425 V Å−1. This suggests that because of the low energy difference between t2g–eg, there could be a transition of an electron from the t2g to eg orbital. As the strength of an applied electric field increases, the ΔEHS–LS gap decreases. The ZPE correction to the electronic energy suggests that at 0.514 V Å−1 electric field, the HS state becomes a ground state while the LS state lies at a higher energy of 2 kJ mol−1, 6 kJ mol−1, and 12 kJ mol−1 in the case of 1, 2 and 3, respectively (see Fig. 3a–c). It is noted that while in the presence of an electric field, the entropy of both HS and LS states decreases, the decrease in the LS state, however, is found to be dominant, leading to an overall decrease in ΔSHL value. Similarly, the ΔHHL value also decreases upon increasing the strength of the applied field.
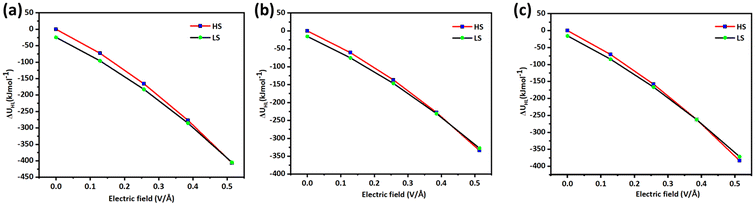 | ||
| Fig. 3 (a), (b) and (c) represent the ZPE corrected HS–LS gap (ΔUHL) in the presence of OEEFs for complexes 1, 2 and 3. | ||
To decipher the role of various exchange–correlation functionals in the HS–LS gap and how they behave under applied electric field conditions, we have performed a limited benchmarking employing GGA to hybrid functionals with a varying percent of HF exchange. We found that, unlike the TPSSh48 functional, others are not suitable for computing the SCO properties of the chosen molecules. The GGA functionals such as PBE53 and BLYP54 were found to overestimate the stability of the LS state yielding a ΔUHL gap of more than 50 kJ mol−1 while the hybrid functionals such as B3LYP57 and PBE058 with HF exchange 20% and 25%, respectively, were found to stabilise the HS state as the ground state yielding a ΔUHL gap of more than −30 kJ mol−1. However, the B3LYP*55,56 with 15% HF exchange behaves similarly to the TPSSh though the energy gap was found to be overestimated (48.2 kJ mol−1). We also computed spin-state energetics with different functionals employing OEEFs and found that independent of the functional employed, the application of 0.1 V Å−1 electric field was found to decrease the ΔUHL gap by ∼0.5–2.0 kJ mol−1 stabilising the HS state (see Fig. 4a, b and Table S11†). All functionals, except for TPSSh, predict no spin-crossover (SCO) behavior under any applied field conditions. This underscores the importance of selecting a suitable exchange–correlation functional that accurately mimics solid-state properties before examining their behavior under electric field conditions. Furthermore, the analysis indicates that the electric field responses are linear and generally consistent with the original results obtained under zero-field conditions.
Spin crossover entropies and transition temperature
The total entropy change (ΔSHL) associated with the LS–HS transition for the molecule under study was computed by DFT employing the same level of theory. The total change in entropy due to the transition could be divided into three parts: (i) electronic, (ii) vibrational and (iii) rotational. The electronic term depends on the change in spin multiplicity, which is constant throughout all considered systems and has a value of 13.38 J K−1 mol−1.75 The contribution to the change in entropy from the rotational degree of freedom will be very small as a change in structure due to the spin transition is minimal and therefore the moment of inertia for the HS and LS states will be similar. The significant contribution to the change in entropy is expected to arise from the vibrations, as vibrational frequencies alter significantly during the spin transition. The contribution to the entropy because of vibrations can be easily calculated within the harmonic approximations at finite temperature using the well-established statistical equation:76 | (1) |
Here, ωi denotes the angular frequency of the vibrational i and N denotes the number of atoms. ħ is the reduced Planck's constant, while R and k are the universal gas constant and Boltzmann constant, respectively.
Once the variation in entropy for both the spin states is estimated the transition temperature (T1/2) can be approximately calculated under the condition of thermodynamic equilibrium by the expression:
 | (2) |
The experimental reported value of T1/2 for 1 is 174 K as a sharp transition occurs at this temperature, while the T1/2↑ (cooling) and T1/2↓ (heating) for 2 (3) were reported to be 180.9 K and 170.2 K (116.5 K and 113.5 K), respectively. To estimate T1/2, Svib and hence ΔSHL were calculated in the range of temperatures from 100–200 K. From Fig. 5a–c, it is clear that the crossing point for ΔSHL and ΔHHL/T for the optimised geometry of 1, 2 and 3 is 134.6, 159.9 and 111.4 K which are T1/2 respectively. While the computed T1/2 is underestimated for 1 from the experimental reported value, for 2 and 3 the agreement is acceptable, given the fact that earlier reports often predict T1/2 values, which are orders of magnitude overestimated.77
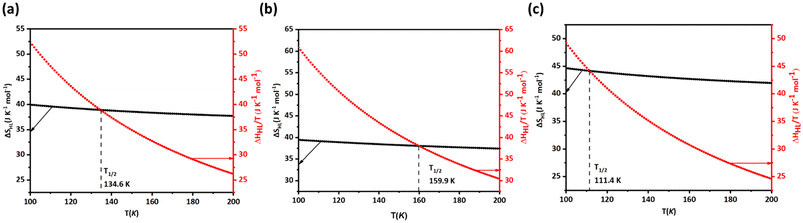 | ||
| Fig. 5 (a), (b) and (c) represent the variation of ΔSHL and ΔHHL/T versus T for 1, 2 and 3 respectively. Here, the crossing point represents the T1/2 of the respective molecule. | ||
In the next step, the same procedure is followed to estimate the T1/2 under an OEEF (see Table 2). From Table 2, it is clear that as the strength of the applied electric field increases, the T1/2 for all studied systems also increases.
| +FZ (V Å−1) | T 1/2 of 1 (K) | T 1/2 of 2 (K) | T 1/2 of 3 (K) |
|---|---|---|---|
| 00 (opt) | 134.6 | 159.9 | 111.4 |
| 0.1285 | 140.0 | 140.5 | 112.1 |
| 0.2570 | 140.3 | 147.1 | 117.9 |
| 0.3855 | 139.7 | 148.9 | 121.3 |
| 0.5140 | 136.7 | 177.1 | 126.6 |
| 0.6425 | 187.3 | 211.0 | 184.3 |
From the above table, we see that from the applied electric field of 0.5140 V Å−1 to 0.6425 V Å−1, the transition temperature increases significantly. This is because, under the electric field of 0.5140 V Å−1, the HS state becomes the ground state, while the LS state lies higher in energy. If we plot OEEF vs. T1/2, all complexes exhibit two regions, with a slight increase in T1/2 (smaller slop) as the field increases till the crossover points, after which a substantial increase is noted (a large slope; see Fig. 6). We also compared the relationship between the ΔEHL and T1/2 (see Fig. S7†). It is found that as the energy difference between the HS and LS states decreases, the T1/2 increases.
Effect of OEEFs on SCO properties of 1 adsorbed at the Au(111) surface (1@Au(111))
Technological applications require the immobilisation of SCO molecules on a substrate. It is found that the SCO properties of a molecule strongly modify after fabrication on the surface, and even a complete quenching of SCO properties occurs many times.26 After careful investigation of the effect of OEEFs on the pristine SCO molecules, we have first time computed their effect on surface-adsorbed SCO molecules using periodic DFT in the VASP package as developed by Neugebauer and Scheffler71 (see the Computational methodology section). To induce the SCO behaviour of molecule 1 at Au(111), an OEEF was applied along the direction perpendicular to the gold surface in positive as well as negative directions (Scheme 1b). The axis applied is similar to the axis chosen for the free molecule and keeping in mind the approach of the STM tip as shown earlier by the work of Coote and co-workers (see Scheme 1).74To start with, both HS and LS states were optimised on the Au(111) surface. The optimised geometries of HS and LS states were found to agree with the previously reported geometries(see Table S12†).26 The average Au–S and Fe–N bond lengths for the optimised geometry of 1LS@Au(111) and 1HS@Au(111) were found to be 2.51, 2.57 and 2.67, 2.71 Å respectively. The S–S distance, S–Fe–S and N–Fe–N undergo significant changes in both the spin states as NCS groups accommodate to bind the Au atoms (see Table S13†). The smaller Au–S distance in the LS state suggests that it gets stabilised on the substrate to a greater extent. This finding is also supported by the higher adsorption energy of the LS state. The Eads for HS and LS states was found to be −305 kJ mol−1 and −322 kJ mol−1. Also, the ΔEHL gap for 1@Au(111) was computed to be 96 kJ mol−1, which suggests that the spin transition of 1 at the Au(111) surface is not possible due to the larger HS–LS gap. We also computed the projected density of states for the bound and unbound state of complex 1. Fig. 7a presents the pDOS of the unbound complex 1 in the LS state. It is clear from Fig. 7a that the highest occupied band has contributions from the Fe 3d orbitals (t2g) and NCS ligands, while the lowest unoccupied band is mainly composed of the phen ligand and a little contribution from Fe 3d unoccupied orbitals (eg). The pDOS of 1LS@Au(111) (Fig. 7b) suggests that after the adsorption of the molecule on the surface, the Fe 3d orbitals and NCS ligand orbitals are getting stabilised by around 1 eV (see Fig. 7b). Furthermore, the difference density plot reveals that there is a significant charge transfer from the molecule to the surface in the case of the LS state and this is essentially associated with the Au–S interaction while in the HS state such charge transfer was found to be relatively small due to a longer Au–S distance (see Fig. 8).
To capture the effect of the electric field, we have performed several single-point calculations in the presence of an electric field at several points in both directions (±FZ, see Table 3). It is found that when the electric field is applied along the −FZ direction, the LS is further stabilised, increasing the ΔEHL gap. This gap decreases significantly when the field is applied along the +FZ direction. While the ΔEHL gap increases up to 228 kJ mol−1 at 0.514 V Å−1 along +FZ, it decreases till 49 kJ mol−1 at −0.514 V Å−1 along the −FZ direction. This trend suggests that applying an electric field along the −FZ direction could induce spin transition behaviour of 1 at the Au(111) surface, a phenomenon hard to witness in Fe SCO complexes with the only exception of FeII((3,5-(CH3)2Pz)3BH)2 exhibiting partial SCO at the Au(111) surface.78
| −FZ (V Å−1) | 0.1285 | 0.2570 | 0.3855 | 0.514 |
| ΔEHL (kJ mol−1) | 85.6 | 75.2 | 63.2 | 49.9 |
Conclusions
In this work, we have studied the effect of oriented external electric fields as external stimuli to induce the spin crossover transition on three complexes, i.e. [Fe(phen)2(NCS)2], [Fe(bt)2(NCS)2] and [Fe(py)2phen(NCS)2]. For the three studied complexes, we found that the application of an external electric field along the pseudo-C2 axis that passes between two –NCS groups induces the elongation of the Fe–N bonds, which eventually reaches the values corresponding to the HS state at any OEEF in the range of 0.4–0.5 V Å−1. The TPSSh computed spin transition temperature was found to be in close agreement with the experimentally reported values. It is observed that in the presence of an applied electric field, the transition temperature for 1, 2 and 3 increases from 134.6 K to 187.3 K, 159.9 K to 211.0 K and 111.4 K to 184.4 K, respectively, with the largest jump of the spin transition temperature seen in complex 3 (∼73 K enhancement at 0.64 V Å−1). A limited benchmarking performed with an additional five exchange–correlation functional suggests their non-suitability for predicting SCO behaviour, and they were found not to improve under electric field conditions.Also, it was observed that after the grafting of complex 1 on the Au(111) substrate, the high-spin (HS) low-spin (LS) gap increased significantly and it became less probable to observe the spin transition as the Au–S bond was found to strengthen the ligand field leading to large stabilisation of the LS state. This is also accompanied by a significant charge transfer. This rationalises the common observation that many Fe(II) complexes exhibiting SCO lose this property upon deposition on metallic surfaces like Au(111). However, our estimation suggests that applying oriented external electric fields along the pseudo-C2 axis to the molecule adsorbed on Au(111) alters the HS–LS gap. This method could potentially serve as a post-fabrication stimulus to induce the desired SCO, thereby paving the way for new developments in this field. To this end, we introduce a new method to adjust the spin-transition temperature in Fe(II) SCO complexes without the need for elaborate chemical design or encountering challenging conditions.
Data availability
The optimized geometries, Cartesian coordinates, tables with bond lengths, other structural data, and energy calculations are available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank SERB (SB/SJF/2019-20/12; CRG/2022/001697) for funding. RKT thanks CSIR, for the fellowship. RP thanks PMRF for the fellowship.References
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 CrossRef.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335 RSC.
- S. K. Kuppusamy and M. Ruben, Angew. Chem., Int. Ed., 2020, 59, 2–22 CrossRef.
- L. Kipgen, M. Bernien, F. Tuczek and W. Kuch, Adv. Mater., 2021, 33, 2008141 CrossRef CAS PubMed.
- M. Salimi, S. Fathizadeh and S. Behnia, Phys. Scr., 2022, 97, 055005 CrossRef CAS.
- G. Hao, A. T. N'Diaye, T. K. Ekanayaka, A. S. Dale, X. Jiang, E. Mishra, C. Mellinger, S. Yazdani, J. W. Freeland and J. Zhang, Magnetochemistry, 2021, 7, 135 CrossRef CAS.
- X. Zhang, P. S. Costa, J. Hooper, D. P. Miller, A. T. N'Diaye, S. Beniwal, X. Jiang, Y. Yin, P. Rosa and L. Routaboul, Adv. Mater., 2017, 29, 1702257 CrossRef PubMed.
- M. Gruber, T. Miyamachi, V. Davesne, M. Bowen, S. Boukari, W. Wulfhekel, M. Alouani and E. Beaurepaire, J. Chem. Phys., 2017, 146, 092312 CrossRef.
- T. Granier, B. Gallois, J. Gaultier, J. A. Real and J. Zarembowitch, Inorg. Chem., 1993, 32, 5305–5312 CrossRef CAS.
- M. Alexandra and J. DerekáWoollins, J. Chem. Soc., Dalton Trans., 1995, 1607–1613 Search PubMed.
- Y. Zhang, J. Chem. Phys., 2019, 151, 134701 CrossRef PubMed.
- A. Mosey, A. S. Dale, G. Hao, A. N'Diaye, P. A. Dowben and R. Cheng, J. Phys. Chem. Lett., 2020, 11, 8231–8237 CrossRef CAS PubMed.
- T. Ekanayaka, G. Hao, A. Mosey, A. Dale, X. Jiang, A. Yost, K. Sapkota, G. Wang, J. Zhang and A. N’Diaye, Magnetochemistry, 2021, 7, 37 CrossRef CAS.
- K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521 CrossRef CAS PubMed.
- F. J. Valverde-Muñoz, A. B. Gaspar, S. I. Shylin, V. Ksenofontov and J. A. Real, Inorg. Chem., 2015, 54, 7906–7914 CrossRef PubMed.
- Y. Zhang, J. Chem. Phys., 2020, 153, 134704 CrossRef CAS PubMed.
- B. Capozzi, J. Xia, O. Adak, E. J. Dell, Z.-F. Liu, J. C. Taylor, J. B. Neaton, L. M. Campos and L. Venkataraman, Nat. Nanotechnol., 2015, 10, 522–527 CrossRef CAS PubMed.
- R. K. Tiwari, R. Nabi, R. L. Kumawat, B. Pathak and G. Rajaraman, Inorg. Chem., 2023, 63, 316–328 CrossRef PubMed.
- G. Hao, R. Cheng and P. Dowben, J. Phys.: Condens. Matter, 2020, 32, 234002 CrossRef CAS PubMed.
- G. Hao, A. S. Dale, R. V. Chopdekar, R. J. Koch, X. Jiang, C. Mellinger, J. Zhang, R. Cheng, X. Xu and P. A. Dowben, J. Phys.: Condens. Matter, 2022, 34, 295201 CrossRef CAS PubMed.
- A. Dhingra, X. Hu, M. F. Borunda, J. F. Johnson, C. Binek, J. Bird, J.-P. Sutter, E. Delahaye, E. D. Switzer and E. Del Barco, J. Phys.: Condens. Matter, 2022, 34, 441501 CrossRef CAS PubMed.
- A. Pronschinske, Y. Chen, G. F. Lewis, D. A. Shultz, A. Calzolari, M. Buongiorno Nardelli and D. B. Dougherty, Nano Lett., 2013, 13, 1429–1434 CrossRef CAS PubMed.
- T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada and P. Ohresser, Nat. Commun., 2012, 3, 938 CrossRef PubMed.
- M. Gruber, V. Davesne, M. Bowen, S. Boukari, E. Beaurepaire, W. Wulfhekel and T. Miyamachi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195415 CrossRef.
- M. Gruber and R. Berndt, Magnetochemistry, 2020, 6, 35 CrossRef CAS.
- R. Sánchez-de-Armas and C. J. Calzado, Phys. Chem. Chem. Phys., 2023, 25, 21673–21683 RSC.
- N. Giaconi, A. L. Sorrentino, L. Poggini, G. Serrano, G. Cucinotta, E. Otero, D. Longo, H. Douib, F. Pointillart and A. Caneschi, Magnetochemistry, 2022, 8, 14 CrossRef CAS.
- S. Yazdani, J. Phillips, T. K. Ekanayaka, R. Cheng and P. A. Dowben, Molecules, 2023, 28, 3735 CrossRef CAS PubMed.
- A. Bousseksou, G. Molnár and G. Matouzenko, Eur. J. Inorg. Chem., 2004, 2004, 4353–4369 CrossRef.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- P. Kot, M. Ismail, R. Drost, J. Siebrecht, H. Huang and C. R. Ast, Nat. Commun., 2023, 14, 6612 CrossRef CAS PubMed.
- T. Nan, Y. Lee, S. Zhuang, Z. Hu, J. D. Clarkson, X. Wang, C. Ko, H. Choe, Z. Chen and D. Budil, Sci. Adv., 2020, 6, eabd2613 CrossRef CAS PubMed.
- G. Wang, T. Hu, Y. Xiong, X. Liu, S. Shen, J. Wang, M. Che, Z. Cui, Y. Zhang and L. Yang, Sci. Bull., 2023, 68, 1632–1639 CrossRef CAS PubMed.
- M. R. Akanda, M. Sohail, M. A. Aziz and A. N. Kawde, Electroanalysis, 2016, 28, 408–424 CrossRef CAS.
- C. Lefter, R. Tan, J. Dugay, S. Tricard, G. Molnár, L. Salmon, J. Carrey, W. Nicolazzi, A. Rotaru and A. Bousseksou, Chem. Phys. Lett., 2016, 644, 138–141 CrossRef CAS.
- A. Sarkar and G. Rajaraman, Chem. Sci., 2020, 11, 10324–10330 RSC.
- R. Nabi, R. K. Tiwari and G. Rajaraman, Chem. Commun., 2021, 57, 11350–11353 RSC.
- A. Swain, R. K. Tiwari, M. Khatua and G. Rajaraman, Inorg. Chem., 2023, 62, 9552–9562 CrossRef CAS PubMed.
- H. Hirao, H. Chen, M. A. Carvajal, Y. Wang and S. Shaik, J. Am. Chem. Soc., 2008, 130, 3319–3327 CrossRef CAS PubMed.
- A. Sen and G. Rajaraman, Inorg. Chem., 2023, 62, 2342–2358 CrossRef CAS PubMed.
- K. Gopakumar, S. Shaik and R. Ramanan, Angew. Chem., 2023, 135, e202307579 CrossRef.
- A. K. Boudalis, J. Robert and P. Turek, Chem. – Eur. J., 2018, 24, 14896–14900 CrossRef CAS PubMed.
- K. Leung, S. B. Rempe, P. A. Schultz, E. M. Sproviero, V. S. Batista, M. E. Chandross and C. J. Medforth, J. Am. Chem. Soc., 2006, 128, 3659–3668 CrossRef CAS PubMed.
- E. Koenig and K. Madeja, Inorg. Chem., 1967, 6, 48–55 CrossRef CAS.
- S. Kulshreshtha, R. Sasikala and E. König, Chem. Phys. Lett., 1986, 123, 215–217 CrossRef CAS.
- R. Claude, J. A. Real, J. Zarembowitch, O. Kahn, L. Ouahab, D. Grandjean, K. Boukheddaden, F. Varret and A. Dworkin, Inorg. Chem., 1990, 29, 4442–4448 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365 CrossRef CAS PubMed.
- O. S. Siig and K. P. Kepp, J. Phys. Chem. A, 2018, 122, 4208–4217 CrossRef CAS PubMed.
- M. t. s. Pápai, G. r. Vankó, C. De Graaf and T. Rozgonyi, J. Chem. Theory Comput., 2013, 9, 509–519 CrossRef PubMed.
- J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105 CrossRef CAS PubMed.
- K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729–4737 CrossRef CAS.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- S. Lebègue, S. Pillet and J. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 024433 CrossRef.
- M. Iskin and C. S. de Melo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024512 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS PubMed.
- P. J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125403 CrossRef.
- M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef CAS PubMed.
- A. Rudavskyi, C. Sousa, C. de Graaf, R. W. Havenith and R. Broer, J. Chem. Phys., 2014, 140, 184312 CrossRef PubMed.
- Y. Zhang, J. Chem. Phys., 2014, 141, 214703 CrossRef PubMed.
- S. De, S. Tewary, D. Garnier, Y. Li, G. Gontard, L. Lisnard, A. Flambard, F. Breher, M. L. Boillot and G. Rajaraman, Eur. J. Inorg. Chem., 2018, 2018, 414–428 CrossRef CAS.
- N. Montenegro-Pohlhammer, R. Sánchez-de-Armas and C. J. Calzado, Chem. – Eur. J., 2021, 27, 712–723 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimised geometries, cartesian coordinates, tables with bond lengths and other structural and energies, etc. See DOI: https://doi.org/10.1039/d4dt00808a |
| This journal is © The Royal Society of Chemistry 2024 |






