Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polarization-dependent effects in vibrational absorption spectra of 2D finite-size adsorbate islands on dielectric substrates†
Benedikt
Zerulla
 *a,
Marjan
Krstić
*a,
Marjan
Krstić
 b,
Shuang
Chen
c,
Zairan
Yu
c,
Dominik
Beutel
b,
Shuang
Chen
c,
Zairan
Yu
c,
Dominik
Beutel
 b,
Christof
Holzer
b,
Christof
Holzer
 b,
Markus
Nyman
b,
Markus
Nyman
 a,
Alexei
Nefedov
a,
Alexei
Nefedov
 c,
Yuemin
Wang
c,
Yuemin
Wang
 c,
Thomas G.
Mayerhöfer
c,
Thomas G.
Mayerhöfer
 d,
Christof
Wöll
d,
Christof
Wöll
 *c and
Carsten
Rockstuhl
*c and
Carsten
Rockstuhl
 *ab
*ab
aInstitute of Nanotechnology, Karlsruhe Institute of Technology (KIT), Kaiserstr. 12, 76131 Karlsruhe, Germany. E-mail: benedikt.zerulla@kit.edu; carsten.rockstuhl@kit.edu
bInstitute of Theoretical Solid State Physics, Karlsruhe Institute of Technology (KIT), Kaiserstr. 12, 76131 Karlsruhe, Germany
cInstitute of Functional Interfaces, Karlsruhe Institute of Technology (KIT), Kaiserstr. 12, 76131 Karlsruhe, Germany. E-mail: christof.woell@kit.edu
dLeibniz Institute of Photonic Technology, Albert-Einstein-Str. 9, 07745 Jena, Germany
First published on 12th April 2024
Abstract
In the last few years, infrared reflection–absorption spectroscopy (IRRAS) has become a standard technique to study vibrational excitations of molecules. These investigations are strongly motivated by potential applications in monitoring chemical processes. For a better understanding of the adsorption mechanism of molecules on dielectrics, the polarization-dependence of an interaction of infrared light with adsorbates on dielectric surfaces is commonly used. Thus, the peak positions in absorption spectra could be different for s- and p-polarized light. This shift between the peak positions depends on both the molecule itself and the dielectric substrate. While the origin of this shift is well understood for infinite two-dimensional adsorbate layers, finite-size samples, which consist of 2D islands of a small number of molecules, have never been considered. Here, we present a study on polarization-dependent finite-size effects in the optical response of such islands on dielectric substrates. The study uses a multi-scale modeling approach that connects quantum chemistry calculations with Maxwell scattering simulations. We distinguish the optical response of a single molecule, a finite number of molecules, and a two-dimensional adsorbate layer. We analyze CO and CO2 molecules deposited on CeO2 and Al2O3 substrates. The evolution of the shift between the polarization-dependent absorbance peaks is first studied for a single molecule, which does not exhibit any shifting at all, and for finite molecular islands, where it increases with increasing island size, as well as for an infinite two-dimensional adsorbate layer. In the latter case, the agreement between the obtained results and the experimental IRRAS data and more traditional three/four-layer model theoretical studies supports the predictive power of the multi-scale approach.
1 Introduction and summary
Infrared reflection–absorption spectroscopy (IRRAS) is one of the most important experimental techniques for characterizing molecular species on solid surfaces.1–4 Its application to metal surfaces is a rather mature field, with extensive experimental data for various molecules for virtually all metals in the periodic table.2,5–7 There is also a well-advanced theoretical understanding through state-of-the-art ab initio calculations concerning binding energies and vibrational frequencies.8,9In contrast, the application of IRRAS to oxides and dielectrics, in general, is much less developed. While experimental IR data for numerous adsorbates on oxide powder samples are widely available,10,11 IRRAS data for macroscopic single crystals of these materials are limited.10–13 This limitation originates from the particular optical properties of dielectrics and has hindered the experimental recording of IRRAS data on oxides until recently. The key difference between metals and semiconductors is the screening of the electric field by metal electrons, affecting the total infrared reflectivity and giving rise to the so-called surface selection rule governing IRRAS on metal surfaces.2,14 This rule states that for metals, usually, only vibrations with a component of the transition dipole moment (TDM) normal to the surface are detectable in IRRAS, while those parallel are screened by the metal electrons. This restriction does not apply to oxides and dielectrics in general, allowing IRRAS data collection using both s- and p-polarized light.15 Notably, IRRAS data for dielectrics show unique, rather counterintuitive characteristics, such as a splitting of peaks recorded for different polarizations.15,16
For weakly absorbing adsorbates, the variation in absorbance peak positions between s- and p-polarized light is minimal, often just a few wavenumbers. Reports on these polarization-dependent shifts are limited due to experimental challenges. Notably, Chabal and colleagues observed minor shifts in Si–H on Si (100) substrates,17 while the first data for oxides were reported by Yang et al.15 demonstrating significant effects of CO on ceria and another dielectric material, CaCO3. Moreover, for strong absorbers such as N2O, this shift can reach up to 20 cm−1.16
It is possible to study chemical processes by means of a combination of in situ spectroscopic methods and theoretical simulations. An instance is the investigation of metal nanoparticle oxidation with plasmonic optical spectroscopy in ref. 18 and 19. Recent developments in infrared spectroscopy have demonstrated the potential of IR spectroscopy, in particular diffuse reflectance IR spectroscopy (DRIFTS) for monitoring chemical processes on oxide powder surfaces,20 especially for operando studies21 in the context of heterogeneous catalysis. A crucial aspect is determining whether polarization-dependent shifts observed for adsorbate vibrational frequencies on single crystals are also present on smaller oxide particles, which could impact the interpretation of powder data. Traditional theoretical models, such as the three-layer model,15 have successfully replicated experimental findings on macroscopic single crystal surfaces but are inadequate for studying finite-size effects, as they assume a dielectric permittivity for a molecular layer being infinitely extended into two dimensions. For a molecular island which consists of only a small number of molecules, this assumption does not hold.
To address this lack of understanding of finite-size effects, we have adopted here a multi-scale ab initio modeling approach which connects density-functional theory (DFT) calculations to self-consistent scattering simulations based on Maxwell's equations, enabling the examination of an extended 2D adsorbate layer, or adlayer in brief, and finite-sized adsorbate islands. This approach aims to better understand the polarization-dependent shift and its relevance to different-sized particles, enhancing the interpretation of experimental data in real-world applications.
In ref. 15, it is explained on a macroscopic level that the reflectance of s-polarized light is determined by the imaginary part of the permittivity of the molecular film associated with the molecular axis. In contrast, the reflectance of the electric field component of the p-polarized light, which is vertical to the film, is determined by the imaginary part of the inverse of this permittivity. The difference between the maxima of both quantities explains the shift between the curves. The electric field component of the p-polarized light, which is vertical to the film, increases with the angle of incidence so that the reflectance of p-polarized light is mainly determined by this component.
Chabal presented that the dielectric permittivity of a 2D adsorbate layer can be phenomenologically modeled.22 This can be further used to compute the optical response of the layer deposited on a substrate. While infinite systems can be described using phenomenological means, as reported in ref. 15, one cannot use material parameters such as the dielectric permittivity for finite islands consisting of only a few molecules. This is because, in an exact sense, the dielectric permittivity can only be used to describe the optical material properties for a spatially infinitely extended media, see eqn (1) of ref. 23 for instance. While the materials of structures considerably larger than the wavelength of illumination continue to be well described by the dielectric permittivity, finite islands that are much smaller than the wavelength consisting of a small number of molecules do not cope with such assumptions.
Here, we demonstrate with our multi-scale ab initio modeling approach for CO and CO2 molecules and two different dielectric substrates that the shifts between the curves for s- and p-polarized light, related to the different reflection conditions for the s-polarized light and the vertical electric field component of the p-polarized light, increase with increasing size of the finite islands. In this regard, it is possible to explain the origin of the shift and to observe the transition from the shift for a single molecule and for small islands toward the shift for the case of the infinite adsorbate layer.
This article is structured as follows. In Section 2, the DFT simulations of the molecules are discussed. In Section 3, the optical response of islands of CO and CO2 molecules on dielectric substrates is analyzed. The conclusions of the article are presented in Section 4. Technical details are presented in the following three sections that serve as appendices. In Appendix A.1, the experimental measurements are described. Appendix A.2 explains the T-matrix formalism, and Appendix A.3 describes the three/four-layer model study.
2 DFT simulations of CO and CO2 molecules
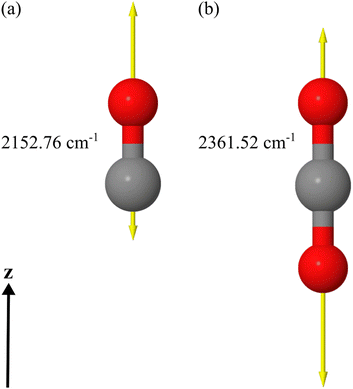
We apply a dedicated multi-scale approach to study the optical response of molecular islands on dielectric substrates. To this end, we calculate the optical properties of individual molecules at the quantum level using time-dependent density functional theory. From these considerations, we assign a polarizability to the molecules. By representing the individual molecule using the polarizability, we use a full-wave Maxwell solver based on a multiple-particle scattering formalism to study the optical response of an infinite periodic arrangement of molecules on a substrate or the response of a finite island of molecules. The finite 2D islands are also periodically arranged into a superlattice, but only for numerical convenience. The lattice constant of the superlattice will be sufficiently large to suppress interaction among the periodically arranged islands and sufficiently small so that diffraction effects do not play a role. Comparing the simulations with experiments, on the one hand, permits us to identify the microscopic origin of the different responses between s- and p-polarized light at oblique incidence studied in the past.15,17,21 On the other hand, by comparing the response between the infinite adsorbate layer and the finite islands, we can pinpoint the spatial extent of an adsorbate island necessary to consider it sufficiently representative of the bulk sample.In our examples, we use DFT to initially optimize the geometry of the molecular structure at the minimum on the potential energy surface of the electronic ground state (presented in Fig. 1(a) and (b)). Once the structure is obtained, we calculate the vibrational and electronic dynamic polarizabilities of the CO and CO2 molecules in the gas phase using a linear-response approach within the time-dependent density functional theory (TDDFT) framework. In the considered spectral domain (mainly 2100–2200 cm−1 for CO and 2300–2500 cm−1 for CO2), the vibrational dynamic polarizability is characterized by a single resonance in the z-component of the polarizability in the chosen coordinate system. The displacement vectors of this vibrational mode are also visualized in Fig. 1 for each molecule, along with an indication of its resonance frequency.
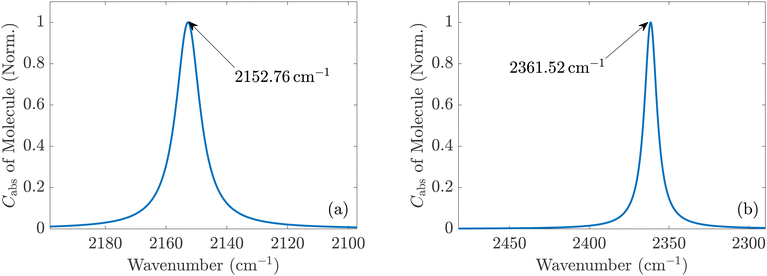
In the DFT calculations, performed with the development version of TURBOMOLE,24 we combined the hybrid PBE0 exchange–correlation functional25,26 and the def2-TZVP basis set.27 The complete damped dynamic polarizability tensors are calculated for the spectral range around the stretching vibrational mode wavenumber for each molecule. In the case of CO, we calculated all polarizability tensors using the DFT/TDDFT method for the range 2180–2285 cm−1 with a resolution of 0.1 cm−1. Calculations were done for all frequencies in the full spectral range from 1 to 4000 cm−1 for the CO2 molecule with the same resolution using the same methods. The damping was set to 5 cm−1 for the half-width at half-maximum of the Lorentzian line shape to simulate the broadening seen in the experiments. Due to the known fact that DFT simulations of single molecules in the gas phase overestimate the frequencies of the vibrational modes of the molecules, all wavenumbers of the spectra were scaled down by a factor of 0.962 to match the experimental values.28 The scaling shifted the spectral window for the CO molecule to the range covering 2097.16–2198.17 cm−1 as visualized in Fig. 2(a). For the CO2 molecule, we focused only on the spectral part presented in Fig. 2(b) after the scaling of wavenumbers was applied. The infrared absorption and the electronic background calculated by DFT in the spectral domain of interest are presented in Fig. S1(a) and (b) in the ESI.†
Finally, the obtained dynamic polarizability tensors are used to construct the T-matrices of an individual molecule. The T-matrix serves as the complete representation of the optical properties of a molecule. This T-matrix can then be used in a full-wave Maxwell solver to simulate the optical response of an infinite or periodically arranged finite island of molecules on a substrate. Please note that only the optical interaction between the molecules themselves and between the molecules and the substrate is considered in these simulations. These multi-scale simulations rely on a previously published workflow.29–31 The simulation of the optical response of the system is performed using the T-matrix-based program suite treams.32–34
Once the computational workflow is clear, we study the optical response of individual molecules in the gas phase and, afterward, the optical response from infinite or finite islands on a substrate. The configurations, we consider, strictly correspond to those considered in experiments already presented in the literature.15
3 Islands of CO and CO2 on dielectric substrates
We apply in this article, for the first time, a multi-scale optical modeling approach29–31 to study finite-size effects on the optical response of molecular islands supported by a dielectric substrate. The starting point for describing the optical response of the molecules is their T-matrix.3.1 Isolated molecules in the gas phase
The T-matrices of isolated molecules in the gas phase calculated with DFT express the vibrational Tvib and the electrical Tel response of the respective molecule in infrared wavelength regions. Although the molecules do not show electronic transitions in this spectral range, the less dispersive contribution of transitions from the visible to UV range has to be considered viaT = Tvib + Tel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . . | (1) |
It should be noted that translational and rotational molecular movements are excluded from the molecular degrees of freedom in the theoretical description. In Fig. 2(a) and (b), the absorption cross sections of a single CO and CO2 molecule with respect to a plane wave with a z-polarized electric field are shown, respectively. They are calculated from the extinction cross section Cext and the scattering cross section Csca,
Cabs = Cext − Csca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , , | (2) |
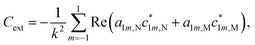 | (3) |
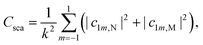 | (4) |
3.2 Islands of CO molecules supported on a substrate
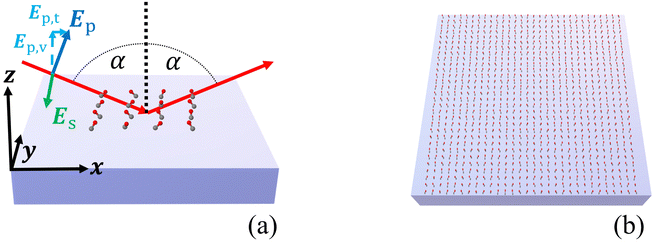
Once we know the spectral properties of the individual molecules, we can study the optical response after they are deposited as islands on top of a substrate. In this subsection, we discuss the case of CO, and in the following subsection, we discuss CO2.The numerical setup shown in Fig. 3(a) is constructed in analogy to the experimental setup for recording IRRAS data for adsorbates on oxide single-crystal surfaces.10,11 The substrate with the molecular adsorbate islands is illuminated from above with a plane wave under oblique incidence in the xz-plane. The angle of incidence was set to α = 80°. The incident plane wave is either s- or p-polarized. In our coordinate system, for normal incidence, s- and p- correspond to a polarization of the electric field along the y- and the x-axis, respectively. For oblique incidence, the polarizations are correspondingly rotated. It has to be noted that in the case of s-polarized light, the electric field of the incident light is perpendicular to the plane of the surface normal and the vector of incidence. In the case of p-polarized light, the electric field consists of a component Ep,v, which is perpendicular to the surface, and a component Ep,t, which is parallel to the surface, see Fig. 3(a).
We consider the adsorption of CO and CO2 on two different dielectric substrates: CeO2(111), characterized by a dielectric permittivity of 5.31,15 and α-Al2O3(0001), characterized by a dielectric permittivity of 3.075.36 These values correspond to refractive indices of 2.30 and 1.75, respectively. We have assumed constant optical properties for both substrates as the frequencies are far off any resonances. For the value of the dielectric permittivity of Al2O3, we have averaged the values of the principal axes from ref. 36, since the anisotropy in this frequency range is very small.
Fig. 3(b) schematically shows an infinite 2D adsorbate layer. In ref. 15, the experimental details of CO molecules on top of a ceria substrate were provided, and we consider here the molecular details as discussed there. Specifically, average tilt angles are assumed, namely 46° for CO, and of 60° for CO2. There might be two contributions to this tilt angle, a static tilt and a “dynamic” tilt caused by frustrated rotations that are thermally occupied.15 The estimated tilt angle for CO2 agrees well with the values found in the three/four-layer model, as we see in Appendix A.3. The azimuthal orientation of the molecule is assumed to be random, in agreement with experimental observations.15 To accommodate this random orientation in our simulations, we average the T-matrix of the molecule across all possible azimuthal angles to express a nominal molecule on the substrate. We will first consider infinite 2D adlayers with a square lattice and a lattice constant of 0.5 nm before considering finite islands. We set the distance between the center of mass of the CO molecules and the surface of the substrate to 0.3446 nm and for the CO2 molecules to 0.3581 nm. These values were computed from the distance between the center of mass and the atom attached to the surface and an estimate for the distance between this atom and the substrate.
To discuss the spectral details, we define the absorbance A for both polarizations as the difference of the negative logarithms of the reflectance R of the molecules on the substrate and the reflectance Rsubs of the bare substrate:
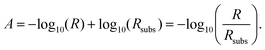 | (5) |
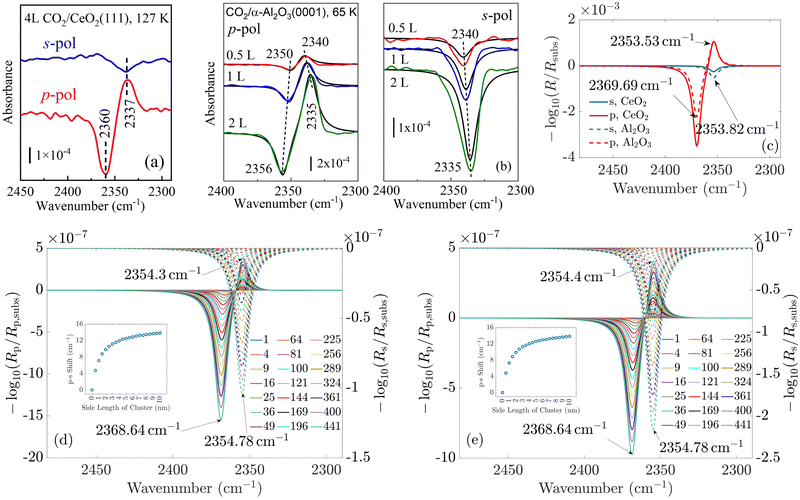
To validate our approach, we compare the optical response of CO molecules with previous experimental results and with theoretical work performed using a phenomenological three-layer model.15 In Fig. 4(a) and (b), the experimentally measured IRRAS data and the simulated spectra for CO molecules on the ceria substrate are displayed. Here, we assume initially an infinite periodic array of the molecule. This corresponds to the situation sketched in Fig. 3(b).
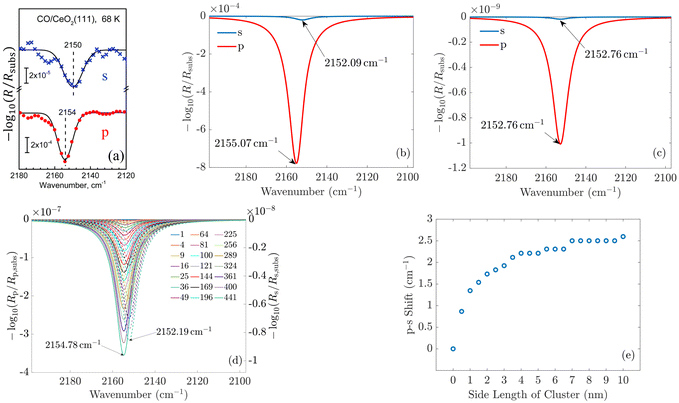 | ||
| Fig. 4 (a) Experimentally measured IRRAS data and (b) simulated spectra of CO molecules on a ceria substrate. The agreement between the measured and the simulated spectra is good. The less-intensive bands observed in the measurement originate from minority CO species adsorbed at defective regions of the surface (oxygen vacancies, step edges). (c) and (d) Show the simulated spectra of a single molecule on the substrate and for increasing island size, respectively. One observes that the shift between the p- and s-spectra shown in (e) increases from zero for one molecule to 2.6 cm−1. In (d), the p-spectra are solid lines, and the s-spectra are dashed lines. Fig. 4(a) is adapted with permission from ref. 15 under a CC BY-NC 3.0 Deed license. Copyright 2020, The Royal Society of Chemistry. | ||
In the experiment and the simulation, the optical response is characterized by a resonance in both s- and p-polarization that occurs in spectral proximity to the resonance of the isolated molecules.
In IRRAS experiments for CO and other molecular species adsorbed on metal surfaces, when the frequency of the IR light matches that of the adsorbed species, the reflectivity always decreases, leading to (positive) peaks in the absorbance spectra.22 On dielectric substrates, the situation is different. According to the three-layer model, for s-polarized light, the reflectivity always increases when hitting the resonance condition, i.e., in normal nomenclature, we would see “negative” absorbance peaks. For p-polarized light, the situation is more complicated, as the electric field consists of a component, which is tangential to the surface, and a component, which is vertical to the surface. The reflectivity can either reduce or increase in resonance, depending on the experimental conditions.10 It is important to note that our multi-scale simulations correctly reproduce the absorbance sign for all the cases studied in this work. In the following, we always refer to the position and total intensity of these “absorption peaks”.
We see a more intense absorbance peak (in the chosen logarithmic scale) for p-polarization than for s-polarization in both experiment and simulation. Generally, the spectra computed using our new ab initio approach are in excellent agreement with the experimental data. As the exact numbers are significant, we have included the information on the spectral position of the resonances in Fig. 4.
For CO molecules, the spectral difference between the resonance positions in s- and p-polarization amounts to 3 cm−1. The agreement of the peak positions between the experimentally measured spectra and the results obtained with our multi-scale ab initio approach is almost perfect. We note that the previous phenomenological description based on the three-layer model15 relies on free parameters such as the layer thickness and oscillator parameters, which are, to some extent, estimated and represent average properties of the probed region. In contrast to that, the present calculations rely on single transition dipoles which are optically coupled to each other via the multi-scale approach. To elaborate on this, in contrast to the macroscopic explanations provided by the three-layer model, the notion of bulk permittivity used to describe the molecular film does not enter our consideration. Instead, we consider the optical response at the level of an individual molecule.
In the next step, we consider adsorbate islands of different sizes to study finite-size effects. As noted in the introduction, such information is rather important for the interpretation of IR data recorded for CO and CO2 adsorbed on the facets exposed by oxide powder particles with sizes down to the tenths of a nm regime. We computed the optical response of finite molecular islands supported on an infinite 2D substrate. Within the variable-sized islands, the molecules continue to be arranged on a quadratic grid with a distance of 0.5 nm between neighboring molecules in the x- and y-directions, containing between 1 and 441 molecules, with a maximum size of 10 × 10 nm2. The T-matrix of the molecules is rotated by the respective tilt angle relative to the z-axis and averaged with respect to the xy-plane. For computational purposes, these square islands on the dielectric substrate are arranged into a periodic two-dimensional (2D) superlattice with a lattice constant of 500 nm. The large separation from adjacent islands guarantees, first, that the interaction between the islands can be neglected such that each 2D island responds individually and, second, that the s- and p-polarizations and their reflectance continue to be well-defined as the substrate is still infinitely extended. Please note that the chosen period of 500 nm continues to be much smaller than the wavelengths of interest. Therefore, only a zeroth diffraction order exists for the considered systems.
The simulated spectra for one molecule and for different sizes of the island are shown in Fig. 4(c) and (d), respectively. From these simulations, we extract the spectral position of the absorbance peaks as a function of the island size, see Fig. 4(d).
We observe no shift in peak position between the s- and the p-spectra for a single adsorbate molecule (Fig. 4(c)). The absorbance peaks are located precisely at the same spectral position. When there is more than one molecule on the island, a clear shift in the peak position occurs when going from s-polarized light to p-polarized light (Fig. 4(e)). This shift increases with the growing island size. For 2 × 2 islands (containing four molecules) with a size of 0.5 nm × 0.5 nm, the shift already amounts to 0.9 cm−1. For islands with 441 molecules, with a size of 10 nm × 10 nm, the shift is 2.6 cm−1. This value is already relatively close to the results for the infinite adlayer. Increasing the island size, which becomes computationally more and more demanding, would lead to a perfect match between the shift and the positions of the peaks between the finite 2D island and the infinite system. From this study, we conclude that on a microscopic level, the interaction between the molecules is necessary to observe a shift between the s- and p-spectra. For a single molecule, the shift does not occur since this molecule does not interact with another one. Based on these results, one can additionally conclude the number of molecules on average contained in an island by measuring the shift between the s- and p-spectra.
3.3 Islands of CO2 molecules supported on a substrate
In the following, we concentrate on CO2 molecules. In Appendix A.1, the experimental measurement is explained in more detail. In Fig. 5, we compare the spectra for CO2 molecules adsorbed on CeO2(111) and α-Al2O3(0001) single-crystal surfaces, respectively. In general, the results for ceria and Al2O3 are very similar. In Fig. 5(a) and (b), the experimentally measured spectra are shown. For comparison, Fig. 5(c) displays the simulation results under the assumption of an infinitely extended lattice. The agreement between the positions of the absorbance peaks in the measured and simulated spectra is good. For the theoretically simulated spectra, the polarization-dependent shift amounts to 15.87 cm−1, which is considerably larger than that for CO molecules (3 cm−1). This is expected, also the three/four-layer-model in combination with dispersion theory predicts that for larger coupling strengths the shift increases (see Fig. 5(b)).22 While the position and the shifts of the peaks slightly differ between the experimental and theoretical results, we observe the same trend in the measured and simulated spectra for both CeO2 and Al2O3 for which the s-peak is very close to the p-peak at lower wavenumbers. The experiment and the phenomenological study for Al2O3 shown in Fig. 5(b) reveals that the change in the amount of used molecules to cover the substrate shifts the peaks, explaining slight disagreements between the experiment and theory. The phenomenological study is explained in more detail in Appendix A.3. In comparison to the spectra for CO molecules, we observe here two peaks for the absorbance spectra related to the p-polarized illumination. In ref. 10 and 11, it is explained that, in general, one observes two peaks in the absorbance spectra of oblique incident p-polarized light for molecules adsorbed on dielectric substrates. One can be related to the vertical component, and the other can be related to the tangential component of the p-polarized electric field. The signs of the absorbance peaks depend on the refractive index of the substrate and the angle of incidence. They are always opposite to each other. We recall that the reflectance of the vertical component of the p-polarized electric field is determined by the inverse of the molecular film permittivity, and the reflectance of the tangential component of the p-polarized electric field, and the s-polarized field is determined by the permittivity. The permittivity and its inverse are, in general, shifted and their imaginary parts have different signs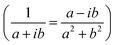 . Therefore, the spectra related to the p-polarized fields have, in general, two peaks, which are shifted from each other and have opposite signs.
. Therefore, the spectra related to the p-polarized fields have, in general, two peaks, which are shifted from each other and have opposite signs.
For CO2, we observe two peaks for the spectra related to the p-polarized field. They are not observable for CO, as the shift between the maxima of the permittivity and its inverse is very small, which can be seen when comparing the p- and s-curves. This also agrees with the oscillator strengths for CO2 in Table 1, which are considerably larger than for CO, see ref. 15. Therefore, the peak related to the tangential component of the p-polarized light is overlayed by the peak of the vertical component of the p-polarized light.
| S/cm−1 | γ/cm−1 |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0/cm−1
0/cm−1 |
ε r,a,∞ | ε r,c,∞ | θ/deg | d/Å | |
|---|---|---|---|---|---|---|---|
| 0.5 L | 519.3 | 14.28 | 2340.8 | 1.61 | 2.38 | 56.5 | 1.31 |
| 1 L | 645.5 | 13.09 | 2338.8 | 1.67 | 2.35 | 57.3 | 1.64 |
| 2 L | 845.5 | 12.72 | 2335.7 | 1.69 | 2.37 | 57.5 | 2.05 |
Lastly, we study the optical response of the CO2 molecular islands on the dielectric substrates as a function of their size. In Fig. 5(d) and (e), we observe, similar to the case of CO discussed above, that with increasing island size, the shift between the absorbance peaks in the s- and p-spectra increases until it is relatively close to the shift of the continuous adlayer. Again, we do not observe a polarization-dependent shift for a single adsorbate molecule. The study of the change of the coverage in Fig. 5(b) demonstrates the same behavior as with the increasing number of used molecules in the experiment, which corresponds to smaller distances between the molecules and, therefore, larger interaction, the shift of the peaks increases. Together with the other results, this finding strongly supports the predictive power of our multi-scale modeling approach.
4 Conclusions
We considered the optical response of differently sized islands of CO and CO2 molecules adsorbed on two prototypic oxidic substrates, CeO2(111) and α-Al2O3(0001). Our ab initio approach reproduces the experimentally observed shift between the absorbance peaks in the reflectance of s- and p-polarized plane waves. The experimentally measured and theoretically simulated results agree very well for an infinite adlayer. It was established that the shift value depends strongly on the properties of the adsorbates, but the dependence on the substrate is rather small. In the analysis of the finite systems, it was observed that the shift between the s- and the p-spectra vanishes for a single, isolated adsorbate molecule. However, already for islands consisting of four molecules, a shift is observed, which increases with increasing island size and converges to the value of the infinite systems already for island sizes of 10 nm × 10 nm. These results imply that with regard to the interpretation of infrared data recorded for oxide powders, size effects can be generally excluded for particle sizes above 10 nm.Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
B. Z. has contributed to the conceptualization, formal analysis, investigation, methodology, validation, visualization, and writing of the original draft. M. K. has contributed to the conceptualization, formal analysis, investigation, methodology, validation, visualization, and writing of the original draft. S. C. has contributed to the formal analysis, investigation, methodology, validation, visualization, and review of the original draft. Z. Y. has contributed to the formal analysis, investigation, methodology, validation, visualization, and review of the original draft. D. B. has contributed to the conceptualization, formal analysis, methodology, development of the software, and review of the original draft. C. H. has contributed to the conceptualization, formal analysis, methodology, development of the software, and review of the original draft. M. N. has contributed to the conceptualization, formal analysis, methodology, and review of the original draft. A. N. has contributed to the conceptualization, formal analysis, investigation, methodology, supervision, validation, visualization and writing of the original draft. Y. W. has contributed to the conceptualization, formal analysis, investigation, methodology, supervision, validation, visualization and writing of the original draft. T. G. M. has contributed to the conceptualization, formal analysis, investigation, methodology, validation, visualization and writing of the original draft. C. W. has contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization and writing of the original draft. C. R. has contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization and writing of the original draft.When it comes to the different investigations that found their way into the manuscript, the contributions are the following ones. The measurements have been performed by S. C. and Z. Y., supervised by A. N., Y. W., and C. W. The DFT-simulations have been performed by M. K., supported by C. H. The full-wave Maxwell solver simulations have been performed by B. Z., supported by D. B., M. N., and supervised by C. R. The three/four-layer-model studies have been performed by T. G. M.
Conflicts of interest
There are no conflicts to declare.A Appendices
A.1 Experimental section
The polarization-resolved IRRAS measurements were conducted using a dedicated ultrahigh vacuum (UHV) apparatus combining a state-of-the-art FTIR spectrometer (Vertex 80v, Bruker Optics GmbH, Germany) with a multi-chamber UHV system (PREVAC, Poland).10 Prior to the IRRAS experiments, the CeO2(111) (SurfaceNet, Germany) and α-Al2O3(0001) (Crystal GmbH, Germany) single crystals were prepared using standard procedures. The ceria surface was pretreated by repeated cycles of sputtering with 1 keV Ar+ and annealing at 800 K in an O2 atmosphere of 1 × 10−5 mbar to form a stoichiometric surface. The α-Al2O3(0001) single crystal was pretreated by repeated cycles of sputtering with 2 keV Ar+ and annealing at 850 K in an O2 atmosphere of 1 × 10−5 mbar. The cleanliness and oxidation states of the samples were monitored by grazing incidence XPS equipped with an R4000 electron energy analyzer (VG Scienta, Sweden). Exposure to CO and CO2 at low temperatures was achieved by backfilling the IR chamber using a leak-valve-based directional doser connected to a tube (2 mm in diameter) that terminated 3 cm from the sample surface. The exposure was carried out at 1.3 × 10−9 mbar in a few steps with a total exposure time of 40 s. Since the hot-cathode ionization gauge, which was used for exposure control, is placed close to the pump and at a 50 cm distance from the sample, the real exposure was, according to our internal calibration, about 100 times higher resulting in a coverage of 4 Langmuir (L). The base pressure during acquisition of IR spectra was 3 × 10−11 mbar. Polarization-resolved IRRA spectra were recorded with both s- and p-polarized light at a fixed grazing incidence of 80°. All spectra shown are difference spectra obtained by subtracting a reference spectrum recorded immediately before adsorption of CO2 or CO at 127 K (cooling with liquid nitrogen) or 65 K (cooling with liquid helium), respectively.A.2 T-matrix formalism
We use the T-matrix formalism to describe the scattering of light at the molecular islands.37 The T-matrix relates the multipolar coefficients of the scattered electric field of an object to the multipolar coefficients of the incident field. In the frequency domain, one expands the total electric field outside a scattering object at point r as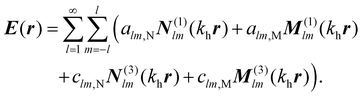 | (6) |
N
(1)lm(khr) and M(1)lm(khr) are incident and N(3)lm(khr) and M(3)lm(khr) are scattered vector spherical waves. For regular waves, N and M are transverse magnetic (TM) and transverse electric (TE) modes, respectively.30,32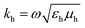 is the wave number with the permeability μh and the permittivity εh of the host medium. All quantities are frequency-dependent. However, we omit the frequency as an explicit argument for better readability. The expansion coefficients alm and clm are related by the T-matrix,
is the wave number with the permeability μh and the permittivity εh of the host medium. All quantities are frequency-dependent. However, we omit the frequency as an explicit argument for better readability. The expansion coefficients alm and clm are related by the T-matrix,
| c = Ta. | (7) |
To compute the dipolar T-matrix of a molecule, eqn (6) from ref. 30 is used,
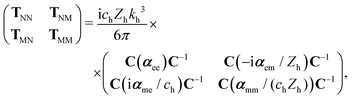 | (8) |
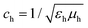 is the speed of light in the medium surrounding the molecules and
is the speed of light in the medium surrounding the molecules and 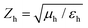 is the corresponding wave impedance.
is the corresponding wave impedance.
The optical response of a two-dimensional lattice of molecules is obtained by solving a multi-scattering problem, where the expansion coefficients a0 of the primary incident field and the expansion coefficients c0,tot of the scattered field of a molecule at the origin of the lattice are determined:32
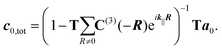 | (9) |
In eqn (9), R is a two-dimensional lattice vector, k|| is the component of the illuminating plane wave parallel to the lattice, and C(3)(−R) is a matrix which translates scattered vector spherical waves to incident vector spherical waves.
Additionally to solving eqn (9), one computes Q-matrices defined in eqn (6)–(9) and (12a) and (12b) in ref. 32 to describe the substrate and the interfaces between the different layers. The combination of the different Q-matrices enables the computation of the reflectance of the entire device.
To describe the scattering of an adsorbate island consisting of N molecules, the molecular island is represented by T-matrices Tnj, which relate the expansion coefficients of the incident field aj at particle j to the expansion coefficients of the total scattered field cn of particle n,
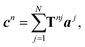 | (10) |
A.3 Three/four-layer-model study of CO2 on Al2O3
For the simulations and the fits of the experimental spectra, we assumed either a three-layer model for CO absorbed on ceria (semi-infinite incidence medium/absorbed CO/semi-infinite substrate) or a four-layer-model for CO2 adsorbed on Al2O3 (semi-infinite incidence medium/absorbed CO2/substrate/semi-infinite exit medium). The incidence medium and exit medium were assumed to be vacuum. Ceria was modelled with a scalar dielectric function, whereas Al2O3 was assumed to be oriented with the c-axis normal to the surface. For the adsorbed layer we employed a matrix approach to compute an orientation-averaged dielectric tensor according to eqn (11):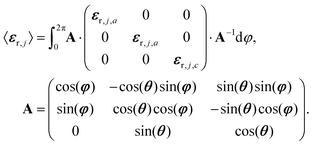 | (11) |
From eqn (11) an effective medium results that is uniaxial and whose optical axis is oriented perpendicular to the interface. The principal dielectric functions, εr,j,a and εr,j,c, were generated by the classical damped harmonic oscillator model,
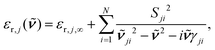 | (12) |
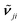 its position and γji the damping. The damping corresponds to the full-width at half-maximum. In comparison, the broadening was set to 5 cm−1 for the half-width at half-maximum for the TDDFT calculations, corresponding to 10 cm−1 for the full-width at half-maximum. εr,j,∞ represents the dielectric background which is due to modes in the UV/Vis spectral region.
its position and γji the damping. The damping corresponds to the full-width at half-maximum. In comparison, the broadening was set to 5 cm−1 for the half-width at half-maximum for the TDDFT calculations, corresponding to 10 cm−1 for the full-width at half-maximum. εr,j,∞ represents the dielectric background which is due to modes in the UV/Vis spectral region.
For the calculation of the reflectances, a unified 4 × 4 matrix formalism was employed.41,42 The experimental absorbance spectra −log10(Rs/Rs,subs) and −log10(Rp/Rp,subs) were baseline corrected by subtracting line functions that were fitted to the data points in non-absorbing regions between 2280 and 2420 cm−1. For the fits of the absorbance bands of CO2, all 7 parameters shown in Table 1 were allowed to vary freely. The distance between maximum and minimum in p-polarized spectra is proportional to the oscillator strength. Correspondingly, the oscillator strengths increase with the increasing number density of CO2 molecules. The damping of the oscillator decreases, but not substantially. The redshift of the oscillator position could be a polarization effect as it increases with number density.43 It is, however, somewhat surprising that neither the εr,a,∞ nor εr,c,∞ change with increasing density, since also the oscillator strengths in the UV/Vis should correlate with changes in density of CO2. The angles θ relative to the surface normal stay approximately constant, while the thickness of the layers d increases. However, it is not clear for a monomolecular or bimolecular layer what this value actually refers to, since we used the same 4 × 4 matrix formalism that is usually applied for homogenous solid layers. The oscillator parameters of Al2O3 were taken over from ref. 44.
Acknowledgements
M. K., D. B., C. W., and C. R. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy via the Excellence Cluster 3D Matter Made to Order (EXC-2082/1-390761711) and from the Carl Zeiss Foundation via the CZF-Focus@HEiKA Program. S. C., Z. Y., A. N., Y. W., and C. W. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - Project-ID 426888090 - SFB 1441. S. C. is grateful for a Postdoc fellowship donated by the Helmholtz Association and China Postdoctoral Council (OCPC). M. K., C. H., and C. R. acknowledge funding from the Volkswagen Foundation. A. N., C. W. and C. R. acknowledge support from the Helmholtz Association via the Helmholtz program “Materials Systems Engineering” (MSE). B. Z., M. N., and C. R. acknowledge support from the KIT through the “Virtual Materials Design” (VIRTMAT) project. We thank Dr Ivan Fernandez-Corbaton for fruitful discussions about scattering simulation methods. M. K. and C. R. acknowledge support from the state of Baden-Warttemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 Cluster) and the HoreKa supercomputer funded by the Ministry of Science, Research and the Arts Baden-Wattemberg and by the Federal Ministry of Education and Research.References
- W. Golden, D. S. Dunn and J. Overend, J. Catal., 1981, 71, 395–404 CrossRef CAS.
- R. G. Greenler, J. Chem. Phys., 1966, 44, 310–315 CrossRef CAS.
- F. M. Hoffmann, Surf. Sci. Rep., 1983, 3, 107–192 CrossRef CAS.
- K. Molt, Fresenius' Z. Anal. Chem., 1984, 319, 743–750 CrossRef CAS.
- M. Trenary, Annu. Rev. Phys. Chem., 2000, 51, 381–403 CrossRef CAS PubMed.
- K. Hinrichs, Reflection Absorption IR Spectroscopy (RAIRS), John Wiley & Sons, Ltd, 2011, ch. 23, pp. 367–375 Search PubMed.
- F. Zaera, Chem. Soc. Rev., 2014, 43, 7624–7663 RSC.
- P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518 CrossRef CAS.
- P. Deglmann and F. Furche, J. Chem. Phys., 2002, 117, 9535–9538 CrossRef CAS.
- Y. Wang and C. Wöll, Chem. Soc. Rev., 2017, 46, 1875–1932 RSC.
- C. Yang and C. Wöll, Adv. Phys. X, 2017, 2, 373–408 CAS.
- A. R. Head, O. Karslıoǧlu, T. Gerber, Y. Yu, L. Trotochaud, J. Raso, P. Kerger and H. Bluhm, Surf. Sci., 2017, 665, 51–55 CrossRef CAS.
- D. Zhang, C. Jansen, O. T. Berg, J. M. Bakker, J. Meyer, A. W. Kleyn and L. B. F. Juurlink, J. Phys. Chem. C, 2022, 126, 13114–13121 CrossRef CAS PubMed.
- R. G. Greenler, D. Snider, D. Witt and R. Sorbello, Surf. Sci., 1982, 118, 415–428 CrossRef CAS.
- C. Yang, W. Wang, A. Nefedov, Y. Wang, T. G. Mayerhöfer and C. Wöll, Phys. Chem. Chem. Phys., 2020, 22, 17129–17133 RSC.
- C. Yang, Y. Cao, P. N. Plessow, J. Wang, A. Nefedov, S. Heissler, F. Studt, Y. Wang, H. Idriss, T. G. Mayerhöfer and C. Wöll, J. Phys. Chem. C, 2022, 126, 2253–2263 CrossRef CAS.
- Y. J. Chabal and K. Raghavachari, Phys. Rev. Lett., 1985, 54, 1055–1058 CrossRef CAS PubMed.
- D. Albinsson, S. Nilsson, T. J. Antosiewicz, V. P. Zhdanov and C. Langhammer, J. Phys. Chem. C, 2019, 123, 6284–6293 CrossRef CAS PubMed.
- S. Nilsson, D. Albinsson, T. J. Antosiewicz, J. Fritzsche and C. Langhammer, Nanoscale, 2019, 11, 20725–20733 RSC.
- C. Wöll, ACS Catal., 2020, 10, 168–176 CrossRef.
- L. Caulfield, E. Sauter, H. Idriss, Y. Wang and C. Wöll, J. Phys. Chem. C, 2023, 127, 14023–14029 CrossRef CAS.
- Y. Chabal, Surf. Sci. Rep., 1988, 8, 211–357 CrossRef CAS.
- R. Venkitakrishnan, Y. Augenstein, B. Zerulla, F. Z. Goffi, M. Plum and C. Rockstuhl, New J. Phys., 2023, 25, 123014 CrossRef.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- CCCBDB Precomputed vibrational scaling factors, 2022, https://cccbdb.nist.gov/vibscalejust.asp.
- B. Zerulla, M. Krstić, D. Beutel, C. Holzer, C. Wöll, C. Rockstuhl and I. Fernandez-Corbaton, Adv. Mater., 2022, 34, 2200350 CrossRef CAS PubMed.
- I. Fernandez-Corbaton, D. Beutel, C. Rockstuhl, A. Pausch and W. Klopper, Chem. Phys. Chem., 2020, 21, 878–887 CrossRef CAS PubMed.
- B. Zerulla, C. Li, D. Beutel, S. Oßwald, C. Holzer, J. Bürck, S. Bräse, C. Wöll, I. Fernandez-Corbaton, L. Heinke, C. Rockstuhl and M. Krstić, Adv. Funct. Mater., 2023, 2301093 CrossRef.
- D. Beutel, A. Groner, C. Rockstuhl and I. Fernandez-Corbaton, J. Opt. Soc. Am. B, 2021, 38, 1782–1791 CrossRef.
- D. Beutel, Treams, https://github.com/tfp-photonics/treams.git, 2023.
- D. Beutel, I. Fernandez-Corbaton and C. Rockstuhl, Comp. Phys. Commun., 2024, 297, 109076 CrossRef CAS.
- M. I. Mishchenko, L. D. Travis and A. A. Lacis, Scattering, Absorption, and Emission of Light by Small Particles, Cambridge University Press, Cambridge, 2002 Search PubMed.
- M. Schubert, T. E. Tiwald and C. M. Herzinger, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8187–8201 CrossRef CAS.
- P. Waterman, Proc. of IEEE, 1965, 53, 805–812 Search PubMed.
- M. Kehry, Y. J. Franzke, C. Holzer and W. Klopper, Mol. Phys., 2020, 118, e1755064 CrossRef.
- M. I. Mishchenko, L. D. Travis and D. W. Mackowski, J. Quant. Spectrosc. Radiat. Transfer, 1996, 55, 535–575 CrossRef CAS.
- D. W. Mackowski, J. Opt. Soc. Am. A, 1994, 11, 2851–2861 CrossRef.
- T. G. Mayerhöfer, O. Ilchenko, A. Kutsyk and J. Popp, Appl. Spectrosc., 2022, 76, 92–104 CrossRef PubMed.
- T. G. Mayerhöfer, Wave Optics in Infrared Spectroscopy - Theory, Simulation and Modelling, Elsevier, Philadelphia, 2024 Search PubMed.
- T. G. Mayerhöfer, O. Ilchenko, A. Kutsyk and J. Popp, Appl. Spectrosc., 2022, 76, 92–104 CrossRef PubMed.
- A. S. Barker, Phys. Rev., 1963, 132, 1474–1481 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00860j |
| This journal is © the Owner Societies 2024 |