Open Access Article
Open Access ArticleHomochiral vs. heterochiral preference in chiral self-recognition of cyclic diols†
Jennifer
Dupont
a,
Beppo
Hartwig
 b,
Katia
Le Barbu-Debus
b,
Katia
Le Barbu-Debus
 a,
Valeria
Lepere
a,
Valeria
Lepere
 a,
Regis
Guillot
a,
Regis
Guillot
 c,
Martin A.
Suhm
c,
Martin A.
Suhm
 b and
Anne
Zehnacker
b and
Anne
Zehnacker
 *a
*a
aInstitut des Sciences Moléculaires d’Orsay (ISMO), CNRS, rue André Rivière, Université Paris-Saclay, F-91405 Orsay, France. E-mail: anne.zehnacker-rentien@universite-paris-saclay.fr
bInstitut für Physikalische Chemie, Georg-August-Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany
cInstitut de Chimie Moléculaire et des Matériaux d’Orsay (ICMMO), 17 Av. des Sciences Université Paris-Saclay, F-91405 Orsay, France
First published on 12th March 2024
Abstract
The structure and clustering propensity of a chiral derivative of cis-1,2-cyclohexanediol, namely, 1-phenyl-cis-1,2-cyclohexanediol (cis-PCD), has been studied under supersonic expansion conditions by combining laser spectroscopy with quantum chemistry calculations. The presence of the phenyl substituent induces conformational locking relative to cis-1,2-cyclohexanediol (cis-CD), and only one conformer of the bare molecule is observed by both Raman and IR-UV double resonance spectroscopy. The homochiral preference inferred for the dimer formation at low enough temperature is in line with the formation of a conglomerate in the solid state. The change in clustering propensity in cis-PCD relative to trans-1,2-cyclohexanediol (trans-CD), which shows heterochiral preference, is explained by the presence of the phenyl substituent rather than the effect of cis-trans isomerism. Indeed the transiently chiral cis-CD also forms preferentially heterodimers, whose structure is very close to that of the corresponding trans-CD dimer.
Introduction
Life is characterised by a strong homochiral preference: all the proteogenic amino acids are of identical absolute configuration, and so are all the sugars, and the reason for the initial dissymmetry between the two enantiomers is still under debate.1–3 It is commonly admitted that non-covalent interactions play a major role in shaping the homochirality of biomolecules. For example the helical structure of an all-L polyalanine peptide is disrupted by the mere presence of a D residue.4 The solid state of chiral molecules contrasts with biomolecules as most of the racemic mixtures crystallise in the form of racemates, in which the unit cell contains both enantiomers that are intimately mixed.5 Racemic mixtures that crystallise as conglomerate are scarcer. They are estimated to form about 5–10% of the total racemic crystals, although DFT-based calculations suggest that thermodynamic conglomerate abundance should actually reach 20% or more.6,7 In these conglomerates, separate crystals of the two enantiomers are formed, which can be further manually separated. An example of such conglomerates is the tartrate salts at the basis of the discovery of chirality by Pasteur.8Several attempts have been reported to assess the homochiral or heterochiral preference in molecular pairs isolated in the gas phase.9,10 The gas-phase dimer structure often differs from that observed in the solid, because the isolated dimer tries to optimise the number of hydrogen bonds. In particular, alcohols or substituted alcohols have been the subjects of many studies, for example the 1-indanol11 or fluoroethanol dimer.12 Bifunctional compounds are especially interesting in this respect as they provide more anchoring points that are expected to favour chiral discrimination.13 Examples include systems with permanent chirality like the methyllactate14–16 or the protonated 1-amino-2-indanol dimers17 or systems showing transient chirality like vicinal diols or aminoalcohols. In the latter systems, the two enantiomers are interconverted by torsion around a CC bond. Tunnelling between the two enantiomers manifests itself by the splitting of the transitions observed in microwave spectroscopy.18 The torsion can be blocked by dimer formation, which allows observing both homochiral and heterochiral dimers, with a preference for heterochiral pairing in the case of the 1,2-ethanediol dimer, whose preferred structure is achiral with S4 symmetry.19 In contrast, the aminoethanol dimer shows homochiral preference.20 Trends for homochiral aggregation are also observed for transiently chiral substituted alcohols such as the trifluoroethanol dimer or large clusters of phenyl-methanol, up to the tetramer.21,22
Information has been gained recently on the chiral preference in the jet-cooled dimer of 1,2-ethanediol, by comparison with one of its cyclohexane analogues, the permanently chiral trans-1,2-cyclohexanediol (trans-CD).23trans-CD shows heterochiral pairing preference in the gas phase due to the formation of a strongly bound dimer optimising the number of hydrogen bonds. The isolated 1,2-ethanediol dimers form the same hydrogen-bond pattern, hence the same heterochiral preference in the gas phase. Heterochiral preference is also observed in the trans-CD solid, which is a racemate.24
In contrast to trans-CD, cis-1,2-cyclohexanediol (cis-CD) is only transiently chiral because of the plane of symmetry that intersects the C1C2 bond when the carbon skeleton is made planar. Moreover, the cis geometry of the substituents will influence the strength of the intramolecular hydrogen bond relative to trans-1,2-cyclohexanediol. trans CD is energetically favoured by 1.9 kJ mol−1 in terms of zero-point-corrected energy at the B3LYP-D3(BJ,abc)/ma-def2-TZVP level of theory. Adding a phenyl substituent results in 1-phenyl-cis-1,2-cyclohexanediol (cis-PCD) that is permanently chiral. Dimer formation and chiral preference are expected to differ between trans-CD, cis-CD and cis-PCD, and may be influenced by the competition between intra- and intermolecular hydrogen bonds formation.12,25 On the other hand, the aromatic π-system adds both steric hindrance and dispersion interactions in cis-PCD and acts as an efficient hydrogen bond acceptor.26 These factors result in a wealth of expected hydrogen bond patterns in the aromatic dimer.
Here, we report the spectroscopic properties of cis-PCD and its dimers under supersonic expansion conditions, as studied by resonance-enhanced multi-photon ionisation (REMPI), Raman scattering, and conformer specific vibrational spectroscopy. The vibrational spectra of the homochiral and heterochiral dimers obtained by double resonance IR-UV spectroscopy are interpreted with the help of density functional theory (DFT) calculations to shed light on the diastereomeric preference in cis-PCD. The interaction patterns observed in the gas phase are compared to those existing in the solid. The structures found thereby are compared to the non-aromatic systems cis- and trans-CD.
Experimental and theoretical methods
1. Experimental methods
cis-PCD (99%) was purchased from Santa Cruz Biotechnology (USA). cis-CD (99%) was bought from Sigma Aldrich. Both samples were used without further purification.The Raman spectroscopy results were obtained using a slit jet at the Institut für Physikalische Chemie. In the following, we will give a description of the measurement conditions for cis-PCD. When conditions differ between cis-PCD and cis-CD, the values for the latter will be given in parentheses. Pure He was used as a carrier gas and continuously expanded at a stagnation pressure of 0.4 bar (1.4 bar for cis-CD) into low vacuum (∼ a few 10−1 mbar). Raman scattering was obtained from a 532 nm cw laser operated at 24 W, with the expansion being irradiated orthogonally 1 mm (1.25 mm for cis-CD) downstream of the nozzle. The scattered light was collected by a photo lens perpendicular to the laser, focussed towards a Czerny–Turner-monochromator and detected by a LN2 cooled CCD camera. An exposure time of 4 min was used with 18 such exposures being averaged (5 for cis-CD) to yield the experimental spectrum. The spectrum was calibrated using Ne lines. The vapour pressure of the diol was enhanced in a heatable saturator kept at 395 K (365 K for cis-CD) with the following tubing and nozzle being heated to 425 K (395 K for cis-CD) to avoid condensation.27
The electronic and vibrational spectroscopy results for cis-PCD were obtained using a pinhole jet at ISMO. The pulsed supersonic beam was produced by expanding 2 bar of helium seeded with the enantiopure or racemic cis-PCD into high vacuum (∼10−6 mbar) through a 200 μm pulsed nozzle (General Valve – Parker).28cis-PCD was put in an oven just prior the expansion and heated at 365 K for the study of the monomer and 400 K for that of the dimer. Mass-resolved electronic spectra were obtained using one-colour resonance-enhanced two-photon ionisation (RE2PI). The UV source (0.02 cm−1 resolution) was generated by doubling the output of a dye laser (Sirah equipped with C540A dye) pumped by the second harmonic of a Nd:YAG laser (Quanta Ray, Spectra Physics). The UV laser beam was mildly focused by a 1 m focal length lens and crossed the skimmed supersonic beam (skimmer of 500 μm diameter) in the interaction zone of a linear time-of-flight (TOF) mass spectrometer (Jordan, one-meter length). The ion signal was detected by a microchannel plate detector (RM Jordan, 25 mm diameter), averaged by an oscilloscope (Lecroy wavesurfer), and processed through a personal computer.
Vibrational spectra were recorded using the IR-UV double resonance method.29,30 A slightly focused (0.5 m focal length lens) IR laser beam (OPO/OPA – Laser Vision – 3 cm−1 resolution) was counter-propagated relative to the UV laser beam and superimposed to it in the source region. After fixing the UV probe laser on selected vibronic transitions of the electronic spectrum, the wavelength of the IR pump laser was scanned in the 3 μm region. The IR absorption was then detected as a depletion of the UV-induced ion signal. The IR pulse was triggered ∼80 ns before the UV pulse to record ground-state vibrational spectra. Synchronisation between the lasers was controlled by a homemade gate generator. The IR spectra were recorded resorting to an active baseline scheme, by measuring the difference in ion signal produced by successive UV laser pulses (one without and one with the IR laser pulse present).31
X-ray diffraction data for compound cis-PCD were collected following the protocol described in the ESI.†
2. Theoretical methods
The potential energy surfaces (PES) of the cis-PCD monomer, its dimers, and those of cis-CD were first explored using the OPLS-2005 force fields with the advanced conformational search implemented in the MacroModel suite, a part of the Schrödinger package.32 Geometry optimization of the structures found thereby with energy below 21 kJ mol−1 and vibrational frequencies calculation were performed using the B3LYP functional combined to the 6-311++G(d,p) basis set,33 and including D3BJ dispersion corrections.34,35 The minimum energy monomers resulting from the PES exploration yield the structures that were observed experimentally (vide infra). Because the structure of the dimers results from a competition between inter- and intra-molecular hydrogen bonds, their formation depends on multiple factors including crossing energy barriers. For this reason, we also included additional dimer structures that would be above 21 kJ mol−1 in the exploration or missed with the force field used, for example hydrogen bond patterns observed in similar systems like trans-CD. These structures were optimised in the same manner. The vibrational spectra were simulated in the frame of the double harmonic approximation at the same level of theory and the absence of imaginary frequencies was checked for all minima found. The harmonic frequencies were scaled by 0.952 to correct for anharmonicity, functional deficiencies and basis set incompleteness.36,37The relative stability of the different conformers was assessed by comparing their relative zero-point-corrected energies ΔE0 and their standard Gibbs free energies ΔG (we suppress the standard sign because only differences are relevant in the present work) relative to the most stable conformation at 300 K. Comparison between ΔE0 and ΔG is especially relevant for dimers, because they are formed at a temperature somewhere between that of the nozzle and the temperature where the expansion is probed. The difference between ΔE0 and ΔG may be viewed as a rough estimate of the uncertainty in the predicted energy ranking. The deformation energy was calculated as the difference in energy between the structure of the monomer in the complex and that of its most stable form.25,38,39 The deformation energy mentioned in what follows is the sum of that of the two monomers.
The nature of the first two electronic excited states and the vertical transition energies were calculated at the TD-DFT level at the same level as the ground state, using 4 excited states. The difference in electronic densities was calculated from the cube files generated by the Gaussian software and using the “cubman” facility. The resulting densities were plotted using the VMD software with an isovalue of 0.001. All these calculations were performed with the Gaussian Package (Version 16 Rev. B.01).40
For the sake of comparison with previously published work and sensitivity analysis with respect to small computational details like three-body-inclusive dispersion correction and basis set variants, the energies and harmonic frequencies were also calculated at the B3LYP-D3(BJ,abc)/ma-def2-TZVP41,42 level using the ORCA (version 5.0.3) program package.43 The theoretical spectra were simulated using the harmonic frequencies scaled by 0.963. Furthermore, a recently proposed empirical model45 was applied to the cis-PCD monomer to account for density functional deficiencies and the missing anharmonicity. Specifically, a correction of −146.0 cm−1 was used to account for the degree of substitution at the 1,2-diol subunit as well as an additional correction of −8 cm−1 due to the phenyl group. In the case of the PCD dimers, for which highly anharmonic low-frequency modes are expected, the Gibbs energy calculations were also conducted using the Quasi Rigid Rotor Harmonic Oscillator (QRRHO) approximation developed by Grimme,44 as a second measure for the uncertainty involved in such calculations. The results and discussion that follow are based on the B3LYP-D3(BJ,abc)/ma-def2-TZVP calculations, unless specified otherwise. The B3LYP-D3BJ/6-311++G(d,p) results are given in the ESI† as well as the comparison with QRRHO.
Results and discussion
The molecule under multi-experimental study, cis-1-phenylcyclohexane-1,2-diol, as well as trans-1,2-cyclohexanediol and cis-1,2-cyclohexanediol are shown in Fig. 1.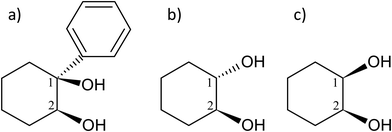 | ||
| Fig. 1 Scheme and atom numbering for (a) (S,S)-(+)-1-phenylcyclohexane-cis-1,2-diol (cis-PCD) (b) (1S,2S)-trans-1,2-cyclohexanediol (trans-CD) (c) cis-1,2-cyclohexanediol (cis-CD). | ||
1. cis-PCD Monomer
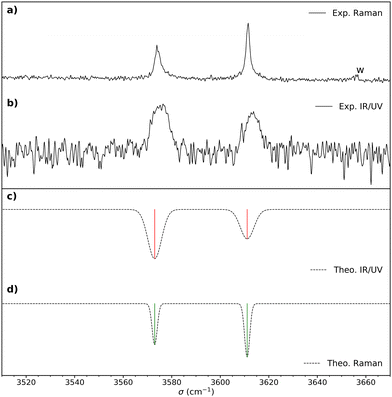 | ||
Fig. 2 (a) Raman spectrum of cis-PCD. “w” denotes a water impurity signal. (b) Double resonance spectrum of the monomer obtained by setting the UV probe on the transition origin at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 cm−1. (c) IR spectrum simulated for the most stable structure M1, shown in Fig. 4, obtained from the B3LYP-D3(BJ,abc)/ma-def2-TZVP empirically corrected harmonic frequencies. (d) Simulated Raman spectrum obtained from the empirically corrected harmonic B3LYP-D3(BJ,abc)/ma-def2-TZVP frequencies. The computed harmonic frequencies have been corrected by a recently proposed empirical correction model (see text and ref. 46). A Gaussian line profile is assumed with a full width at half maximum of 4 cm−1 and 1.5 cm−1 for the IR/UV and Raman spectra, respectively. Scaled B3LYP-D3(BJ,abc)/ma-def2-TZVP or B3LYP-D3(BJ)/6-311++G(d,p) harmonic frequencies calculations yield similar results. 766 cm−1. (c) IR spectrum simulated for the most stable structure M1, shown in Fig. 4, obtained from the B3LYP-D3(BJ,abc)/ma-def2-TZVP empirically corrected harmonic frequencies. (d) Simulated Raman spectrum obtained from the empirically corrected harmonic B3LYP-D3(BJ,abc)/ma-def2-TZVP frequencies. The computed harmonic frequencies have been corrected by a recently proposed empirical correction model (see text and ref. 46). A Gaussian line profile is assumed with a full width at half maximum of 4 cm−1 and 1.5 cm−1 for the IR/UV and Raman spectra, respectively. Scaled B3LYP-D3(BJ,abc)/ma-def2-TZVP or B3LYP-D3(BJ)/6-311++G(d,p) harmonic frequencies calculations yield similar results. | ||
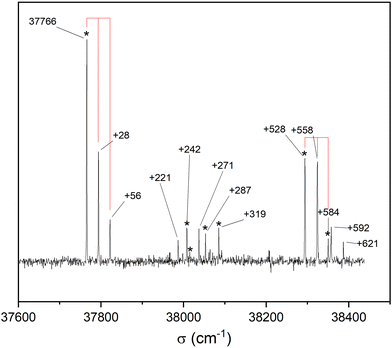
Fig. 3 shows the S1 ← S0 spectrum of the cis-PCD monomer. The strong transition origin at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 cm−1 is followed by a progression built on a low-frequency mode of 28 cm−1. The same progression appears in combination with the Herzberg–Teller allowed mode at +528 cm−1.
766 cm−1 is followed by a progression built on a low-frequency mode of 28 cm−1. The same progression appears in combination with the Herzberg–Teller allowed mode at +528 cm−1.
IR-UV double resonance spectra have been recorded by setting the UV probe on all the transitions marked by * in Fig. 3; that obtained by probing the transition origin is displayed in Fig. 2b. They are identical whatever the probe wavelength, showing unambiguously that only one conformer exists under pinhole jet conditions too. The spectrum shows two bands, both being down-shifted relative to a free ν(OH), at 3575 and 3613 cm−1, very close to the Raman spectroscopy values (Fig. 2a).
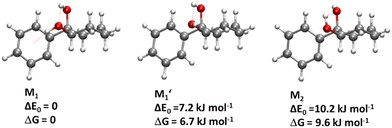
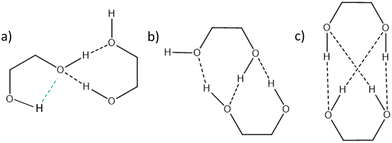
We are thus left with the three structures shown in Fig. 4, together with their energetics (Gibbs energy ΔG and ZPE-corrected energy ΔE0). Their energetics are summarised in Table S1 of the ESI.† They all show the phenyl and the O2H in equatorial position, and the O1H in axial position. They all involve a sterically constrained OH⋯O intramolecular interaction. We shall discuss their energetics in terms of relative Gibbs energies and ZPE-corrected energy ΔE0 at the B3LYP-D3(BJ,abc)/ma-def2-TZVP level. The energetics (relative Gibbs energy ΔG and ZPE-corrected energy ΔE0) and geometrical parameters at the B3LYP-D3BJ/6-311G++(d,p) level are listed in Table S2 of the ESI.† These structures will be called M (like monomer) with the index 1 or 2 when the OH on the carbon atom 1 or 2 is acting as a hydrogen bond donor, respectively. Both M1 and 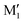 show an O1H⋯O2 interaction. They only differ by a rotation of O2H that allows a weak O2H⋯π interaction to take place in M1 and not in
show an O1H⋯O2 interaction. They only differ by a rotation of O2H that allows a weak O2H⋯π interaction to take place in M1 and not in 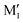 . M1 is thus stabilised by 6.7 kJ mol−1 relative to
. M1 is thus stabilised by 6.7 kJ mol−1 relative to 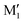 , in terms of ΔG. This value can be taken as an estimation of the OH⋯π interaction energy. M2 shows a hydrogen bond in the opposite direction, namely, an O2H⋯O1 interaction and is much less stable than M1 because no OH⋯π interaction is possible in M2 due to steric reasons. Notwithstanding the difference in hydrogen bond directions, the backbones are very similar in
, in terms of ΔG. This value can be taken as an estimation of the OH⋯π interaction energy. M2 shows a hydrogen bond in the opposite direction, namely, an O2H⋯O1 interaction and is much less stable than M1 because no OH⋯π interaction is possible in M2 due to steric reasons. Notwithstanding the difference in hydrogen bond directions, the backbones are very similar in 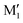 and M2. The Gibbs energy of M2 relative to M1 is 9.6 kJ mol−1, which allows roughly assessing the difference between O2H⋯O1 and O1H⋯O2 interactions to ∼3 kJ mol−1. The energy barrier for converting
and M2. The Gibbs energy of M2 relative to M1 is 9.6 kJ mol−1, which allows roughly assessing the difference between O2H⋯O1 and O1H⋯O2 interactions to ∼3 kJ mol−1. The energy barrier for converting 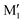 to M1 is calculated at 2.5 kJ mol−1 and is overcome in our experimental conditions,45 therefore only M1 is expected to be observed. The energy ranking is the same if one considers ΔE0 or the values obtained at the B3LYP-D3BJ/6-311G++(d,p) level (see Tables S1 and S2, ESI†), the values obtained with the various approaches differing by less than 10%.
to M1 is calculated at 2.5 kJ mol−1 and is overcome in our experimental conditions,45 therefore only M1 is expected to be observed. The energy ranking is the same if one considers ΔE0 or the values obtained at the B3LYP-D3BJ/6-311G++(d,p) level (see Tables S1 and S2, ESI†), the values obtained with the various approaches differing by less than 10%.
The splitting of the calculated frequencies of M1 matches well the experimental one, whatever the method used. The empirical scaling model developed for diols also predicts the absolute wavenumbers very well, although cis-PCD was not part of the training set.46ν(O1H) (3574.0 for the Raman and 3575 for the IR-UV results) is much lower than its counterpart in the related structure of cis-CD (3648 cm−1),46 as expected from the presence of an O1H⋯π interaction. Moreover, also ν(O2H) (3611.5 for the Raman and 3613 for the IR-UV results) is lower in frequency, which points towards a cooperative effect between the two hydrogen bonds, as observed also for intermolecular hydrogen bonds.26,47,48 The intramolecular hydrogen bond is hindered and far from linearity (θ(O1HO2) = 115° and d(O1H⋯O2) = 2.22 Å in M1), which explains the limited downshift of ν(O1H) compared to intermolecular OH⋯O interactions.
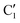 , C1, C2 by analogy and for a better comparison. C1′ is the dominant form and corresponds to
, C1, C2 by analogy and for a better comparison. C1′ is the dominant form and corresponds to 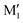 in cis-PCD. Although the experimentally observed conformers C1,
in cis-PCD. Although the experimentally observed conformers C1, 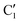 , and C2 of cis-CD are similar to M1,
, and C2 of cis-CD are similar to M1, 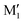 , M2 of cis-PCD, respectively, the energetic ordering is different. The stability of the first two conformers is inverted due to the possibility of an OH⋯π interaction in M1 and not in
, M2 of cis-PCD, respectively, the energetic ordering is different. The stability of the first two conformers is inverted due to the possibility of an OH⋯π interaction in M1 and not in 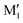 , which does not intervene in cis-CD.46 The Gibbs energy difference between the two most stable conformers of cis-PCD is large (6.7 kJ mol−1), as is ΔE0 (7.2 kJ mol−1), due to the OH⋯π hydrogen bond. This, in addition to the small interconversion barrier (2.5 kJ mol−1), explains that only M1 is observed in cis-PCD. In both cis-CD and cis-PCD, one of the hydroxyl substituents is in equatorial and the other one in axial position. In cis-PCD, the equatorial position of the bulky phenyl substituent is favoured to decrease the 1-3 diaxial interactions, and the most stable structure has its O2H group in equatorial and its O1H in axial position, with an
, which does not intervene in cis-CD.46 The Gibbs energy difference between the two most stable conformers of cis-PCD is large (6.7 kJ mol−1), as is ΔE0 (7.2 kJ mol−1), due to the OH⋯π hydrogen bond. This, in addition to the small interconversion barrier (2.5 kJ mol−1), explains that only M1 is observed in cis-PCD. In both cis-CD and cis-PCD, one of the hydroxyl substituents is in equatorial and the other one in axial position. In cis-PCD, the equatorial position of the bulky phenyl substituent is favoured to decrease the 1-3 diaxial interactions, and the most stable structure has its O2H group in equatorial and its O1H in axial position, with an 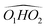 angle of 115°.
angle of 115°.
cis/trans isomerism also influences the diol structure. The two OH substituents are in equatorial position in trans-CD, hence equivalent. Two monomers with a different orientation of the accepting OH are calculated, corresponding to an 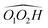 angle of 145° and 110°, respectively (M and M′ in reference,23 here renamed T′ and T for better distinction and analogy), akin to
angle of 145° and 110°, respectively (M and M′ in reference,23 here renamed T′ and T for better distinction and analogy), akin to 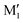 and M1 in cis-PCD, notwithstanding the axial or equatorial position. In the absence of other interactions, T and T′ are almost isoenergetic. They differ in energy by about 1 kJ mol−1 and their interconversion barrier is of the order of 4 kJ mol−1. The two of them are therefore observed under slit jet conditions.23
and M1 in cis-PCD, notwithstanding the axial or equatorial position. In the absence of other interactions, T and T′ are almost isoenergetic. They differ in energy by about 1 kJ mol−1 and their interconversion barrier is of the order of 4 kJ mol−1. The two of them are therefore observed under slit jet conditions.23
2. Dimers
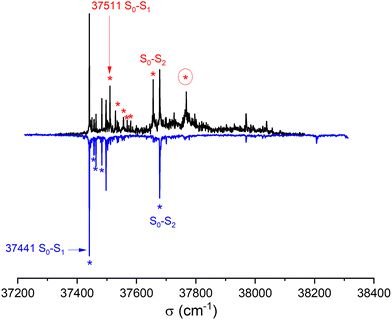
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441 cm−1) of the homochiral dimer is downshifted in energy relative to that of the monomer by 325 cm−1, a value slightly larger than that observed for other aromatic dimers like the anisole dimer (∼240 cm−1) or the 1-indanol dimer (∼250 cm−1).11,49 The intense transition origin is followed by low-frequency modes located at 15, 22, 42, 56 cm−1. An intense band also appears at 237 cm−1 from the S1 ← S0 origin, i.e. −88 cm−1 from the monomer origin. It probably corresponds to the S2 ← S0 origin. Interestingly, only a weak combination band involving the 22 cm−1 mode is observed, pointing towards different Franck Condon activity for the S1 ← S0 and S2 ← S0 transitions. The other bands observed in the spectrum correspond to the Herzberg–Teller allowed mode of the benzene ring in S1 (528 cm−1 from the S1 ← S0 origin) or S2 (528 cm−1 from the S2 ← S0 origin). The strong decrease in band intensity at higher energy points towards the onset of non-radiative processes, which were not apparent in the monomer.
441 cm−1) of the homochiral dimer is downshifted in energy relative to that of the monomer by 325 cm−1, a value slightly larger than that observed for other aromatic dimers like the anisole dimer (∼240 cm−1) or the 1-indanol dimer (∼250 cm−1).11,49 The intense transition origin is followed by low-frequency modes located at 15, 22, 42, 56 cm−1. An intense band also appears at 237 cm−1 from the S1 ← S0 origin, i.e. −88 cm−1 from the monomer origin. It probably corresponds to the S2 ← S0 origin. Interestingly, only a weak combination band involving the 22 cm−1 mode is observed, pointing towards different Franck Condon activity for the S1 ← S0 and S2 ← S0 transitions. The other bands observed in the spectrum correspond to the Herzberg–Teller allowed mode of the benzene ring in S1 (528 cm−1 from the S1 ← S0 origin) or S2 (528 cm−1 from the S2 ← S0 origin). The strong decrease in band intensity at higher energy points towards the onset of non-radiative processes, which were not apparent in the monomer.
The spectrum of racemic cis-PCD clearly shows additional bands, which are due to the heterochiral dimer. The downshift of the S1 ← S0 transition origin of the heterochiral dimer (37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 cm−1) is smaller (255 cm−1 from the monomer origin). A low-frequency pattern similar to that of the homochiral dimer is observed near the S1 ← S0 origin, with bands at 18, 45, 57 cm−1 from the S1 ← S0 origin. An additional weak band appears at 70 cm−1. The band tentatively assigned to the S2 ← S0 origin, located at 145 cm−1 from the S1 ← S0 origin, also shows a larger down shift relative to the monomer than the homochiral dimer (110 cm−1). The same decrease in band intensity at higher energy is observed as for the homochiral dimer. Still, an intense band is observed at +257 cm−1 of the S1 ← S0 origin, a point to which we shall come back later.
511 cm−1) is smaller (255 cm−1 from the monomer origin). A low-frequency pattern similar to that of the homochiral dimer is observed near the S1 ← S0 origin, with bands at 18, 45, 57 cm−1 from the S1 ← S0 origin. An additional weak band appears at 70 cm−1. The band tentatively assigned to the S2 ← S0 origin, located at 145 cm−1 from the S1 ← S0 origin, also shows a larger down shift relative to the monomer than the homochiral dimer (110 cm−1). The same decrease in band intensity at higher energy is observed as for the homochiral dimer. Still, an intense band is observed at +257 cm−1 of the S1 ← S0 origin, a point to which we shall come back later.
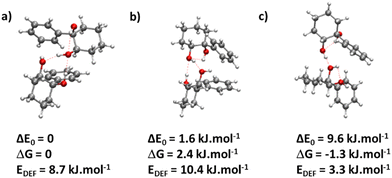
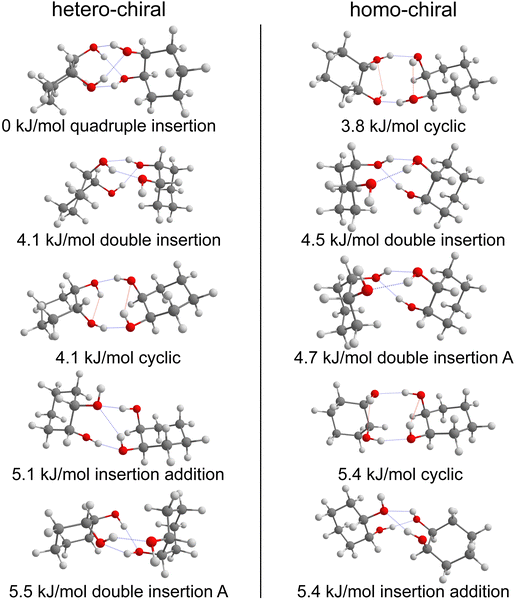
The most stable calculated homochiral structure (Fig. 7a) meets these requirements. The other calculated structures are shown in Fig. S1 of the ESI,† together with their 6-311G++(d,p) energetics. Their interactive 3-D structures are given in the ESI† structures file. Their energetic data calculated at the B3LYP-D3(BJ,abc)/ma-def2-TZVP level are listed in Table S1 (ESI†). The simulated spectra are shown in Fig. S2 (ESI†).
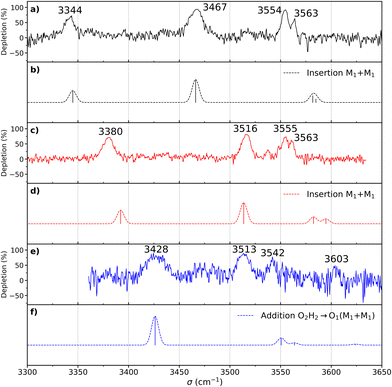
The most stable homochiral structure is built from the most stable monomers M1 and is what we shall call an “insertion” complex. The O2H group of one of the monomers, called “guest” in what follows and denoted by the subscript “g”, inserts into the intramolecular hydrogen bond of the other monomer, called “host” and denoted by “h”. The intramolecular O1gH⋯O2g hydrogen bond of the guest is retained while its O2gH⋯π contact is disrupted to the benefit of the strong intermolecular O2gH⋯O2h interaction. The dangling O2hH interacts with the aromatic ring of the guest. The intramolecular O1hH⋯O2h hydrogen bond of the host is disrupted to the benefit of two strong intermolecular O2gH⋯O2h and O1hH⋯O2g interactions. The intramolecular hydrogen bond of the guest is hardly modified relative to the M1 monomer (θ(O1gHO2g) = 116° and d(O1g⋯HO2g) = 2.19 Å vs. 115° and 2.22 Å). In contrast, the host undergoes strong deformation, which explains the large deformation energy (10.4 kJ mol−1). The experimental spectrum is readily assigned on the basis of this geometry (Fig. 6a and b). The bands observed at 3344 and 3467 cm−1 are assigned to the ν(O1hH) and ν(O2gH), respectively. The doublet at 3554/3563 cm−1 is assigned to ν(O2hH) and ν(O1gH), respectively.
More conformational diversity is observed for the heterochiral dimer and a different vibrational spectrum is obtained for the probe set on the transition located at 257 cm−1 of the S1 ← S0 transition origin or for the probe set on the S1 ← S0 transition origin or any of the other bands. The spectrum with the probe set on the S1 ← S0 origin (Fig. 6c) shows four transitions, at 3380, 3516, 3555 and 3563 cm−1. It is attributed to the most stable (at 0 K) calculated structure (Fig. 7b), which is very similar to the homochiral dimer described above. A similar insertion structure is calculated with similar hydrogen bonds, with a deformation energy of the same order as the corresponding homochiral complex. The spectrum simulated for this structure is in excellent agreement with the experimental findings (Fig. 6c and d). The assignments of the bands at 3380 and 3516 cm−1 or the doublet at 3555/3563 cm−1 parallel that of the homochiral dimer.
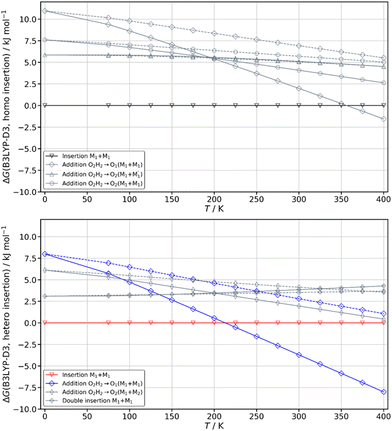
The spectrum obtained when probing the band at +257 cm−1 (band marked with an encircled asterisk in Fig. 5) shows a different pattern, with a smaller down-shift of the ν(OH) frequencies. Four bands appear at 3428, 3513, 3542, 3603 cm−1. Based on agreement between simulated and experimental frequencies, it is assigned to an addition complex (linear structure), which is high in energy at 0 K but predicted to become competitive at higher temperature (see Fig. 8 and Table S1, ESI†). The other calculated heterochiral structures are shown in Fig. S2 of the ESI,† together with their 6-311G++(d,p) energetics. Their interactive 3-D structures are given in the ESI† structures file. The addition complex is built from a M1 monomer acting as a donor, which adds to a M1 monomer via a strong intermolecular hydrogen bond. The donor and the acceptor will be denoted by the subscript “d” or “a”, respectively. They both keep their intramolecular hydrogen bond O1H⋯O2 intact. Because the geometry of the monomer within the complex is very close to that of the bare monomers (no disruption of the intramolecular hydrogen bonds), the deformation energy is very low (3.3 kJ mol−1). The dangling O2dH of the donor is involved in a strong intermolecular O2dH⋯O1a hydrogen bond while that of the acceptor is involved in the same OH⋯π interaction as the monomer. There is a rather large uncertainty in energy ranking as the addition dimer is less stable by 8.0 kJ mol−1 in terms of ΔE0 but more stable by 3.7 kJ mol−1 than the insertion heterodimer in terms of Gibbs energy at 300 K. This uncertainty mainly arises from the fact that the insertion complexes are tighter than addition complexes; the evolution of the Gibbs free energy as a function of the temperature is in favour of the latter as one can already see from the large discrepancy between ΔG and ΔE0 provided in Fig. 7. The temperature at which the complexes are formed in the out-of-equilibrium supersonic expansion is not known but the fact that we see both heterochiral complexes, the insertion one being dominant, seems to indicate that the temperature at which the complexes are formed is higher than 100 K (see Fig. 8). As expected for rigid complexes, the insertion and double insertion dimers show little variation of their relative ΔG as a function of the temperature. This contrasts to the addition complexes, in particular the heterochiral addition O2H2 → O1 (M1 + M1) dimer to which one of the experimentally observed spectra is assigned. The observation of this dimer provides an indirect measurement of the jet conformational temperature, which can be estimated at similar values using different basis set; a switch from ma-def2-TZVP to 6-311G++(d,p) would suggest a slightly different conformational temperature (175 K vs. 150 K). However, one should not overestimate the robustness of this estimate, as a different way of dealing with the entropy of very low frequency vibrations44 would suggest very different conformational temperature. Resorting to the QRRHO corrections would result in a less realistic temperature above 300 K (dashed lines in Fig. 8).
3. Comparison between homo and heterochiral dimers
A similar insertion structure is observed for both homochiral and heterochiral dimers, with similar hydrogen bonds and deformation energies. A structural difference lies in the fact that, due to the stereochemical constraints, the aromatic rings are facing each other in the heterochiral dimer while they are on opposite sides of the homochiral dimer. An increase in temperature strongly favours the addition dimers (see Fig. 8) because addition complexes are less rigid, which makes them favoured at high temperature, entropic effects being more important there than the intrinsic hydrogen bond strength. Still, the insertion dimer is the most stable structure for the homochiral dimer, at 0 K and 300 K alike. For the heterochiral complex, the addition dimer is strongly stabilised at 300 K (by 3.7 kJ mol−1) relative to the insertion. The same is obtained to a lesser extent (0.5 kJ mol−1) using the B3LYP-D3BJ/6-311G++(d,p) values. However, a larger stability of the addition relative to the insertion heterochiral dimer would be in contradiction with the more intense and numerous bands assigned to the latter in the REMPI spectrum. Assuming that the oscillator strength of the electronic transition and ionisation efficiency are identical for both heterochiral structures, these experimental findings would suggest a larger abundance of the insertion heterochiral dimer in our experimental conditions. Hence, the temperature at which the two heterochiral dimers are formed is likely lower than 300 K.The calculated value of the chirodiastaltic energy is different whether ΔE0 or ΔG is considered (see Fig. 8 and Table S1, ESI†), and also depends on the level of theory used. Homochiral preference is obtained at 0 K whatever the method used; ΔE0(hom-het) amounts to 1.6 kJ mol−1 at the B3LYP-D3(BJ,abc)/ma-def2-TZVP level and 1.7 kJ mol−1 for B3LYP-D3BJ/6-311G++(d,p), respectively. Note that when ΔE0 is considered, the most stable homo- and heterochiral complexes are both insertion structures but when ΔG at 300 K is considered the most stable heterochiral structure is the addition dimer that would energetically win over the homochiral dimer by 1.3 kJ mol−1 at 300 K. Changing the basis set from ma-def2-TZVP to 6-311G++(d,p) reverses this trend and retrieves the homochiral preference (by 2.3 kJ mol−1) at 300 K.
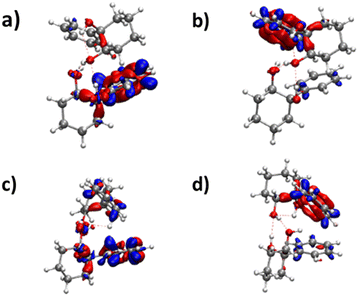
The frequencies located on O2gH and O1hH are lower in the homochiral than the heterochiral dimer, suggesting stronger hydrogen bonds in the former. Non-covalent (NCI) calculations59,60 indeed indicate a slightly larger electron density for the intermolecular hydrogen bonds of the homochiral dimer (0.199 and 0.177 vs. 0.197 and 0.175 for the heterochiral dimer). This observation is compatible with a larger stability of the homochiral dimer, although it should be taken with caution as stronger hydrogen bonds do not always correlate with an overall larger stability.61 Introducing the QRRHO approximation allows retrieving a chirodiastaltic Gibbs free energy in favour of the homochiral dimer (1.8 kJ mol−1), and an insertion heterochiral complex more stable than the addition structure, but would suggest a conformational temperature in the jet close to room temperature. Still, there are concordant indications in favour of a homochiral preference, although each taken separately (energy at 0 K, relative intensities in the electronic spectrum, down shift of the ν(OH)) is not sufficiently conclusive.
The heterochiral dimer shows more conformational flexibility than the homochiral one as it exists in two forms. A larger conformational flexibility has been observed already for the less stable configuration of chiral systems, for example heterochiral peptides, or protonated methyl tartrate dimers,52,62,63 or the homochiral 1-indanol dimer.11 A larger conformational flexibility of the homochiral adduct was observed as well for the trans-CD dimer for which the most stable calculated dimer is heterochiral.23
4. Comparison with cis- and trans-1,2-cyclohexanediol
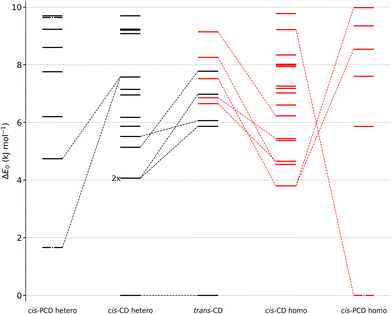
We shall now compare the structures described above to those obtained for similar systems, namely, cis- and trans-CD. The hydrogen bond patterns observed for the most stable dimers of the three systems at low temperature are sketched in Fig. 10. Further possible hydrogen bond patterns are sketched in Fig. S5 of the ESI.† The energetics of the cis-CD, trans-CD and cis-PCD dimers are summarised in Fig. 11.The Raman spectrum of cis-CD,46 taken with experimental conditions optimised for dimer formation, is shown in Fig. 12. It has one dominant band at 3419 cm−1, which is predicted to arise mainly from the most stable transiently heterochiral dimer, whereas the most likely similarly abundant transiently homochiral dimer is spread over several conformations and weaker transitions at lower and mostly at higher wavenumber. The lack of conformational selectivity prevents any further spectral assignment, but the calculations suggest that the homo- and heterochiral dimers have a very different hydrogen bond topology. Similar to trans-CD, a heterochiral quadruple insertion dimer is predicted to be the most stable dimer with other hetero- and homochiral dimers being significantly higher in energy, although not quite as pronounced as for trans-CD (ΔE0(hom-het) for cis-CD is 3.8 kJ mol−1vs. 6.6 kJ mol−1 for trans-CD at the B3LYP-D3/ma-def2-TZVP level). The analogy to trans-CD also holds for the homochiral dimers with the most stable ones being close in energy as well as structurally related. Of these four dimers a cyclic structure (two intermolecular and two intramolecular hydrogen bonds) is energetically favoured. The somewhat surprising similarity between cis-CD and trans-CD can be explained by the fact that the O–C–C–O dihedral angles of the diol subunit are still quite similar. Hence, the fact that the chiral preference in cis-PCD is inverted can most likely be attributed to the introduction of the phenyl group. The most stable homochiral cyclic (double addition) pattern contrasts to that at play in the homochiral cis-PCD dimer that involves two intermolecular and one intramolecular OH⋯O interactions. This is because the aromatic ring electrons compete with the oxygen as a hydrogen bond acceptor; both homochiral and heterochiral cis-PCD insertion dimers involve indeed an OH⋯π interaction.
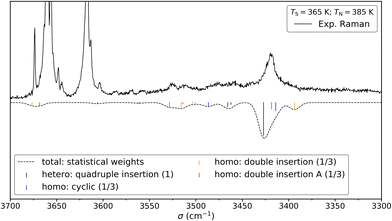 | ||
Fig. 12 Comparison between the experimental (top) and simulated (bottom) Raman spectrum of cis-CD in 1.4 bar of helium. The saturator (365 K) and nozzle (385 K) temperatures have been optimised for dimer formation. Reasonable agreement can be found between the simulation and the experiment. See Fig. 13 for depiction of the corresponding structures. For the simulation, it is assumed that homo- and heterochiral dimers are formed with equal likelihood. Furthermore, the three most stable homo-dimers are assumed to be isoenergetic and therefore the homo population is equally spread among them. Since the most stable heterochiral dimer is energetically unrivalled one arrives at statistical weights of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3 1/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3 1/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3 (quadruple insertion: cyclic: double insertion: double insertion A). Such an approach was previously successfully used for trans-CD. The simulation assumes Gaussian profile with a FWHM of 8 cm−1. 1/3 (quadruple insertion: cyclic: double insertion: double insertion A). Such an approach was previously successfully used for trans-CD. The simulation assumes Gaussian profile with a FWHM of 8 cm−1. | ||
Calculations confirm that there is little similarity between the most stable complexes of cis-PCD and cis-CD in a 10 kJ mol−1 window (see Fig. 11 and Fig. 13). The conformational locking induced by the phenyl on the cis-PCD monomer also exists for its dimers, as shown by the much higher density of structures for cis-CD. The insertion dimer is indeed the only homochiral stable structure in a 5 kJ mol−1 window at low temperature (see Fig. 8). In cis-PCD, the chirodiastaltic energy favours the homochiral complex. This contrasts to what is calculated for trans-CD or cis-CD for which the most stable calculated dimer is the heterochiral one (ΔE0 = 6.6 kJ mol−1 and 3.8 kJ mol−1, respectively, at the B3LYP-D3/ma-def2-TZVP level) due to its structure (quadruple insertion) that optimises the number of hydrogen bonds.
The energetics sketched in Fig. 11 illustrate the main points of the comparison between the different systems. The lesser density of structures for cis-PCD, independently of chirality, illustrates the conformational locking induced by the aromatic ring. Both cis- and trans-CD show heterochiral preference with a quadruple insertion structure, which contrast with cis-PCD that shows homochiral preference. On a common energy scale where the most stable dimer irrespective of relative chirality is aligned, the most stable homochiral dimer of cis-CD is destabilised by ∼5 kJ mol−1 when adding an aromatic ring, because of the steric hindrance brought by the latter. Conversely, the most stable homochiral cis-PCD dimer is stabilised by ∼9 kJ mol−1 relative to the equivalent in CD.
5. Structure of the solid state
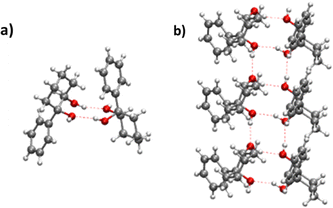
(R,R) enantiopure and racemic cis-PCD samples have been dissolved in ethanol and allowed to crystallise slowly, resulting in long needle-shaped crystals. The X-ray diffraction pattern of both samples has been recorded following the procedure described in the ESI.† The enantiopure crystal belongs to the monoclinic Sohncke group C2, characterised by a two-fold rotation axis and a two-fold screw axis. The unit cell, displayed in Fig. 14a, contains two non-equivalent monomers interacting via two intermolecular hydrogen bonds, in what can be called an addition structure. The superimposed structure of the two monomers are shown in Fig. S6 of the ESI.† The structure of one of the monomers is close to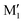 , with an O1H1···O2 hydrogen bond, while the other is close to M2 with an O2H2···O1 interaction. The dangling OH of each monomer binds to the monomer of same nature in a neighbouring dimer, resulting in long hydrogen-bonded chains that explain the needle-like appearance of the crystal (Fig. 14b). The racemic cis-PCD is a conglomerate composed of a 50/50 mixture of (R,R) and (S,S) crystals. In the solid phase as well, homochiral preference is therefore observed. This contrasts to trans-CD whose racemic crystal crystallises as a racemate in the C2/c space group, which contains an inversion centre.24 The asymmetric unit is a trans-CD monomer that converts into its enantiomer via the inversion operation, resulting in a similar addition dimer, with monomers in a geometry intermediate between M and M′ (
, with an O1H1···O2 hydrogen bond, while the other is close to M2 with an O2H2···O1 interaction. The dangling OH of each monomer binds to the monomer of same nature in a neighbouring dimer, resulting in long hydrogen-bonded chains that explain the needle-like appearance of the crystal (Fig. 14b). The racemic cis-PCD is a conglomerate composed of a 50/50 mixture of (R,R) and (S,S) crystals. In the solid phase as well, homochiral preference is therefore observed. This contrasts to trans-CD whose racemic crystal crystallises as a racemate in the C2/c space group, which contains an inversion centre.24 The asymmetric unit is a trans-CD monomer that converts into its enantiomer via the inversion operation, resulting in a similar addition dimer, with monomers in a geometry intermediate between M and M′ (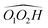 angle of 131°).
angle of 131°).
Conclusion
The spectroscopic study of the chiral diol cis-PCD and its dimer emphasises several differences relative to the previously studied permanently chiral trans-CD and the transiently chiral cis-CD diols further explored in this work. First, the steric hindrance due to the bulky phenyl ring, in addition to its hydrogen bond acceptor capability that allows formation of an OH⋯π hydrogen bond, induces conformational locking in cis-PCD relative to cis-CD and decreases the number of populated conformers. cis-PCD exists therefore in one conformer only under supersonic jet conditions. The most stable structure of both homochiral and heterochiral dimers of cis-PCD at low temperature is an insertion structure, with the O2H group of the guest inserted in the intramolecular hydrogen bond of the host. With increasing temperature, competition by more floppy addition complexes sets in, first in the heterochiral case, as also evidenced by experiment. The recently observed tunneling splitting present in one of the homo dimers of trans-CD should not be of concern for cis-PCD given the large structural changes relative to trans-CD that do not readily allow for a conversion between equivalent conformers.64 The homochiral preference observed for cold cis-PCD contrasts to what was observed in trans-CD and cis-CD for which the predicted heterochiral preference is explained by the formation of an outstandingly stable heterochiral dimer that optimises the number of possible hydrogen bonds via a quadruple insertion structure. Due to the strong similarities between cis-CD and trans-CD, it is clear that the changes in clustering propensity of cis-PCD are due to the presence of the phenyl substituent rather than the consequences of cis-trans isomerism. These findings at the molecular level parallel those in the crystal, as racemic cis-PCD is a conglomerate while trans-CD is a racemate.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455 and 405832858 for computational resources is acknowledged. We acknowledge the computing centre MésoLUM managed by ISMO (UMR8214) and LPGP (UMR8578), University Paris-Saclay (France).References
- I. Myrgorodska, C. Meinert, S. V. Hoffmann, N. C. Jones, L. Nahon and U. J. Meierhenrich, ChemPlusChem, 2017, 82, 74–87 CrossRef CAS PubMed.
- J. Podlech, Cell. Mol. Life Sci., 2001, 58, 44–60 CrossRef CAS PubMed.
- W. A. Bonner, Origins of Life and Evolution of the Biosphere, 1995, vol. 25, pp. 175–190 Search PubMed.
- R. Sudha and M. F. Jarrold, J. Phys. Chem. B, 2005, 109, 11777–11780 CrossRef CAS PubMed.
- T. Rekis, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 307–315 CrossRef CAS PubMed.
- C. Brandel, S. Petit, Y. Cartigny and G. Coquerel, Curr. Pharm. Des., 2016, 22, 4929–4941 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, J. E. Hein and E. R. Johnson, Cryst. Growth Des., 2016, 16, 6055–6059 CrossRef CAS.
- L. Pasteur, C. R. Acad. Sci., 1853, 37, 162 Search PubMed.
- A. Zehnacker, Int. Rev. Phys. Chem., 2014, 33, 151–207 Search PubMed.
- A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992 CrossRef CAS PubMed.
- J. Altnoeder, A. Bouchet, J. J. Lee, K. E. Otto, M. A. Suhm and A. Zehnacker-Rentien, Phys. Chem. Chem. Phys., 2013, 15, 10167–10180 RSC.
- X. C. Liu, N. Borho and Y. J. Xu, Chem. – Eur. J., 2009, 15, 270–277 CrossRef CAS PubMed.
- W. H. Pirkle and T. C. Pochapsky, Chem. Rev., 1989, 89, 347–362 CrossRef CAS.
- N. Borho and M. A. Suhm, Org. Biomol. Chem., 2003, 1, 4351–4358 RSC.
- N. Borho and M. A. Suhm, Phys. Chem. Chem. Phys., 2004, 6, 2885–2890 RSC.
- T. B. Adler, N. Borho, M. Reiher and M. A. Suhm, Angew. Chem., Int. Ed., 2006, 45, 3440–3445 CrossRef CAS PubMed.
- A. Bouchet, J. Klyne, S.-I. Ishiuchi, O. Dopfer, M. Fujii and A. Zehnacker, Phys. Chem. Chem. Phys., 2018, 20, 12430–12443 RSC.
- D. F. Plusquellic, F. J. Lovas, B. H. Pate, J. L. Neill, M. T. Muckle and A. J. Remijan, J. Phys. Chem. A, 2009, 113, 12911–12918 CrossRef CAS PubMed.
- F. Kollipost, K. E. Otto and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 4591–4595 CrossRef CAS PubMed.
- P. Asselin, B. Madebene, P. Soulard, R. Georges, M. Goubet, T. R. Huet, O. Pirali and A. Zehnacker-Rentien, J. Chem. Phys., 2016, 145 Search PubMed.
- R. Medel, A. Camiruaga, R. T. Saragi, P. Pinacho, C. Perez, M. Schnell, A. Lesarri, M. A. Suhm and J. A. Fernandez, Phys. Chem. Chem. Phys., 2021, 23, 23610–23624 RSC.
- T. Scharge, T. Haber and M. A. Suhm, Phys. Chem. Chem. Phys., 2006, 8, 4664–4667 RSC.
- B. Hartwig, M. Lange, A. Poblotzki, R. Medel, A. Zehnacker and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 1122–1136 RSC.
- S. Jahnigen, A. Zehnacker and R. Vuilleumier, J. Phys. Chem. Lett., 2021, 12, 7213–7220 CrossRef CAS PubMed.
- N. Seurre, J. Sepiol, K. Le Barbu-Debus, F. Lahmani and A. Zehnacker-Rentien, Phys. Chem. Chem. Phys., 2004, 6, 2867–2877 RSC.
- N. Seurre, J. Sepiol, F. Lahmani, A. Zehnacker-Rentien and K. Le Barbu-Debus, Phys. Chem. Chem. Phys., 2004, 6, 4658–4664 RSC.
- R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 25538–25551 RSC.
- D. Scuderi, K. Le Barbu-Debus and A. Zehnacker, Phys. Chem. Chem. Phys., 2011, 13, 17916–17929 RSC.
- R. N. Pribble and T. S. Zwier, Science, 1994, 265, 75–79 CrossRef CAS PubMed.
- S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352 CrossRef CAS.
- A. Sen, A. Bouchet, V. Lepère, K. Le Barbu-Debus, D. Scuderi, F. Piuzzi and A. Zehnacker-Rentien, J. Phys. Chem. A, 2012, 116, 8334–8344 CrossRef CAS PubMed.
- R. A. Marta, R. H. Wu, K. R. Eldridge, J. K. Martens and T. B. McMahon, Int. J. Mass Spectrom., 2010, 297, 76–84 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. BenNasr, A. Pérez-Mellor, I. Alata, V. Lepere, N. E. Jaidane and A. Zehnacker, Faraday Discuss., 2018, 212, 399–419 RSC.
- M. D. Halls, J. Velkovski and H. B. Schlegel, Theor. Chem. Acc., 2001, 105, 413 Search PubMed.
- K. Le Barbu-Debus, in Chiral Recognition in the Gas Phase, ed. A. Zehnacker, CRC Press Taylor and Francis, Boca Raton, 2010, ch. 4, pp. 47–59 Search PubMed.
- N. Borho, M. A. Suhm, K. Le Barbu-Debus and A. Zehnacker, Phys. Chem. Chem. Phys., 2006, 8, 4449–4460 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- B. Hartwig and M. A. Suhm, Phys. Chem. Chem. Phys., 2021, 23, 21623–21640 RSC.
- M. Broquier, F. Lahmani, A. Zehnacker-Rentien, V. Brenner, P. Millie and A. Peremans, J. Phys. Chem. A, 2001, 105, 6841–6850 CrossRef CAS.
- R. W. Larsen and M. A. Suhm, J. Chem. Phys., 2006, 125, 154314 CrossRef PubMed.
- A. Zehnacker, F. Lahmani, E. Breheret, J. P. Desvergne, H. BouasLaurent, A. Germain, V. Brenner and P. Millie, Chem. Phys., 1996, 208, 243–257 CrossRef CAS.
- N. M. Kidwell, B. Nebgen, L. V. Slipchenko and T. S. Zwier, J. Chem. Phys., 2019, 151, 084313 CrossRef PubMed.
- U. Erlekam, M. Frankowski, G. von Helden and G. Meijer, Phys. Chem. Chem. Phys., 2007, 9, 3786–3789 RSC.
- J. Dupont, R. Guillot, V. Lepère and A. Zehnacker, J. Mol. Struct., 2022, 1262, 133059 CrossRef CAS.
- A. Pérez-Mellor, I. Alata, V. Lepere and A. Zehnacker, J. Mol. Spectrosc., 2018, 349, 71–84 CrossRef.
- K. Le Barbu, F. Lahmani and A. Zehnacker-Rentien, J. Phys. Chem. A, 2002, 106, 6271–6278 CrossRef CAS.
- K. Le Barbu, F. Lahmani, M. Mons, M. Broquier and A. Zehnacker, Phys. Chem. Chem. Phys., 2001, 3, 4684–4688 RSC.
- C. E. H. Dessent, W. D. Geppert, S. Ullrich and K. Muller-Dethlefs, Chem. Phys. Lett., 2000, 319, 375–384 CrossRef CAS.
- M. Mons, I. Dimicoli, B. Tardivel, F. Piuzzi, V. Brenner and P. Millie, J. Phys. Chem. A, 1999, 103, 9958–9965 CrossRef CAS.
- C. J. Gruenloh, F. C. Hagemeister, J. R. Carney and T. S. Zwier, J. Phys. Chem. A, 1999, 103, 503–513 CrossRef CAS.
- R. Chaudret, B. d Courcy, J. Contreras-Garcia, E. Gloaguen, A. Zehnacker-Rentien, M. Mons and J. P. Piquemal, Phys. Chem. Chem. Phys., 2014, 16, 9876–9891 RSC.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- P. Hurtado, F. Gamez, S. Hamad, B. Martinez-Haya, J. D. Steill and J. Oomens, J. Chem. Phys., 2012, 136 Search PubMed.
- V. Lepere, K. Le Barbu-Debus, C. Clavaguera, D. Scuderi, G. Piani, A.-L. Simon, F. Chirot, L. MacAleese, P. Dugourd and A. Zehnacker, Phys. Chem. Chem. Phys., 2016, 18, 1807–1817 RSC.
- K. Le Barbu-Debus, D. Scuderi, V. Lepere and A. Zehnacker, J. Mol. Struct., 2020, 1205, 127583 CrossRef CAS.
- F. Xie, W. Sun, B. Hartwig, D. A. Obenchain and M. Schnell, Angew. Chem., Int. Ed., 2023, 62(37), e202308273 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2277624. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp00351a |
| This journal is © the Owner Societies 2024 |