Searching for stable copper borozene complexes in CuB₇⁻ and CuB₈⁻

Abstract

Copper has been shown to be an important substrate for the growth of borophenes. Copper–boron binary clusters are ideal platforms to study the interactions between copper and boron, which may provide insight about the underlying growth mechanisms of borophene on copper substrates. Here we report a joint photoelectron spectroscopy and theoretical study on two copper-doped boron clusters, CuB₇⁻ and CuB₈⁻. Well resolved photoelectron spectra are obtained for the two clusters at different wavelengths and are used to understand the structures and bonding properties of the two CuB_n⁻ clusters. We find that CuB₈⁻ is a highly stable borozene complex, which possesses a half-sandwich structure with a Cu⁺ species interacting with the doubly aromatic η⁸-B₈²⁻ borozene. The CuB₇⁻ cluster is found to consist of a terminal copper atom bonded to a double-chain B₇ motif, but it has a low-lying isomer composed of a half-sandwich structure with a Cu⁺ species interacting with an open-shell η⁷-B₇²⁻ borozene. Both ionic and covalent interactions are found to be possible in the binary Cu–B clusters, resulting in different structures.

---

1 Introduction

The electron deficiency of boron gives rise to a variety of bulk allotropes with cage structures.^1–3 Boron-based nanotubes with a triangular boron layer were also proposed after the discovery of carbon nanotubes.^4,5 However, a triangular boron layer is too electron-rich, which results in out-of-plane distortions.^6,7 Theoretical calculations suggested that a triangular boron lattice with hexagonal vacancies could be perfectly planar.^8,9 Combined experimental and theoretical studies have revealed the structures of various boron clusters.^10–19 Different from bulk boron materials, finite boron clusters have been found predominantly to possess two-dimensional (2D) structures consisting of B₃ triangles decorated with vacancies of different shapes, where the 2D structures are stabilized by delocalized σ and π bonds throughout the cluster plane.^20,21 The C_6v planar B₃₆ cluster with a central hexagonal vacancy provided the first experimental evidence for the viability of a graphene-like planar boron sheet (a.k.a. borophene).²² The B₃₅⁻ cluster was also found to contain a planar structure with a double hexagonal vacancy, providing a more flexible building block for borophenes.²³ Borophenes have been successfully realized on various metal substrates,^24,25 becoming a new class of 2D materials.^26,27 The discovery of the B₄₀ cage marks the first all-boron fullerene (borospherene).²⁸ The B₄₈⁻ cluster was confirmed to be the first bilayer boron cluster,^29,30 suggesting the possibility of bilayer borophenes that have also been successfully prepared on coinage metal substrates.^31,32 Theoretical analyses for the formation of bilayer borophenes on the copper substrate suggested that electron transfers from the metal substrate to the first layer of boron play an important role in the growth of the bilayer borophene.³¹ To fully understand the growth mechanisms of borophenes, it is important to study the interactions between boron and the underlying metal substrates at the atomic level. Metal–boron binary clusters provide ideal model systems.

Significant amounts of work have been done on metal-doped boron clusters over the past two decades.^18,33,34 The study on transition-metal-doped boron clusters has uncovered various novel structures including metal-centered molecular wheels,^35–37 metallo-boron nanotubes^38–40 and metallo-borophenes.^33,41,42 The B₇⁻, B₈⁻ and B₉⁻ clusters were among the first few boron clusters jointly studied by photoelectron spectroscopy (PES) and computational chemistry.^12,43 B₉⁻ was found to possess a perfect D_8h structure with σ and π double aromaticity. The closed-shell B₇³⁻ and B₈²⁻, possessing similar double aromaticity, were first found in the AlB₇, PrB₇, and LiB₈⁻ clusters.^44–46 During a recent study on a series of LnB₈⁻ clusters (Ln = La, Pr, Tb, Tm, Yb), the similarity between the π bonding in B₇³⁻, B₈²⁻ and B₉⁻ and that in the series of prototypical hydrocarbons, C₅H₅⁻, C₆H₆ and C₇H₇⁺, was recognized and the name “borozene” was proposed for the series of doubly aromatic boron motifs.⁴⁷ Several B₇³⁻ and B₈²⁻ borozene complexes have been realized recently in multiple metal-doped boron clusters, even in a boron oxide cluster.^48–50

Copper–boron binary clusters (Cu_xB_y⁻) are ideal systems to study the interactions between copper and boron atoms at the atomic levels, which may help develop a better understanding of the growth of borophenes on copper substrates. Our recent study on Cu₂B₈⁻ revealed a Cu₂⁺–[B₈²⁻] borozene complex,⁵¹ in which the charge transfer from the copper atoms to the boron motif is similar to what was suggested in the growth of bilayer borophenes on copper substrates.³¹ Smaller di-copper-doped boron clusters Cu₂B_n⁻ (n = 3–7) were also studied recently, revealing competitions between covalent and ionic interactions in determining the cluster structures.^52,53 In this article, we report a combined experimental and computational study on two mono-copper-doped boron clusters, CuB₇⁻ and CuB₈⁻, to probe the Cu–boron bonding and search for stable copper borozene complexes. Well-resolved photoelectron spectra are obtained for the two clusters at different wavelengths and are combined with theoretical calculations to understand the structures and bonding of the two CuB_n⁻ clusters. CuB₈⁻ is found to be a highly stable metal borozene complex, which possesses a half-sandwich structure with a Cu⁺ species coordinated by the η⁸-B₈²⁻ borozene. On the other hand, CuB₇⁻ is found to consist of a terminal copper atom bonded to a double-chain B₇ motif with strong covalent Cu–B covalent bonding, while the borozene complex consisting of the open-shell η⁷-B₇²⁻, is a low-lying isomer present in the experiment as a minor species. We have also found strong electron correlation effects in the two clusters and a multi-reference method was required to calculate their electron detachment energies.

2 Experimental and theoretical methods

2.1. Experimental methods

The experiments were conducted using a PES apparatus consisting of a laser vaporization cluster source, a time-of-flight (TOF) mass spectrometer, and a 3.5-meter-long magnetic bottle photoelectron analyzer. Details of the experimental apparatus can be found elsewhere.¹⁷ The CuB₇⁻ and CuB₈⁻ clusters were formed by laser vaporization of a hot-pressed Cu/¹¹B disk target prepared using a natural isotope Cu powder and a ¹¹B-enriched (97%) boron powder. The laser-induced plasma was quenched by a helium carrier gas pulse seeded with 5% argon. Clusters formed inside the nozzle were mixed with the carrier gas and underwent a supersonic expansion to create a cold cluster beam. After passing a skimmer, anionic clusters from the collimated beam were extracted perpendicularly into the TOF mass spectrometer. The CuB₇⁻ and CuB₈⁻ clusters were mass-selected and decelerated before photodetachment. Three different photon energies were used in the current study, including 355 nm (3.496 eV) and 266 nm (4.661 eV) from a Nd:YAG laser, and 193 nm (6.424 eV) from an ArF excimer laser. Photoelectrons were collimated by the magnetic bottle with >90% collecting efficiency and analyzed in the 3.5-meter-long electron TOF tube. The photoelectron kinetic energies were calibrated using the known transitions of the Bi⁻ atomic anion. The kinetic energy (E_k) resolution (ΔE_k/E_k) of the apparatus was around 2.5%, which was around 25 meV for 1 eV electrons.

2.2. Theoretical methods

We utilized the Coalescence Kick (CK) algorithm⁵⁴ for the global minimum (GM) search. The CK algorithm randomly generated numerous structures that coalesced to the center of mass based on a predetermined parameter derived from the covalent radii of the involved atoms. In the first step, the generated structures of CuB₇/CuB₇⁻ and CuB₈/CuB₈⁻ were optimized to local minima in their respective lower (singlet/doublet) and higher (triplet/quartet) spin states at the MN15/def2-SVP level.^55,56 Large populations of the initial structures were considered for each stoichiometry, spin state, and charge states (Table S1, ESI†). The slightly larger population sizes for the anions were due to their greater tendency for dissociation. Calculations at this step were performed using the Gaussian16 suite.⁵⁷

In the second step, the non-dissociated structures found by the CK procedure in the first step were re-optimized and harmonic frequencies were calculated at the PBE0/def2-TZVPD level,^58–62 applying the UKS formalism for all cases regardless of the studied multiplicity. Additionally, the RIJCOSX approximation⁶³ with the universal def2/J auxiliary basis set^64,65 was used to accelerate the calculations, achieving SCF convergence with VeryTight criterion (TolE = 1e-9). For geometry optimization, we used the default NORMALOPT criterion. Isomers within 15 kcal mol⁻¹ from the lowest energy structure were evaluated at the CCSD(T)/aug-cc-pVQZ level,^66–69 with zero-point energy (ZPE) corrections at the PBE0/def2-TZVPD level. The wave functions for all GM structures and low-lying isomers were examined by the wave function stability test to ensure that the calculations converged to the ground states.⁷⁰ Unstable structures were re-converged towards the broken-symmetry solution, and their geometries were subsequently re-optimized. The first vertical detachment energy (VDE₁) was calculated at the PBE0/def2-TZVPD and CCSD(T)/aug-cc-pVQZ levels as the energy difference between the anion and the corresponding neutral species, both at the geometry of the anion. Higher VDEs were calculated employing PBE0/def2-TZVPD (time-dependent density functional theory, TD-DFT⁷¹) and the multireference NEVPT2^72,73/aug-cc-pVTZ^66–69 approach for both clusters and an additional reference approach IP-EOM-CCSD⁷⁴/aug-cc-pVQZ for CuB₈⁻, in all cases at the geometry of the corresponding anion. Due to the large number of MOs, the domain-based local pair natural orbital [DLPNO-CCSD(T) and DLPNO-CCSD] approximation^75–77 was applied with “TightPNO” settings to obtain an accurate energy. Quasi-restricted orbitals⁷⁸ (QROs) obtained from the UHF reference wavefunctions were applied to eliminate the influence of possible spin-contamination. The adiabatic detachment energy (ADE) was calculated as the energy difference between the anion and the corresponding neutral structure at their respective reoptimized geometries. Chemical bonding of the GM and selected isomers was analyzed employing the adaptive natural density partitioning (AdNDP) algorithm,⁷⁹ as implemented in the Multiwfn software.⁸⁰ The described calculations were performed via the ORCA 5.04 suite.^81,82 All ORCA computations were performed with the “defgrid3” settings for integration grids and C₁ point group symmetry. Visualization of molecular structures and the AdNDP results was performed using ChemCraft.⁸³

3 Experimental results

Photoelectron spectra of CuB₇⁻ and CuB₈⁻ taken at three different wavelengths are presented in Fig. 1 and 2, respectively. For each cluster, the observed PES bands are labeled with letters (X, A, B…) and the measured VDEs are given in Tables 1 and 2, respectively, where they are compared with the theoretical results. The label X′ in Fig. 1 refers to potential contributions from a low-lying isomer of CuB₇⁻. Band X in each spectrum represents the electron detachment transition from the ground state of the anion to that of the corresponding neutral, while bands A, B, C,… indicate detachment transitions to excited neutral states. The ADEs are determined by drawing a straight line at the leading edge of the ground state detachment transition and then adding the instrumental resolution, as given in Table 3, where they are also compared with the theoretical results. The ADE is equivalent to the electron affinity (EA) of the corresponding neutral cluster.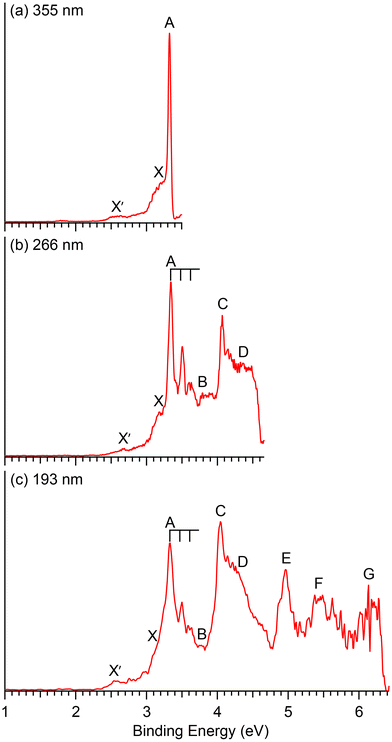

Fig. 1 Photoelectron spectra of CuB₇⁻ at (a) 355 nm (3.496 eV), (b) 266 nm (4.661 eV) and (c) 193 nm (6.424 eV).

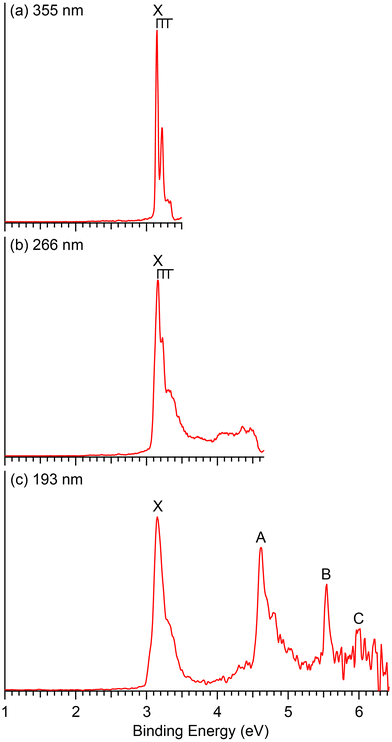Fig. 2 Photoelectron spectra of CuB₈⁻ at (a) 355 nm (3.496 eV), (b) 266 nm (4.661 eV) and (c) 193 nm (6.424 eV).

Table 1 The experimental vertical detachment energies (VDEs) in eV of CuB₇⁻ compared with theoretical VDEs for the GM structure (C_s, ²A′). VDE₁ was calculated at CCSD(T)/aug-cc-pVQZ. Higher VDEs were computed at NEVPT2(14,12)/aug-cc-pVTZ

	Final state and electron configuration	VDE (exp)^a	VDE (theo)
a The experimental uncertainty is ±0.02 eV.
X	^1A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^0}	3.17	3.26
A	^3A′′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^1(27a′)^1}	3.34	3.46
B	^1A′′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^1(27a′)^1}	3.79	3.68
C	^3A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^1(6a′′)^2(27a′)^1}	4.07	3.99
	^1A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^1(6a′′)^2(27a′)^1}		4.21
D	^3A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^1(26a′)^2(6a′′)^2(27a′)^1}	∼4.4	4.39
	^3A′′{…(22a′)^2(5a′′)^1(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		4.56
E	^1A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^2(25a′)^1(26a′)^2(6a′′)^2(27a′)^1}	4.97	4.97
	^3A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^1(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		5.04
F	^1A′{…(22a′)^2(5a′′)^2(23a′)^2(24a′)^1(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}	∼5.5	5.49
	^1A′′{…(22a′)^2(5a′′)^1(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		5.56
	^3A′{…(22a′)^1(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		5.59
	^1A′{…(22a′)^1(5a′′)^2(23a′)^2(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		5.62
	^3A′{…(22a′)^2(5a′′)^2(23a′)^1(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}		5.72
G	^nA′{…(22a′)^2(5a′′)^2(23a′)^1(24a′)^2(25a′)^2(26a′)^2(6a′′)^2(27a′)^1}	∼6.1	5.92

---

Table 2 The experimental vertical detachment energies (VDEs) in eV of CuB₈⁻ compared with theoretical VDEs for the GM structure (C_7v, ¹A₁). VDE₁ was calculated at CCSD(T)/aug-cc-pVQZ. Higher VDEs were computed at NEVPT2(17,12)/aug-cc-pVTZ

	Final state and electron configuration	VDE (exp)^a	VDE (theo)
a The experimental uncertainty is ±0.02 eV.
X	^2E1{…(3e2)^4(2e3)^4(11a1)^2(6e1)^4(7e1)^3}	3.15	3.07
A	^2E1{…(3e2)^4(2e3)^4(11a1)^2(6e1)^3(7e1)^4}	4.62	4.63
B	^2nA1{…(3e2)^4(2e3)^4(11a1)^1(6e1)^4(7e1)^4}	5.54	5.65
C	^2E3{…(3e2)^4(2e3)^3(11a1)^2(6e1)^4(7e1)^4}	∼6	6.02
	^2E2{… (3e2)^3(2e3)^4(11a1)^2(6e1)^4(7e1)^4}		6.15

---

Table 3 Comparison of the experimental ADE and VDE₁ (in eV) with theoretical values calculated at the PBE0/def2-TZVPD and CCSD(T)/aug-cc-pVQZ levels of theory for the GM structures of CuB₇⁻ and CuB₈⁻ and Iso1 and Iso2 of CuB₇⁻

	Final state	ADE (exp)^a	VDE (exp)^a	ADE (theo)		VDE1 (theo)
				CCSD(T)	PBE0	CCSD(T)	PBE0
a The experimental uncertainty is ±0.02 eV.
CuB7^−
GM	^1A′	2.98	3.17	2.91	3.17	3.26	3.23
Iso1	^3A2	2.41	2.63	2.37	2.13	2.46	2.32
Iso2	^1A′			2.15	2.01	2.43	2.30
CuB8^−
GM	^2E1	3.13	3.15	3.02	2.99	3.07	3.04

---

3.1. CuB₇⁻

The photoelectron spectra of CuB₇⁻ are complicated due to its open-shell nature (Fig. 1). The first PES band X is relatively weak and broad, yielding a VDE₁ of 3.17 eV and an estimated ADE of 2.98 eV. An intense and sharp peak is observed near the detachment threshold at 355 nm (Fig. 1a), which represents the 0–0 transition for band A, for which a short vibrational progression is resolved in the 266 nm spectrum (Fig. 1b). The VDE of band A is measured to be 3.34 eV and the vibrational spacing is ∼1150 cm⁻¹. A weak band B is discernable at 3.79 eV. A sharp and intense feature C is observed at 4.07 eV, followed by a congested broad feature around ∼4.4 eV designated as D. In the 193 nm spectrum, a well-defined band E is observed at 4.97 eV, whereas two broad features F and G can be tentatively identified at ∼5.5 eV and ∼6.1 eV, respectively. A weak broad feature X′ is also observed on the low binding energy side at ∼2.6 eV, which is likely due to the presence of a low-lying isomer.

3.2. CuB₈⁻

The photoelectron spectra of CuB₈⁻ appear very simple with only four well-separated detachment transitions (Fig. 2), suggesting a highly symmetric and closed-shell cluster. A short vibrational progression is observed for the ground state transition (band X) with a spacing of ∼600 cm⁻¹. The VDE, defined by the sharp 0–0 transition, is 3.15 eV, while the ADE is estimated from its leading edge to be 3.13 eV to account for possible unresolved low-frequency vibrations. The sharp and short vibrational progression for the ground state transition indicates a small geometry change between the ground state of the anion and that of the neutral CuB₈. No more major detachment transitions are observed in the 266 nm spectrum (Fig. 2b), except some weak and broad signals above 4 eV, which may be due to contributions from impurities. The masses of both Cu₂B₂⁻ (m/z = 148–152) and B₁₄⁻ (m/z = 154) are close to that of CuB₈⁻ (m/z = 151–153) and they could be candidates for the weak signals.¹³ At 193 nm (Fig. 2c), two strong and sharp bands A and B are clearly observed at VDEs of 4.62 eV and 5.54 eV, respectively. A relatively weak band C is also discernible at a VDE around 6 eV on the high binding energy side with poor signal-to-noise ratios.

4 Theoretical results

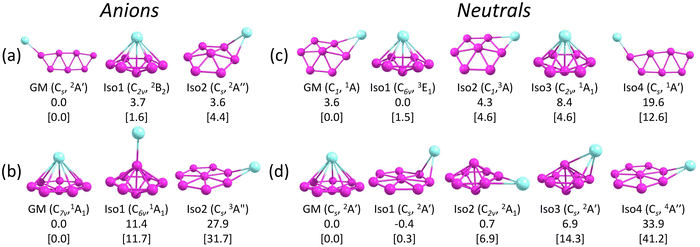
Fig. 3 presents the GM structures of CuB₇⁻ and CuB₈⁻ and their neutral counterparts with several low-lying isomers arranged by the relative energies at the CCSD(T) level of theory. Additional low-lying structures are shown in Fig. S1 and S2 (ESI†) for the anions and neutrals, respectively. Recently, the structures of the neutral CuB₇ and CuB₈ species were examined at the DFT level of theory.⁸⁴ While some of the previously reported structures agree with the current CCSD(T) relative energy ordering, several of them are substantially different, highlighting the importance of employing more accurate methods along with experimental verification. The coordinates of the GM of CuB₇⁻ and CuB₈⁻ and low-lying isomers of CuB₇⁻ and the corresponding neutrals are provided in the xyz format as an additional zip file in the ESI.†

Fig. 3 The GM structures and selected low-lying isomers of (a) CuB₇⁻, (b) CuB₈⁻, (c) CuB₇, and (d) CuB₈. Point groups and spectroscopic states are shown in the parentheses. Relative energies in kcal mol⁻¹ are given at PBE0/def2-TZVPD, with the CCSD(T)/aug-cc-pVQZ values shown in brackets.

4.1. CuB₇⁻ and CuB₇

Several low-lying isomers are identified for CuB₇⁻, as shown in Fig. 3a. The GM structure (C_s, ²A′) features a planar double-chain B₇ motif with the Cu atom bonded to one of the two apex boron atoms. The electronic stability of this structure can be glimpsed by its large SOMO–LUMO gap (alpha electrons) of 3.12 eV at the PBE0/def2-TZVPD level. The first low-lying isomer, Iso1 (C_2v, ²B₂), which is only 1.6 kcal mol⁻¹ above the GM structure at CCSD(T), adopts a half-sandwich structure, with the Cu atom located above a hexagonal B₇ motif. Similar half-sandwich architectures were previously found in other complexes involving the η⁷-B₇³⁻ borozene motif.^44,45,50 However, Iso1 of CuB₇⁻ (C_2v, ²B₂) is one electron short of a B₇³⁻ borozene configuration, which is why it is not the GM. The B₇ motif in Iso1 is similar to the first low-lying isomer of the bare B₇⁻ cluster.⁴³ The second low-lying isomer, Iso2 (C_s, ²A′′), which is 4.4 kcal mol⁻¹ above the GM structure, is another derivative of the distorted hexagonal B₇ motif, where the Cu atom is bonded to its edge bridging two boron atoms. All other isomers are at least 11.0 kcal mol⁻¹ higher in energy than the GM structure (Fig. S1A, ESI†). Electron detachment from CuB₇⁻ leads to significant destabilization of the double chain structure, making it energetically less stable by 12.6 kcal mol⁻¹ than the GM structure of neutral CuB₇ at CCSD(T) (Fig. 3c). The GM and the first three low-lying isomers of neutral CuB₇ all feature the hexagonal B₇ motif, differing in the position of the Cu atom and in the spin states, as shown in Fig. 3c.

4.2. CuB₈⁻ and CuB₈

The GM of CuB₈⁻ (C_7v, ¹A₁) adopts a half-sandwich structure (Fig. 3b), in which the B₈ motif is quasi-planar with the central B atom slightly moving out of the B₇ plane by 0.35 Å away from the Cu atom relative to the planar bare B₈.¹² The large HOMO–LUMO gap of 3.05 eV indicates the high electronic stability of the CuB₈⁻ GM. In contrast to CuB₇⁻, the closest low-lying isomer of CuB₈⁻, Iso1, is 11.7 kcal mol⁻¹ higher in energy than the GM at the CCSD(T) level. The high stability of the C_7v CuB₈⁻ GM is related to the high stability of the B₈²⁻ borozene.⁴⁷ Iso1 of CuB₈⁻ (C_6v, ¹A₁) has a 3D bipyramidal boron framework bonded to Cu at the top, which is reminiscent of the umbrella structure of B₉O⁻ [B₈(BO)⁻].⁵⁰ In the next isomer, Iso2 (C_s, ³A′′), which is 31.7 kcal mol⁻¹ higher than the GM, the Cu atom is bonded to the edge of the planar B₈ moiety, similar to the GM of AuB₈⁻.⁴⁹ More high energy isomers for CuB₈⁻ are given in Fig. S1B (ESI†). Electron detachment from the GM of CuB₈⁻ leads to a minor geometry reorganization, reducing its symmetry from C_7v to C_s in the GM of the open-shell CuB₈ (²A′) (Fig. 3d). However, Iso1 of CuB₈ (C_s, ²A′) is almost degenerate with the GM, where the Cu atom is bonded to the edge of the planar B₈ motif. Iso2 of CuB₈ (C_2v, ²A₁), which is 6.9 kcal mol⁻¹ above the GM, consists of a bipyramidal B₈ motif with the Cu atom bonded to its equator. The potential energy surface of neutral CuB₈ is much flatter in comparison with that of the anion.

5 Discussion

5.1. Comparison between experiment and theory

The GM structures of CuB₇⁻ and CuB₈⁻ are verified by comparison with the experimental PES data. The computed ADE and VDE₁ values at both the PBE0/def2-TZVPD and CCSD(T)/aug-cc-pVQZ levels of theory for the GM structures of CuB₇⁻ and CuB₈⁻ and the two low-lying isomers of CuB₇⁻ are compared with the experimental data in Table 3.

5.1.1. Strong electron correlation effects in CuB₇⁻ and CuB₈⁻ and suitable methods to compute higher VDEs. The MOs for the GM and low-lying isomers of CuB₇⁻ are displayed in Fig. S3–S5 (ESI†) and those for the GM of CuB₈⁻ are shown in Fig. S6 (ESI†). Since the GM of CuB₈⁻ possesses a closed-shell electron configuration, each fully occupied MO results in one electron detachment channel, leading to a doublet final state and relatively simple PE spectra. In contrast, electron detachment from the open-shell doublet CuB₇⁻ cluster yields both singlet and triplet final states, resulting in significantly more complicated spectral features. To compute higher detachment channels for boron-metal clusters, we have usually used the TD-DFT method⁷¹ and have found that it generally gives satisfactory results suitable for the interpretation of experimental PES data.^44–53 However, we discovered surprisingly that the TD-DFT method was no longer reliable for CuB₇⁻ (Fig. S7, ESI†) and CuB₈⁻ (Fig. S8, ESI†). In particular, TD-DFT completely failed for CuB₈⁻ beyond the second detachment channel (Fig. S8, ESI†). Therefore, we have tested alternative and more expensive methods to compute the VDEs for CuB₇⁻ and CuB₈⁻.

We first applied the accurate IP-EOM-CCSD/aug-cc-pVQZ approach⁷⁴ for the closed-shell CuB₈⁻ as a reference method and found that it gave excellent results in comparison with the experiment (Fig. S8, ESI†). However, the IP-EOM-CCSD method cannot be used for the open-shell CuB₇⁻. We next examined the multi-reference method, NEVPT2(17,12),^68,69 for CuB₈⁻ and found that it also gave excellent results similar to those using the IP-EOM-CCSD method (Fig. S8, ESI†). Finally, we used the NEVPT2(14,12) method to compute higher VDEs for CuB₇⁻ (Fig. S7, ESI†). For consistency and accuracy, we will use the multi-reference NEVPT2 results to compare with the PE spectra of CuB₇⁻ and CuB₈⁻, as shown in Fig. 4. The calculated VDEs for higher detachment channels of the GM structures at the NEVPT2/aug-cc-pVTZ level of theory are compared with the experimental results in Tables 1 and 2 for CuB₇⁻ and CuB₈⁻, respectively.

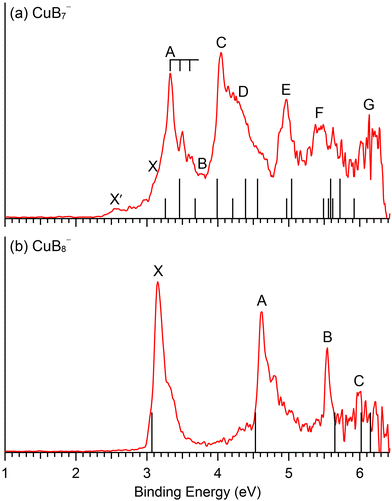Fig. 4 Comparison between the 193 nm PE spectra and the computed VDEs (vertical bars) for the GM of (a) CuB₇⁻ and (b) CuB₈⁻. In (a), the short bars correspond to singlet final states and the longer bars correspond to triplet final states. See Fig. S11 (ESI†) delineating potential contributions of the low-lying isomers of CuB₇⁻ to the weak X′ signals.

5.1.2. CuB₇⁻. The calculated ADE/VDE₁ values for the GM of CuB₇⁻ are 2.91/3.26 eV at the CCSD(T) level, in good agreement with the experimental data of 2.98/3.17 eV for the X band (Table 3). The first VDE corresponds to electron detachment from the SOMO, mostly localized on the apex boron atom in the double chain B₇ framework opposite to the Cu atom (Fig. S3, ESI†). This orbital is ready to bond to another Cu atom to form the closed-shell Cu₂B₇⁻ cluster.⁵² The removal of the SOMO electron results in significant structural changes (Fig. S9, ESI†): the B–B bonds between the apex boron atom and its two neighbors are significantly shortened, as well as a large in-plane bond angle change between the Cu–B bond relative to the B₇ framework. These large geometry changes are consistent with the broad X band observed in the PE spectra (Fig. 1).

Electron detachment from the HOMO (6a′′) yields a triplet and singlet final state with computed VDEs of 3.46 and 3.68 eV, respectively, in good accord with the observed A and B bands at 3.34 and 3.79 eV (Table 1). The HOMO of CuB₇⁻ is a π orbital in the B₇ motif (Fig. S3, ESI†). Electron detachment from this orbital is expected to induce in-plane B–B stretching vibrations. While we could not compute the vibrational frequencies for the triplet excited state of the corresponding neutral CuB₇, the computed B–B stretching frequencies for the ground state, ranging from 1313 cm⁻¹ (ν₃) to 1054 cm⁻¹ (ν₅) (Fig. S10, ESI†), are consistent with the observed frequency of ∼1150 cm⁻¹ for band A. Detachment from the HOMO−1 (26a′) gives rise to a computed VDE of 3.99 eV for the triplet final state, in good agreement with the measured VDE of 4.07 eV for band C. The calculated VDE for the singlet final state from detachment of the HOMO−1 (4.21 eV) and those for the triplet final states from detachment from the HOMO−2 (25a′) (4.39 eV) and HOMO−5 (5a′′) (4.56 eV) are close to band C and to each other, consistent with the broad overlapping band D. The computed VDE for the singlet final state from detachment from the HOMO−2 (4.97 eV) and that for the triplet final state from detachment from the HOMO−3 (24a′) (5.04 eV) are close to each other and are in excellent agreement with the well-resolved band E at 4.97 eV. A dense manifold of detachment channels is found in the higher binding energy side, consistent with the congested bands F and G. The overall computed VDEs match well with the complex experimental PES pattern (Fig. 4a), providing considerable credence to the double chain GM structure of CuB₇⁻. It should be noted that the PE spectral pattern of CuB₇⁻ displays some resemblance to that of Cu₂B₇⁻,⁵² which is closed-shell with a similar double chain structure and gives much better resolved PE spectra because each occupied MOs only result in one double final state.

The computed ADE/VDE₁ values for Iso1 (C_2v, ²B₂) of 2.37/2.46 eV agree with the observed values of 2.41/2.63 eV for the minor X′ band (Table 3), suggesting its presence experimentally due to its close energy relative to the GM (Fig. 3a). Higher VDEs of Iso1 would be masked by the dominant signals of the C_s GM. Iso2 (C_s, ²A′′) can be ruled out because no PES signals were observed near its calculated ADE/VDE₁ at 2.15/2.43 eV. The observation of Iso1 provides further evidence for the identified GM for CuB₇⁻.

5.1.3. CuB₈⁻. The GM of CuB₈⁻ (C_7v, ¹A₁) is significantly more stable than other isomers (Fig. 3b), suggesting no other isomers were present experimentally. The closed-shell and highly symmetric GM of CuB₈⁻ gives rise to a very simple PES pattern. The computed ADE/VDE₁ values of 3.02/3.07 eV at CCSD(T) for the C_7v CuB₈⁻ are in good agreement with the experimental value of 3.13/3.15 eV (Table 3). Electron detachment from the HOMO (7e₁) (Fig. S6, ESI†) leads only to minor structural reorganization for the neutral ground state (Fig. S12, ESI†), breaking the C_7v symmetry to C_s and resulting in a short vibrational progression. The 600 cm⁻¹ vibrational frequency observed for the X band is consistent with the computed frequencies for both the ν₁₀ (601 cm⁻¹) and ν₁₁ (593 cm⁻¹) modes (Fig. S13, ESI†), either of which would lead to a structural distortion from C_7v to C_s in the neutral final state. The very small geometry change upon electron detachment in the CuB₈ neutral is in accord with the high stability of the B₈ borozene framework.⁴⁷

The second detachment channel for CuB₈⁻ is from the HOMO−1 (6e₁) with a computed VDE of 4.63 eV, in excellent agreement with band A at 4.62 eV. There are unresolved vibrational features for band A. The third detachment channel is from the HOMO−2 (11a₁) with a computed VDE of 5.65 eV, agreeing well with the observed VDE of band B at 5.54 eV. Band B is an extremely sharp peak without any discernible vibrational feature, in agreement with the nondegenerate 11a₁ HOMO−2, which is mainly a σ bonding MO on the B₇ ring of the B₈ motif with a small contribution from the Cu 3d_z2 orbital (Fig. S6, ESI†). The fourth and fifth detachment channels from the HOMO−3 (2e₃) and HOMO−4 (3e₂) give similar computed VDEs of 6.02 eV and 6.16 eV, respectively, in good agreement with the weak band C at ∼6 eV. The excellent agreement between the simple spectral pattern observed for CuB₈⁻ and the computed VDEs (Fig. 4b) provides unequivocal evidence for the C_7v GM structure of CuB₈⁻.

5.2. Borozenes and the chemical bonding in the CuB₇⁻ and CuB₈⁻ clusters

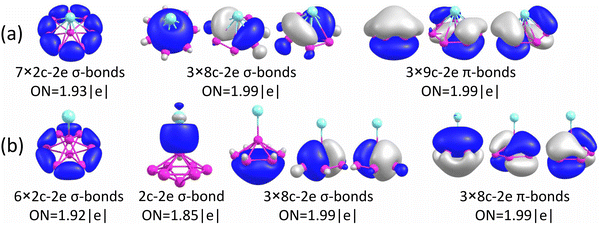
The chemical bonding for the GM and Iso1 structures of CuB₇⁻ and CuB₈⁻ is analyzed using the AdNDP method, as shown in Fig. 5 and 6, respectively. In all cases, the Cu 3d electrons are found primarily as five 3d lone pairs, i.e., one-center two electron (1c–2e) AdNDP elements, and they are omitted from the figures for clarity. The occupation numbers (ONs) for the Cu 3d electron pairs are found to be in the range of 2.00–1.91|e|, consistent with the fact that they are essentially non-bonding localized electron pairs on the Cu atom in each cluster.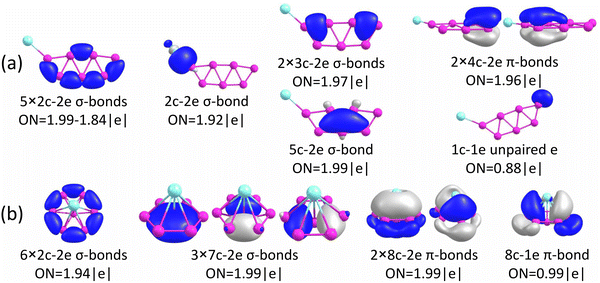

Fig. 5 Results from AdNDP bonding analyses for (a) the GM of CuB₇⁻ (C_s, ²A′) and (b) Iso1 of CuB₇⁻ (C_2v, ²B₂).

Fig. 6 Results from AdNDP bonding analyses for (a) the GM of CuB₈⁻ (C_7v, ¹A₁) and (b) Iso1 of CuB₈⁻ (C_6v, ¹A₁).

5.2.1. CuB₇⁻. The GM of CuB₇⁻ consists of a boron double chain structure bonded to the Cu atom at one of the two apex boron atoms via a two-center two-electron (2c–2e) Cu–B σ-bond with ON = 1.92|e| (Fig. 5a). The periphery of the boron framework is characterized by five 2c–2e B–B σ-bonds with ON = 1.99–1.84|e| and two 3c–2e B–B–B σ-bonds with ON = 1.97|e| (in lieu of the two missing peripheral 2c–2e B–B σ-bonds, which have appreciably lower ON values of 1.64–1.60|e|). The planarity of the cluster is supported by the presence of one delocalized 5c–2e σ-bond with ON = 1.99|e| and two delocalized 4c–2e π-bonds with ON = 1.96|e|. The doublet spin state of CuB₇⁻ arises from the unpaired electron on the apex boron atom located farthest from the Cu atom. The double chain motif is a higher energy isomer for B₇⁻,⁴³ which is stabilized by the Cu−B covalent bond. The further derivative of this double-chain structure was investigated for Cu₂B₇⁻, resulting from the addition of the second Cu atom to the unpaired electron of the apex boron atom, forming a highly stable closed-shell cluster, as reported recently.⁵² Similar double chain structures and bonding have also been found in Au₂B₇⁻ and H₂B₇⁻.^85,86 The double chain structure of B₇ is stabilized by the covalent bonds between the apex boron atoms with the Cu (or Au/H) atoms.

Iso1 of CuB₇⁻ possesses a half-sandwich structure, which is only 1.6 kcal mol⁻¹ higher in energy than the double chain GM (Fig. 3a) and can be viewed as Cu coordinated by the hexagonal B₇⁻. The GM of B₇⁻ has a C_6v structure with a triplet ground state.⁴³ As shown recently, adding two electrons to B₇⁻ leads to the closed-shell doubly aromatic B₇³⁻ borozene with six delocalized σ and six delocalized π electrons.⁴⁷ The B₇³⁻ closed-shell electron configuration was first realized in the C_6v PrB₇, i.e., [Pr³⁺][ B₇³⁻] with a half-sandwich structure.⁴⁵ However, Cu can only contribute one valence electron to B₇⁻, resulting in the doublet state for Iso1 of CuB₇⁻ with one partially filled π orbital (Fig. S4, ESI†). The ensuing Jahn–Teller distortion in the open shell Iso1 would lead to the C_2v symmetry. The AdNDP results reveal precisely this bonding picture, as shown in Fig. 5b. In addition to the six peripheral 2c–2e B–B σ-bonds on the B₇ motif, we observe three delocalized 7c–2e σ bonds, two 8c–2e π bonds, and one 8c–1e π bond. Hence, the half-sandwich Iso1 of CuB₇⁻ can be viewed as [Cu⁺][B₇²⁻], which is one electron short of the closed-shell B₇³⁻ borozene configuration. Clearly, ionic interactions are dominant between Cu and the B₇ motif in Iso1, whereas in the double chain GM of CuB₇⁻ the Cu−B covalent interaction dominates. The NPA charge of Cu in the double chain GM of CuB₇⁻ is only +0.29|e|, consistent with more covalent interactions, in comparison to a value of +1.00|e| in the ionic Iso1 of CuB₇⁻. The missing π electron in the [Cu⁺][B₇²⁻] open-shell borozene complex is the reason why Iso1 has slightly lower stability compared to the double chain GM structure.

5.2.2. CuB₈⁻. The AdNDP analyses reveal a simple bonding picture for the GM of CuB₈⁻ (Fig. 6a): seven peripheral 2c–2e B–B σ-bonds, three delocalized σ bonds, and three delocalized π bonds. In other words, it is an electron-precise doubly aromatic B₈²⁻ borozene complex, [Cu⁺][B₈²⁻], which underlies its overwhelming stability relative to other isomers of CuB₈⁻ (Fig. 3b). The NPA charge of +1.00|e| on Cu in the GM of CuB₈⁻ indicates that Cu basically donates its 4s electron to the B₈ motif to fulfill the closed-shell B₈²⁻ borozene electron configuration. Notably, in the previously studied Cu₂B₈ cluster,⁵¹ a similar structural motif was found. It consists of a B₈²⁻ borozene with a Cu₂ dimer located atop, forming a charge-transfer complex [Cu₂⁺][B₈²⁻]. In the GM of neutral CuB₈, one π electron is detached, leading to its symmetry breaking from C_7v to C_s and also a reduction of stability relative to the low-lying isomers (Fig. 3d). It was previously found that the high stability of the B₈²⁻ borozene even stabilized the rare +1 oxidation state of lanthanides in a series of LnB₈⁻ complexes, i.e., [Ln⁺][B₈²⁻].⁴⁷

As shown above for the CuB₇⁻ cluster and other Cu–B clusters,^51–53 Cu can interact with boron clusters both covalently and ionically. We have found that in CuB₈⁻ the position of the Cu atom around the B₈²⁻ borozene molecular wheel dictates the degree of covalent interactions between the Cu atom and the borozene framework. For example, the shift of the Cu atom from the center position to the edge, and ultimately to the side in a planar structure, results in a decrease of the NPA charge on the Cu atom from +1.00|e| to +0.76|e|, and finally to +0.67|e| (Fig. S14A, ESI†). Thus, just like that in the case of Iso1 of CuB₇⁻ discussed above, the half-sandwich structure facilitates the most significant charge transfer from Cu to the B₈ motif and leads to the formation of the stable closed-shell C_7v [Cu⁺][B₈²⁻] borozene complex. Previously, it was found that the LiB₈⁻ cluster also had the C_7v [Li⁺][B₈²⁻] structure,⁴⁶ and all the LnB₈⁻ clusters had similar C_7v [Ln⁺][B₈²⁻] structures.⁴⁷

Interestingly, the GM of AuB₈⁻ is known to consist of the B₈ wheel with the Au atom bonded at the side,⁴⁹ due to the fact that Au tends to engage in strong covalent bonding as a result of the strong relativistic effects.^87,88 The C_7v AuB₈⁻ structure, which has the strongest ionic interactions, is not even a minimum on the potential energy surface with two imaginary frequencies (Fig. S14B, ESI†). The GM of AuB₈⁻ exhibits the lowest charge transfer, i.e., the strongest covalent interaction between Au and B, as shown in Fig. S14B (ESI†) and also previously.⁴⁹ Furthermore, unlike transition metal doped boron clusters,^35–37 the Cu©B₈⁻ molecular wheel structure is disfavored, less stable than the GM by 45.3 kcal mol⁻¹ (Fig. S1B, ESI†), owing to the lacking of d–p covalent interactions between Cu and the B₈ ring.⁸⁹

The chemical bonding of the umbrella-shaped low-lying Iso1 of CuB₈⁻ is also very interesting. It is identical to that found in the umbrella-shaped B₉O⁻ cluster, i.e., [B₈–BO]⁻,⁵⁰ by replacing the BO unit with the Cu atom. The central B atom can be viewed as forming a covalent bond with the Cu atom, while sharing its three valence electrons with the hexagonal B₇ unit to fulfill the B₇³⁻ borozene configuration. Thus, both the GM and the low-lying isomer of CuB₈⁻ involve the borozene motifs, the B₈²⁻ borozene in the GM and the B₇³⁻ borozene in Iso1. These results provide further confirmation of the high stability of the borozenes B₇³⁻ and B₈²⁻.

6 Conclusions

We report a joint photoelectron spectroscopy and theoretical study of two Cu-doped boron clusters CuB₇⁻ and CuB₈⁻. Well-resolved photoelectron spectra are obtained for the two clusters and are combined with theoretical calculations to understand their structures and bonding. The global minimum of CuB₇⁻ consists of a double-chain B₇ boron motif with a copper atom covalently bonded to one of its two apex boron atoms, whereas the low-lying isomer of CuB₇⁻ is found to be a half-sandwich structure involving the open-shell B₇²⁻ borozene. The global minimum of CuB₈⁻ reveals a highly stable copper–borozene complex with a copper atom coordinated by the η⁸-B₈²⁻ borozene. The current results provide not only new examples of borozene complexes, but also further insight about the interactions between copper and boron atoms and the competition between covalent and ionic interactions. The strong electron correlation effects found in the CuB₇⁻ and CuB₈⁻ clusters will also have implications for understanding the electronic structure of other copper–boron systems.

Data availability

The data that supports the findings of this study is available from the corresponding authors upon reasonable request.

Author contributions

L. S. W., I. A. P., and A. I. B. designed the project. W. J. C. and H. W. C. with help from D. F. Y. performed the experiment. A. S. P. performed the theoretical calculations and bonding analyses. W. J. C., A. S. P., I. A. P., and L. S. W. wrote and edited the manuscript. All authors helped to analyze the experimental and theoretical results.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The experiment done at Brown University was supported by the National Science Foundation (CHE-2053541). Computational resources from the ARCC HPC cluster of the University of Akron are gratefully acknowledged. I.A.P. acknowledges the start-up funding from the University of Akron.

References

1. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
2. E. D. Jemmis and D. L. V. K. Prasad, J. Solid State Chem., 2006, 179, 2768–2774.
3. A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867.
4. A. Gindulyte, W. N. Lipscomb and N. L. Massa, Inorg. Chem., 1998, 37, 6544–6545.
5. I. Boustani and A. Quandt, Europhys. Lett., 1997, 39, 527–532.
6. I. Boustani, A. Quandt, E. Hernandez and A. Rubio, J. Chem. Phys., 1999, 110, 3176–3185.
7. M. H. Evans, J. D. Joannopoulos and S. T. Pantelides, Phys. Rev. B, 2005, 72, 045434.
8. H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501.
9. X. Yang, Y. Ding and J. Ni, Phys. Rev. B, 2008, 77, 041402.
10. H. J. Zhai, L. S. Wang, A. N. Alexandrova and A. I. Boldyrev, J. Chem. Phys., 2002, 117, 7917–7924.
11. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai, L. S. Wang, E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2003, 107, 1359–1369.
12. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
13. H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833.
14. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
15. E. Oger, N. R. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
16. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
17. L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142.
18. T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
19. S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744.
20. D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 251–268.
21. A. I. Boldyrev and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 11589–11605.
22. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
23. W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260.
24. A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, et al. , Science, 2015, 350, 1513–1516.
25. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
26. S. Y. Xie, Y. Wang and X. B. Li, Adv. Mater., 2019, 31, 1900392.
27. Y. V. Kaneti, D. P. Benu, X. Xu, B. Yuliarto, Y. Yamauchi and D. Golberg, Chem. Rev., 2022, 111, 1000–1052.
28. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
29. W. J. Chen, Y. Y. Ma, T. T. Chen, M. Z. Ao, D. F. Yuan, Q. Chen, X. X. Tian, Y. W. Mu, S. D. Li and L. S. Wang, Nanoscale, 2021, 13, 3868–3876.
30. L. Sai, X. Wu, N. Gao, J. Zhao and R. B. King, Nanoscale, 2017, 9, 13905–13909.
31. C. Chen, H. Lv, P. Zhang, Z. Zhuo, Y. Wang, C. Ma, W. Li, X. Wang, B. Feng, P. Cheng, X. Wu, K. Wu and L. Chen, Nat. Chem., 2022, 14, 25–31.
32. X. Liu, Q. Li, Q. Ruan, M. S. Rahn, B. I. Yakobson and M. C. Hersam, Nat. Mater., 2022, 21, 35–40.
33. W. L. Li, X. Chen, T. Jian, T. T. Chen, J. Li and L. S. Wang, Nat. Rev. Chem., 2017, 1, 0071.
34. J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123.
35. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
36. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
37. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
38. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
39. T. Jian, W. L. Li, I. A. Popov, G. V. Lopez, X. Chen, A. I. Boldyrev, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 154310.
40. W. L. Li, T. Jian, X. Chen, H. R. Li, T. T. Chen, X. M. Luo, S. D. Li, J. Li and L. S. Wang, Chem. Commun., 2017, 53, 1587–1590.
41. W. L. Li, T. Jian, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2016, 55, 7358–7363.
42. T. Jian, W. L. Li, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Chem. Sci., 2016, 7, 7020–7027.
43. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2004, 108, 3509–3517.
44. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Chem. Phys., 2011, 135, 104301.
45. T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 6916–6920.
46. A. N. Alexandrova, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3552–3554.
47. W. L. Li, T. T. Chen, W. J. Chen, J. Li and L. S. Wang, Nat. Commun., 2021, 12, 6467.
48. W. J. Chen, M. Kulichenko, H. W. Choi, J. Cavanagh, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2021, 125, 6751–6760.
49. W. J. Chen, Y. Y. Zhang, W. L. Li, H. W. Choi, J. Li and L. S. Wang, Chem. Commun., 2022, 58, 3134–3137.
50. W. J. Tian, W. J. Chen, M. Yan, R. Li, Z. H. Wei, T. T. Chen, Q. Chen, H. J. Zhai, S. D. Li and L. S. Wang, Chem. Sci., 2021, 12, 8157–8164.
51. M. Kulichenko, W. J. Chen, H. W. Choi, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Vac. Sci. Technol., 2022, 40, 042201.
52. A. S. Pozdeev, W. J. Chen, M. Kulichenko, H. W. Choi, A. I. Boldyrev and L. S. Wang, Solid State Sci., 2023, 142, 107248.
53. A. S. Pozdeev, W. J. Chen, H. W. Choi, M. Kulichenko, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2023, 127, 4888–4896.
54. A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2011, 134, 224304.
55. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
56. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
57. M. J. Frisch, et al., Gaussian 16, revision A.03, Gaussian, Inc., Wallingford, CT, 2009.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
60. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
61. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
62. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
63. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
64. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
65. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
66. H. J. Monkhorst, Int. J. Quantum Chem., 2009, 12, 421–432.
67. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
68. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
69. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
70. R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052.
71. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
72. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
73. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
74. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
75. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
76. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
77. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
78. F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222.
79. D. Yu Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
80. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
81. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78.
82. F. Neese, WIREs Comput. Mol. Sci., 2018, 8, 1327.
83. G. A. Zhurko, Chemcraft - Graphical Software for Visualization of Quantum Chemistry Computations. Ivanovo, Russia, 2005, https://www.chemcraftprog.com.
84. P. L. Rodríguez-Kessler, A. Vasquez-Espinal and A. Munoz-Castro, Polyhedron, 2023, 243, 116538.
85. H. J. Zhai, L. S. Wang, D. Y. Zubarev and A. I. Boldyrev, J. Phys. Chem. A, 2006, 110, 1689–1693.
86. W. L. Li, C. Romanescu, T. Jian and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 13228–13231.
87. P. Pyykkö, Chem. Rev., 1988, 88, 563–594.
88. L. S. Wang, Phys. Chem. Chem. Phys., 2010, 12, 8694–8705.
89. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00296b

‡ These authors contributed equally to this work.

---