Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimizing through-space interaction for singlet fission by using macrocyclic structures†
Zhangxia
Wang
a,
Xuexiao
Yang
a,
Haibo
Ma
 *b and
Xiaoyu
Xie
*c
*b and
Xiaoyu
Xie
*c
aSchool of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210023, China
bQingdao Institute for Theoretical and Computational Sciences, Qingdao Institute of Frontier and Interdisciplinary Science, Shandong University, Qingdao 266237, China. E-mail: haibo.ma@sdu.edu.cn
cDepartment of Chemistry, University of Liverpool, Liverpool L69 3BX, UK. E-mail: xiaoyu@liverpool.ac.uk
First published on 2nd May 2023
Abstract
There is great interest in the exploitation of singlet fission (SF) materials to improve the power conversion efficiency (PCE) of solar cells. Usually, ultrafast SF is achieved as an intermolecular process (xSF). However, it isn’t easy to precisely tune crystal packing in the experiment. In contrast, electronic structural properties can be exactly tuned in intramolecular SF (iSF) materials by changing different linkers. Nevertheless, few designs can achieve ultrafast SF in iSF materials. In this work, we use macrocyclic structures to maintain the π–π packing between two pentacenes and optimize through-space interaction in iSF. First, we conduct a detailed discussion on the experimentally discovered bipentacene macrocycle (BPc) and phenylene-linked bipentacene (BP1) by performing high-level electronic structure calculations and molecular dynamics (MD) sampling. The calculated iSF rates are in good agreement with experimental measurements. More importantly, the macrocyclic scaffold in BPc only plays a role in restricting the relative position of two pentacenes and does not affect the electronic coupling between excited states. Accordingly, 19 optimal structures are screened out from 97 initial candidates, and those 19 systems exhibit remarkably efficient iSF features with unprecedented ultrafast time constants (tens of femtoseconds).
1 Introduction
Singlet fission (SF) is a photophysical process typical of some organic compounds, where a high-energy singlet state splits into two low-energy triplet states. Compared with conventional semiconductor materials, SF materials generate two excitons from one single absorbed photon, which can achieve photocurrent multiplication theoretically.1,2 It has been demonstrated that sensitizing solar cells using singlet fission can reduce thermalization losses and improve light sensitivity.3–9 To break the 45% power conversion efficiency limit of conventional photovoltaic devices,1 scientists have devoted great efforts to unravelling the SF mechanisms10–17 and discovering more effective SF materials.18–26An efficient SF process requires sufficiently large electronic coupling between two chromophores in addition to satisfying the energy level matching conditions (E(S1) ≥ 2E(T1) and E(T2) ≥ 2E(T1)).18 Usually, electronic couplings originate from close packing between adjacent chromophores in intermolecular singlet fission (xSF, see in Fig. 1a). It is generally believed that slip-stacked packing is beneficial to singlet fission.21,27–30 Wang et al. illustrated that slip-stacked packing could increase the SF rate by more than an order of magnitude compared to cofacial stacking of pentacene through nonadiabatic molecular dynamics calculations.29 In both experiment and calculation work, people can modulate molecular packing and electronic properties by introducing either the heteroatom in the backbone or terminally halogenated modification,31–39 changing the side groups40–45 or adding spacer molecules between SF chromophores.46 However, in crystalline media, photophysical processes depend not only on crystal packing but also on the influence of many other factors, such as crystallinity, morphology, and defects.47–53 Despite creative endeavours in this regard, tuning electronic properties in the solid state is experimentally challenging because interchromophoric interaction is highly sensitive to slight changes in chromophore arrangement.
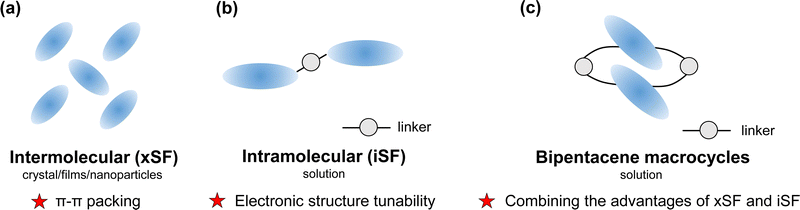 | ||
| Fig. 1 Summary of characteristics in (a) intermolecular singlet fission (xSF) and (b) intramolecular singlet fission (iSF) and (c) the design strategy for bipentacene macrocycles. | ||
During the past decade, intramolecular singlet fission (iSF) has attracted many research interests because of its precise tunability of number, connectivity, and interchromophoric interactions.54–66 Moreover, the iSF process can be easily tuned by changing the chemical composition of the linker (Fig. 1b). Since 2015, dimers,22,67,68 oligomers69–74 and polymers75 of chromophore molecules (e.g., acene or rylene) have been discovered for iSF. Among the chromophores, pentacene and tetracene are the most extensively studied because of their high charge mobility and well energy level matching for SF.18,76–78 It has been recently reported that introducing different linkers between the two pentacenes can change singlet fission rates by orders of magnitude (from femtosecond to nanosecond).54,60,79
Can we take advantage of the molecular control inherent in iSF to help the challenging control of packing in xSF? (Fig. 1c). Are there other ways to achieve slip-stacked packing between chromophores? Over a half-century, the synthesis of structurally specific macrocycles has developed rapidly,80–82 providing the possibility to synthesize chromophore-containing macrocycles. This idea was verified by Tilley's group in 2020.83 They reported two types of pentacene-containing macrocycles: pentacene dimerized macrocycles, and pentacene trimerized macrocycles. The pentacene dimerized macrocycle (marked as 1b in their work) exhibits an ideal SF rate (13.8 ps) and triplet yield (170%) in chloroform solution. Similarly, Yoshizawa et al.84 demonstrated that the macrocyclic framework facilitates the interaction between three adjacent pentacene units, resulting in efficient SF in solution. According to the SF behaviour brought by the structure specificity of macrocycles, it looks promising to design a variety of ideal SF materials.
Before designing bipentacene macrocycles, it is necessary to find out how iSF occurs in the macrocycles. There are two driving forces in iSF systems: through-space and through-bond interactions. It has been proved theoretically and experimentally that through-bond interactions play a crucial role for many bipentacenes, such as the well-known ortho-, meta- and para-pentacene dimers.56,85 For ortho-pentacene dimers, the calculated total coupling is 16.4 meV, and the coupling of the through-space model is 1.57 meV (about 10% of the total one).86 Furthermore, the through-space interactions dominate the iSF process in some covalently bridged bipentacenes with unique spatial proximity of the two pentacenes.60,79,87–90 According to previous experimental and theoretical experience on bipentacenes, we speculate that the through-space interactions of the bipentacene macrocycles are the key factor in the occurrence of iSF, but is it the dominant factor? In addition to the role of structural confinement mentioned in the experiment, does the rigid scaffold have other functions? These issues need to be adequately addressed before designing bipentacene macrocycles.
In this work, we present an accurate quantitative study for clarifying the above mechanism controversial issues in iSF with macrocyclic structures by taking the experimentally discovered bipentacene macrocycle and phenylene-linked bipentacene (see Fig. 2). Our calculations combining high-level electronic structure calculations, molecular dynamics (MD) sampling, and Fermi golden rule achieve good agreement with experimental measurements for iSF rates. We find the macrocyclic structure can maintain the optimal π–π stacking of two pentacenes in solution. Furthermore, based on these new findings, we suggest 97 macrocyclic scaffolds with different lengths to help the two pentacene units optimize their packing structure. Then 19 optimal structures are screened out from these 97 candidates, and the detailed quantum chemical calculations reveal that these systems can exhibit remarkably efficient iSF features with ultrafast time constants of unprecedented tens of femtoseconds. The work presented here opens a new scenario for designing new molecules to improve the singlet fission efficiency by combining the advantages of both close π–π stacking in xSF and chemical diversity in iSF.
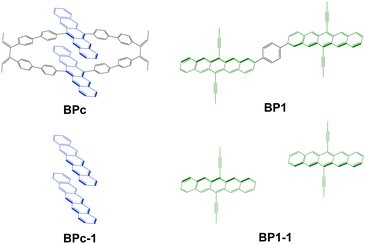 | ||
| Fig. 2 Model molecules studied in this work. BPc is used to model 1b studied in ref. 83, and BP1 is used to model the same molecule studied in ref. 54. BPc-1 and BP1-1 are the corresponding truncated models. | ||
2 Methodologies and computational details
2.1 Model systems
To explore the mechanism of BPc singlet fission, we adopt the molecules in Fig. 2 as our model systems. The phenylene-linked bipentacene (BP1) is included in our study to visually compare the difference between the macrocycle and the general covalently bridged bipentacene. BPc-1 and BP1-1 are through-space models formed by removing the linkers and replacing the broken bonds with hydrogen atoms. Here, the triisopropylsilyl moieties in BP1 are replaced with methyl groups to reduce computational complexity. Due to the high conformational flexibility of BP1 in solution, we perform a potential energy surface relaxed scan by scanning the dihedral angle in the range of 0–360° in increments of 5° and optimizing the remaining geometrical parameters for every point. Four local minima are found, and energy barriers between all conformations are small (<3.2 kcal mol−1, Fig. S1, ESI†). Four local minima are reoptimized using the density functional theory (DFT) with the hybrid functional B3LYP in combination with Grimme's atom pairwise dispersion corrections with BeckeJohnson damping (D3BJ).91,92 The 6-31G(d) basis set is used, and the solvent model density (SMD) continuum solvation model93 is considered to simulate the chloroform solution environment. All bipentacene macrocycles are calculated with the same method to get the ground state geometry. In this work, all DFT calculations are performed in Gaussian16 software.942.2 Electronic structures for singlet fission
Within a dimer picture, singlet fission involves the spin-conserved internal electronic conversion from a local singlet excited state (S0S1) into the triplet pair state (1(TT)) and the subsequent decoupling of this state to two free triplet excitons:| S0S1 → 1(TT) → T1 + T1 | (1) |
The first process is a prerequisite for obtaining free triplet states, and we focus only on this electronic conversion process in this work. In pentacene-based dimers, the common mechanism in the formation of 1(TT) is the superexchange mechanism,12,18,86,95–98 whereby the fission process proceeds through virtual charge-transfer (CT) states which may be energetically high. Therefore, two local excited states (S1S0, S0S1), two CT states (AC and CA with ‘C’ and ‘A’ meaning cation and anion monomers) and one triplet pair state (TT) are considered in our diabatic Hamiltonian.
Due to the multi-excitation nature of the triplet pair states, multi-configurational wavefunction theory (WFT) methods are applied to investigate the electronic structures and construct diabatic Hamiltonians for singlet fission in these molecules. In our work, the complete active space self-consistent field (CASSCF) method is used to calculate the electronic structure of the excited states relevant for singlet fission.99 Since each chromophore's highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) is usually considered to provide the most important information for the investigation of singlet fission, CASSCF(4e, 4o) calculations are performed with the ANO-L-VDZP basis set. After that, we employ the Pipek–Mezey localization method on the orbitals in active space to get the orthonormal orbitals localized on just one single pentacene molecule. By defining the diabatic states with these local orbitals (five states as mentioned before for bipentacenes shown in Fig. S2, ESI†), the diabatic Hamiltonian of each molecule is then constructed. All WFT calculations here are carried out by using the OpenMOLCAS package.100
2.3 Singlet fission rate
To introduce vibration mode and model the rate of fission kSF, the Fermi golden rule is used in our case,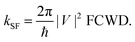 | (2) |
Based on the frequency analysis, there are many low-frequency modes (also see Fig. S7 in ESI†) of iSF systems which strongly affect the distance between two pentacene units, and, consequently, the electronic coupling terms (i.e., strong nonlocal exciton–vibration coupling). While the energies of states are more sensitive to high-frequency modes (e.g., C–C stretch around 1400 cm−1), contributing dominantly to the relaxation of vibrational states and the FCWD term. These two types of vibration modes are separately treated in eqn (2) to evaluate the rate of SF.
Low-frequency modes are included in the calculation of effective electronic coupling terms, which can be obtained from the diabatic Hamiltonian elements in Section 2.2 by the following formula:101
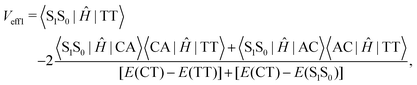 | (3) |
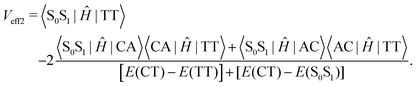 | (4) |
For the low-frequency modes, MD simulation is applied to investigate their role in the stability as well as SF rate. Under the frozen mode approximation,102 the fluctuation of effective electronic couplings due to their strong coupling with low-frequency modes is considered a static disorder, and |V|2 is the averaged using conformation sampling via the MD simulation. In detail, a solvent model containing chloroform molecules is established in the Materials Studio 2019 software103 for molecular dynamics simulation. According to the experimental conditions, both BPc and BP1 undergo singlet fission in dilute solutions, so the initial value of the solution density is set to the density of chloroform solvent (1.48 g cm−3). The universal force field (UFF) is adopted depending on the sample properties and the application ranges of various force fields.104 One BPc or BP1 molecule and 2000 chloroform molecules are placed into a periodic cell (Fig. S3, ESI†). Before MD simulations, we optimize the periodic cell with 5000 iterations using the geometry optimization task in the Forcite module. The related geometry optimization parameters are set as follows: the morphological optimization algorithm is set as Smart, and the quality is set as Ultrafine. The Ewald summation method is used for electrostatic interactions, and the atom-based summation method is used for the van der Waals interactions, where the cutoff distance is set to 15.5 Å. Afterwards, the optimized configurations are further refined by subjecting them to dynamic progress to ensure that the systems reach equilibrium and obtain enough sampled trajectory snapshots to compute the SF rates. The NVT ensemble is adopted in the MD simulations. The temperature is controlled at 300 K, and the total simulation time provided is 5 ns with the time step of 1 fs, and 10 snapshots were selected for the average of effective coupling with a time interval of 0.5 ns.
The high-frequency parts are related to the FCWD term, which can be calculated as the overlap between the spectrum of initial and final states:105
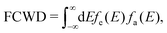 | (5) |
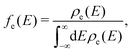 | (6) |
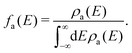 | (7) |
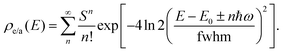 | (8) |
In this work, E0, ω and fwhm are extracted from experimental absorption spectra of the monomeric model compound for BP1 (TIPS pentacene) and BPc (pentacene). Reorganization energy λ is calculated by time-dependent DFT (TDDFT) with Tamm–Dancoff approximations (TDA) at B3LYP/6-31G(d) level. All parameters are listed in Table S1 (ESI†).
Since the experiment gaps between LE and TT states are applied for the FCWD and rate calculation, Veff1 and Veff2 would not be distinguished in practice in a specific snapshot based on the QC calculation, and they are averaged to compute the final |V|2.
3 Results and discussion
3.1 Through-space/through-bond interaction
Singlet fission systems have two driving forces: through-space and through-bond interactions. The through-space situation means that two chromophores have spatial orbital overlap due to the special close packing. In contrast, through-bond means that the linker orbitals are strongly coupled to both chromophores, enhancing the effective interaction between chromophores. In order to explore the driving force of bipentacenes, we take BPc and BP1 as our model systems, where BP1 is the representative of the through-bond iSF system.First, we calculate the electronic Hamiltonian of BPc, BP1 and their corresponding through-space systems (BPc-1 and BP1-1) at equilibrium molecular geometries. As shown in Fig. 3a, all electronic couplings (absolute values) are close in BPc and BPc-1, indicating that the presence or absence of a macrocyclic scaffold does not affect the coupling between electronic states. The through-space interaction dominates the iSF process in BPc. Moreover, Hamiltonian elements (the full Hamiltonian can be found in ESI†) are similar to references’ works in xSF systems. E.g., coupling terms29,99 and energy gap between LE and TT state (around 0.35–0.55 eV) compared to experimental results106,107 (0.47 eV), suggesting that the linker weakly affects the electronic structure of the pentacene unit. In the BP1 system (Fig. 3b), the couplings are almost zero after removing the phenylene linker, which intuitively shows that the component of through-space interaction can be ignored. Similar results can be found in the other three equilibrium structures of BP1 (Fig. S6, ESI†). It should be noted that the couplings between CT states and TT states are strictly zero due to the high structural symmetry (C2h) of the equilibrium geometry of BPc. In this case, singlet fission is driven by the excitation of symmetry-breaking interchromophoric vibrations, which is the same mechanism as the thermal activation of rubrene.108,109,110 As shown below, the couplings become no-zero for MD sampled trajectories with symmetry-breaking molecular structures (Tables S14–S33, ESI†). However, the direct two-electron couplings between S0S1/S1S0 and TT states are negligible, even for MD samples, implying that BPc undergoes a CT-mediated superexchange process to generate TT states.
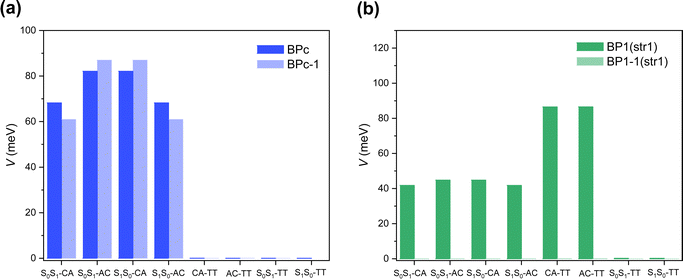 | ||
| Fig. 3 Electronic couplings (absolute values) between different diabatic states at equilibrium structures of (a) BPc and (b) BP1. | ||
Furthermore, we analyze the contributions of the linkers to the one- and two-electron integrals according to the explicit expressions of the off-diagonal matrix elements (see ESI† for the detailed expressions). In general (for both BP1/BPc), two-electron integrals among HOMOs and LUMOs play major roles in determining the magnitudes of the electronic couplings between CT and TT states but not the Fock coupling between local HOMO and LUMO. At the same time, the couplings between LE states and CT states are predominated by the Fock interaction (i.e., HOMO–HOMO/LUMO–LUMO effective electronic coupling), which is controlled by opposite real one-electron integral and shielding interaction of occupied orbitals (Coulomb and exchange terms).
For BP1, all terms show significant reductions from BP1 to BP1-1, implying the high contribution of through-bond interaction. The effective one-electron integral terms of BP1-1 are two orders of magnitude lower than that of BP1, leading to a significant reduction in the coupling of S0S1/S1S0–CT and CT–TT. After removing the linker, the two-electron integrals of BP1 equilibrium structures between CT and TT states are reduced from 70–80 meV to 0–2 meV. The reductions of one-electron integrals in all coupling terms and two-electron integrals in coupling between CT and TT states come from the absence of a linker component in local HOMO/LUMO orbitals. At the same time, the reduction of Coulomb interaction comes from the contribution of occupied linker orbitals. In particular, the exchange interactions of Fock coupling (K), which are sensitive to the distance, are negligible compared to one-electron integral and Coulomb interaction terms.
For BPc, exchange terms play important roles for couplings in both BPc and BPc-1, due to the strong π–π interaction between two pentacene units, i.e., through-space interaction dominates singlet fission in BPc. All components between BPc and BPc-1 are comparable, which also suggests the minor role of the linker in BPc. That is, the macrocycle only acts as a structural constraint. We also notice the equilibrium structure of the BPc (Table S12, ESI†): one-electron and Coulomb terms change a lot from BPc to BPc-1, but the Fock couplings obtained by adding one-electron, Coulomb and exchange interaction terms are not much different.
Second, we perform MD simulations to capture the effect of electronic couplings fluctuation for the reason that BPc and BP1 have large flexibility in the solution environment. The calculated effective electronic couplings of 10 samples are shown in Fig. 4. We can find that couplings between different samples change over two orders of magnitude in both systems, reflecting that the influence of thermal fluctuation on the SF rate also exceeds two orders of magnitude. Therefore, we take the effective coupling average of 10 samples, and the calculated SF rates achieve an unprecedented good agreement with the experimental values (Table 1). Compared to BP1, BPc undergoes faster singlet fission (the calculated time constants of BPc and BP1 are 10.3 ps and 228.8 ps, respectively). Similar to the results under the static structure, the macrocyclic scaffolds keep two pentacenes persistent π–π packing in MD, leading to singlet fission through spatial coupling in BPc.
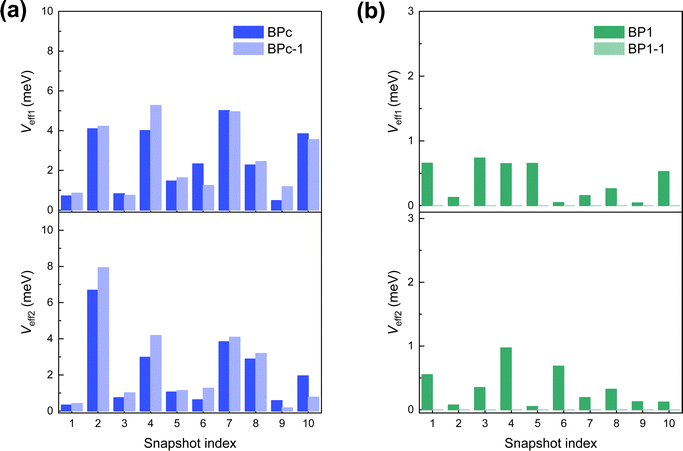 | ||
| Fig. 4 Effective electronic couplings (absolute values) at 10 molecular dynamics snapshots of (a) BPc and (b) BP1. Absolute values of Veff1 and Veff2 of the superexchange process are calculated by eqn (3) and (4), respectively. | ||
3.2 Expanding the chemical space
Since only BPc has been found experimentally on bipentacene macrocycles, we try to get more ideal bipentacene materials through theoretical simulation. Based on the above findings, we change the macrocyclic scaffold to achieve π–π stacking of two pentacenes, which is similar to BPc. Because the linker plays the role of structural support in the iSF process, its choice will be numerous for both conjugated and unconjugated ones. Moreover, the slipped distance between pentacenes will be easily regulated by linkers of different lengths.To construct bipentacene macrocyclic scaffolds, we explore a large number of macrocyclic molecules discovered in recent experiments,111–116 as shown in the most left column of molecules in Fig. S8 (ESI†), where we select 25 existing linkers. H, L, T represent the slipped distances between the centre of mass of two pentacenes along the vertical, longitudinal and transverse axes, respectively (Fig. 5a). Among these bipentacene structures, except for a few molecules (43, 69, 73, 82, and 87 in Fig. S8, ESI†), the rest molecules have almost no displacement along the transverse axis due to the short and symmetric linkers. The relationship between xSF efficiency in pentacene dimers and the longitudinal and transverse displacements of the molecular backbones have been unravelled by Wang et al.29 upon self-consistent fewest switches surface hopping (SC-FSSH) non-adiabatic simulations in conjunction with ab initio and semiempirical electronic structure calculations. They pointed out that the xSF rate can be increased by more than an order of magnitude by tuning the intermolecular packing, especially in the slipped stacked configurations with a shift of one ring along the transverse direction and an offset of one or two rings along the longitudinal axis are superior for SF (the local regions indicated by I, II, III and IV showed in Fig. 5b). The V and VI regions have the large CT character of the photoexcited state, which is found to be not essential for efficient SF.
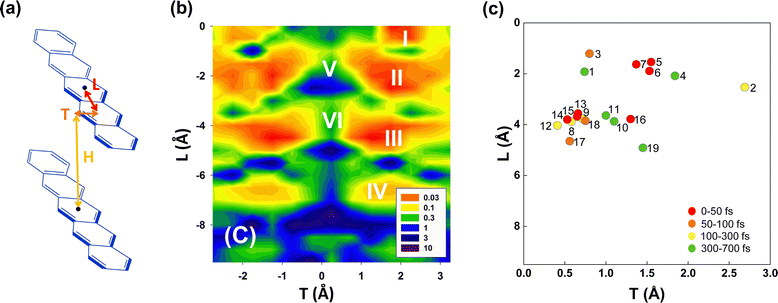 | ||
| Fig. 5 (a) Model molecular packing in designed bipentacene macrocycles. H, L and T are the slipped distances between the centre of mass of the two pentacenes along the vertical, longitudinal and transverse axes, respectively. (b) Relationship between SF time constant (in ps) and pentacene slipped distances (H = 3.4 Å). Reproduced with permission.29 Copyright 2014, American Chemical Society. (c) Calculated SF time constants of 19 screened bipentacene macrocycles. | ||
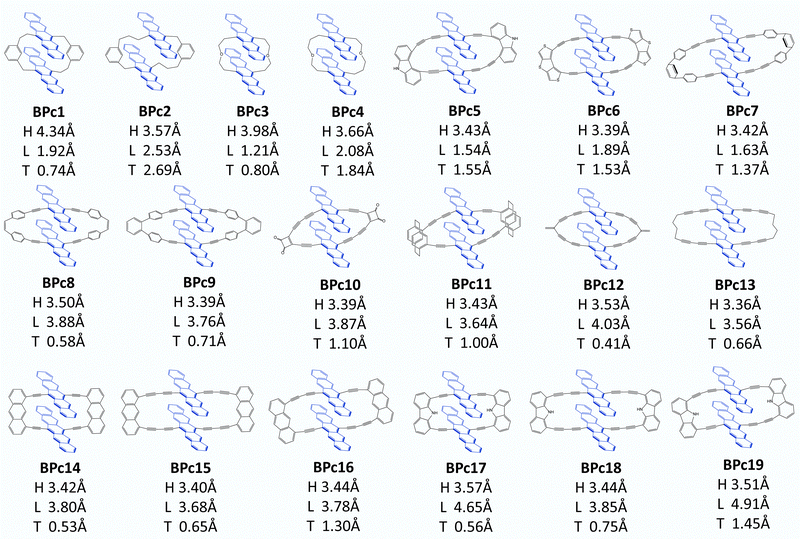
Following Wang et al.'s suggestion29 on slipping along the transverse direction about 2 Å to produce ultrafast xSF, we modify the experimentally existing linkers by enlarging conjugated length (e.g., molecule 6 compared to 5 in Fig. S8, ESI†) or introducing asymmetric structures, (e.g., 7, 8 compared to 5 in Fig. S8, ESI†), and 97 candidate molecules are designed finally. Then we perform structure optimization of these molecules in chloroform solvent by the computational method given in Section 2.1. There are five molecules (1, 2, 3, 86, and 91 in Fig. S8, ESI†) whose distances in the vertical direction exceed 4 Å, and the remaining 92 molecules, regardless of the length of the linker, maintain H at about 3.5 Å under the π–π interaction of two pentacenes. Furthermore, the two pentacenes in 1, 2 and 3 molecules are too far apart because the scaffold is too short and rigid. For 86 and 91, phenylenes form a large steric hindrance in the macrocycle. Obviously, these molecules are not optimal for SF. Next, we select 26 molecules located exactly in several localized regions indicated by I, II, III, and IV based on the displacement of the longitudinal and transverse axes. In order to observe whether the designed materials can maintain intramolecular pentacene stacking in the solution, we also perform MD calculations at room temperature and find that the distances between pentacenes in 7 systems are enlarged (>6 Å) in chloroform solution, which does not meet the requirements and will not be considered further. In the end, 19 optimal systems are screened out (see Fig. 6) for the iSF rate calculation using a similar procedure of BPc.
The calculated iSF rates are shown in Fig. 5c (see Table S35 for detailed results, ESI†). The calculated iSF time constants of the 19 systems are all in the magnitudes of a few tens or hundreds of femtoseconds, which is rare in the current experimental and theoretical works for iSF, indicating that our design strategy is promising to guide the synthesis of new ultrafast iSF materials. In addition, one may notice that the optimal system is concentrated around L being 4 Å and 2 Å, and T being 0.5–3 Å, which is completely consistent with the calculation results predicted in Fig. 5b (corresponding to their II/III region). This also verifies that iSF in the macrocycle is mainly related to the relative position of the chromophores but insensitive to the type and length of the macrocycle linkers. That is, similar ultrafast rates of xSF processes can be achieved by macrocyclic structures. We have found seven systems with SF time constants below 50 fs (marked with red dots in Fig. 5c), three systems between 50 and 100 fs (BPc9), and four systems between 100 and 300 fs. The time constant of BPc1 (587.0 fs) is larger than that of other systems due to its largest displacement of 4.34 Å in the vertical direction. Similarly, the couplings of CT–TT for all materials are sufficiently large to exceed tens of meV, while the couplings of S0S1/S1S0–CT are less than 2 meV, indicating that they undergo a superexchange process. In conclusion, the designed 19 materials have well demonstrated the potential of singlet fission and exhibited a superior iSF rate to BPc. We noted that the initial condition might influence the dynamic behaviour and results of the rate.117 Therefore, we also calculated rates of all systems using a different initial state, the bright eigenstate (i.e., with the largest transition dipole) of the subspace of the LE states. The results of rates are slightly different, but the overall relationship between rates and packing is similar (see Table S35 and Fig. S9 in ESI†).
The bipentacene macrocycle consists of three parts: two pentacenes, two conjugated/covalent centres, and two legs connected to one conjugated/covalent centre (a total of four legs in one molecule). From the perspective of macrocycle selection, we give the following design recommendations: (1) suitable conjugate length of legs (e.g., two triple bonds or one triple bond plus one phenyl) is needed for the design of macrocyclic singlet fission materials. Too short legs (e.g., 1, 5 in Fig. S8, ESI†) cannot guarantee the common π–π stacking, which ensures the strong through-space interaction or provide much-restricted conformation space of the bipentacene. Too long legs (e.g., 78, 83 in Fig. S8, ESI†) have large displacements along longitudinal and transverse axes, making the interaction for singlet fission weak. (2) Introducing asymmetric legs is recommended to ensure the static displacement shift along the transverse axis, even if the vibration effect is not considered. In this case, one triple bond for one leg and two triple bonds for another is an appropriate proposal, which makes the value of L in the suitable region (I/II/III Fig. 5b). While linkers with three triple bonds for another leg show large L, which is out of the fast-rate regions (e.g., 8, 12 in Fig. S8, ESI†). In addition, there are contorted and bent features of the pentacene unit in some macrocyclic molecules, e.g., BPc2 in Fig. 6, implying the possible role of macrocyclic linker on the electronic structure of chromophore for SF.
Here, we constrain partial degrees of freedom in bipentacene via a macrocyclic structure. Compared to the conventional iSF system, the macrocycle enforces two chromophore units to be face-to-face (π–π packing) by using two linkers instead of one along the transverse axis. Consequently, there are strong through-space interactions for singlet fission. Two linkers along the longitudinal axis can also be considered in the future. Unlike crystalline structures, the restriction using linkers is much more controllable. For example, the appropriate choice of the length of legs ensures the strong π–π interaction and suitable displacement along the longitudinal and transverse axes. The introduction of asymmetric legs provides static displacement-shift along the transverse axis if the degree of freedom along transverse axes is controlled (as shown in our case), even if the thermal effect is not considered.
4 Conclusions
Based on the electronic structure analysis, the macrocyclic model is proven to be a good framework for iSF molecule design since the distance between chromophores can be highly controlled by its linker and the linker does not involve the electronic structure for SF. Therefore, design rules for packing xSF material can be used for the designing and preliminary searching of novel macrocyclic iSF molecules. Furthermore, an approach to calculating the SF rate is performed based on the Fermi golden rule and the rates of candidates are evaluated to conform to the high efficiency of these candidates.Though our computational exploration is limited to 97 bipentacene macrocycles, their wide tunability is demonstrated. Our preliminary calculations on alternative linkers indicate that the same principles can be readily applied to similar materials systems. For example, two linkers can be connected longitudinally, pentacene can be replaced with other chromophores such as tetracene, and various linkers can be selected.
In addition, we find the macrocyclic structure maintains the ideal π–π stacking of two pentacenes in solution and promotes the occurrence of ultrafast intramolecular singlet fission. Based on the aforementioned ideas, we design 97 candidate macrocyclic scaffolds, from which 19 promising new bipentacene macrocycles are proposed. The designed 19 materials display potential singlet fission and exhibited a superior iSF rate (fs). Here, we provide a novel design idea to optimize through-space interaction for intramolecular singlet fission using macrocyclic structures. Incorporating two pentacenes into a macrocycle is undoubtedly a good idea for iSF molecule design and can inspire more material discoveries.
Author contributions
H. M. and X. X. conceived the project. Z. W. designed the molecules and carried out the calculations. X. Y. and X. X. helped with the calculation process and provided inspiring suggestions for improvement. All the authors contributed to the data analysis and writing of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2022YFA1503103) and the National Natural Science Foundation of China (grant no. 22073045).Notes and references
- M. Hanna and A. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 1–12 Search PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS.
- M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn and M. G. Bawendi, et al. , Nature, 2019, 571, 90–94 CrossRef CAS PubMed.
- L. Yang, M. Tabachnyk, S. L. Bayliss, M. L. Bohm, K. Broch, N. C. Greenham, R. H. Friend and B. Ehrler, Nano Lett., 2015, 15, 354–358 CrossRef CAS PubMed.
- J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. Van Voorhis and M. A. Baldo, Acc. Chem. Res., 2013, 46, 1300–1311 CrossRef CAS.
- J. Xia, S. N. Sanders, W. Cheng, J. Z. Low, J. Liu, L. M. Campos and T. Sun, Adv. Mater., 2017, 29, 1601652 CrossRef.
- R. W. MacQueen, M. Liebhaber, J. Niederhausen, M. Mews, C. Gersmann, S. Jäckle, K. Jäger, M. J. Tayebjee, T. W. Schmidt and B. Rech, et al. , Mater. Horiz., 2018, 5, 1065–1075 RSC.
- X. Qiao and D. Ma, Mater. Sci. Eng., R, 2020, 139, 100519 CrossRef.
- W.-L. Chan, T. C. Berkelbach, M. R. Provorse, N. R. Monahan, J. R. Tritsch, M. S. Hybertsen, D. R. Reichman, J. Gao and X.-Y. Zhu, Acc. Chem. Res., 2013, 46, 1321–1329 CrossRef CAS.
- K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X.-Y. Zhu, Chem. Rev., 2019, 119, 4261–4292 CrossRef CAS PubMed.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- R. M. Young and M. R. Wasielewski, Acc. Chem. Res., 2020, 53, 1957–1968 CrossRef CAS.
- Y. Yao, Phys. Rev. B, 2016, 93, 115426 CrossRef.
- K.-W. Sun and Y. Yao, J. Chem. Phys., 2017, 147, 224905 CrossRef.
- L. Xue, X. Song, Y. Feng, S. Cheng, G. Lu and Y. Bu, J. Am. Chem. Soc., 2020, 142, 17469–17479 CrossRef CAS PubMed.
- L. Wang, T.-S. Zhang, L. Fu, S. Xie, Y. Wu, G. Cui, W.-H. Fang, J. Yao and H. Fu, J. Am. Chem. Soc., 2021, 143, 5691–5697 CrossRef CAS.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299 CrossRef CAS PubMed.
- S. Ito, T. Nagami and M. Nakano, J. Photochem. Photobiol., C, 2018, 34, 85–120 CrossRef CAS.
- T. Hasobe, S. Nakamura, N. V. Tkachenko and Y. Kobori, ACS Energy Lett., 2021, 7, 390–400 CrossRef.
- Ö. H. Omar, D. Padula and A. Troisi, ChemPhotoChem, 2020, 4, 5223–5229 CrossRef.
- J. Wen, Z. Havlas and J. Michl, J. Am. Chem. Soc., 2015, 137, 165–172 CrossRef CAS PubMed.
- D. Padula, Ö. H. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416 RSC.
- T. Nagami, R. Sugimori, R. Sakai, K. Okada and M. Nakano, J. Phys. Chem. A, 2021, 125, 3257–3267 CrossRef CAS PubMed.
- H. Miyamoto, K. Okada, K. Tokuyama and M. Nakano, J. Phys. Chem. A, 2021, 125, 5585–5600 CrossRef CAS PubMed.
- E. A. Buchanan and J. Michl, J. Am. Chem. Soc., 2017, 139, 15572–15575 CrossRef CAS PubMed.
- L. Wang, Y. Olivier, O. V. Prezhdo and D. Beljonne, J. Phys. Chem. Lett., 2014, 5, 3345–3353 CrossRef CAS.
- S. Ito, T. Nagami and M. Nakano, Phys. Chem. Chem. Phys., 2017, 19, 5737–5745 RSC.
- Y.-D. Zhang, Y. Wu, Y. Xu, Q. Wang, K. Liu, J.-W. Chen, J.-J. Cao, C. Zhang, H. Fu and H.-L. Zhang, J. Am. Chem. Soc., 2016, 138, 6739–6745 CrossRef CAS.
- N. Alagna, J. Han, N. Wollscheid, J. L. Perez Lustres, J. Herz, S. Hahn, S. Koser, F. Paulus, U. H. Bunz and A. Dreuw, et al. , J. Am. Chem. Soc., 2019, 141, 8834–8845 CrossRef CAS PubMed.
- T. Geiger, S. Schundelmeier, T. Hummel, M. Ströbele, W. Leis, M. Seitz, C. Zeiser, L. Moretti, M. Maiuri and G. Cerullo, et al. , Chem. – Eur. J., 2020, 26, 3420–3434 CrossRef CAS.
- C. Zeiser, L. Moretti, T. Geiger, L. Kalix, A. M. Valencia, M. Maiuri, C. Cocchi, H. F. Bettinger, G. Cerullo and K. Broch, J. Phys. Chem. Lett., 2021, 12, 7453–7458 CrossRef CAS.
- Y. Wu, K. Liu, H. Liu, Y. Zhang, H. Zhang, J. Yao and H. Fu, J. Phys. Chem. Lett., 2014, 5, 3451–3455 CrossRef CAS.
- R. D. Pensack, E. E. Ostroumov, A. J. Tilley, S. Mazza, C. Grieco, K. J. Thorley, J. B. Asbury, D. S. Seferos, J. E. Anthony and G. D. Scholes, J. Phys. Chem. Lett., 2016, 7, 2370–2375 CrossRef CAS.
- Y.-Y. Liu, C.-L. Song, W.-J. Zeng, K.-G. Zhou, Z.-F. Shi, C.-B. Ma, F. Yang, H.-L. Zhang and X. Gong, J. Am. Chem. Soc., 2010, 132, 16349–16351 CrossRef CAS PubMed.
- J. Herz, T. Buckup, F. Paulus, J. Engelhart, U. H. Bunz and M. Motzkus, J. Phys. Chem. Lett., 2014, 5, 2425–2430 CrossRef CAS PubMed.
- K. Bhattacharyya and A. Datta, J. Phys. Chem. C, 2019, 123, 19257–19268 CrossRef CAS.
- C. Sutton, N. R. Tummala, D. Beljonne and J.-L. Bredas, Chem. Mater., 2017, 29, 2777–2787 CrossRef CAS.
- Z. Tang, S. Zhou, H. Liu, X. Wang, S. Liu, L. Shen, X. Lu and X. Li, Mater. Chem. Front., 2020, 4, 2113–2125 RSC.
- K. Bhattacharyya and A. Datta, J. Phys. Chem. C, 2017, 121, 1412–1420 CrossRef CAS.
- R. D. Pensack, A. J. Tilley, C. Grieco, G. E. Purdum, E. E. Ostroumov, D. B. Granger, D. G. Oblinsky, J. C. Dean, G. S. Doucette and J. B. Asbury, et al. , Chem. Sci., 2018, 9, 6240–6259 RSC.
- C. Cao, G.-X. Yang, J.-H. Tan, D. Shen, W.-C. Chen, J.-X. Chen, J.-L. Liang, Z.-L. Zhu, S.-H. Liu and Q.-X. Tong, et al. , Mater. Today Energy, 2021, 21, 100727 CrossRef CAS.
- A. K. Pal, K. Bhattacharyya and A. Datta, J. Chem. Theory Comput., 2019, 15, 5014–5023 CrossRef CAS PubMed.
- K. Broch, J. Dieterle, F. Branchi, N. Hestand, Y. Olivier, H. Tamura, C. Cruz, V. Nichols, A. Hinderhofer and D. Beljonne, et al. , Nat. Commun., 2018, 9, 1–9 CrossRef CAS.
- S. R. Yost, J. Lee, M. W. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao and K. Johnson, et al. , Nat. Chem., 2014, 6, 492–497 CrossRef CAS.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS PubMed.
- R. D. Pensack, A. J. Tilley, S. R. Parkin, T. S. Lee, M. M. Payne, D. Gao, A. A. Jahnke, D. G. Oblinsky, P.-F. Li and J. E. Anthony, et al. , J. Am. Chem. Soc., 2015, 137, 6790–6803 CrossRef CAS PubMed.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS PubMed.
- J. N. Mastron, S. T. Roberts, R. E. McAnally, M. E. Thompson and S. E. Bradforth, J. Phys. Chem. B, 2013, 117, 15519–15526 CrossRef CAS PubMed.
- D. Lubert-Perquel, E. Salvadori, M. Dyson, P. N. Stavrinou, R. Montis, H. Nagashima, Y. Kobori, S. Heutz and C. W. Kay, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- M. L. Williams, I. Schlesinger, C. E. Ramirez, R. M. Jacobberger, P. J. Brown, R. M. Young and M. R. Wasielewski, J. Phys. Chem. C, 2022, 126, 10287–10297 CrossRef CAS.
- S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller and X. Roy, et al. , J. Am. Chem. Soc., 2015, 137, 8965–8972 CrossRef CAS PubMed.
- S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss and J. Wu, et al. , Adv. Funct. Mater., 2015, 25, 5452–5461 CrossRef CAS.
- J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 CrossRef CAS.
- C. Hetzer, D. M. Guldi and R. R. Tykwinski, Chem. – Eur. J., 2018, 24, 8245–8257 CrossRef CAS PubMed.
- T. Sakuma, H. Sakai, Y. Araki, T. Mori, T. Wada, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. A, 2016, 120, 1867–1875 CrossRef CAS PubMed.
- A. Akdag, A. Wahab, P. Beran, L. Rulisek, P. I. Dron, J. Ludvik and J. Michl, J. Org. Chem., 2015, 80, 80–89 CrossRef CAS PubMed.
- E. Kumarasamy, S. N. Sanders, M. J. Tayebjee, A. Asadpoordarvish, T. J. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low and D. W. Paley, et al. , J. Am. Chem. Soc., 2017, 139, 12488–12494 CrossRef CAS PubMed.
- N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190 CrossRef CAS PubMed.
- T. Yamakado, S. Takahashi, K. Watanabe, Y. Matsumoto, A. Osuka and S. Saito, Angew. Chem., Int. Ed., 2018, 130, 5536–5541 CrossRef.
- A. T. Gilligan, E. G. Miller, T. Sammakia and N. H. Damrauer, J. Am. Chem. Soc., 2019, 141, 5961–5971 CrossRef CAS PubMed.
- M. Chen, M. D. Krzyaniak, J. N. Nelson, Y. J. Bae, S. M. Harvey, R. D. Schaller, R. M. Young and M. R. Wasielewski, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8178–8183 CrossRef CAS.
- L. M. Yablon, S. N. Sanders, K. Miyazaki, E. Kumarasamy, G. He, B. Choi, N. Ananth, M. Y. Sfeir and L. M. Campos, Mater. Horiz., 2022, 9, 462–470 RSC.
- S. Paul and V. Karunakaran, J. Phys. Chem. B, 2022, 126, 1054–1062 CrossRef CAS PubMed.
- G. He, K. R. Parenti, L. M. Campos and M. Y. Sfeir, Adv. Mater., 2022, 34, 2203974 CrossRef CAS PubMed.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741–2804 RSC.
- Y. Duan, G. Zhang, X. Liu, F. Shi, T. Wang, H. Yan, H. Xu and L. Zhang, J. Org. Chem., 2022, 87, 8841–8848 CrossRef CAS PubMed.
- Z. Wang, H. Liu, X. Xie, C. Zhang, R. Wang, L. Chen, Y. Xu, H. Ma, W. Fang and Y. Yao, et al. , Nat. Chem., 2021, 13, 559–567 CrossRef CAS PubMed.
- J. Kim, H. T. Teo, Y. Hong, J. Oh, H. Kim, C. Chi and D. Kim, Angew. Chem., Int. Ed., 2020, 59, 20956–20964 CrossRef CAS PubMed.
- N. V. Korovina, C. H. Chang and J. C. Johnson, Nat. Chem., 2020, 12, 391–398 CrossRef CAS PubMed.
- Y. Hong, M. Rudolf, M. Kim, J. Kim, T. Schembri, A.-M. Krause, K. Shoyama, D. Bialas, M. I. Röhr and T. Joo, et al. , Nat. Commun., 2022, 13, 1–11 Search PubMed.
- C. Lin, T. Kim, J. D. Schultz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2022, 1–8 Search PubMed.
- G. He, L. M. Yablon, K. R. Parenti, K. J. Fallon, L. M. Campos and M. Y. Sfeir, J. Am. Chem. Soc., 2022, 144, 3269–3278 CrossRef CAS PubMed.
- T. Okamoto and Z. Bao, J. Am. Chem. Soc., 2007, 129, 10308–10309 CrossRef CAS PubMed.
- S. K. Park, T. N. Jackson, J. E. Anthony and D. A. Mourey, Appl. Phys. Lett., 2007, 91, 063514 CrossRef.
- T. Nagami, H. Miyamoto, R. Sakai and M. Nakano, J. Phys. Chem. C, 2021, 125, 2264–2275 CrossRef CAS.
- I. Papadopoulos, J. Zirzlmeier, C. Hetzer, Y. J. Bae, M. D. Krzyaniak, M. R. Wasielewski, T. Clark, R. R. Tykwinski and D. M. Guldi, J. Am. Chem. Soc., 2019, 141, 6191–6203 CrossRef PubMed.
- V. Marti-Centelles, M. D. Pandey, M. I. Burguete and S. V. Luis, Chem. Rev., 2015, 115, 8736–8834 CrossRef CAS PubMed.
- G. Gil-Ramrez, D. A. Leigh and A. J. Stephens, Angew. Chem., Int. Ed., 2015, 54, 6110–6150 CrossRef PubMed.
- M.-X. Wang, Acc. Chem. Res., 2012, 45, 182–195 CrossRef CAS PubMed.
- H. M. Bergman, G. R. Kiel, R. J. Witzke, D. P. Nenon, A. M. Schwartzberg, Y. Liu and T. D. Tilley, J. Am. Chem. Soc., 2020, 142, 19850–19855 CrossRef CAS PubMed.
- K. Kuroda, K. Yazaki, Y. Tanaka, M. Akita, H. Sakai, T. Hasobe, N. V. Tkachenko and M. Yoshizawa, Angew. Chem., Int. Ed., 2019, 131, 1127–1131 CrossRef.
- S. R. Reddy, P. B. Coto and M. Thoss, J. Phys. Chem. Lett., 2018, 9, 5979–5986 CrossRef CAS PubMed.
- H.-H. Lin, K. Y. Kue, G. C. Claudio and C.-P. Hsu, J. Chem. Theory Comput., 2019, 15, 2246–2253 CrossRef CAS PubMed.
- A. Sharma, S. Athanasopoulos, Y. Li, S. N. Sanders, E. Kumarasamy, L. M. Campos and G. Lakhwani, J. Phys. Chem. Lett., 2022, 13, 8978–8986 CrossRef CAS PubMed.
- B. S. Basel, C. Hetzer, J. Zirzlmeier, D. Thiel, R. Guldi, F. Hampel, A. Kahnt, T. Clark, D. M. Guldi and R. R. Tykwinski, Chem. Sci., 2019, 10, 3854–3863 RSC.
- R. D. Ribson, G. Choi, R. G. Hadt and T. Agapie, ACS Cent. Sci., 2020, 6, 2088–2096 CrossRef CAS PubMed.
- A. Aster, F. Zinna, C. Rumble, J. Lacour and E. Vauthey, J. Am. Chem. Soc., 2021, 143, 2361–2371 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc.Wallingford CT, 2016 Search PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103 CrossRef PubMed.
- N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618 CrossRef CAS PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, S. R. Reddy, B. T. Phelan, M. D. Krzyaniak, M. K. Volland, P. B. Coto, R. M. Young and T. Clark, et al. , Chem, 2018, 4, 1092–1111 CAS.
- S. Lukman, K. Chen, J. M. Hodgkiss, D. H. Turban, N. D. Hine, S. Dong, J. Wu, N. C. Greenham and A. J. Musser, Nat. Commun., 2016, 7, 1–13 Search PubMed.
- X. Xie and A. Troisi, J. Chem. Theory Comput., 2021, 18, 394–405 CrossRef PubMed.
- I. Fdez Galvan, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, et al. , J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef CAS PubMed.
- C. E. Miller, M. R. Wasielewski and G. C. Schatz, J. Phys. Chem. C, 2017, 121, 10345–10350 CrossRef CAS.
- A. Montoya-Castillo, T. C. Berkelbach and D. R. Reichman, J. Chem. Phys., 2015, 143, 194108 CrossRef PubMed.
- BIOVIA, Dassault Systèmes, BIOVIA Materials Studio, version: 2019, San Diego: Dassault Systèmes, 2019.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- Z.-Q. You and C.-P. Hsu, J. Phys. Chem. A, 2011, 115, 4092–4100 CrossRef CAS PubMed.
- E. Heinecke, D. Hartmann, R. Müller and A. Hese, J. Chem. Phys., 1998, 109, 906–911 CrossRef CAS.
- D. Smith, S. Tretiak, R. Martin, X. Chi, B. Crone, A. Ramirez and A. Taylor, Phys. Rev. Lett., 2009, 102, 017401 CrossRef PubMed.
- H. Tamura, M. Huix-Rotllant, I. Burghardt, Y. Olivier and D. Beljonne, Phys. Rev. Lett., 2015, 115, 107401 CrossRef PubMed.
- K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989 CrossRef CAS PubMed.
- X. Xie, A. Santana-Bonilla, W. Fang, C. Liu, A. Troisi and H. Ma, J. Chem. Theory Comput., 2019, 15, 3721–3729 CrossRef CAS PubMed.
- K. Miki and K. Ohe, Eur. J. Chem., 2020, 26, 2529–2575 CrossRef CAS PubMed.
- Q. Shi, X. Wang, B. Liu, P. Qiao, J. Li and L. Wang, Chem. Commun., 2021, 57, 12379–12405 RSC.
- J. J. Christensen, D. J. Eatough and R. M. Izatt, Chem. Rev., 1974, 74, 351–384 CrossRef PubMed.
- S. Toyota, Chem. Rev., 2010, 110, 5398–5424 CrossRef CAS PubMed.
- M. Iyoda, J. Yamakawa and M. J. Rahman, Angew. Chem., Int. Ed., 2011, 50, 10522–10553 CrossRef CAS PubMed.
- M. A. Majewski and M. Stepien, Angew. Chem., Int. Ed., 2019, 58, 86–116 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2014, 141, 074705 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01077e |
| This journal is © The Royal Society of Chemistry 2023 |