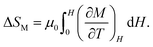Open Access Article
Open Access ArticleGiant caloric effects in charge–spin–lattice coupled transition-metal oxides
Yuichi
Shimakawa
 * and
Yoshihisa
Kosugi
* and
Yoshihisa
Kosugi
Institute for Chemical Research, Kyoto University, Gokasho, Uji, Kyoto 611-0011, Japan. E-mail: shimak@scl.kyoto-u.ac.jp; Fax: +81-774-38-3118; Tel: +81-774-38-3110
First published on 6th January 2023
Abstract
The caloric effects of solids can provide us with highly efficient and environmentally friendly energy systems. Exploring novel caloric materials is challenging but critically important in developing future technologies. Typical solid caloric effects are magnetocaloric, electrocaloric, and barocaloric effects induced respectively by magnetic fields, electric fields, and pressure, and materials showing large caloric responses through the effects attract lots of recent attention. In this perspective article, novel transition-metal oxides that show giant caloric effects are highlighted. The compounds are NdCu3Fe4O12 and BiCu3Cr4O12 containing unusually high valence states of transition-metal ions and show charge transitions to relieve the electronic instabilities. The charge, spin, and lattice degrees of freedom in the compounds are strongly correlated and the primarily induced charge transitions cause unusual first-order magnetic phase transitions that provide significant latent heat. Importantly, the large latent heat can be utilized through the caloric effects in multiple ways. The details of the giant caloric effects in the charge–spin–lattice coupled transition-metal oxides are summarized and the mechanism of the effects is discussed.
10th Anniversary StatementEffective thermal management is one of the critical issues that need to be resolved if we are to achieve the United Nations Sustainable Development Goals (SDGs). Fundamental science to address this issue is of main interest to the Journal of Materials Chemistry A, and the journal has contributed a lot for the development of novel materials in this research field. We celebrate the 10th anniversary of the Journal of Materials Chemistry A and are sure that the journal will have a large influence on energy- and environment-related research all over the world. |
Introduction
Materials showing caloric effects attract lots of recent attention because of their potential for highly effective and environmentally friendly thermal control applications.1–5 The caloric effects of solids can provide refrigeration systems that are innovative compared to the widely used conventional vapor compressive cooling systems, which account for a large amount of the current world's energy consumption.6,7 Multiple ways of controlling thermal properties by the caloric effects are known and the representatives are magnetocaloric, electrocaloric, and barocaloric effects induced respectively by applying magnetic fields, electric fields, and pressure.8–12 The magnetocaloric effects have been intensively studied for decades, and materials containing atoms with large magnetic moments show large effects.13–16 The electrocaloric effects are found in ferroelectric and pyroelectric compounds.17–19 Some of the materials showing the magnetocaloric or electrocaloric effect are also reported to show the barocaloric effect.11,20,21 Large barocaloric effects were also observed in plastic crystals.22 The effects are of great interest in recent years and much of this interest has been focused on the development of materials that show large caloric effects.Large caloric responses are expected to occur in the vicinity of phase transitions of the first order.3,4,23 When temperature changes, some materials exhibit a first-order transition accompanying large latent heat. If the large latent heat can be accessed by driving an external field, the giant caloric effect can be achieved. Although solid–liquid phase transitions like solidification or liquefaction often provide large latent heat, handling of liquid-phase materials is difficult.24,25 Solid–solid phase transitions, on the other hand, are attractive in terms of safety and chemical stability when the materials are used in devices. Exploring solid materials showing large caloric effects is challenging, but finding and developing new solid caloric materials are strongly demanded.
We here focus on the caloric effects of phase transitions in solids, especially phase transitions in charge–spin–lattice coupled transition-metal oxides. In some transition-metal oxides, the d orbitals of transition-metal ions are strongly hybridized with the 2p orbitals of coordinated oxygen ions, and as a result, the charge, spin, and lattice degrees of freedom are strongly correlated.26–29 In such a transition-metal oxide, electric, magnetic, and structural transitions can occur concomitantly, and as a result, the entropies of the order parameters of the charge, spin, and lattice degrees of freedom could combine to produce a significant latent heat. Interesting examples were recently found in oxide materials containing unusually high-valence-state transition-metal ions.30,31 A phase transition was primarily induced by relieving the electronic instability of the unusually high valence state of the constituent transition-metal ion, and drastic changes in electronic, magnetic, and structural properties occurred concomitantly. Significant latent heat associated with phase transition was observed, and more importantly, the observed large latent heat was accessed by applying external fields. Therefore, giant caloric effects were confirmed. The details of the giant caloric effects found in A-site-ordered perovskite structure oxides containing the unusually high-valence Fe or Cr are highlighted and the mechanism of the effects is discussed.
Giant barocaloric effect in NdCu3Fe4O12
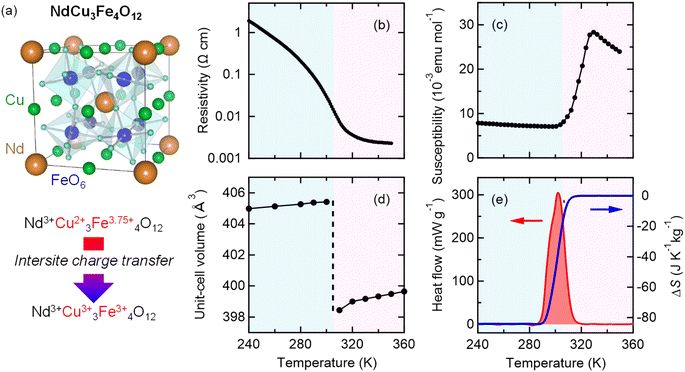
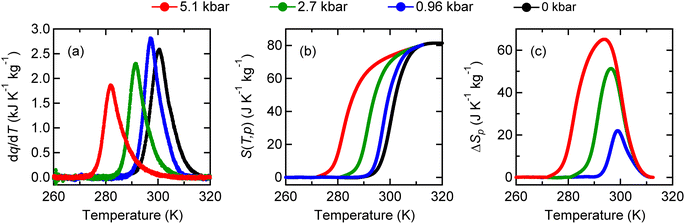
NdCu3Fe4O12 is synthesized by a solid–state reaction under high-pressure and high-temperature conditions, which are typically 9 GPa and 1050 °C.30,32 The resultant compound crystallizes in an A-site-ordered quadruple perovskite structure and contains the unusually high-valence Fe3.75+ ions at the B site of a fundamental perovskite structure.32–34 (see a schematic model of the crystal structure in Fig. 1a.32,35,36) Compared to typical stable valence states for Fe in oxides like 2+ (Fe2+) in FeO and 3+ (Fe3+) in Fe2O3,37–40 a valence state more than 3+ is unusually high and not readily stabilized.41,42 The Fe3.75+ state in the present compound is confirmed by 57Fe Mössbauer spectroscopy and bond-valence-sum results. Because the Fe3.75+ state is unusually high and unstable, when temperature decreases, a charge transition is induced to relieve its electronic instability. The high-temperature Nd3+Cu32+Fe43.75+O12 phase changes to the low-temperature Nd3+Cu33+Fe43+O12 phase by the intersite charge transfer transition (3Cu2+ + 4Fe3.75+ → 3Cu3+ + 4Fe3+). The details of this charge transition are given in previous papers.42–44 An important point is that the low-lying d orbitals of the unusually high-valence Fe ions are significantly hybridized with the 2p orbitals of octahedrally coordinated oxygen ions, giving rise to strong correlations in the charge, spin, and lattice degrees of freedom. At the intersite charge transfer transition in the compound, significant changes in electronic transport, magnetic, and lattice properties occur concomitantly. With decreasing temperature, as shown in Fig. 1b–d, first-order-type metal-to-insulator transition, paramagnetism-to-antiferromagnetism transition, and transition of unit-cell expansion are observed. Importantly, significant latent heat, 25.5 kJ kg−1, is also observed to be provided by the intersite charge transfer phase transition (Fig. 1e). The corresponding entropy change associated with the transition is estimated to be 84.2 J K−1 kg−1, which is larger than the largest entropy change near room temperature reported in the inorganic caloric material (MnNiSi)0.62(FeCoGe)0.38 (62 J K−1 kg−1).45The large latent heat associated with the intersite charge transfer transition in NdCu3Fe4O12 is also accessible by applying pressure. In other words, the large entropy change can be utilized through the barocaloric effect. As shown in Fig. 2a, the heat flow peak in differential thermal analysis (DTA) measurements shifts to a lower temperature. The peak signal decreases with increasing pressure, suggesting that the first-order transition slightly weakens due to a missing latent heat under pressure.46–48 The corresponding entropy changes S(T, p) and the pressure-induced isothermal entropy changes, ΔSp = S(T, p) − S(T, 0), as a function of temperature at various measured pressures are also respectively shown in Fig. 2b and c. When 5.1 kbar pressure is applied the maximum isothermal entropy change reaches 65.1 J K−1 kg−1 at 293.9 K, which corresponds to 77% of the total entropy change associated with the intersite charge transfer transition under ambient conditions. The value is much larger than those reported in known giant barocaloric materials like the NiMnIn alloy (24.4 J K−1 kg−1) and Mn3GaN (22.3 J K−1 kg−1),11,12 and is comparable to the largest barocaloric change reported in (MnNiSi)0.62(FeCoGe)0.38 (74 J K−1 kg−1).45 The pressure-induced adiabatic temperature change, as estimated from the relationship ΔT = T(S, 0) − T(S, p), reaches 13.7 K at the intersite charge transfer phase transition temperature. The values are quite large and therefore the giant barocaloric effect is indeed realized in NdCu3Fe4O12 with intersite charge transfer phase transition.
Giant barocaloric and magnetocaloric effects in BiCu3Cr4O12
The analogue A-site-ordered quadruple perovskite BiCu3Cr4O12 (Fig. 3a), which is synthesized by a solid–state reaction under high-pressure (9 GPa) and high-temperature (1000 °C) conditions, contains the unusually high-valence Cr3.75+ ions at the B site.31,49 In contrast to the intersite charge transfer transition in NdCu3Fe4O12, the compound shows charge disproportionation transition of Cr3.75+ to Cr3+ and Cr4+ (4Cr3.75+ → Cu3+ + 3Cr4+) at 190 K to relieve its electronic instability. The high-temperature Bi3+Cu32+Cr43.75+O12 phase thus changes to the low-temperature Bi3+Cu32+Cr3+Cr34+O12 phase, and the first-order-type transitions in electronic transport, magnetic, and lattice properties are observed, as respectively shown in Fig. 3b–d. The phase transition behaviors confirm that the charge, spin, and lattice degrees of freedom are strongly correlated in the compound. Similar to NdCu3Fe4O12, significant latent heat is associated with the phase transition, as shown in Fig. 3e. Differential scanning calorimetry measurement gives a latent heat of 5.23 kJ kg−1 and the corresponding entropy change of 28.2 J K−1 kg−1.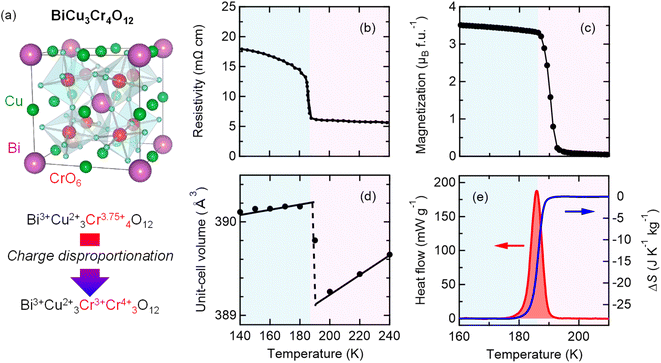 | ||
Fig. 3 (a) Crystal structure of A-site-ordered perovskite BiCu3Cr4O12. Bi and Cu ions are ordered at a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and B-site Cr ions form CrO6 octahedra. The compound shows a charge disproportionation transition at 190 K. Temperature dependences of the (b) resistivity, (c) magnetization, and (d) unit-cell volume of BiCu3Cr4O12. The resistivity data were taken from ref. 49. (e) Heat flow of BiCu3Cr4O12 measured by differential scanning calorimetry (left axis) and corresponding entropy change ΔS referred to the value at 210 K (right axis). 3, and B-site Cr ions form CrO6 octahedra. The compound shows a charge disproportionation transition at 190 K. Temperature dependences of the (b) resistivity, (c) magnetization, and (d) unit-cell volume of BiCu3Cr4O12. The resistivity data were taken from ref. 49. (e) Heat flow of BiCu3Cr4O12 measured by differential scanning calorimetry (left axis) and corresponding entropy change ΔS referred to the value at 210 K (right axis). | ||
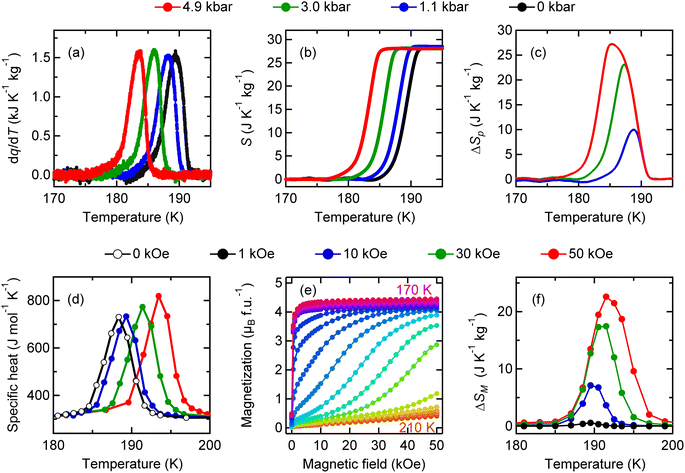
The latent heat associated with the charge disproportionation transition in BiCu3Cr4O12 is also accessible by applying pressure, as in the case of the barocaloric effect in NdCu3Fe4O12. The calorimetric curves can be shifted to a lower temperature by applying pressure, as shown in Fig. 4a. The entropy changes as a function of temperature at various pressures are also shown in Fig. 4b. The maximum isothermal entropy change is found to be 27.2 J K−1 kg−1 at 189 K under a pressure of 4.9 kbar (Fig. 4c). The 4.9 kbar-pressure-induced adiabatic temperature change reaches 4.8 K.
An important difference from the charge-transferred antiferromagnet NdCu3Fe4O12 is that the charge-disproportionated BiCu3Cr4O12 is a ferrimagnet. Because the ferrimagnetic transition is accompanied by the charge disproportionation transition due to strong charge–spin–lattice coupling, the latent heat associated with the charge disproportionation transition can also be accessed by driving magnetic fields as well as pressure. As shown in Fig. 4d, specific heat-capacity curves recorded under magnetic fields shift to higher temperatures, indicating the magnetocaloric effect in the compound. Because the specific heat capacity measured with a relaxation method shown in the figure often underestimates the actual latent heat for a first-order transition,50 the magnetic entropy change ΔSM is evaluated from isothermal magnetization measured in various magnetic fields (Fig. 4e) with the following relationship:
Although the barocaloric and magnetocaloric effects in BiCu3Cr4O12 are experimentally demonstrated separately, the “multicaloric effect”, where the entropy change is accessed by applying both pressure and a magnetic field simultaneously, can also be achieved because the charge, spin, and lattice degrees of freedom are strongly correlated. Actually, the charge disproportionation transition temperature can be modified by applying both pressure and a magnetic field simultaneously. The results further lead to an idea of triple ways of controlling the caloric effects, i.e., barocaloric, magnetocaloric, and electrocaloric effects in the charge–spin–lattice coupled compound. Even for an antiferromagnetic compound like NdCu3Fe4O12, whose thermal properties cannot be controlled by applying magnetic fields, a multicaloric effect comprising both barocaloric and electrocaloric effects is possibly observed.
Giant caloric responses in the charge–spin–lattice coupled system
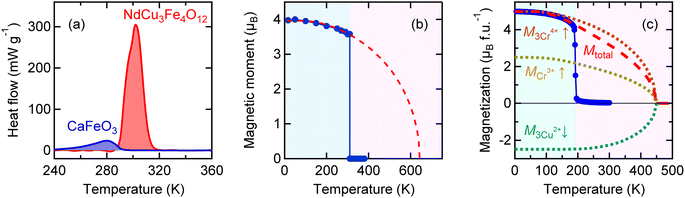
The charge transitions induced by relieving the electronic instabilities, like the intersite charge transfer transition in NdCu3Fe4O12 and the charge disproportionation transition in BiCu3Cr4O12, give large latent heats that can be utilized as caloric effects. However, not all charge transitions give enough latent heat to be a practical caloric effect. Fig. 5a displays the result of a specific heat measurement for the perovskite CaFeO3, which shows a charge disproportionation transition of the unusually high-valence Fe4+ (2Fe4+ → Fe3+ + Fe5+) at 290 K.51,52 Although the charge disproportionation transition temperature is close to the intersite charge transfer transition temperature (305 K) of NdCu3Fe4O12, the observed latent heat 3.67 kJ kg−1 is much smaller than that observed in NdCu3Fe4O12 (25.5 kJ kg−1). The latent heat is even small compared to that caused by charge disproportionation transition of BiCu3Cr4O12 at 190 K (5.23 kJ kg−1). It is noted that in CaFeO3 the antiferromagnetic transition, which stabilizes a helical magnetic structure, occurs at 115 K and is not accompanied by the charge disproportionation transition.53 Note also that the structural changes at the charge disproportionation transition temperature are small. Thus, the correlation of the charge, spin, and lattice degrees of freedom in CaFeO3 does not seem to be so strong, in contrast to the cases of NdCu3Fe4O12 and BiCu3Cr4O12.An important common feature in the phase transitions in NdCu3Fe4O12 and BiCu3Cr4O12 is that the charge, spin, and lattice properties change concomitantly. The most prominent feature concerns the first-order-type magnetic transitions induced by the charge transitions.30,54 When we see the magnetic transitions of the compounds, the behaviors are completely different from a typical second-order transition driven by the usual magnetic interactions and observed in many magnetic materials. In NdCu3Fe4O12 the development of the Fe magnetic moment, which is obtained from the analysis of temperature-dependent neutron magnetic diffraction data, is first order as shown in Fig. 5b. The projected magnetic transition temperature extrapolated from the fitting with a Brillouin function to the temperature-dependent refined magnetic moments (643 K) is more than twice as high as the charge transition temperature (305 K). Note also that the projected magnetic transition temperature is comparable to the magnetic transition temperatures due to Fe3+–O–Fe3+ superexchange magnetic interaction of simple perovskite-structure antiferromagnets LnFe3+O3 (Ln = lanthanides).55,56 The magnetic transition behaviour observed in BiCu3Cr4O12 is similar, as shown in Fig. 5c. A large ferrimagnetic magnetization of about 5μB f.u.−1, which originates from the antiferromagnetically coupled A-site Cu (Cu2+ with S = 1/2) and B-site Cr (Cr3+ with S = 3/2 and Cr4+ with S = 1) spins, is observed below the charge disproportionation transition temperature of 190 K. A fit to the temperature-dependent magnetization data with a Brillouin function gives an extrapolated magnetic transition temperature of about 450 K.
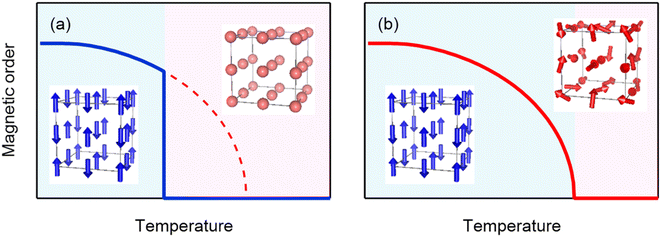
In both cases “intrinsic” magnetic transition temperatures are much higher than the “actual” magnetic transition temperature induced by the charge transitions. This implies that the energy gain caused by the charge delocalization is larger than that caused by the magnetic order, and as a result, the actual magnetic transition is suppressed to the temperature at which the charge transition occurs. The charge transition, where the charges are localized to relieve the electronic instability, seems to cause a change like one in which the magnetic moments abruptly appear and simultaneously order themselves (see Fig. 6). The magnetic entropy, which intrinsically has to be gradually changed below the magnetic transition temperature, is thus abruptly yielded by the very sharp first-order magnetic (=charge) transition. If we assume a simple order–disorder transition model in the antiferromagnetic NdCu3Fe4O12, for example, the magnetic entropy change ΔSM of the Fe3+ (S = 5/2) moment is expected to be R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) = 79 J K−1 kg−1, which is more than 90% of the observed total entropy change (84.2 J K−1 kg−1). Most of the magnetic entropy seems to change at the charge transition temperature. It is therefore reasonable to conclude that the magnetic entropy change plays an important role in giving rise to the observed large latent heat in the present charge–spin–lattice coupled systems.
ln(2S + 1) = 79 J K−1 kg−1, which is more than 90% of the observed total entropy change (84.2 J K−1 kg−1). Most of the magnetic entropy seems to change at the charge transition temperature. It is therefore reasonable to conclude that the magnetic entropy change plays an important role in giving rise to the observed large latent heat in the present charge–spin–lattice coupled systems.
The above key feature of the first-order-like magnetic transition induced primarily by the charge transition gives us an idea for designing novel materials with large caloric responses. An unusual valence state of the constituent transition-metal ions in a charge–spin–lattice coupled system is important to induce a charge transition to relieve its electronic instability. The transition-metal ions at the ground state should be magnetic, and the strong magnetic interaction between the magnetic ions would make the material's intrinsic magnetic transition temperature high. The large magnetic moment of the ions would also be advantageous for contributing the large entropy change. If this magnetic transition is suppressed by the delocalized charge instability, the magnetic transition would be induced primarily by the charge transition in a first-order form. An essential point is that the intrinsic magnetic transition temperature should be higher than the charge transition temperature. At the first-order magnetic transition induced by the charge transition, the magnetic entropy, which intrinsically has to be changed gradually below the intrinsic magnetic transition temperature, would thus be abruptly yielded. The lattice entropy change caused by the structural change due to the charge change of the constituent ions would additionally contribute to the total entropy change caused by the phase transition.
Conclusions
The caloric effects of novel charge–spin–lattice coupled transition-metal oxides, NdCu3Fe4O12 and BiCu3Cr4O12 containing respectively unusually high-valence Fe3.75+ and Cr3.75+, are highlighted. In the compounds, the charge, spin, and lattice degrees of freedom are strongly correlated, and the charge transitions, which are induced primarily by relieving the electronic instabilities, cause unusual first-order phase transitions. A significant latent heat of 25.5 kJ kg−1 and the corresponding large entropy change of 84.2 J K−1 kg−1 are observed to be caused by the intersite charge transfer transition of NdCu3Fe4O12. The large latent heat is accessed by applying pressure through the barocaloric effect. The maximum isothermal entropy change reaches 65.1 J K−1 kg−1 when 5.1 kbar pressure is applied, and the pressure-induced adiabatic temperature change is estimated to be 13.7 K at the intersite charge transfer phase transition temperature. BiCu3Cr4O12 shows a latent heat of 5.23 kJ kg−1 and the corresponding entropy change of 28.2 J K−1 kg−1 caused by the charge disproportionation transition. The compound shows both barocaloric and magnetocaloric effects, i.e., multiple caloric effects. The adiabatic temperature changes reach 3.9 K for the 50 kOe magnetic field and 5.4 K for the 4.9 kbar pressure, and thus practical thermal controls are achieved in multiple ways.In the phase transitions in NdCu3Fe4O12 and BiCu3Cr4O12, the charge, spin, and lattice degrees of freedom are strongly correlated, and the first-order-type magnetic transitions are induced primarily by the charge transitions. The magnetic transition behaviors are completely different from a typical second-order transition driven by the usual magnetic interactions and observed in many magnetic materials. The “intrinsic” magnetic transition temperatures are much higher than the “actual” magnetic transition temperatures induced by the charge transitions. The magnetic transitions are suppressed to the temperatures at which the charge transitions occur. The magnetic entropy, which intrinsically has to be changed gradually below the magnetic transition temperature, is thus abruptly yielded by the first-order magnetic (=charge) transition. This unusual magnetic entropy change plays an essential role for the giant caloric responses in the charge–spin–lattice coupled oxides.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the fruitful discussion with Asaya Fujita at AIST Chubu. The work highlighted here was done in collaboration with Masato Goto, Zhenhong Tan, Chen Chen, and Daisuke Kan at ICR, Kyoto University, Takashi Saito and Takashi Kamiyama at KEK, Wei-Tin Chen at National Taiwan University, Yu-Chun Chuang and Hwo-Shuenn Sheu at NSRRC, Masahiko Isobe and Hidenori Takagi at the Max Planck Institute for Solid State Research, Kenji Yoshii at the Japan Atomic Energy Agency, and Masaichiro Mizumaki at the Japan Synchrotron Radiation Research Institute. This work was partly supported by Grants-in-Aid for Scientific Research (No. 16H02266, 16H00888, 19H05823, 20K20547, 20H00397, 22J15128, and 22KK0075) and by grants for the Integrated Research Consortium on Chemical Sciences and the International Collaborative Research Program of the Institute for Chemical Research in Kyoto University from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. This work was also supported by the Japan Society for the Promotion of Science Core-to-Core Program (A) Advanced Research Networks.Notes and references
- A. Gschneidner, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479–1539 CrossRef.
- M. Valant, Prog. Mater. Sci., 2012, 57, 980–1009 CrossRef CAS.
- S. Fähler, U. K. Rößler, O. Kastner, J. Eckert, G. Eggeler, H. Emmerich, P. Entel, S. Müller, E. Quandt and K. Albe, Energy Technol., 2012, 14, 10–19 Search PubMed.
- X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450 CrossRef CAS PubMed.
- L. Mañosa and A. Planes, Adv. Mater., 2017, 29, 1603607 CrossRef PubMed.
- A. M. Omer, Renew. Sustain. Energy Rev., 2008, 12, 2265–2300 CrossRef CAS.
- J. M. Calm, Int. J. Refrig., 2008, 31, 1123–1133 CrossRef CAS.
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270 CrossRef CAS PubMed.
- B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821 CrossRef CAS PubMed.
- D. Matsunami and A. Fujita, Appl. Phys. Lett., 2015, 106, 042901 CrossRef.
- L. Mañosa, D. González-Alonso, A. Planes, E. Bonnot, M. Barrio, J. L. Tamarit, S. Aksoy and M. Acet, Nat. Mater., 2010, 9, 478–481 CrossRef PubMed.
- D. Matsunami, A. Fujita, K. Takenaka and M. Kano, Nat. Mater., 2015, 14, 73–78 CrossRef CAS PubMed.
- G. V. Brown, J. Appl. Phys., 1976, 47, 3673–3680 CrossRef CAS.
- V. K. Pecharsky and K. A. Gschneidner, Phys. Rev. Lett., 1997, 78, 4494–4497 CrossRef CAS.
- M. P. Annaorazov, S. A. Nikitin, A. L. Tyurin, K. A. Asatryan and A. K. Dovletov, J. Appl. Phys., 1996, 79, 1689–1695 CrossRef CAS.
- H. Wada and H. Tanabe, Appl. Phys. Lett., 2001, 79, 3302–3304 CrossRef CAS.
- X. Moya, E. Stern-Taulats, S. Crossley, D. González-Alonso, S. Kar-Narayan, A. Planes, L. Mañosa and N. D. Mathur, Adv. Mater., 2013, 25, 1360–1365 CrossRef CAS PubMed.
- B. Nair, T. Usui, S. Crossley, S. Kurdi, G. G. Guzmán-Verri, X. Moya, S. Hirose and N. D. Mathur, Nature, 2019, 575, 468–472 CrossRef CAS PubMed.
- D. Matsunami and A. Fujita, Appl. Phys. Lett., 2015, 106, 042901 CrossRef.
- E. Stern-Taulats, P. Lloveras, M. Barrio, E. Defay, M. Egilmez, A. Planes, J. L. Tamarit, L. Mañosa, N. D. Mathur and X. Moya, APL Mater., 2016, 4, 091102 CrossRef.
- E. A. Mikhaleva, I. N. Flerov, M. V. Gorev, M. S. Molokeev, A. V. Cherepakhin, A. V. Kartashev, N. V. Mikhashenok and K. A. Sablina, Phys. Solid State, 2012, 54, 1832–1840 CrossRef CAS.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. ichiro Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS PubMed.
- E. Stern-Taulats, T. Castán, L. Mañosa, A. Planes, N. D. Mathur and X. Moya, MRS Bull., 2018, 43, 295–298 CrossRef.
- N. Zhang, Y. Yuan, X. Cao, Y. Du, Z. Zhang and Y. Gui, Adv. Eng. Mater., 2018, 20, 1–30 Search PubMed.
- A. Fallahi, G. Guldentops, M. Tao, S. Granados-Focil and S. Van Dessel, Appl. Therm. Eng., 2017, 127, 1427–1441 CrossRef.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 55, 418–421 CrossRef CAS PubMed.
- F. M. F. de Groot, M. Grioni, J. C. Fuggle, J. Ghijsen, G. A. Sawatzky and H. Petersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5715–5723 CrossRef CAS PubMed.
- N. A. Spaldin and M. Fiebig, Science, 2005, 309, 391–3922 CrossRef CAS PubMed.
- N. A. Spaldin, S. W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38–43 CrossRef.
- Y. Kosugi, M. Goto, Z. Tan, A. Fujita, T. Saito, T. Kamiyama, W. T. Chen, Y. C. Chuang, H. S. Sheu, D. Kan and Y. Shimakawa, Adv. Funct. Mater., 2021, 31, 2009476 CrossRef CAS.
- Y. Kosugi, M. Goto, Z. Tan, D. Kan, M. Isobe, K. Yoshii, M. Mizumaki, A. Fujita, H. Takagi and Y. Shimakawa, Sci. Rep., 2021, 11, 12682 CrossRef CAS PubMed.
- Y. Shimakawa, Inorg. Chem., 2008, 47, 8562–8570 CrossRef CAS PubMed.
- Y. W. Long, N. Hayashi, T. Saito, M. Azuma, S. Muranaka and Y. Shimakawa, Nature, 2009, 458, 60–63 CrossRef CAS PubMed.
- Y. W. Long, T. Salto, T. Tohyama, K. Oka, M. Azuma and Y. Shimakawa, Inorg. Chem., 2009, 48, 8489 CrossRef CAS PubMed.
- A. N. Vasil’ev and O. S. Yolkova, Low Temp. Phys., 2007, 33, 895 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- E. R. Jette and F. Foote, J. Chem. Phys., 1933, 1, 9 Search PubMed.
- R. M. Hazen and R. Jeanloz, Rev. Geophys., 1984, 22, 37 CrossRef CAS.
- L. Pauling and S. B. Hendricks, J. Am. Chem. Soc., 1925, 47, 781 CrossRef CAS.
- H. E. Hoefer, G. P. Brey, B. Schulz-Dobrick and R. Oberhaensli, Eur. J. Mineral., 1994, 6, 407 CrossRef CAS.
- F. D. Romero and Y. Shimakawa, Chem. Commun., 2019, 55, 3690–3696 RSC.
- Y. Shimakawa, J. Phys. D Appl. Phys., 2015, 48, 504006 CrossRef.
- W. T. Chen, T. Saito, N. Hayashi, M. Takano and Y. Shimakawa, Sci. Rep., 2012, 2, 449 CrossRef PubMed.
- Y. Shimakawa, M. W. Lufaso and P. M. Woodward, APL Mater., 2018, 6, 086106 CrossRef.
- T. Samanta, P. Lloveras, A. U. Saleheen, D. L. Lepkowski, E. Kramer, I. Dubenko, P. W. Adams, D. P. Young, M. Barrio, J. L. Tamarit, N. Ali and S. Stadler, Appl. Phys. Lett., 2018, 112, 021907 CrossRef.
- M. Bratko, E. Lovell, A. D. Caplin, V. Basso, A. Barcza, M. Katter and L. F. Cohen, Phys. Rev. B, 2017, 95, 064411 CrossRef.
- K. Morrison, M. Bratko, J. Turcaud, A. Berenov, A. D. Caplin and L. F. Cohen, Rev. Sci. Instrum., 2012, 83, 033901 CrossRef CAS PubMed.
- K. Morrison, A. Dupas, Y. Mudryk, V. K. Pecharsky, K. A. Gschneidner, A. D. Caplin and L. F. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134421 CrossRef.
- M. Etter, M. Isobe, H. Sakurai, A. Yaresko, R. E. Dinnebier and H. Takagi, Phys. Rev. B, 2018, 97, 195111 CrossRef CAS.
- J. C. Lashley, M. F. Hundley, A. Migliori, J. L. Sarrao, P. G. Pagliuso, T. W. Darling, M. Jaime, J. C. Cooley, W. L. Hults, L. Morales, D. J. Thoma, J. L. Smith, J. Boerio-Goates, B. F. Woodfield, G. R. Stewart, R. A. Fisher and N. E. Phillips, Cryogenics, 2003, 43, 369–378 CrossRef CAS.
- M. Takano, N. Nakanishi, Y. Takeda, S. Naka and T. Takada, Mater. Res. Bull., 1977, 12, 923 CrossRef CAS.
- Y. Takeda, S. Naka, M. Takano, T. Shinjo, T. Takada and M. Shimada, Mater. Res. Bull., 1978, 13, 61 CrossRef CAS.
- P. M. Woodward, D. E. Cox, E. Mosphopoulou, A. W. Sleight and S. Morimoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 844 CrossRef CAS.
- W. T. Chen, Y. Long, T. Saito, J. P. Attfield and Y. Shimakawa, J. Mater. Chem., 2010, 20, 7282–7286 RSC.
- D. Treves, M. Eibschütz and P. Coppens, Phys. Lett., 1965, 18, 216–217 CrossRef CAS.
- I. S. Lyubutin, T. V. Dmitrieva and A. S. Stepin, J. Exp. Theor. Phys., 1999, 88, 590–597 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |