Single-atom catalysis enabled by high-energy metastable structures

Abstract

Owing to limited degrees of freedom, the active sites of stable single-atom catalyst (SAC) often have one structure that is energetically much lower than other local-minimum structures. Thus, the SAC adopts one lowest-energy structure (LES) with an overwhelmingly larger proportion than any other high-energy metastable structure (HEMS), and the LES is commonly assumed to be solely responsible for the catalytic performance of an SAC. Herein, we demonstrate with SACs anchored on CeO₂ that the HEMS of an SAC, even though its proportion remains several orders of magnitude lower than the LES throughout the catalytic reaction, can dictate catalysis with extraordinary activity arising from its unique coordination environment and oxidation state. Thus, we unravel the key role of HEMS-enabled catalysis in single-atom catalysis, which shakes the common assumption in the studies of SACs and urges new developments in both experiment and theory to identify and exploit catalysis via HEMSs.

---

Introduction

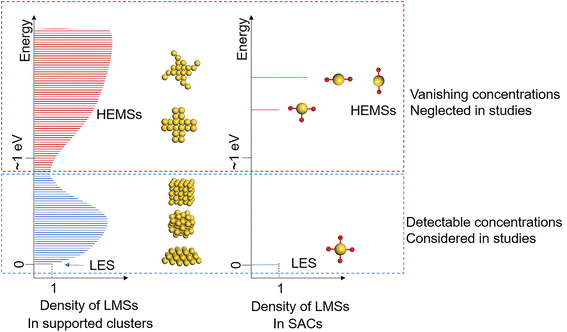
Dynamic processes in heterogeneous catalysis have attracted great attention in recent years, owing to the rapid development of operando characterization techniques, which provide molecular-level insights into the catalytic process and thus promote the understanding of active sites under reaction conditions.^1–6 However, it remains a grand challenge for experiments to elucidate the atomistic mechanisms at relevant microscopic timescales for the dynamic processes in heterogeneous catalysis. First-principles modeling presents a theoretical probe to unveil more fundamental and essential aspects, thus shedding light on the structure–performance relationship and catalyst design.^7,8

An intricate yet fundamental aspect is the dynamic structural evolution of active sites coupled with catalytic mechanisms,⁹ and this has been well exemplified by theoretical studies of catalysis on supported clusters and nanoparticles.^7,8,10,11 The active sites of these catalysts are composed of multiple atoms and thus possess large degrees of freedom, which result in ensembles of local-minimum structures (LMSs) that are energetically close¹² and thus accessible to catalysis, based on the Boltzmann distribution.⁸ In addition, the LMSs in the accessible ensembles can vary with the reaction atmosphere, which is induced by adsorptions.^13,14 These impose challenging complications on deciphering the structure–performance relationships of these catalysts.

Nevertheless, as the number of LMSs exponentially decreases with the system size,¹² the scenario becomes intrinsically different when the size of the active site is pushed to the limit of a single atom, i.e., the concept of a single-atom catalyst (SAC). Since it was first proposed in 2011,¹⁵ the SAC has developed into a promising design concept for highly efficient heterogeneous catalysts,^16–19 and it also serves as an ideal model for the study of the structure–performance relationship of catalytic active sites, owing to its well-defined local structure with precise tunability.^16,20 This exactly arises from the fact that because of the limited degrees of freedom, the active sites of stable SACs often present one lowest-energy structure (LES) dominant in quantity, and the other local minima are high-energy metastable structures (HEMSs) in negligibly low concentrations, as illustrated in Fig. 1.

Fig. 1 Schematic illustration of densities of LMSs in supported clusters and SACs. Similar to the electronic density of states for the electronic structure, each LMS is a state of the atomic structure of the system, and the density of LMSs presents the number of all possible LMSs, i.e., the degeneracy, at each energy level for the atomic structure of the system. Arising from large degrees of freedom, supported clusters possess many LMSs that are energetically close to the LES, but the LMSs in SACs other than the LES usually are HEMSs with extremely low concentrations. Because of this intrinsic difference, it is necessary to consider the ensemble catalysis on supported clusters, while a clear structure–performance relationship is commonly assumed for the SAC, based on its LES.

Thus, it is a sensible and common practice for both experiment and theory to assume that the LES of an SAC is solely responsible for its catalytic performance, and a clear structure–performance relationship can be established. Yet, it has been reported that SACs can reversibly switch between different structures, including cluster forms and varying coordinations,^9,21,22 in which the different structures are energetically close and thus are accessible with detectable concentrations, while the HEMSs remain reasonably ignored.

Herein, we found that the HEMSs of SACs can significantly contribute to catalysis, even though they remain at negligibly low concentrations throughout the catalytic cycle, which is thus often overlooked in both experiment and theory. By investigating the local minimum structures and phase diagrams of transition metal M (M = Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) SACs (M₁) anchored on the CeO₂ (110) surface (M₁/CeO₂) with density functional theory (DFT) calculations, we identified that under a reductive environment, both Au₁/CeO₂ and Pt₁/CeO₂ possess a HEMS of the same type that is energetically higher than the LES by over 0.7 eV and is thus with a negligibly low concentration less than 10⁻⁵. However, we demonstrated that this HEMS of Au₁/CeO₂ and Pt₁/CeO₂ SACs plays a key role in delivering the catalysis of reduction reactions by its much higher activity arising from the unique oxidation state of M₁, and it is thus the HEMS that enables the catalytic performance of SACs for these reactions.

Computational methodology

All periodic DFT calculations were performed with the Vienna ab initio simulation package (VASP).^23–25 The projector augmented wave (PAW)²⁶ method was used for the interactions between the core and valence electrons. The valence electron densities were described by plane-wave basis sets with an energy cutoff of 400 eV.²⁵ The exchange-correlation energies were calculated using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional,²⁷ and the spin-unrestricted Kohn–Sham scheme²⁸ was adopted. To partially account for the strong correlation of Ce 4f electrons, a Hubbard U correction was applied, with U − J = 4.5 eV.^29,30 The D3 correction was included to describe the van der Waals interactions.³¹

The thresholds for converging the electronic wavefunctions and atomic structures are 10⁻⁶ eV for the energy and 0.02 eV Å⁻¹ for the maximal force, respectively. The calculated lattice constant (5.418 Å) and Ce–O bond (2.360 Å) length of the CeO₂ bulk are consistent with experimental results.³² The CeO₂ (110) surface was then modeled by a p(3 × 2) 5-layer supercell with the bottom 3 layers fixed, and a 15 Å vacuum gap was included to separate the periodic images along the z-axis. A 2 × 2 × 1 Monkhorst–Pack grid was used to sample the Brillouin zone. Dipole correction along the z-axis was applied.

The Gibbs free energy corrections (including enthalpic and entropic terms) of gas-phase molecules and surface-adsorbed species were calculated with the ideal gas approximation and the harmonic approximation for the vibrational degrees of freedom using the thermochemistry modules of the Atomic Simulation Environment (ASE).³³

Comparisons between electronic affinities with and without relativistic effects were obtained using the ADF program,³⁴ which uses all-electron Slater-type orbitals as basis sets. The relativistic effects are included in the Hamiltonian via the zero-order regular approximation (ZORA).³⁵

Microkinetic modeling was conducted using CatMAP³⁶ to explicitly investigate the catalytic kinetics under varying conditions. The partial pressures of all the gas phase reactants were set to 1 bar, while the partial pressures of the gas phase products were set to 0.1 bar for C₂H₂ and 10⁻¹⁵ bar for HCOOH to ensure overall exothermic reactions with positive net forward reaction rates. Note that the extremely low partial pressure of HCOOH is in accordance with the experimental conditions (see the note in the ESI†).

Results and discussion

Local-minimum structures and phase diagrams of M₁/CeO₂ SACs

The M₁/CeO₂ SACs present an important family and have been widely studied because of their promising applications^37–41 and theoretical values.^42–44 We first investigated all possible LMSs for the twelve groups 8–11 transition metal M₁/CeO₂ SACs (M = Fe–Cu, Ru–Ag, Os–Au), and calculated their phase diagrams under different redox atmospheres (additional details can be found in the ESI discussion and Fig. S1–S12†).

The most stable phase, i.e., the LES of the active site, on each M₁/CeO₂ SAC widely changes with varying atmosphere. In particular, the coordination number of M to O (CN_O) varies among different LESs. In the reductive condition represented by the pressure of H₂ (p_H2), the phase diagrams (Fig. S11 and S12†) indicate that all the M₁/CeO₂ SACs retain a particular type of LES with a CN_O of 2 (labeled as the M_subO-2 type) in a wide temperature range at p_H2 of 1 bar.

In the LES of the M_subO-2 type, the single-atom M is anchored at the O vacancy site and bonds to the two nearest O atoms to form an O–M–O configuration (Fig. 2a). The M atom can lose one of the M–O bonds to form an M–O configuration, and this is labeled as the M_subO-1 type (Fig. 2a). Only with M = Cu, Pd, Pt, and Au, can the M₁/CeO₂ SAC adopt M_subO-1 as a LMS.

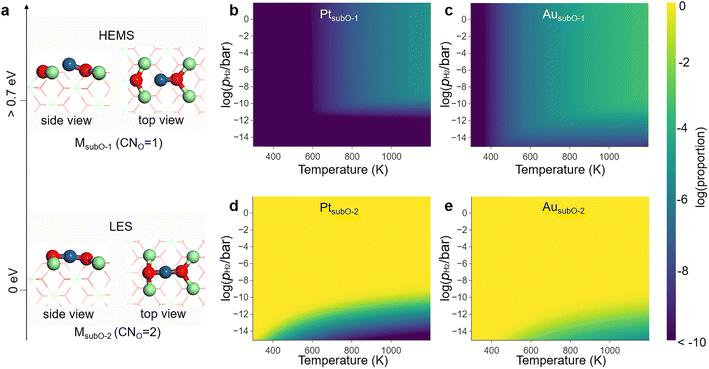Fig. 2 (a) The M_subO-1 and M_subO-2 types of structures for active sites in the M₁/CeO₂ SACs. The two are well separated in energy by more than 0.7 eV, with the M_subO-2 type being the LES and the M_subO-1 type being the HEMS under reductive conditions. The energy gap results in the extremely low concentrations of (b) Pt_subO-1 and (c) Au_subO-1 in the phase diagrams, while the concentrations of (d) Pt_subO-2 and (e) Au_subO-2 dominate the phase diagrams of active sites in the corresponding M₁/CeO₂ SACs under varying temperatures and p_H2 (in logarithmic scale). Note that the number of atoms for M_subO-1 and M_subO-2 are the same, while the dependence of the phase diagram on p_H2 arises from the competition among all 8 types of SAC structures considered in Fig. S2–S8,† for which the numbers of O atoms are different.

Under the reducing environment with the standard p_H2, M_subO-2 is the LES, and M_subO-1 is the HEMS that is over 0.7 eV higher in energy (Fig. 2a and Table S1†). Therefore, the concentrations of HEMS (M_subO-1) are less than 10⁻⁵ in the phase diagrams of the active sites of M₁/CeO₂ SACs (Fig. 2b and c), and the active sites dominantly adopt the LES (M_subO-2) (Fig. 2d and e). Conventionally, the catalytic performance by such a HEMS has often been overlooked for further investigation. However, this HEMS (M_subO-1) has an unusually low CN_O of only 1 (Fig. 2a), and such a highly unsaturated coordination mode of the single-atom M may spark extraordinarily high catalytic activity. Therefore, we further scrutinized the role of this HEMS of the M_subO-1 type in catalysis, in comparison with that of the LES of the M_subO-2 type.

Catalytic performance by the LES and HEMS

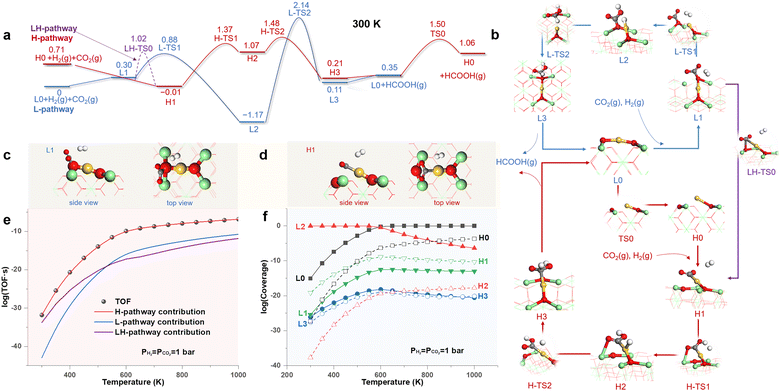
To obtain a panoramic understanding of the contribution of HEMS to catalysis, we investigated the CO₂ hydrogenation reaction (CO₂HR) on the Au₁/CeO₂ SAC and the semi-hydrogenation of acetylene (SHA) on the Pt₁/CeO₂ SAC, which are typical slow and fast catalytic reactions, respectively.^45,46 Both reactions introduce a reducing environment, and thus, the two M₁/CeO₂ SACs adopt the M_subO-2 type as the LES under the standard conditions, with the M_subO-1 type as the HEMS (Fig. 2).

Fig. 3a shows the free energy profiles of the reaction pathways for CO₂HR catalyzed by the LES (L-pathway) and the HEMS (H-pathway) of the Au₁/CeO₂ SAC under standard conditions, with structures of all states illustrated in Fig. 3b. In the L-pathway, starting from the LES of the M_subO-2 type (L0), the CO₂ molecule prefers to bind with the surface O atom to form a carbonate group (L1, Fig. 3c) instead of weak physisorption on the positively charged Au₁ site of L0 (Fig. S13†). H₂ then easily dissociates into H⁺ and H⁻ on the Lewis pair composed of the carbonate group and Au₁ site (L2) with a small barrier of 0.58 eV (L-TS1). Subsequently, H⁻ attacks the carbonate group to produce HCOOH (L3), which, however, poses a formidable barrier of 3.31 eV (L-TS2).

Fig. 3 (a) Free energy profiles (in eV) of CO₂HR on the Au₁/CeO₂ SAC following pathways enabled by the LES (L-pathway) and HEMS (H-pathway). (b) Structures of all states. Configurations of CO₂ activation on (c) the LES and (d) the HEMS. Calculated (e) turnover frequency (TOF) and (f) coverages of states as functions of temperature.

In contrast to the L-pathway, CO₂ in the H-pathway can spontaneously and directly bind to the Au₁ site in the HEMS of the M_subO-1 type (H1, Fig. 3d) with a bent configuration, indicating a chemisorbed CO₂. It is subsequently hydrogenated by H₂via an Eley–Rideal (ER) mechanism with a barrier of 1.38 eV (H-TS1) to form the co-adsorbed COOH and H on Au₁ (H2), which combine to produce HCOOH (H3) by overcoming a small barrier of 0.31 eV (H-TS2). Upon releasing HCOOH, the Au₁ site transforms to L0, which recovers H0 by overcoming a barrier of 1.15 eV.

Fig. 3c and d highlights the key difference between the CO₂ activation modes driven by the two types of active sites, i.e., the LES of the M_subO-2 type activates CO₂ on its O site to form a carbonate group, while the HEMS of the M_subO-1 type chemisorbs CO₂ directly on its Au₁ site to form a bent CO₂.

In addition, we investigated the direct transformation of L0 to H1 upon the adsorption of CO₂ on Au. This, however, requires the C atom of CO₂ to approach the positively charged Au₁ site of L0, which leads to a large repulsion, and it is more favored for the C atom of CO₂ to bind to the surface O to form L1. Thus, the transformation from L0 to H1 follows a detour through L1 with a barrier of 1.02 eV (LH-TS0 in Fig. 3a) referenced to L0, and this forks to a new pathway labelled as the LH-pathway.

The three pathways, in fact, compose a complex reaction network via common states, and thus, they all contribute to the kinetics of catalysis. Therefore, we performed microkinetic modeling³⁶ of this complex reaction network. The results (Fig. 3e) show that the H-pathway dominates the contribution to the TOF, and is larger than those of the L- and LH-pathways by several orders of magnitude. Nevertheless, Fig. 3f shows that the coverages of states in the H-pathway (H0–H3) are extremely small (<10⁻¹⁹ at 300 K and <10⁻⁴ even at 1000 K), and thus, they remain marginal and barely detectable. In contrast, the state (L2 or L0) in the L-pathway dominates the Au₁/CeO₂ SAC surface at all temperatures considered. Therefore, it is in fact the HEMS with a miniscule concentration, instead of the LES, that drives the CO₂HR on the Au₁/CeO₂ SAC, and the extraordinary catalytic ability of the HEMS arises from the unique oxidation state of its Au₁ site to activate CO₂, as discussed later.

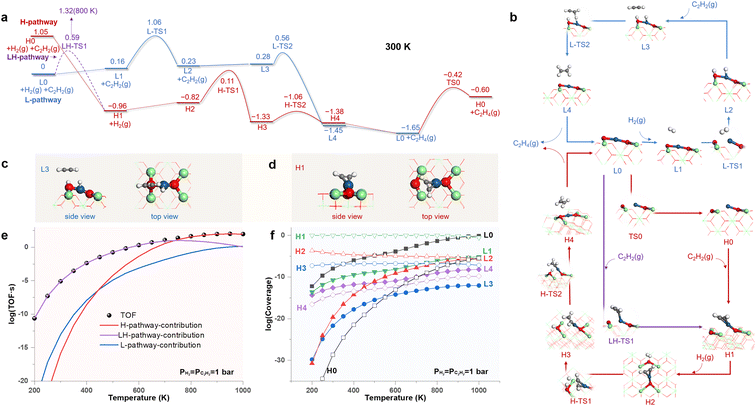
Fig. 4a shows the free energy profiles of the reaction pathways for SHA catalyzed by the LES (L-pathway) and the HEMS (H-pathway) of the Pt₁/CeO₂ SAC under standard conditions, with the structures of all states illustrated in Fig. 4b. In the L-pathway, the LES of the M_subO-2 type (L0) prefers the physisorption of H₂ (L1) to that of C₂H₂ and delivers the dissociative chemisorption of H₂ (L2) by overcoming a barrier of 0.90 eV (L-TS1). Subsequently, C₂H₂ consumes the adsorbed H atoms (L3, Fig. 4c) through an ER mechanism with a small barrier of 0.28 eV (L-TS2) and produces C₂H₄.

Fig. 4 (a) Free energy profiles (in eV) of SHA on the Pt₁/CeO₂ SAC following pathways enabled by the LES (L-pathway) and the HEMS (H-pathway). (b) Structures of all states. Configurations of C₂H₂ activation on (c) the LES and (d) the HEMS. Calculated (e) turnover frequency (TOF) and (f) coverages of states as functions of temperature.

In contrast to L0, H0 in the H-pathway favors strong bonding to C₂H₂ (H1, Fig. 4d), which is exothermic by 2.01 eV. Such strong adsorption of C₂H₂ can couple with the transformation of active sites and leads to a low barrier of 0.59 eV at 300 K (LH-TS1 in Fig. 4a). This forks to a new pathway labeled as the LH-pathway (Fig. 4a) that involves the coupling of C₂H₂ adsorption and L0–H1 site transformation. However, this low barrier rapidly increases with temperature due to the entropic contribution of gas phase C₂H₂, and it reaches 1.32 eV at 800 K (LH-TS1 in Fig. S15†). Thus, the transformation of the active site is decoupled from the chemisorption of C₂H₂, favoring the direct transformation from H0 to H1 at temperatures higher than 710 K (Fig. S15† shows the scenario at 800 K), and this recovers the H-pathway with the initial state of H0.

In the H- and LH-pathways, upon the chemisorption of C₂H₂ (H1), H₂ then hydrogenates the adsorbed C₂H₂via an ER mechanism to produce C₂H₄ by sequentially overcoming two barriers of 0.93 eV (H-TS1) and 0.27 eV (H-TS2). Upon releasing C₂H₄, the H-pathway reaches L0, which recovers H0 via a barrier of 1.23 eV (TS0).

Fig. 4c and d highlights the key difference between the C₂H₂ activation modes driven by the two types of active sites. The LES of the M_subO-2 type cannot adsorb C₂H₂, and instead, it activates H₂ to the adsorbed H atoms on its Pt and O sites, which then activate C₂H₂. In contrast, the HEMS of the M_subO-1 type can directly chemisorb C₂H₂ on its Pt₁ site.

We further performed microkinetic modeling³⁶ of the complex reaction network composed of all three pathways in Fig. 4a. The results in Fig. 4e show that the LH-pathway dominates the contribution to the TOF at low temperatures, and the H-pathway dominates the contribution to the TOF at high temperatures. Fig. 4f shows that the Pt₁/CeO₂ SAC surface is dominated by H1 at most of the temperatures because of the strong adsorption of C₂H₂ on the HEMS. Thus, the adsorption state derived from the HEMS is detectable in this scenario, but the HEMS itself (H0) retains a negligibly small coverage (<10⁻³⁰ to 10⁻⁸). Nevertheless, the coverage of LES (L0) increases with temperature and then dominates the Pt₁/CeO₂ SAC surface at 1000 K. Therefore, the HEMS drives the SHA on the Pt₁/CeO₂ SAC at high temperatures, and LES drives the SHA at low temperatures. The extraordinary catalytic ability of the HEMS arises from the unique oxidation state of its Pt₁ site to activate C₂H₂, as discussed below.

Negatively charged M₁ in the HEMS

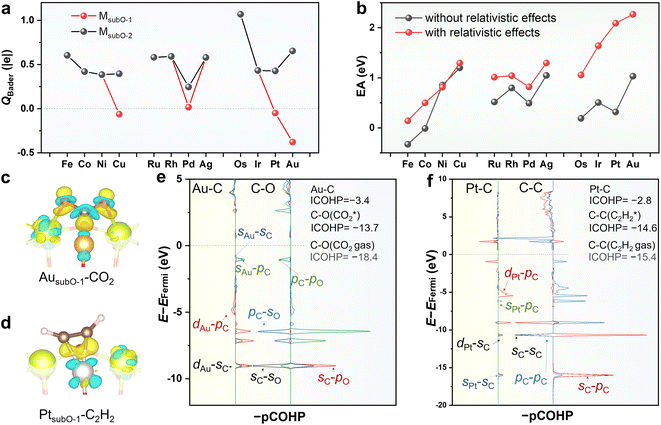
The oxidation state (OS) of the single-atom metal (M₁) in the SAC is a key characteristic denoting its catalytic capability.^47,48 The M₁'s in most SACs supported on metal oxides are positively charged,⁴⁹ but their OSs may substantially change as the catalytic reaction proceeds.^21,22,50 Such evolution of the OS in the SAC may stem from the emergence of metastable states and play a key role in catalysis.⁵¹

We investigated the OSs of M₁'s in the M₁/CeO₂ SACs. Fig. 5a shows the results of the Bader charge analysis,^52,53 which indicates that the M₁'s in the LES (M_subO-2 type) of all M₁/CeO₂ SACs are positively charged, but the Pt₁ and Au₁ in the HEMS (M_subO-1 type) are negatively charged. The Hartree potential difference (ΔV_H)^54,55 in Fig. S17† also implies similar conclusions. Together with the spin population analysis (Fig. S18†), our results suggest that the OSs of Pt₁ and Au₁ in the HEMS are both −1.

Fig. 5 (a) Bader charges (Q_Bader) of M₁ in the M_subO-1 and M_subO-2 types of M₁/CeO₂ SACs. (b) Calculated electronic affinity (EA) of gas-phase metal atoms with and without the relativistic effects. The differential electron density contours of (c) CO₂ adsorption on Au_subO-1 and (d) C₂H₂ adsorption on Pt_subO-1 (cyan indicates a decrease in electron density, and yellow indicates an increase in electron density upon adsorption). Projected crystal orbital Hamilton population (pCOHP) analyses of (e) CO₂ adsorption on the HEMS of Au₁/CeO₂ and (f) C₂H₂ adsorption on the HEMS of Pt₁/CeO₂. E − E_Fermi is the energy level referenced to the Fermi level.

We further calculated the 1s core level shifts of Pt₁ and Au₁ (Table S2†), and the results also indicated that the OSs of Pt₁ and Au₁ in the HEMS are −1. Although there are no clear-cut methods to determine the OS, various analyses provided strong evidence indicating that Pt₁ and Au₁ in the HEMS are negatively charged. This may be similar to the case of negatively charged Au SAC on CuO, which was experimentally observed by in situ scanning tunneling microscopy (STM) imaging and X-ray photoelectron spectroscopy (XPS) in a reducing environment.⁵⁶

To understand why Pt and Au can reach negatively charged states, we calculated the electron affinities (EAs) of gas phase metal atoms with and without the relativistic effects (Fig. 5b). If no relativistic effects were taken into account, Pt and Au would have similar EAs to those of Pd and Ag, which were much less likely to take electrons from the support. With including the relativistic effects, Pt and Au possess the largest EAs among all metals. This arises from the contraction and thus stabilization of the 6s orbitals introduced by relativistic effects,^57–60 which enables Pt and Au to hold extra electrons.

The negatively charged Au₁ and Pt₁ in the HEMSs serve as strong electron donors that can deliver facile activation of CO₂ and C₂H₂. The differential electron density contour in Fig. 5c illustrates significant electron transfer from Au₁ to CO₂ that subsequently results in a bent CO₂^δ−. The bent CO₂^δ− forms strong bonding with Au s and d orbitals, as shown by the projected crystal orbital Hamilton population (pCOHP) analysis of Au–C in Fig. 5e, with an integrated COHP (ICOHP) of −3.4 eV. Consequently, the ICOHP of the C–O bond in CO₂ increases from −18.4 eV to −13.7 eV upon adsorption, indicating the presence of greatly weakened C–O bonds.

Similarly, the differential charge density contour in Fig. 5d shows significant electron transfer from Pt₁ to bonding with C₂H₂ that results in a bent C₂H₂, implying a transition from the sp hybridization of C to sp² hybridization. The pCOHP analysis of Pt–C in Fig. 5d indicates strong bonding between C and the s and d orbitals of Pt, with an ICOHP of −2.8 eV. As a result, the C–C bond in C₂H₂ is weakened, as revealed by the increase in the ICOHP of C–C from −15.4 eV to −14.6 eV.

Conclusions

In summary, we demonstrated that the HEMS can play a key role in single-atom catalysis, as illustrated by the two case studies of CO₂HR catalyzed on Au₁/CeO₂ and SHA on Pt₁/CeO₂, in which the HEMS is overwhelmingly outnumbered by the LES, yet dictates the catalytic performance due to the extraordinarily high activities that arise from the unique oxidation state of M₁ in the HEMS. However, there is difficulty in experimentally detecting these HEMSs with unique oxidation states because of their extremely low concentrations (H0 in Fig. 3f and 4f) that barely reach the detection limits of operando characterization techniques. Also, there is difficulty in discovering them with normal ab initio molecular dynamics simulations because the high formation energies of HEMSs render extremely low probabilities (as rare events) according to the Boltzmann distribution.

Our finding shakes the common assumption in the studies of SAC that the LES, which is much lower in energy by approximately 1 eV than any other HEMS, is responsible for the catalytic performance of the SAC. Therefore, this urges developments of new methodologies and techniques in experiment and theory to scrutinize the role of HEMS in the structure–performance relationship of SAC. Moreover, the HEMS in SACs may be further promoted and thus exploited with external fields, as in the scenarios of electrochemistry and photochemistry.

Data availability

The dataset of optimized SAC structures in this work is available at the following DOI: 10.5281/zenodo.7638276. The rest of the datasets supporting this work's conclusions are available in the ESI.†

Author contributions

H. X. and Z. X. conceived and designed the study. Z. X. conducted all the theoretical modeling. Z. X. and H. X. wrote the initial manuscript. All authors contributed to the revisions of the manuscript and approved the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 22122304 and 92261111), the National Key Research and Development Project (2022YFA1503000), the Tsinghua University Initiative Scientific Research Program (20221080065), and the China Postdoctoral Science Foundation (2020M680507). We are grateful to the Center of High-Performance Computing at Tsinghua University for providing computational resources.

References

1. F. Tao and P. A. Crozier, Atomic-scale observations of catalyst structures under reaction conditions and during catalysis, Chem. Rev., 2016, 116, 3487–3539.
2. J. Dou, Z. Sun, A. A. Opalade, N. Wang, W. Fu and F. Tao, Operando chemistry of catalyst surfaces during catalysis, Chem. Soc. Rev., 2017, 46, 2001–2027.
3. H. Xu, D. Rebollar, H. He, L. Chong, Y. Liu, C. Liu, C.-J. Sun, T. Li, J. V. Muntean, R. E. Winans, D.-J. Liu and T. Xu, Highly selective electrocatalytic CO₂ reduction to ethanol by metallic clusters dynamically formed from atomically dispersed copper, Nat. Energy, 2020, 5, 623–632.
4. W. Xi, K. Wang, Y. Shen, M. Ge, Z. Deng, Y. Zhao, Q. Cao, Y. Ding, G. Hu and J. Luo, Dynamic co-catalysis of Au single atoms and nanoporous Au for methane pyrolysis, Nat. Commun., 2020, 11.
5. L. Zhang, R. Long, Y. Zhang, D. Duan, Y. Xiong, Y. Zhang and Y. Bi, Direct observation of dynamic bond evolution in single-atom Pt/C₃N₄ catalysts, Angew. Chem., Int. Ed., 2020, 59, 6224–6229.
6. J. Li and J. Gong, Operando characterization techniques for electrocatalysis, Energy Environ. Sci., 2020, 13, 3748–3779.
7. B. Zandkarimi and A. N. Alexandrova, Surface-supported cluster catalysis: Ensembles of metastable states run the show, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1420.
8. Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Ensembles of metastable states govern heterogeneous catalysis on dynamic interfaces, Acc. Chem. Res., 2020, 53, 447–458.
9. L. Liu and A. Corma, Evolution of isolated atoms and clusters in catalysis, Trends Chem., 2020, 2, 383–400.
10. H. Zhai and A. N. Alexandrova, Local fluxionality of surface-deposited cluster catalysts: the case of Pt₇ on Al₂O₃, J. Phys. Chem. Lett., 2018, 9, 1696–1702.
11. G. Sun and P. Sautet, Metastable structures in cluster catalysis from first-principles: structural ensemble in reaction conditions and metastability triggered reactivity, J. Am. Chem. Soc., 2018, 140, 2812–2820.
12. F. H. Stillinger, Exponential multiplicity of inherent structures, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 48–51.
13. Y. G. Wang, D. Mei, V. A. Glezakou, J. Li and R. Rousseau, Dynamic formation of single-atom catalytic active sites on ceria-supported gold nanoparticles, Nat. Commun., 2015, 6, 6511.
14. Y. He, J.-C. Liu, L. Luo, Y.-G. Wang, J. Zhu, Y. Du, J. Li, S. X. Mao and C. Wang, Size-dependent dynamic structures of supported gold nanoparticles in CO oxidation reaction condition, Proc. Natl. Acad. Sci., 2018, 115, 7700–7705.
15. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Single-atom catalysis of CO oxidation using Pt₁/FeO_x, Nat. Chem., 2011, 3, 634–641.
16. X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-atom catalysts: a new frontier in heterogeneous catalysis, Acc. Chem. Res., 2013, 46, 1740–1748.
17. A. Wang, J. Li and T. Zhang, Heterogeneous single-atom catalysis, Nat. Rev. Chem., 2018, 2, 65–81.
18. J.-C. Liu, Y. Tang, Y.-G. Wang, T. Zhang and J. Li, Theoretical understanding of the stability of single-atom catalysts, Natl. Sci. Rev, 2018, 5, 638–641.
19. H.-Y. Zhuo, X. Zhang, J.-X. Liang, Q. Yu, H. Xiao and J. Li, Theoretical understandings of graphene-based metal single-atom catalysts: stability and catalytic performance, Chem. Rev., 2020, 120, 12315–12341.
20. X. Cui, W. Li, P. Ryabchuk, K. Junge and M. Beller, Bridging homogeneous and heterogeneous catalysis by heterogeneous single-metal-site catalysts, Nat. Catal., 2018, 1, 385–397.
21. F. Maurer, J. Jelic, J. Wang, A. Gänzler, P. Dolcet, C. Wöll, Y. Wang, F. Studt, M. Casapu and J.-D. Grunwaldt, Tracking the formation, fate and consequence for catalytic activity of Pt single sites on CeO₂, Nat. Catal., 2020, 3, 824–833.
22. N. Daelman, M. Capdevila-Cortada and N. López, Dynamic charge and oxidation state of Pt/CeO₂ single-atom catalysts, Nat. Mater., 2019, 18, 1215–1221.
23. G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
24. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47, 558.
25. G. Kresse and J. Furthmüller, Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169–11186.
26. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758–1775.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
28. W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138.
29. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method, J. Phys.: Condens. Matter, 1997, 9, 767–808.
30. Z.-Q. Huang, T. Zhang, C.-R. Chang and J. Li, Dynamic frustrated lewis pairs on ceria for direct nonoxidative coupling of methane, ACS Catal., 2019, 9, 5523–5536.
31. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
32. J. F. Lee, M. T. Tang, W. C. Shih and R. S. Liu, Ce K-edge EXAFS study of nanocrystalline CeO₂, Mater. Res. Bull., 2002, 37, 555–562.
33. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002.
34. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
35. E. v. Lenthe, J. G. Snijders and E. J. Baerends, The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules, J. Chem. Phys., 1996, 105, 6505–6516.
36. A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, CatMAP: a software package for descriptor-based microkinetic mapping of catalytic trends, Catal. Lett., 2015, 145, 794–807.
37. L. Nie, D. Mei, H. Xiong, B. Peng, Z. Ren, X. I. P. Hernandez, A. DeLaRiva, M. Wang, M. H. Engelhard, L. Kovarik, A. K. Datye and Y. Wang, Activation of surface lattice oxygen in single-atom Pt/CeO₂ for low-temperature CO oxidation, Science, 2017, 358, 1419–1423.
38. C. Yang, X. Yu, S. Heißler, P. G. Weidler, A. Nefedov, Y. Wang, C. Wöll, T. Kropp, J. Paier and J. Sauer, O₂ activation on ceria catalysts—the importance of substrate crystallographic orientation, Angew. Chem., Int. Ed., 2017, 56, 16399–16404.
39. L. Ye, X. Duan, S. Wu, T.-S. Wu, Y. Zhao, A. W. Robertson, H.-L. Chou, J. Zheng, T. Ayvalı, S. Day, C. Tang, Y.-L. Soo, Y. Yuan and S. C. E. Tsang, Self- regeneration of Au/CeO₂ based catalysts with enhanced activity and ultra-stability for acetylene hydrochlorination, Nat. Commun., 2019, 10, 914.
40. V. Muravev, G. Spezzati, Y.-Q. Su, A. Parastaev, F.-K. Chiang, A. Longo, C. Escudero, N. Kosinov and E. J. M. Hensen, Interface dynamics of Pd–CeO₂ single-atom catalysts during CO oxidation, Nat. Catal., 2021, 4, 469–478.
41. Y. Wang, Z. Chen, P. Han, Y. Du, Z. Gu, X. Xu and G. Zheng, Single-atomic Cu with multiple oxygen vacancies on ceria for electrocatalytic CO₂ Reduction to CH₄, ACS Catal., 2018, 8, 7113–7119.
42. W. Song and E. J. M. Hensen, Mechanistic aspects of the water–gas shift reaction on isolated and clustered Au atoms on CeO₂(110): a density functional theory study, ACS Catal., 2014, 4, 1885–1892.
43. Z. Cheng, B. J. Sherman and C. S. Lo, Carbon dioxide activation and dissociation on ceria (110): A density functional theory study, J. Chem. Phys., 2013, 138, 014702.
44. Y. Tang, Y.-G. Wang, J.-X. Liang and J. Li, Investigation of water adsorption and dissociation on Au₁/CeO₂ single-atom catalysts using density functional theory, Chinese J. Catal., 2017, 38, 1558–1565.
45. R. Sun, Y. Liao, S.-T. Bai, M. Zheng, C. Zhou, T. Zhang and B. F. Sels, Heterogeneous catalysts for CO₂ hydrogenation to formic acid/formate: from nanoscale to single atom, Energy Environ. Sci., 2021, 14, 1247–1285.
46. Z. Sun, S. Wang and W. Chen, Metal single-atom catalysts for selective hydrogenation of unsaturated bonds, J. Mater. Chem. A, 2021, 9, 5296–5319.
47. J.-X. Liang, J. Lin, J. Liu, X. Wang, T. Zhang and J. Li, Dual metal active sites in an Ir₁/FeO_x single-atom catalyst: a redox mechanism for the water-gas shift reaction, Angew. Chem., Int. Ed., 2020, 59, 12868–12875.
48. Z. Li, Y. Chen, S. Ji, Y. Tang, W. Chen, A. Li, J. Zhao, Y. Xiong, Y. Wu, Y. Gong, T. Yao, W. Liu, L. Zheng, J. Dong, Y. Wang, Z. Zhuang, W. Xing, C.-T. He, C. Peng, W.-C. Cheong, Q. Li, M. Zhang, Z. Chen, N. Fu, X. Gao, W. Zhu, J. Wan, J. Zhang, L. Gu, S. Wei, P. Hu, J. Luo, J. Li, C. Chen, Q. Peng, X. Duan, Y. Huang, X.-M. Chen, D. Wang and Y. Li, Iridium single-atom catalyst on nitrogen-doped carbon for formic acid oxidation synthesized using a general host–guest strategy, Nat. Chem., 2020, 12, 764–772.
49. R. Lang, X. Du, Y. Huang, X. Jiang, Q. Zhang, Y. Guo, K. Liu, B. Qiao, A. Wang and T. Zhang, Single-atom catalysts based on the metal–oxide interaction, Chem. Rev., 2020, 120, 11986–12043.
50. J. Li, Y. Tang, Y. Ma, Z. Zhang, F. Tao and Y. Qu, In Situ Formation of Isolated Bimetallic PtCe Sites of Single-Dispersed Pt on CeO₂ for Low-Temperature CO Oxidation, ACS Appl. Mater. Interface, 2018, 10, 38134–38140.
51. L. Liu and A. Corma, Identification of the active sites in supported subnanometric metal catalysts, Nat. Catal., 2021, 4, 453–456.
52. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
53. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111.
54. Y.-G. Wang, Y. Yoon, V.-A. Glezakou, J. Li and R. Rousseau, The role of reducible oxide–metal cluster charge transfer in catalytic processes: new insights on the catalytic mechanism of CO oxidation on Au/TiO₂ from ab initio molecular dynamics, J. Am. Chem. Soc., 2013, 135, 10673–10683.
55. N. A. Deskins, R. Rousseau and M. Dupuis, Localized electronic states from surface hydroxyls and polarons in TiO₂(110), J. Phys. Chem. C, 2009, 113, 14583–14586.
56. X. Zhou, Q. Shen, K. Yuan, W. Yang, Q. Chen, Z. Geng, J. Zhang, X. Shao, W. Chen, G. Xu, X. Yang and K. Wu, Unraveling charge state of supported Au single-atoms during CO oxidation, J. Am. Chem. Soc., 2018, 140, 554–557.
57. P. Pyykko and J. P. Desclaux, Relativity and the periodic system of elements, Acc. Chem. Res., 1979, 12, 276–281.
58. P. Pyykko, Relativistic effects in structural chemistry, Chem. Rev., 1988, 88, 563–594.
59. P. Pyykkö, Theoretical chemistry of gold, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
60. P. Pyykkö, Relativity, gold, closed-shell interactions, and CsAu·NH₃, Angew. Chem., Int. Ed., 2002, 41, 3573–3578.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06962h

---