Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterising flow with continuous aeration in an oscillatory baffle flow reactor using residence time distribution†
Rylan
Cox
 *a,
Konstantinos
Salonitis
a,
Susan A.
Impey
a and
Evgeny
Rebrov
*a,
Konstantinos
Salonitis
a,
Susan A.
Impey
a and
Evgeny
Rebrov
 bc
bc
aSchool of Aerospace, Transport and Manufacturing, Cranfield University, Cranfield MK43 0AL, UK. E-mail: rylan.cox@cranfield.ac.uk
bSchool of Engineering, Department of Chemical Engineering and Chemistry, University of Warwick, Coventry CV4 7AL, UK
cEindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
First published on 30th August 2023
Abstract
Multi-phase flow occurs in many reactions with gas, an integral part of the reaction. This study assesses the synergistic impact of continuous aeration and velocity ratio on mixing conditions within an oscillatory baffled flow reactor to enhance the degree of plug flow, quantified by a tanks-in-series (TiS) model. A bubbly flow regime is shown in all experiments. In most cases, the TiS value was reduced with gas flow, and a maximum TiS value of 23.6 was achieved at a velocity ratio of 3.8 at 225 ml min−1 in a counter-current direction. Single-phase runs and co-current multi-phase runs produced maximum TiS values of 23.5 and 18.2 respectively at a velocity ratio of 2.2. Regardless of the gas flow rate, the velocity ratio was found to be the most influential factor that dictates the level of plug flow within the OBR. A predictive model is developed and used to maximise the mixing efficiency by determining the level of plug flow within the OBR at selected amplitudes, frequencies, and gas flow rates.
1 Introduction
Continuous flow technology for materials processing can improve industrial performance and economics.1 One such system is an oscillatory baffled flow reactor (OBR) which is said to have improved mixing and enhanced heat and mass transfer over conventional batch systems.2,3 An OBR has been used in different applications which include bioprocessing, crystallisation, synthetic chemistry, biofuels and several others.4–7 A conventional OBR, a continuous flow reactor, contains periodic constrictions known as baffles, and an oscillatory motion is applied to the fluid.8 Eddies are generated on either side of the constrictions for uniform mixing along the reactor length.9 Usually operated within a laminar flow range over turbulent flow due to the parabolic flow pattern of liquid through a smooth tube which is not found due to chaotic mixing within turbulent flow.10 The baffles act as a restriction to the laminar boundary layers at the walls, whilst the oscillatory motion added to the parabolic velocity gradient, particularly during the back stroke of the oscillation, drags the central high velocity fluid back into the vicinity of the low velocity which adheres to the walls. Meanwhile, the eddy generation prevents mixing dead spots behind or in front of the baffles. This combination of laminar flow and oscillatory motion increases the radial diffusion towards the wall and provides a uniform velocity gradient along the length of the reactor.11 This flow profile promotes plug flow behaviour and allows mixing to be independent of the net flow allowing a wide range of residence time and plug flow reactor type behaviour.12 The level of plug flow is quantified either with an axial dispersion model or a tanks-in-series (TiS) model, controlled through the oscillatory frequency and amplitude.13A range of studies investigating residence time distribution (RTD) within OBRs conclude near plug flow can be achieved with a range of parameters depending on the design and operating conditions.2,14–16 Dimensionless numbers are usually associated with the OBR to provide initial guidelines for operational parameters that provide near plug flow using eqn (1) for net Reynolds number (Ren), which determines the net flow. Eqn (2) for oscillatory Reynolds number (Reo), which determines the intensity of mixing and eqn (3) for Strouhal number (St) which determines the propagation of eddies between each constriction.12
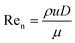 | (1) |
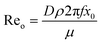 | (2) |
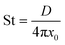 | (3) |
As the OBR is operated under laminar conditions mixing is provided through the oscillatory motion and the eddies that are formed on either side of the baffle on the up or downstroke respectively.12 Reo which describes the oscillatory motion, is an adaption of the Ren.17 The oscillatory parameters frequency and amplitude are what control the size of the vortices either side of the baffle and therefore the intensity of mixing within an inter baffled zone as shown by several numerical and PIV studies.12,18–20 Furthermore, the oscillatory parameter 2πfx0 combined with the net flow is what controls the maximum velocity fluid velocity.21 As the fluid is accelerated past the baffle, separation occurs which forms a toroidal vortex downstream of the baffle. In the reverse stroke, the vortex is removed by the reversal of flow, pulling the vortices away from the wall and back into the main flow path which in turn forms a second vortex on the back side of the baffle.12 For single phase flow this mixing mechanism allows scaling linearly by maintaining dimensionless numbers.8 Unlike conventional stirred tank reactors (STRs), the linear scaling of OBRs allows momentum transfer conditions through plug flow characterisation studies to be predicted when transitioning process screening experiments at a lab scale to pilot plants.22 The batch process residence time can then be equated to a flow rate and reactor length whilst operating with a narrow RTD.8 Maintaining RTDs with high TiS values is crucial in maintaining near plug flow conditions within the liquid phase of an OBR and therefore ensuring each inter baffle zone acts as a CSTR in series. Several studies have quantified the level of plug flow either through the TiS model or dispersion model, equated the operational parameters to their respective dimensionless numbers and used these as a basis for scale up methodologies.8,9,11,12,15,16,22–32
Several studies have also been conducted in multiphase to evaluate the OBRs gas–liquid mass transfer within single baffled columns both numerically and experimentally. In these studies however, only a single column is used with a headspace with the focus on mass transfer, gas hold-up, bubble size and flow regimes concluding improved mass transfer over conventional systems.3,33–40 Many of these studies correlate similar findings in which oscillation parameters play a vital role in enhancing mass transfer, gas hold-up and bubble size, identifying its need for both optimising the level of plug flow and its gas–liquid interaction. As the oscillatory intensity increases, either through increasing amplitude or frequency, the bubbles no longer act in a plug flow manner. Thus, there is a longer bubble residence time within the reactor which increases the gas–liquid contact time. Furthermore, the motion around the baffles from generated eddies causes the bubbles to continuously coalesce and break up within each inter baffled zone resulting in a smaller Sauter-mean diameter.35 Break-up is likely caused due to the induced increase in velocity and strength of interaction between oscillating liquid and sharp-edged baffles, essentially as the oscillatory velocity or oscillatory Reynolds number increases the intermediate vortex scale increases to break bubbles up more often.13,39 This increases the bubble surface area to volume ratio and results in an increase in mass transfer and gas hold-up as bubble sizes reduce. Although several studies on mass transfer have correlated the same there has been little to no observation of the impact of aeration in scaling up a multi-pass OBR with several channels, how the bubbles will impact the OBRs near plug flow behaviour and the ability of oscillatory propagation through the reactor. One study identified that smaller bubble diameters result in smaller levels of localised fluid recirculation.2,13,41,42 As water is an incompressible fluid, in single-phase investigations there will be little to no oscillation dampening through fluid compression but rather frictional losses and momentum changes.2,42 The transition to a multiphase gas–liquid system provides a compressible phase, the gas, which could exhibit oscillation dampening. Additionally, due to significant differences in physical properties between gas and liquid, the interaction between these two phases may have an impact on the liquid RTD. This may generate localised recirculation loops from passing bubbles, causing a deviation away from near plug flow into mixed flow like that of STRs.
To the best of the authors' knowledge no investigation has been made to identify the impacts of aeration on OBR RTD curves, nor has this been discussed regarding the possibilities of scaling up through a multi-pass system. The closest resemblance of RTD studies with gas–liquid flow is that of continuous bubble columns. Bubble columns are simply large tanks with a continuous input of gas at the base of the column. The bubbles rise under buoyancy causing liquid recirculation providing mixing and gas–liquid mass transfer.3 Bubbles act similarly in the OBR as bubble columns however the addition of oscillation and baffles add a secondary force causing bubbles to break up and reverse in direction.3 In continuous operation, OBRs must be full of liquid to ensure the oscillatory motion propagates throughout the entire system to create eddies around the baffles and provide uniform mixing. The flow regime will have an impact on the RTD of the liquid phase which will change depending on the gas flow rate, column diameter, and oscillatory parameters.3,8,34,37 Several chemical or bioprocess reactions require multiphase gas–liquid flow. To operate these reactions in a continuous manner the reactor must have sparging points along the length where excess can be removed to minimise disruption to the flow. Deviations from plug flow into mixed flow, oscillation dampening, or localised liquid recirculation will reduce the benefits of an OBR leading to arguments that the technology is no better than a complex tubular reactor system.
It is important to understand how the RTD curves are affected when transitioning into gas–liquid multiphase flow. Using data from previous studies, the development of models that can predict the level of plug flow at different aeration conditions can synergistically provide a valuable understanding of parameters that can provide high mass transfer and gas hold-up whilst simultaneously knowing the associated level of plug flow for such chosen parameters.
Although the OBR has been proven to enhance gas–liquid mass transfer within the OBR there has been no study on RTDs when operated as a gas–liquid system. This research investigates experimentally the liquid phase RTD within an OBR. The aim is to evaluate different oscillatory parameters, gas flow rates and directions on the RTD. Any impact on oscillatory propagation due to the implementation of membranes is measured and assessed to minimise disruption to near plug flow. Based on selected parameters and using a design of experiments (DOE) approach, the study evaluates how factors and their interactions influence the level of plug flow. A central-composite design (CCD) methodology is used to identify the influence of gas flow rate, amplitude, and frequency. A predictive model is built that can maximise plug flow by achieving a narrow liquid phase RTD under a constant gas flow rate and determine suitable parameters to provide enhanced mass transfer and maximise the level of plug flow. The flow is modelled and quantified using the tanks-in-series model to determine the level of plug flow with the TiS number set as the response for the predictive model.43
2 Materials and methods
2.1 Experimental setup
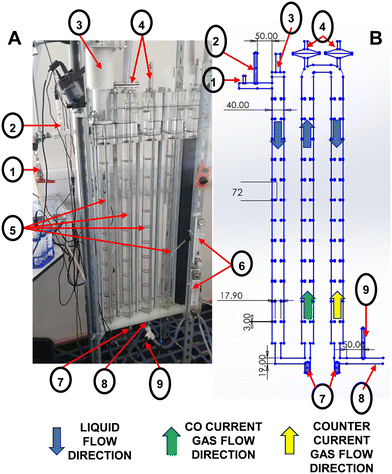
An oscillatory baffled flow reactor (OBR) with five columns connected with U-bends was constructed and assembled in a vertical orientation. The experimental rig is displayed in Fig. 1A; the operated system contained three baffled columns, each baffle was 3 mm in thickness and spaced 72 mm centre to centre from one another. The orifice diameter was 17.9 mm to ensure a constriction ratio of 20%. Each baffled column contained twelve baffles and was connected via a set of U bends. The top U bend has venting modules centrally aligned with the second and third baffled column, whilst the lower connecting U bend had a sparger fitted in either column two or three. A schematic of the dimensions and parts can be identified in Fig. 1B along with a detailed summary in a previous study.42 Oscillatory motion was provided by a scotch yolk mechanism capable of amplitudes from 0.5–12 mm and frequencies of 0.05–2 Hz. Amplitude was pre-calibrated during manufacture with a zero-datum line followed by 1 mm incremental ruler marks to set the amplitude. To ensure there was no change of amplitude during oscillation locking rods were fitted to the oscillatory mechanism and fastened. Frequencies were measured manually using a FINIATE professional digital tachometer. Gas sparging could be provided at the base of columns 2–5 only, with the first column that is connected to the oscillatory mechanism not provided with any gas. Air was used for all multiphase flow experiments and provided by a Cole-Parmer air diaphragm vacuum/pressure pump WZ-79202-05. The gas line was connected to two mechanical gas flow meters with a range of 0.01–2.1 L min−1 which is equivalent to an aeration rate between 0.0125–2.63 (volumetric flow rate of air per volume of liquid in a single column per minute (m3 air)/(m3 of liquid within the column)/min). The gas control was connected to a 0.2 μm Swagelok filter and a blue, cylindrical, ceramic pond stone with a diameter of 23 mm and height of 33 mm. The sparger type was kept constant in all experiments, as it was found to have no impact on mass transfer.35,39 The OBR design allowed gas to be input in both co-current and counter-current directions to the liquid flow and assessed by swapping the air inlet location to a riser or downer column within the system. Due to the length of each experiment only the first three columns were used. In co-current gas was only sparged in column 2, whereas in counter-current gas was sparged in column 3 only as shown in Fig. 1B. For this study, the scope was to identify the impact of co-current and counter current independently, hence only one column was sparged with gas at any one point unless stated otherwise. The top connecting U-bends each have a port centrally aligned to the columns connected to venting columns containing 15D07MI semi-permeable oleophobic membranes provided by Sartorius. Two distinct types of venting devices were used with different surface areas to evaluate different gas flow rates and membrane impact on oscillation dampening. To allow rapid removal of excess gas and prevent bubble build-up within the U-bend, each venting device was connected to an Edwards RV8 vacuum pump. Both vacuum pumps were operated continuously during aeration experiments. Fresh, clean tap water was used as the bulk fluid in all experiments with the fluid properties remaining constant in all experiments. Tap water was fed into a buffer tank before being pumped into the reactor to negate any impact of water pressure from the tap. Properties were kept constant by continuously monitoring a constant water temperature at a value of 21 ± 2 °C. Water was provided at a constant flow rate of 500 ml min−1. The experimental setup used for all experiments is given in Fig. 1A.2.2 Oscillation dampening
Before all experiments, the reactor was filled with water and cycled a minimum of five times to ensure removal of any prior impurities and air. All experiments were conducted at ambient room temperature. Once flushed completely, column four was partially drained of liquid to the halfway point. A line gauge (ruler) was attached to the column with the 0-point aligned to the water level. Measurement of oscillation dampening was taken with no net flow. Different membrane sizes and oscillatory parameters without air were assessed to determine if the size of the membrane produced oscillation dampening over a range of parameters. To accurately monitor the water level on the line gauge a Samsung S10+ phone camera with slow-motion video recording was used to view the water level. Oscillation dampening was attempted with aeration but stopped due to inaccurate and varied results. This is attributed to fluctuating gas hold up, at high frequencies (2 Hz) and amplitudes greater than 6 mm, coupled with fluctuations in gas removal rates. The continual oscillatory motion causes the partial pressure differential at the membrane surface to vary the gas removal and therefore the gas hold up. Therefore, this section discusses oscillation dampening caused by membrane surface area, amplitude, and frequency with no gas input. Fig. 2 identifies the two different membrane housings used. The membrane surface area was set when using two metal membrane housings at 1.57 cm2, using one white poly-lactic acid (PLA) housing and a stainless steel 316 housing at 102 cm2, and when using 2 PLA membrane housings at 201 cm2.2.3 Design of experiments
Rather than conducting a full factorial design of experiments (DOE) of oscillatory amplitude, frequency, and gas flow rate a face Centred Composite Design (CCD) was selected. This was to both minimise runs and build secondary models without the need for a full three-level factorial requiring more experiments.44 The response in this case was the TiS number (N) or quantitative level of plug flow, with continuous factors amplitude, (x1), frequency, (x2) and gas flow rate (x3) at two levels. Each factor is given in Table 1. The range of amplitude and frequency were selected to provide a wide range of velocity ratios and based on previous studies that maximise plug-flow and mass transfer; whereas gas flow was set at the two extremes within the systems capabilities.3,42 Centre points which were the median of each factor are included with all experiments replicated twice whilst the centre points were replicated 4 times.| Factor | Value | Unit |
|---|---|---|
| Amplitude | 2, 6.5, 11 | mm |
| Frequency | 0.3, 1.15, 2 | Hz |
| Velocity ratio | 0.57–20.85 | (—) |
| Gas flow rate | 0, 225, 400 | ml min −1 |
The CCD consists of eight factorial points, two centre points and six axial points enabling a model to provide three main effects, three two-way interactions and three quadratic effects.45 The full table of experiments along with dimensionless values given in Table 2 consists of 32 runs in total. DOE software JMP® 17 Pro was used to generate the DOE, analyse data, and develop a predictive response surface model to maximise the TiS number and determine factor impact and interactions. Data was displayed through scatter plots generated in Microsoft Excel or using JMP Pro 17®.
| Amplitude (mm) | Frequency (Hz) | Gas flow (ml min−1) |
|---|---|---|
| 2 | 0.3 | 50 |
| 11 | 0.3 | 50 |
| 6.5 | 1.15 | 50 |
| 2 | 2 | 50 |
| 11 | 2 | 50 |
| 6.5 | 0.3 | 225 |
| 2 | 1.15 | 225 |
| 6.5 | 1.15 | 225 |
| 6.5 | 1.15 | 225 |
| 11 | 1.15 | 225 |
| 6.5 | 2 | 225 |
| 2 | 0.3 | 400 |
| 11 | 0.3 | 400 |
| 6.5 | 1.15 | 400 |
| 2 | 2 | 400 |
| 11 | 2 | 400 |
The predictive model equation is built-up of seven terms related to the factors and their interactions. Each term within the model is either linear, square or the interaction between factors.45 Analysis of variance (ANOVA) was used to determine the influence of each term with the response being the TiS number. Each term is associated with a coefficient to determine the level of fit as per regression analysis between experimental values and model predicted values. The significance of each term is provided by a p-value, which is the probability of the term having no significant effect. Therefore, a step-wise elimination of p-values was conducted on all terms with a p-value >0.05 before the final model was completed. p-Values required due to hierarchical requirements of other terms were kept.22
2.4 Deconvolution and residence time distribution
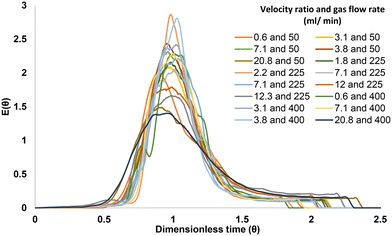
To quantify the impact of aeration and the level of plug flow tracer experiments were conducted to produce RTD curves. The tanks-in-series (TiS) model was used to quantitatively evaluate the RTD curves.43 RTD curves were produced by injection of 5 ml potassium hydroxide tracer (0.1 M) 200 mm upstream of the reactor inlet, followed by 40 ml of tap water to ensure all tracer was injected into the flow path and not remaining within the injection ports. Injection of both tracer and water was conducted over a 3.5 s period. The pH was monitored 50 mm from the inlet and outlet of the reactor using a Mettler Toledo LE407 pH probe with a measured response time of 10 seconds. The data was live streamed into Excel using data streaming software at an interval of 1 s which was found to produce well-shaped RTD curves as shown in Fig. 4 Each experiment ended when the outlet pH returned to its starting value. The pH data was converted into hydroxide ion concentration before determining the TiS number (N), using the TiS model. Near plug flow is achieved when N > 10, and mixed flow occurs when N < 3.8,22,31,32 Thus, to achieve adequate plug flow, a minimum of 3 baffled columns were used each containing 12 baffled zones within the OBR. This satisfies the design criteria to ensure that more than 15 inter-baffled cavities are available to achieve the criterion of N > 10.8 It is stated that the number of inter-baffled zones within an OBR is equal to the theoretical maximum of TiS.22 Perfect pulse injections are only found in ideal scenarios, to combat any mixing between the tracer injection point and reactor entry a deconvolution was conducted to remove any initial tracer dispersion. Furthermore, all measurements were offset by 10 seconds to account for the response time of the pH probe in a similar method to Abbott et al.22 Before deconvolution, pH was converted to hydroxide ion concentration before deconvolution was conducted through the inverse fast Fourier transformation within the time domain. The true outlet signal (E) was calculated by the inverse fast Fourier transformation between the measured inlet and outlet signals as described in eqn (4)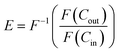 | (4) |
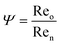 | (5) |
3 Results and discussion
3.1 Oscillation dampening with membranes and aeration
The OBR operates by applying oscillatory motion through periodic constrictions along each column to ensure uniform mixing throughout. If the connecting U-bend fills with air and the oscillations do not propagate into the next column it will minimise any mixing downstream. The maximum level of aeration that can then be input into the system is equal to the maximum rate of aeration removal. The problem becomes more complex with increasing the turbulence within the reactor as the gas hold-up also increases.3 The maximum level of air removal within the system is relative to the membrane flux and therefore the surface area of the membrane. Three different membrane sizes were evaluated at their maximum aeration removal.Fig. 3 displays the fluid amplitude at different frequencies and set amplitudes with a change in the membrane surface area. At low frequencies, the membrane surface area has little to no impact on the achieved oscillation motion within the fourth riser column. Each set amplitude matches the fluid amplitude and are correlated linearly. When the frequency increases to 1 Hz, the set amplitude of oscillation is equal to the observed fluid oscillation in the fourth column. Furthermore, membrane surface area has a negligible impact on fluid oscillation.
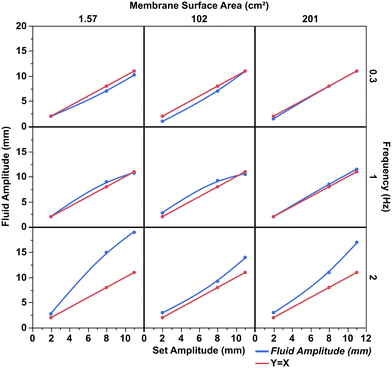 | ||
| Fig. 3 Displaying the different liquid oscillation (achieved amplitude mm) vs. the set amplitude (mm) with different membrane surface areas and frequencies. | ||
Upon increasing the frequency to 2 Hz it is noted the fluid oscillation is much greater than the set oscillation amplitude. In previous cases, the fluid oscillates at the same amplitude as the set amplitude but for all amplitudes evaluated (at 2 Hz), there is an increase in achieved fluid oscillation. Thus, 2 mm, 8 mm and 11 mm set amplitudes increased to an average fluid oscillation of 3 mm, 12 mm, and 17 mm, respectively. These results are comparable with a study by Briggs et al., who experienced a similar phenomenon in a commercial 15 mm nominal diameter (DN15) OBR.2 The reason for the increase in fluid oscillation is due to the additional energy added to the system from faster piston acceleration with increased frequency. The additional energy is maintained within the fluid momentum propelling the liquid down the reactor before flow reversal of the piston upstroke. Furthermore, due to the inclusion of baffles, the fluid in the radial centre travels with a greater velocity than at the sides due to the constrictions. At an amplitude of 2 mm the achieved fluid oscillation remains constant regardless of membrane area, however, once the amplitude reaches 8 and 11 mm there is a noticeable drop in fluid amplitude against set amplitude with different membrane areas. The highest fluid oscillation is achieved with the smallest membrane area, reaching a fluid oscillation of 15 mm and 19 mm for 8 mm and 11 mm set amplitudes, respectively. As the membrane area increases from 1.57 cm2 to 102 cm2 there is a decrease in fluid oscillation to 9 mm and 14 mm for 8 mm and 11 mm set amplitudes, respectively. A similar decrease is observed for the largest membrane surface area of 201 cm2, where both set amplitudes at 8 and 11 mm produced a fluid oscillation of 10 and 16 mm, respectively.
An increase in membrane area at high frequencies causes some degree of oscillation dampening downstream. This can be attributed to the membrane flexing back and forth within its housing due to the fluid oscillation. One way to minimise the oscillation dampening due to the membranes would be to introduce fixed supports within the membrane housing whilst minimising surface area blockage. This will prevent the membranes from absorbing the oscillatory kinetic motion, so it is translated through the fluid only whilst removing excess gas.
3.2 Flow regime and bubble interaction
The interaction of oscillatory motion on bubbles within the OBR has a profound effect, as reported in several mass transfer studies using an OBR.3,33,34,37–39,46 Ahmed et al. investigated the impact of flow regime and mass transfer with different designs of OBR, including a single orifice OBR, as a function of oscillatory parameters and gas flow rate.3 They conclude the OBR was able to produce different flow regimes including bubble, churn, and slug flow depending on the gas flow rate and oscillatory Reynolds number. In the same study, the authors found bubbly flow is present to an aeration rate of 0.56 volumetric flow rate of air per volume of liquid in a single column per minute.3 During their experimental study, the motion and size of the bubbles would alter, coinciding with the oscillatory motion.• At velocity ratios of 3.8 and below the bubbles would coalesce together. The bubbles rise the column with no interference from the oscillatory motion to the path. The bubbles, ranging in diameter from 5–20 mm, were acting under buoyancy alone.
• At a velocity ratio of 7.1 the bubbles temporarily stagnate within the baffled column from flow reversal by the oscillatory piston. However, bubble sizes remain large with coalescence occurring as the bubbles rise the column to 20 mm diameter. A visualisation study conducted by Ranganathan simulating gas–liquid flow within an OBR, found at frequencies <1 Hz, a large amount of bubble coalescence occurs behind the baffles.36
• At velocity ratios of 12 and 12.3, the impact of flow reversal becomes more pronounced on the bubbles, as they stagnate for a longer period. The bubble size is also smaller (<5 mm diameter on average) with no visible sign of large bubbles present in the entire column. Bubbles exhibit full bubble reversal behind the baffles where the turbulence is greatest.
• Finally at a velocity ratio of 20.8, full flow reversal is identified in all locations within the column, not just behind the baffles but in the centre of the inter-baffled zone. Bubbles break-up around the baffles ensuring a smaller visual mean bubble diameter distribution within the baffled column. This finding is similar as noted in previous studies.3,35,36
In this study, to ensure only oscillatory parameters and gas flow rates were being investigated the largest membrane was selected for all experiments to ensure a wide range of gas flow rates could be achieved. In all the co-current studies performed in this current study, the flow regime remained, within the bubble flow regime attributed to a gas flow rate no greater than 0.56 volumetric flow rate of air per volume of liquid in a single column per minute. This is under the stated threshold for single orifice baffles to achieve churn flow as pointed out by Ahmed et al.3 Similarly Ahmed et al. in another study identified that when scaling up the OBR to tube diameters of 50 mm or greater, only the bubbly flow regime is present.37 However, there was no identification of slug flow within the baffled column at any of the velocity ratios or gas flow rates within this present study which is in contradiction to the data generated by Ahmed et al.3
This study also investigated the impact of counter-current flow. The setup was done by moving the gas injection point to the base of the next adjacent column. Selected velocity ratios were 1.9, 2.2, 3.8, 7.1 and 20.8 at gas flow rates of 225, 225, 50, 400 and 50 ml min−1, respectively. It was expected that similar observations to those described earlier in the co-current flow would be found. All experiments remained within the bubbly flow regime. However, on the application of oscillatory motion and aeration the bubbles, regardless of oscillatory parameters or gas flow rate, acted under buoyancy alone with no reversal, stagnation, or rapid bubble coalescence or bubble break-up. The initial conclusions are the bubbles dampened all oscillations in that column. However, there is visible fluid oscillation at the top of the column where the gas was escaping, fluid oscillation at the outlet tube, and on the mechanical pressure gauge, at the outlet of the reactor. Which matches the same levels as co-current studies. The reason for this phenomenon would need further investigation to provide clarity as to why the oscillation has no direct impact on the bubbles as it does in the co-current experiments.
3.3 Quantifying aeration impact on the level of plug flow
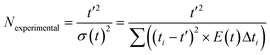 | (6) |
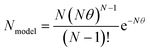 | (7) |
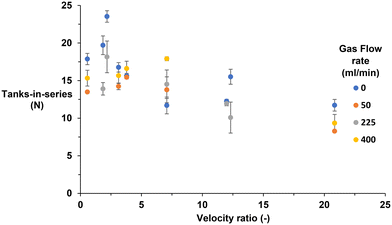 | ||
| Fig. 5 Experimental mean TiS value based upon the velocity ratio, with no gas flow and gas flow rates 50, 225 and 400 ml min−1. The error bar represents the variation between replicates. | ||
Fig. 5 shows that for most velocity ratios, the TiS number is higher with no aeration present (blue) compared with aeration. Surprisingly, a velocity ratio of 7.1 presents the lowest TiS value with no aeration. This is a result contrary to all other velocity ratios in the range assessed.
• At zero aeration, the TiS value is maximum around a value of 2.2, which correlates with a previous study conducted in the same system.42 With gas flowing at a rate of 50 ml min−1 the TiS value remains between 13.5 and 15.5 across a velocity ratio of 0.6 to 3.8. The value begins to decline once a velocity ratio of 7.1 is reached. The lowest TiS value of 8.3 occurs at a velocity ratio of 20.1.
• A similar scenario was found with gas flow rates of 225 ml min−1, however, there is a significant initial rise in TiS value (18.2) at a velocity ratio of 2.2 before sharply declining, reaching its lowest value of 10.1 at a velocity ratio of 12.3.
• Finally for a gas flow rate of 400 ml min−1 again a similar trend to the previous gas flow rate is exhibited. This time, a maximum TiS value of 17.9 was reached at a velocity ratio of 7.1 before rapidly declining to a TiS number of 9.34 at a velocity ratio of 20.8.
Within all the tested gas flow rates the TiS > 13 at velocity ratios between 0.6–7.1. The TIS values all rapidly decline, reaching their lowest value at a velocity ratio of 20.8.
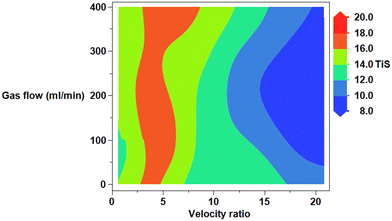
To the authors' knowledge this is the first reported study to investigate the RTD within an OBR for multiphase flow. The closest to such a system is the bubble tank, although the bubble tank does not exhibit oscillatory motion or baffles. For a fixed velocity ratio, it would be expected that as the aeration rate increases the TiS number would reduce. With an increase in velocity ratio and gas flow rate, the gas hold-up in an OBR increases.3,36,37,39,50 In bubble columns an increase in gas results in more liquid circulation and a higher liquid dispersion.51,52 Therefore, the increase in gas flow rate should decrease the TiS value, however, this is not the case. In most of the velocity ratios where three different gas flow rates are used the maximum gas flow rate appears to provide the highest TiS number followed by 225 and then 50 ml min−1. To visualise the variation of TiS with both velocity ratio and gas flow rate, the experimental data was plotted through a contour plot in Fig. 6. The interaction of oscillatory motion overpowers the negative impact of aeration, by minimising dispersion and providing some degree of plug flow. In bubble columns, the motion of bubbles through the centre line causes an uneven radial density across the column diameter, which results in liquid recirculation and increases axial dispersion.52 In an OBR the bubbles have more bubble stagnation points and bubbles break up at a faster rate at higher velocity ratios. However, as the liquid turbulence also increases this explains why the zero air experiments at high velocity ratios result in low TiS values. When evaluating axial dispersion in packed or tray bubble columns it was identified the axial dispersion of tracer reduces dramatically compared with an empty bubble column.51 In the same way the baffles could be acting as constraints which maintain a high degree of plug flow similar to packed bubble columns.
Palaskar et al. investigated perforated plates within bubble columns and the effect on axial dispersion and found as the percentage free area in the radial direction decreases, the resistance to the gas phase increases and generates a uniform gradient distribution.52 This in turn reduces liquid recirculation and therefore minimises axial dispersion. This explains why there is a level of plug flow present at gas flow rates and velocity ratios <20. The impact of gas viscosity, gas density or liquid surface tension was not evaluated in this study.
To identify each term's effect on the TiS number an effect summary was produced which identified the p-value associated with each term. The p-value is the probability of likelihood that a term has an impact on the TiS value when changed. The p-values of each term are shown in Table 3. Factor terms that are required due to cross-factor interactions or polynomials are denoted with a ^. The software develops a predictive model using the data predicting the TiS number. Each term is given a coefficient on its effect on the TiS number shown in “parameter estimates”. Parameter estimates indicate the increase or decrease in TiS number when the value is increased by one. For example, if the frequency increases from 1 to 2 Hz the TiS value will reduce by 1.29. The likelihood of this happening is then dictated by the parameter estimates p-value.
| Source | p-Value | Parameter estimates | p-Value parameter estimates |
|---|---|---|---|
| Amplitude | 0.00001 | −1.95 | <0.0001 |
| Amplitude *frequency | 0.00006 | −1.94 | 0.0015 |
| Frequency *frequency | 0.00085 | −2.52 | 0.0129 |
| Frequency (Hz) ^ | 0.00147 | −1.29 | <0.0001 |
| Gas flow (ml min−1) | 0.01292 | 0.96 | 0.0009 |
| Gas flow *gas flow | 0.04681 | 1.33 | 0.0468 |
Finally, the derived model equation which predicts the TiS value based on the selected terms above is given in eqn (8). The equation coefficients are calculated through the DoE whilst the coefficients produced are the intercept, three main effect coefficients, three two-way interaction coefficients and the three quadratic effect coefficients. All are left in fraction form to prevent decimal rounding errors.
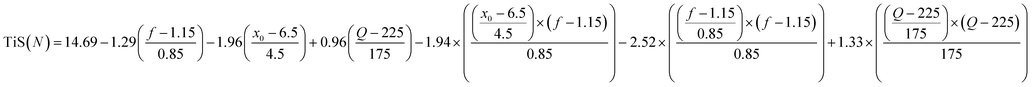 | (8) |
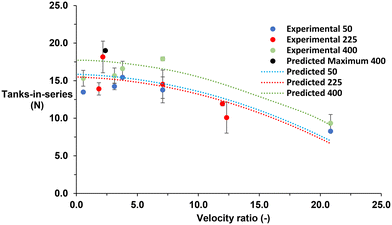
The equation was able to predict a maximum TiS value of 19 at parameters 2 mm amplitude, 1.26 Hz frequency and 400 ml min−1 gas flow rate. This prediction gives a velocity ratio of 2.38 and expects a higher TiS value to be achieved compared with all the other parameters experimentally evaluated. However, the velocity ratio remains within the optimal range for maximising TiS in single-phase reports.18,22Fig. 7 displays the predicted TiS values against the experimental values. The maximum predicted TiS value is denoted by a black point. When looking at the predicted value of TiS against the experimental all points lie close to the actual experimental TiS indicating a high level of fit of the model compared with the experimental data.
Although the model can predict TiS using amplitude and frequency only, both parameters can be combined through the oscillatory Reynolds number (eqn (2)) along with the net flow via the Reynolds number (eqn (1)) to calculate the velocity ratio (eqn (5)). The model can therefore be used at a range of scales, providing the dimensionless numbers remain constant between scales to predict the TiS. It is critical to mention that the model generated within this study contains a saddle point by which the maximum TiS value is theoretically infinite outside of the tested parameter range. Without expanding the factor range the model should only be used within the tested range. Furthermore, the model was derived using the largest membrane size only. Any oscillation dampening induced by the membrane is not factored into the model.
When operating aeration in a counter-current direction there was a visible increase in TiS number for the majority of the parameters as shown in Fig. 8. All counter-current parameters were able to perform some degree of plug flow whereas the co-current found that the velocity ratio of 20.8 exhibited a TiS value under 10, which tends towards mixed flow.13 A similar trend was observed with the counter-current TiS values which present an increasing TiS number initially up to a value of 23.6 at a velocity ratio of 3.8. The TiS values then begin to fall reaching its lowest value of 10.3 at a velocity ratio of 20.8. The trend almost matches the co-current results however their maximum TiS value is achieved at a velocity ratio of 2.2 rather than 3.8 in the counter-current experiments. Additionally, the co-current TiS value was much higher at a velocity ratio of 7.1 compared with the counter-current results. To determine the difference in OBR efficiency between the values eqn (9) is used. This equation is based on the maximum theoretical TiS value the OBR can produce. As the number of inter-baffled zones can each act as a CSTR, then the maximum number of TiS is equal to the number of inter-baffled zones providing there are above 15 zones, although true plug flow is not achieved until TiS number of at least 50.8,13 It takes the experimental TiS value and divides it by the number of inter-baffled zones within the experimental flow path of the reactor to provide a percentage for the actual number of TiS against the potential number of TiS.
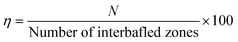 | (9) |
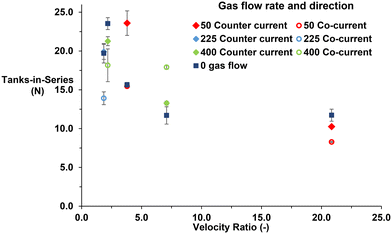 | ||
| Fig. 8 Scatter plot of TiS values with different velocity ratios, aeration conditions and gas flow direction. | ||
The range of actual tanks in series against the potential number of TiS between co-current to counter-current for parameters where counter-current exhibits a greater TiS is between 5–21%.
From this study, the flow regime changes from co-current to counter-current with bubbles acting under buoyancy alone in a plug flow manner. With co-current, the oscillatory motion changes the bubble flight path and size. Small bubbles get entangled within the high velocity eddy recirculation, whereas large bubbles formed from bubble coalescence are dragged from the centre of the eddies to the external sections of the vortex as identified by Al-Abduly et al.39 In counter-current however, it was visually observed that there was little interaction with the eddies generated either side of the baffle and the bubbles meaning they travelled under buoyancy alone. This enabled an increase in TiS values for counter-current which can be explained by the flow regime and generation of eddies within the liquid phase. The influence of eddy generation around the baffles within the liquid phase when the bubbles are acting in a counter-current direction is enough to minimise axial dispersion. A second visual observation was the lack of interaction between oscillatory motion-induced eddies and the bubbles does not reduce the localised liquid recirculation caused by the bubbles when they rise, but instead become entangled within the eddies generated either side of the baffles. This prevents axial dispersion of the tracer and maintains some degree of plug flow. Furthermore, if the bubbles were to be dragging the tracer against the direction of liquid flow i.e., in a counter-current direction then the RTD curves would exhibit non-symmetrical curves with a tail at the end implying back mixing is not the case.42,53
3.4 Application in multi-phase OBRs
To operate a continuous multi-pass OBR in multiphase gas–liquid operation, there must be locations where gas can be sparged and any excess removed with minimal impact on the flow. Section 3.1 describes the impact of oscillation dampening at high frequencies and amplitudes. The results from this work have found that high velocity ratios (a combination of high amplitudes and frequencies) will reduce the TiS value. This is found true for both multiphase and single-phase processes within an OBR.22,42 Therefore the process will have to prioritise either gas–liquid mass transfer which is improved at higher velocity ratios (>5) or maintaining near plug flow conditions by maintaining a velocity ratio in the optimal lower range, (2 < 4).3,34,37 The predictive statistical model in this study can help to balance the two values by maximising aeration whilst maintaining some degree of plug flow within the OBR. Although the net flow has not been investigated within this work, maintaining the velocity ratio using Ren and Reo can help to factor in the net flow. To validate this a future investigation should be made to identify the impact of net flow on multiphase as its impact has been conducted previously in single phase.12,22,23,54 There are limits to this model which have briefly been discussed in the previous section. Firstly, the parameter range available is confined to those within this study. Although the tested gas flow rate range is particularly high (maximum 0.5 volumetric flow rate of air per volume of liquid in a single column per minute) the range of amplitudes and frequencies within this study are mid-range compared to previous mass transfer study ranges.2,3,38 The model does not account for oscillation dampening induced by the membranes themselves. Only the large membrane was used for all experimental work as the membrane selection was done for the sole purpose of providing a wide range of gas flow rates therefore any oscillation dampening exhibited for the parameters would have been experienced at every gas flow rate regardless of the amplitude and frequencies.The results from this work have suggested that like single-phase flow, velocity ratios within the range of 2–4 are more suited for the flow to tend towards plug flow characteristics. This may not be suitable in practice if the multiphase system also requires solids. For high solid content processes where particle suspension is required, low velocity ratios may not be suitable, causing settling within the reactor.55 Furthermore, multiphase gas–solid–liquid is not taken into consideration within this model which may cause the equation to function inaccurately owing to the impact of solids within the fluid. A few studies have identified the impact of solids on axial dispersion, oscillation dampening and mass transfer. The studies conclude that solid particle oscillation dampening will occur downstream within the reactor as solid content increases, additionally, axial dispersion of solids and liquids within an OBR will vary based upon the radial mixing velocities.41,56 However solid content up to a concentration of 20% has no impact on mass transfer.57
Moving to commercial scales requires the reactor volume or throughput for low value high volume products to be increased by a few factors. For bubble columns scaling through tube diameter increases axial dispersion, whereas for OBRs, providing the dimensionless number is maintained throughout scales.8,51,52,58 Previous studies have indicated that the single orifice may not be the most suitable design for multiphase scale-up to ensure high mass transfer with plug flow. Therefore, the design should shift to a multi-orifice baffled design due to its increased resistance to gas flow which will minimise fluid recirculation caused by bubbles and increased mass transfer coefficient.37,52 This will also prevent the requirement of large amplitudes and low frequencies in operation and prevent loss of mixing intensities and length when scaling through diameter.5 For scale-up through the column diameter it seems a likely scenario for the OBR however producing a multi pass for multiphase operation combined with membranes, solids and aeration will potentially lead to a reactor that halfway down will have zero oscillatory motion within the fluid flow and revert to net flow laminar mixing profiles only. Without a pilot scale investigation, it cannot be certain that the OBR can be scaled in this capacity.
4 Conclusion
This study successfully characterised liquid phase axial dispersion in a gas–liquid OBR with multiple columns. Three gas flow rates, three amplitudes and three frequencies were assessed, with aeration in two gas–liquid configurations. Maximum TiS values of 23.5, 23.6 and 18.2 were observed under single phase, counter-current and co-current two-phase flow at velocity ratios of 2.2, 3.8 and 2.2, respectively. The velocity ratio remains the main factor that determines the level of plug flow irrespective of gas flow rate or flow direction. A predictive statistical model was developed to maximise TiS value by varying amplitude, frequency, and gas flow rate in the OBR reactor for process optimisation.Author contributions
R. C.: design, methodology, investigation, formal analysis, writing original draft, visualization, and conceptualization. E. R., S. A. I., and K. S.: revisions of the original draft, supervision, funding acquisitions, and conceptualization. All authors have read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. C. thanks Engineering and Physical Research Council (EPSRC) (Budget code EP/L016389/1) for funding his doctoral research. The funders had no role in the study experimental plan, system design, data collection, analysis, the decision to publish, or preparation of the article. The authors acknowledge the facilities provided by Cranfield University to allow experiments to take place and funding for the manufacture of the reactor, Cranfield Workshop for manufacturing the reactor and Electronic, Power, and Drive laboratories for their 3D printing facilities. We also thank Cranfield Forensic Institute for the provision of laboratory space funded by SEMLEP through the Local Growth Fund and Cranfield University.References
- K. Plumb, Continuous processing in the pharmaceutical industry: Changing the mind set, Chem. Eng. Res. Des., 2005, 83(6 A), 730–738 CrossRef CAS.
- N. E. B. Briggs, J. McGinty, C. McCabe, V. Raval, J. Sefcik and A. J. Florence, Heat Transfer and Residence Time Distribution in Plug Flow Continuous Oscillatory Baffled Crystallizers, ACS Omega, 2021, 6(28), 18352–18363, DOI:10.1021/acsomega.1c02215.
- S. M. R. Ahmed, A. N. Phan and A. P. Harvey, Mass transfer enhancement as a function of oscillatory baffled reactor design, Chem. Eng. Process., 2018, 130, 229–239 CrossRef CAS.
- P. Bianchi, J. D. Williams and C. O. Kappe, Oscillatory flow reactors for synthetic chemistry applications, J. Flow Chem., 2020, 10, 475–490 CrossRef CAS.
- M. R. S. Abbott, A. P. Harvey, G. V. Perez and M. K. Theodorou, Biological processing in oscillatory baffled reactors: Operation, advantages and potential, Interface Focus, 2013, 3(1) DOI:10.1098/rsfs.2012.0036.
- N. Masngut, A. P. Harvey and J. Ikwebe, Potential uses of oscillatory baffled reactors for biofuel production, Biofuels, 2010, 605–619, DOI:10.4155/bfs.10.38.
- T. McGlone, N. E. B. Briggs, C. A. Clark, C. J. Brown, J. Sefcik and A. J. Florence, Oscillatory Flow Reactors (OFRs) for Continuous Manufacturing and Crystallization, Org. Process Res. Dev., 2015, 19(9), 1186–1202 CrossRef CAS.
- P. Stonestreet and A. P. Harvey, A mixing-based design methodology for continuous oscillatory flow reactors, Chem. Eng. Res. Des., 2002, 80(1), 31–44 CrossRef CAS.
- X. Ni, M. R. Mackley, A. P. Harvey, P. Stonestreet, M. H. I. Baird and N. V. Rama Rao, Mixing through oscillations and pulsations -A guide to achieving process enhancements in the chemical and process industries, Chem. Eng. Res. Des., 2003, 81(3), 373–383 CrossRef CAS , Available from: https://reader.elsevier.com/reader/sd/pii/S026387620372320X?token=D9F1085A8A700FEFF27E2F5E0D0719F6F9F46DE8320E785CB29E5100672D2D2250A590EC2F1D050A291F5A50FABE5A08.
- C. R. Brunold, J. C. B. Hunns, M. R. Mackley and J. W. Thompson, Experimental observations on flow patterns and energy losses for oscillatory flow in ducts containing sharp edges, Chem. Eng. Sci., 1989, 44(5), 1227–1244 CrossRef CAS.
- X. Ni, A study of fluid dispersion in oscillatory flow through a baffled tube, J. Chem. Technol. Biotechnol., 1995, 64(2), 165–174 CrossRef CAS.
- P. Stonestreet and P. M. J. Van Der Veeken, The effects of oscillatory flow and bulk flow components on residence time distribution in baffled tube reactors, Chem. Eng. Res. Des., 1999, 77(8), 671–684 CrossRef CAS.
- M. Avila, B. Kawas, D. F. Fletcher, M. Poux, C. Xuereb and J. Aubin, Design, performance characterization and applications of continuous oscillatory baffled reactors, Chem. Eng. Process., 2021, 108718 Search PubMed , Available from: https://www.sciencedirect.com/science/article/pii/S0255270121004025.
- J. R. McDonough, S. Murta, R. Law and A. P. Harvey, Oscillatory fluid motion unlocks plug flow operation in helical tube reactors at lower Reynolds numbers (Re ≤ 10), Chem. Eng. J., 2019, 358, 643–657 CrossRef CAS.
- A. N. Phan, A. Harvey and J. Lavender, Characterisation of fluid mixing in novel designs of mesoscale oscillatory baffled reactors operating at low flow rates (0.3-0.6ml/min), Chem. Eng. Process.: Process Intesif., 2011, 50(3), 254–263 CrossRef CAS , Available from: https://reader.elsevier.com/reader/sd/pii/S0255270111000432?token=DA4007FA476AB2FD428258055F4F1CFB48A27BCC61DE644DFA24CDD331812CF946DBBAC3DDDBBFF4FC989F6694376491.
- X. Ni and N. E. Pereira, Parameters affecting fluid dispersion in a continuous oscillatory baffled tube, AIChE J., 2000, 46(1), 37–45, DOI:10.1002/aic.690460106.
- W. K. Sern, M. S. Takriff, S. K. Kamarudin, M. Z. M Talib and N Hasan, Numerical Simulation Of Fluid Flow Behaviour On Scale Up Of Oscillatory Baffled Column, Journal of Engineering Science and Technology, 2012, 7(11), 119–130 Search PubMed.
- M. Avila, D. F. Fletcher, M. Poux, C. Xuereb and J. Aubin, Mixing performance in continuous oscillatory baffled reactors, Chem. Eng. Sci., 2020, 219 Search PubMed , Available from: https://hal.archives-ouvertes.fr/hal-02735360.
- X. Ni, H. Jian and A. Fitch, Evaluation of Turbulent Integral Length Scale in an Oscillatory Baffled Column Using Large Eddy Simulation and Digital Particle Image Velocimetry, Chem. Eng. Res. Des., 2003, 81(8), 842–853 CrossRef CAS.
- M. Manninen, E. Gorshkova, K. Immonen and X. W. Ni, Evaluation of axial dispersion and mixing performance in oscillatory baffled reactors using CFD, J. Chem. Technol. Biotechnol., 2013, 88(4), 553–562, DOI:10.1002/jctb.3979.
- M. Zheng and M. Mackley, The axial dispersion performance of an oscillatory flow meso-reactor with relevance to continuous flow operation, Chem. Eng. Sci., 2008, 63(7), 1788–1799 CrossRef CAS , Available from: https://reader.elsevier.com/reader/sd/pii/S0009250907009050?token=25ABA28785B812B575250794545F765961C1CD4BE6CE9FBB336FBEA6B7C9AFA8C0110C0A971CA3B64361AD43C0BC041D.
- M. S. R. Abbott, A. P. Harvey and M. I. Morrison, Rapid determination of the Residence Time Distribution (RTD) function in an Oscillatory Baffled Reactor (OBR) using a Design of Experiments (DoE) approach, Int. J. Chem. React. Eng., 2014, 12(1), 575–586 Search PubMed.
- A. P. Harvey, M. R. Mackley and P. Stonestreet, Operation and Optimization of an Oscillatory Flow Continuous Reactor, Ind. Eng. Chem. Res., 2001, 40(23), 5371–5377, DOI:10.1021/ie0011223.
- H. Jian and X. Ni, A numerical study on the scale-up behaviour in oscillatory baffled columns, Chem. Eng. Res. Des., 2005, 83(10 A), 1163–1170 CrossRef CAS , Available from: https://pdf.sciencedirectassets.com/276837/1-s2.0-S0263876205X86087/1-s2.0-S0263876205728161/main.pdf?X-Amz-Security-Token=IQoJb3JpZ2luX2VjECsaCXVzLWVhc3QtMSJGMEQCIBsORxSXyuKRzdqZzPcbD%2Bo9VqKpAgMANioYZpbcalZ0AiB3ox%2FcEmBZC6X%2FzEExA%2BNSgRKm%2Fg5ZTII1wK.
- M. R. Mackley and X. Ni, Experimental fluid dispersion measurements in periodic baffled tube arrays, Chem. Eng. Sci., 1993, 48(18), 3293–3305 CrossRef CAS.
- M. R. Mackley and X. Ni, Mixing and dispersion in a baffled tube for steady laminar and pulsatile flow, Chem. Eng. Sci., 1991, 46(12), 3139–3151 CrossRef CAS.
- X. Ni and C. C. Stevenson, On the effect of gap size between baffle outer diameter and tube inner diameter on the mixing characteristics in an oscillatory-baffled column, J. Chem. Technol. Biotechnol., 1999, 74(6), 587–593, DOI:10.1002/%28SICI%291097-4660%28199906%2974%3A6%3C587%3A%3AAID-JCTB87%3E3.0.CO%3B2-C.
- X. Ni, G. Brogan, A. Struthers, D. C. Bennett and S. F. Wilson, A systematic study of the effect of geometrical parameters on mixing time in oscillatory baffled columns, Chem. Eng. Res. Des., 1998, 76(5 A5), 635–642 CrossRef CAS , Available from: https://pdf.sciencedirectassets.com/276837/1-s2.0-S0263876298X85370/1-s2.0-S0263876298716880/main.pdf?X-Amz-Security-Token=IQoJb3JpZ2luX2VjEBkaCXVzLWVhc3QtMSJHMEUCIQCe4vv4GV%2FrmlakVZAxVJQuQIRX7gzNIf3yh5%2F9v3IZ%2BgIgK9QI%2BRbzWY8RfGzxj4ubDmd0qGCB1Q3bj2gO.
- X. Ni, Y. S. De Gélicourt, M. H. I. I. Baird and N. V. R. R. Rao, Scale-up of single phase axial dispersion coefficients in batch and continuous oscillatory baffled tubes, Can. J. Chem. Eng., 2001, 79(3), 444–448, DOI:10.1002/cjce.5450790318.
- N. Reis, A. P. Harvey, M. R. Mackley, A. A. Vicente and J. A. Teixeira, Fluid mechanics and design aspects of a novel oscillatory flow screening mesoreactor, Chem. Eng. Res. Des., 2005, 83(4 A), 357–371 CrossRef CAS.
- A. N. Phan and A. P. Harvey, Characterisation of mesoscale oscillatory helical baffled reactor-Experimental approach, Chem. Eng. J., 2012, 180, 229–236 CrossRef CAS.
- A. N. Phan and A. Harvey, Development and evaluation of novel designs of continuous mesoscale oscillatory baffled reactors, Chem. Eng. J., 2010, 159(1–3), 212–219 CrossRef CAS.
- M. S. Lucas, N. M. Reis and G. Li Puma, Intensification of ozonation processes in a novel, compact, multi-orifice oscillatory baffled column, Chem. Eng. J., 2016, 296, 335–339 CrossRef CAS.
- A. Ferreira, J. A. Teixeira and F. Rocha, O2 mass transfer in an oscillatory flow reactor provided with smooth periodic constrictions, Individual characterization of kL and a, Chem. Eng. J., 2015, 262, 499–508 CrossRef CAS.
- M. S. N. Oliveira and X. W. Ni, Effect of hydrodynamics on mass transfer in a gas-liquid oscillatory baffled column, Chem. Eng. J., 2004, 99(1), 59–68 CrossRef CAS.
- P. Ranganathan, Numerical Simulation of a Gas–Liquid Oscillatory Baffled Column Focusing on Hydrodynamics and Mass Transfer, Ind. Eng. Chem. Res., 2022, 61(26), 9443–9455 CrossRef CAS.
- S. M. R. Ahmed, A. N. Phan and A. P. Harvey, Scale-Up of Gas-Liquid Mass Transfer in Oscillatory Multiorifice Baffled Reactors (OMBRs), Ind. Eng. Chem. Res., 2019, 58(15), 5929–5935 CrossRef CAS.
- C. A. L. Graça, R. B. Lima, M. F. R. Pereira, A. M. T. Silva and A. Ferreira, Intensification of the ozone-water mass transfer in an oscillatory flow reactor with innovative design of periodic constrictions: Optimization and application in ozonation water treatment, Chem. Eng. J., 2020, 389, 124412 CrossRef.
- A. Al-Abduly, P. Christensen, A. Harvey and K. Zahng, Characterization and optimization of an oscillatory baffled reactor (OBR) for ozone-water mass transfer, Chem. Eng. Process., 2014, 84, 82–89 CrossRef CAS.
- F. Almeida, F. Rocha, J. A. Teixeira and A. Ferreira, The influence of electrolytes in aqueous solutions on gas-liquid mass transfer in an oscillatory flow reactor, Chem. Eng. Sci., 2022, 263, 118048 CrossRef CAS.
- G. Jimeno, Y. C. Lee and X. W. Ni, The effect of particle size on flow in a continuous oscillatory baffled reactor using CFD, Can. J. Chem. Eng., 2022, 100(S1), S258–S271 CrossRef CAS.
- R. Cox, K. Salonitis, E. Rebrov and S. A. S. A. Impey, Revisiting the Effect of U-Bends, Flow Parameters, and Feasibility for Scale-Up on Residence Time Distribution Curves for a Continuous Bioprocessing Oscillatory Baffled Flow Reactor, Ind. Eng. Chem. Res., 2022, 61(30), 11181–11196, DOI:10.1021/acs.iecr.2c00822.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, New York, 3rd edn, 1998, vol. 38, pp. 321–326 Search PubMed.
- D. C. Montgomery, Design and Analysis of Experiments, Wiley, 10th edn, 2013, pp. 320–349 Search PubMed.
- SAS Institute Inc., JMP 16 Documentation Library, Cary, NC, 16th edn, 2021, p. 6702 Search PubMed.
- N. Reis, R. N. Pereira, A. A. Vicente and J. A. Teixeira, Enhanced gas-liquid mass transfer of an oscillatory constricted-tubular reactor, Ind. Eng. Chem. Res., 2008, 47(19), 7190–7201, DOI:10.1021/ie8001588.
- D. S. Slavnić, L. V. Živković, A. V. Bjelić, B. M. Bugarski and N. M. Nikačević, Residence time distribution and Peclet number correlation for continuous oscillatory flow reactors, J. Chem. Technol. Biotechnol., 2017, 92(8), 2178–2188 CrossRef.
- D. González-Juárez, J. P. Solano, R. Herrero-Martín and A. P. Harvey, Residence time distribution in multiorifice baffled tubes: A numerical study, Chem. Eng. Res. Des., 2017, 118, 259–269 CrossRef.
- J. R. McDonough, M. F. Oates, R. Law and A. P. Harvey, Micromixing in oscillatory baffled flows, Chem. Eng. J., 2019, 361, 508–518 CrossRef CAS.
- N. Reis, C. N. Gonçalves, A. A. Vicente and J. A. Teixeira, Proof-of-concept of a novel micro-bioreactor for fast development of industrial bioprocesses, Biotechnol. Bioeng., 2006, 95(4), 744–753 CrossRef CAS PubMed.
- M. Shah, A. A. Kiss, E. Zondervan, J. Van Der Schaaf and A. B. De Haan, Gas holdup, axial dispersion, and mass transfer studies in bubble columns, Ind. Eng. Chem. Res., 2012, 51(43), 14268–14278 CrossRef CAS.
- S. N. Palaskar, J. K. De and A. B. Pandit, Liquid phase RTD studies in sectionalized bubble column, Chem. Eng. Technol., 2000, 23(1), 61–69 CrossRef CAS.
- J. A. Oliva, K. Pal, A. Barton, P. Firth and Z. K. Nagy, Experimental investigation of the effect of scale-up on mixing efficiency in oscillatory flow baffled reactors (OFBR) using principal component based image analysis as a novel noninvasive residence time distribution measurement approach, Chem. Eng. J., 2018, 351, 498–505 CrossRef CAS.
- J. Muñoz-Cámara, D. Crespí-Llorens, J. P. Solano and P. Vicente, Baffled tubes with superimposed oscillatory flow: Experimental study of the fluid mixing and heat transfer at low net Reynolds numbers, Exp. Therm. Fluid Sci., 2021, 123, 110324 CrossRef , Available from: https://linkinghub.elsevier.com/retrieve/pii/S0894177720308220.
- M. S. R. Abbott, G. Valente Perez, A. P. Harvey and M. K. Theodorou, Reduced power consumption compared to a traditional stirred tank reactor (STR) for enzymatic saccharification of alpha-cellulose using oscillatory baffled reactor (OBR) technology, Chem. Eng. Res. Des., 2014, 92(10), 1969–1975 CrossRef CAS.
- I. I. Onyemelukwe, Z. K. Nagy and C. D. Rielly, Solid-liquid axial dispersion performance of a mesoscale continuous oscillatory flow crystalliser with smooth periodic constrictions using a non-invasive dual backlit imaging technique, Chem. Eng. J., 2020, 382, 122862 CrossRef CAS.
- A. Ferreira, P. O. Adesite, J. A. Teixeira and F. Rocha, Effect of solids on O2 mass transfer in an oscillatory flow reactor provided with smooth periodic constrictions, Chem. Eng. Sci., 2017, 170, 400–409 CrossRef CAS.
- K. Wadaugsorn, S. Limtrakul, T. Vatanatham and P. A. Ramachandran, Mixing Characteristics of Gas and Liquid Phases in Bubble Column Reactors from Virtual Tracer Simulation, Ind. Eng. Chem. Res., 2018, 57(42), 14064–14079 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00065f |
| This journal is © The Royal Society of Chemistry 2023 |