Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring effects of polymeric stabiliser molecular weight and concentration on emulsion production via stirred cell membrane emulsification†
Mohamed S.
Manga
,
Lucy
Higgins
,
Akshai A.
Kumar
 ,
Benjamin T.
Lobel
,
Benjamin T.
Lobel
 ,
David W.
York
and
Olivier J.
Cayre
,
David W.
York
and
Olivier J.
Cayre
 *
*
School of Chemical and Process Engineering, Faculty of Engineering and Physical Sciences, University of Leeds, Leeds, LS2 9JT, UK. E-mail: o.j.cayre@leeds.ac.uk
First published on 7th November 2023
Abstract
The impact of polymer emulsifier diffusion rates and droplet formation kinetics are critical for effective control of emulsion droplet size and stability during the membrane emulsification process. It is expected that the molecular weight of a polymer stabiliser will play a significant role in the resultant emulsion due to the low energy nature of the emulsion formation mechanism and dependence on emulsifier diffusion inherent in a membrane emulsification system. Dodecane in water emulsions were formed via membrane emulsification at various concentrations and molecular weights of a polyvinyl alcohol polymer. Emulsion attributes were quantified via laser diffraction and optical microscopy over time. These data were then related to the diffusion time of polymers of different molecular weight at various concentrations via pendent droplet tensiometry. It was found that molecular weight of a polymeric stabiliser and subsequent diffusion to the interface have a significant impact on droplet size, dispersity and stability. Larger polymeric stabilisers were slower to diffuse to the interface, resulting in highly stable larger droplets, while smaller polymers quickly adsorbed to the interface but offered limited steric stabilisation and thus resulted in significant droplet coalescence. Combination of both high and low molecular weight polymers as stabilisers was observed to result in emulsions of low dispersity and controllable sizes for extremely low concentration of polymer.
1. Introduction
Membrane emulsification allows scientists and engineers to control the formation of emulsion droplets more efficiently than with standard stochastic methods of emulsification. The slow build-up of the droplet population in the system ensures that all droplets produced with this method experience significantly more homogeneous shear forces as compared to highly chaotic high shear mixing or high-pressure homogenisation.1,2 Furthermore, membrane emulsification processes allow formulators to better tune the design of the emulsions themselves, particularly the choice of emulsifier properties, by taking into account the need for rapidly populating the droplet surface. This plays a significant role in droplet detachment from the membrane (via controlling interfacial tension (IFT)),3–5 and to ensure efficient droplet stabilisation in the continuous phase once released from the membrane surface.6–8 The latter requirement is a key aspect of retaining the narrow size distribution of droplets, particularly as most membrane emulsification devices are used to produce batch emulsions, subsequently processed into a final formulation, which takes the form of a more complex emulsion, particle or microcapsule product.9,10In a standard emulsification process, the choice of stabiliser type and concentration is generally based on the ability of the emulsifiers to reduce the interfacial tension and to provide an energy barrier against droplet aggregation and coalescence. Often, the diffusion and adsorption of the emulsifier to the interface in the emulsification process can be disregarded as the chaotic (and typically long – >1 min) emulsification process results in many contacts between the newly formed droplet interface and the emulsifiers in the system. However, in a membrane emulsification process, the diffusion rate and adsorption rate of the emulsifier to the surface of the growing droplets on the membrane and once detached, becomes important to control the process effectively in an environment that is comparatively less sheared.4,11,12
In membrane emulsification processes, the production of droplets at a pore has two stages; (i) droplet growth and (ii) droplet detachment. The droplet size achieved at the time of detachment from the membrane is dependent on a balance of the forces acting on the droplet to move from the first stage to the second.3,13 As a droplet grows, new interface is formed onto which surface-active emulsifiers (typically surfactants or polymers) can adsorb from the bulk to lower the IFT. Once the droplet detaches, the process of emulsifier adsorption from the bulk onto the emulsion droplet surface continues until an equilibrium is reached. Throughout this process, the kinetics of adsorption is affected by the molecular characteristics of the emulsifier such as molecular weight (Mw), concentration and the location of the solvophilic and solvophobic moieties.8 In particular for polymeric emulsifiers, the molecular weight will dictate the diffusion time taken for the polymer to travel from the bulk to the interface.14 The interplay between the droplet expansion rate and the emulsifier adsorption rate will yield a dynamic IFT.3–5,15 It has been reported using microfluidic techniques that, using fast adsorbing emulsifiers (e.g. surfactants and low molecular weight polymers), a dynamic IFT close to the equilibrium value can be achieved within the droplet formation time, although this is only achieved at high emulsifier concentrations.16–18 In this case, the rapid reduction in IFT facilitates the production of smaller droplets.
When using interfacially-active polymers (often a standard choice for formulators because of their non-toxicity and ability to affect rheological properties) preventing/limiting coalescence once the droplets detach from the membrane relies on providing an efficient steric barrier at the interface.19 Achieving this stabilisation generally requires the use of medium to high molecular weight polymers. However, high molecular weight polymers will adsorb relatively slowly to the droplet interface with an adsorption time likely to be comparable to the droplet formation time in a membrane emulsification process, or possibly even slower. The droplet interface will typically have an incomplete emulsifier coverage at the time of droplet detachment from the membrane and the corresponding dynamic IFT will be high (in some cases similar to that of a bare oil–water interface) resulting in the formation of larger drops prior to detachment.4,20 Upon detachment, these droplets will likely undergo some degree of coalescence in the bulk.11,21,22 To compensate for the slow diffusion times of the large molecular weight polymer, the polymer is generally used in high concentrations but, in some cases, this can also lead to depletion–flocculation processes that also diminish emulsion stability.23,24
In this study we investigate the possibility of preparing emulsions of narrow size distribution via a stirred cell membrane emulsification device using poly(vinyl alcohol) of various molecular weights as an emulsifier. Specifically, we demonstrate that using mixtures of low Mw and high Mw PVA allows for production of well-controlled emulsion droplet sizes by taking advantage of the faster adsorption of the low Mw polymer and the enhanced steric stabilisation provided by the high Mw polymer. In doing so, we open up avenues for producing well-controlled emulsions in this membrane emulsification device at very low overall concentrations of polymer stabilisers (0.1 wt%).
2. Materials and methodology
2.1. Materials
In this study, poly(vinyl alcohol) (PVA, Sigma-Aldrich) was used to stabilise oil-in-water emulsions. The PVA molecular weights and degree of hydrolysis (% of hydrophilic alcohol moieties responsible for the steric interactions, versus the hydrophobic acetate moieties, which drive adsorption at the interface)25 as specified by the supplier are summarised in Table 1. The following reagents were used as received; n-dodecane (purity ≥99%, Sigma-Aldrich), sodium hydroxide (NaOH, purity ≥97%, Sigma-Aldrich), citric acid (purity ≥99.5%, Sigma-Aldrich), isopropanol (purity ≥99%, Acros Organics). All water used was Milli-Q (Merck Millipore, 18.2 MΩ cm at 25 °C), unless otherwise stated.| PVA sample | Molecular weight (kDa) | Hydrolysis extent (%) |
|---|---|---|
| LMw-PVA-88 | 13–23 | 87–89 |
| LMw-PVA-98 | 13–23 | 98 |
| HMw-PVA-88 | 85–124 | 87–89 |
| HMw-PVA-99 | 85–124 | 99 |
2.2. Preparation of PVA solutions
The stock 2 wt% PVA aqueous solutions were prepared by dissolving the PVA powders in water by stirring (350 rpm) at 95 °C for at least 2 hours under reflux. The solution was then allowed to cool to room temperature and was left to stir for a further 24 hours. This stock solution was diluted with water to obtain the different polymer solution concentrations required which were used as the continuous phase for emulsification.2.3. Production of emulsions using stirred cell membrane emulsification
Emulsification studies were conducted using a stirred cell equipped with hydrophilic nickel disc membrane (Micropore Technologies Ltd, Redcar, U.K.). A 24 V DC motor was used to drive a paddle stirrer above the membrane surface to create the necessary shear for droplet detachment. The nickel disc membrane used had a pore diameter of 20 μm with a pitch of 200 μm. The total volume of continuous phase used in each experiment was 90 mL. The continuous phase (containing the PVA emulsifier) was allowed to wet the membrane for 20 min prior to injecting the oil phase through the membrane. The oil injection rate (0.1 mL min−1) was selected based on the emulsion size distribution obtained using 2 wt% LMw-PVA-88 in preliminary experiments (Fig. S1†). The injection rate was controlled using a syringe pump (Harvard Apparatus) and a total of 10 mL of n-dodecane was injected. All the emulsification experiments were undertaken at room temperature (i.e. 18 ± 2 °C). After each experiment, the membrane was cleaned by immersion in 0.1 M NaOH and sonication for 15 min, followed by immersion in 0.1 M citric acid. The membrane was further cleaned using a detergent solution (Decon 90), thoroughly rinsed in isopropanol and water before being finally dried in an oven before use.2.4. Production of emulsions via high shear homogenisation
n-Dodecane in water emulsions with a disperse phase volume fraction of 10 vol% were prepared using an IKA T25 Ultra-Turrax homogeniser operating at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 2 min. For these emulsions LMw-PVA-88 and HMw-PVA-88 were used as the stabilisers at 2 different concentrations for comparison with the membrane emulsification systems. The total volume of emulsion produced was 20 mL.
000 rpm for 2 min. For these emulsions LMw-PVA-88 and HMw-PVA-88 were used as the stabilisers at 2 different concentrations for comparison with the membrane emulsification systems. The total volume of emulsion produced was 20 mL.
2.5. Characterisation
The coefficient of variation (CV, eqn (1)) was calculated from the standard deviation (σ) and average droplet diameter (dav):
| CV(%) = (σ/dav) × 100%. | (1) |
The emulsion droplet size distributions were also measured via laser diffraction using a Malvern Mastersizer 2000 (Malvern Instruments Ltd, U.K.) equipped with a Hydro 2000SM sample dispersion unit. A HeNe laser operating at 633 nm, and a solid-state blue laser operating at 466 nm were used to size each emulsion. The stirring rate was adjusted to 1000 rpm to avoid creaming of the emulsion during analysis, which matched the stirring speed used in the stirred cell membrane emulsification experiments. Aqueous PVA solutions were used as the continuous phase (flowing through the cell) matching the molecular weight, degree of hydrolysis and concentration used to prepare the emulsion being analysed. After each measurement, the cell was rinsed once with isopropanol, followed by three rinses with water. The glass walls of the cell were carefully wiped with a lint-free lens cleaning tissue to avoid contamination across samples. The width of the droplet size distribution was expressed as a span value where,
| Span = (dv90 − dv10)/dv50. | (2) |
3. Results and discussion
3.1 Effect of PVA molecular weight and concentration
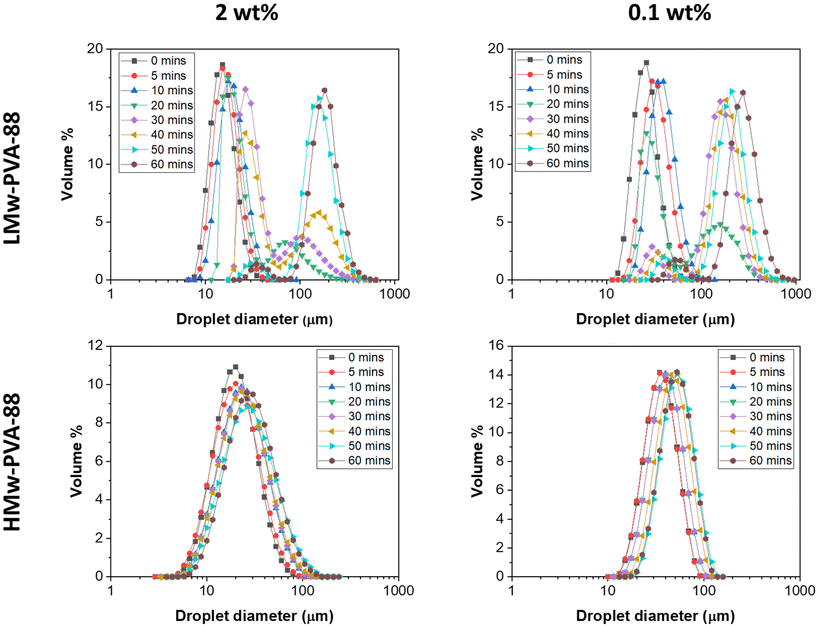
Emulsifiers play a crucial role in membrane emulsification processes, by adsorbing at the liquid–liquid interface to influence both the rates of droplet detachment from the membrane and the droplet coalescence rate in the bulk after detachment.31,32 Both these phenomena influence the final droplet size and size distribution obtained. In the case of polymer emulsifiers, their rate of interfacial adsorption from the bulk (significantly slower than that of short chain surfactants) plays a particularly important role in controlling these phenomena. To probe the impact of the PVA polymeric stabiliser properties on the characteristics of emulsions prepared with the stirred-cell membrane emulsification process in this work, the effects of polymer molecular weight and concentration were first investigated. The impact of hydrolysis degree was also investigated, but it was found that the emulsions made with PVA polymers with a 98–99% hydrolysis degree were highly unstable and therefore were not subjected to further study (see Fig. S2 in the ESI†).Initial screening experiments were performed to probe the impact of PVA molecular weight and polymer concentration on the resulting droplet size distribution of n-dodecane in water emulsions first using a standard high-shear emulsification method. Here, we used an ultra-turrax homogeniser, which imparts high energy into the system to form the droplets and thus limits the influence of polymer diffusion/adsorption time on the droplet formation process. The PVA polymers used for this study were LMw-PVA-88 and HMw-PVA-88 at two different concentrations (0.1 and 2 wt%). The emulsions were prepared with a dispersed phase volume of 10%. The size distribution of the prepared emulsion was regularly measured over a period of 60 min. Here, the emulsion was allowed to evolve and a periodic sample was characterised to follow the droplet size and the potentially associated droplet coalescence (Fig. 1).
For LMw-PVA-88 stabilised emulsions at a polymer concentration of 0.1 wt%, a mean droplet diameter of ∼20 μm is measured at t = 0 As the emulsion evolved, an increase in the mean droplet size could be observed along with a broadening of the size distribution. At t = 20 min, a bi-modal droplet size distribution was seen with the primary peak occurring around ∼20 μm and a broad second peak centred at 170 μm. This is indicative of droplet coalescence. Between 20 and 60 min, the height of the primary peak slowly diminished whilst the secondary peak increased with a shift towards a larger size (max peak value at ∼300 μm). Relatively rapid emulsion coalescence was also observed when using a polymer concentration of 2 wt%, however, after 40 min in this case, the position of the secondary peak remained stationary (max peak value at ∼190 μm). In comparison, emulsions stabilised with HMw-PVA-88 (at both 0.1 and 2 wt% polymer concentrations) resulted in monomodal droplet size distributions over the 60 min of measurement time. For both the concentrations tested, the mean droplet size also slowly increased over time, indicative of some limited droplet coalescence in these systems. Increasing the polymer concentration appeared to limit this coalescence rate further.
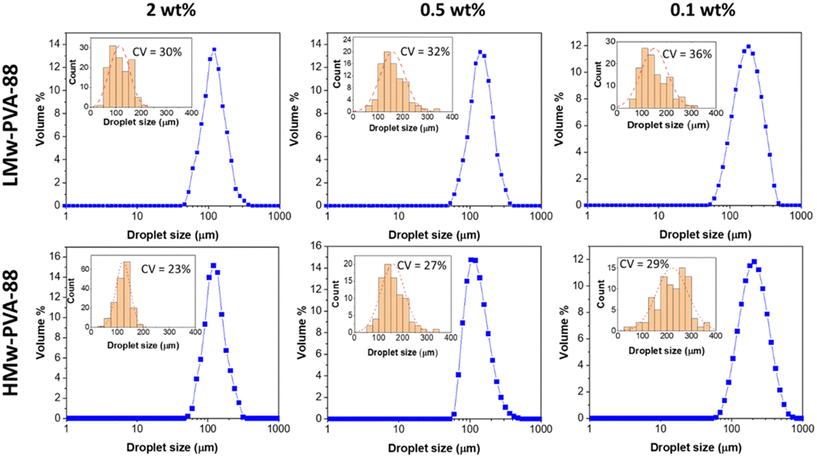
As previously outlined, the membrane emulsification process allows for less shear and a more homogenous shear profile compared to the chaotic process experienced in the ultra-turrax homogeniser. In this emulsification method, better control of the final emulsion characteristics should be possible when using polymer stabilisers, while taking into account the polymer diffusion time and adsorption properties. Here, we used both LMw-PVA-88 and HMw-PVA-88 polymers at different concentrations to verify the role of the PVA characteristics in controlling the droplet size and associated size distribution obtained with the stirred-cell membrane emulsification method. The corresponding emulsion droplet size distributions of emulsions prepared with both of these polymers for different concentrations are presented in Fig. 2. This study was conducted to obtain emulsions with a dispersed phase volume fraction of 10% at a fixed stirrer paddle speed of 1000 rpm and an oil injection rate of 0.1 mL min−1. The paddle speed and oil injection rate were initially selected based on values reported in literature elsewhere.20,33,34 We then verified successful production of n-dodecane in water emulsions with these parameters using the selected emulsifiers for this work.
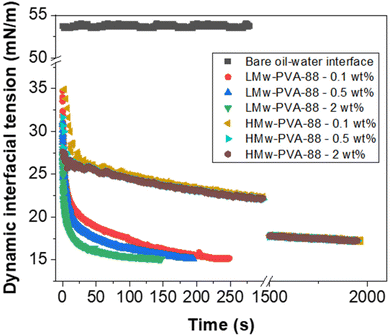
Fig. 2 demonstrates that, as expected, when the PVA concentration is decreased from 2 to 0.1 wt% using LMw-PVA-88, the resulting droplet size distribution shifts to higher sizes (with an average diameter increasing from 120 μm to 182 μm) and becomes broader (CV increases from 30% to 36%). These data are concordant with the histograms (and fitted distributions) obtained via image analysis of droplets from optical micrographs (shown as insets in Fig. 2 top row). The increase in droplet size with decreasing stabiliser concentration can be partially explained by probing the dynamic IFT (Fig. 3). The IFT force is responsible for holding a growing droplet at the membrane surface by resisting the influence of the drag force (as inertial and buoyancy forces are deemed to be negligible for micron sized droplets).35–37 By decreasing the IFT, the droplets detach sooner from the membrane pore, which results in smaller droplets being produced. In addition, lower concentration of stabilisers can also decrease droplet stability after detachment from the membrane due to reduced droplet surface coverage. Although the rate of change of the IFT in the measurements shown in Fig. 3 is significantly slower than the droplet growth rate on the membranes, differences noted between the various concentrations can illustrate the differences in polymer adsorption rates on the growing droplets on the membrane surface for the same concentrations. Fig. 3 illustrates that, for the LMw polymer at 2 wt%, the IFT equilibrium value (∼15 mN m−1) is achieved in around 130 s, which increases to 225 s at a concentration of 0.1 wt%. As expected, these data demonstrate that, as the polymer concentration is decreased, the time taken for the PVA molecules to (i) diffuse from the bulk to the interface (ii) successfully adsorb and (iii) unfold and conform to allow maximum surface coverage, will increase.38,39
In order to confirm the anticipated behaviour of the four polymer stabilisers used in this work, we used existing understanding of this membrane emulsification device,20 including the radial profile of shear stress caused by the paddle, to calculate the droplet lifetime on the membrane for all four polymer conditions. A force balance between the capillary and drag forces acting on a droplet at the membrane pore is used to perform these calculations,
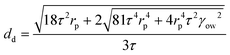 | (3) |
The predicted droplet size based on a paddle rotation speed of 1000 rpm (τ = 10.6 Pa) at an oil injection rate of 0.1 mL min−1 was subsequently used to calculate the droplet lifetime on the membrane for each PVA polymer studied in this work and for two different IFT values, both for a bare interface and at equilibrium adsorption (Table 2). These calculated characteristic droplet lifetimes can then be contrasted with the polymer chain diffusion time (across the length scale approximated as the inter-polymer chain distance).
| (1) PVA Samplea | (2) Radius of gyration (nm) | (3) Calculated inter-polymer chain distance (nm) | (4) Time taken for polymer to diffuse distance in columnb 3 (ms) | (5) Predicted droplet diameter at equilibrium IFT value (μm) | (6) Lifetime of droplet on membrane pore based on droplet size in column 5 (s) | (7) Predicted droplet diameter for a bare oil–water IFT value (∼53 mN m−1) (μm) | (8) Lifetime of droplet on membrane pore based on droplet size in column 7 (s) |
|---|---|---|---|---|---|---|---|
Data are calculated using eqn (3) for an oil injection rate of 0.1 mL min−1. The radius of gyration for the polymer chains is based on Flory's approximation.40 The predicted droplet size (at a paddle stirrer speed of 1000 rpm) in the stirred cell membrane unit is based on the relationship developed by Kosvintsev et al.20 The lifetime of the droplet was calculated based on the time taken to produce a droplet volume with a particular size (columns 5 and 7) at an injection rate of 0.1 mL min−1 across ∼126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pores (based on 20 μm pore size, 200 μm pitch, porosity 0.9%) with 2% of pores being active at any point in time (see ESI† for detailed calculations).41,42a Discussion of the values calculated in the case of the highly hydrolysed polymer can be found in the ESI (Table S1†).b Diffusion coefficient was calculated from the Stokes–Einstein relationship, using the radius of gyration (2). 000 pores (based on 20 μm pore size, 200 μm pitch, porosity 0.9%) with 2% of pores being active at any point in time (see ESI† for detailed calculations).41,42a Discussion of the values calculated in the case of the highly hydrolysed polymer can be found in the ESI (Table S1†).b Diffusion coefficient was calculated from the Stokes–Einstein relationship, using the radius of gyration (2). |
|||||||
| LMw-PVA-88 | 4.8–6.5 | 69–92 | 0.056–0.13 | 120 | 1.4 | 220 | 8.5 |
| HMw-PVA-88 | 13–15 | 177–214 | 0.91–1.6 | 124 | 1.5 | 221 | 8.5 |
For the low molecular weight system (LMw-PVA-88), the polymer diffusion time is fast and, provided that rapid/efficient adsorption occurs upon polymer chains reaching the vicinity of the droplet surface, a potentially rapid reduction in the IFT can drive faster droplet detachment, resulting in initially smaller droplets. However, as demonstrated in Fig. 1, these droplets rapidly coalesce due to poor steric stabilisation. This is supported by the tensiometry data (Fig. 3), which highlights that, although there is a rapid decrease in the IFT using the low Mw polymer, the timescales required to achieve equilibrium is in the order of ∼102 s. Additionally, when using HMw-PVA-88 the polymer diffusion time is still fast compared to the calculated droplet lifetime but does provide a smaller time window for efficient polymer attachment on the growing droplet as compared to the lower MW PVA polymer. If we instead assume that the interface is bare upon detachment (i.e. an IFT of 53 mN m−1), owing to the long timescales of interfacial tension decay recorded in the tensiometry measurements (Fig. 3), then the droplet will grow to a predicted size of ∼220 μm taking approximately 8.5 s to form before detachment occurs. In the case of the higher MW, even small amounts of adsorbed polymer will lead to more effective steric stabilisation (i.e. larger droplets that are likely more stable). In reality the droplets will experience a dynamic IFT with a value somewhere between that of a bare interface and that at equilibrium. This will impact both the droplet size upon detachment and its lifetime on the membrane pore (Fig. 4).
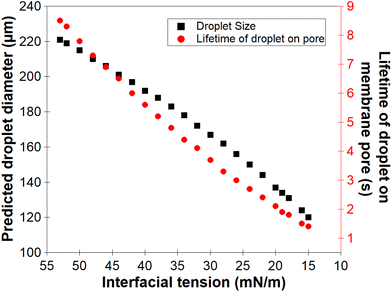 | ||
| Fig. 4 Calculated relationship between the dynamic interfacial tension of a n-dodecane–water interface (from a bare interface to an equilibrium interfacial tension) in presence of PVA and the predicted droplet size formed at the membrane pore using eqn (3) and also the corresponding droplet lifetime before detachment from the membrane. | ||
In practice, the droplets emerging from the membrane will not experience the equilibrium IFT of the oil–water interface measured in Fig. 3 (in the presence of polymer stabiliser), as the droplet growth rate is likely greater than the rate of polymer adsorption under these conditions (even though polymer diffusion is faster than the droplet lifetime on the membrane).43,44 Thus, when producing PVA-stabilised droplets from the membrane emulsification device, droplets detaching from the membrane will likely only possess an incomplete polymer coverage on their surface. It is clear that further adsorption of polymer from the bulk onto the droplets will be required to form an efficient steric layer on the droplet surface. At the same time, droplet coalescence will also occur, which can increase the size distribution of the final droplets produced by the technique.
When HMw-PVA-88 was used, the average droplet size and associated CV values also increased with decreasing polymer concentration. In addition, the average droplet sizes obtained are larger than those obtained with the low molecular weight system (LMw-PVA-88). This should be considered while remaining cognisant of the tensiometry data presented in Fig. 3, for which the reduction in IFT from 53 to 26 mN m−1 in ∼25 s (when using 0.5 wt% of HMw-PVA-88), is small and slow in comparison to when using the same concentration of LMw-PVA-88 (from 53 to 18 mN m−1 over the same period). Furthermore, achieving an equilibrium value with these larger molecules takes around 10 times longer. However, the emulsions obtained at 0.5 wt% HMw-PVA-88 do exhibit CV values that are much lower compared to those obtained with the LMw-PVA-88 system, thus confirming that coalescence of droplets in the bulk significantly influences the resulting emulsion properties, and perhaps more than their rate of detachment from the membrane surface. The bulk coalescence is heavily influenced by operational conditions (flow rate, stirring rate) which will play a larger role in the final characteristics of the emulsion formed than the interfacial tension evolution during droplet detachment as outlined in eqn (3). Indeed, as demonstrated by Table 2 and Fig. 4, IFT primarily serves to determine the lifetime of the droplet at the membrane surface. Thus, the use of high Mw polymers for more efficient droplet stabilisation in the bulk at the expense of fast polymer adsorption (and consequent decrease in IFT) on the growing droplet on the membrane surface may be advantageous. Similar results were obtained for smaller droplets produced through high shear homogenisation in a study by Lankveld and Lyklema using n-paraffin as the oil and 88% hydrolysed PVA as the polymeric stabiliser.45 These authors found that the mass of polymer chains adsorbed at the interface increased with molecular weight. It was reasoned that this was because a thicker layer was present at the interface for the polymers of higher molecular weight (improved steric stabilisation ability), as a result of the polymer loops being longer. It was also implied that the distribution of the polymer chain between the interface and the bulk aqueous phase shifts to favour the interface at higher molecular weights. This results in significant lateral constriction of the chains at the interface aiding droplet stability and may also explain the decrease in the CV value observed in our case for HMw-PVA-88 in Fig. 2.
It is common practise in the development of emulsion formulations to load the continuous phase with a polymeric stabiliser concentration that is far in excess of what is required to stabilise the created total interfacial area. As a result, the partitioning of polymer chains can be such that the remaining amount of polymer in the bulk continuous phase is substantially larger than what adsorbs at the droplet surface. This highlights a number of potential limitations in the preparation of such emulsions: (i) material waste, (ii) increased cost, (iii) environmental pollution and potentially (iv) enhanced emulsion instability driven by depletion forces.46 Thus, in this article, we explore the possibility of producing better controlled polymer-stabilised emulsions via membrane emulsification by balancing the need for controlled detachment of droplets from membranes and efficient stabilisation in the continuous phase, which should also help reduce the polymer concentration utilised for emulsion stabilisation. Consequently, we first investigate the influence of PVA polymer stabiliser molecular weight at low polymer concentrations (0.1 wt%) over increased timescales before using both LMw-PVA-88 and HMw-PVA-88 in combination to drive improvements in droplet size, stability and dispersity.
In the membrane emulsification experiments the total time taken to form an emulsion with a disperse volume fraction of ∼10 vol% using a 0.1 mL min−1 oil injection rate is 100 min after which droplet characterisation is performed. This means that there is an opportunity for the droplets to evolve with production time as the volume fraction increases and therefore the final measured droplet size may not be indicative of the droplet size that detaches from the membrane pore. To investigate this, emulsions stabilised with 0.1 wt% LMw-PVA-88 and HMw-PVA-88 were prepared again with the high shear homogeniser (see Fig. S3 in the ESI†). The emulsions were then left to stand for 60 min and then measured to track the droplet evolution for another 60 min (total of 120 minutes) to compare to the membrane emulsification process more reliably. In this case, when using LMw-PVA-88 over the time period studied, the emulsion droplets undergo a significant level of coalescence, whilst droplets prepared in the presence of HMw-PVA-88 are found to be stable over that time period.
3.2. Mixing low and high molecular weight polymers
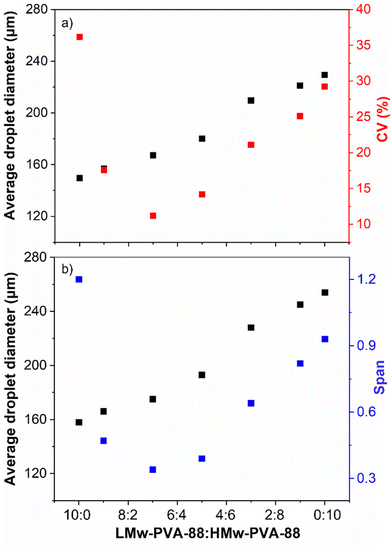
As demonstrated in Fig. 3, the lower molecular weight polymer can reduce the IFT faster than the higher molecular weight PVA and will enable detachment of smaller droplets from the membrane but is unable to prevent droplet coalescence over the timescales of the emulsification procedure due to the low steric layer thickness formed on the droplet surface (Fig. 1 and S3†). In contrast, the higher molecular weight polymer provides a thick steric layer, which ensures longer term droplet stability. On this basis, we attempted to optimise emulsion size and stability by exploiting the benefits provided by each of the two different molecular weights. This was achieved by producing emulsions stabilised by varied ratios (by volume) of LMw-PVA-88 and HMw-PVA-88 (Fig. 5).Although there are a number of studies in the literature using co-emulsifiers/stabilisers such as (i) particle–surfactant,47–49 (ii) polymer–surfactant,50–52 and (iii) mixed polymer systems etc.,53 to the best of our knowledge, this is the first time a study investigates the blending of two molecular weights of the same polymer and its effect on droplet size and emulsion stability for systems produced in a membrane emulsification device. Here, it was hypothesised that a mixed volume ratio of the two (at a typically low polymer concentration of 0.1 wt%) would potentially allow for significant improvement of the droplet size distribution obtained using the stirred cell membrane. Fig. 5 shows the average droplet diameter and the corresponding CV values as a function of the ratio between LMw-PVA-88 and HMw-PVA-88 for these experiments. The smallest average droplet size and largest CV value is observed when the continuous phase contains 100% LMw-PVA-88. This is expected due to the relatively fast detachment of the droplet from the membrane and subsequent rapid coalescence as outlined above (Fig. 1). As the volume ratio of LMw-PVA-88 to HMw-PVA-88 in the continuous phase is decreased, the average droplet size increases in a linear fashion. Interestingly, as the LMw-PVA-88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMw-PVA-88 volume ratio is changed from 10
HMw-PVA-88 volume ratio is changed from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to 7
0 to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 there is a significant decrease in the CV value from 36% to 11%, reflecting a narrowing of the droplet size distribution. This change in droplet size distribution could also be observed via optical microscopy, which Fig. 6 illustrates for a small number of emulsion droplets. It is suggested that this narrow size distribution is due to the competitive adsorption of the two molecular weights at the oil–water interface. Initially the adsorption is dominated by the smaller chains of LMw-PVA-88 which are able to diffuse quickly to the growing interface (diffusion rates presented in Table 2), which reduces the IFT leading to rapid droplet detachment from the membrane pore and smaller droplet size. This is then followed by the adsorption of the larger HMw-PVA-88 chains, which adsorb at the interface more strongly than the LMw-PVA-88 chains, that can result in a thick steric layer forming around the droplets limiting the droplet coalescence rate and thus helping decrease the CV value of the final emulsion. At a LMw-PVA-88
3 there is a significant decrease in the CV value from 36% to 11%, reflecting a narrowing of the droplet size distribution. This change in droplet size distribution could also be observed via optical microscopy, which Fig. 6 illustrates for a small number of emulsion droplets. It is suggested that this narrow size distribution is due to the competitive adsorption of the two molecular weights at the oil–water interface. Initially the adsorption is dominated by the smaller chains of LMw-PVA-88 which are able to diffuse quickly to the growing interface (diffusion rates presented in Table 2), which reduces the IFT leading to rapid droplet detachment from the membrane pore and smaller droplet size. This is then followed by the adsorption of the larger HMw-PVA-88 chains, which adsorb at the interface more strongly than the LMw-PVA-88 chains, that can result in a thick steric layer forming around the droplets limiting the droplet coalescence rate and thus helping decrease the CV value of the final emulsion. At a LMw-PVA-88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMw-PVA-88 ratio of 7
HMw-PVA-88 ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 this competitive adsorption is optimised resulting in the production of stable droplets of very narrow size distribution.
3 this competitive adsorption is optimised resulting in the production of stable droplets of very narrow size distribution.
At an equal ratio of both polymers (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
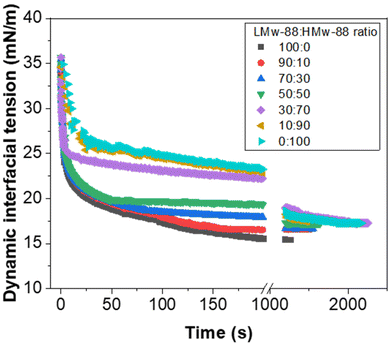
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the CV value was observed to increase up to 14% and continued to increase as the ratio of HMw-PVA-88 increased, reaching 29% at 100% HMw-PVA-88. As the ratio of HMw-PVA-88 increased, the number of fast-adsorbing LMw-PVA-88 chains in the system decreased, which is likely driving poorly covered emulsion droplets detaching from the membrane. In addition to the slow diffusion time of the HMw-PVA-88 chains, these conditions resulted in enhanced coalescence in the bulk until a sufficient droplet surface coverage was obtained. This hypothesis can be interrogated by studying the timescales needed to obtain an equilibrium IFT value from additional tensiometry measurements (Fig. 7).
1), the CV value was observed to increase up to 14% and continued to increase as the ratio of HMw-PVA-88 increased, reaching 29% at 100% HMw-PVA-88. As the ratio of HMw-PVA-88 increased, the number of fast-adsorbing LMw-PVA-88 chains in the system decreased, which is likely driving poorly covered emulsion droplets detaching from the membrane. In addition to the slow diffusion time of the HMw-PVA-88 chains, these conditions resulted in enhanced coalescence in the bulk until a sufficient droplet surface coverage was obtained. This hypothesis can be interrogated by studying the timescales needed to obtain an equilibrium IFT value from additional tensiometry measurements (Fig. 7).
As illustrated in Fig. 7 (also earlier in Fig. 3), when the continuous phase contains >50% of 0.1 wt% LMw-PVA-88 the initial decrease in IFT is rapid. As the ratio of HMw-PVA-88 increases beyond 2000 s, the time taken to reach the final IFT increases due to the larger diffusion time of the higher molecular weight polymers. Furthermore, the final IFT value also increases with the HMw-PVA-88 proportion. It should be noted that, at very high HMw-PVA-88 proportions, the final IFT values still approach the values obtained for the high LMw-PVA-88 ratio samples. This again highlights the impact and importance of the polymer diffusion time to the surface of the droplets both during the pendent drop measurements and during the detachment of droplets from the membrane with, in this case, the final droplet stabilisation in the bulk also drastically affected by these kinetics. In addition to this, examination of Fig. 7 suggests that the droplets growing on the membrane for experiments using 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 LMw-PVA-88
5 LMw-PVA-88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMw-PVA-88 ratios exhibit broadly similar behaviour. Thus, one can assume that initial rapid IFT drops allow for relatively rapid droplet detachment (Fig. 4) within this ratio window and that the differences found for the values of span and CV% in Fig. 5, with a minimum at the 7
HMw-PVA-88 ratios exhibit broadly similar behaviour. Thus, one can assume that initial rapid IFT drops allow for relatively rapid droplet detachment (Fig. 4) within this ratio window and that the differences found for the values of span and CV% in Fig. 5, with a minimum at the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 LMw-PVA-88
3 LMw-PVA-88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMw-PVA-88 ratio appear to be dictated by the availability of the larger polymer to provide an efficient steric barrier for droplet stabilisation in the bulk.
HMw-PVA-88 ratio appear to be dictated by the availability of the larger polymer to provide an efficient steric barrier for droplet stabilisation in the bulk.
As noted earlier the adsorption timescales to obtain an equilibrium tension value are significantly longer than those experienced during emulsification and therefore the dynamic IFT will be bounded within the IFT for a bare oil–water interface and one at equilibrium as presented earlier in Fig. 4. The change in droplet size shown in Fig. 5 & 6 ranges from 150 to 230 μm and is concordant with the predicted sizes in Fig. 4. By combining these findings with the tensiometry data presented in Fig. 3, it is apparent that the minimum IFT that can be achieved before droplet detachment occurs from the membrane pore is around 25 mN m−1. It should be noted however that in reality when the droplets form at the membrane pore, competitive interfacial adsorption between the two molecular weight polymers will occur,8 which could be investigated further for a more precise understanding of the adsorbed polymer film composition if required. However, the data in this article demonstrate that by optimising the molecular weight blend of a PVA polymer in the continuous phase, it is possible to produce droplets with well controlled size distributions using membrane emulsification technologies at a fraction of the polymer concentration used in traditional emulsification processes.
4. Conclusion
Dodecane in water emulsions were prepared using both membrane emulsification and traditional homogenisation techniques with both high and low Mw polyvinylalcohol as emulsifiers. High Mw polymers resulted in well-stabilised larger droplets, while low Mw polymers formed smaller droplets that relatively quickly coalesced into larger droplets. These findings were consistent using both high energy emulsification and membrane emulsification. The size and stability of emulsions produced with each emulsifier molecular weight was attributed to the balance between the ability of the polymer to sterically stabilise an emulsion droplet and the diffusion time required for adsorption to the droplet interface. Specifically, the use of low Mw polymer, which can quickly diffuse to the droplet interface but provides limited resistance to coalescence, resulted in emulsions of a wide size distribution. Conversely, high Mw polymer was slow to adsorb to the interface, allowing increased droplet growth, but once adsorbed demonstrated superior stability and relatively narrow size distribution. These overall behaviours were observed at concentrations ranging from 0.1 to 2 wt% of each polymer. Finally, we demonstrate that due to the rapid initial diffusion low Mw polymer and increased stability of high Mw polymer, an optimum ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 resulted in a significant decrease in emulsion CV and span at a polymer concentration of 0.1 wt%, when prepared with the membrane emulsification process (out of the range of ratios tested in these experiments). This work demonstrates that, by tuning polymer molecular weights and ratios between polymers of different MWs, emulsions of controlled size, dispersity and stability may easily be formed via membrane emulsification at extremely low polymer concentrations. These findings should be of significant interest to both research and industrial formulations, allowing for well controlled emulsions to be formed using minimal quantities of polymeric stabilisers.
3 resulted in a significant decrease in emulsion CV and span at a polymer concentration of 0.1 wt%, when prepared with the membrane emulsification process (out of the range of ratios tested in these experiments). This work demonstrates that, by tuning polymer molecular weights and ratios between polymers of different MWs, emulsions of controlled size, dispersity and stability may easily be formed via membrane emulsification at extremely low polymer concentrations. These findings should be of significant interest to both research and industrial formulations, allowing for well controlled emulsions to be formed using minimal quantities of polymeric stabilisers.
Author contributions
Mohamed S. Manga: conceptualisation, methodology, investigation, validation, writing – original draft. Lucy Higgins: methodology, investigation. Akshai A. Kumar: methodology, investigation. Benjamin T. Lobel: writing – review and editing. David W. York: supervision, resources. Olivier J. Cayre: conceptualisation, supervision, writing – review and editing, funding acquisition, formal analysis.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work is funded by Innovate UK, (Grant number: TS/R000646/1) and the EPSRC (EP/V027646/1). The authors would like to thank Micropore Ltd and International Paints Ltd for the fruitful discussions and technical support throughout. Finally, the authors would like to acknowledge the help of Mr Robert Harris for his assistance in various technical matters that were essential for this study.References
- H. P. Schuchmann and H. Schubert, Eng. Life Sci., 2003, 3, 67–76 CrossRef CAS.
- G. T. Vladisavljević, in Current Trends and Future Developments on (Bio-) Membranes, ed. A. Basile and C. Charcosset, Elsevier, 2019, pp. 167–222 Search PubMed.
- V. Schröder, O. Behrend and H. Schubert, J. Colloid Interface Sci., 1998, 202, 334–340 CrossRef.
- S. van der Graaf, C. G. P. H. Schroën, R. G. M. van der Sman and R. M. Boom, J. Colloid Interface Sci., 2004, 277, 456–463 CrossRef CAS PubMed.
- M. Rayner, G. Trägårdh and C. Trägårdh, Colloids Surf., A, 2005, 266, 1–17 CrossRef CAS.
- E. Dickinson, Soft Matter, 2008, 4, 932–942 RSC.
- D. Guzey and D. J. McClements, Adv. Colloid Interface Sci., 2006, 128–130, 227–248 CrossRef CAS PubMed.
- D. J. McClements and S. M. Jafari, Adv. Colloid Interface Sci., 2018, 251, 55–79 CrossRef CAS PubMed.
- C. Charcosset, I. Limayem and H. Fessi, J. Chem. Technol. Biotechnol., 2004, 79, 209–218 CrossRef CAS.
- S. M. Joscelyne and G. Trägårdh, J. Membr. Sci., 2000, 169, 107–117 CrossRef CAS.
- M. S. Manga, O. J. Cayre, R. A. Williams, S. Biggs and D. W. York, Soft Matter, 2012, 8, 1532–1538 RSC.
- K. Schroën, J. de Ruiter and C. Berton-Carabin, ChemEngineering, 2020, 4, 63 CrossRef.
- S. J. Peng and R. A. Williams, Chem. Eng. Res. Des., 1998, 76, 894–901 CrossRef CAS.
- M. H. Friedman, Principles and Models of Biological Transport, Springer Berlin, Heidelberg, 1986 Search PubMed.
- G. De Luca, A. Sindona, L. Giorno and E. Drioli, J. Membr. Sci., 2004, 229, 199–209 CrossRef CAS.
- K. Muijlwijk, E. Hinderink, D. Ershov, C. Berton-Carabin and K. Schroën, J. Colloid Interface Sci., 2016, 470, 71–79 CrossRef CAS PubMed.
- K. Wang, Y. C. Lu, J. H. Xu and G. S. Luo, Langmuir, 2009, 25, 2153–2158 CrossRef CAS PubMed.
- J. H. Xu, P. F. Dong, H. Zhao, C. P. Tostado and G. S. Luo, Langmuir, 2012, 28, 9250–9258 CrossRef CAS PubMed.
- A. Patil and M. S. Ferritto, Polymers for Personal Care and Cosmetics, American Chemical Society, 2013 Search PubMed.
- S. R. Kosvintsev, G. Gasparini, R. G. Holdich, I. W. Cumming and M. T. Stillwell, Ind. Eng. Chem. Res., 2005, 44, 9323–9330 CrossRef CAS.
- Q. Yuan, O. J. Cayre, M. Manga, R. A. Williams and S. Biggs, Soft Matter, 2010, 6, 1580–1588 RSC.
- M. S. Manga, T. N. Hunter, O. J. Cayre, D. W. York, M. D. Reichert, S. L. Anna, L. M. Walker, R. A. Williams and S. R. Biggs, Langmuir, 2016, 32, 4125–4133 CrossRef CAS PubMed.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS.
- A. Jones and B. Vincent, Colloids Surf., 1989, 42, 113–138 CrossRef CAS.
- T. F. Tadros, A. Vandamme, B. Levecke, K. Booten and C. Stevens, Adv. Colloid Interface Sci., 2004, 108, 207–226 CrossRef PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- R. Aveyard and D. Haydon, Trans. Faraday Soc., 1965, 61, 2255–2261 RSC.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
- S. Zeppieri, J. Rodríguez and A. L. López de Ramos, J. Chem. Eng. Data, 2001, 46, 1086–1088 CrossRef CAS.
- K. Kandori, K. Kishi and T. Ishikawa, Colloids Surf., 1991, 61, 269–279 CrossRef CAS.
- I. Kobayashi, M. Yasuno, S. Iwamoto, A. Shono, K. Satoh and M. Nakajima, Colloids Surf., A, 2002, 207, 185–196 CrossRef CAS.
- M. S. Manga and D. W. York, Langmuir, 2017, 33, 9050–9056 CrossRef CAS PubMed.
- X. Pan, D. York, J. A. Preece and Z. Zhang, Powder Technol., 2012, 227, 43–50 CrossRef CAS.
- J. Santos, L. A. Trujillo-Cayado, N. Calero and J. Muñoz, AIChE J., 2014, 60, 2644–2653 CrossRef CAS.
- J. Santos, G. T. Vladisavljević, R. G. Holdich, M. M. Dragosavac and J. Muñoz, Chem. Eng. Res. Des., 2015, 98, 59–69 CrossRef CAS.
- M. Rayner and G. Trägårdh, Desalination, 2002, 145, 165–172 CrossRef CAS.
- R. J. Hunter, Foundations of Colloid Science, Vol II, Clarendon, Oxford, 1989, pp. 992–1052 Search PubMed.
- A. Bąk and W. Podgórska, Chem. Eng. Res. Des., 2016, 108, 88–100 CrossRef.
- P. J. Flory, Statistical Mechanics of Chain Molecules, Wiley-Interscience, New York, 1969 Search PubMed.
- G. T. Vladisavljevic and H. Schubertb, Desalination, 2002, 144, 167–172 CrossRef CAS.
- E. Egidi, G. Gasparini, R. G. Holdich, G. T. Vladisavljević and S. R. Kosvintsev, J. Membr. Sci., 2008, 323, 414–420 CrossRef CAS.
- S. Van der Graaf, C. Schroën, R. Van der Sman and R. Boom, J. Colloid Interface Sci., 2004, 277, 456–463 CrossRef CAS PubMed.
- P. S. Silva, S. Morelli, M. M. Dragosavac, V. M. Starov and R. G. Holdich, Colloids Surf., A, 2017, 532, 77–86 CrossRef CAS.
- J. M. G. Lankveld and J. Lyklema, J. Colloid Interface Sci., 1972, 41, 475–483 CrossRef CAS.
- J.-L. Salager, N. Marquez, A. Graciaa and J. Lachaise, Langmuir, 2000, 16, 5534–5539 CrossRef CAS.
- R. Pichot, F. Spyropoulos and I. T. Norton, J. Colloid Interface Sci., 2012, 377, 396–405 CrossRef CAS PubMed.
- B. P. Binks, A. Desforges and D. G. Duff, Langmuir, 2007, 23, 1098–1106 CrossRef CAS PubMed.
- R. Pichot, F. Spyropoulos and I. T. Norton, J. Colloid Interface Sci., 2010, 352, 128–135 CrossRef CAS PubMed.
- L. B. Petrovic, V. J. Sovilj, J. M. Katona and J. L. Milanovic, J. Colloid Interface Sci., 2010, 342, 333–339 CrossRef CAS PubMed.
- J. S. Nambam and J. Philip, J. Colloid Interface Sci., 2012, 366, 88–95 CrossRef CAS PubMed.
- A. A. Sharipova, S. B. Aidarova, B. Z. Mutaliyeva, A. A. Babayev, M. Issakhov, A. B. Issayeva, G. M. Madybekova, D. O. Grigoriev and R. Miller, Colloids Interfaces, 2017, 1, 3 CrossRef CAS.
- F. Wang, X. Fang and Z. Zhang, Sol. Energy Mater. Sol. Cells, 2018, 176, 381–390 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3py00948c |
| This journal is © The Royal Society of Chemistry 2023 |