Spectroscopic analysis of vibrational coupling in multi-molecular excited states†
Sebastian
Hammer‡
 *a,
Theresa
Linderl
b,
Kristofer
Tvingstedt
*a,
Theresa
Linderl
b,
Kristofer
Tvingstedt
 a,
Wolfgang
Brütting
a,
Wolfgang
Brütting
 b and
Jens
Pflaum
b and
Jens
Pflaum
 *ac
*ac
aExperimental Physics VI, Julius Maximilian University Würzburg, 97074 Würzburg, Germany. E-mail: sebastian.hammer@mail.mcgill.ca; jpflaum@physik.uni-wuerzburg.de
bInstitute of Physics, University of Augsburg, 86135 Augsburg, Germany
cBavarian Center for Applied Energy Research, 97074 Würzburg, Germany
First published on 1st November 2022
Abstract
Multi-molecular excited states accompanied by intra- and inter-molecular geometric relaxation are commonly encountered in optical and electrooptical studies and applications of organic semiconductors as, for example, excimers or charge transfer states. Understanding the dynamics of these states is crucial to improve organic devices such as light emitting diodes and solar cells. Their full microscopic description, however, demands sophisticated tools such as ab initio quantum chemical calculations which come at the expense of high computational costs and are prone to errors by assumptions as well as iterative algorithmic procedures. Hence, the analysis of spectroscopic data is often conducted at a phenomenological level only. Here, we present a toolkit to analyze temperature dependent luminescence data and gain first insights into the relevant microscopic parameters of the molecular system at hand. By means of a Franck–Condon based approach considering a single effective inter-molecular vibrational mode and different potentials for the ground and excited state we are able to explain the luminescence spectra of such multi-molecular states. We demonstrate that by applying certain reasonable simplifications the luminescence of charge transfer states as well as excimers can be satisfactorily reproduced for temperatures ranging from cryogenics to above room temperature. We present a semi-classical and a quantum-mechanical description of our model and, for both cases, demonstrate its applicability by analyzing the temperature dependent luminescence of the amorphous donor–acceptor heterojunction tetraphenyldibenzoperiflanthene:C60 as well as polycrystalline zinc-phthalocyanine to reproduce the luminescence spectra and extract relevant system parameters such as the excimer binding energy.
New conceptsMulti-molecular excited states, i.e. excimers or charge-transfer (CT) states, whose formation is accompanied by significant reorganization of the on-site molecular geometry, are commonly encountered in organic optoelectronic devices, such as light emitting diodes or photovoltaic cells. They mediate the central photo-physical processes and, thus, determine the performance of devices. Analysis and modelling of the related spectroscopic data are important tools to develop an understanding of their formation and relaxation processes. Here, we present a Franck–Condon-based approach using a single effective inter-molecular vibrational mode to explain the temperature dependent luminescence of these states. In contrast to commonly applied simplifications, we demonstrate that by employing ground and excited state potentials of different shape the temperature dependent luminescence spectra can be successfully explained without the need for an ad hoc assumption on energetic disorder from structural inhomogeneities. Already the qualitative analysis of the linewidth asymmetry and the shift of the emission maximum as a function of temperature reveals key features of the underlying potential energy surface. We give a detailed derivation of the model and explain how to employ it to fit temperature dependent emission spectra of CT and excimer states, making it readily applicable to analyze a variety of different material systems. |
1 Introduction
The photo-physics of molecular semiconductors is usually described by excitons, i.e. partially delocalized electronically excited molecular states, and their interaction with neighboring entities, which is summarized by Kasha's exciton theory.1 As the electronic coupling of adjacent molecules depends on their relative orientation, the underlying crystal structure strongly affects the photo-physics and their dynamics in molecular aggregates,2–4 one prominent example being the occurrence of Davydov-splitting.5,6However, as it has been shown in recent studies on more complex compounds, Kasha theory only provides a simplistic picture of the underlying physical mechanisms7,8 as it, for instance, ignores molecular vibrations as well as deformation of the crystalline lattice and its molecular constituents upon excitation. To overcome these shortcomings, one approach is to only consider the smallest possible unit of the system at hand that is necessary to describe its photo-physics and to calculate all adiabatic nuclear and electronic relaxations involved at a full quantum-mechanical level.8,9 The main disadvantage of this approach, apart from the huge computational effort, is the inherent confinement of the excitation to a few molecules as the interaction with more distant molecules is only considered as a mean dielectric screening of the central molecular group. If the crystallinity of the system and its intra-molecular vibrations are taken into account, the excitation can be described in terms of an exciton–polaron, i.e. a photo-excited state within a single crystal, which is dressed by intra-molecular vibrations extending to adjacent molecules.10 Formally, the description is given by a Holstein–Peierls model which takes into account both the vibrational energy and the reorganization due to vibronic coupling of the excited state.7 This approach, however, treats the crystal's molecular constituents as fixed in position and, hence, is not suited to describe states originating from inter-molecular reorganization. Only recently Bialas and Spano successfully extended the Holstein–Peierls approach to describe inter-molecular geometry relaxation and the subsequent radiative relaxation.11
Emission from excited states which emerge from inter-molecular geometry relaxation, e.g. excimers or exciplexes (vide infra), is common in molecular single crystals as well as polycrystalline thin films2,12–14 and is often found in organic light emitting diodes (OLEDs)15–18 and solar cells.19,20 Usually, the emission from such states is characterized by a broad and unstructured spectrum which is considerably red shifted compared to the single molecule emission.2,21,22 A unique feature of such excited multi-molecular states is the temperature dependence of their emission spectrum showing a characteristic broadening with increasing temperature11,23–25
For donor–acceptor heterojunctions in solar cells it has been common since many years to describe the absorption and emission spectra of charge-transfer (CT) states in terms of Marcus theory according to which the inter- and intra-molecular geometrical relaxation is mediated by low energy vibrations. Two main concepts have emerged: in the picture of dynamic disorder the broadening of the spectra is solely the product of inter- and intra-molecular vibrations.24,26–29 The static and dynamic disorder based modelling, in contrast, includes an energetic disorder term in the range of 50 meV to 100 meV to account for structural inhomogeneities. This is the main reason for the broad spectra recorded at low temperatures and the finite line width found for the extrapolation to T → 0 K while low energy vibronic transitions only influence the spectra at higher temperatures.30–34 Both pictures describe the experimental observations in various material systems well and, as a consequence, no general consensus has emerged, so far.
Here, we present a model that explains the temperature dependent evolution of the luminescence spectra of multi-molecular excited states solely by their relaxation within a modified potential energy surface (PES) after excitation and the subsequently induced inter-molecular vibrations. We introduce a semi-classical as well as a quantum-mechanical description based on a displaced harmonic oscillator model which, different from other approaches, is based on unequal ground and excited state potentials. We show that the evolution of the luminescence spectra with temperature is sufficient to qualitatively assess the potential energy landscape along the geometric relaxation coordinate. Finally, our model is validated for a prototypical charge-transfer system, comprising tetraphenyldibenzoperiflanthene (DBP) and fullerene C60,32 as well as for the excimer system zinc-phthalocyanine (ZnPc). We demonstrate that the proposed model is indeed able to reproduce all spectral key features of the emission over a broad temperature range and, thus, yields access to the essential parameters characterizing the system's PES, such as the vibrational energy quantum of the inter-molecular modes as well as binding and relaxation energies.
2 Modeling multi-molecular emission
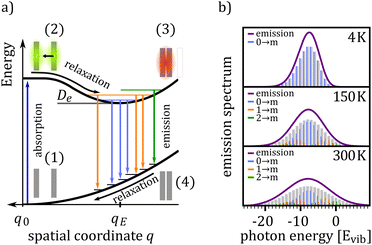
Fig. 1(a) shows the excitation scheme of a simple bi-molecular excitation within a geometric relaxation model: two molecules located on adjacent lattice sites at equilibrium distance q0 mark the starting point of the excitation–relaxation cycle (1). By photo-excitation the molecule is brought into an excited state, yielding a delocalized Frenkel exciton (2). This state evolves now, accompanied by an adiabatic relaxation of the inter-molecular geometry, to a lower lying excited state, for which (i) the inter-molecular geometry is different from that of the ground state equilibrium position and (ii) the corresponding wavefunction is primarily delocalized over adjacent molecules constituting the final dimer state. For the case shown in Fig. 1(a), the inter-molecular distance between the two molecules is reduced from q0 to qE and the excitation delocalizes equally over both monomers (3). For two identical molecules this state is commonly referred to as an excimer, a portmanteau of excited and dimer. In case of a dimer comprising a donor and acceptor molecule, this results in either a charge-transfer (CT) complex or an exciplex (excited complex), depending on the ground state interaction.35 For the sake of generality, we will call such a state X-dimer from here on, deliberately leaving the underlying resonance interaction unspecified. The X-dimer entity, bound by its electronic potential, is subject to inter-molecular vibrations. Due to the different geometry compared to the surrounding crystal, these vibrations are confined to the dimer entity and, in a first approximation, are decoupled from the crystal phonons. The X-dimer's vibrational states become thermally occupied forming a vibrationally and electronically excited dimer state which, finally, can decay radiatively to the ground state. In the diabatic Franck–Condon picture, the electronic transitions are much faster than the attending changes in the inter-molecular geometry which leads to the generation of a hot ground state, i.e. an electronic ground state dressed by high energy phonons (4). The crystal relaxes back to its equilibrium position via thermalization.From the description above, it becomes clear that some simplifications have been made in the description of the formation and relaxation processes. First of all, the excited state interaction leading to the geometric relaxation has not been specified in detail, which actually is not necessary for the phenomenological description of the X-dimer's photon emission. In the case of excimer formation, exciton resonance36,37 and also a CT state12 have been proposed as the driving forces behind geometrical relaxations but, meanwhile, the consensus prevailed that only an adiabatic mixing of Frenkel and CT excitons can fully explain the observed phenomena.11,15,25,38–41 For example, in crystalline pentacene, the first excited state is known to have a significant admixture of CT character42,43 and a considerable geometric reorganization accompanies its photo-excitation.44 In fact, Tvingstedt et al. successfully used a displaced harmonic oscillator model using inter- and intra-molecular vibrational modes to describe the emission of CT states formed at donor–acceptor hetero-junctions.24 The evolution from the initial excitation towards the excimer state is often considered as a single-step process,22,45–47 but a two step process via an intermediate state has been proposed, too,48,49 which can be part of the adiabatic evolution towards the relaxed excimer geometry.25 Furthermore, the geometric reorganization upon photo-excitation usually comprises more than just one motion.40,50 For example, calculations revealed the pyrene excimer formation to be governed by a superposition of a lateral convergence as shown in Fig. 1(a) and a horizontal sliding motion.46 For perlyene bisimide (PBI) dimers, a relative rotation of the stacked PBI dimer is predicted to govern the geometric relaxation upon photo-excitation.9,25 This means, the relaxation path shown in Fig. 1(a) between configurations (2) and (3) should be interpreted as an energetically steered pathway along which the system relaxes towards a local minimum of its PES and, hence, q can be interpreted as a generalized coordinate. This implies that the inter-molecular vibrations of the relaxed dimer state in configuration (3) are composed of several vibrational modes, e.g. shifting and sliding motions.46,50,51 We will show that for many applications, the assumption of one dominant vibrational mode governing the vibronic transitions, as it is commonly applied for intra-molecular vibrations in molecular spectroscopy, can be a useful strategy to satisfactorily explain X-dimer emission spectra and to obtain first insights into the system's PES and relaxation pathways.
For the case of a single vibrational mode coupled to the X-dimer and its electronic ground state, the emission process is a transition from an electronically excited dimer state |X,n〉 at vibrational state n to the electronic ground state |G,m〉 in its vibrationally excited state m. The probability of thermal population of the vibrationally excited state |X,n〉 at temperature T is given by the Boltzmann probability 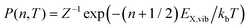 with the canonical partition function
with the canonical partition function 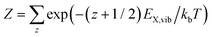 and EX,vib as the vibrational energy quantum of the X-dimer potential. In a Franck–Condon picture, the emission spectrum52 is then given by
and EX,vib as the vibrational energy quantum of the X-dimer potential. In a Franck–Condon picture, the emission spectrum52 is then given by
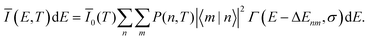 | (1) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |X〉|2 describes the overall intensity of the electronic transition at a given temperature and is proportional to the transition dipole matrix element. The temperature dependence accounts for any non-radiative decay or thermal population of the excited state directly influencing the luminescence intensity. This overall intensity is then distributed over the individual vibronic transitions |X,n〉 → |G,m〉 and, hence, does not influence the shape of the spectra which is why, in the following, we incorporate it in the lineshape functions Γ such that
|X〉|2 describes the overall intensity of the electronic transition at a given temperature and is proportional to the transition dipole matrix element. The temperature dependence accounts for any non-radiative decay or thermal population of the excited state directly influencing the luminescence intensity. This overall intensity is then distributed over the individual vibronic transitions |X,n〉 → |G,m〉 and, hence, does not influence the shape of the spectra which is why, in the following, we incorporate it in the lineshape functions Γ such that 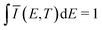 . If ground state and X-dimer potential are of the same form, i.e. both resemble that of a displaced harmonic oscillator model, Thomas Keil derived a general expression for the Franck–Condon factor53 given by
. If ground state and X-dimer potential are of the same form, i.e. both resemble that of a displaced harmonic oscillator model, Thomas Keil derived a general expression for the Franck–Condon factor53 given by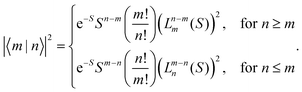 | (2) |
Fig. 1(b) shows the emission line shape of an X-dimer at three different temperatures calculated from eqn (1) utilizing the displaced harmonic oscillator approximation (2) with a vibrational energy quantum of 12 meV and a Huang–Rhys parameter of S = 8. The calculated stick spectra displayed in grey indicate the intensity at steps of the vibrational energy with 0 marking the energy of the vibronic 0–0 transition on the energy axis. The contribution of the individual vibrational levels of the X-dimer is color coded. The superposition of Gaussian lineshape functions with a line width of 10 meV for each vibronic emission generates the broad envelope. Evidently, at 4 K the emission is dominated by transitions from the X-dimer's vibrational ground state and the large vibronic coupling (S = 8) causes a preferential transition to high vibrationally excited levels of the ground state resulting in an asymmetric emission line shape with a pronounced low energy flank. With increasing temperature, higher vibrational levels of the X-dimer are populated and contribute to the overall emission yielding a redistribution of emission intensity between the different vibronic transitions. This leads to a broadening of the emission spectrum while simultaneously the intensity maximum decreases. Although the displaced harmonic oscillator model can be used to describe the emission of CT states,24,28 the assumption of the same inter-molecular potential for the electronic ground and excited state turns out to be justified only at first approximation taking into account the large geometric reorganizations expected upon X-dimer formation. Therefore, in the following we present an extended approach to this problem based on different ground and excited state potentials treated in a semi-classical as well as a quantum mechanical description.
2.1 Semi-classical description
The semi-classical description treats the X-dimer's inter-molecular vibrations as a quantum mechanical harmonic oscillator while classically approximating the ground state energy spectrum to be continuous as suggested by Birks and Kazzaz.23 This approximation holds true under two conditions:(i) The displacement of the oscillators is large in relation to the vibrational energy quantum of the final state55 leading to a population of vibrational states with large quantum numbers.56,57
(ii) The vibrational energy quantum of the final state, here the ground state, is smaller or of the same order of magnitude as the line width parameter, i.e. EG,vib ≲ 2σ.
The final states described by condition (i) are characterized by wave functions whose largest amplitude and, thus, contribution, is located at the classical turning points of the oscillator,56,57 concentrating the transition probability described by the Franck–Condon factor in eqn (1) to a small region of the nuclear displacement58 Δq → 0. Condition (ii) ensures that the individual vibronic transitions are close in energy justifying a continuous ground state energy spectrum resulting from the potential R(q).
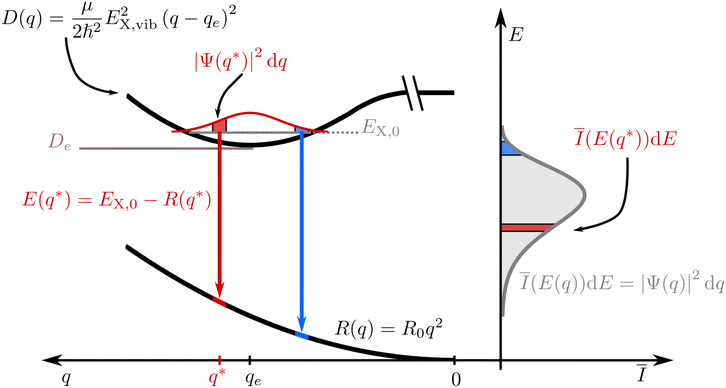
Without loss of generality, we now define the sign of the general nuclear displacement coordinate q to be positive along the path on the PES towards the new energetic minimum after photo-excitation which defines the X-dimer's fully relaxed geometry. Furthermore, the equilibrium position in the electronic ground state is set to q0 : = 0, as shown in Fig. 2. Here, the excimer equilibrium position qe has a positive value and in the picture of a lateral convergence described in Fig. 1(a), qe = |qE − q0| is the absolute value of molecular displacement of both entities forming the X-dimer with respect to the ground state equilibrium q0. In the semi-classical picture, the ground state potential is given as
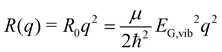 | (3) |
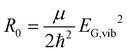 expressed by the reduced mass59μ and the vibrational energy quantum of the ground state oscillator. In the same manner the X-dimer potential can be expressed as
expressed by the reduced mass59μ and the vibrational energy quantum of the ground state oscillator. In the same manner the X-dimer potential can be expressed as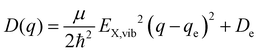 | (4) |
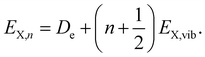 | (5) |
| E(q*) = EX,n − R(q*). | (6) |
| Ī(E(q*))dE = |Ψ(q*)|2dq. | (7) |
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) n(E) for each vibrationally excited state |X,n〉. Assuming harmonic oscillator wave functions Ψn for the X-dimer, the emission from the vibrational ground state |X,0〉 → |G〉 plotted as the grey spectrum in Fig. 2 is given by
n(E) for each vibrationally excited state |X,n〉. Assuming harmonic oscillator wave functions Ψn for the X-dimer, the emission from the vibrational ground state |X,0〉 → |G〉 plotted as the grey spectrum in Fig. 2 is given by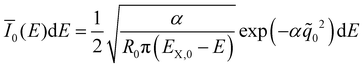 | (8) |
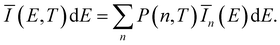 | (9) |
2.2 Quantum mechanical description
The quantum mechanical description of the X-dimer emission spectrum is given by the general expression in eqn (1). Thus, for two displaced harmonic oscillators with distinct potentials, the Franck–Condon factor |〈m|n〉|2, defining the intensity for the transition |X,n〉 → |G,m〉, needs to be evaluated. For a ground state and an excited state described by the potentials (3) and (4) with the harmonic oscillator wave functions Φm and Ψn, respectively, the overlap integral of the Franck–Condon factor is formally expressed by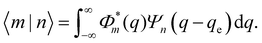 | (10) |
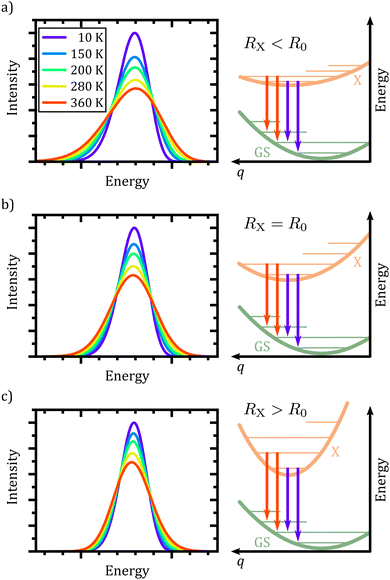
At this point, it is appropriate to evaluate if and how the emission spectra of non-equal harmonic oscillators deviate from the “ideal” case, i.e. the analytically solvable case of equal ground and excited state potentials. For this purpose we have simulated the emission spectra of three prototypical cases for comparison by means of eqn (1) and (10). The resulting emission spectra Ī(E,T)dE are displayed in Fig. 3 for a shallow (RX < R0, cf.Fig. 3(a)), an equal (RX = R0, cf.Fig. 3(b)), and a steep excited state potential (RX < R0, cf.Fig. 3(c)) at different temperatures. For the sake of comparability, the ground state potential R0, the X-dimer's energetic and spatial offsets, De and qe, as well as the line width parameter σ were kept constant while only varying the strength of the excited state potential 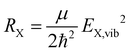 . At low temperatures, the emission spectra of all three cases show an asymmetric flank towards lower energies. Moreover, an increase in temperature leads to a broadening of the emission spectra while the intensity of the emission maximum decreases as higher vibrational levels of the excited state are populated and hence, the intensity from the |X,0〉 → |G,m〉 transitions shifts to vibronic side bands |X,n〉 → |G,m〉. For the case of equal potentials (Fig. 3(b)) the asymmetry vanishes with increasing temperature and a Gaussian line shape develops as expected by the semi-classical analytical solution.53 For the shallow potential of the excited state (Fig. 3(a)), the emission profile is highly asymmetric showing a broad tail into the low energy region. For low temperatures, the spectrum's high energy flank is defined by a sharp cut-off which blurs with rising temperature while at the same time, the emission maximum slightly shifts towards higher energies. Moreover, the overall line width is much larger in comparison with the other two cases. The emission spectra in the case of the steep excited state potential (Fig. 3(c)) have, compared to the other cases, narrow emission profiles, albeit still in the order of 100 meV and show only a slight asymmetry on the high energy flank, becoming more pronounced at higher temperatures. However, the maximum of the emission spectrum shifts to lower energies with rising temperature. Additional details of the peak shifts, the spectral broadening, the asymmetry of the emission spectra as well as computational details are available in the ESI† as Note 3.
. At low temperatures, the emission spectra of all three cases show an asymmetric flank towards lower energies. Moreover, an increase in temperature leads to a broadening of the emission spectra while the intensity of the emission maximum decreases as higher vibrational levels of the excited state are populated and hence, the intensity from the |X,0〉 → |G,m〉 transitions shifts to vibronic side bands |X,n〉 → |G,m〉. For the case of equal potentials (Fig. 3(b)) the asymmetry vanishes with increasing temperature and a Gaussian line shape develops as expected by the semi-classical analytical solution.53 For the shallow potential of the excited state (Fig. 3(a)), the emission profile is highly asymmetric showing a broad tail into the low energy region. For low temperatures, the spectrum's high energy flank is defined by a sharp cut-off which blurs with rising temperature while at the same time, the emission maximum slightly shifts towards higher energies. Moreover, the overall line width is much larger in comparison with the other two cases. The emission spectra in the case of the steep excited state potential (Fig. 3(c)) have, compared to the other cases, narrow emission profiles, albeit still in the order of 100 meV and show only a slight asymmetry on the high energy flank, becoming more pronounced at higher temperatures. However, the maximum of the emission spectrum shifts to lower energies with rising temperature. Additional details of the peak shifts, the spectral broadening, the asymmetry of the emission spectra as well as computational details are available in the ESI† as Note 3.
In conclusion, the spectral features of the X-dimer's temperature dependent emission spectra allows for the identification of the relation between the ground and excited state potential and, hence, enable a direct categorization by means of the three cases presented above.
3 Analyzing optical spectra
Following up on the previous theoretical discussion on modeling the luminescence spectra of a multi-molecular excited state, we will now put the developed model in its semi-classical as well as quantum-mechanical form to the test and explore their respective scope of application. For this purpose we choose a CT as well as an excimeric system. We analyze their temperature dependent luminescence spectra, managing both, to evaluate the applicability of our mathematical models and extract relevant parameters of each system. Furthermore, we will discuss the differences between an amorphous system and a crystalline system for which temperature dependent lattice extensions can no longer be neglected.3.1 CT emission
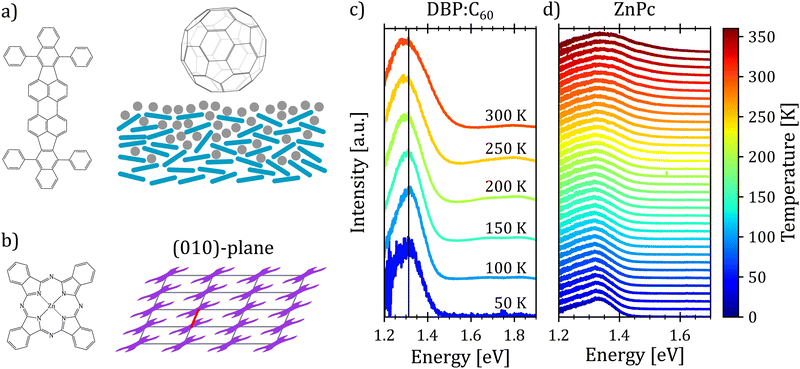
First, we turn to an amorphous donor–acceptor system comprising an intermixed heterojunction of tetraphenyldibenzoperiflanthene (DBP) as the donor and fullerene C60 as the acceptor previously published in ref. 32. DBP belongs to the well-known class of perylene dyes. As compared to its parent compound diindenoperylene (DIP), it has an extended π-conjugated core and, most importantly, four rotatable phenyl rings at the indeno groups at each side of the perylene core. This changes orientation in thin films from upright standing in the case of DIP to lying down on the substrate for DBP. It was introduced as a novel donor in organic photovoltaics by Fujishima et al.60 because of its better light absorption due to the favorable molecular orientation. Both neat films of DBP and its co-evaporated blends with C60 are amorphous, however, with the mentioned preferential in-plane orientation of the optical transition dipole moment of DBP61 (cf.Fig. 4(a)).Fig. 4(c) shows the temperature dependent electroluminescence (T-EL) of the DBP–C60 heterojunction from room temperature down to 50 K. The emission comprises two main features: a pronounced peak at 1.3 eV and a weaker one at 1.8 eV, the latter growing in intensity with rising temperature. While the emission at higher energies is associated with monomer emission of the donor and acceptor molecules,32 the emission feature of interest is the CT emission at 1.3 eV. As evident, the spectra show a broadening as well as a slight red shift of the emission maximum with increasing temperature. Furthermore, we note that the shape of the spectra also undergoes changes with temperature. For low temperatures, the spectra present an asymmetric shape with a broader flank at the low energy side. With increasing temperature, the emission spectra broaden and the asymmetry slightly shifts towards the high energy side. Hence, the presented phenomenological behavior is consistent with the emission spectra of an X-dimer with a steeper excited state potential compared to the ground state. This qualitative match with the simulated characteristics of an X-dimer encourages us to put the above presented model to a quantitative test.
Taking the previous main findings on the spectral features into account, we can set a parameter space to fit the overall dataset within the presented X-dimer model using eqn (1). At first, we assume a Gaussian line shape function Γ for each vibronic transition with a temperature independent line width σ. The emission energy of a single vibronic transition |X,n〉 → |G,m〉 is given by
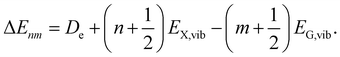 | (11) |
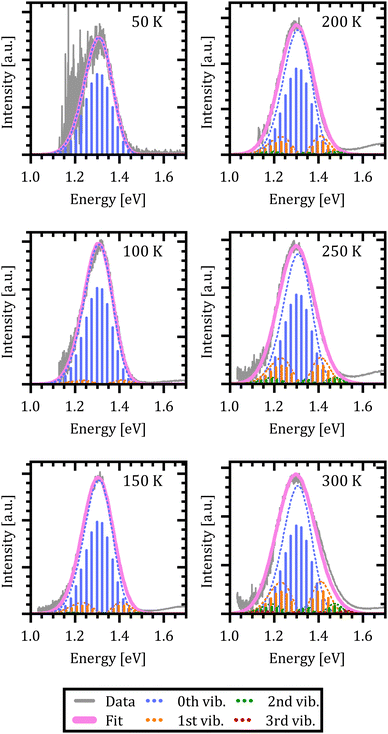
The results are shown in Fig. 5. The resulting emission spectrum is given by the magenta curve while the experimental data are depicted in grey. The envelope emission spectrum is broken down into its individual contributions from the respective X-dimer's vibrational levels which is indicated by the color coding of the individual emission spectra for each level, i.e. blue for vibrational ground state emission, orange for emission from the first excited state, etc. The individual vibronic transitions to the ground state are given by the stick spectra whose heights mark the maximum of the respective Gaussian line shape. The emission spectra are reproduced very well over the full temperature range, despite the use of only a single parameter set. The slight deviation on the high energy side for T = 300 K is attributed to the overlap with the broad monomer emission at around 1.8 eV, which becomes more pronounced as the CT emission broadens with rising temperature.
The extracted fit parameters are listed in Table 1. First of all, we notice a slightly stronger X-state potential as expected from the qualitative analysis of the evolution of the spectra with temperature. However, for a quantitative assessment of the extracted parameters we need to compare the results to already established analytical models such as Marcus theory26,27 and its derivative including static as well as dynamical disorder by Burke et al.30 performed by Linderl et al. in an earlier publication.32 In these approaches the emission spectrum is described by a Gaussian line shape as
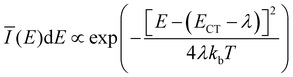 | (12) |
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) + σB2/2kbT to account for static disorder by introducing the disorder parameter σB. Note that here, the static disorder not only influences the line width of the emission spectra but also the Stokes shift. Combining room temperature electroluminescence and incident photon to current efficiency measurements Linderl et al.32 extracted ECT,M = 1.49 eV from the Marcus approach and ẼCT,B = 1.55 eV and σB = 55 meV from the Burke approach for the DBP–C60 heterojunctions. The corresponding parameter from the X-dimer model is the energetic offset De which coincides very well with the all dynamical Marcus model but misses the Burke model by about 60 meV. As the X-dimer model accounts for static broadening only on the scale of vibronic transitions and attributes the overall line broadening to an overall dynamical effect, these correspondences are not surprising. Calculating the observed energetic offset from the Burke model by ECT,B = ẼCT,B − σB2/2kb300 K ≈ 1.49 eV a good agreement between all three models is achieved. For the second key parameter, the reorganization energy, the Marcus and Burke model yield λM = 0.18 eV and
+ σB2/2kbT to account for static disorder by introducing the disorder parameter σB. Note that here, the static disorder not only influences the line width of the emission spectra but also the Stokes shift. Combining room temperature electroluminescence and incident photon to current efficiency measurements Linderl et al.32 extracted ECT,M = 1.49 eV from the Marcus approach and ẼCT,B = 1.55 eV and σB = 55 meV from the Burke approach for the DBP–C60 heterojunctions. The corresponding parameter from the X-dimer model is the energetic offset De which coincides very well with the all dynamical Marcus model but misses the Burke model by about 60 meV. As the X-dimer model accounts for static broadening only on the scale of vibronic transitions and attributes the overall line broadening to an overall dynamical effect, these correspondences are not surprising. Calculating the observed energetic offset from the Burke model by ECT,B = ẼCT,B − σB2/2kb300 K ≈ 1.49 eV a good agreement between all three models is achieved. For the second key parameter, the reorganization energy, the Marcus and Burke model yield λM = 0.18 eV and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) B = 0.12 eV, respectively. In the X-dimer model, there is no direct analogue, as first of all, by definition the quantum mechanical treatment does not consider a continuous reorganization energy and, second, the excited and ground state have different potentials which excludes a single reorganization energy. However, we can estimate a mean reorganization energy for the hot ground state after emission by the Huang–Rhys parameter54S via
B = 0.12 eV, respectively. In the X-dimer model, there is no direct analogue, as first of all, by definition the quantum mechanical treatment does not consider a continuous reorganization energy and, second, the excited and ground state have different potentials which excludes a single reorganization energy. However, we can estimate a mean reorganization energy for the hot ground state after emission by the Huang–Rhys parameter54S via| λG = SEG,vib = R0qe2 | (13) |
| Parameter | Fitted value | |
|---|---|---|
| X-state vib. energy | E X,vib | (27.5 ± 0.5) meV |
| Ground state vib. energy | E G,vib | (23.6 ± 0.2) meV |
| Energetic offset | D e | (1.485 ± 0.002) eV |
| Oscillator displacement | q e | 0.09 Å |
| Static disorder | σ | (13.9 ± 0.5) meV |
From the above evaluation of our X-dimer model, two main conclusions can be drawn: first of all, the temperature dependent spectra can be reproduced over a large temperature range with a single set of parameters, explaining simultaneously the asymmetric line shape at low temperatures, the line broadening with temperature and the red shift of the peak maximum. Second, the comparison to well established models based on Marcus theory confirms similar values for the inherent key parameters of the system, namely the relative energetic position of ground and excited state as well as the line broadening parameter. Even though a one-to-one comparison is not straightforward, the analysis suggests that conventional approaches lead to an overestimation of the reorganization energy of the ground state after population by radiative transitions from the excited state.
3.2 ZnPc excimer emission
In the next step, we test the described model on a prototypical excimer system, the molecular semiconductor zinc-phthalocyanine (ZnPc) (Fig. 4(a)). ZnPc thin films prepared by vacuum sublimation usually adapt the crystallographic α-phase with one molecule per unit cell and a P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry leading to a slip stack arrangement within the film plane (cf. Fig. 4(b)).64,65 The characteristic broad, asymmetric luminescence peak is commonly assigned to an alleged excimer emission.66 We assume that the excimer forms along the short crystallographic a-axis (red line in Fig. 4(b)) via convergence of two adjacent monomers, as its characteristic emission is suppressed in the crystallographic β-phase67 as well as in mixtures with fluorinated ZnPc derivatives68 hinting at steric hindrance of excimer formation. Recent calculations suggest a strong CT admixture to the lowest excited state in the ZnPc α polymorph69,70 while the lowest excited state is of pure excitonic nature in the crystallographic β-phase,70 corroborating the hypothesis of excimer formation as a preferred relaxation pathway.
symmetry leading to a slip stack arrangement within the film plane (cf. Fig. 4(b)).64,65 The characteristic broad, asymmetric luminescence peak is commonly assigned to an alleged excimer emission.66 We assume that the excimer forms along the short crystallographic a-axis (red line in Fig. 4(b)) via convergence of two adjacent monomers, as its characteristic emission is suppressed in the crystallographic β-phase67 as well as in mixtures with fluorinated ZnPc derivatives68 hinting at steric hindrance of excimer formation. Recent calculations suggest a strong CT admixture to the lowest excited state in the ZnPc α polymorph69,70 while the lowest excited state is of pure excitonic nature in the crystallographic β-phase,70 corroborating the hypothesis of excimer formation as a preferred relaxation pathway.
To compare the semi-classical description with the full quantum mechanical treatment, we first performed temperature dependent photoluminescence (T-PL) measurements on a ZnPc α-phase thin film from 20 K to 360 K to obtain a reference dataset of excimer emission spectra. The spectra are shown in Fig. 4(d). As can be seen, with increasing temperature the emission shows the typical broadening and the shape of the spectra changes as well. At low temperatures the spectra present an asymmetry towards the low energy tail. As the temperature rises, the asymmetry shifts towards the high energy flank, indicating a steeper X-dimer potential compared to the ground state. Interestingly, the maximum of the spectra shifts towards higher energies with increasing temperature in contradiction with the simulations before. However, so far, we have not included any thermal expansion or contraction of the underlying crystal lattice, as the amorphous DBP–C60 heterostructure could be fully described without, even though, molecular semiconductors can have up to two orders of magnitude larger expansion coefficients71–73 compared to inorganic compounds.74,75 A change in the ground state crystal lattice is likely to change the X-dimer's spatial displacement coordinate as well as the ground state potential slope which is common for molecular crystals and can be identified by shifts in phonon frequency with temperature.76–78 As these parameters strongly influence the overlap of the nuclear wave functions in the crystalline aggregate, the spectral barycenter and also the maximum of the emission spectra are highly dependent on R0(T) and qe(T) which have to be regarded as functions of temperature and cannot be assumed constant in crystalline materials.
Using the same rationale as before, we will first apply the quantum mechanical description to fit the data using eqn (1) while estimating the Franck–Condon factors numerically by eqn (10) as the asymmetry of the spectra suggests dissimilar ground and X-state potentials. Furthermore, in a first approximation, we assume that the excimer potential is only weakly influenced by the thermal expansion of the crystal lattice. Therefore, the energetic offset to the ground state De as well as the X-state potential Re and as such EX,vib are set to be constant and independent of temperature.79 The ground state potential oscillator constant R0(T) as well as the spatial displacement coordinate qe(T) are chosen as free parameters. To select a reasonable start value for the X-dimer's vibrational energy quantum we use an independent approach, following the proposed approximation of Birks et al.23 The full-width at half-maximum (FWHM) at a given temperature T can be approximated by
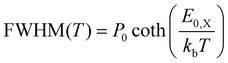 | (14) |
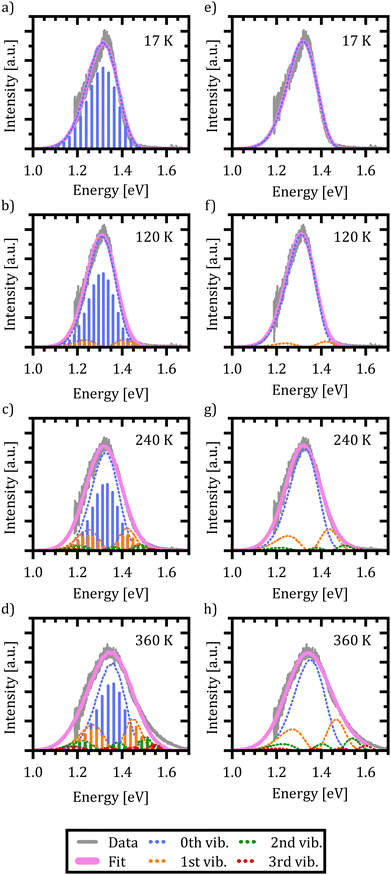
In Fig. 6(a)–(d) the resulting spectra and vibrational transitions are shown for exemplary emission spectra at 17 K, 120 K, 240 K and 360 K (see Fig. S6 in the ESI† for full dataset). The color coding and presentation of the experimental data and the simulated spectra are similar to Fig. 5 where different colors depict emission from different vibrational levels of the X-dimer state and single vibronic transitions are shown as stick spectra.
Again, the X-dimer model is able to correctly describe the individual experimental emission spectra at a high level. For low temperatures, a slight deviation on the low energy side of the spectra is apparent, leading to a small mismatch between the measured and simulated emission maxima. Yet, the overall line shape is still reproduced very well and with increasing temperature, this mismatch disappears. At 120 K the emission from the first vibrational level becomes apparent, although 94% of the intensity is still clustered in the ground state emission. The thermal population of the vibrational levels and, thereby, the increasing contribution to the emission spectra lead to the buildup of an asymmetric high energy flank in the emission spectra. At 240 K only 78% of the intensity stems from ground state emission while about 17% is contributed by the first vibrational level as the second largest contribution. Finally, at 360 K only 58% of the emitted photons come from the vibrational ground state, while about a quarter stem from the first and 10% from the second vibrationally excited state, while the rest are distributed over higher vibrational levels. At high temperatures T > 300 K, the chosen model fails to completely reproduce the high energy flank above 1.5 eV. Notably, the incapacity to fully describe the asymmetric flanks is most pronounced at high temperatures (cf. Fig. 6(d) for 360 K). We attribute this shortcoming to the simplification of deliberately assuming only a single effective inter-molecular vibrational mode. As the thermal population of vibrational modes is the dominant factor determining the spectral envelope,51 this simplification may well lead to minor deviations at the extreme ends of the temperature range. Nevertheless, the modelling of the experimental spectra by our dimer approach including a single main mode is still able to reproduce the overall emission spectra while keeping the parameter space for the fitting procedure to a reasonable size. Furthermore, the fitting parameters still enable us to quantify the main parameters determining the potential energy landscape. It is noteworthy that at sufficiently high temperatures, the harmonic approximation implied in our model might lose validity which may lead to certain deviations in the fit, as well.
Using the reduced mass of two ZnPc molecules μ = mZnPc/2 = 577.916 u/2 the fit reveals a vibrational energy quantum of EX,vib = (24.7 ± 0.1) meV for the excimer state. The energetic offset of the excimer potential is estimated as De = 1.49 eV. Estimating the singlet exciton energy in the crystalline α-phase from the lowest Q-band absorption as about 1.7 eV to 1.8 eV,65,68,81 this puts the excimer binding energy in the range of 200 meV to 300 meV. As the ground state potential and the X-dimer's spatial displacement are functions of temperature, the absolute values vary (see Fig. S4, ESI†), and their temperature dependencies are strongly correlated which will be discussed in greater detail below. The vibrational energy quantum of the ground state varies between 22 meV to 25 meV putting it quite close to the excited state potential. Here, the highest energies are found for low and high temperatures, while a constant minimum plateau establishes between 100 K and 230 K. The spatial displacement, i.e. the reduction of the distance between two neighboring ZnPc monomers, is in the range of 0.08 Å to 0.11 Å with an inverse behaviour with temperature with respect to the vibrational energy. This is a reasonable result when compared to other excimer systems for which similar values in reduction of the inter-molecular distance have been reported.23,25,40,46,50,51
Last but not least, we conduct the above excimer analysis also with the semi-classical approach. For this purpose eqn (9) was fitted to each emission spectrum with R0, qe and De as free parameters by a least square method of the SciPy package.82 Again, to minimize the number of correlated free parameters, we assume the X-state potential as constant with temperature and set it to the fixed value determined from the FWHM using eqn (14). This leads to a slight overestimation of the vibrational energy compared to the results of the quantum-mechanical fit, but, as will be shown below, still yields reasonable results in the reproduction of the emission lineshape and hence gives an opportunity to test the semi-classical approach without any input from the full quantum mechanical model. Six vibrational levels of the excimer were simulated for the emission spectra.
Fig. 6(e)–(h) exemplarily show the fitted emission spectra at 17 K, 120 K, 240 K and 360 K for direct comparison with the quantum mechanical approach (see Fig. S7 in the ESI† for full dataset). As before, the resulting lineshape is given in magenta, while the individual contributions of the X-dimer's vibrational levels are color coded. Generic to the semi-classical description, the individual emissions are given by a continuous spectral density rather than discrete individual transitions. The individual vibronic spectra correspond well to the respective envelope spectra from the quantum mechanical calculation shown in Fig. 6(a)–(d). Furthermore, despite the higher vibrational energy of the excimer potential, the fractional contributions of the individual vibrational levels to the overall emission intensity are quite similar. At 17 K only the vibrational ground state contributes to the emission. As before, at 120 K the vibrational ground state emission accounts for the largest share of the emission intensity with about 94% with the next vibrational level starting to significantly contribute as well. Only at higher temperatures slight deviations from the quantum mechanical model occur. At 240 K the ground state emission amounts to 77% and the first vibrational state is at 18%, while for 360 K still 63% of the emission stems from the vibrational ground state followed by the first vibrational level at 24%, the second at 9% and the rest distributed across higher levels. The fifth excited state contributes only 0.5% at this temperature. Interestingly, the shortcomings in the reproduction of the high temperature spectra are similar to the quantum-mechanical approach, which is plausible if the deviation is caused by the simplification of using just one single vibrational mode. Before discussing the extracted parameters of the excimer's PES, one more limitation of the semi-classical model needs to be addressed, namely the singularity occurring at high emission energies. As already mentioned in the discussion of eqn (8), the energy dependent expression in the denominator of the square-root term leads to a limitation of eqn (9) to emission energies below EX,n = De + (n + 1/2)EX,vib, i.e. to the singularity of the highest simulated vibrational X-dimer level line shape EX,n − E. From the quantum mechanical treatment before, we know that the excimeric energy offset De is in the order of about 1.5 eV, and hence the simulated emission spectra will be limited to an energy range below EX,5 ≈ 1.67 eV. This means that for temperatures above 300 K, the emerging high energy flank of the spectra cannot be simulated completely. This can be recognized as a discontinuity in the fitting parameters R0, qe and De at 330 K where the least square algorithm shifts the emission spectra to higher energies in order to reproduce the experimental data as can be seen in Fig. S5 (ESI†).
Below this temperature, the fitting routine works very well. In fact, the obtained energetic offset as a function of temperature is constant at (1.55 ± 0.01) eV without any prior assumption on its behavior with temperature and only 60 meV higher compared to the quantum mechanical model. Moreover, the ground state potential shows a similar behavior with temperature and is characterized by similar parameters between (21.6 ± 0.3) meV and (24.7 ± 0.3) meV compared to the quantum mechanical model. The same holds true for the spatial displacement with values between 0.10 Å and 0.13 Å.
To summarize, first and foremost, we have proven that we can consistently describe the emission of crystalline α-phase ZnPc thin films and its evolution with temperature with the presented X-dimer model based on a single inter-molecular vibrational mode. Hence, our results strongly suggest that the characteristics of photo- and electroluminescence67 are indeed the result of an excimer formation located 200 meV to 300 meV below the free exciton. The lack of free exciton luminescence suggests that there is no energetic barrier between the two states, leading to an exothermic instantaneous population of the excimer state. As the dominant mechanism we suggest a convergence of two adjacent molecules, reducing the inter-molecular distance by about 0.1 Å. Our results further suggest that especially at high temperatures, a second vibrational mode is likely to contribute to the emission as well. By means of the overall comparison, we showed that a semi-classical approach can be well suited to describe the measured excimer emission as long as the inherent limitations are carefully considered.
4 Discussion
Regardless of its successful application to two inherently different molecular systems, in the following, we will discuss potential pitfalls and shortcomings of the proposed X-dimer model, as well as strategies to overcome those. Applying the X-dimer model to extract the material inherent parameters without any additional information on the ground and X-state potentials can be challenging and obtained results should be treated cautiously. The parameters defining the ground and the excited state potential as well as the oscillator displacement are highly correlated as they mutually contribute to the spectral broadening, which is indicated by their high co-variance values. In conventional Franck–Condon based models this drawback is usually circumvented by combining these three parameters in the Huang–Rhys parameter which then effectively describes the spectral broadening by a single parameter. However, this approach fails for materials where the asymmetry in line shape, especially at higher temperatures, refers to different ground state and excited state potentials. Nevertheless, there exist strategies to reduce the free parameter space and to control these uncertainties for certain cases. For example in the above presented analysis of the ZnPc excimer, the experimental data allow for an estimation of the X-dimer's zero point energy by means of the semi-classical approximation of the FWHM (14) which can be either used as a reliable start value for the fitting procedure, as demonstrated for the quantum mechanical approach, or even eliminate the parameter at all by assuming it to be a fixed value, as shown for the semi-classical approach. Furthermore, as demonstrated by Birks et al.23 the low temperature spectra allow to infer the ground state potential parameter R0 and the X-state displacement qe, because the low temperature emission spectra are dominated by transitions from the X-dimer's vibrational ground state to ground state phonons. As a consequence, a thorough evaluation of the dataset taking the limits of the underlying model into account has to be performed before detailed analysis.With these conditions in mind, it is however possible to gain considerable insights into the photophysical processes of multi-molecular excited states by directly evaluating the temperature dependent spectrally resolved steady state luminescence. As demonstrated on different material systems the one dimensional PES can be extracted, that reveals, within the discussed limitations, the reorganization energies after photo emission, the inter-molecular displacement as well as the binding energies.
5 Conclusion
In this contribution we presented the X-dimer model to analyse the temperature dependence of luminescence spectra of multi-molecular excited states originating from Franck–Condon like transitions between inter-molecular vibrational levels. We evaluated this model for two different material systems, the CT emission of the amorphous donor–acceptor bulk heterojunction DBP–C60 and the excimer emission of α-ZnPc crystalline thin films. The emission of both systems was reproduced very well by the presented model and the extracted parameters agree with that of established benchmark models.From our analysis we conclude that there is no need to include a significant contribution by static disorder to explain broad spectral line shapes even at low temperatures, which seems reasonable for amorphous systems but appears rather counter intuitive for crystalline aggregates such as α-ZnPc. Rather, our results suggest that a manifold of vibronic transitions between low energy inter-molecular vibrations is indeed sufficient to describe the emission over a large temperature range and, hence, supports the picture of dynamic broadening as suggested previously in various forms.24,26–29
In summary, by the two seminal material examples and the information gained by applying our X-dimer model, we want to encourage a more extended analysis of emission spectra which by their lineshape and temperature dependence indicate a multi-molecular origin.
6 Methods
Sample preparation and characterization
DBP–C60 devices are prepared via thermal evaporation on a 30 nm thick poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) film coated on an indium-tin-oxide (ITO) covered glass substrate. The 50 nm active layer (DBP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C60, molar ratio 1
C60, molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) is enclosed by neat 5 nm DBP and 10 nm C60 layers. A 5 nm bathocuproine (BCP) exciton blocking layer is added on top to prevent quenching at the 100 nm aluminium (Al) cathode. The total layer structure is ITO/PEDOT:PSS/DBP/DBP:C60/C60/BCP/Al. Morphological characterization confirming the amorphous nature of the donor–acceptor bulk heterojunction as well as a detailed description of the sample preparation is given in ref. 32.
2) is enclosed by neat 5 nm DBP and 10 nm C60 layers. A 5 nm bathocuproine (BCP) exciton blocking layer is added on top to prevent quenching at the 100 nm aluminium (Al) cathode. The total layer structure is ITO/PEDOT:PSS/DBP/DBP:C60/C60/BCP/Al. Morphological characterization confirming the amorphous nature of the donor–acceptor bulk heterojunction as well as a detailed description of the sample preparation is given in ref. 32.
ZnPc thin films were prepared via vacuum sublimation of ZnPc, purified by twofold gradient sublimation, at a base pressure of 10−9 mbar while controlling the deposition rate and film thickness by using a quartz crystal microbalance. A film of 30 nm was evaporated on a 200 nm thick thermal oxide layer on top of a silicon wafer at a rate of 10 Å min−1. These crystalline films grow in the thermodynamically metastable α-phase and are composed of small crystallites (lateral dimensions about 20 nm to 50 nm) with a high crystallinity along the out-of-plane direction (as large as the film thickness as determined by X-ray diffraction analyses).67
Optical measurements
Temperature dependent electroluminescence measurements are described in ref. 32. Specifically, the spectra were recorded using a liquid-nitrogen-cooled CCD camera (PyLoN:100BR_eXcelon, Princton Instruments) coupled with a spectrometer (SP2300i, Princton Instruments) with spectral sensitivity in the wavelength range of approximately 300–1000 nm. The measurements were performed under a constant dc voltage drive (2 V in all cases shown in this work) from a Keithley source meter. The samples were transferred into a liquid-helium-cooled cryostat (Cryovac) with an inert gas atmosphere (approximately 300 mbar He) without air exposure.Temperature dependent photoluminescence measurements on ZnPc thin films were performed at 685 nm cw-excitation with a Coherent OBIS LS/LX solid state laser. The sample was mounted on a cold finger in a CryoVac helium cryostat with a silicon diode as a temperature sensor located at the sample position for reliable temperature measurements and control. The laser was focused onto the sample via a OLYMPUS SLMPLNx 50 (NA = 0.35, 50× magnification) long working distance objective. The luminescence signal was captured through the same objective and guided to a Princeton Instruments Acton SP-2500i spectrometer with a PIXIS 100BR eXcelon peltier cooled CCD camera. Spectra were recorded at each temperature with an acquisition time of 60 s after a 15 min delay to ensure thermal equilibrium. The spectra were background corrected before analysis.
Code availability
We provide the xDimer python package containing the functions to simulate luminescence spectra within the semi-classical and quantum-mechanical X-dimer model on a Zenodo repository at https://doi.org/10.5281/zenodo.6707037.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SH gratefully acknowledges funding from the German Research Foundation (DFG) through the project 490894053. Financial support by the Bavarian State Ministry of Science, Research and the Arts within the collaborative research network “Solar Technologies go Hybrid (SolTech)” is gratefully acknowledged by WB and JP. JP acknowledges funding from the German Research Foundation (DFG) within the project PF385/12-1. WB acknowledges funding from the German Research Foundation (DFG) within the project BR 1728/14-2.Notes and references
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- J. Gierschner and S. Y. Park, J. Mater. Chem. C, 2013, 1, 5818 RSC.
- F. C. Spano and D. Beljonne, in The WSPC Reference on Organic Electronics: Organic Semiconductors, ed. J.-L. Brédas and S. R. Marder, World Scientific, Singapore, 2016, ch. 4, vol. 1, pp.93–130 Search PubMed.
- B. Gieseking, T. Schmeiler, B. Müller, C. Deibel, B. Engels, V. Dyakonov and J. Pflaum, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205305 CrossRef.
- A. S. Davydov, J. Exp. Theor. Phys., 1948, 18, 210–218 CAS.
- A. S. Davydov, Sov. Phys. Usp., 1964, 7, 145–178 CrossRef.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- B. Engels and V. Engel, Phys. Chem. Chem. Phys., 2017, 19, 12604–12619 RSC.
- R. F. Fink, J. Seibt, V. Engel, M. Renz, M. Kaupp, S. Lochbrunner, H.-M. Zhao, J. Pfister, F. Würthner and B. Engels, J. Am. Chem. Soc., 2008, 130, 12858–12859 CrossRef CAS PubMed.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS.
- A. L. Bialas and F. C. Spano, J. Phys. Chem. C, 2022, 126, 4067–4081 CrossRef CAS.
- J. Ferguson, J. Chem. Phys., 1958, 28, 765–768 CrossRef CAS.
- J. Tanaka, Bull. Chem. Soc. Jpn., 1963, 36, 1237–1249 CrossRef CAS.
- J. Hausch, A. J. Berges, C. Zeiser, T. Rammler, A. Morlok, J. Bredehöft, S. Hammer, J. Pflaum, C. J. Bardeen and K. Broch, J. Phys. Chem. C, 2022 DOI:10.1021/acs.jpcc.1c09297.
- J. Kalinowski, Mater. Sci.-Pol., 2009, 27, 735–756 CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS.
- M. Sarma and K.-T. Wong, ACS Appl. Mater. Interfaces, 2018, 10, 19279–19304 CrossRef CAS.
- N. Bunzmann, S. Weissenseel, L. Kudriashova, J. Gruene, B. Krugmann, J. V. Grazulevicius, A. Sperlich and V. Dyakonov, Mater. Horiz., 2020, 7, 1126–1137 RSC.
- C. Deibel, T. Strobel and V. Dyakonov, Adv. Mater., 2010, 22, 4097–4111 CrossRef CAS.
- K. Vandewal, Annu. Rev. Phys. Chem., 2016, 67, 113–133 CrossRef CAS PubMed.
- J. B. Birks and L. G. Christophorou, Proc. R. Soc. London, Ser. A, 1964, 277, 571–582 CAS.
- T. Förster, Angew. Chem., Int. Ed. Engl., 1969, 8, 333–343 CrossRef.
- J. B. Birks and A. A. Kazzaz, Proc. R. Soc. London, Ser. A, 1968, 304, 291–301 Search PubMed.
- K. Tvingstedt, J. Benduhn and K. Vandewal, Mater. Horiz., 2020, 7, 1888–1900 RSC.
- Y. Hong, W. Kim, T. Kim, C. Kaufmann, H. Kim, F. Würthner and D. Kim, Angew. Chem., Int. Ed., 2022, 61, e202114474 CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- K. Vandewal, K. Tvingstedt, J. V. Manca and O. Inganäs, IEEE J. Sel. Top. Quantum Electron., 2010, 16, 1676–1684 CAS.
- J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. McGarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053 CrossRef CAS.
- C. Göhler, M. Saladina, Y. Wang, D. Spoltore, J. Benduhn, K. Leo and C. Deibel, Phys. Rev. Appl., 2021, 15, 064009 CrossRef.
- T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123 CrossRef.
- F.-J. Kahle, A. Rudnick, H. Bässler and A. Köhler, Mater. Horiz., 2018, 5, 837–848 RSC.
- T. Linderl, T. Zechel, A. Hofmann, T. Sato, K. Shimizu, H. Ishii and W. Brütting, Phys. Rev. Appl., 2020, 13, 024061 CrossRef CAS.
- A. Melianas, N. Felekidis, Y. Puttisong, S. C. J. Meskers, O. Inganäs, W. M. Chen and M. Kemerink, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23416–23425 CrossRef CAS.
- J. Yan, E. Rezasoltani, M. Azzouzi, F. Eisner and J. Nelson, Nat. Commun., 2021, 12, 3642 CrossRef CAS PubMed.
- V. Belova, P. Beyer, E. Meister, T. Linderl, M.-U. Halbich, M. Gerhard, S. Schmidt, T. Zechel, T. Meisel, A. V. Generalov, A. S. Anselmo, R. Scholz, O. Konovalov, A. Gerlach, M. Koch, A. Hinderhofer, A. Opitz, W. Brütting and F. Schreiber, J. Am. Chem. Soc., 2017, 139, 8474–8486 CrossRef CAS PubMed.
- T. Förster, Pure Appl. Chem., 1962, 4, 121–134 CrossRef.
- T. Förster, Pure Appl. Chem., 1963, 7, 73–78 Search PubMed.
- T. Azumi and S. P. McGlynn, J. Chem. Phys., 1964, 41, 3131–3138 CrossRef CAS.
- T. Azumi, A. T. Armstrong and S. P. McGlynn, J. Chem. Phys., 1964, 41, 3839–3852 CrossRef CAS.
- D. Casanova, Int. J. Quantum Chem., 2015, 115, 442–452 CrossRef CAS.
- C. E. Ramirez, S. Chen, N. E. Powers-Riggs, I. Schlesinger, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2020, 142, 18243–18250 CrossRef CAS.
- N. J. Hestand, H. Yamagata, B. Xu, D. Sun, Y. Zhong, A. R. Harutyunyan, G. Chen, H.-L. Dai, Y. Rao and F. C. Spano, J. Phys. Chem. C, 2015, 119, 22137–22147 CrossRef CAS.
- L. Craciunescu, S. Wirsing, S. Hammer, K. Broch, A. Dreuw, F. Fantuzzi, V. Sivanesan, P. Tegeder and B. Engels, J. Phys. Chem. Lett., 2022, 13, 3726–3731 CrossRef CAS.
- H. Seiler, M. Krynski, D. Zahn, S. Hammer, Y. W. Windsor, T. Vasileiadis, J. Pflaum, R. Ernstorfer, M. Rossi and H. Schwoerer, Sci. Adv., 2021, 7, eabg0869 CrossRef CAS.
- J. B. Birks, Rep. Prog. Phys., 1975, 38, 903–974 CrossRef CAS.
- J. Hoche, H.-C. Schmitt, A. Humeniuk, I. Fischer, R. Mitrić and M. I. S. Röhr, Phys. Chem. Chem. Phys., 2017, 19, 25002–25015 RSC.
- J. Hoche, M. Flock, X. Miao, L. N. Philipp, M. Wenzel, I. Fischer and R. Mitric, Chem. Sci., 2021, 12, 11965–11975 RSC.
- R. E. Cook, B. T. Phelan, R. J. Kamire, M. B. Majewski, R. M. Young and M. R. Wasielewski, J. Phys. Chem. A, 2017, 121, 1607–1615 CrossRef CAS PubMed.
- R. D. Pensack, R. J. Ashmore, A. L. Paoletta and G. D. Scholes, J. Phys. Chem. C, 2018, 122, 21004–21017 CrossRef CAS.
- J. Gierschner, H.-G. Mack, D. Oelkrug, I. Waldner and H. Rau, J. Phys. Chem. A, 2003, 108, 257–263 CrossRef.
- A. Warshel and E. Huler, Chem. Phys., 1974, 6, 463–468 CrossRef CAS.
- The term “emission spectrum” denoted with Ī(E)dE refers to the actual transition strength and not the experimentally measured photon flux I(E)dE which can be transformed via Ī(E)dE = I(E)dE/E3 (ref. 83).
- T. H. Keil, Phys. Rev., 1965, 140, A601–A617 CrossRef.
- M. de Jong, L. Seijo, A. Meijerink and F. T. Rabouw, Phys. Chem. Chem. Phys., 2015, 17, 16959–16969 RSC.
- In terminology usually reserved for oscillators with the equal potential, this results in a very large Huang–Rhys parameter which corresponds to a primarily population of vibrational states with large quantum numbers.
- F. E. Williams and M. H. Hebb, Phys. Rev., 1951, 84, 1181–1183 CrossRef CAS.
- M. Lax, J. Chem. Phys., 1952, 20, 1752–1760 CrossRef CAS.
- In mathematical terms this states the existence of an injective relation between the vibrational energy of the final state R and the nuclear displacement q ↦ R.
- The reduced mass could in principle be any mass parameter describing the oscillatory motion, e.g. the mass inertia for a torsional rocking mode.
- D. Fujishima, H. Kanno, T. Kinoshita, E. Maruyama, M. Tanaka, M. Shirakawa and K. Shibata, Sol. Energy Mater. Sol. Cells, 2009, 93, 1029–1032 CrossRef CAS.
- S. Grob, M. Gruber, A. N. Bartynski, U. Hörmann, T. Linderl, M. E. Thompson and W. Brütting, Appl. Phys. Lett., 2014, 104, 213304 CrossRef.
- For a vibrational energy of 25 meV the Boltzmann probility to populate the 5th vibrationally excited state is 1.4% at 400 K.
- M. Newville, T. Stensitzki, D. B. Allen and A. Ingargiola, LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python, 2014 DOI:10.5281/zenodo.11813.
- P. Erk, CCDC 112723: Experimental Crystal Structure Determination, 2004.
- I. Bruder, J. Schöneboom, R. Dinnebier, A. Ojala, S. Schäfer, R. Sens, P. Erk and J. Weis, Org. Electron., 2010, 11, 377–387 CrossRef CAS.
- W. Bała, M. Wojdyła, M. Szybowic, M. Drozdowski, A. Grodzicki and P. Piszczek, J. Optoelectron. Adv. Mater., 2009, 11, 264 Search PubMed.
- S. Hammer, T. Ferschke, G. V. Eyb and J. Pflaum, Appl. Phys. Lett., 2019, 115, 263303 CrossRef.
- L. Graf, K. Ortstein, L. P. Doctor, M. Naumann, J. Beyer, J. Heitmann, K. Leo and M. Knupfer, AIP Adv., 2021, 11, 025230 CrossRef CAS.
- S. Feng, Y.-C. Wang, Y. Ke, W. Liang and Y. Zhao, J. Chem. Phys., 2020, 153, 034116 CrossRef CAS.
- S. Feng, Y.-C. Wang, W. Liang and Y. Zhao, Phys. Chem. Chem. Phys., 2022 10.1039/d1cp03600a.
- A. R. J. P. Ubbelohde, I. Woodward and H. H. Dale, Proc. R. Soc. London, Ser. A, 1943, 181, 415–427 CAS.
- T. Siegrist, C. Besnard, S. Haas, M. Schiltz, P. Pattison, D. Chernyshov, B. Batlogg and C. Kloc, Adv. Mater., 2007, 19, 2079–2082 CrossRef CAS.
- S. Haas, B. Batlogg, C. Besnard, M. Schiltz, C. Kloc and T. Siegrist, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 205203 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Cengage Learning, 1st edn, 1976 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press Taylor & Francais Group, Boca Raton, 2014, vol. 95 Search PubMed.
- R. G. D. Valle, E. Venuti, L. Farina, A. Brillante, M. Masino and A. Girlando, J. Phys. Chem. B, 2004, 108, 1822–1826 CrossRef.
- E. Venuti, R. G. D. Valle, L. Farina, A. Brillante, M. Masino and A. Girlando, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104106 CrossRef.
- M. Pinterić, S. Roh, S. Hammer, J. Pflaum, M. Dressel and E. Uykur, J. Mater. Chem. C, 2022 10.1039/D1TC04297A.
- This assumption can be thought of as a deliberate reduction of free parameters by reasonably simplifying the exact physical representation.
- C. Amovilli and N. H. March, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 2846–2849 CrossRef CAS.
- M. Brendel, S. Krause, A. Steindamm, A. K. Topczak, S. Sundarraj, P. Erk, S. Höhla, N. Fruehauf, N. Koch and J. Pflaum, Adv. Funct. Mater., 2015, 25, 1565–1573 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef CAS.
- J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2013, 4, 3316–3318 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Mathematical and computational details of semi-classical and quantum-mechanical model description, further evaluation of peak shifts and spectral asymmetry, details of fit parameters and fit curves for zinc-phthalocyanine excimer emission. See DOI: https://doi.org/10.1039/d2mh00829g |
| ‡ Present address: Center for the Physics of Materials, Department of Physics and Department of Chemistry, McGill University, Montreal, QC H3A 2K6, Canada. |
| This journal is © The Royal Society of Chemistry 2023 |