Influence of oxidation on the magnetism of small Co oxide clusters probed by Stern–Gerlach deflection†
Kobe
De Knijf
 *a,
Johan
van der Tol
a,
Piero
Ferrari
*a,
Johan
van der Tol
a,
Piero
Ferrari
 a,
Sandrien
Scholiers
a,
Gao-Lei
Hou
a,
Sandrien
Scholiers
a,
Gao-Lei
Hou
 b,
Peter
Lievens
b,
Peter
Lievens
 a and
Ewald
Janssens
a and
Ewald
Janssens
 *a
*a
aQuantum Solid-State Physics, Department of Physics and Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium. E-mail: kobe.deknijf@kuleuven.be; ewald.janssens@kuleuven.be
bMOE Key Laboratory for Non-Equilibrium Synthesis and Modulation of Condensed Matter, School of Physics, Xian Jiaotong University, Xi'an, 710049, P. R. China
First published on 30th November 2022
Abstract
We report on the magnetic properties of small neutral suboxide ConOm (n = 5–18 and m = 0–10, m ≤ n) clusters produced by laser vaporisation and gas aggregation. Their magnetism is probed experimentally by means of Stern–Gerlach magnetic deflection. The results imply that the cobalt atoms couple ferromagnetically not only in pure Con clusters, as known from previous investigations, but also in their oxidized counterparts. It was found that the magnetic moment per cobalt atom is mostly enhanced in the oxide clusters with respect to the pure cobalt clusters and generally increases with the oxygen content in the studied composition range. The spin magnetism of selected clusters is also investigated by density functional theory (DFT) calculations. The computations allow to attribute the effect of oxidation on the magnetic response of the ConOm clusters to electron transfer from the cobalt 3d and 4s valence orbitals to oxygen. The cobalt 3d levels preferentially donate electrons of minority spin, but both spin orientations are involved in the transfer of cobalt 4s electrons.
1 Introduction
Transition metal oxides play an important role in a vast variety of valuable applications.1–4 In particular, Co oxides can be used as catalysts,4,5 gas sensors,6 and in the development of magnetic recording media.7 Moreover, Co oxide nanoparticles are candidates to inhibit cancer cell growth8,9 and have great potential as antimicrobial agents.2,8 More specifically, there is a lot of interest in magnetic nanoparticles because they are promising candidates for diverse applications such as drug delivery, tissue engineering, biosensing, magnetic resonance imaging, ultrahigh density data storage, and magneto-electric memory devices.10 Also, clusters with interesting properties could potentially be assembled into larger nanostructured materials.11 Furthermore, in the interest of developing fundamental understanding of the evolution of magnetism with size and composition from single atoms to the bulk, small clusters are ideal test systems.It is well known that the physical and chemical properties of few-atom clusters can be distinctively different from those of their bulk counterparts with possibly even drastic differences between successive sizes.12,13 This is also the case for cobalt oxide clusters which have been the subject of several theoretical and experimental studies examining various properties. Experimentally, efforts were undertaken to investigate them by means of photofragmentation,14,15 photoelectron spectroscopy,16 and infrared vibrational spectroscopy.17 Also the role of cobalt oxide clusters as catalysts18 and their reaction with different gases19 have been studied. However, the magnetism of these clusters in the size range of this work has not yet been probed experimentally. In contrast, several theoretical studies explored the magnetism of cobalt oxide clusters.
A systematic DFT computational study on the magnetic properties of neutral and cationic ConO0,+m clusters (n = 3–8, m = 1–10) was carried out by Aguilera-del-Toro and coworkers.20 In line with multiphoton dissociation experiments, their calculations for the charged species confirmed n = m as the favoured stoichiometry, the loss of O2 as the preferred fragmentation channel, and the particular high stability of Co4O4+. For the latter cluster they found indications that the local spin magnetic moments at the Co sites closely resemble those of metallic Co4 and Co4+, with additional significant contributions of the oxygen atoms to the total spin magnetic moment. Because of the parallel coupling of all local spin magnetic moments in Co4O4+, its total spin magnetic moment is about 30% larger than that of the Co4+ cation. More generally, their DFT calculations predict the series of (CoO)n+ (n = 2–6) clusters to be stabilized by a high spin magnetic moment and that the spin-polarisation of the Co atoms is not quenched by the oxygen. The high stability of the Co4O4+ cation was suggested by Tung et al.21 as well, and photodissociation mass spectrometry also indicated that Co2O2+ and Co4O3+ could be particularly stable. In addition, Zayed et al.22 reported the remarkable structural stability of Co4O0,+4 determined by mass spectrometry, and confirmed by DFT computations for the neutral counterpart.
In another study, Gutsev et al. performed DFT calculations on the geometries, total spin magnetic moments, polarizabilities and binding energies of neutral (FeO)n, (CoO)n, and (NiO)n clusters for n = 1–10. In all cases, they found relatively low spin multiplicities.23 In contrast to the neutral cobalt oxides in ref. 20 with non-vanishing total spin magnetic moments, it was concluded that the total spin magnetic moments of the bare neutral Fen and Con clusters are strongly reduced in their corresponding oxides. Ferromagnetic ordering was only found in the nickel oxides (NiO)n for n = 3, 4, 9, and 10, whereas (FeO)2, (CoO)2, (FeO)4, (CoO)4, (FeO)6, (CoO)6, and (NiO)5 were found to be antiferromagnetic singlets. All other clusters in the (FeO)n and (CoO)n series as well as (NiO)7 and (NiO)8 were identified as being ferrimagnetic.
Recently, Geng et al. reported on a special class of neutral oxygen-passivated metal oxides with a cubic structure and special aromatic stability, termed ‘metalloxocubes’, for which enhanced stabilities of M13O0,±8 (M = Fe, Co or Ni) clusters were observed.24 In particular, the Co13O8 cluster has a prominent abundance in the resultant mass spectrum when neutral cobalt clusters, produced by a laser evaporation source, were allowed to interact with He gas enriched with a large oxygen content. First-principles calculations attributed the stability of this cluster to a perovskite-like body-centered cubic structure and cubic aromaticity from multicenter Co–Co metal–metal bonding. Their computations predict Co13O8 to have a large total spin magnetic moment of about 30 μB in its lowest energy state.
In the following, we present the results obtained by Stern–Gerlach magnetic deflection as well as DFT analysis on the magnetic properties of small ConOm (n = 5–18, m = 0–10) clusters. We start with a description of the methodology and of the applied models to determine the experimental magnetic moments. Because of the importance of the cluster temperature in these models, attention is devoted to asses this temperature before examining the magnetism. Finally, the ferromagnetic coupling between the cobalt atoms and the influence of electron transfer from cobalt to oxygen on the magnetism is discussed.
2 Methodology
2.1 Experimental methodology
A schematic overview of the experimental setup, in more detail described in ref. 25, is provided in the ESI† (see Fig. S1). We used a pulsed (10 Hz) laser ablation source to produce a molecular beam of clusters. The source body is a copper block that has a 3 mm diameter formation channel. The second harmonic (532 nm) of a pulsed Nd-YAG laser (Continuum Minilite II) is directed onto a translating rectangular cobalt target. The resulting evaporated material nucleates and grows into clusters in the formation channel by collisions with the atoms of a carrier gas, introduced by a pulsed supersonic valve (Jordan TOF Products, Inc.) at a backing pressure of 5 bar. A mixture of He and a small amount of oxygen (ca. 0.06 mol%) was used as the carrier gas, leading to the formation of cobalt suboxides, including some pure cobalt clusters. A cryogenic system, consisting of a cold head (Leybold COOLPOWER 10 MD) pneumatically driven by a closed helium circuit from a compressor unit (Leybold COOLPAK 6000 H), provides for the cooling of the source. Hereto, a conducting copper braid serves as the connection between the source and the cold head. The temperature of the formation channel was estimated to be 49 ± 2 K by a sensor on the outside of the source body. However, the actual temperature of the clusters inside the source is more reliably determined from a velocity distribution analysis,26 as will be elaborated further, and was found to be slightly lower: 41 ± 4 K.During their time spent in the source, the clusters are carried towards the nozzle of the formation channel, after which they expand in vacuum. The direction of the molecular beam exiting the source is denoted by x. More downstream, a skimmer removes most of the carrier gas, and the combination of a rotating chopper wheel and pulsed postionisation later in the setup selects clusters within a very narrow velocity range: here 537 ± 4 m s−1, around the mean value (525.9 ± 0.1 m s−1) of the average velocities of all cluster sizes in this study. A highly directional molecular beam for the magnetic deflection experiment is further achieved by means of two slit collimators, each with an opening of 0.45 mm. The collimated beam is then steered through a 2.6 mm opening between the 20 cm long poles of a Rabi type magnet, ensuring a fairly constant magnetic field gradient (about 350 T m−1) along the cluster path. Neutral clusters can be deflected from their straight path by the magnet and the degree of deflection depends on the projection of their magnetic moment along the magnetic field direction. The direction of deflection is denoted by z and is orthogonal to x. About 80 cm after exiting the magnet, the clusters are subject to the aforementioned postionisation by the UV light (157 nm) of an F2 excimer laser (Coherent ExciStar XS). The profile of this excimer laser is elongated along the deflection direction by a cylindrical lens to ensure that deflected clusters are ionized as well, and to prevent multiple photon absorption and fragmentation. The specific laser profile is estimated from a series of atomic yttrium deflection experiments, and is found to be non-uniform. The resulting profile is taken into account to assess the position dependent ionisation efficiency and to reconstruct the deflection profiles of the clusters. Once ionized, the charged clusters are extracted in the y direction, orthogonally to the x–z plane (see ESI,† Fig. S1), into a reflectron time-of-flight mass spectrometer with a position sensitive microchannel plate delay line detector (surface concept GmbH) that is able to record simultaneously the position and arrival time of each cluster.
2.2 Computational methodology
DFT calculations on selected cobalt oxide clusters, Co6Om (m = 0, 4, 5, 6) and Co7Om (m = 0, 3, 4, 5), were conducted using the ORCA 5.0 software package.27 The hybrid PBE0 functional28 was employed, in conjunction with the def2-TZVP basis set.29 Tight convergency criteria were used for the self-consistent field27 and geometry optimisation cycles. The structures of neutral cobalt clusters, Con, were investigated earlier by a combination of IR-UV two-colour vibrational spectroscopy and DFT calculations.30 The geometries of Co6 and Co7 were taken from this work and reoptimized at the PBE0/def2-TZVP level for different multiplicities. Initial geometries of the cobalt oxide clusters were taken from the computational work of ref. 20 and reoptimized at the same level of theory. Additional possible structural isomers were generated from scratch by randomly positioning the different atoms and geometry optimisation, but no configurations of lower energy were found than the ones in ref. 20. In all cases, different spin multiplicities were considered. Bader partial electron charges and Wiberg bond indices were calculated using the Multiwfn software,31 whereas the natural population analysis (NPA) scheme was used to compute partial atomic charges and spin densities with the NBO software.322.3 Interpretation of the magnetic deflection profiles
In a Stern–Gerlach experiment, a beam of atoms splits in 2J + 1 beamlets.33 Here, J is the total electronic angular momentum quantum number. By applying this well established behaviour to atomic yttrium deflections, the magnetic field gradient, δzB, was determined. The latter is needed to determine the relation between the z-component of the magnetic moment, μz, and the deflection, d, of a particle in the experimental setup. By applying the expression for the force on a magnetic dipole in a magnetic field34 to a cluster in the setup, it is found that: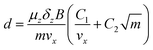 | (1) |
| = cmμz, | (2) |
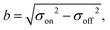 | (3) |
In contrast to atoms and apart from the trivial case of being non-magnetic, the response of a cluster to a magnetic field can manifest itself in a variety of observed deflection profiles. In the following, we will discuss two models able to describe the responses of the studied clusters. It is also worth mentioning that for specific clusters with one magnetic atom in a non-magnetic host an atom-like behaviour has been observed,35 giving rise to discrete or overlapping beamlets, and combinations of all described responses are possible as well.36
On the one hand, spin-rotation coupling can destroy spin quantisation through avoided crossings.36,37 The avoided-crossing model (ACM) proposes an explanation for the most frequently observed case of a single sided deflection (SSD) towards the high field pole, resulting from the ability of the magnetic moment to rotate in the field direction. The description also holds at low temperatures where traditional vibrational behaviour no longer applies. This model ascribes single sided deflections to different energy levels in the rotation-Zeeman diagram developing more uniform slopes with increasing magnetic fields. The negative of the slope corresponds to μz = −δE/δB associated with an energy level with energy E in a magnetic field B. Thermal population of energy levels with slightly different slopes in the rotation-Zeeman diagram can cause an accompanied broadening of the deflection profile. Another possible cause of broadening is the variation in sensed magnetic fields as discussed further below. For low μzB but sufficiently high magnetic fields for the energy level slopes to reach the linearly decreasing regime in the rotation-Zeeman diagram, it is found that the magnetisation can be approximated by the Curie law:37
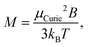 | (4) |
On the other hand, magnetic anisotropy can cause the magnetic moment to be strongly locked to the geometry of the cluster. In this case the magnetic moment rotates with the cluster as a whole and the magnetic field only broadens the beam profile without net deflection. In terms of the ACM, this behaviour could be treated as a case where some, but not all, crossings are avoided. Although in principle the avoided-crossing model is a suitable theory to interpret the complex nature of any deflection profile, we lack the information to properly construct the rotation-Zeeman diagram. Because of this, we quantify this response using the adiabatic rigid rotor model (ARRM),38–40 treating the clusters as a canonical ensemble of rigid spherical rotors at a rotational temperature Trot. In this model, the magnitude of the magnetic moment, μ, can be estimated for weak magnetic fields, i.e. μB ≪ kBTrot, as follows. The distribution of μz is given by:
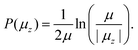 | (5) |
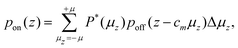 | (6) |
3 Results
3.1 Mass spectrum
The cluster source produces a distribution of clusters of different sizes and compositions, allowing the determination of magnetic properties for different species simultaneously under the same experimental conditions. However, because of mass overlap between different compositions, not all sizes can be readily identified. Here, we studied ConOm (n = 5–18) clusters in the 280–1200 u range (Fig. 1). The production conditions were optimized to have the highest intensities for cobalt suboxides, i.e. m ≤ n, where m = 0–10. Two datasets were measured with different oxygen to cobalt ratios in the source. All other experimental conditions were the same. The dataset for the series with n = 5–10 was obtained for a relative lower oxygen content than the dataset for the series with n = 11–18.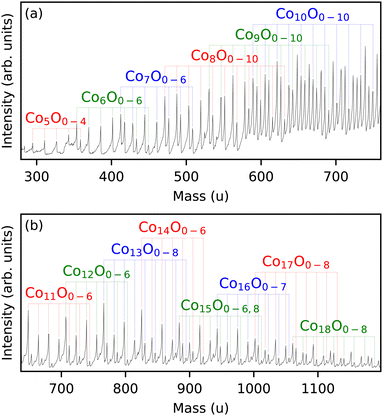 | ||
| Fig. 1 Mass spectrum of the ConOm clusters in (a) the 280–750 u and (b) 650–1200 u ranges. The identified clusters are labelled. | ||
Care was taken in the identification process by ensuring no or minimal estimated overlap in the mass spectrum with neighbouring sizes. Knowing that the mass difference between Co3 and O11 is slightly less than 1 u, overlap can arise between ConOm and Con−3Om+11. For all identified sizes in Fig. 1, minimal estimated overlap was guaranteed by considering only those n values for which the average integrated intensity of Con−3O8,9,10 is only a small percentage of the one of ConO0,1. This assures that the Con−3Om clusters with m ≥ 11 don't significantly contaminate the ConOmm ≤ 10 intensities. For n = 5–9 this overlap is zero, for n = 10–18 it is less than about 15%.
3.2 Velocity distributions and temperature
To study the evolution of magnetism as a function of stoichiometry, a properly thermalized source is required. Hereto we measured the velocity distributions26 prior to the actual deflection experiment. Intensity distributions are measured by selecting different chopper wheel and postionisation timings and hence transmitted velocities. Examples of velocity distributions are shown in Fig. 2a and b. As described in ref. 26, such a distribution f(vx) can be modelled by: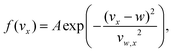 | (7) |
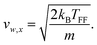 | (8) |
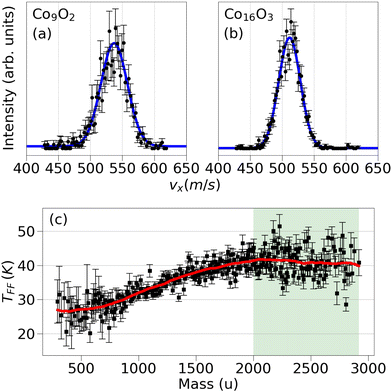 | ||
| Fig. 2 Velocity distributions of (a) Co9O2 and (b) Co16O3. The blue curve corresponds to the fit function of eqn (7) (apart from a constant noise level). Clearly, most clusters of the smaller mass move faster than the ones of the heavier mass with the distributions of Co9O2 and Co16O3 displaying maxima at 537 ± 1 m s−1 and 511.6 ± 0.3 m s−1, respectively. (c) Translational temperatures in free flight as a function of cluster mass. The shaded region corresponds to clusters with a TFF converging to the source temperature. The red curve is a guide to the eye. | ||
3.3 Magnetism
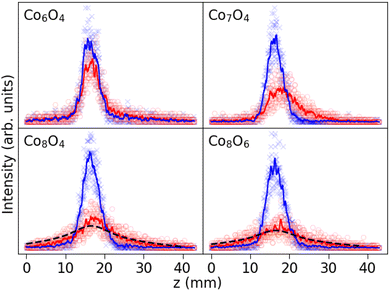
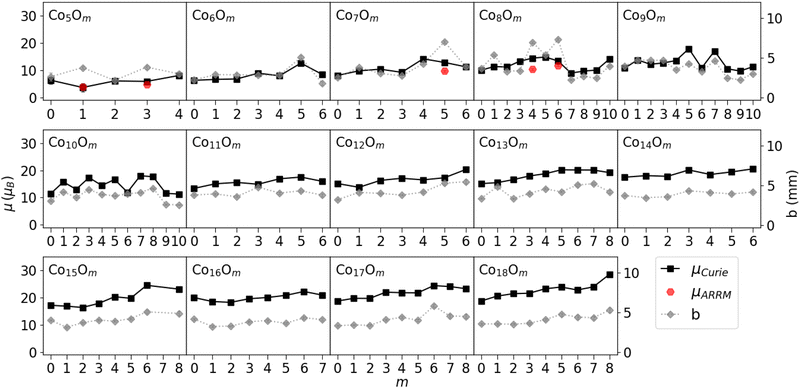
A selection of measured beam profiles is shown in Fig. 3. Beam profiles of all studied ConOm clusters are available in the ESI† Fig. S3–S5. Most beam profiles in our experiment display an SSD, although five clusters show signs of locked moment behaviour, i.e. Co5O1, Co5O3, Co7O5, Co8O4, and Co8O6. The measured magnetic moments obtained by means of the Curie law and ARRM are presented in Fig. 4, together with the broadenings computed according to eqn (3). When discussing tendencies involving μCurie, systematic uncertainties are left out. Systematic uncertainties originate from uncertainties in the determination of the magnetic field, the temperature of the clusters inside the source, atomic deflection calibration parameters and setup constants. Non-systematic uncertainties arise only from the discrete Poisson-distributed counts on the position channels of the detector. Systematic uncertainties on μCurie are for most clusters in the range of 1–2 μB. This value does not incorporate the model uncertainty on the use of the Curie law, which as discussed below is the largest unknown.It is important to recognize that the application of both the Curie law and ARRM has some restrictions. On the one hand, asymetric broadenings in the deflected beam profiles normally occur if the ARRM weak field condition is not satisfied, an effect that becomes stronger with increasing magnetic fields.39,40 In the present study, the set of clusters showing ARRM behaviour display a vanishingly small to noticeable deflection towards the high field pole, while strictly speaking no net deflection is expected. Because all ARRM deflection profiles are reasonably well symmetric, we consider the above procedure to extract the ARRM magnetic moments by the application of eqn (6) still reliable. On the other hand, while the ACM is appropriate for all cluster sizes and temperature regimes, the applicability of the Curie law emerging from the model is not straightforward. It is more appropriate to examine the variation of magnetism with cluster stoichiometry, rather than the absolute values of the magnetic moments. Secondly, the avoided-crossing model was derived for ferromagnetic pure cobalt clusters ignoring the orbital contribution to the magnetism.37 Orbital quenching is a good approximation for bulk first row transition metals41 and for bulk cobalt, the latter having an orbital magnetic moment per atom μL that is only about 10% of its spin magnetic moment per atom μS.42,43 In contrast, X-ray magnetic circular dichroism (XMCD) studies of singly-ionized Con+ clusters reveal that, for the size range of the experiment, the orbital contribution to the magnetic moment per atom is significant, but generally diminishes with increasing cluster size.44,45 These studies quote μL/μS ratios from about 60% for n = 5 to about 25% for n = 17. To our knowledge, no results have been reported about the orbital contributions in the corresponding cobalt oxide clusters. Furthermore, an adequate estimation of the temperature that should be used in the Curie law is challenging. The total magnetic moments determined by means of the Curie law in Fig. 4 are calculated for the case the population of all energy levels is stagnant upon exiting the source. Because we have a well thermalized source, as explained above, this is equivalent of using the source temperature as the relevant temperature. In reality though, the relevant temperature in the Curie law might be subject to cooling effects, meaning that the obtained values for μCurie are upper limits.
From Fig. 4, some conclusions can be drawn. (1) With increasing number of cobalt atoms, the clusters become more magnetic. This is in line with the ferromagnetic nature of macroscopic Co and pure Co clusters.37,41,46 (2) Overall there is also a tendency of increasing magnetic moment with increasing number of oxygen atoms. For the smaller ConOm clusters with n = 5–10, μCurie displays fluctuations as a function of m, but the increasing trend is noticeable for n = 5–8. A clear odd-even staggering is present in the Co9Om (m = 4–8) and Co10Om (m = 0–7) series with higher magnetic moments for clusters with an odd number of oxygen atoms. For n = 11–18 the magnetic moment increases almost monotonically with the number of oxygen atoms. (3) For most clusters, the broadening is in the range from 2.0 to 5.5 mm, except in 3 noticeable cases: Co7O5, Co8O4, and Co8O6, whose deflection profiles are classified as rigid rotor behaviour. All broadenings are significantly greater than zero, which implies a magnetic response of all studied clusters. There is no clear increase in broadening with n as is the case for the magnetic moment, although on average the broadenings are relatively lower in the Co5,6Om series as compared to the rest. Mostly the broadening for all series in Fig. 4 closely resembles the trends in μCurie as a function of m. Remarkable exceptions are the clusters with identified ARRM response, which have a broader deflection profile than the neighbouring clusters. (4) Despite the limitations in applicability, discussed in the previous paragraph, the Curie law and ARRM yield similar magnetic moment values. Because of the different ways these magnetic moments were obtained, this correspondence is reassuring for both methods to deduce the presented values. Moreover, in all rigid rotor cases μCurie ≳ μARRM, which is consistent with the idea that the calculated μCurie values provide an upper limit. Observations (1) and (2) will be explored in more detail in the discussion section, taking also into account the results of the DFT calculations.
The investigated species include the Co13O8 system, which was reported to have a special stability and a high magnetic moment by Geng et al.24 We found no particularly high intensity for this cluster in the mass spectrum, nor an enhanced magnetic moment compared to other members of the Co13Om series. The total effective magnetic moment of Co13O8, calculated by means of the Curie law, is 19 ± 2 μB, about 65% of the effective total spin magnetic moment (about 29 μB) computed by Geng et al.24
3.4 DFT calculations
In order to get a more qualitative insight into the mechanism that is responsible of producing the observed trends in magnetic moment, especially the increasing magnetism with the addition of oxygen, we investigated the Co6Om (m = 0, 4, 5, 6) and Co7Om (m = 0, 3, 4, 5) series computationally. These size ranges were chosen because the experiments revealed a strong oxygen concentration dependence with a local maximum in μ at m = 5 and 4 for the Co6Om and Co7Om series, respectively. We must emphasize that the DFT calculations presented here only take into account the spin contribution to the magnetic moment, in addition to the intrinsic assumption that the wavefunctions of the clusters can be described by a single configuration.47 Experimentally, though, total magnetic moments, estimated by μCurie and μARRM, are obtained that cannot be decomposed into spin and orbital parts.The strong interaction between cobalt and oxygen, also known from previous studies,15 shows up in different properties of the clusters. First, the lowest energy structures of all calculated clusters (presented in Fig. 5) have a large number of Co–O bonds. More specifically, in the case of Co6Om, it was found that the oxygen atoms adopt positions with a high Co coordination. Geometries where two oxygens coordinate directly are not stable. For the Co7Om series, the lowest energy geometries of the clusters show that all oxygen atoms adopt threefold Co-coordinated sites. Second, the density of states of the calculated Co6 oxides (see ESI,† Fig. S2) reveals that the cobalt d-states strongly hybridize with the oxygen valence states. Third, Wiberg bond indices, measuring the average number of electron pairs (i.e. ‘bonds') shared by two atoms, indicate a strong Co–O interaction. The calculated values for both series can be found in ESI,† Tables S2 and S4. Although there is notable spread on the calculated bond indices, some general characteristics are observed. With the exception of one cobalt atom in Co7O3, all other cobalt atoms are bound to oxygen. On average, the Wiberg bond indices for Co–O bonds lie between 0.7 and 0.8 for Co6Om, and between 0.8 and 0.9 for Co7Om, reflecting the formation of single bonds. In general, the pairs of adjacent Co atoms have Wiberg bond indices around 0.56 for Co6, but those values decrease to 0.26, 0.23, and 0.33 for Co6Om with m = 4, 5, and 6 respectively. In the case of Co7Om, these Co–Co indices also decrease on average from 0.41 for pure Co7, to 0.30, 0.27, and 0.24 for m = 3, 4, and 5 respectively. Solely for three Co–Co pairs in Co7O3, of which only one cobalt atom is bound to oxygen, the Co–Co index increases to 0.60. In general, the Wiberg bond indices indicate that oxygen interacts more strongly with Co in comparison with the interaction between Co pairs and also weakens the cobalt–cobalt interaction. Also they suggest that metal–metal bonds survive in the oxidized clusters and this could be an important reason for why the magnetism survives in the studied clusters.
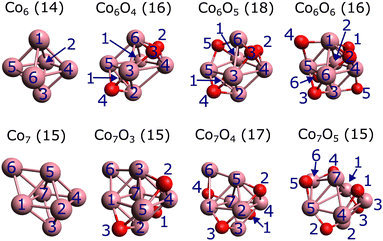 | ||
| Fig. 5 Lowest-energy geometries of the Co6Om (m = 0, 4, 5, 6) and Co7Om (m = 0, 3, 4, 5) clusters, calculated at the PBE0/def2-TZVP level. The associated computed total spin magnetic moments μs in Bohr magnetons are shown in parenthesis. The labels of the cobalt (purple) and oxygen (red) atoms correspond to the designations in Tables 1 and 2, and in the ESI,† Tables S1–S4. | ||
Partial charge analysis reveals a major charge redistribution in the clusters due to the presence of oxygen. Partial charges in a molecular system depend to a large extent on the method employed to define such a partial charge, because partial charge is not a quantum observable. Here, three methods were employed in order to corroborate the consistency of results, namely the Löwdin, NPA, and Bader schemes. The partial electron charges for all calculated Co6,7Om clusters according to the three schemes can be found in the ESI,† (Tables S1 and S3). Qualitatively, similar results are obtained for all schemes. All three methods indicate that oxygen accepts electrons from cobalt. This can for example be inferred from Table 1 showing the local partial electron charges for the Co6,7Om clusters using the Bader scheme. Although, on average, the Bader and Löwdin scheme for Co6Om predicts the largest transfer for the m = 5 cluster, which was experimentally found to possess the largest magnetic moment in the m = 0–6 series, the general trend for Co6Om and Co7Om is an increasing amount of charge transfer for increasing oxygen content.
| Co6 | Co6O4 | Co6O5 | Co6O6 | Co7 | Co7O3 | Co7O4 | Co7O5 | |
|---|---|---|---|---|---|---|---|---|
| Co(1) | −0.01 | 0.83 | 1.22 | 1.01 | 0.01 | 0.40 | 0.76 | 0.77 |
| Co(2) | 0.01 | 0.84 | 0.77 | 0.84 | −0.01 | 0.69 | 0.73 | 0.75 |
| Co(3) | −0.01 | 0.83 | 0.88 | 1.05 | −0.00 | 0.46 | 0.70 | 0.84 |
| Co(4) | 0.00 | 0.91 | 0.76 | 0.98 | −0.01 | 0.82 | 0.79 | 0.71 |
| Co(5) | 0.00 | 0.66 | 1.21 | 0.96 | −0.02 | 0.71 | 0.53 | 0.77 |
| Co(6) | 0.01 | 0.65 | 1.21 | 0.87 | 0.02 | 0.49 | 0.34 | 0.85 |
| Co(7) | — | — | — | — | 0.02 | −0.11 | 0.86 | 1.15 |
| O(1) | — | −1.18 | −1.21 | −0.96 | — | −1.15 | −1.17 | −1.19 |
| O(2) | — | −1.18 | −1.21 | −0.96 | — | −1.16 | −1.17 | −1.18 |
| O(3) | — | −1.18 | −1.20 | −1.00 | — | −1.17 | −1.16 | −1.18 |
| O(4) | — | −1.18 | −1.21 | −0.99 | — | — | −1.20 | −1.16 |
| O(5) | — | — | −1.22 | −0.92 | — | — | — | −1.13 |
| O(6) | — | — | — | −0.89 | — | — | — | — |
The calculated total spin magnetic moment μs for the lowest energy configuration of Co6 is 14 μB, a value that increases to 16 μB for Co6O4 and to 18 μB for Co6O5. For Co6O6, it decreases to 16 μB. In the Co7Om series, the obtained values are 15, 15, 17, and 15 μB, for Co7, Co7O3, Co7O4, and Co7O5, respectively. Qualitatively, all these trends are consistent with the experimental observations.
Fig. 6 compares the computed spin magnetic moments in this work with the ones from a previous study of Aguilera-del-Toro et al.20 The experimental magnetic moments are also included to qualitatively compare the calculated and measured trends as a function of oxygen content. Quantitative comparison between the computed and experimental values is not appropriate because of the different contributions to the concerned magnetic moments. There is a good correspondence between our calculated spin magnetic moments and the ones from ref. 20. In particular, both calculations predict Co6O5 to have a slightly larger spin magnetic moment than its immediate neighbours, with the values in this work to be consistently 2 μB larger than the ones obtained by Aguilera-del-Toro et al.20 For the Co7Om series, apart from m = 4, the exact same values are obtained in our work and ref. 20. In general, the experimental magnetic moments are significantly smaller than the predicted ones. Overall though, the theoretically obtained trends agree well with the progression of μCurie for growing m, except for Co7Om≥4 and Co8Om≥6.
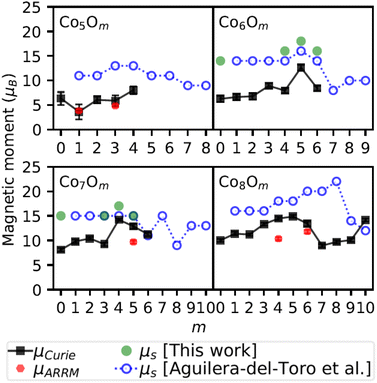 | ||
| Fig. 6 Comparison between the experimental effective total magnetic moments μCurie and μARRM, and the calculated total spin magnetic moments, 2SμB, with S the total spin quantum number, obtained in this work and by Aguilera-del-Toro et al.20 for the lowest energy structures of the neutral ConOm clusters in the range n = 5–8. All magnetic moment values are in Bohr magnetons. Systematic uncertainties on μCurie are not included in the error bars. | ||
In order to explore the agreement between the experimental results and our calculations further, natural electron configurations per atom were computed using the natural orbital decomposition. The results can be retrieved from the ESI,† Tables S5–S12. From these natural electron configurations, local spin magnetic moments were derived. Table 2 lists the calculated μs values per atom for the Co6,7Om series, that will be discussed below.
| Co6 | Co6O4 | Co6O5 | Co6O6 | Co7 | Co7O3 | Co7O4 | Co7O5 | |
|---|---|---|---|---|---|---|---|---|
| Co(1) | 2.33 | 2.27 | 2.65 | 2.55 | 2.05 | 1.94 | 2.11 | 2.14 |
| Co(2) | 2.34 | 2.25 | 2.90 | 2.53 | 2.16 | 2.07 | 2.11 | 2.10 |
| Co(3) | 2.33 | 2.27 | 2.35 | 2.57 | 2.46 | 2.05 | 2.07 | 2.29 |
| Co(4) | 2.34 | 2.34 | 2.92 | 1.17 | 2.20 | 2.26 | 2.21 | 2.07 |
| Co(5) | 2.34 | 2.78 | 2.66 | 2.51 | 2.10 | 2.07 | 2.52 | 2.15 |
| Co(6) | 2.34 | 2.77 | 2.63 | 2.51 | 1.97 | 2.08 | 2.60 | 0.70 |
| Co(7) | — | — | — | — | 2.06 | 1.82 | 2.25 | 2.53 |
| O(1) | — | 0.34 | 0.42 | 0.25 | — | 0.28 | 0.25 | 0.23 |
| O(2) | — | 0.32 | 0.42 | 0.30 | — | 0.22 | 0.24 | 0.26 |
| O(3) | — | 0.32 | 0.35 | 0.41 | — | 0.22 | 0.29 | 0.22 |
| O(4) | — | 0.34 | 0.33 | 0.39 | — | — | 0.33 | 0.11 |
| O(5) | — | — | 0.37 | 0.56 | — | — | — | 0.18 |
| O(6) | — | — | — | 0.25 | — | — | — | — |
4 Discussion
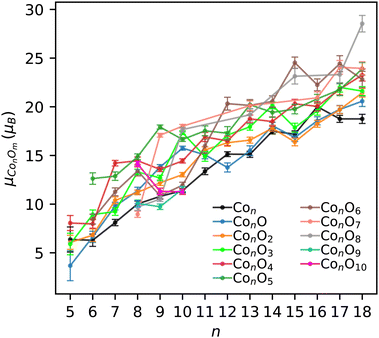
An indication of the ferromagnetic nature of the ConOm clusters was already provided in Fig. 4. This aspect can be inferred further from Fig. 7, showing the experimental total magnetic moments of all ConOm clusters as a function of the number of cobalt atoms n. The m = 9 and 10 series only contain three points, which is too little to observe a distinctive trend. All other fixed-m series display a clear tendency of increasing magnetic moments with growing n. This trend implies a ferromagnetic coupling between the cobalt atoms, both in the pure and oxidized cobalt clusters. This is consistent with the ferromagnetic nature of pure Con clusters reported in ref. 37, 46, 48–50.Before investigating the experimental data in more detail, it is instructive to first elaborate on the computational results of the natural orbital decomposition for the eight selected Co6,7Om clusters. These findings will then be used to provide further insight in the interpretation of the measured magnetic moments. Outcomes of this DFT analysis are presented in Fig. 8 for Co6O4 and Co7O4. Population analysis revealed that in both the pure and oxidized Co6,7Om clusters, the local cobalt magnetic moments are mainly caused by the 3d electrons. There is a smaller contribution of the 4s electrons that can be either parallel or antiparallel with respect to the 3d levels. On average, the 4s spin moments contribute about 4% to the local cobalt magnetic moment, but there are some atoms where the 4s electrons contribute between 0.1 and 0.3 μB. The net cobalt 4s magnetic moment, also found to be either positive or negative, was determined to be on average 3% of the total cluster's magnetic moment. The electronic ground state configuration of the free cobalt atom is [Ar]3d74s2. Following Hunds rules, there are three unpaired electrons in the 3d subshell. In general, the cobalt atoms in the computationally investigated clusters have a decreased spin magnetic moment in comparison with the corresponding value of 3 μB of the free cobalt atom.
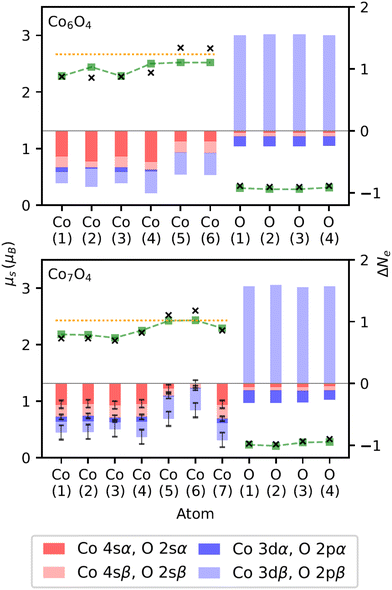 | ||
| Fig. 8 Magnetic and orbital characteristics for each atom (labeled according to Fig. 5) in Co6O4 and Co7O4, resulting from the natural orbital decomposition. The black crosses are the total spin magnetic moments, μs, of the respective atoms (left scale). The green dashed curves depict the local μs values obtained by only taking into account the cobalt 3d electrons and oxygen 2p electrons for the cobalt and oxygen atoms, respectively. Marked by the orange dotted line is the value of the average μs per cobalt atom, calculated as the total spin magnetic moment of the cluster divided by the number of cobalt atoms. The red and blue bars visualize the change in the number of electrons per orbital type and spin orientation (see legend) upon oxidation. Each population change, ΔNe, represents a decreasing (negative) or increasing (positive) number of electrons with respect to the corresponding reference (see text). The height of each bar in the stack corresponds with the actual ΔNe value (right scale). Uncertainties on ΔNe (see text) smaller than 0.01 are not shown for better viewing. | ||
The local spin magnetic moments of the oxygen atoms are nearly entirely due to the 2p orbitals. In all computationally investigated clusters, the oxygen spin magnetic moments are much lower than the corresponding value of 2.0 μB of the free oxygen atom. From the calculated μs values for the selected Co6,7Om clusters with m > 0 (see Table 2), it was derived that the mean spin magnetic moment per oxygen atom is about 13% of the mean spin magnetic moment per cobalt atom. With respect to the entire cluster, the net contribution of oxygen to the total magnetic moment is found to be 6% on average. These numbers suggest a non-negligible, but rather small contribution of oxygen to the value of the total spin magnetic moment, μs,tot, of the examined clusters. Consequently, with n representing the number of cobalt atoms in a cluster, the value of μs,tot/n, portrayed by the orange dotted line in Fig. 8, in general gives a good first order estimation of the local cobalt magnetic moments.
In agreement with the experimental findings, all local cobalt spin magnetic moments align parallel, implying a ferromagnetic coupling between them both in the pure and oxidized clusters. Also the spin magnetic moments of all oxygen atoms are oriented parallel with those of the cobalt atoms.
Apart from two exceptions, the DFT calculations indicate that the cobalt atoms in the investigated clusters populate their 3d orbitals analogously to Hund's first rule, with about 5 electrons of α-spin in all cobalt 3d orbitals. We will refer to this observation of maximizing the 3d spin in the discussion of the experimental results. As evidenced by the previous discussion of the local cobalt magnetic moments, there are more 3d electrons of β-spin for the cobalt atoms in the clusters than in the free cobalt atom. On the contrary, the occupation of the cobalt 4s orbitals in all clusters is lower than in the free cobalt atom for both spin orientations.
We also examined the effect of oxidation on the population of the cobalt 4s and 3d orbitals, and the oxygen 2s and 2p orbitals of the selected Co6,7Om clusters. Hereto, we calculated the population changes, ΔNe, for these orbitals upon oxidation, where Ne denotes the number of electrons of one particular spin in one particular orbital type. The results are presented in Fig. 8. For every cobalt or oxygen atom in the oxidized ConOm clusters, each ΔNe resembles the difference in Ne for that atom with respect to the corresponding value averaged over all cobalt atoms in the associated pure Con cluster or for the free oxygen atom, respectively. While there is almost no variation in local Ne values of the 4s and 3d orbitals for both spin orientations over the constituent cobalt atoms in Co6, there is notable spread on the average Ne values of Co 4sα, Co 4sβ, and Co 3dβ in the case of Co7. This spread is the cause of the error bars in Fig. 8. In general upon oxidation, a decreasing Ne is noticed for the cobalt atoms in the oxidized clusters for 4s electrons of both spin orientations and also for 3d electrons of β-spin. The amount of 3d electrons of α-spin remains almost unchanged. With respect to the free oxygen atom, we see a large increase in oxygen 2p electrons of β-spin, but a similar number of oxygen 2p electrons of α-spin and oxygen 2s electrons of both spin orientations.
The analysis of the population changes not only shows that there is charge transfer from cobalt to oxygen upon oxidation, but also suggests that this transfer arises from the cobalt 3d and 4s valence orbitals to oxygen 2p β orbitals. While cobalt 4s electrons of both spin orientations are involved in the transfer, the electron donation from the cobalt 3d states emanates mainly from the β orbitals. These transfers determine the magnetic response of an oxidized cluster. We will further interpret the influence of oxygen on the magnetism of the experimentally studied clusters, by adhering to this mechanism arising from the DFT calculations.
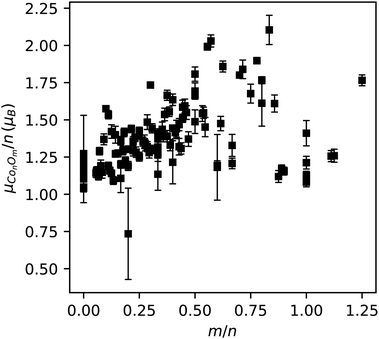
The experimental magnetic moments per number of cobalt atoms in a cluster, μConOm/n, are presented in Fig. 9 as a function of the oxygen-to-cobalt ratio m/n. Because of potential non-vanishing oxygen magnetic moments, the quantities μConOm/n do not correspond directly to the average magnetic moment of a cobalt atom in the clusters (except for pure Con), but since the contribution of the oxygen atoms is rather small (cf. DFT calculations), μConOm/n can be interpreted as a first order approximation of the local cobalt magnetic moments. Consequently, the data in Fig. 9 indicates that the magnetic moment per cobalt atom is enhanced for most oxide clusters with respect to the pure cobalt clusters and also grows larger with increasing m/n. However, it seems that a turning point arises around m/n ≈ 0.75, where the magnetic moment per cobalt atom tends to decrease as more oxygen is added. The experimental magnetic moments per cobalt atom of the eight computationally investigated clusters are all smaller than the corresponding mean spin magnetic moments per cobalt atom from the DFT calculations, on the average by an amount of 0.7 μB.
For the metallic Con clusters, the measured magnetic moments per cobalt atom range from 1.0 ± 0.1 μB for Co18 up to 1.3 ± 0.3 μB for Co5. These values are significantly lower than the ones reported by other deflection48,51 and theoretical52,53 studies. Also, in contrast to these studies our values lie below the bulk value of 1.7 μB.46,49,51 But it should be noted that the results of these studies do not agree well. The most probable explanation for the differences in magnetic moments derived from the deflection studies of Knickelbein48 and Xu et al.,51 but also for the differences between these two studies and this study, is likely to be the difficulty in determining the relevant temperature and precise magnetic field in the approximative Curie law. An accurate assessment of the magnetic field can indeed be complicated in practice by large applied gradients, as in this study.
To explore the data in Fig. 9 in more detail, we will only take the spin contribution to the magnetic moment into account. Furthermore, the DFT calculations imply that the cobalt 4s electrons play a minor role in the magnetism of the investigated clusters. Therefore, it is also useful to regard μConOm/n as a first order approximation of the magnetic moment per cobalt atom caused only by the 3d electrons, the actual values of which are estimated to lie within an extra uncertainty interval of 0.2 μB on top of the error bars in Fig. 9. We arrived at this typical additional uncertainty by considering characteristic values for the contributions of the oxygen atoms and the cobalt 4s electrons from the DFT calculations. As put forward by the DFT calculations, we will further assume that the cobalt 3d orbitals are filled by maximizing the total electron spin.
Because a single electron contributes one Bohr magneton to the total spin magnetic moment, the interpretation of Fig. 9 suggests that pure cobalt clusters have an increased 3d occupancy with respect to the free cobalt atom. Whereas the latter has 3 unpaired 3d electrons giving rise to a spin magnetic moment of 3 μB, all measured Con clusters must have less unpaired electrons in the 3d levels (corresponding to an increased 3d occupancy), in a range slightly more than one.
The initial rise in local cobalt magnetic moments with increasing oxygen-to-cobalt ratios can be explained as oxygen taking away β spin electrons from the cobalt 3d orbitals. Around the turning point, each cobalt atom has a maximal magnetic moment of about 2 μB, indicating that oxygen was not able to take away all 3d β spin as the latter would give the cobalt atoms a magnetic moment of 5 μB. Even if we incorporate a maximal uncertainty on the interpreted cobalt 3d magnetic moments of Fig. 9, estimated to be 1 μB on the values, the data suggests that the occupation of the cobalt 3d levels is never less than for the free cobalt atom. This is in full agreement with the findings of the DFT calculations. As a rough estimate, the oxidation process is able to maximally increase the magnetic moments of the cobalt atoms by about 1 Bohr magneton. As such, maximally about n 3d electrons are donated from the cobalt to m oxygen atoms, on average leading to a maximal transfer of n/m = 1/0.75 ≈ 1.3 3d electrons to each oxygen atom.
Different types of interaction for different sizes and compositions could explain the large scattering around m/n = 0.75. Because of this, we can only speculate about the behaviour at oxygen-to-cobalt ratios higher than 0.75, where the magnetic moments appear to reduce. In line with our reasoning, the only possibility for this decline is a diminishing charge transfer of 3d β electrons from the cobalt to oxygen, leaving the cobalt atoms with less unpaired electrons in the 3d orbitals.
We also investigated the effect of oxygen on the local cobalt magnetic moments by considering a non-vanishing oxygen contribution. Hereto we estimated the average magnetic moment per oxygen atom to be 13% of the average magnetic moment per cobalt atom for all clusters, a percentage taken from the DFT calculations. For this situation, we obtain a very similar behaviour as the one in Fig. 9 with slightly lower magnetic moments per cobalt atom, reinforcing the evidence for the increase of the local cobalt magnetic moments with relative oxygen composition.
Similar conclusions could also be drawn for small Co oxide cations ConOm+ (n = 2, 3 and 1 ≤ m ≤ 4) that were studied in ref. 54. The DFT calculations in that work also revealed an increase in the total spin magnetic moment of the Co oxide clusters as the oxygen content grows, due to an increasing number of unpaired electrons in the 3d4s shell of the cobalt atoms accompanied with the donation of electrons to atomic oxygen bonds by a cobalt atom.
5 Conclusions
A Stern–Gerlach magnetic deflection experiment has been conducted on neutral gas phase ConOm (n = 5–18 and m = 0–10) clusters, produced by laser ablation and gas aggregation. In addition, DFT calculations of structural, electronic, and magnetic properties have been performed for a selection of Co6,7Om clusters.Experimentally, we found evidence for ferromagnetic coupling between the cobalt atoms both in the pure cobalt clusters and in their oxidized counterparts, with oxygen reinforcing the ferromagnetic coupling between the cobalt atoms. The magnetic moment per cobalt atom in the oxidized clusters is, for most clusters, enhanced with respect to the pure cobalt clusters and largely displays an increasing tendency with growing relative oxygen content.
The DFT calculations confirm the ferromagnetic coupling between the cobalt atoms in the pure and oxidized cobalt clusters. In addition, the small spin magnetic moments on the oxygen atoms were found to align parallel with Co in all calculated clusters. The computations demonstrate an increased 3d level population per cobalt atom with respect to the free cobalt atom for all investigated clusters. This is consistent with the discussion of the experimental results. We found a qualitative agreement between the trends of the predicted and measured total cluster magnetic moments, although they do not agree quantitatively.
The following mechanism was proposed to explain the magnetism of the studied clusters. Both in the pure and oxidized cobalt clusters the magnetic response is mainly determined by the cobalt 3d electrons, and to a much lesser extent by the cobalt 4s and oxygen 2p orbitals. Upon oxidation, there is electron transfer from the 3d and 4s valence states of the cobalt atoms to oxygen. The cobalt 3d orbitals donate mainly electrons of minority spin, but there is no spin preference towards emptying the cobalt 4s states. The different occupations of the energy levels taking part in this transfer cause the size-to-size variations in cluster magnetic moments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by the Research Foundation Flanders (project G0A0519N) and by the KU Leuven Research Council (C14/18/073 and C14/22/103). P. F. acknowledges the FWO for a Senior postdoctoral grant. The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the FWO and the Flemish Government.References
- F. Hasannezhad, L. Naji and M. Arvand, Mater. Sci. Semicond. Process., 2022, 139, 106333 CrossRef CAS.
- A. Raghunath and E. Perumal, Int. J. Antimicrob. Agents, 2017, 49, 137–152 CrossRef CAS PubMed.
- K. Kalantar-zadeh, J. Z. Ou, T. Daeneke, A. Mitchell, T. Sasaki and M. S. Fuhrer, Appl. Mater. Today, 2016, 5, 73–89 CrossRef.
- H. Osgood, S. V. Devaguptapu, H. Xu, J. Cho and G. Wu, Nano Today, 2016, 11, 601–625 CrossRef CAS.
- S. Lee, A. Halder, G. A. Ferguson, S. Seifert, R. E. Winans, D. Teschner, R. Schlögl, V. Papaefthimiou, J. Greeley, L. A. Curtiss and S. Vajda, Nat. Commun., 2019, 10, 954 CrossRef PubMed.
- J. Park, X. Shen and G. Wang, Sens. Actuators, B, 2009, 136, 494–498 CrossRef CAS.
- V. Skumryev, S. Stoyanov, Y. Zhang, G. Hadjipanayis, D. Givord and J. Nogués, Nature, 2003, 423, 850–853 CrossRef CAS PubMed.
- N. Arsalan, E. H. Kashi, A. Hasan, M. E. Doost, B. Rasti, B. A. Paray, M. Z. Nakhjiri, S. Sari, M. Sharifi, K. Shahpasand, K. Akhtari, S. Haghighat and M. Falahati, Int. J. Nanomed., 2020, 15, 4607–4623 CrossRef PubMed.
- I. K. Kgosiemang, R. Lefojane, P. Direko, Z. Madlanga, S. Mashele and M. Sekhoacha, Inorg. Nano-Met. Chem., 2020, 50, 1070–1080 CrossRef CAS.
- Magnetic Nanoparticles: A New Platform for Drug Delivery, ed. K. S. Joshy, T. Sabu and V. K. Thakur, Springer Nature Singapore Pte Ltd., 2021 Search PubMed.
- T. Morisato, N. Jones, S. Khanna and Y. Kawazoe, Comput. Mater. Sci., 2006, 35, 366–370 CrossRef CAS.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- P. Jena and A. W. Castleman, Jr., Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10560–10569 CrossRef CAS PubMed.
- C. J. Dibble, S. T. Akin, S. Ard, C. P. Fowler and M. A. Duncan, J. Phys. Chem. A, 2012, 116, 5398–5404 CrossRef CAS PubMed.
- N. T. Mai, S. T. Ngo, P. Lievens, E. Janssens and N. T. Tung, J. Phys. Chem. A, 2020, 124, 7333–7339 CrossRef CAS PubMed.
- A. Pramann, K. Koyasu, A. Nakajima and K. Kaya, J. Phys. Chem. A, 2002, 106, 4891–4896 CrossRef CAS.
- C. N. van Dijk, D. R. Roy, A. Fielicke, T. Rasing, A. C. Reber, S. N. Khanna and A. Kirilyuk, Eur. Phys. J. D, 2014, 68, 357 CrossRef.
- F. Jiao and H. Frei, Angew. Chem., Int. Ed., 2009, 48, 1841–1844 CrossRef CAS PubMed.
- Y. Xie, F. Dong, S. Heinbuch, J. J. Rocca and E. R. Bernstein, Phys. Chem. Chem. Phys., 2010, 12, 947–959 RSC.
- R. H. Aguilera-del Toro, F. Aguilera-Granja, A. Vega and L. C. Balbás, Phys. Chem. Chem. Phys., 2014, 16, 21732–21741 RSC.
- N. T. Tung, N. M. Tam, M. T. Nguyen, P. Lievens and E. Janssens, J. Chem. Phys., 2014, 141, 044311 CrossRef PubMed.
- A. O. H. Zayed, M. N. Daud and S. M. Zain, J. Alloys Compd., 2017, 695, 2513–2518 CrossRef CAS.
- G. L. Gutsev, K. G. Belay, K. V. Bozhenko, L. G. Gutsev and B. R. Ramachandran, Phys. Chem. Chem. Phys., 2016, 18, 27858–27867 RSC.
- L. Geng, M. Weng, C.-Q. Xu, H. Zhang, C. Cui, H. Wu, X. Chen, M. Hu, H. Lin, Z.-D. Sun, X. Wang, H.-S. Hu, J. Li, J. Zheng, Z. Luo, F. Pan and J. Yao, Natl. Sci. Rev., 2021, 8, nwaa201 CrossRef CAS PubMed.
- J. van der Tol, PhD thesis, KU Leuven, 2019.
- J. van der Tol and E. Janssens, Phys. Rev. A, 2020, 102, 022806 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. M. Bakker, J. Jalink, D. Dieleman and A. Kirilyuk, J. Phys.: Condens. Matter, 2018, 30, 494003 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- Quantum mechanics, ed. B. H. Bransden and C. J. Joachain, Pearson Education Ltd, 2nd edn, 2000 Search PubMed.
- T. H. Boyer, Am. J. Phys., 1988, 56, 688–692 CrossRef.
- U. Rohrmann and R. Schäfer, Phys. Rev. Lett., 2013, 111, 133401 CrossRef PubMed.
- M. Gleditzsch, T. M. Fuchs and R. Schäfer, J. Phys. Chem. A, 2019, 123, 1434–1444 CrossRef CAS PubMed.
- X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054430 CrossRef.
- G. F. Bertsch and K. Yabana, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 1930–1932 CrossRef CAS PubMed.
- M. B. Knickelbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 014424 CrossRef.
- U. Rohrmann, S. Schäfer and R. Schäfer, J. Phys. Chem. A, 2009, 113, 12115–12121 CrossRef CAS PubMed.
- N. A. Spaldin, Magnetic materials, Cambridge University Press, 2nd edn, 2013 Search PubMed.
- R. M. Moon, Phys. Rev., 1964, 136, A195–A202 CrossRef.
- C. T. Chen, Y. U. Idzerda, H.-J. Lin, N. V. Smith, G. Meigs, E. Chaban, G. H. Ho, E. Pellegrin and F. Sette, Phys. Rev. Lett., 1995, 75, 152–155 CrossRef CAS PubMed.
- V. Zamudio-Bayer, K. Hirsch, A. Langenberg, A. awicki, A. Terasaki, B. von Issendorff and J. T. Lau, J. Phys.: Condens. Matter, 2018, 30, 464002 CrossRef CAS PubMed.
- S. Peredkov, M. Neeb, W. Eberhardt, J. Meyer, M. Tombers, H. Kampschulte and G. Niedner-Schatteburg, Phys. Rev. Lett., 2011, 107, 233401 CrossRef CAS PubMed.
- I. M. L. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1682–1684 CrossRef CAS PubMed.
- P. Ferrari and S. Gómez-Coca, Phys. Chem. Chem. Phys., 2022, 24, 23128–23134 RSC.
- M. B. Knickelbein, J. Chem. Phys., 2006, 125, 044308 CrossRef PubMed.
- F. W. Payne, W. Jiang, J. W. Emmert, J. Deng and L. A. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094431 CrossRef.
- J. Jalink, PhD thesis, Radboud Universiteit Nijmegen, 2014.
- X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. Lett., 2005, 95, 237209 CrossRef PubMed.
- J. L. Rodríguez-López, F. Aguilera-Granja, K. Michaelian and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174413 CrossRef.
- J. Guevara, F. Parisi, A. M. Llois and M. Weissmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 13283–13287 CrossRef CAS.
- H. T. Pham, N. T. Cuong, N. M. Tam, V. D. Lam and N. T. Tung, Chem. Phys. Lett., 2016, 643, 77–83 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A schematic overview of the experimental setup, a brief explaination about the determination of the magnetic field, results from the DFT calculations on selected Co6,7Om clusters (including the density of states of Co6Om, partial electron charges, Wiberg bond indices, and natural electron configurations), and beam profiles of all identified ConOm clusters. See DOI: https://doi.org/10.1039/d2cp05202d |
| This journal is © the Owner Societies 2023 |