Formation of magnetic anionic electrons by hole doping
Jingyu
He
a,
Yuanzheng
Chen
 b,
Zishen
Wang
ac,
Ming
Yang
b,
Zishen
Wang
ac,
Ming
Yang
 d,
Tong
Yang
d,
Lei
Shen
d,
Tong
Yang
d,
Lei
Shen
 e,
Xiaoguang
Xu
f,
Yong
Jiang
f,
Jianwei
Chai
g,
Lai Mun
Wong
g,
Shijie
Wang
e,
Xiaoguang
Xu
f,
Yong
Jiang
f,
Jianwei
Chai
g,
Lai Mun
Wong
g,
Shijie
Wang
 *g,
Yuan Ping
Feng
*g,
Yuan Ping
Feng
 *ac and
Jun
Zhou
*ac and
Jun
Zhou
 *g
*g
aDepartment of Physics, National University of Singapore, Singapore 117551, Singapore. E-mail: phyfyp@nus.edu.sg
bSchool of Physical Science and Technology, Southwest Jiaotong University, Chengdu 610031, China
cCenter for Advanced Two-Dimensional Materials (CA2DM), National University of Singapore, Singapore 117546, Singapore
dDepartment of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong SAR, China
eDepartment of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore
fSchool of Materials Science and Engineering, University of Science and Technology Beijing, Beijing, 100083, China
gInstitute of Materials Research & Engineering, A*STAR (Agency for Science, Technology and Research), 2 Fusionopolis Way, Innovis, Singapore 138634, Singapore. E-mail: sj-wang@imre.a-star.edu.sg; zhou_jun@imre.a-star.edu.sg
First published on 18th April 2022
Abstract
Electrides intrinsically hold some unique properties arising from the anionic electrons such as the low work function from their loosely bound nature and extended distribution due to their absence of restriction from atomic orbitals. Leveraging these properties, via first-principles calculations, we firstly propose a new nonmagnetic semiconducting electrene ZrCl2 ([ZrCl2]2+·2e−), which is stable and can be easily exfoliated from its experimentally grown parent layered bulk. Moreover, a spontaneous spin splitting of the anionic electrons and consequently a nonmagnetic–magnetic phase transition are revealed in monolayer ZrCl2 at a critical doping concentration of 5.0 × 1014 cm−2. Assisted by the low-energy effective model, constrained random phase approximation simulation, and Anderson's theory, we demonstrate the mechanism of d0 magnetism in the doped monolayer ZrCl2 and confirm the dual localized and extended nature of these magnetic anionic electrons. These results enable electric-field controllable magnetism in electrenes, showing potential for novel spintronic applications.
Introduction
The experimental growth of truly two-dimensional (2D) magnets CrI3 and CrGeTe3 in 2017 has ignited research enthusiasm in the materials community for low-dimensional magnetism.1,2 Hitherto, this group of materials has burgeoned and a wide spectrum of emergent properties have been reported such as controllable magnetic phase transition by external stimuli and spin-valley coupled excitonic physics, making them appealing for new spintronic and valleytronic applications.3–6 However, the origin of the magnetic moments of the most reported 2D magnets is akin to the conventional three-dimensional magnetic materials, that is, from the magnetic elements (Fe, Cr, V, and Mn), in which the d orbitals are partially occupied such as in the recently reported FeX3 (X = F, Cl, Br and I) and Janus VSeTe systems.7–11On the other hand, the so-called d0 magnetism, which does not involve magnetic elements, has been known for a while.12–14 To achieve such unconventional magnetism, a shift of the Fermi level (EF) by carrier doping, defect formation, or functionalities, is usually needed to obtain partially filled p orbitals, which increases the density of states (DOS) at the Fermi level.15–17 This facilitates a Stoner-type itinerant magnetic instability, which can be triggered by N(EF)I > 1, where N(EF) is the density of states at the Fermi energy and I represents the Stoner parameter, respectively.18 However, due to the less localized nature of p orbitals than d orbitals, the Stoner parameters of d0 systems are usually smaller than that of typical 3d ferromagnets. This suggests that the d0 magnetic instability is mainly driven by the high N(EF). As a result, materials with Mexican-hat-induced van Hove singularities with power-law divergent DOS are ideal examples for d0 magnetism.19–22
Recently, an intrinsic d0 magnetism has been proposed in monolayer electrides (coined as electrenes).23–25 This is based on electrenes being electron-rich and their excess electrons localizing at the interstitial sites at the center of cation “cages” (called anionic electrons).26 The localized nature of the anionic electrons leads to a strong correlation (thus a large I) and a narrow bandwidth [thus a high N(EF)], both of which promote the system to meet the Stoner criterion and induce spontaneous splitting of the anionic electrons. Such atomic orbital-free magnetic anionic electrons represent a novel pathway for d0 magnetism, which does not require a van Hove singularization in the DOS. Besides, the wavefunctions of magnetic anionic electrons have extended tails and their overlap results in a strong direct ferromagnetic (FM) coupling between them.23
To take advantage of both the tunability of carrier doping and the unique dual nature of anionic electrons, it is interesting to explore the possibility of a charge doping induced magnetism in non-magnetic electrenes. The benefit of this concept is threefold. Firstly, the 2D nature of electrenes allows the application of gate voltage for carrier doping.16,27 Whereas conventional chemical doping in bulk materials suffers from low carrier density, high expenses at damaging the system's transport properties, and technological limitations, the gate-controlled electrostatic doping has been shown to be a useful technique for both electron and hole doping, achieving high carrier densities exceeding 1015 cm−2 and is reversible and non-destructive as well as allowing the electrical control of magnetism.28 Secondly, the localized nature of anionic electrons provides a good condition to fulfill the Stoner criterion by shifting the Fermi level. Finally, their loosely bound nature leads to the low work function of electrenes, which would further facilitate the hole doping of electrenes.
To exemplify this concept, via first-principles simulations, we first propose a new electrene, i.e., a ZrCl2 monolayer. It is a non-magnetic semiconductor, which can be easily exfoliated from the experimentally grown parent bulk structure and is dynamically and thermodynamically stable. More importantly, our results confirm that its anionic electrons become spin-polarized after a critical hole doping concentration of 5.0 × 1014 cm−2. The induced magnetic anionic electrons also demonstrate a unique dual localized and extended nature, and thus a large magnetic exchange coupling. These results pave the way to generate tunable magnetic electrenes for novel spintronic applications.
Methods
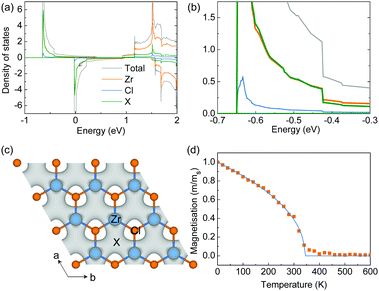
All the density functional theory (DFT) calculations were performed using the Vienna ab initio Simulation Package (VASP 6.1.0)29,30 with the Perdew–Burke–Ernzerhof (PBE) approximation for the exchange–correlation functional and the frozen-core all-electron projector augmented wave (PAW) method for the electron–ion interaction.31 The plane wave expansion was found to be well converged at a cutoff energy of 450 eV. A Γ-centered 15 × 15 × 1 k-point grid was used to sample the reciprocal space. The structures were fully relaxed until the energy and force were converged to 10−6 eV and 0.001 eV Å−1, respectively. The thickness of the vacuum layer was set to around 30 Å to eliminate the interaction between the images resulting from the periodic boundary conditions. The Wannier function was constructed from the results of the DFT calculations using the procedure of maximal localization using the Wannier90 package as implemented in VASP.32 Interstitial-centered maximally-localised Wannier functions (MLWFs) from interstitial s orbitals have been used as initial guesses to construct the MLWFs of the anionic electrons, which were used for further constrained random phase approximation (cRPA) calculations and the long-energy effective model.33,34The Monte Carlo simulations are based on the Heisenberg model and are performed using the VAMPIRE package.35 The simulated spin system contains 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 spins. At each temperature, the orientations of spins were initially randomized, and all the spins were first thermalized for 10, 000 equilibrium steps and then by 50, 000 averaging steps to derive the thermal equilibrium magnetization. The simulated temperature dependent magnetization is fitted to the Curie–Bloch equation in the classical limit M(T) = (1 − T/Tc)β, where β is the critical exponent.
800 spins. At each temperature, the orientations of spins were initially randomized, and all the spins were first thermalized for 10, 000 equilibrium steps and then by 50, 000 averaging steps to derive the thermal equilibrium magnetization. The simulated temperature dependent magnetization is fitted to the Curie–Bloch equation in the classical limit M(T) = (1 − T/Tc)β, where β is the critical exponent.
Results and discussion
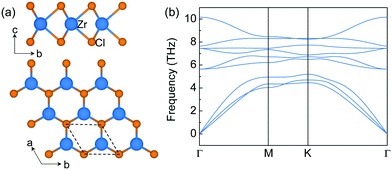
The structure of monolayer ZrCl2 is shown in Fig. 1a. It is composed of a middle layer of Zr atoms sandwiched by two Cl atomic layers in trigonal prismatic coordination. This structure resembles an H-phase MoS2 structure with a space group of P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2. It is interesting to note that the layered bulk 3R ZrCl2, containing three H-phase ZrCl2 monolayers in one unit cell, has been experimentally synthesized in the 1970s.36 However, the experimental report of the monolayer limit of H-phase ZrCl2 is still missing. To explore the synthesizability of monolayer ZrCl2, its exfoliation energy is estimated from the difference of the energy per atom between bulk and monolayer structures and compared to that of graphene and electrene Ca2N. The exfoliation energy of ZrCl2 (69.0 meV per atom) is much lower than that of electrene 2D Ca2N (260.0 meV per atom) and comparable to that of graphene (67.0 meV per atom).37 It is noted that, besides graphene,38 the electrene Ca2N has also been experimentally exfoliated, and the anionic electrons in Ca2N are well retained in the monolayer limit.39,40 Thus, our results indicate that monolayer ZrCl2 could be exfoliated in the experiment. Besides, the dynamic stability of monolayer ZrCl2 is proved by the phonon band structure (see Fig. 1b) as evidenced by the absence of imaginary frequencies. Its thermodynamical stability is confirmed by the energy above hull,41 which is 0 eV per atom, indicating its stability against decomposition and phase transition.42
m2. It is interesting to note that the layered bulk 3R ZrCl2, containing three H-phase ZrCl2 monolayers in one unit cell, has been experimentally synthesized in the 1970s.36 However, the experimental report of the monolayer limit of H-phase ZrCl2 is still missing. To explore the synthesizability of monolayer ZrCl2, its exfoliation energy is estimated from the difference of the energy per atom between bulk and monolayer structures and compared to that of graphene and electrene Ca2N. The exfoliation energy of ZrCl2 (69.0 meV per atom) is much lower than that of electrene 2D Ca2N (260.0 meV per atom) and comparable to that of graphene (67.0 meV per atom).37 It is noted that, besides graphene,38 the electrene Ca2N has also been experimentally exfoliated, and the anionic electrons in Ca2N are well retained in the monolayer limit.39,40 Thus, our results indicate that monolayer ZrCl2 could be exfoliated in the experiment. Besides, the dynamic stability of monolayer ZrCl2 is proved by the phonon band structure (see Fig. 1b) as evidenced by the absence of imaginary frequencies. Its thermodynamical stability is confirmed by the energy above hull,41 which is 0 eV per atom, indicating its stability against decomposition and phase transition.42
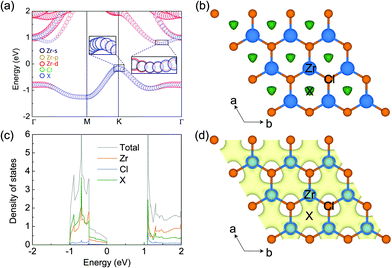
The electronic properties of monolayer ZrCl2 are shown in Fig. 2. It is clear that ZrCl2 is a nonmagnetic semiconductor with an indirect PBE gap of 0.94 eV between the valence band maximum at the K point and conduction band minimum along the ΓK path, which are mainly composed of the states from the interstitial sites (denoted as X) and both the Zr d orbitals and X sites, respectively. It is interesting to note that the valence band, which spans from around −1.0 to 0.0 eV, is well separated from other bands. This suggests that the two electrons occupying the isolated valence band have minimal hybridization with other orbitals. In addition, based on the preferred oxidization state of Zr4+ and Cl− ions, ZrCl2 is an intrinsic electron-rich material with 2 excess electrons per formula unit (f.u.), thus it can be written as [ZrCl2]2+·2e−. These two facts are typical features of electrides, in which the excess electrons localize at the interstitial site and are loosely bound to the cation framework.
To evince the electride nature of ZrCl2, we performed simulations on the electron localization function (ELF), projected density of states (PDOS), and partial charge for the isolated band. As shown by the ELF in Fig. 2b, a remarkable number of electrons localize at the interstitial centers of the hexagons, performing as anionic electrons (X). To further confirm the existence of interstitial localized electrons in this material, we put a pseudo-atom (an empty sphere) at site X and project DOS on it. As shown by PDOS of ZrCl2 in Fig. 2c, the valence band is contributed mostly by the pseudo-atom X. Such contribution is also evidenced by the real-space distribution of the valence band decomposed charge densities (see Fig. 2d). These results clearly demonstrate that the 2 excess electrons of ZrCl2, which fully occupy the valence band, localize at the interstitial sites as anionic electrons, proving the electride nature of ZrCl2. Thus, we refer to the valence band as an anionic electron band in the following sections.
One of the unique features of electrides is their low work function, because anionic electrons are loosely bound in electrides, and they can easily “escape” from the lattice, making electrides efficient thermionic emitters.43 The calculated work function of monolayer ZrCl2 is 3.85 eV, which is comparable with that of another electrene Y2C44 but lower than those of monolayer transition metal dichalcogenides (TMDs).45 Recently, a remarkable high doping concentration of ∼4 × 1014 cm−2 has been experimentally applied to 2D semiconductor CrGeTe3.46 For a direct comparison, the work function of CrGeTe3 is also calculated, which is 4.97 eV, much higher than that of ZrCl2, suggesting the experimental feasibility of heavy doping of ZrCl2. This motivated us to further investigate the doping effects on monolayer ZrCl2.
Hole doping of a series of concentrations up to 10.0 × 1014 cm−2 (equivalent to 1 hole per f.u.) with an incremental step of 0.5 × 1014 cm−2 has been applied to the monolayer ZrCl2. As shown by the doping concentration-dependent magnetic moments in Fig. 3, a transition from the intrinsic nonmagnetic nature of ZrCl2 to a magnetic state happened at around 5.0 × 1014 cm−2. The magnetic moment of the system further increases with the hole doping concentration and reaches 1 μB per f.u. at 10.0 × 1014 cm−2 (1 hole per f.u.), implying the full spin polarization of the anionic electron band. Such a hole-induced spin polarization can be understood by the Stoner criterion N(EF)I > 1. As shown in Fig. 2c, the anionic electron band consists of two regions, below and above around −0.5 eV, with high and low DOS, respectively. This is in line with the dual localized and extended nature of anionic electrons as proposed in ref. 18. The hole doping shifts the Fermi level to a lower energy region, which first enters the low DOS zone of −0.5 to 0 eV, where the Stoner criterion is not met due to the small N(EF). This explains why monolayer ZrCl2 remains nonmagnetic under the doping concentration from 0 to 4.50 × 1014 cm−2. At around 0.5 eV, there is a sudden surge of DOS, which leads to the sudden increase of magnetic moments at a doping concentration of around 5.0 × 1014 cm−2.
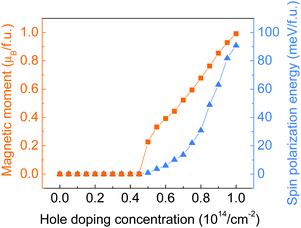 | ||
| Fig. 3 Total magnetic moment (in orange) and spin polarization energy (in blue) of monolayer ZrCl2 with regards to the hole doping concentration. | ||
To study the stability of the magnetic state of the hole-doped ZrCl2, the spin polarization energy, which is defined as the energy difference between the nonmagnetic and ferromagnetic states, is calculated for each doping concentration. Positive values indicate a preference for the ferromagnetic order. As shown by the blue triangles in Fig. 3, the spin polarization energy is positive from the onset of the magnetic state. The spin polarization energy continues to increase with the doping concentration and reaches 90.8 meV per f.u. at 10.0 × 1014 cm−2.
The origin of the magnetic moments in the hole-doped ZrCl2 is further studied by using a hole concentration of 8.0 × 1014 cm−2 as an example, under which the total magnetic moment is 0.68 μB per f.u. As indicated by the projected density of states shown in Fig. 4a, the magnetic moments come from the spin-splitting of the anionic electron band. And the contribution of the anionic electron site X (green line in Fig. 4a and the inset) is comparable to that of the Zr atom (orange line in Fig. 4a), suggesting the formation of magnetic anionic electrons. The spin density shown in Fig. 4b also confirms that the magnetic moments of the system are mainly from the interstitial sites.
The magnetic anionic electrons have been shown to possess interesting properties such as a dual localized and extended nature.23 While the localization leads to the formation of magnetic moments, the overlap of the extended tails of the anionic electron wave function produces a strong long-distance direct FM coupling.23 Unfortunately, such characteristics of the anionic electron cannot be fully captured by conventional DFT. To confirm such properties of the magnetic anionic electrons in hole-doped monolayer ZrCl2, a low-energy effective model is adopted for the anionic electron bands under the hole doping concentration of 8.0 × 1014 cm−2, the Hamiltonian of which based on the second quantization is given as follows. 33,34
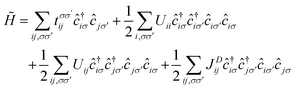
| (1) |
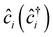 , tij, Uii, Uij and JDij are site indices, spin indices, creation (annihilation) operators, hopping parameters, on-site Coulomb, off-site Coulomb, and off-site direct-exchange interactions, respectively. The magnitude of Coulomb and exchange interactions can be mapped by the constrained random phase approximation based on the interstitial-centered MLWFs for the anionic electrons. In this work, we focus on the interactions between the nearest neighbouring magnetic anionic electrons.
, tij, Uii, Uij and JDij are site indices, spin indices, creation (annihilation) operators, hopping parameters, on-site Coulomb, off-site Coulomb, and off-site direct-exchange interactions, respectively. The magnitude of Coulomb and exchange interactions can be mapped by the constrained random phase approximation based on the interstitial-centered MLWFs for the anionic electrons. In this work, we focus on the interactions between the nearest neighbouring magnetic anionic electrons.
The calculated parameters are U00 = 1.99 eV, U01 = 1.34 eV, t01 = 76.80 meV and JD01 = 31.86 meV. Compared with the anionic electrons in the H-phase LaBr2, the on-site Coulomb interaction is smaller while the off-site direct-exchange interactions and hopping integrals are larger for hole-doped ZrCl2.23 This suggests that the anionic electrons in ZrCl2 are more delocalized, as supported by its larger bandwidth (∼1.0 eV) than that of H-phase LaBr2 (∼0.5 eV). Nevertheless, the Coulomb interactions and hopping integrals of hole-doped ZrCl2 still satisfy the condition U00 > U01 ≫ t01, which facilitates the application of Anderson's model. As a result, the overall isotropic exchange interactions of the hole-doped ZrCl2 monolayer can be determined as follows.47
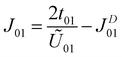 | (2) |
Conclusions
In summary, we identify a new nonmagnetic semiconducting electrene [ZrCl2]2+·2e−, which is both kinetically and thermodynamically stable and can be exfoliated from the experimentally grown layered bulk. Taking advantage of the low work function of electrene, our research further shows that at a critical hole doping concentration of 5.0 × 1014 cm−2, the anionic electrons in monolayer ZrCl2 undergo spontaneous spin splitting. Our combined low-energy effective model, cRPA simulation, and Anderson's model confirm the dual localized and extended nature of the hole-induced magnetic anionic electrons in ZrCl2 and their strong ferromagnetic exchange coupling. Our results utilize the intrinsic properties of electrenes to introduce low-dimensional magnetism to non-magnetic systems, paving the way for controllable novel spintronic applications.Author contributions
Z. J., S. J. W. and Y. P. F. conceived the idea. J. H. performed the DFT calculations with input from Z. J., S. J. W. and Y. P. F. All authors analysed the data. Z. J. and J. H. wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Education, Singapore, under its MOE Tier 1 Awards R-144-000-441-114 & R-144-000-413-114. We acknowledge the computational resources supported by the National Supercomputing Centre (NSCC) Singapore and Centre of Advanced 2D Materials (CA2DM) HPC infrastructure.References
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- C. Gong and X. Zhang, Science, 2019, 363, 706 CrossRef PubMed.
- B. Huang, M. A. McGuire, A. F. May, D. Xiao, P. Jarillo-Herrero and X. Xu, Nat. Mater., 2020, 19, 1276–1289 CrossRef CAS PubMed.
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419 CrossRef CAS PubMed.
- K. S. Burch, D. Mandrus and J. G. Park, Nature, 2018, 563, 47–52 CrossRef CAS PubMed.
- Z. Guan, J. Wang, J. Huang, X. Wu, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 22491–22498 CrossRef CAS.
- M. Zhang, Z. Guan, Z. Yang, X. Hu, X. Wang, Y.-Z. Long and C. Huang, Chem. Mater., 2020, 32, 9001–9007 CrossRef CAS.
- Z. Guan and S. Ni, Nanoscale, 2020, 12, 22735–22742 RSC.
- Z. Guan and S. Ni, ACS Appl. Mater. Interfaces, 2020, 12, 53067–53075 CrossRef CAS.
- Z. Guan and S. Ni, ACS Appl. Electron. Mater., 2021, 3, 3147–3157 CrossRef CAS.
- J. M. D. Coey, Nat. Mater., 2019, 18, 652–656 CrossRef CAS PubMed.
- H. Peng, H. J. Xiang, S. H. Wei, S. S. Li, J. B. Xia and J. Li, Phys. Rev. Lett., 2009, 102, 017201 CrossRef PubMed.
- J. M. D. Coey, Solid State Sci., 2005, 7, 660–667 CrossRef CAS.
- R. R. Nair, M. Sepioni, I. L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199–202 Search PubMed.
- M. M. Ugeda, I. Brihuega, F. Guinea and J. M. Gomez-Rodriguez, Phys. Rev. Lett., 2010, 104, 096804 CrossRef CAS.
- J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870 CrossRef CAS.
- E. C. Stoner, Proc. R. Soc. London, Ser. A, 1938, 165, 372–414 Search PubMed.
- T. Cao, Z. Li and S. G. Louie, Phys. Rev. Lett., 2015, 114, 236602 CrossRef PubMed.
- L. Seixas, A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2016, 116, 206803 CrossRef CAS PubMed.
- Y. Wang, Q. Zhang, Q. Shen, Y. Cheng, U. Schwingenschlögl and W. Huang, J. Mater. Chem. C, 2017, 5, 4520–4525 RSC.
- L. Guan and J. Tao, Phys. Rev. Appl., 2017, 8, 064019 CrossRef.
- J. Zhou, Y. P. Feng and L. Shen, Phys. Rev. B, 2020, 102, 180407(R) CrossRef.
- J. Zhou, X. Song, M. Yang, J. Chai, N. L. M. Wong, L. Shen, S. Wang and Y. P. Feng, J. Mater. Chem. C, 2021, 9, 16576–16580 RSC.
- X. Sui, J. Wang, C. Yam and B. Huang, Nano Lett., 2021, 21, 3813–3819 CrossRef CAS PubMed.
- J. L. Dye, Science, 2003, 301, 607–608 CrossRef CAS PubMed.
- S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549–553 CrossRef CAS PubMed.
- A. M. Goldman, Annu. Rev. Mater. Res., 2014, 44, 45–63 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- V. V. Mazurenko, A. N. Rudenko, S. A. Nikolaev, D. S. Medvedeva, A. I. Lichtenstein and M. I. Katsnelson, Phys. Rev. B, 2016, 94, 214411 CrossRef.
- I. V. Solovyev, Z. V. Pchelkina and V. V. Mazurenko, CrystEngComm, 2014, 16, 522–531 RSC.
- R. F. Evans, W. J. Fan, P. Chureemart, T. A. Ostler, M. O. Ellis and R. W. Chantrell, J. Phys.: Condens. Matter, 2014, 26, 103202 CrossRef CAS PubMed.
- A. Cisar, J. D. Corbett and R. L. Daake, Inorg. Chem., 1979, 18, 836–843 CrossRef CAS.
- J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 86 CrossRef PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- D. L. Druffel, K. L. Kuntz, A. H. Woomer, F. M. Alcorn, J. Hu, C. L. Donley and S. C. Warren, J. Am. Chem. Soc., 2016, 138, 16089–16094 CrossRef CAS PubMed.
- J. S. Oh, C. J. Kang, Y. J. Kim, S. Sinn, M. Han, Y. J. Chang, B. G. Park, S. W. Kim, B. I. Min, H. D. Kim and T. W. Noh, J. Am. Chem. Soc., 2016, 138, 2496–2499 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- G. Hautier, A. Jain, S. P. Ong, B. Kang, C. Moore, R. Doe and G. Ceder, Chem. Mater., 2011, 23, 3495–3508 CrossRef CAS.
- Y. Toda, S. W. Kim, K. Hayashi, M. Hirano, T. Kamiya, H. Hosono, T. Haraguchi and H. Yasuda, Appl. Phys. Lett., 2005, 87, 254103 CrossRef.
- W. Meng, X. Zhang, Y. Liu, X. Dai, H. Gao and G. Liu, J. Mater. Chem. C, 2021, 9, 15477–15487 RSC.
- C. Gong, H. Zhang, W. Wang, L. Colombo, R. M. Wallace and K. Cho, Appl. Phys. Lett., 2013, 103, 053513 CrossRef.
- I. A. Verzhbitskiy, H. Kurebayashi, H. Cheng, J. Zhou, S. Khan, Y. P. Feng and G. Eda, Nat. Electron., 2020, 3, 460–465 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- A. Kabiraj, M. Kumar and S. Mahapatra, npj Comput. Mater., 2020, 6, 35 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |