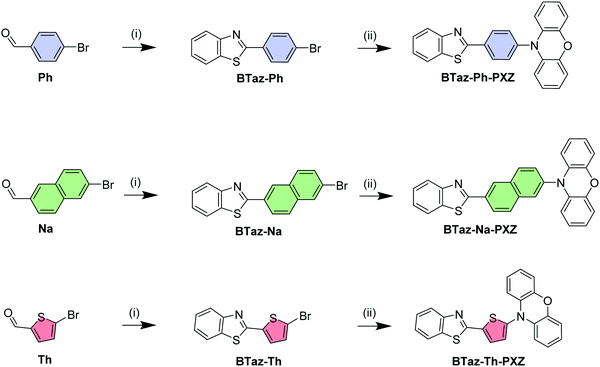
Bridge control of photophysical properties in benzothiazole-phenoxazine emitters – from thermally activated delayed fluorescence to room temperature phosphorescence†
Simon
Paredis
ab,
Tom
Cardeynaels
 abc,
Jasper
Deckers
abc,
Jasper
Deckers
 ab,
Andrew
Danos
ab,
Andrew
Danos
 d,
Dirk
Vanderzande
d,
Dirk
Vanderzande
 ab,
Andrew P.
Monkman
ab,
Andrew P.
Monkman
 d,
Benoît
Champagne
d,
Benoît
Champagne
 c and
Wouter
Maes
c and
Wouter
Maes
 *ab
*ab
aHasselt University, Institute for Materials Research (IMO-IMOMEC), Design & Synthesis of Organic Semiconductors (DSOS), Agoralaan 1, 3590 Diepenbeek, Belgium. E-mail: wouter.maes@uhasselt.be
bIMOMEC Division, IMEC, Wetenschapspark 1, 3590 Diepenbeek, Belgium
cUniversity of Namur, Laboratory of Theoretical Chemistry, Theoretical and Structural Physical Chemistry Unit, Namur Institute of Structured Matter, Rue de Bruxelles 61, 5000 Namur, Belgium
dOEM group, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
First published on 5th January 2022
Abstract
The bridging phenyl group in a fluorescent phenoxazine-benzothiazole donor–acceptor dyad is replaced by either a naphthalene or a thiophene moiety to probe the influence of a more extended conjugated system or the presence of a sulfur-containing heteroaromatic spacer on the emissive properties. These seemingly small structural alterations strongly affect the relative positions of the excited states, the fluorescence intensity, and the emission mechanism. Consequently, thermally activated delayed fluorescence (TADF) is observed at longer timescales for the materials with phenyl and naphthalene linkers, whereas the thiophene group promotes room temperature phosphorescence (RTP), both in the solid state and in solution, and enhances singlet oxygen generation. Phosphorescence in solution at ambient temperature from a purely organic molecule without heavy halogen functionalisation is quite rare, and this unique property calls for further specific attention.
Introduction
Purely organic molecules that emit light upon applying an electric current are highly attractive because of their strong potential for organic light-emitting diodes (OLEDs).1,2 These electroluminescent properties arise from the radiative decay of excitons,3 which are electrically generated in an excited singlet or triplet state with a statistical probability of 25 and 75%, respectively.4,5 The transition from the first singlet excited state to the ground state (S1 → S0, i.e. fluorescence) represents an exchange between two electronic states with identical spin multiplicity and as such is a spin-allowed transition,6 generally with a lifetime in the nanoseconds regime. On the other hand, the transition from the first triplet excited state to the ground state (T1 → S0, i.e. phosphorescence) occurs between two electronic states with different spin multiplicity and is therefore a spin-forbidden and considerably slower transition (typically in the order of microseconds).6,7While the second generation OLED devices are able to harvest triplet excitons by spin–orbit coupling (SOC) enhanced phosphorescence from heavy metal complexes, the third generation focusses on triplet up-conversion strategies to achieve near-unity internal quantum efficiency and singlet emission. There are three leading mechanisms for the indirect generation and emission of singlet excited states, i.e. thermally activated delayed fluorescence (TADF), hybridised local and charge-transfer (HLCT) emission, and triplet–triplet annihilation (TTA).8 TADF is the most promising emission mechanism for highly efficient exciton harvesting and it has become a very popular strategy to enhance OLED efficiency in recent years.9,10 For TADF to occur, the first excited singlet state and the first two excited triplet states, which are mixed by vibronic coupling, should be in close proximity (<200 meV).11 This small energy difference enables transitions between the relevant excited states (S1 ⇄ T1,2). Consequently, if the transition rate from the triplet excited state to the singlet excited state, i.e. reverse intersystem crossing (rISC), is higher than other (non)radiative pathways from the triplet states, the singlet excited state will be (re)populated.12 As a result, a delayed emission occurs from the singlet excited state, with the same energy as regular fluorescence. Since the delayed fluorescence relies on slow rISC from triplet states, it occurs with lifetimes in the microseconds regime. TADF emitters can thus harvest excitons from both the singlet and triplet states, affording highly efficient light-emitting devices.13
Organic molecules exhibiting TADF generally consist of a combination of an electron-donating (D) and an electron-accepting (A) part. While the size of the singlet–triplet splitting is largely determined by the frontier molecular orbital overlap, the rational design of a D–A or push–pull dyad showing TADF remains challenging because of the complex interplay between the excited state energy levels.14 As a result, other phenomena such as room temperature phosphorescence (RTP) are sometimes observed in molecules designed to show TADF emission. It is only in recent years that purely organic RTP, not relying on the SOC of metallic ions in organometallic phosphors, has risen to prominence.15–17 Besides the need for sufficient SOC, a second criterion for RTP needs to be met, i.e. the suppression of non-radiative transitions caused by vibrational losses and collisions. This collisional quenching can be reduced by fixing the emitting molecules in a solid-state environment, as is typically done for OLEDs. On the other hand, RTP in solution has been rarely observed due to the high molecular mobility in a solvent medium, favouring non-radiative transitions.18,19
While a large number of TADF emitters can be found in the literature, and many make use of a π-bridge between the donor and acceptor parts of the molecule, only a few reports exist about the influence of this π-bridge on the photophysical properties of a given molecule and whether or not the π-bridge can be used to tune the emissive properties of the fluorophore. It has been illustrated that the introduction of such π-bridges,20,21 and the addition of substituents such as methyl,22 trifluoromethyl,23 nitrile,24 or extra phenyl groups21,25–27 onto these bridges, has a great impact on the emissive properties (e.g. colour, quantum yield, rate of (r)ISC) by restricting the rotational freedom, altering the acceptor strength, and/or increasing the space between donor and acceptor. In this work, 10-(4-(benzo[d]thiazol-2-yl)phenyl)-10H-phenoxazine (BTaz-Ph-PXZ; Scheme 1), a fluorescent molecule already reported to show green TADF emission by Adachi et al.,28 is used as a suitable scaffold to perform such an investigation. The bridging phenyl moiety is systematically replaced by either a naphthalene (BTaz-Na-PXZ) or a thiophene unit (BTaz-Th-PXZ). We find that by altering the bridging unit, the energy of the excited triplet states changes, while keeping the excited singlet state energies relatively similar. Consequently, these dyads all have the same emission colour, but the emission mechanisms and their efficiencies are very different, controlled by the bridge. These emission kinetics and mechanisms are elucidated from (time-resolved) photophysical measurements in solution and in film, and corroborated by dedicated quantum-chemical calculations.
Results and discussion
Benzothiazole (BTaz) is used here as a small acceptor molecule, which has already shown great potential in other fields of organic electronics such as organic photovoltaics (OPVs),29 organic field-effect transistors (OFETs),30,31 and OLEDs.32 This acceptor unit is combined with phenoxazine (PXZ), a strong donor moiety commonly used in the field of TADF as it tends to give rise to stable high-energy triplet states and it has a large dihedral angle with adjacent groups.33–35 To finalise the design, a phenyl,28 naphthyl, or thienyl group is introduced as a π-bridge between the donor and the acceptor to obtain a clear separation of the highest occupied and lowest unoccupied molecular orbital (HOMO and LUMO, respectively). The starting materials for the dyad synthesis are the three respective aromatic bridge molecules substituted with a bromine and an aldehyde group on the appropriate positions. First, the aldehyde functionality was reacted with 2-aminothiophenol in the presence of sodium metabisulfite, a nontoxic inorganic oxidant,36 to yield the benzothiazole unit. Afterwards, a Buchwald–Hartwig cross-coupling reaction was performed to attach the phenoxazine unit, affording BTaz-Ph-PXZ, BTaz-Na-PXZ, and BTaz-Th-PXZ (Scheme 1). Details on the synthesis procedures and characterization data are provided in the ESI.†The geometries of the three D–A chromophores were optimised using density functional theory (DFT) calculations with M06/6-311G(d).37 Time dependent DFT (TDDFT) calculations were additionally performed to estimate the singlet and triplet energies using a modified LC-BLYP (ω = 0.17 bohr−1) exchange correlation (XC) functional, which is optimised for TADF research,38,39 with the Tamm–Dancoff approximation (TDA) and the 6-311G(d) basis set. TDDFT calculations were done using the polarizable continuum model (PCM) in cyclohexane to simulate a non-polar environment. The orbital spatial distributions were obtained from single-point calculations that are performed during the TDDFT calculations and are hence obtained using the same LC-BLYP/6-311G(d) method. All calculations were performed using the Gaussian16 package.40 The charge-transfer (CT) character of the involved states was investigated by looking at the differences of ground and excited state electron densities. These were characterised by the distance over which the electronic charge is transferred (dCT) and the related change in dipole moment (Δμ), which were calculated according to the work of Le Bahers and coworkers.41 The PySOC program was used to calculate the SOC values using the same XC functional, basis set, and PCM treatment as for the TDDFT calculations.42
DFT geometry optimizations illustrated that the PXZ moiety is nearly perpendicular (i.e. ±90° torsion angle) with respect to the aromatic unit linking PXZ and BTaz, as shown in Fig. 1. Moreover, the bridging unit is in all cases coplanar with the benzothiazole group, making it electronically a part of the acceptor rather than a simple non-interacting bridge. The optimised geometries and the corresponding HOMO and LUMO spatial distributions reveal that the HOMO is (mostly) located on the PXZ moiety, while the LUMO is spread over the BTaz-Ar unit, resulting in well-separated HOMO–LUMO topologies and suggesting strong CT character of the lowest-energy excited singlet state. This CT nature is also visualised in Fig. S1 (ESI†), where the difference in electron density between the ground and (different) excited states is shown. A clear CT character is observed in the first singlet and the first triplet for BTaz-Ph-PXZ, while the second singlet state seems to show some CT character from the PXZ donor unit to the phenyl bridge. CT character is also observed in the first and second singlet and the second triplet state in the case of BTaz-Na-PXZ, and in the first singlet and second triplet state for BTaz-Th-PXZ. The calculated excitation energies for the most relevant excited states are listed in Table 1. The first two excited triplet states are close in energy to the first excited singlet state, potentially allowing TADF. Furthermore, for the three compounds, the dominant HOMO–LUMO nature of the vertical transition towards the first excited singlet state, together with the CT distance and the change in dipole moment (listed in Table 2), demonstrates the substantial CT character. For other relevant excited states, the nature of the transitions is not always from HOMO to LUMO, leading to more localised excitonic states and smaller values for both dCT and Δμ (Table 2). The distributions of the other molecular orbitals taking part in these transitions (i.e. HOMO−1 and LUMO+1) are shown in Fig. 1. UV-Vis absorption spectra were simulated (Fig. S2, ESI†) and are dominated by a band at higher energy than the aforementioned CT states, which often have negligible absorption cross-section. A dihedral angle of 10° was considered to account for the vibrational freedom of the PXZ moiety with respect to the rest of the molecule.
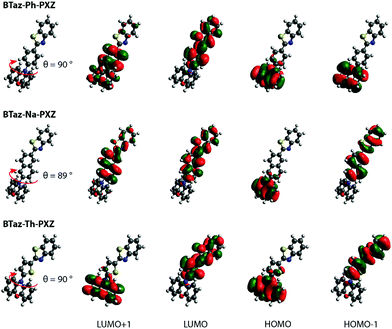 | ||
| Fig. 1 HOMO–LUMO spatial distributions for BTaz-Ph-PXZ, BTaz-Na-PXZ, and BTaz-Th-PXZ. Isocontour values of 0.02 (a.u.) were used for all orbitals. | ||
| Compound | S1 (eV) | fS1 | S2 (eV) | fS2 | T1 (eV) | T2 (eV) | ΔES1−T1 (eV) | ΔES1−T2 (eV) |
|---|---|---|---|---|---|---|---|---|
| BTaz-Ph-PXZ | 2.96 | <0.001 | 3.56 | <0.001 | 2.94 | 3.04 | 0.02 | −0.08 |
| BTaz-Na-PXZ | 2.97 | <0.001 | 3.56 | 0.001 | 2.81 | 2.90 | 0.16 | 0.07 |
| BTaz-Th-PXZ | 2.86 | <0.001 | 3.78 | 0.013 | 2.78 | 2.85 | 0.08 | 0.01 |
| Compound | S1 | S2 | T1 | T2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nature | d CT (Å) | Δμ (D) | Nature | d CT (Å) | Δμ (D) | Nature | d CT (Å) | Δμ (D) | Nature | d CT (Å) | Δμ (D) | |
| BTaz-Ph-PXZ | H→L | 3.79 | 21.42 | H→L+1 | 1.89 | 6.64 | H→L | 3.77 | 20.70 | H→L+1 | 0.17 | 0.39 |
| BTaz-Na-PXZ | H→L | 3.85 | 21.55 | H→L+1 | 3.64 | 16.34 | H−1→L | 0.15 | 0.22 | H→L | 3.58 | 16.02 |
| BTaz-Th-PXZ | H→L | 3.50 | 19.03 | H→L+1 | 0.54 | 1.49 | H−1→L | 0.35 | 0.67 | H→L | 3.49 | 18.88 |
To better understand which states are dominating the UV-vis absorption spectra, the TDDFT investigation was expanded to the 5th excited singlet. The higher singlet excited states (i.e. S3–S5) show localised character on different parts of the molecule depending on the excited state and the π-bridge (Fig. S1 and Table S2, ESI†). For S3, the excited state is localised on the Ar-PXZ part for BTaz-Ph-PXZ and BTaz-Na-PXZ, and on the BTaz-Ar part for BTaz-Th-PXZ, whereas the opposite is true for S4. The 5th singlet excited state shows localization on the Ar-PXZ part for the phenyl bridged compound, whereas it is localised on the BTaz-Ar part for the naphthalene and thiophene bridged compounds. Overall, the simulated absorption profiles (Fig. S2, ESI†) are in close agreement with the experimental spectra (vide infra, Fig. 2).
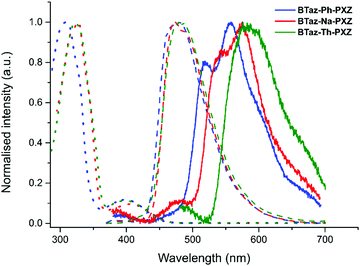
Steady-state absorption spectra (in toluene) and both fluorescence and phosphorescence emission spectra (in zeonex film) of the three push–pull dyes are shown in Fig. 2 (and the data can be found in Table 3). For all three molecules, the absorption consists of one intense main peak and one minor peak at longer wavelength. Based on the TDDFT calculations, we can attribute the weak absorption band around 400 nm to direct CT absorption (see also Fig. S2, ESI†), whereas the intense peak around 320 nm can be attributed to locally excited (LE) singlet states. For all three compounds, the fluorescence spectra in film are very similar, while the phosphorescence peaks differ both in emission wavelength and in shape. Therefore, we can conclude that upon changing the π-bridge, the singlet excited state remains relatively unaffected, while the energy and the nature of the triplet excited state does change considerably.
The nature of the absorption and emission features of the three dyes was further analysed by solvatochromic experiments (Fig. S3 and Table S4, ESI†). Emission spectra were recorded in three different solvents, i.e. methylcyclohexane, toluene, and chloroform. In all three solvents, two emission peaks were observed. The lower energy emission peak shows a strong red-shift upon increasing solvent polarity, which occurs due to the stabilisation of states with CT character in more polar solvents. The solvatochromic red-shift confirms the presence of a CT state and it is therefore suggested that the structureless low energy emission peaks in toluene and chloroform originate from CT emission. The vibronic structured emission peak in methylcyclohexane on the other hand suggests emission from an LE state.
The higher energy emission in all three solvents shows little influence of the solvent polarity and could therefore be originating from LE states, giving rise to dual LE and CT emission. A possible explanation for this observation could be the occurrence of dual stable conformations of the PXZ donor unit with respect to the bridging moiety.43 Relaxed potential energy surface scans were performed for all compounds (Fig. S4, ESI†), using the M06/6-311G(d) method, and the perpendicular orientation between the donor and bridge units was found to be the most stable one by more than 13 kJ mol−1. This corresponds to a Boltzmann population of more than 99% for the perpendicular orientation, indicating that it is highly unlikely for the higher energy emission to be originating from a coplanar (metastable) conformer. Further investigation of the compounds in solution revealed signs of degradation under the influence of light (Fig. S5, ESI†). To verify this photodegradation, the steady-state absorption and emission of all three compounds was measured in chloroform with intermittent periods of LED (λexc = 325 nm) irradiation (Fig. S6, ESI†). It is clear that exposure to light gives rise to a relative increase in the lower energy absorption, located in the same spectral region as the CT absorption, and higher energy emission bands. This is more abundant in chloroform with respect to toluene and increases within the series from the phenyl to the thienyl spacer. These spectral changes are likely caused by photodegradation of the benzothiazole unit,44,45 although 1H NMR spectra recorded after irradiation did not show clear signs of degradation (Fig. S7, ESI†).
| Compound | λ abs (nm) | ε (M−1 cm−1) | λ em (nm) | Φ f,atm,sol | Φ f,inert,sol | Φ f,atm,film | Φ f,inert,film | Φ Δ |
|---|---|---|---|---|---|---|---|---|
| a Absorption maxima in toluene solution. b Molar extinction coefficients at the absorption maxima in toluene solution. c Fluorescence emission maxima in zeonex film. d Photoluminescence quantum yields in toluene solution under normal atmosphere determined vs. quinine (Φf = 0.58, λexc = 347 nm in 0.1 M H2SO4). e Fluorescence quantum yields in toluene solution under inert atmosphere determined vs. quinine (λexc = 347 nm). f Absolute PLQYs in zeonex using an integrating sphere in air at room temperature. g Absolute PLQYs in zeonex using an integrating sphere in inert atmosphere at room temperature. h Singlet oxygen quantum yields in toluene solution determined vs. coronene (ΦΔ = 0.90, λexc = 325 nm in toluene) by monitoring the absorbance of 1,3-DPBF at 414 nm. | ||||||||
| BTaz-Ph-PXZ | 308 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
479 | 0.22 | 0.35 | 0.12 | 0.48 | 0.33 |
| 401 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||||
| BTaz-Na-PXZ | 327 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
473 | 0.13 | 0.17 | 0.13 | 0.18 | 0.46 |
| 405 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||||
| BTaz-Th-PXZ | 323 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
481 | 0.02 | 0.03 | 0.09 | 0.11 | 0.59 |
| 402 | 2700 | |||||||
The fluorescence quantum yields in toluene solution and zeonex film under normal and inert atmosphere (Φf,atm and Φf,inert) of all three compounds were then determined (Table 3) to gauge their luminescent properties. The results obtained for BTaz-Ph-PXZ are similar to the values achieved by Adachi et al. (λem,toluene = 512 nm, Φf,atm,toluene = 0.17, Φf,inert,toluene = 0.33), within the margin of error, proving that our method accurately reproduces the literature values.28 A decrease of the fluorescence quantum yield in solution under atmospheric conditions can be observed when changing the phenyl (Φf = 0.22) linker to naphthyl (Φf = 0.13), while the fluorescence almost vanishes for the thienyl bridge (Φf = 0.02). When performing the same measurements under inert atmosphere, it is clear that the fluorescence quantum yield improves significantly for the phenyl and naphthyl linkers (to Φf = 0.35 and 0.17, respectively), whereas the value remains very low for the thienyl linker. This is a first indication that BTaz-Ph-PXZ and BTaz-Na-PXZ could benefit from some kind of triplet up-conversion mechanism as oxygen is no longer able to quench the intermittent triplet states in degassed solution. In zeonex film, the photoluminescence quantum yields (PLQYs) follow the same trend as in solution. The PLQYs are again lower in air than under inert atmosphere and the thienyl linked molecule has a lower PLQY than the phenyl and naphthyl counterparts. Since the zeonex matrix is a solid host, rotational and vibrational modes are more restricted and this is especially beneficial for BTaz-Th-PXZ, which seems to suffer from large non-radiative losses in solution. On the other hand, BTaz-Ph-PXZ seemingly fluoresces less in solid film as opposed to in toluene solution. The increases going from air to inert atmosphere are even more significant in zeonex film (Table 3).
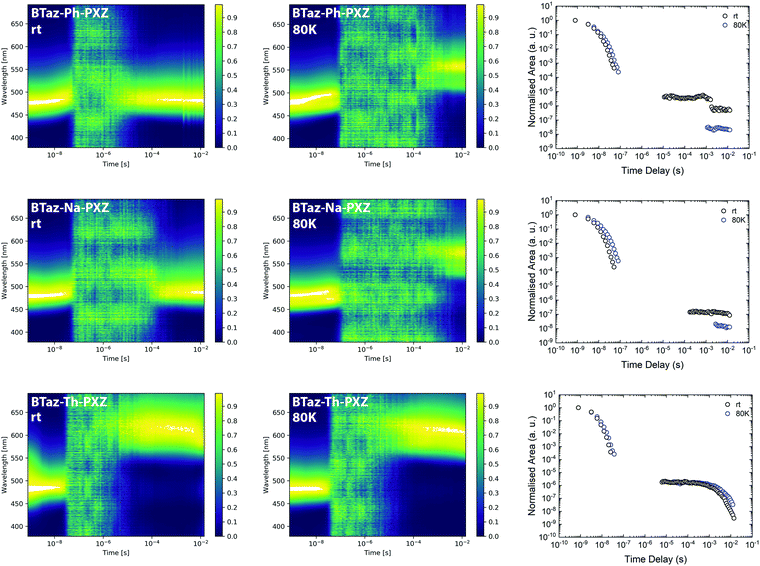
Time-resolved emission spectroscopy (TRES) experiments in a zeonex host (at 1 w/w% loading), with a polarity similar to methylcyclohexane, were then performed to unravel the detailed emission mechanisms. The contour maps of the normalised TRES experiments for the three compounds at room temperature and at 80 K are shown in Fig. 3 (left and middle) and individual spectra extracted at different time intervals are provided in Fig. S8–S10 (ESI†). The prompt fluorescence, which vanishes within the first 100 ns, shows a small red-shift in the initial period, which is most pronounced for BTaz-Ph-PXZ and BTaz-Na-PXZ. This red-shift could be the result of a combination of emission from excited singlet states with slightly different molecular geometries, typically caused by different dihedral angles between the donor and acceptor unit. These differences in geometry will affect the radiative lifetime, ISC rate, etc. Afterwards, the emission falls below the detection limit of the detector until a time delay in the microseconds regime. Thereafter, delayed emission at room temperature occurs with the same energy as the prompt fluorescence in the case of BTaz-Ph-PXZ and BTaz-Na-PXZ. This suggests TADF or TTA to occur, as in both cases the delayed emission originates from the same emissive singlet state, and confirms our earlier hypothesis of a triplet up-conversion mechanism being at work. At 80 K, the delayed emission for both compounds is slightly red-shifted with respect to the prompt emission and can be attributed to phosphorescence. In contrast, the delayed emission for BTaz-Th-PXZ at room temperature is already strongly red-shifted compared to the prompt fluorescence and the contour maps of the TRES experiments recorded at room temperature and 80 K (Fig. 3, left and middle) are almost identical. This is further supported by looking at the individual emission spectra obtained at various time delays during the emission decays. The emission spectrum for the phosphorescence of BTaz-Th-PXZ is similar to the spectra of its delayed emission at room temperature (Fig. S9, ESI†). Therefore, we can conclude that the delayed emission of BTaz-Th-PXZ is due to RTP. The latter is also visible in the steady-state emission spectrum under inert atmosphere (Fig. S11, ESI†).
To distinguish between TADF and TTA as the delayed emission mechanism for BTaz-Ph-PXZ and BTaz-Na-PXZ, laser energy experiments were performed (Fig. S12, ESI†). The dependence of emission intensity on excitation laser energy was measured by attenuation of the excitation beam with reflective neutral density filters. Throughout the entire experiment, the slope of the log–log plot remained unity, suggesting TADF as the emission mechanism in both cases. Moreover, BTaz-Th-PXZ also showed a slope of ∼1, confirming RTP emission.
The emission decays for all three compounds, presented as the normalised integrated area versus time at room temperature and at 80 K (Fig. 3, right), give more insight into the kinetics of the emission. All compounds show prompt emission at room temperature and at 80 K, with a nanoseconds lifetime (Table 4). A relatively long-lived and intense delayed emission is seen for BTaz-Ph-PXZ and BTaz-Na-PXZ at room temperature. At 80 K, the lower intensity and longer timescale of the emission is due to the disappearance of the delayed emission and appearance of phosphorescence, confirming a temperature dependent mechanism such as TADF. In the case of BTaz-Th-PXZ, the decay of the total emission at room temperature and at 80 K is nearly identical, confirming RTP. The lifetimes of the prompt and delayed components in zeonex have been obtained via biexponential fitting of the decay curves (Table 4). While BTaz-Ph-PXZ and BTaz-Na-PXZ have similar lifetimes for the prompt fluorescence, BTaz-Th-PXZ has a clearly shorter lifetime. The lifetimes of the delayed components in zeonex are very large, indicating that rISC is not very efficient in these materials.
| Compound | Sample | τ prompt (ns) | τ delayed (μs) |
|---|---|---|---|
| a Lifetime of the emission as obtained using a biexponential fit. A weighted average of the two lifetimes was made. b Accurate lifetimes cannot be determined. | |||
| BTaz-Ph-PXZ | Zeonex | 4.7 | −b |
| Toluene | 13.7 | 143.7 | |
| Chloroform | 9.1 | 5.2 | |
| BTaz-Na-PXZ | Zeonex | 4.6 | −b |
| Toluene | 6.2 | 64.8 | |
| Chloroform | 10.2 | 15.8 | |
| BTaz-Th-PXZ | Zeonex | 2.8 | 1.5 × 103 |
| Toluene | 2.6 | 106.6 | |
| Chloroform | 2.4 | 33.2 | |
With the information from the time-resolved emission at 80 K (phosphorescence) and the steady-state emission spectra in zeonex (Fig. 2), it is possible to determine the triplet and singlet energy, respectively, by looking at the onset of the emission (Table 5). As expected from the theoretical calculations, the singlet energies are comparable for all three compounds. However, a significant decrease is observed for the triplet energy within the series, from 2.55 eV (phenyl) to 2.34 eV (thienyl). As the S0→T1 vertical excitation is mostly located on the BTaz-π-linker part of the molecule (Fig. S1, ESI†), it makes sense that the experimental triplet energy is most influenced by the structural changes. The increased delocalization for the naphthyl with respect to the phenyl linker stabilises the triplet state energy and the heteroaromatic thiophene seemingly has an even larger stabilizing effect. As a result, the experimental singlet–triplet energy splitting increases upon moving from BTaz-Ph-PXZ to BTaz-Th-PXZ. The theoretical calculations predicted BTaz-Na-PXZ to have the largest ΔEST and this discrepancy with respect to the experimental results can be related to the way the singlet–triplet gap is determined, i.e. via the difference between two vertical excitation energies for TDDFT or via the onset of the prompt fluorescence and phosphorescence for the experimental results. While these experimental singlet–triplet splittings are relatively large for BTaz-Ph-PXZ (0.30 eV) and BTaz-Na-PXZ (0.37 eV), they make the thermal up-conversion (rISC) difficult, but not impossible.23 For BTaz-Th-PXZ, on the other hand, the ΔEST (0.49 eV) is too large for rISC to occur and therefore the radiative transition from the triplet excited state to the singlet ground state becomes plausible.
| Compound | E S (eV)a | E T (eV)b | ΔEST (eV)c |
|---|---|---|---|
| a Taken from the onset of the steady-state emission in zeonex film. b Taken from the onset of the phosphorescence emission at ms timescales at 80 K in zeonex film. c Calculated as ES − ET. | |||
| BTaz-Ph-PXZ | 2.85 | 2.55 | 0.30 |
| BTaz-Na-PXZ | 2.83 | 2.46 | 0.37 |
| BTaz-Th-PXZ | 2.83 | 2.34 | 0.49 |
To get a deeper understanding of the photophysical properties of the three compounds in solution, and more particular BTaz-Th-PXZ, TRES experiments were performed in degassed toluene (ε = 2.38) and chloroform (ε = 4.81) at a concentration of 50 μM. The contour maps and the decay plots of BTaz-Ph-PXZ measured at room temperature in these two solvents are shown in Fig. S13 (ESI†). In both cases, the contour plots clearly show delayed emission originating from the same excited state as the prompt fluorescence, suggesting TADF. The polarity of the solvent, however, does have an effect on the emission wavelength as BTaz-Ph-PXZ emits at 530 nm in toluene, whereas it emits at 575 nm in chloroform, implying strong excited state stabilisation in more polar environments. Consistent with the solid-state measurements, BTaz-Na-PXZ shows similar properties as BTaz-Ph-PXZ, as shown in Fig. S14 (ESI†). The contour maps and decay plots in toluene and chloroform also show TADF in both solvents for BTaz-Na-PXZ, albeit a bit less intense than for BTaz-Ph-PXZ. The thienyl variant BTaz-Th-PXZ shows relatively intense delayed emission in solution, with reasonably long lifetimes of 33.2 μs and 106.6 μs in chloroform and toluene, respectively (Table 4). Strongly red-shifted with respect to the prompt fluorescence (Fig. 4 and Fig. S15, ESI†) and similar to its behaviour in zeonex, this is assigned to RTP. This is somewhat surprising as phosphorescence at room temperature in solution has only rarely been observed for halogen-free purely organic compounds due to the strong competition between the typically slow phosphorescence and the relatively fast non-radiative decay pathways (collisional quenching and internal conversion). We note, however, that the relatively low solution PLQYs (both with and without the presence of oxygen, Table 3) indicate quenching processes are still strongly active, and the RTP we do observe originates only from the small population of molecules for which triplet emission outcompetes quenching.
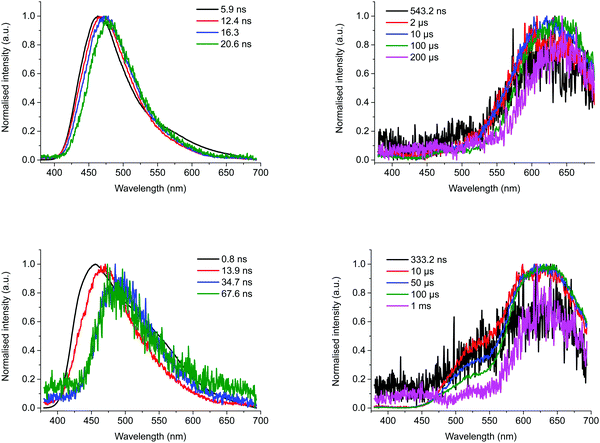 | ||
| Fig. 4 Snapshots of the emission at various time scales during prompt (left) and delayed emission (right) for BTaz-Th-PXZ at room temperature in chloroform (top) and in toluene (bottom) solution. | ||
Since we observe TADF for the phenyl and naphthyl linked compounds and RTP for the thienyl bridged material, triplet excited states play a crucial role in the (time-resolved) photophysics of these materials. Independent of the exact emission process, molecular oxygen can lead to quenching of excited triplet states to undergo a transition from its triplet ground state to the singlet excited state (3O2 + Tn → 1O2 + S0). Singlet oxygen formation can thus be used as an indirect method to prove triplet formation in photosensitizers.46 This is also at the origin of the difference in PLQY in air and under inert atmosphere for compounds showing triplet up-conversion or triplet emission. Singlet oxygen quantum yields (ΦΔ, Table 3) were measured using a relative method in which the reaction of a 1O2 scavenger (1,3-diphenylisobenzofuran, 1,3-DPBF) is monitored via UV-Vis absorption spectroscopy while the photosensitizer (i.e. the BTaz compound) is illuminated using a secondary light source (Fig. S16, ESI†). The singlet oxygen quantum yields follow the opposite trend of the PLQYs, with BTaz-Th-PXZ (ΦΔ = 0.59) showing the largest value, followed by BTaz-Na-PXZ (ΦΔ = 0.46) and BTaz-Ph-PXZ (ΦΔ = 0.33).
These values, in combination with the PLQYs under inert atmosphere, can be rationalised by looking at the experimental singlet–triplet splittings of these materials (Table 5). The phenyl and naphthyl linked molecules both show TADF, so transitions from the triplet state to the ground state are in competition with the rISC pathway. The phenyl bridged molecule has a smaller ΔEST, which means that the rISC rate will be higher and thus the singlet oxygen quantum yield will be lower than that of BTaz-Na-PXZ. BTaz-Th-PXZ shows RTP, which means that the transitions from the triplet excited state are in competition with radiative relaxation to the ground state. This is a spin-forbidden process and combined with the low PLQY, a large amount of triplet excitons are required to see the phosphorescence. Due to its large ΔEST, the rISC pathway is not viable for this molecule and the triplet excitons are trapped until (non-)radiative decay allows them to relax back to the ground state. The results can also be interpreted in terms of the ISC rate. While it is not straightforward to derive the ISC rate from the emission decays, the 1O2 quantum yields show that ISC is most efficient in BTaz-Th-PXZ when compared to BTaz-Na-PXZ and BTaz-Ph-PXZ.
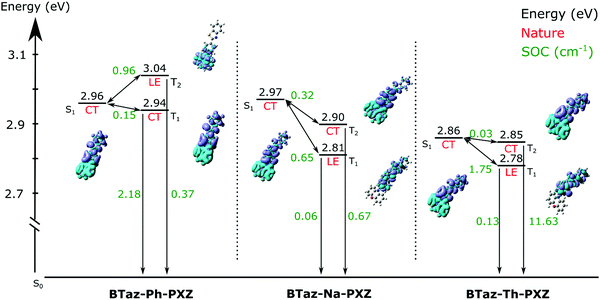
As mentioned before, the singlet oxygen quantum yields are related to the ISC and, when applicable, rISC rates. Apart from the energy difference between the involved excited states, the spin–orbit coupling between them also plays a crucial role. For BTaz-Ph-PXZ, the T1→S0 transition has a large SOC value in comparison to the other two compounds (Fig. 5). It must be noted that for BTaz-Ph-PXZ the first excited triplet state has significant CT character and the second excited triplet state has LE character, whereas the inverse is true for BTaz-Na-PXZ and BTaz-Th-PXZ (Table 2 and Fig. 5). Therefore, we need to compare this value with the T2→S0 transition for the naphthyl and thienyl linked compounds. Indeed, in comparison with the LE triplet states, the triplet states with CT character have the largest SOC value for the transition to S0. For BTaz-Ph-PXZ, the rISC pathway is likely outcompeting the radiative triplet decay to the ground state due to the higher-lying triplet state and smaller ΔEST. For BTaz-Na-PXZ, the SOC values for both the T1/T2→S0 transitions are small and these are therefore unlikely to occur.
BTaz-Th-PXZ has a very large SOC value for the T2→S0 transition and the T1–T2 energy splitting is only 0.07 eV, making vibronic mixing between these two states possible. The aforementioned, in combination with the relatively large ΔEST, is likely giving rise to the RTP that we observe in the TRES experiments. To enable rISC between excited states of different multiplicities, vibrational mixing of the CT and LE triplet states is required and this is plausible because of the small energy difference (0.07 eV, Table 1) between the two states. For the ISC pathway, the S1→T1 and S1→T2 transitions are investigated. Since the S1 state is of CT character for all compounds, according to the El Sayed rule,47 we expect the largest SOC values to be found for the CT→LE transition, which corresponds to the S1→T2 transition for BTaz-Ph-PXZ and to the S1→T1 transition for BTaz-Na-PXZ and BTaz-Th-PXZ. The phenyl linked molecule has a slightly higher SOC value than the naphthyl linked molecule for the CT→LE transition, but T2 is also higher in energy than S1 for BTaz-Ph-PXZ, whereas both T2 and T1 are lower in energy than S1 for BTaz-Na-PXZ (Fig. 5). Therefore, the S1→T2 ISC transition is not available for BTaz-Ph-PXZ and this could explain why the naphthyl variant has a higher triplet formation yield. BTaz-Th-PXZ has the highest SOC value for the ISC process, as is also reflected in the singlet oxygen quantum yields. Heavy atoms, such as sulfur, are known to afford stronger SOC effects, leading to higher ISC rates, and thereby increasing the chance for RTP to occur.48–54 In addition, the ground and excited state energy difference densities (Fig. 5 and Fig. S1, ESI†) show that the thiophene unit is involved in all transitions under investigation for BTaz-Th-PXZ, increasing the influence of the central sulfur atom on the SOC values. These results indicate that the thienyl linker imposes a significantly higher tendency to give ISC.
Conclusions
In this work, we presented the design and synthesis of three small molecule benzothiazole-π-bridge-phenoxazine emitters, each with a different aromatic bridging moiety. An extended photophysical study was performed, both in solution and in zeonex film. The fluorescence quantum yield goes down when changing the phenyl bridge to naphthyl and even further to thienyl, whereas the opposite is true for the ability to generate singlet oxygen. The emission mechanism, first in the solid state, was studied using time-resolved emission spectroscopy by doping the emitters in a zeonex matrix. These measurements showed that the emission wavelength is similar for all three dyads, although they possess different triplet energies. Consequently, thermally activated delayed fluorescence was seen for BTaz-Ph-PXZ and (somewhat weaker) for BTaz-Na-PXZ, whereas room temperature phosphorescence was noticed for BTaz-Th-PXZ, even in solution. The observation of phosphorescence in solution correlates with the high singlet oxygen generation and possibly opens up applications in other fields such as (image-guided) photodynamic therapy.55–57 Altering the π-bridge thus has a drastic effect on the excited/ground-state transition rates governing the emission mechanism, which consequently has a significant impact on the photophysical properties. These results provide further insights into the relationship between the bridging moiety and the photophysical properties of D-π-A type small-molecule emitters and contribute to the future development of applications relying on different types of emission from purely organic molecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Research Foundation – Flanders (FWO Vlaanderen) for financial support (projects G087718N, G0D1521N, I006320N, GOH3816NAUHL, the Scientific Research Community ‘Supramolecular Chemistry and Materials’ (W000620N), and PhD scholarship S. Paredis). The calculations were performed on the computers of the ‘Consortium des équipements de Calcul Intensif (CÉCI)’ (http://www.ceci-hpc.be), including those of the ‘UNamur Technological Platform of High-Performance Computing (PTCI)’ (http://www.ptci.unamur.be), for which we gratefully acknowledge the financial support from the FNRS-FRFC, the Walloon Region, and the University of Namur (Conventions No. 2.5020.11, GEQ U.G006.15, U.G018.19, 1610468, and RW/GEQ2016). A. Danos and A. P. Monkman are supported by EU Horizon 2020 Grant Agreement No. 732013 (HyperOLED) and EPSRC grant EP/T02240X/1.References
- J. Kalinowski, in Electrical and Related Properties of Organic Solids, Springer, Netherlands, Dordrecht, 1997, pp. 167–206 Search PubMed.
- L. Wang, L. Xiao, H. Gu and H. Sun, Adv. Opt. Mater., 2019, 7, 1801154 CrossRef.
- M. R. Narayan and J. Singh, in Excitonic and Photonic Processes in Materials, ed. J. Singh, R. T. Williams, Springer, 2015, pp. 229–251 Search PubMed.
- M. Segal, M. A. Baldo, R. J. Holmes, S. R. Forrest and Z. G. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 075211 CrossRef.
- T. Tsujimura, OLED Display Fundamentals and Applications, John Wiley & Sons, Inc., Hoboken, New Jersey, 2017 Search PubMed.
- D. T. Yonemoto, C. M. Papa, C. Mongin and F. N. Castellano, J. Am. Chem. Soc., 2020, 142, 10883–10893 CrossRef CAS PubMed.
- R. Chen, Y. Tang, Y. Wan, T. Chen, C. Zheng, Y. Qi, Y. Cheng and W. Huang, Sci. Rep., 2017, 7, 6225 CrossRef PubMed.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- X. Liang, Z. Tu and Y. Zheng, Chem. – Eur. J., 2019, 25, 5623–5642 CrossRef CAS PubMed.
- L. B. McGown and K. Nithipatikom, Appl. Spectrosc. Rev., 2000, 35, 353–393 CrossRef CAS.
- J. Gibson, A. P. Monkman and T. J. Penfold, Chem. Phys. Chem., 2016, 17, 2956–2961 CrossRef CAS PubMed.
- P. Data and Y. Takeda, Chem. – Asian J., 2019, 14, 1613–1636 CrossRef CAS PubMed.
- Q. Wei, N. Fei, A. Islam, T. Lei, L. Hong, R. Peng, X. Fan, L. Chen, P. Gao and Z. Ge, Adv. Opt. Mater., 2018, 6, 1800512 CrossRef.
- N. A. Kukhta and M. R. Bryce, Mater. Horiz., 2021, 8, 33–55 RSC.
- Z. An, C. Zheng, Y. Tao, R. Chen, H. Shi, T. Chen, Z. Wang, H. Li, R. Deng, X. Liu and W. Huang, Nat. Mater., 2015, 14, 685–690 CrossRef CAS PubMed.
- L. Gu, H. Shi, L. Bian, M. Gu, K. Ling, X. Wang, H. Ma, S. Cai, W. Ning, L. Fu, H. Wang, S. Wang, Y. Gao, W. Yao, F. Huo, Y. Tao, Z. An, X. Liu and W. Huang, Nat. Photonics, 2019, 13, 406–411 CrossRef CAS.
- J. Xu, A. Takai, Y. Kobayashi and M. Takeuchi, Chem. Commun., 2013, 49, 8447 RSC.
- B. Ventura, A. Bertocco, D. Braga, L. Catalano, S. D’Agostino, F. Grepioni and P. Taddei, J. Phys. Chem. C, 2014, 118, 18646–18658 CrossRef CAS.
- Q. Zhang, H. Kuwabara, W. J. Potscavage, S. Huang, Y. Hatae, T. Shibata and C. Adachi, J. Am. Chem. Soc., 2014, 136, 18070–18081 CrossRef CAS PubMed.
- W. Wei, Z. Yang, X. Chen, T. Liu, Z. Mao, J. Zhao and Z. Chi, J. Mater. Chem. C, 2020, 8, 3663–3668 RSC.
- P. Stachelek, J. S. Ward, P. L. dos Santos, A. Danos, M. Colella, N. Haase, S. J. Raynes, A. S. Batsanov, M. R. Bryce and A. P. Monkman, ACS Appl. Mater. Interfaces, 2019, 11, 27125–27133 CrossRef CAS PubMed.
- J. S. Ward, A. Danos, P. Stachelek, M. A. Fox, A. S. Batsanov, A. P. Monkman and M. R. Bryce, Mater. Chem. Front., 2020, 4, 3602–3615 RSC.
- H. L. Lee, K. H. Lee, J. Y. Lee and W. P. Hong, J. Mater. Chem. C, 2019, 7, 6465–6474 RSC.
- K. H. Lee, S. O. Jeon, Y. S. Chung, M. Numata, H. Lee, E. K. Lee, E. S. Kwon, M. Sim, H. Choi and J. Y. Lee, J. Mater. Chem. C, 2020, 8, 1736–1745 RSC.
- L. Xue, B. Cui, S. Xie and S. Yin, J. Phys. Chem. Lett., 2019, 10, 302–308 CrossRef CAS PubMed.
- Y. Gao, Y. Geng, Y. Wu, M. Zhang and Z.-M. Su, Dyes Pigm., 2017, 145, 277–284 CrossRef CAS.
- Y. Sagara, K. Shizu, H. Tanaka, H. Miyazaki, K. Goushi, H. Kaji and C. Adachi, Chem. Lett., 2015, 44, 360–362 CrossRef CAS.
- L. Mohammad, Q. Chen, A. Mitul, J. Sun, D. Khatiwada, B. Vaagensmith, C. Zhang, J. Li and Q. Qiao, J. Phys. Chem. C, 2015, 119, 18992–19000 CrossRef CAS.
- G. K. Dutta, S. Guha and S. Patil, Org. Electron., 2010, 11, 1–9 CrossRef CAS.
- Y. Wang and T. Michinobu, J. Mater. Chem. C, 2016, 4, 6200–6214 RSC.
- A. Mabrouk, A. Azazi and K. Alimi, J. Phys. Chem. Solids, 2010, 71, 1225–1235 CrossRef CAS.
- F. Li, M. Li, J. Fan, Y. Song, C.-K. Wang and L. Lin, J. Phys. Chem. A, 2020, 124, 7526–7537 CrossRef CAS PubMed.
- W. Che, Y. Xie and Z. Li, Asian J. Org. Chem., 2020, 9, 1262–1276 CrossRef CAS.
- B. Sk, S. Sharma, A. James, S. Kundu and A. Patra, J. Mater. Chem. C, 2020, 8, 12943–12950 RSC.
- A. A. Weekes, M. C. Dix, M. C. Bagley and A. D. Westwell, Synth. Commun., 2010, 40, 3027–3032 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. J. Penfold, J. Phys. Chem. C, 2015, 119, 13535–13544 CrossRef CAS.
- T. Cardeynaels, S. Paredis, J. Deckers, S. Brebels, D. Vanderzande, W. Maes and B. Champagne, Phys. Chem. Chem. Phys., 2020, 22, 16387–16399 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- K. Wang, C.-J. Zheng, W. Liu, K. Liang, Y.-Z. Shi, S.-L. Tao, C.-S. Lee, X.-M. Ou and X.-H. Zhang, Adv. Mater., 2017, 29, 1701476 CrossRef PubMed.
- E. Borowska, E. Felis and J. Kalka, Chem. Eng. J., 2016, 304, 852–863 CrossRef CAS.
- X. Han, X. Zhang, L. Zhang, M. Pan and J. Yan, R. Soc. Open Sci., 2018, 5, 180322 CrossRef PubMed.
- J. R. Kanofsky, in Singlet Oxygen: Applications in Biosciences and Nanosciences, 2016, Volume 1, p. 11 Search PubMed.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- J. Deckers, T. Cardeynaels, L. Lutsen, B. Champagne and W. Maes, ChemPhysChem, 2021, 22, 1488–1496 CrossRef CAS PubMed.
- T. Cardeynaels, S. Paredis, A. Danos, D. Vanderzande, A. P. Monkman, B. Champagne and W. Maes, Dyes Pigm., 2021, 186, 109022 CrossRef CAS.
- T. Cardeynaels, S. Paredis, A. Danos, A. Harrison, J. Deckers, S. Brebels, L. Lutsen, D. Vanderzande, A. P. Monkman, B. Champagne and W. Maes, Dyes Pigm., 2021, 190, 109301 CrossRef CAS.
- S. Hirata, Adv. Opt. Mater., 2017, 5, 1700116 CrossRef.
- P. Pander, A. Swist, R. Motyka, J. Soloducho, F. B. Dias and P. Data, J. Mater. Chem. C, 2018, 6, 5434–5443 RSC.
- N. A. Kukhta, R. Huang, A. S. Batsanov, M. R. Bryce and F. B. Dias, J. Phys. Chem. C, 2019, 123, 26536–26546 CrossRef CAS.
- J. S. Ward, R. S. Nobuyasu, A. S. Batsanov, P. Data, A. P. Monkman, F. B. Dias and M. R. Bryce, Chem. Commun., 2016, 52, 2612–2615 RSC.
- R. R. Allison, G. H. Downie, R. Cuenca, X.-H. Hu, C. J. Childs and C. H. Sibata, Photodiagn. Photodyn. Ther., 2004, 1, 27–42 CrossRef CAS PubMed.
- J. P. Celli, B. Q. Spring, I. Rizvi, C. L. Evans, K. S. Samkoe, S. Verma, B. W. Pogue and T. Hasan, Chem. Rev., 2010, 110, 2795–2838 CrossRef CAS PubMed.
- J. Deckers, T. Cardeynaels, H. Penxten, A. Ethirajan, M. Ameloot, M. Kruk, B. Champagne and W. Maes, Chem. – Eur. J., 2020, 26, 15212–15225 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc04885f |
| This journal is © The Royal Society of Chemistry 2022 |