Open Access Article
Open Access ArticleModeling the roles of rigidity and dopants in single-atom methane-to-methanol catalysts†
Haojun
Jia
 ab,
Aditya
Nandy
ab,
Aditya
Nandy
 ab,
Mingjie
Liu
ab,
Mingjie
Liu
 a and
Heather J.
Kulik
a and
Heather J.
Kulik
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +1-617-253-4584
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 4th January 2022
Abstract
Doped graphitic single-atom catalysts (SACs) with isolated iron sites have similarities to natural enzymes and molecular biomimetics that can convert methane to methanol via a radical rebound mechanism with high-valent Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediates. To understand the relationship of SACs to these homogeneous analogues, we use range-separated hybrid density functional theory (DFT) to compare the energetics and structure of the direct metal-coordinating environment in the presence of 2p (i.e., N or O) and 3p (i.e., P or S) dopants and with increasing finite graphene model flake size to mimic differences in local rigidity. While metal–ligand bond lengths in SACs are significantly shorter than those in transition-metal complexes, they remain longer than SAC mimic macrocyclic complexes. In SACs or the macrocyclic complexes, this compressed metal–ligand environment induces metal distortion out of the plane, especially when reactive species are bound to iron. As a result of this modified metal-coordination environment, we observe SACs to simultaneously favor the formation of the metal–oxo while also allowing for methanol release. This reactivity is different from what has been observed for large sets of square planar model homogeneous catalysts. Overall, our calculations recommend broader consideration of dopants (e.g., P or S) and processing conditions that allow for local distortion around the metal site in graphitic SACs.
O intermediates. To understand the relationship of SACs to these homogeneous analogues, we use range-separated hybrid density functional theory (DFT) to compare the energetics and structure of the direct metal-coordinating environment in the presence of 2p (i.e., N or O) and 3p (i.e., P or S) dopants and with increasing finite graphene model flake size to mimic differences in local rigidity. While metal–ligand bond lengths in SACs are significantly shorter than those in transition-metal complexes, they remain longer than SAC mimic macrocyclic complexes. In SACs or the macrocyclic complexes, this compressed metal–ligand environment induces metal distortion out of the plane, especially when reactive species are bound to iron. As a result of this modified metal-coordination environment, we observe SACs to simultaneously favor the formation of the metal–oxo while also allowing for methanol release. This reactivity is different from what has been observed for large sets of square planar model homogeneous catalysts. Overall, our calculations recommend broader consideration of dopants (e.g., P or S) and processing conditions that allow for local distortion around the metal site in graphitic SACs.
1. Introduction
Single-atom catalysts (SACs) are emergent catalysts that contain isolated single metal atoms dispersed on supports, which are frequently graphitic.1–7 SACs capture the inherent advantages of both homogeneous and heterogeneous catalysts by combining active site tunability with scalability.8,9 Nevertheless, the applicability of structure–property relationships derived from homogeneous or heterogeneous catalysts to predict the reactivity of SACs remains an outstanding question. Low site density and the short-lived, variable nature of SAC active sites10,11 fundamentally challenge many experimental techniques that bulk average over all sites, which limits the analysis of individual active sites. The harsh pyrolysis conditions used for SAC synthesis generate a distribution of active sites.12,13 Due to a lack of control over active site configuration, relationships between the structure of the SAC active site and the catalytic activity are challenging to deconvolute via experiment.14,15 Moreover, because the sub-nm scale can challenge even the highest-resolution spectroscopic probes that are sensitive to local variations in chemical environment,10,11 the structures, reactivity, and selectivity of SACs are poorly understood from an experimental perspective. Computational modeling enables us to study active site configurations of SACs with atomic precision, and can elucidate the effects of metal-local environment variation in SACs.In doped graphene SACs, some or all of the metal-coordinating atoms are substituted with different atoms that lead to formation of vacancies (e.g., a double vacancy) where the metal atom can bind to form the SAC active site.16 N-doped graphene, generated with nitrogen dopants, is the most common example of a support used in SACs.12,14,17–20 The identity of the coordinating atom alone, however, does not govern structure–property relationships, as different hybridization environments of the same element (e.g., pyridinic N vs. pyrrolic N) can lead to distinct SAC reactivity.8,19 Similarly, different coordinating atom identities provide distinct ligand field strengths which could influence SAC properties and catalysis.21–29
The properties that make SACs attractive also make them challenging to study with conventional computational modeling using density functional theory (DFT). The trade-offs between representing the system as an infinite model simulated with periodic boundary conditions (PBCs) versus as a finite model flake must be considered when simulating SACs. PBCs naturally reproduce the extended nature of crystalline materials.30,31 However, the higher cost of exact exchange in plane wave PBC calculations typically motivates the use of generalized-gradient approximation (GGA) functionals that can be sensitive to delocalization error,32,33 especially for the localized d orbitals of embedded transition-metal atoms.2,32,34–37 Additionally, PBCs may enforce unnecessary symmetry and rigidity in the metal-local environment in disordered SACs, which are known to exhibit curvature.27 Finite models,38 conversely, are more tractable for higher-cost methods (e.g., range-separated GGA hybrid functionals) that suffer less from delocalization error. The extent to which finite-size effects can influence predictions of SAC properties remains unclear.2,39
Using computation to understand structure–activity relationships in SACs is important because they are of the highest interest in catalyzing challenging reactions where only homogeneous catalysts have been successful. Strategies for SAC design require understanding which aspects of homogeneous catalysts can be preserved in an extended, heterogeneous catalyst. Two recent studies on molecular 14-membered pyridinic macrocycles, which are the smallest synthesized SAC mimics, show promise for the oxygen reduction reaction (ORR) in fuel cells.40,41 C–H bond activation42–46 (e.g., for methane-to-methanol conversion) remains an outstanding challenge due to the high bond dissociation energy of methane. The activity, selectivity, and stability must be addressed for scalable C–H activation catalyst design.21,22,47–49 Although many earth-abundant mid-row 3d transition-metal complexes (TMCs) have been demonstrated as homogeneous catalysts, the reactivity and selectivity in direct methane-to-methanol conversion under mild conditions of these TMCs is still very limited.49,50 Previous studies14,51–53 have shown that SACs can activate inert C–H bonds, but the differences in reactivity for C–H bond activation between SACs and TMCs remains unknown.
In this work, we investigate the effects of local structure on SAC reactivity for the challenging reaction of partial oxidation of methane to methanol. First, we calculate stability and structural properties of increasingly large SAC models to establish a benchmark of using finite models to simulate periodic graphene systems. We carry out a comprehensive structural study, comparing the metal–ligand bond lengths of 5- or 6-membered ring SACs, 14-membered macrocycles that most closely represent SACs, and octahedral TMCs for a range of candidate dopant atoms. Finally, we compare reaction energetics for methane-to-methanol conversion in SAC models to those that have been previously observed for TMCs22 to understand the role the rigid graphitic environment can play in tuning SAC reactivity in comparison to analogous TMCs.
2. Model systems
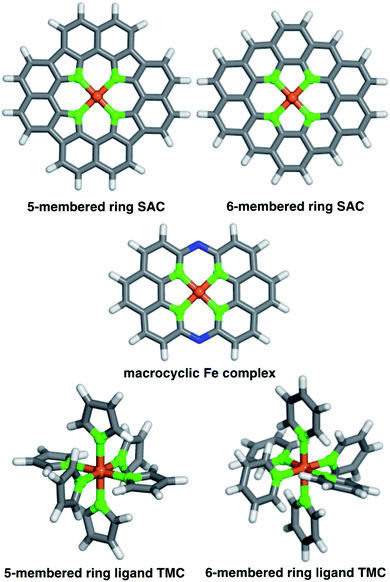
We studied two possible Fe(II) finite graphitic SAC models with identical metal-coordinating atoms of one of four elements (i.e., N, O, P, and S) in 5- or 6-membered rings within the graphene model (Fig. 1). First, we obtained a 58-atom graphene flake model from a data set of structures54 that were optimized using density functional tight binding. We used this initial model to construct a so-called FeX4C10 SAC model (where X = N, O, P, or S) with the chemical formula C36X4H16Fe that corresponds to all metal-coordinating atoms in 6-membered rings, i.e., pyridinic N for X = N. To construct this SAC model, we created a divacancy in the center of the graphene sheet, replaced the four nearest carbon atoms with a given metal-coordinating atom, and placed an Fe atom in the middle of the divacancy (ESI Fig. S1†). To study the size dependence of 6-membered ring SACs, we built model systems from increasingly large flakes ranging from 58 to 398 atoms, with all starting structures derived from the same database.54Next, we studied a FeX4C12 compound (i.e., chemical formula C40X4H16Fe), where all metal-coordinating atoms were in 5-membered rings (i.e., pyrrolic N for X = N, Fig. 1). We built the initial C46H16 structure in Avogadro v1.2.0,55 and formed the SAC model by removing two C atoms from the center and replacing the inward-facing C atoms of the remaining 5-membered rings with the metal-coordinating atoms (ESI Fig. S1†). This model was not studied in flakes of increasing radius due to ambiguities associated with the fact that formation of a five-membered ring requires formation of a likely unstable neighboring eight-membered ring in an otherwise defect-free model.
To understand the relationship between SACs and analogous molecular species, we also studied a recently experimentally characterized40 14-membered macrocyclic Fe(II) complex (Fig. 1). The 14-membered macrocyclic structure has been synthesized and characterized40 for the case of X = N, and we also study it by replacing N with the other three dopants (i.e., C24X4H12N2Fe, where X = N, O, P, or S) we study in the SAC models. To build all molecules, we either worked directly from the experimental crystal structure40 of C24N4H12N2Fe or by replacing the relevant dopant atoms. Finally, as a further point of comparison, we also constructed homoleptic mononuclear octahedral transition-metal complexes (TMCs) with monodentate ligands that are considerably more flexible than the other systems studied (Fig. 1). Initial structures of these TMCs with five- or six-membered ring ligands, i.e., N-coordinating pyrrole and pyridine, O-coordinating furan and 4H-pyran, P-coordinating phosphole and phosphinine, and S-coordinating thiophene and 4H-thiopyran, ligands were built using the molSimplify toolkit56 with both ligand force-field pre-optimization and trained metal–ligand bond length features enabled.57
3. Computational details
Gas-phase geometry optimizations and single-point energy calculations were performed using density functional theory (DFT) with a developer version of the GPU-accelerated electronic structure code TeraChem v1.9.58 The range-separated hybrid functional ωPBEh59 (default ω = 0.2 Bohr−1) was employed for all calculations with the LACVP* composite basis set, which consists of a LANL2DZ effective core potential60,61 for transition metals and the 6-31G* basis for all other atoms. The ωPBEh functional was chosen to avoid unphysical HOMO–LUMO gap closing that has been observed in larger systems with global hybrids.62,63 All singlet spin state calculations were carried out in a spin-restricted formalism, while other calculations (i.e., metal–hydroxo intermediates) were carried out in a spin-unrestricted formalism that employed level shifting64 of 1.0 for majority-spin virtual orbitals and 0.1 Ha for minority-spin virtual orbitals to enable the convergence of the self-consistent field (SCF). The default SCF convergence threshold of 3 × 10−5 Ha for the direct inversion of the iterative subspace (DIIS) error was applied. We focus on singlet states to isolate the effect of angular distortion on catalyst energetics in SACs in comparison to a prior data set of molecular complexes that showed angular distortion had no effect.22 While for these catalysts, intermediate-spin energetics are generally more favorable, trends in dopant-specific energetics are preserved (ESI Tables S1–S3†).Geometry optimizations were carried out with the translation-rotation-internal coordinate (TRIC)65 optimizer, using default tolerances of 4.5 × 10−4 hartree per Bohr for the maximum gradient, and 1 × 10−6 hartree for the change in SCF energy between steps. In the constrained calculations, the position of each atom in the SAC model along the z-direction was kept fixed to maintain a planar geometry. Converged unrestricted (i.e., metal–hydroxo) calculations were removed from the data set following established protocols22,66,67 if: (i) the expectation value of the S2 operator, 〈S2〉, deviated from its expected value of S(S + 1) by >1 μB2 or (ii) the Mulliken spin density on the metal differed from the spin multiplicity by >1 μB.
For the four classes of systems studied, complexes were simulated with iron assumed to be in a formal Fe(II) oxidation state when no catalytic ligand was present, meaning that the total charge of the overall model could vary. We simulated N- and P-coordinating 5-membered (6-membered) ring SAC models with net charges of −2 (+2), but all O- and S-coordinating SAC models with both 5-membered and 6-membered rings were simulated with a net charge of +2 to satisfy the octet rule (ESI Table S4†). We simulated all 14-membered macrocycles with a +2 net charge (ESI Table S4†). The formal charges assigned to the TMC ligands were neutral, except for pyrrole and phosphole, which were assigned a −1 charge (ESI Table S4†).
For catalytic intermediates of SAC models, the resting state SACs (i.e., square-planar Fe(II) complexes) were optimized first. An oxygen atom was added to these SACs at a distance of 1.65 Å, after which the geometry of the metal–oxo intermediate was optimized. Following the procedure developed in ref. 22, the optimized metal–oxo intermediate was used as the starting point for the metal–hydroxo species, which was generated by adding an H atom and re-optimizing in a doublet spin state. That metal–hydroxo structure was then used to generate the methanol-bound singlet intermediate by adding a methyl group to the optimized metal–hydroxo structures using an in-house Python script.
To determine the relative stability of SAC models, we computed the complexation energies of SACs, E(SAC), relative to the bare, doped flake model, E(flake), and a gas-phase low-spin Fe(II) ion, E(Fe(II)). The complexation energy, indicates the relative stabilization energy that the flake provides to the metal and is evaluated as follows:
| E(complexation) = E(SAC) − E(flake) − E(Fe(II)) | (1) |
In addition, we carry out an analysis on scaled metal–ligand bond lengths, drel(Fe–X), evaluated relative to the sum of covalent radii of each ligand element, X, with iron:
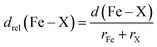 | (2) |
4. Results and discussion
4.1 Size effects of graphene flakes on SAC properties
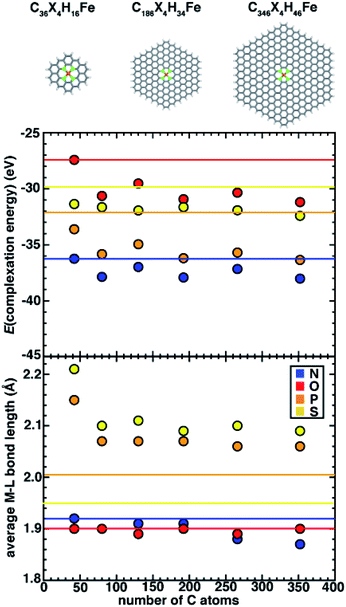
Simulating SACs requires consideration of the trade-offs between representing the system as an infinite model simulated with periodic boundary conditions (PBCs) versus as a finite (i.e., flake) model. Thus, we first aim to understand the approach to an asymptotic limit in model flakes that can be systematically increased in size (i.e., with 6-membered rings coordinating the metal). We focus on evaluating the effect of model size on both overall and local geometric properties as well as the stability (i.e., complexation energy). To determine the size effects of graphene flakes on SAC properties, we study six sizes of doped 6-membered ring graphene flakes ranging from a minimal model that is 13.6 Å in size (C36X4H16Fe, where X = N, O, P, or S) to a larger, 35.0 Å model (C346X4H46Fe, ESI Fig. S2†). We estimate the size of the flake models by the distance between the most distant H atoms prior to optimization. After full geometry optimization, we observe that the SACs with 2p coordinating elements (i.e., N and O) remain planar, while SACs with 3p coordinating elements (i.e., P and S) become distorted. For smaller flake sizes, complexation energies (see Computational details) are less favorable, and they generally approach asymptotic limits with a flake size of 186 carbon atoms (i.e., 225 atoms total), after which they no longer change significantly (Fig. 2). For all flake sizes, the relative stability (i.e., N > P > S > O) is unchanged, but the absolute stability, especially of O- and S-doped models, is somewhat more sensitive to model size (Fig. 2).Since the observed sensitivity of absolute complexation energies has some dependence on graphene flake size, we next investigated whether these changes were associated with differences in structure with increasing model size. When no constraints are applied during geometry optimization, the SACs with 2p (e.g., N and O) coordinating elements remained planar regardless of model size, whereas SACs with 3p (e.g., P and S) coordinating elements are distorted in a manner that is sensitive to the size of the model (Fig. 2). While complexation energies were sensitive to model size for both 2p and 3p elements, we aimed to separately determine if the distortion observed in 3p-coordinating SAC models also depends on model size. We first quantify the global distortion of these models by measuring the distance between the centers of mass of planar and distorted structures. We divide this measure by the size of the SAC model to estimate the size-independent degree of distortion. For all 3p-coordinating SACs, we observe decreased flake distortion with larger graphene models, which is consistent with expectations that larger model sizes should constrain the metal and reduce the degree of distortion (ESI Fig. S3 and Table S5†).
Although all 3p-coordinating SACs exhibit out-of-plane distortion, P-coordinating SACs are more distorted than corresponding S-coordinating SACs for the same model size (ESI Fig. S3 and Table S5†). This observation is surprising because it occurs despite only minor differences in covalent radii between P and S (1.07 and 1.05 Å, respectively). Since the center-of-mass-measured distortion may be influenced by metal-distal carbon atoms, we also measured the metal-local root-mean-square deviation (RMSD) of the metal and four coordinating atoms of P- and S-doped SACs with increasingly large models. We observe that the local RMSD values between the optimized and initial structures of the metal and the four metal-coordinating atoms of P- and S-doped SACs decrease when the flakes become larger, suggesting that increasing model size indeed leads to more constrained metal coordination (ESI Fig. S4†). Thus, observations of flake distortion based on the overall out-of-plane bending and local RMSD-based measures indicates that distortion decreases with increasing model size.
On the basis of the observation of the noticeable distortion, we aimed to understand its impact on the metal–ligand bond lengths of the increasingly large SACs because metal–ligand bond lengths are critical for understanding spin states68 and catalytic properties.21,22 We thus also analyzed the metal–ligand bond lengths of the increasingly large SAC models (Fig. 2 and ESI Table S6†). Consistent with the effects of reduced distortion for larger graphene models, we observe a general trend that metal–ligand bond lengths reduce with increasing SAC size (e.g., from 2.21 Å for the smallest C36S4H16Fe to 2.09 Å for the largest C346S4H46Fe). Thus, in terms of electronic effects of these shortened bond lengths, we can expect that metal sites in increasingly large SACs experience stronger ligand fields (i.e., due to shorter metal–ligand bond lengths). Nevertheless, despite these model-size-dependent trends, relative bond lengths (S > P ≫ N ∼ O) are qualitatively preserved across all flake sizes (Fig. 2). Furthermore, in contrast to complexation energies, we observe fast convergence for metal–ligand bond lengths with the size of SAC models from the second-smallest (i.e., C74X4H22Fe) flake onward, where changes in bond lengths are observed only for 3p elements or between the smallest and larger models (Fig. 2).
While quantitative differences are apparent for the smallest model sizes, qualitative trends in dopant-dependent complexation energies and bond lengths hold for all model sizes (Fig. 2). Thus, in order to aid comparison to macrocycles (i.e., 14-membered rings), TMCs, and alternative coordination within 5-membered-ring-coordinating SAC models, our subsequent analysis focuses on the smallest (i.e., C36X4H16Fe) 6-membered ring SAC model. We note that this means that the finite-size effects cannot be disregarded, but we expect the qualitative comparison of dopant-dependent SAC properties will hold.
4.2 Structural comparisons of SAC models and molecular complexes
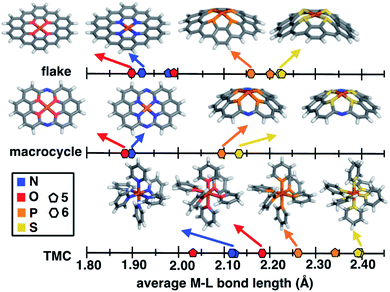
Despite evident structural similarities of SACs and single-site homogeneous catalysts, the relationship to similarities in their catalytic activities is only partially understood.40,41,69 We thus first investigate the structural role that the rigid graphitic environment plays in altering the metal-local environment in SACs in comparison to homogeneous catalysts. To isolate the effect of graphene rigidity on SAC structural properties, we compare the metal–ligand bond lengths of three distinct systems: (i) finite models of SACs, (ii) a recently synthesized40 rigid molecular complex believed to represent the local coordination environment in SACs, and (iii) mononuclear octahedral transition-metal complexes (TMCs, Fig. 1).The covalent radius of 2p dopants (i.e., N and O) is smaller than that of 3p dopants (i.e., P and S), but the graphitic environment always constrains the metal–ligand bond distance to be equivalent in comparison to molecular catalysts with low-denticity ligands. Nevertheless, a competing effect observed in the 3p-doped SACs (see Sec. 4.1) is that the metal and its coordinating atoms are distorted out of the plane (ESI Fig. S5†). To further isolate the effect of this distortion, we compare unconstrained 5- and 6-membered ring SAC models with constrained geometry optimizations in which we fix all atoms to lie in the same plane (i.e., the xy plane). As should be expected, applying this constraint leads to even shorter metal–ligand bond lengths in 3p-doped SAC models relative to the corresponding unconstrained structures (Fig. 3 and ESI Table S7†). Thus, the unfavorable SAC distortion that occurs is compensated for by lowering the degree of metal–ligand bond compression that is highly unfavorable when all atoms are constrained to lie in the same plane. For the smaller 2p dopants, the degree of compression is small enough that no distortion out of the plane is observed (ESI Fig. S6†).
Focusing on the 3p-coordinating SACs, 5-membered ring SACs exhibit more severe distortion relative to 6-membered ring SACs, likely due to the ability of this structure to accommodate larger dopant–dopant distances upon distortion (ESI Table S8†). Specifically comparing the individual 3p dopants, we observe a slight increase in distortion for P-coordinating SAC models relative to S-coordinating models (i.e., 5- or 6-membered ring SACs), consistent with the somewhat larger covalent radius of P than S (ESI Table S9†).
To put the distortion and compression of the bond lengths in SACs in perspective, we compare them to TMC bond lengths. The metal–ligand bond lengths of freely optimized SAC models span a large, 0.32 Å range, from 1.89 Å in O-doped 6-membered ring SACs to 2.21 Å for S-doped 6-membered ring SACs (Fig. 3 and ESI Table S7†). When the ligands can move freely in mononuclear octahedral TMCs, we observe both longer overall bonds and a somewhat larger range (0.35 Å) from O-coordinating furan (2.03 Å) to S-coordinating thiophene (2.38 Å). Thus, the SAC metal–ligand bond length is significantly compressed for all dopants in comparison to analogous TMCs by around 0.1 to 0.2 Å. The 14-membered macrocyclic complexes have very similar structural characteristics to the SACs due to the comparable rigidity. The O-doped 14-membered macrocyclic complexes have equivalently short metal–ligand bonds (i.e., 1.88 Å) to those in the SACs, and the structure is even less accommodating of the larger dopants, with the longest observed metal–ligand bond length in the S-coordinating model (i.e., 2.12 Å) corresponding to both shorter bond lengths and smaller overall range (i.e., 0.24 Å) of dopant-dependent bond lengths than for either SACs or TMCs. The fact that the metal–ligand bonds of the 14-membered macrocycle more closely resemble those of our SACs than TMCs is expected, given previous observations of similarities in activity between SACs and the macrocycle.40
As a specific example, metal–ligand bonds in TMCs with 5- and 6-membered ring ligands (e.g., 2.03 Å and 2.17 Å for furan and 4H-pyran) are consistently longer than those in analogous 5- and 6-membered ring SACs (e.g., 1.99 Å and 1.89 Å for O-doped 5- and 6-membered ring SACs). The shorter bond lengths of SACs (e.g., 1.92 Å in an N-doped 6-membered ring SAC and 2.11 Å in a pyridine TMC) indicate the influence of SAC rigidity on the active site. To quantify this effect on more equal footing between 2p and 3p dopants, we analyze scaled metal–ligand bond lengths, drel(Fe–X), relative to the sum of covalent radii of each ligand element, X, with iron (see eqn (2)) (ESI Table S9†). Using spin-state-dependent definitions of covalent radii,68 a drel(Fe–X) of around 0.90–0.95 is typical for a low-spin TMC. The drel(Fe–X) values are significantly shorter than this value in all SACs and 14-membered macrocycles, especially for the cases with 3p-coordination (ESI Table S10†). The 3p-coordinating 14-membered macrocycles have more compressed metal–ligand bonds (e.g., drel: 0.78 in the S-doped macrocycle) compared to equivalent SACs (e.g., drel: 0.87 and 0.89 in 5- and 6-membered ring SACs). Both absolute bond lengths and their trends are fairly insensitive to exchange-correlation functional, and most DFT functionals predict experimental bond lengths of transition metal complexes well.70 To validate this expectation, we compare our optimized bond lengths to those of the crystal structure of the 14-membered macrocycles and confirm the metal–ligand bond lengths are in good agreement (i.e., within around 0.05 Å).
Motivated by quantitative structural differences among 5- and 6-membered ring SACs and 14-membered macrocycles, we estimate the relative stability of these coordination environments (i.e., by computing the complexation energies). While all structures form favorably relative to the chosen reference in our energetic evaluation, we find that N-doped SACs and N-doped 14-membered macrocycles have the most favorable complexation energies of the systems studied. Due to the less crowded metal-coordination environment, complexation energies of 5-membered ring SACs are more favorable than the corresponding 6-membered ring SACs with the same coordinating atoms (ESI Table S11†). The complexation energy in the distorted 3p-coordinating SACs is up to 1.5 eV more favorable than the constrained case (ESI Table S11†). Overall, the coordination atom type and local chemical environment (i.e., five-membered or six-membered rings and degree of rigidity) both significantly influence the metal–ligand bond lengths and corresponding complexation energy of the systems. Constraining 3p-coordinating SACs to be planar reduces metal–ligand bond lengths in a manner that is likely unrealistic for 3p dopants, potentially leading to poor models of the structural environment in simulations that naturally enforce such a constraint (e.g., in calculations with PBCs).
4.3 Relating structural and catalytic properties of SACs
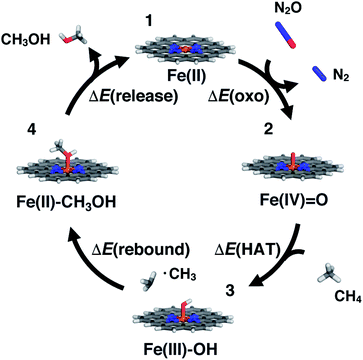
SACs with Fe(II) centers bear strong similarity to single-site homogeneous and biological catalysts capable of challenging reactions such as selective partial methane oxidation to methanol. To understand the relationship between catalytic properties of SACs and homogeneous counterparts for partial methane oxidation, we compare SAC reaction energetics to those from 385 low-spin Fe(II) TMCs studied previously.22 For consistency with this prior work,22 we evaluate the reaction energetics for the radical rebound mechanism71 of methane-to-methanol conversion on both fully optimized and partially constrained SAC models. In brief, to follow the radical rebound mechanism71 we start from the resting state structure (1) and form a high-valent terminal Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (2) via two-electron oxidation (Fig. 4). We evaluate the oxo formation energy, ΔE(oxo), using the common oxidant nitrous oxide, N2O,72,73 as the oxygen atom source
O (2) via two-electron oxidation (Fig. 4). We evaluate the oxo formation energy, ΔE(oxo), using the common oxidant nitrous oxide, N2O,72,73 as the oxygen atom source| ΔE(oxo) = E(2) − E(1) + E(N2) − E(N2O) | (3) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O catalyzes hydrogen atom transfer (HAT) from methane to form methyl radical. We calculate the ΔE(HAT) energy as
O catalyzes hydrogen atom transfer (HAT) from methane to form methyl radical. We calculate the ΔE(HAT) energy as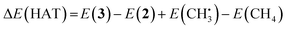 | (4) |
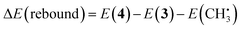 | (5) |
To complete the catalytic cycle, the SAC must then release the methanol and return to the resting state (1, see Fig. 4). We compute the energetics of methanol release, ΔE(release), as
| ΔE(release) = E(1) + E(CH3OH) − E(4) | (6) |
For the above formal oxidation states, we confirmed we converged to these states in our calculations by carrying out Mulliken spin density analysis (ESI Table S12†). The closed-shell calculations ensure that a nominal Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediate is studied during oxo formation, as determined by the total charge of the system. For the open-shell Fe(III)–OH species, the spin is localized on the metal (ESI Table S12†). These observations were corroborated by natural bonding orbital analysis that confirmed that changes in the coordinating atoms (e.g., N vs. O or S) did not dramatically change the degree of charge localized on the metal (ESI Table S13†). We also confirmed that formation of the metal–oxo was generally more favorable than oxygen addition to the organic coordinating atoms, except in the case of P-doped structures that could form a μ-oxo not feasible in the presence of the metal (ESI Table S14†). While the present work allows us to evaluate the radical rebound mechanism, we have not addressed the well-known selectivity challenges for methane to methanol conversion.74,75 Future work should also address whether favorable methanol activation could in fact be a limiting factor in SACs or if the scaling relationship can be broken between activation on methane versus methanol.
O intermediate is studied during oxo formation, as determined by the total charge of the system. For the open-shell Fe(III)–OH species, the spin is localized on the metal (ESI Table S12†). These observations were corroborated by natural bonding orbital analysis that confirmed that changes in the coordinating atoms (e.g., N vs. O or S) did not dramatically change the degree of charge localized on the metal (ESI Table S13†). We also confirmed that formation of the metal–oxo was generally more favorable than oxygen addition to the organic coordinating atoms, except in the case of P-doped structures that could form a μ-oxo not feasible in the presence of the metal (ESI Table S14†). While the present work allows us to evaluate the radical rebound mechanism, we have not addressed the well-known selectivity challenges for methane to methanol conversion.74,75 Future work should also address whether favorable methanol activation could in fact be a limiting factor in SACs or if the scaling relationship can be broken between activation on methane versus methanol.
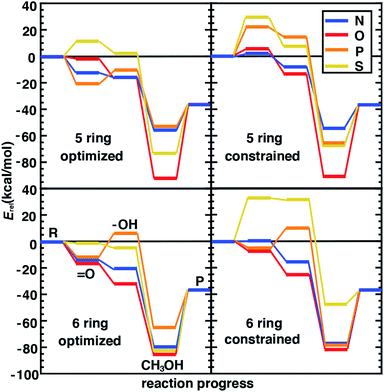
Following our observations of differences in the stability of distorted and constrained 3p-doped SACs, we would expect such constraints to also alter catalytic properties. In addition, the nature of the surrounding coordination environment (i.e., 5-membered vs. 6-membered rings), and the elements coordinating the metal are expected to also play a role in determining catalytic properties. Although for N- and O-doped 5- and 6-membered ring SAC models, constraints did not have any effect on the resting state structure and thus were not expected to influence reaction energetics, we do observe some differences between constrained and unconstrained structures (Fig. 5 and ESI Table S7†). These differences in 2p-coordinated SACs arise due to distortion favored in the reaction intermediates that were absent in the resting state (e.g., especially the metal–oxo, Fig. 5). When unconstrained, the metal–oxo, –hydroxo, and methanol–bound intermediates all exhibit out-of-plane metal distortion of around 5–10°, consistent with prior results21 (ESI Fig. S6†). Because this distortion is generally largest for the metal–oxo, this intermediate is most strongly destabilized for constrained SACs, which in turn influences both oxo formation and hydrogen atom transfer energetics (Fig. 5).
The distortion observed in unconstrained P- and S-doped SAC models was expected to have a much more noticeable effect on the reaction coordinate because it affected resting state energetics. Indeed, while some intermediates are similar in energy (e.g., the methanol-bound intermediate in S-coordinating 5-membered ring SACs) with and without constraints, the likely rate-limiting steps of oxo formation and HAT are more favorable in the structures that allow for distortion with 3p-coordinating SACS (Fig. 5). We attribute the differences in energetics to differences in the bond lengths rather than angles because the distortion largely moves the metal out of the plane simultaneously with the dopants. This observation is also consistent with our prior studies22 that suggest bond length was most important for tuning singlet Fe(II) reaction thermodynamics in TMCs. Overall, our analysis suggests that the freely optimized SACs with 3p dopants (e.g., P-doped, five-membered ring SACs) are competitive with more well studied N-doped SACs because methanol release energetics are relatively favorable without strongly destabilizing oxo or HAT formation (Fig. 5). We focus here on low-spin states to isolate the effect of angular distortion on catalyst energetics in SACs in comparison to this prior data set. We observe general trends are preserved (e.g., for Fe/N systems with five-membered versus six-membered rings) if we had instead computed intermediate-spin energetics (ESI Tables S1–S3†).
We next compare the catalytic performance of these SAC models with the set of previously studied TMCs.22 The TMCs from our previous study have four coordinating minimal model ligands in a square pyramidal geometry constrained to specific metal–ligand bond lengths that correspond to both slightly stretched and compressed bonds with respect to their equilibrium values (i.e., by around 0.2 Å) along with out-of-plane distortions (i.e., the dihedral of the metal with three ligand atoms) of the metal coordination environment. In comparison to these TMCs, we had observed that the SAC structure compresses the metal–ligand bond length to the lower end of the range or even shorter (see Sec. 4.2). In combination with the distinct local environment around the metal-coordinating atoms, SAC models exhibit significantly different energetics from those of the TMCs. Generally, SAC models exhibit more thermoneutral ΔE(oxo) while displaying comparable ΔE(HAT) and ΔE(release) to TMCs from prior work (Fig. 6). These observations are not strongly sensitive to the choice of hybrid DFT exchange-correlation functional, instead suggesting distinct reactivity between the SAC models and TMCs (ESI Fig. S7 and S8†).
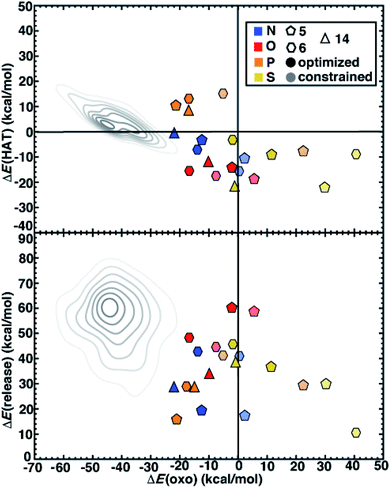 | ||
| Fig. 6 ΔE(oxo) vs. ΔE(HAT) (top) and ΔE(oxo) vs. ΔE(release) (bottom) reaction energies (in kcal mol−1) of representative TMCs from prior work22 compared to 5-membered (pentagons) and 6-membered (hexagons) ring SAC models along with 14-membered macrocyclic Fe complexes (triangles). The SACs and macrocycles are colored by the metal-coordinating atoms in the ligands, as indicated in inset legend. The TMCs from prior work are the full low-spin Fe(II) subset from the square pyramidal constrained (SQ) set of ref. 22. The kernel density estimates of the distributions for the TMC set are colored in gray and shown as contour lines with decreasing saturation in 7 evenly spaced levels. The SACs are distinguished by full geometry optimization (opaque) and constrained optimization (translucent). | ||
Despite distinct reaction energetics for SACs and TMCs with common metal-coordinating atoms, there are some notable cases where the two types of catalysts have comparable properties (ESI Fig. S9 and S10†). Several O-doped SACs behave similarly to the square pyramidal Fe(II) TMCs with O-atom coordination in a somewhat stretched (i.e., 10° out-of-plane distortion and 2.2 Å bond distance) structure (ESI Fig. S10†). This correspondence in energetics does not coincide with correspondence in structure, as the SAC has significantly more compressed metal–ligand bonds (1.9 Å). Somewhat surprisingly, we find more comparable reaction energies between SACs and TMCs in tetragonal equilibrium geometries from prior work22 which contain axial ligands that are not present in our SAC models (ESI Fig. S11†). Because the distal axial ligand tends to make oxo formation more favorable relative to that for compounds in the more structurally equivalent square planar set, the energetics of these TMCs coincide more with the SACs (ESI Fig. S12 and S13†). Overall, SACs increase the favorability for oxo formation, which we attribute to rigidity from the graphene flake strengthening the ligand field and stabilizing a high-valent metal–oxo without requiring the presence of an axial ligand common to TMCs and biological catalysts.
Next, we return to the energetics for the 14-membered macrocycle, which we would expect to behave more comparably to SAC models than to TMCs, despite also being a molecular complex. Reaction energetics are largely consistent between the macrocycles and the 6-membered ring SAC models, although some small differences are observed (Fig. 6). For the 14-membered macrocycle in comparison to SACs, the relative position of N-doped and P-doped models in terms of their ΔE(oxo) vs. ΔE(HAT) favorability is altered (Fig. 6). This reversal of 2p- and 3p-doped favorability is not observed for the O- and S-doped cases (Fig. 6). Overall, the N-doped 14-membered macrocycles exhibit more favorable oxo formation energy than the corresponding N-coordinating 6-membered ring SAC model. We attribute the differences between the two N-doped catalysts to be due to the shorter metal–ligand bond length of the 14-membered macrocycle (1.88 Å) relative to the 6-membered ring SAC model (1.92 Å) in the metal–oxo intermediate along with a larger out-of-plane distortion (19° vs. 11°, ESI Fig. S14†). Structures for the P-doped cases are more comparable, leading to similar energetics and explaining the change in relative favorability (ESI Fig. S14 and Table S7†).
The results compared here focus on reaction energetics due to scaling relations between the reaction thermodynamics and kinetic barriers in this work. Nevertheless, we selected representative favorable N-doped SACs for follow up analysis of the barriers as well (ESI Fig. S15 and S16†). From this analysis, we confirm that favorable thermodynamics for N-doped SACs in five-membered rings indeed correspond to relatively modest barrier heights for oxo formation and HAT (ESI Fig. S15 and S16†). This observation supports our focus on more computationally affordable reaction energetics in our large-scale screen.
5. Conclusions
While single-atom catalysts (SACs) consisting of metal atoms embedded in doped graphene represent promising catalysts, the extent to which design principles derived from homogeneous or heterogeneous catalysts, such as the applicability of scaling relations, can be extended to SACs remains largely unknown. Here, we focused on understanding the relationship between SAC structure and tradeoffs in key reaction steps in the selective partial oxidation of methane to methanol via a radical rebound mechanism at single Fe(II) sites.After confirming that qualitative conclusions about the dopant-dependent structural and stability properties on model SACs were invariant to model size, we carried out a systematic comparison of SACs to TMCs and macrocyclic mimics of SACs using range-separated hybrid DFT. We observed differences in the degree of distortion around the Fe(II) metal center depending on the dopant type. In the resting state, we observed that 2p-coordinating species favored planar structures, whereas significant distortion was observed with 3p dopants. We attributed this difference to differences in the relative covalent radii of these dopants, where the penalty for forming a very short metal–dopant bond in the 3p cases was so large that distortion of the graphitic substrate was preferred. In comparison to transition-metal complexes, SAC model metal–ligand bond lengths were considerably shorter, corresponding to a stronger ligand field, and recently characterized macrocyclic complexes exhibited the shortest metal–ligand bond lengths. Even with this significant compression in the bonding environment, P-doped SACs had energetics competitive with more well studied N-doped systems, with favorable methanol release and exothermic oxo formation. These steps were less favorable if we constrained the structures to be planar. Combined with our observations of model-size-dependent distortion at the metal center, these observations suggest that processing of doped graphitic catalysts that influences flexibility around the catalytic active site should influence reactivity.
Overall, analysis of the doped graphitic SAC reaction energetics indicated distinct behavior for most SAC models in comparison to prior work on TMCs, with SACs having more thermoneutral ΔE(oxo) while displaying comparable ΔE(HAT) and ΔE(release) to TMCs. While we attribute this effect to differences in ligand field, we observed that a set of TMCs with an axial ligand that is absent in our SAC models had more comparable oxo formation energetics. Overall, these results highlight the potential of SACs for altering the energetics of methane-to-methanol conversion by constraining metal–ligand bond distances to values distinct from those typically accessed by more flexible homogeneous catalysts.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was funded by the National Science Foundation (grant numbers CBET-1704266 and CBET-1846426) as well as a National Science Foundation Graduate Research Fellowship under Grant #1122374 (to A. N.). H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund, an AAAS Marion Milligan Mason Award, and an Alfred P. Sloan Fellowship in Chemistry, which supported this work. This work was carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. The authors thank Adam H. Steeves for providing a critical reading of the manuscript.References
- B. T. Qiao, A. Q. Wang, X. F. Yang, L. F. Allard, Z. Jiang, Y. T. Cui, J. Y. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed.
- X. F. Yang, A. Q. Wang, B. T. Qiao, J. Li, J. Y. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed.
- N. J. O'Connor, A. S. M. Jonayat, M. J. Janik and T. P. Senftle, Nat. Catal., 2018, 1, 531–539 CrossRef.
- B. Peters and S. L. Scott, J. Chem. Phys., 2015, 142, 104708 CrossRef PubMed.
- H. Y. Zhuo, X. Zhang, J. X. Liang, Q. Yu, H. Xiao and J. Li, Chem. Rev., 2020, 120, 12315–12341 CrossRef CAS PubMed.
- K. Jiang, S. Siahrostami, A. J. Akey, Y. B. Li, Z. Y. Lu, J. Lattimer, Y. F. Hu, C. Stokes, M. Gangishetty, G. X. Chen, Y. W. Zhou, W. Hill, W. B. Cai, D. Bell, K. R. Chan, J. K. Norskov, Y. Cui and H. T. Wang, Chem, 2017, 3, 950–960 CAS.
- K. Jiang, S. Siahrostami, T. T. Zheng, Y. F. Hu, S. Hwang, E. Stavitski, Y. D. Peng, J. Dynes, M. Gangisetty, D. Su, K. Attenkofer and H. T. Wang, Energy Environ. Sci., 2018, 11, 893–903 RSC.
- F. Liu, T. H. Yang, J. Yang, E. Xu, A. Bajaj and H. J. Kulik, Front. Chem., 2019, 7, 219 CrossRef CAS PubMed.
- A. Q. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- H. L. Fei, J. C. Dong, M. J. Arellano-Jimenez, G. L. Ye, N. D. Kim, E. L. G. Samuel, Z. W. Peng, Z. Zhu, F. Qin, J. M. Bao, M. J. Yacaman, P. M. Ajayan, D. L. Chen and J. M. Tour, Nat. Commun., 2015, 6, 8668 CrossRef CAS PubMed.
- A. Wang and T. Zhang, Nat. Energy, 2016, 1, 15019 CrossRef CAS.
- A. Zitolo, V. Goellner, V. Armel, M. T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937 CrossRef CAS PubMed.
- W. G. Liu, L. L. Zhang, W. S. Yan, X. Y. Liu, X. F. Yang, S. Miao, W. T. Wang, A. Q. Wang and T. Zhang, Chem. Sci., 2016, 7, 5758–5764 RSC.
- W. G. Liu, L. L. Zhang, X. Liu, X. Y. Liu, X. F. Yang, S. Miao, W. T. Wang, A. Q. Wang and T. Zhang, J. Am. Chem. Soc., 2017, 139, 10790–10798 CrossRef CAS PubMed.
- M. J. Dzara, K. Artyushkova, M. T. Sougrati, C. Ngo, M. A. Fitzgerald, A. Serov, B. Zulevi, P. Atanassov, F. Jaouen and S. Pylypenko, J. Phys. Chem. C, 2020, 124, 16529–16543 CrossRef CAS.
- K. Jiang and H. T. Wang, Chem, 2018, 4, 194–195 CAS.
- X. J. Cui, H. B. Li, Y. Wang, Y. L. Hu, L. Hua, H. Y. Li, X. W. Han, Q. F. Liu, F. Yang, L. M. He, X. Q. Chen, Q. Y. Li, J. P. Xiao, D. H. Deng and X. H. Bao, Chem, 2018, 4, 1902–1910 CAS.
- L. Yang, D. J. Cheng, X. F. Zeng, X. Wan, J. L. Shui, Z. H. Xiang and D. P. Cao, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6626–6631 CrossRef CAS PubMed.
- T. Mineva, I. Matanovic, P. Atanassov, M. T. Sougrati, L. Stievano, M. Clemancey, A. Kochem, J. M. Latour and F. Jaouen, ACS Catal., 2019, 9, 9359–9371 CrossRef CAS.
- Y. C. Li, X. F. Liu, L. R. Zheng, J. X. Shang, X. Wan, R. M. Hu, X. Guo, S. Hong and J. L. Shui, J. Mater. Chem. A, 2019, 7, 26147–26153 RSC.
- T. Z. H. Gani and H. J. Kulik, ACS Catal., 2018, 8, 975–986 CrossRef CAS.
- A. Nandy and H. J. Kulik, ACS Catal., 2020, 10, 15033–15047 CrossRef CAS.
- T. A. Betley, Y. Surendranath, M. V. Childress, G. E. Alliger, R. Fu, C. C. Cummins and D. G. Nocera, Philos. Trans. R. Soc., B, 2008, 363, 1293–1303 CrossRef CAS PubMed.
- A. Kazaryan and E. J. Baerends, ACS Catal., 2015, 5, 1475–1488 CrossRef CAS.
- K. Yuan, D. Lutzenkirchen-Hecht, L. B. Li, L. Shuai, Y. Z. Li, R. Cao, M. Qiu, X. D. Zhuang, M. K. H. Leung, Y. W. Chen and U. Scherf, J. Am. Chem. Soc., 2020, 142, 2404–2412 CrossRef CAS PubMed.
- X. H. Li, X. X. Yang, L. T. Liu, H. Zhao, Y. W. Li, H. Y. Zhu, Y. Z. Chen, S. W. Guo, Y. N. Liu, Q. Tan and G. Wu, ACS Catal., 2021, 11, 7450–7459 CrossRef CAS.
- H. S. Shang, X. Y. Zhou, J. C. Dong, A. Li, X. Zhao, Q. H. Liu, Y. Lin, J. J. Pei, Z. Li, Z. L. Jiang, D. N. Zhou, L. R. Zheng, Y. Wang, J. Zhou, Z. K. Yang, R. Cao, R. Sarangi, T. T. Sun, X. Yang, X. S. Zheng, W. S. Yan, Z. B. Zhuang, J. Li, W. X. Chen, D. S. Wang, J. T. Zhang and Y. D. Li, Nat. Commun., 2020, 11, 3049 CrossRef CAS PubMed.
- J. Q. Zhang, Y. F. Zhao, C. Chen, Y. C. Huang, C. L. Dong, C. J. Chen, R. S. Liu, C. Y. Wang, K. Yan, Y. D. Li and G. X. Wang, J. Am. Chem. Soc., 2019, 141, 20118–20126 CrossRef CAS PubMed.
- B. Z. Lu, Q. M. Liu and S. W. Chen, ACS Catal., 2020, 10, 7584–7618 CrossRef CAS.
- S. H. Yoo, M. Todorova, D. Wickramaratne, L. Weston, C. G. Van de Walle and J. Neugebauer, npj Comput. Mater., 2021, 7, 58 CrossRef CAS.
- B. R. Goldsmith, E. D. Sanderson, D. Bean and B. Peters, J. Chem. Phys., 2013, 138, 204105 CrossRef PubMed.
- H. J. Kulik, J. Chem. Phys., 2015, 142, 240901 CrossRef PubMed.
- A. M. Patel, S. Ringe, S. Siahrostami, M. Bajdich, J. K. Norskov and A. R. Kulkarni, J. Phys. Chem. C, 2018, 122, 29307–29318 CrossRef CAS.
- C. A. Gaggioli, S. J. Stoneburner, C. J. Cramer and L. Gagliardi, ACS Catal., 2019, 9, 8481–8502 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- P. Mori-Sanchez, A. J. Cohen and W. T. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- A. Calborean, C. Morari and P. Maldivi, J. Comput. Chem., 2018, 39, 130–138 CrossRef CAS PubMed.
- J. Li, X. Li, H. J. Zhai and L. S. Wang, Science, 2003, 299, 864–867 CrossRef CAS PubMed.
- T. Marshall-Roth, N. J. Libretto, A. T. Wrobel, K. J. Anderton, M. L. Pegis, N. D. Ricke, T. Van Voorhis, J. T. Miller and Y. Surendranath, Nat. Commun., 2020, 11, 7343 Search PubMed.
- M. Moriya, R. Takahama, K. Kamoi, J. Ohyama, S. Kawashima, R. Kojima, M. Okada, T. Hayakawa and Y. Nabae, J. Phys. Chem. C, 2020, 124, 20730–20735 CrossRef CAS.
- G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639 CrossRef CAS PubMed.
- J. H. Lunsford, Catal. Today, 2000, 63, 165–174 CrossRef CAS.
- Z. Z. Lan and S. M. Sharada, Phys. Chem. Chem. Phys., 2018, 20, 25602–25614 RSC.
- Z. Z. Lan and S. M. Sharada, Phys. Chem. Chem. Phys., 2020, 22, 7155–7159 RSC.
- P. L. Liao, R. B. Getman and R. Q. Snurr, ACS Appl. Mater. Interfaces, 2017, 9, 33484–33492 CrossRef CAS PubMed.
- A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Nørskov, Nat. Mater., 2017, 16, 225–229 CrossRef CAS PubMed.
- V. L. Sushkevich, D. Palagin, M. Ranocchiari and J. A. van Bokhoven, Science, 2017, 356, 523 CrossRef CAS PubMed.
- C. Jones, D. Taube, V. R. Ziatdinov, R. A. Periana, R. J. Nielsen, J. Oxgaard and W. A. Goddard, Angew. Chem., Int. Ed., 2004, 116, 4726–4729 CrossRef.
- Z. J. An, X. L. Pan, X. M. Liu, X. W. Han and X. H. Bao, J. Am. Chem. Soc., 2006, 128, 16028–16029 CrossRef CAS PubMed.
- K. Harrath, X. H. Yu, H. Xiao and J. Li, ACS Catal., 2019, 9, 8903–8909 CrossRef CAS.
- J. Y. Yuan, W. H. Zhang, X. X. Li and J. L. Yang, Chem. Commun., 2018, 54, 2284–2287 RSC.
- X. Tan, H. A. Tahini and S. C. Smith, J. Phys. Chem. C, 2021, 125, 12628–12635 CrossRef CAS.
- M. Fernandez, H. Q. Shi and A. S. Barnard, Carbon, 2016, 103, 142–150 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, Chem. Sci., 2017, 8, 5137–5152 RSC.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- H. J. Kulik, J. Y. Zhang, J. P. Klinman and T. J. Martinez, J. Phys. Chem. B, 2016, 120, 11381–11394 CrossRef CAS PubMed.
- C. M. Isborn, N. Luehr, I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2011, 7, 1814–1823 CrossRef CAS PubMed.
- V. R. Saunders and I. H. Hillier, Int. J. Quantum Chem., 1973, 7, 699–705 CrossRef.
- L. P. Wang and C. C. Song, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- A. Nandy, J. Z. Zhu, J. P. Janet, C. R. Duan, R. B. Getman and H. J. Kulik, ACS Catal., 2019, 9, 8243–8255 CrossRef CAS.
- C. R. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, J. Chem. Theory Comput., 2019, 15, 2331–2345 CrossRef CAS PubMed.
- M. G. Taylor, T. Yang, S. Lin, A. Nandy, J. P. Janet, C. R. Duan and H. J. Kulik, J. Phys. Chem. A, 2020, 124, 3286–3299 CrossRef CAS PubMed.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS.
- M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, J. Chem. Theory Comput., 2008, 4, 1449–1459 CrossRef PubMed.
- J. T. Groves and G. A. McClusky, J. Am. Chem. Soc., 1976, 98, 859–861 CrossRef CAS.
- D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma, K. Lee, F. Bonino, V. Crocella, J. Yano, S. Bordiga, D. G. Truhlar, L. Gagliardi, C. M. Brown and J. R. Long, Nat. Chem., 2014, 6, 590–595 CrossRef CAS PubMed.
- M. Barona, S. Ahn, W. Morris, W. Hoover, J. M. Notestein, O. K. Farha and R. Q. Snurr, ACS Catal., 2020, 10, 1460–1469 CrossRef CAS.
- A. A. Latimer, A. Kakekhani, A. R. Kulkarni and J. K. Nørskov, ACS Catal., 2018, 8, 6894–6907 CrossRef CAS.
- M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017, 56, 16464–16483 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08502f |
| This journal is © The Royal Society of Chemistry 2022 |