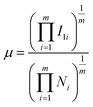Theoretical investigation on hydrogenation of dinitrogen triggered by singly dispersed bimetallic sites

Abstract

The conversion of molecular dinitrogen into ammonia is one of the most important chemical processes, which involves the inert N≡N bond activation and multi-step hydrogenation. To meet the requirements of complicated catalytic processes, single-cluster catalysts (SCCs) have emerged as a promising platform to trigger synergistic effects. Herein, we present a systematic investigation on the stability and activity of a series of singly dispersed bimetallic catalysts, M₁Co_n/CoO_x SCCs, for the hydrogenation of dinitrogen by first-principles calculations. Our results indicate that late transition metals are prone to form stable singly dispersed bimetallic clusters by doping the O vacancy on CoO surfaces. Due to the low oxidation state of the doped metals in the stable M₁Co_n/CoO_x SCCs, the chemisorption of N₂ is enhanced by the multiple “pull–push effect” of the isolated bimetallic sites. Subsequently, an improved electron descriptor (μ) is proposed to effectively estimate the correlation between the favorable bridging N₂ adsorption energies and the essential electronic characteristics of M₁Co_n/CoO_x SCCs, in which the influence of the metal d orbital electrons and the intrinsic 1st ionization energy are considered. We focus on the first hydrogenation in the associative mechanism on the multicenter of M₁Co_n/CoO_x SCCs, and the Pd₁Co₄/CoO_x SCC is proposed to exhibit superior charge buffer capacity towards thermal dinitrogen hydrogenation. Furthermore, a superimposed evaluation strategy associates the activity of nitrogen fixation on SCCs with certain intrinsic features of multi-active sites at both static and kinetic states. The present work not only provides a potential candidate for the thermal N₂-to-NH₃ conversion, but also sheds insights into the rational design of heterogeneous catalysts for thermal nitrogen fixation.

---

1. Introduction

Ammonia (NH₃) is a vital chemical for agriculture and industry and it can be directly synthesized on a large scale through the Haber–Bosch process (N₂ + 3H₂ → 2NH₃) under harsh conditions, in which the nitrogen and hydrogen atoms do not react until the strong N≡N and H–H bonds have been broken (the dissociative mechanism).¹ However, the reaction mechanism in enzymes is quite different, in which N₂ molecules are hydrogenated initially before N–N cleavage (the associative mechanism).² The principal obstacle of the thermal N₂-to-NH₃ conversion essentially lies in the inert N≡N bond activation and multi-step hydrogenation. Inspired by biological nitrogen fixation to improve the Haber–Bosch process, extensive efforts have been made to search for sustainable and clean methods for ammonia production, as well as effective catalysts with high performance.³

As the bridge of homogeneous catalysts and heterogeneous catalysts, single-atom catalysts (SACs) with well-defined single-atom dispersion on the surfaces^4,5 exhibit high selectivity and activity, as well as maximizing the utilization efficiency of supported metal atoms.^6,7 To adapt to the requirements of complicated catalytic reactions and break the limitation of a single adsorption site, single-cluster catalysts (SCCs), singly dispersed metal clusters anchored on nonmetallic supports with natural pores or defects, have emerged as promising candidates in the field of heterogeneous catalysis.^8–14 Singly dispersed bimetallic clusters anchored on the oxide surface (M₁A_n/AO_x) can be regarded as a typical category of SCCs, in which an oxygen atom on the metal oxide (AO_x) surface is substituted by a guest metal atom (M).¹⁵

It is noteworthy that the guest metal M in M₁A_n/AO_x shows a strong charge rearrangement.¹⁶ For example, the oxygen vacancy on the CeO₂ surface results in very stable anchoring sites for the Au adatom, which binds at the O vacancy site with two Ce nearest neighbors, forming AuCe₂ clusters.¹⁷ The charge transfer occurs from the reduced oxide surface to the supported metal atom, which results in a negatively charged Au^δ− adatom and leads to the formation of Au–Ce bonds. Benefiting from the presence of metal–metal bonds and the special electronic state of M₁A_n, which could trigger synergistic effects, singly dispersed bimetallic sites have been considered as a promising platform for complicated catalytic reactions, such as the reduction of NO to N₂ on the Pd₁Co_n/Co₃O₄ catalyst,⁸ and methanol partial oxidation (MPO) on the Ir₁Zn_n/ZnO catalyst.⁹ In our previous work,¹⁸ a high degree of N≡N triple bond activation occurs in a bridging manner over the Co–Rh bond of the bimetallic SCC Rh₁Co₃/CoO, and the co-adsorption of reactants is favorable on isolated Rh₁Co₃ sites, which are proposed to be directly hydrogenated to form the NNH intermediate in the thermal N₂-to-NH₃ conversion.¹² The catalytic ability of M₁A_n SCCs arises from both the electronic effect of doped low-valent metal M that serves as a charge buffer, and the complementary role of synergic metal A in catalysis, which offer more possibilities for bond cleavage/formation and contribute to achieving unique catalytic properties different from SACs. Additionally, active clusters in SCCs strongly prefer to bind adsorbates with certain sites, and such adsorbate-induced reconstructions can dynamically generate active sites during catalytic reactions, which is known as the cluster fluxionality and also partially responsible for the high catalytic activity of SCCs.^19,20

Due to the Brønsted–Evans–Polanyi (BEP) relation, the dissociation barrier of N₂ and the desorption energies of NH_x are limited by the adsorption energy of the N atom.^21–23 Rather than the N₂ dissociative adsorption, the NNH associative mechanism on the multicenter of SCCs can bypass the BEP relation.¹⁴ The electrochemical N₂ reduction reactions on SCCs have been proposed as one of the most attractive alternatives for the production of NH₃.^{1,10,13,24–33} However, the energy variation changes significantly when the chemical potential is increased by applying a negative electric potential because hydrogen is not entering as H₂ but as protons and electrons, H⁺ and e⁻.³⁴ The mechanism of thermal N₂-to-NH₃ conversion is totally different because of the definite activation energy of the reaction, in which H transfer, M–H bond cleavage and N–H bond formation should be considered intensively.

Using first-principles calculation, we present a systematic investigation on the stability and activity of a series of M₁Co_n/CoO_x SCCs for dinitrogen activation. Here, the electron descriptor of singly dispersed bimetallic sites is adopted to analyze the correlation between the favorable bridging N₂ adsorption energies and the intrinsic properties of M₁Co_n/CoO_x SCCs. We focus on the first hydrogenation in the associative mechanism of dinitrogen fixation and the correlation factors of dinitrogen hydrogenation triggered by bimetallic SCCs are discussed. Our results demonstrated that the Pd₁Co₄/CoO_x SCC exhibits superior charge buffer capacity towards thermal dinitrogen hydrogenation. The correlation of the activation energy in this work sheds insights into the rational design of heterogeneous catalysts for thermal nitrogen fixation.

2. Computational details

The calculations were based on spin-polarized density functional theory methods, as implemented in the Vienna Ab initio Simulation Package (VASP version 5.4) with projector-augmented wave pseudopotential.^35,36 The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional was used to describe the exchange–correlation interaction of valence electrons.³⁷ In this work, we have not included the vdW correction, because the commonly used approach for including the vdW interaction, such as the D3 correction, may lead to overestimation of chemisorption energies.³⁸ The cutoff energy for the plane wave basis set was taken as 400 eV. A Monkhorst-Pack grid of size 2 × 2 × 1 was used to sample the surface Brillouin zone. To partially correct the strong electron-correlation property of cobalt monoxide, DFT+U calculations were carried out with the parameter of U_eff = 3.0 eV for Co.³⁹ The convergence criterion of electronic iteration was set at 10⁻⁵ eV for energy and 0.03 eV Å⁻¹ for the maximal force. The transition states were obtained by relaxing the force <0.02 eV Å⁻¹ by using the dimer method. Atomic charges were calculated using the atom-in-molecule (AIM) theory proposed by Bader.⁴⁰

The CoO (011) surface was represented by a periodic slab model with vacuum layers of 12 Å constructed using the cubic CoO with cell parameters of a = b = c = 4.2667 Å. Since CoO is antiferromagnetic and has atomic moment on cobalt atoms, the primitive cubic unit cell of CoO was used to build the surface slab, which was previously proved to be the most energetically stable configuration for CoO.¹⁸ The slab model contains five layers of 60 atoms, and the three top-layer slabs of the surface were allowed to relax while the other layers were frozen during the geometry optimization.

3. Results and discussion

3.1 Stability and electronic structures of M₁Co_n/CoO_x SCCs

Different vacancies on the surface exhibit quite different binding capacities with the same doped metal.⁴¹ To evaluate the thermodynamic stabilities of SACs (doping the Co vacancy) and SCCs (doping the O vacancy) on the CoO surface as shown in Fig. 1, binding energies between 24 transition metals and the CoO surface with different vacancy defects were taken into consideration.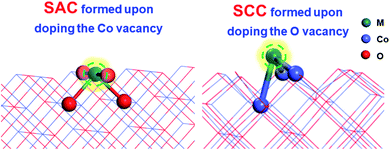

Fig. 1 The model structures of SACs (doping the Co vacancy) and SCCs (doping the O vacancy) on the CoO surface.

The binding energy E_b(SCC) of M₁ anchored on the O vacancy is calculated as,

E_b(SCC) = E_SCC − E_M1 − E_Ov

where E_SCC is the energy of the resulting M₁Co_n/CoO_x SCCs, E_M1 refers to the energy of the bulk phase of M per atom and E_Ov represents the energy of the CoO surface with the O vacancy. The binding energy E_b(SAC) of M₁ anchored on the Co vacancy is calculated as,

E_b(SAC) = E_SAC − E_M1 − E_Cov

where E_SAC is the energy of the resulting M₁/Co_x−1O_x SACs, E_M1 refers to the energy of the bulk phase of M per atom and E_Cov represents the energy of the CoO surface with the Co vacancy.

Based on the stronger binding energies as shown in Fig. 2, it was suggested that early transition metals are prone to form SACs with doping the Co vacancy on the CoO surface, while late transition metals (Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) can more easily generate SCCs with doping the O vacancy. In addition, the previous calculations suggest that the host metal oxide surfaces CoO(011) could stabilize most of the guest metal atoms (Ni, Ru, Ir, etc.) due to large energy barriers, which proves that the doped metal atoms are kinetically stable and not prone to migrate out of the surface O vacancy.⁴² The stable configurations of M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) and corresponding computed electron density difference maps are displayed in Fig. S1.† It is noteworthy that pure late transition metal surfaces are limited by the adsorption of molecular nitrogen and the first proton transfer step (N₂ + H⁺ + e⁻ → *NNH) on the volcano plots for ammonia formation.² For this reason, the following discussion focuses on the first hydrogenation of dinitrogen to reveal the activity of M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) in dinitrogen fixation.

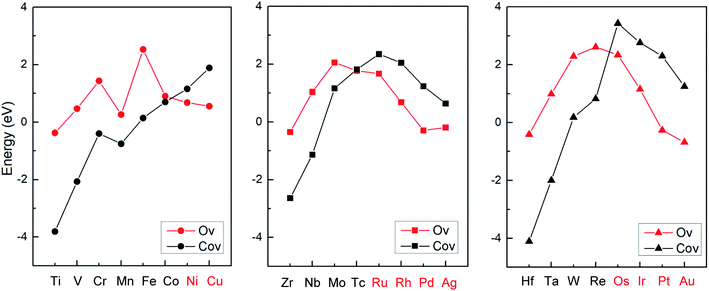Fig. 2 Binding energies between 24 transition metals and the CoO surface with different vacancy defects.

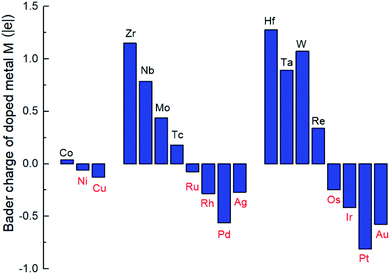
From Bader charge analysis, it is shown that the doped metals are negatively charged in the stable SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) as shown in Fig. 3. With the most negative charge in the period, the Bader charge on doped Pd and Pt is −0.56|e| and −0.81|e|, respectively. The results indicate that late transition metals (Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) are prone to be further reduced to obtain electrons and form singly dispersed bimetallic clusters with neighboring Co atoms in the process of metal doping to the O vacancy on the CoO surface. The phenomenon is related to the intrinsic electron characteristics of the doped transition metals, which can be reflected by the first ionization energy and the electron affinity energy as displayed in Fig. S2.† In the same period, the smaller the first ionization energy is, the more easily electrons are lost; the larger the electron affinity energy is, the more easily electrons are obtained. Therefore, early transition metals with smaller first ionization energy and electron affinity are more prone to lose electrons; while late transition metals with larger first ionization energy and electron affinity are more likely to gain electrons during doping with the O vacancy on the CoO surface, leading to the relatively stable singly dispersed bimetallic clusters, M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au).

Fig. 3 Bader charge of the doped metal M in M₁Co_n/CoO_x SCCs.

The composition of the singly dispersed bimetallic cluster, M₁Co_n, can be referenced to the Co–M distance between the doped metal M and neighboring Co atoms. The key bond lengths of Co–M in M₁Co_n/CoO_x SCCs are listed in Table S1.† It is noteworthy that the representation of composition is related to the distance criterion to some extent. The strong metal–metal interaction of the supported bimetallic cluster can be further confirmed by the overlap of the projected d-orbitals of the doped M and the neighboring Co atoms as illustrated in Fig. S3.† The present work can help to understand the formation of SCCs synthesized in the experiments so far, such as the Pd₁Co_n/Co₃O₄ catalyst⁸ and Ir₁Zn_n/ZnO catalyst,⁹ as well as give more insights into the development of SCCs into singly dispersed bimetallic clusters anchored on the oxide surface (M₁A_n/AO_x).

3.2 Adsorption of N₂ and H₂ on M₁Co_n/CoO_x SCCs

The adsorption of the N₂ molecule on SCCs is vital to activate the inert N≡N triple bond, and also meaningful for subsequent hydrogenation.⁴³ Owing to the low oxidation state of the doped metals in the stable M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au), the isolated bimetallic sites have the potential to enhance the chemisorption of N₂ to effectively activate the N≡N triple bond.

For these stable M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au), the adsorption configurations of dinitrogen with the end-on and the bridging modes are considered. The corresponding adsorption energies and the N–N bond lengths are listed in Table S2.† The N–N bond lengths in the bridging mode are in the range from 1.171 Å (Ir) to 1.205 Å (Pt), and the N–N bond lengths in the end-on mode are in the range from 1.118 Å (Au) to 1.151 Å (Os). The results show that the N₂ adsorption species with the bridging mode have a longer N–N bond length than those in the end-on mode on all M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au), which implies the stronger activation of the bridging N₂ and the stronger π-backdonation from the bimetallic sites of M₁Co_n/CoO_x SCCs to N₂. In addition, the bridging adsorption configurations of N₂ on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) are more stable than the corresponding end-on adsorption configurations. The adsorption energies of the bridging mode range from −3.18 eV(Os) to −0.04 eV(Au), and the adsorption energies of the end-on mode range from −1.91 eV(Ir) to 0.29 eV(Au). For N₂ adsorption on M₁Co_n/CoO_x SCCs (M = Ag, Au), the end-on configuration of N₂ is physisorption, which indicates that it is difficult for the adsorption and activation of N₂ to take place.

Furthermore, the electronic properties and the charge transfer induced by N₂ adsorption are discussed. As convinced by the projected density of states (PDOS) in Fig. S4,† for the bridging adsorption configurations of N₂ on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au), there is strong d–π* orbital coupling above or below the Fermi energy level, as well as obvious overlap between the d orbitals of M₁Co_n and the occupied orbitals of adsorbed N₂, contributing the multiple “pull–push effect”,¹¹ which could be considered as the reservoir for storing or supplying d electrons when needed. The strong interaction between the dinitrogen unit and bimetallic sites of M₁Co_n/CoO_x SCCs is mainly caused by the “acceptance–donation” of electrons,⁴⁴ which is mostly associated with the unoccupied and occupied d orbitals of the doped metal and neighboring cobalt. As shown in Fig. S5 and S6,† the charge density difference of adsorbed N₂ on SCCs further confirms the electron transfer between M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) and the adsorbed N₂, which shows that more electrons transfer from M₁Co_n/CoO_x SCCs to the bridging N₂ than to the end-on N₂ at the isovalue of 0.05 e Å⁻³. Obviously, the electron enrichment and decrease mainly occur between M₁Co_n/CoO_x SCCs and N₂, implying that M₁Co_n/CoO_x SCCs act as both electron donors and acceptors, which is well consistent with the PDOS analysis above.

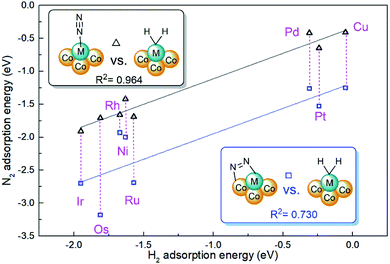
The cooperative effect of hydrogen adsorption is also an important issue of active site stability for dinitrogen activation.⁴⁵ For most doped metals of M₁Co_n/CoO_x SCCs, dissociative H₂ adsorption configurations are available, and corresponding adsorption energies are in the range from −1.95 eV(Ir) to −0.05 eV(Cu) as listed in Table S2.† However, M₁Co_n/CoO_x SCCs (M = Ag, Au) have no interaction with dihydrogen due to the full π-states of the doped metal. Nørskov and co-workers drew the volcano curves to describe the catalytic performance for hydrogen evolution on different metal surfaces,⁴⁶ and also proposed that Au and Ag are unreactive metals for the HER. As shown in Fig. 4, it was also found that there is a linear correlation with an R² of 0.964 between the H₂ adsorption energy and the end-on N₂ adsorption energy on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Os, Ir, Pt), which indicates the active limitation of single sites for the adsorbed species. In contrast, the linear relationship between the energies of bridging N₂ adsorption and H₂ adsorption is rough with an R² of 0.730, which means that the bridging adsorption on the bimetallic active site is beneficial to break through the restriction of catalytic nature of the single active metal.

Fig. 4 Relationship between N₂ adsorption and H₂ adsorption on M₁Co_n/CoO_x SCCs.

In an attempt to gain further insight into the relationship between the properties of the active site and the stability of bridging N₂-adsorbed species on M₁Co_n/CoO_x SCCs, an improved electronic descriptor (μ) was introduced, in which the influence of the metal d orbital electrons and the intrinsic 1st ionization energy were considered comprehensively.¹¹ The electron descriptor (μ) of the SCC is calculated using the following formula,

where N is the number of d orbital electrons for the doped metal atom or Co in the M₁Co_n cluster, I₁ is the 1st ionization energy of the doped metal atom or Co, and m = n + 1, which represents the sum of atoms in the singly dispersed bimetallic cluster, M₁Co_n. The parameters of I₁, N, and μ for M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) are listed in Table S3.† Due to the bridging N₂ adsorption configurations caused by the electron transfer from bimetallic d states to the antibonding orbitals of dinitrogen, it is found that the descriptor μ of M₁Co_n is related to the adsorption energies of bridging N₂ configurations adsorbed on the bimetallic sites as shown in Fig. 5. The relationship may be ascribed to the integrated electronic capability of SCCs. Therefore, the descriptor μ would be used as a referenced index to associate the intrinsic electronic properties of multiple sites with the cooperative adsorption.

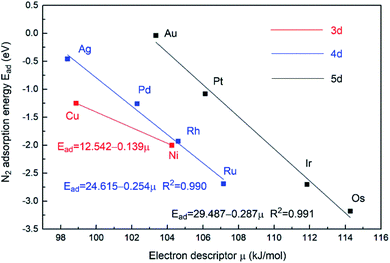Fig. 5 Relationship between bridging N₂ adsorption energies at bimetallic sties and the electron descriptor μ of M₁Co_n/CoO_x SCCs.

3.3 Hydrogenation of N₂ on M₁Co_n/CoO_x SCCs

Catalytic activities of SCCs originate from their ability for the bridging N₂ activation and dissociative H₂ activation, which is related to the intrinsic electronic properties of SCCs as discussed above. Followed by the favorable N₂ bridging adsorption, hydrogen is added in the form of H₂ molecules. The thermodynamically advantageous configurations for the co-adsorption of N₂ and H₂ on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Os, Ir, Pt) are shown in Fig. S7,† and they play an important role in the associative mechanism. In the thermal N₂-to-NH₃ conversion, the bridging N₂ at the bimetallic site in co-adsorption provides more possible ways for subsequent hydrogenation, either the alternating pathway or the evolutionary distal pathway.¹² From this viewpoint, multi-active sites on SCCs have certain advantages to overcome the limitation of SACs when complicated multi-steps are involved.

The energy of favorable co-adsorption (E_co) is linear to the energy of bridging N₂ adsorption with an R² of 0.885 as shown in Fig. S8,† indicating that N₂ bridging adsorption plays a leading role in the stability of the co-adsorption configuration. Due to the lower co-adsorption energies compared to the corresponding dinitrogen adsorption energies, it is suggested that the dissociative adsorption of H₂ on SCCs has an enhanced influence on the stability of the co-adsorption on SCCs. Therefore, the electronic descriptor of singly dispersed bimetallic sites, μ of SCCs, also correlates with the adsorption energy of co-adsorption in the same period.

The adsorbed bridging dinitrogen unit on SCCs can be further activated by H transferring to form NNH* from I to II as shown in Fig. 6a, which plays a critical role in the subsequent steps to generate ammonia. To evaluate the reactivity of the first step in dinitrogen hydrogenation on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Os, Ir, Pt), the activation energy barriers (E_a) and the reaction energies (E_r) are calculated using the following formulas, E_a = E_TSI-II − E_I and E_r = E_II-I − E_I, respectively. The activation energy barriers are in the range of 1.65 eV(Pd) to 3.09 eV(Ir) and the reaction energies range from −0.05 eV(Pd) to 0.87 eV(Ir) as listed in Table S4.†Fig. 6b shows the linear proportional relationship between the energy barrier and the reaction energy in the same period. In addition to the lowest activation energy barrier from I to II, the reaction energy of Pd₁Co₄/CoO_x SCC is negative, which suggests that the H transferred NNH* intermediate is more stable than the co-adsorption of N₂ and H₂. The complete reaction pathway for the N₂-to-NH₃ thermal conversion on the Pd₁Co₄/CoO_x SCC follows the alternating hydrogenation mechanism as shown in Fig. S9,† in which the N–N bond cleavage is not the rate-determining step.

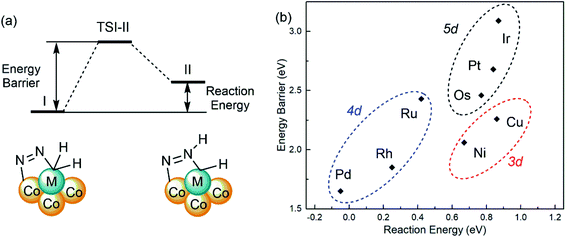Fig. 6 (a) Schematic diagram for H transferring on SCCs from I to II. (b) The linear proportional relationship between the energy barrier and the reaction energy.

As we proposed previously, the doped metal with large charge buffer capacity and low N₂ reduction activation energy is the ideal candidate for ammonia synthesis.¹² The negatively charged doped metals on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Os, Ir, Pt) could be regarded as electron reservoirs, which have the potential to regulate the charge variation in the dinitrogen hydrogenation. According to the Bader charge difference of doped M (Δξ_M) between I and II, the doped Pd exhibits minimal charge fluctuations, and Δξ_M is correlated with E_r with an R² of 0.821 as shown in Fig. S10.† However, the correlation of Δξ_M and E_a is poor with an R² of 0.457. To gain improved insight into hydrogenation of dinitrogen triggered by singly dispersed bimetallic sites, the essential electronic characteristics of SCCs, the co-adsorption energies, and the changes of geometric structures should be combined to explore the correlation of the activation energies.

When the bridging dinitrogen is hydrogenated to *NNH on M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Os, Ir, Pt), occupation of the π* orbitals in *NNH facilitates the increase of N–N bond length. Besides the N–N bond activation, the process also involves M–H bond cleavage and N–H bond formation. These bond length variations from I to II are listed in Table S5.† The root mean square deviation (RMSD) of these key bonds between I and II could be used to measure the variations of two geometric structures on the same bimetallic sites, which should also be related to the activation energy barrier. That is, the activation energy should be considered as the contribution of resisting the combined effects of geometric changes and the charge rearrangement, which is defined as the descriptor (α) calculated using the following formula, α = RMSD_bond × Δξ_M. Based on the descriptor α, the correlation with E_a is improved with an R² of 0.570. If the essential electronic characteristics of SCCs (μ) are stacked up to define the descriptor (β) with the formula of β = RMSD_bond × Δξ_M × μ, the R² of the linear relationship between β and E_a is 0.684. If the co-adsorption energy (E_co) is continued to stack, the descriptor (γ) is defined with the formula of γ = RMSD_bond × Δξ_M × μ × E_co, and the R² of the linear relationship between γ and E_a is 0.719. Therefore, the improved descriptors from α to γ with informative data could associate the activity of nitrogen fixation on SCCs with some intrinsic features of multi-active sites at static and kinetic states. Similar to the previously used descriptors, the complexity of the model increases exponentially with the number of the considered features.⁴⁷

4. Conclusion

In summary, we performed DFT calculations to systematically investigate the stability and activity of a series of singly dispersed bimetallic catalysts, M₁Co_n/CoO_x SCCs, in the hydrogenation of dinitrogen. Firstly, it is demonstrated that early transition metals with smaller first ionization energy and electron affinity are more prone to lose electrons, and are preferred to form relatively stable M₁/Co_x-1O_x SACs by doping with the Co vacancy on the CoO surface; while late transition metals with larger first ionization energy and electron affinity are more likely to gain electrons during doping with the O vacancy, leading to the relatively stable singly dispersed bimetallic clusters, M₁Co_n/CoO_x SCCs (M = Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, Au). Secondly, the strong interaction between the bridging dinitrogen unit and bimetallic sites of M₁Co_n/CoO_x SCCs is mainly caused by the “acceptance–donation” of electrons, which is mostly associated with the unoccupied and occupied d orbitals of the doped metal with negative charge and neighboring cobalt. Based on the descriptor identification, the correlation between the favorable bridging N₂ adsorption energies and the integrated electronic capability of M₁Co_n/CoO_x SCCs is effectively estimated. Furthermore, it is suggested that the activation energy barrier of dinitrogen hydronation should be related to the overlay of the essential electronic characteristics of SCCs and the N₂/H₂ co-adsorption energy at the static state, as well as the changes of geometric structures and charge arrangements in the kinetic process. We finally concluded that the Pd₁Co₄/CoO_x SCC is the most promising M₁Co_n/CoO_x SCC for the thermal dinitrogen hydrogenation due to the superior charge buffer capacity. Overall, the present work can help to understand the formation of SCCs synthesized in the experiments so far, as well as shed insights into the development of SCCs into singly dispersed bimetallic clusters anchored on the oxide surface (M₁A_n/AO_x) for the thermal N₂-to-NH₃ conversion.

Author contributions

X.-L. Ma, and J. Li conceived and designed the project. X.-L. Ma, Y. Yang and W.-Z. Yao carried out the calculations. X.-L. Ma, Y. Yang, L.-M. Xu and H. Xiao discussed the results and prepared the manuscript. All the authors reviewed and contributed to this paper.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (21902182), the Fundamental Research Funds for the Central Universities (2021YQHH04) and the Training Program of Innovation and Entrepreneurship for Undergraduates (C202003262).

References

1. G. Qing, R. Ghazfar, S. T. Jackowski, F. Habibzadeh, M. M. Ashtiani, C. P. Chen, M. R. Smith III and T. W. Hamann, Chem. Rev., 2020, 120, 5437–5516.
2. E. Skulason, T. Bligaard, S. Gudmundsdottir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jonsson and J. K. Norskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245.
3. Q. Wang, J. Guo and P. Chen, J. Energy Chem., 2019, 36, 25–36.
4. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
5. J.-C. Liu, Y. Tang, Y.-G. Wang, T. Zhang and J. Li, Natl. Sci. Rev., 2018, 5, 638–641.
6. A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
7. J. Liu, ACS Catal., 2016, 7, 34–59.
8. L. Nguyen, S. Zhang, L. Wang, Y. Li, H. Yoshida, A. Patlolla, S. Takeda, A. I. Frenkel and F. Tao, ACS Catal., 2016, 6, 840–850.
9. L. Nguyen, S. Zhang, L. Tan, Y. Tang, J. Liu and F. F. Tao, ACS Sustainable Chem. Eng., 2019, 7, 18793–18800.
10. B. Han, H. Meng, F. Li and J. Zhao, Catalysts, 2020, 10, 974.
11. X. Zheng, Y. Liu and Y. Yao, Chem. Eng. J., 2021, 426, 130745.
12. X. L. Ma, J. C. Liu, H. Xiao and J. Li, J. Am. Chem. Soc., 2018, 140, 46–49.
13. G. Zheng, L. Li, Z. Tian, X. Zhang and L. Chen, J. Energy Chem., 2021, 54, 612–619.
14. J.-C. Liu, X.-L. Ma, Y. Li, Y.-G. Wang, H. Xiao and J. Li, Nat. Commun., 2018, 9, 1–9.
15. N. López and F. Illas, J. Phys. Chem. B, 1998, 102, 1430–1436.
16. R. Rousseau, V.-A. Glezakou and A. Selloni, Nat. Rev. Mater., 2020, 5, 460–475.
17. M. F. Camellone and S. Fabris, J. Am. Chem. Soc., 2009, 131, 10473–10483.
18. S. Zhang, L. Nguyen, J. X. Liang, J. Shan, J. J. Liu, A. I. Frenkel, A. Patlolla, W. Huang, J. Li and F. F. Tao, Nat. Commun., 2015, 6, 7938.
19. B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048.
20. B. Zandkarimi and A. N. Alexandrova, J. Phys. Chem. Lett., 2019, 10, 460–467.
21. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42.
22. T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217.
23. S. Dahl, A. Logadottir, C. J. H. Jacobsen and J. K. Nørskov, Appl. Catal., A, 2001, 222, 19–29.
24. Y. Gambo, S. Adamu, A. A. Abdulrasheed, R. A. Lucky, M. S. Ba-Shammakh and M. M. Hossain, Appl. Catal., A, 2021, 609, 117914.
25. H. Zhang, C. Cui and Z. Luo, J. Phys. Chem. C, 2020, 124, 6260–6266.
26. C. Yao, N. Guo, S. Xi, C. Q. Xu, W. Liu, X. Zhao, J. Li, H. Fang, J. Su, Z. Chen, H. Yan, Z. Qiu, P. Lyu, C. Chen, H. Xu, X. Peng, X. Li, B. Liu, C. Su, S. J. Pennycook, C. J. Sun, J. Li, C. Zhang, Y. Du and J. Lu, Nat. Commun., 2020, 11, 4389.
27. M. Li, Y. Cui, X. Zhang, Y. Luo, Y. Dai and Y. Huang, J. Phys. Chem. Lett., 2020, 11, 8128–8137.
28. C. Cui, H. Zhang and Z. Luo, Nano Res., 2020, 13, 2280–2288.
29. Z. W. Chen, L. X. Chen, M. Jiang, D. Chen, Z. L. Wang, X. Yao, C. V. Singh and Q. Jiang, J. Mater. Chem. A, 2020, 8, 15086–15093.
30. D. Ma, Z. Zeng, L. Liu, X. Huang and Y. Jia, J. Phys. Chem. C, 2019, 123, 19066–19076.
31. X. Zhang, A. Chen, Z. Zhang and Z. Zhou, J. Mater. Chem. A, 2018, 6, 18599–18604.
32. Z. W. Chen, J. M. Yan and Q. Jiang, Small Methods, 2018, 3, 1800291.
33. J.-C. Chen, H. Cao, J.-W. Chen, S.-J. Qian, G.-J. Xia, Y.-G. Wang and J. Li, J. Phys. Chem. C, 2021, 125, 19821–19830.
34. M. Boudart, J. Am. Chem. Soc., 1952, 74, 1531–1535.
35. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
36. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. B. Liu, L. Cheng, L. Curtiss and J. Greeley, Surf. Sci., 2014, 622, 51–59.
39. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
40. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
41. M. Ha, D. Y. Kim, M. Umer, V. Gladkikh, C. W. Myung and K. S. Kim, Energy Environ. Sci., 2021, 14, 3455–3468.
42. N. Liu, X.-L. Ma, J. Li and H. Xiao, J. Phys. Chem. C, 2021 DOI:10.1021/acs.jpcc.1c07706.
43. M. Zafari, A. S. Nissimagoudar, M. Umer, G. Lee and K. S. Kim, J. Mater. Chem. A, 2021, 9, 9203–9213.
44. W. Zhao, L. Chen, W. Zhang and J. Yang, J. Mater. Chem. A, 2021, 9, 6547–6554.
45. C. Ling, Y. Zhang, Q. Li, X. Bai, L. Shi and J. Wang, J. Am. Chem. Soc., 2019, 141, 18264–18270.
46. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
47. M. Zafari, D. Kumar, M. Umer and K. S. Kim, J. Mater. Chem. A, 2020, 8, 5209–5216.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08350c

---