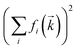Open Access Article
Open Access ArticleFlexibility is the key to tuning the transport properties of fluorinated imide-based ionic liquids†
Frederik
Philippi
 a,
Daniel
Rauber
a,
Daniel
Rauber
 b,
Oriele
Palumbo
b,
Oriele
Palumbo
 c,
Kateryna
Goloviznina‡
d,
Jesse
McDaniel
e,
David
Pugh
c,
Kateryna
Goloviznina‡
d,
Jesse
McDaniel
e,
David
Pugh
 f,
Sophia
Suarez
g,
Carla C.
Fraenza
h,
Agilio
Padua
f,
Sophia
Suarez
g,
Carla C.
Fraenza
h,
Agilio
Padua
 d,
Christopher W. M.
Kay
d,
Christopher W. M.
Kay
 bi and
Tom
Welton
bi and
Tom
Welton
 *a
*a
aDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, London W12 0BZ, UK. E-mail: t.welton@imperial.ac.uk
bDepartment of Chemistry, Saarland University, Campus B2.2, Saarbrücken, Germany
cConsiglio Nazionale delle Ricerche, Istituto dei Sistemi Complessi, Piazzale Aldo Moro 5, 00185 Rome, Italy
dLaboratoire de Chimie, École Normale Supérieure de Lyon, CNRS, 69364 Lyon, France
eSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
fDepartment of Chemistry, King's College London, 7 Trinity Street, London SE1 1DB, UK
gDepartment of Physics, Brooklyn College of CUNY, Brooklyn, New York, 11210, USA
hDepartment of Physics and Astronomy, Hunter College of CUNY, New York, 10065, USA
iLondon Centre for Nanotechnology, University College London, 17–19 Gordon Street, London WC1H 0AH, UK
First published on 3rd August 2022
Abstract
Ionic liquids are becoming increasingly popular for practical applications such as biomass processing and lithium-ion batteries. However, identifying ionic liquids with optimal properties for specific applications by trial and error is extremely inefficient since there are a vast number of potential candidate ions. Here we combine experimental and computational techniques to determine how the interplay of fluorination, flexibility and mass affects the transport properties of ionic liquids with the popular imide anion. We observe that fluorination and flexibility have a large impact on properties such as viscosity, whereas the influence of mass is negligible. Using targeted modifications, we show that conformational flexibility provides a significant contribution to the success of fluorination as a design element. Contrary to conventional wisdom, fluorination by itself is thus not a guarantor for beneficial properties such as low viscosity.
Introduction
Room temperature ionic liquids have moved up from a scientific curiosity to widespread use across science and technology.1–6 However, the realisation of these applications often faces obstacles, and the plateau of productivity is not yet reached.7–10 The main reason for this is the vast chemical space of all possible ionic liquids which rules out purely empirical selection criteria, making it difficult to choose an ionic liquid for a specific application.3,4,11 Ionic liquids are in general expensive and often difficult to work with, which further limits the number of candidates that can be explored. It is thus desirable to identify general concepts and design elements from a purposefully selected subset of ionic liquids.12–16 Such design elements would provide invaluable shortcuts when choosing an ionic liquid, reducing the need for empirical study to only a few promising candidates.The high viscosity of most ionic liquids presents a major challenge for practical applications.17,18 In this regard, ionic liquids are different to classical molecular solvents.19,20 A high viscosity complicates practical handling and slows down other transport properties such as electrical conductivity or diffusion. This reduces the performance of devices when ionic liquids are used, for example in lithium-ion batteries or organic solar cells. Hence, design elements which can influence the viscosity – and transport properties in general – are of critical importance.
Traditionally, design elements are identified in form of ‘structure–property relationships’.21–25 This means that changes to the molecular structure of an ionic liquid (such as the length of an alkyl side chain) are correlated with changes observed in the properties (such as the viscosity). However, this approach is often flawed by confounding variables. For example, changing the length of an alkyl side chain will have impacts on flexibility, mass, volume, and dispersion interactions. Instead, it is desirable to aim for targeted modifications, i.e. well defined changes to just one isolated variable.26 Where this is not possible, it is advisable to at least consider the potential impact of confounding variables.
In this work, we will focus on targeted modifications of the popular bis(trifluoromethylsulfonyl)imide [NTf2]− anion, which was introduced by Bonhôte et al. in 1996.27 Ionic liquids with this anion are now widely used as they generally have beneficial properties such as low melting points and low viscosities.28–30 These beneficial properties are commonly attributed to the high degree of fluorination and the conformational flexibility of the [NTf2]− anion.31–38 The high degree of fluorination leads to delocalisation of the negative charge, thus reducing the basicity and coordination tendency of the anion. The conformational flexibility of the [NTf2]− anion is due to the presence of two conformers, trans and cis, Fig. 1. These conformers are separated by a small barrier, hence the [NTf2]− anion is able to change shape quickly.
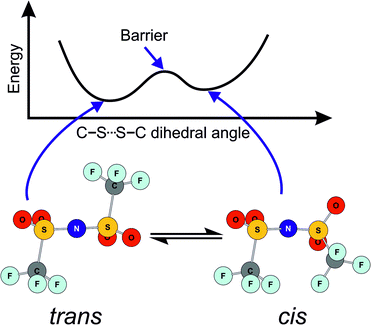 | ||
| Fig. 1 Schematic of the two minimum energy conformers of the [NTf2]− anion, and of the energy as a function of the C–S⋯S–C dihedral angle. Adapted from ref. 39. | ||
The CF3 groups are relatively large, and rotation around the N–S bonds requires significant sweep volume.39 Hence, changes in conformation also change the shape of the [NTf2]− anion significantly. In the ionic liquid, such bulky imide anions move by ‘slithering’ through the little free space available; however, this interpretation is currently debated.36,40 Accordingly, conformational flexibility is not relevant for anions which have small side groups and thus little sweep volume, such as the bis(fluorosulfonyl)imide [NFs2]− anion.35,36,39
We have previously demonstrated the importance of conformational flexibility by comparing two ionic liquids with similar anions, 1-butyl-3-methylimidazolium acetyl(trifluoromethylsulfonyl)imide ([C4C1im][NTfAc]) and 1-butyl-3-methylimidazolium (methylsulfonyl)(2,2,2-trifluoroacetyl)imide ([C4C1im][NMsTFA]).39 In this work, we study several targeted modifications of [C4C1im][NTf2] with a broad range of theoretical and experimental methods. In doing so, we are able to disentangle the effects of fluorination and conformational flexibility and provide a consistent picture of the relative importance of these design elements.
Detailed understanding of the effects of anion fluorination will enable the design of novel anions with similar or better performance in the future. This is especially important in the light of recent reports indicating that some fluorinated anions are persistent environmental contaminants.41–44 The insights in this work provide a starting point for the research on novel anions with lowered fluorine content without having to compromise on ionic liquid performance.
Materials and methods
Ab initio simulations
Full computational details can be found in the literature,39,45 previously unpublished results are given in the ESI.† The Gaussian 09 software package was used for the ab initio simulations in this work.46 Symmetry processing was bypassed for all calculations. The SCF convergence criterion was set to at least 10−9 on the density matrix and 10−7 on the energy. A pruned integration grid with 99 radial shells and 590 angular points per shell was used. Two-dimensional potential energy scans were performed at the MP2/cc-pVTZ//B3LYP-GD3BJ/6-311+G(d,p) level of theory. All electrons were included for the single point energies of stationary points (full MP2), whereas only valence electrons were used for the 2D potential energy surface scans (frozen core MP2) to save computational time. Volumes were calculated for the minimum energy conformer using the Multiwfn software package.47,48 The grid point spacing for the volume analysis was 0.15 bohr, with the wavefunction at the B3LYP-GD3BJ/6-311+G(d,p) level of theory with SCF convergence tightened to 10−10 on the density matrix and 10−8 on the energy.Physicochemical properties
Physicochemical properties were measured as described previously.45 Consistency of the physicochemical characterization with literature data was confirmed for [C4C1im][NTf2] and showed good agreement, see ESI.† Prior to all chemical measurements, the ionic liquids were dried in high vacuum with stirring for at least two days and handled using Schlenk techniques, glove box and NMR port. Information about water content is given in the ESI.†Thermal transitions
Thermal behaviour of the investigated ionic liquids in the range of 153 to 393 K was investigated by differential scanning calorimetry (DSC) on a DSC 1 STARe (Mettler Toledo, Germany) equipped with a liquid nitrogen cooling system. For the measurement, approximately 10 mg of the sample were weighed into an aluminium crucible inside a glove box and the filled crucible was then hermetically sealed. The sample was then subjected to heating from 298 to 393 K with a heating rate of +1 °C min−1, followed by a 5 min isothermal step at 393 K to remove thermal history of the sample. The samples were then cooled to 153 K with a cooling rate of −1 °C min−1, followed by a 5 min isothermal step and heating to 298 K with +1 °C min−1. Glass transitions were determined using the midpoint methods, while the other thermal events are given as the peak maximum.Viscosity
Shear dependent viscosity η was measured on a Physica MCR301 rheometer (Anton Paar, Austria) on a vibration isolated table using a setup with cone-plate geometry. The cone had a nominal diameter of 49.95 mm and a distance between its tip and the plate of 0.101 mm. All measurements were conducted under nitrogen atmosphere to avoid water uptake. After thermal equilibration the viscosities of the samples were measured by applying 30 different shear rates from 5 to 80 s−1 with linear spacing. For each shear rate the data over 15 seconds was averaged. As ionic liquids at all temperatures showed no shear rate dependence (Newtonian fluid behaviour), the results for each measured temperature were averaged. The temperature dependent viscosity curves were constructed by repeating this procedure in 5 K steps from 298.15 K to 378.15 K. Maximum temperature deviation during the measurements was ±0.01 K. The uncertainty of the viscosity values is ±1.5% as estimated from multiple measurements of the same sample, comparison to literature values and temperature dependent viscosity standards.Molecular dynamics simulations
Polarisable MD simulations were run using the LAMMPS49 software package, version 7 Aug 2019, ttdamp branch (the temperature grouped Nosé–Hoover thermostat (tgNH) is available in the USER-DRUDE package since version 24 Dec 2020).50,51 We used the CL&Pol/TG-NH force field as described previously,51–54 with the standard force field parameters for the [C4C1im]+ cation and the [NTf2]− anion.55–57 The procedure of force field extension to [CHTf2]− anion is described in ESI.† The initial LAMMPS data files were created using fftool (https://github.com/paduagroup/fftool) and Packmol58 with 512 cations and 512 anions in a periodic cubic box, explicit polarisation effects were introduced using polariser and scaleLJ scripts (https://github.com/paduagroup/clandpol). Details on the simulation setup are given in the ESI.†The prealpha software package was used for processing of the trajectory and for the calculation of the intermittent dihedral autocorrelation function, the mean squared and mean quartic displacements, rotational autocorrelation functions, charge arm distributions, and conformer distribution histograms. Source code, executable, input files and manual are available on Github (https://github.com/FPhilippi/prealpha).
SAXS patterns have been calculated using the TRAVIS software package, code version Jan 01 2019.59–61 The dynamic charge–charge correlation structure factor Scharge(k,t) is utilised to characterise relaxation dynamics in the ILs, and the details of this calculation are provided in ESI.† The code for dynamic charge–charge correlation structure factors is available on Github (https://github.com/jmcdaniel43/Structure_factor_FFT).
Results and discussion
Overview of targeted modifications
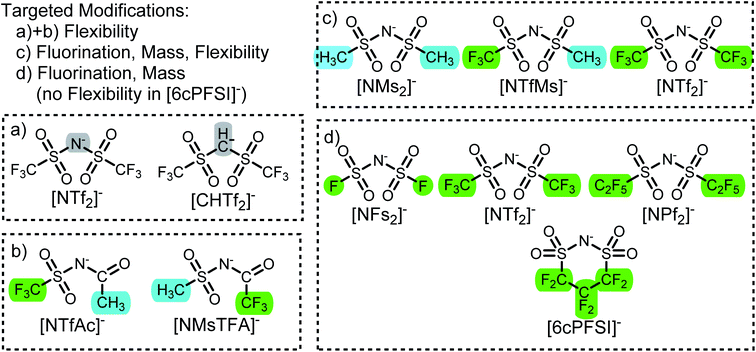
In this work we use targeted modifications of the [NTf2]− anion as a base structure to investigate the influence of conformational flexibility, fluorination, and mass. The targeted modifications are all accessible synthetically and are summarised in Fig. 2.The geometry of the [NTf2]− anion can be defined by two C–S–N–S dihedral angles, describing the rotation around each of the N–S bonds. The corresponding potential energy surface (PES) as a function of these two dihedral angles is shown in Fig. 3a. There are two unique minima, corresponding to the trans and cis conformers. For better comparison, we will use a threshold of 15 kJ mol−1 (shown as dotted lines) to define thermally accessible regions in the PES in this work.
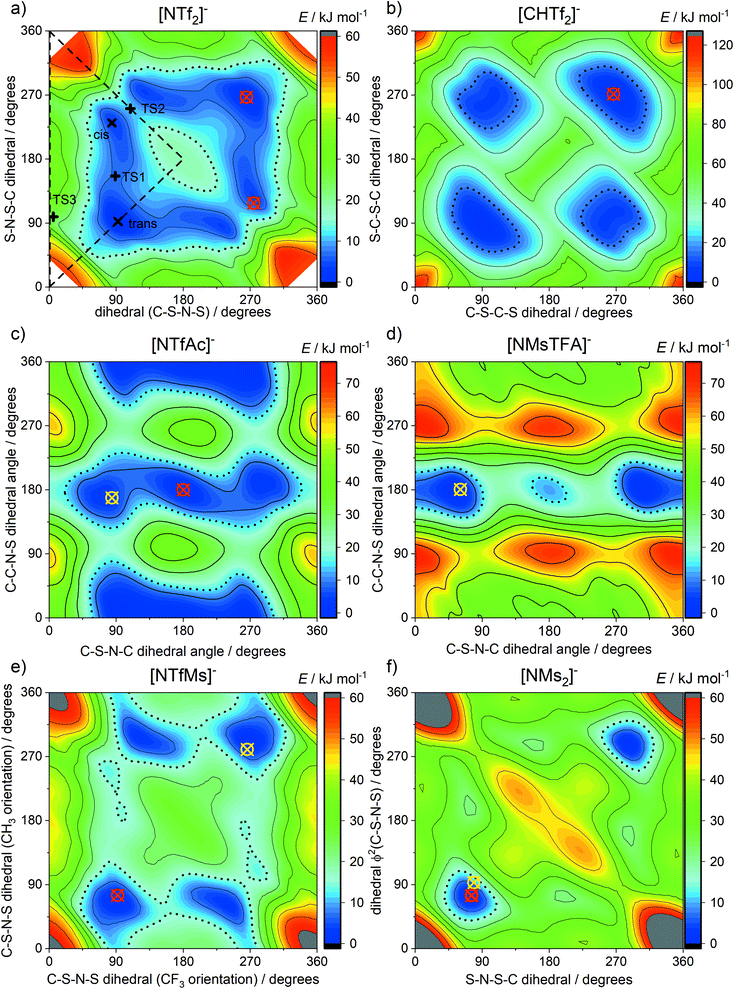 | ||
| Fig. 3 Potential energy surfaces of (a) [NTf2]−, (b) [CHTf2]−, (c) [NTfAc]−, (d) [NMsTFA]−, (e) [NTfMs]−, (f) [NMs2]−. Crosses indicate experimental dihedral angles obtained from crystal structures, red for anions and yellow for their corresponding free acids. See ESI† for details, and CSD deposition number 236629 and 236630 for [NTf2]−.101,102 Long dashed lines enclose the symmetrically unique region. The 15 kJ mol−1 isolines are drawn with black dots. | ||
The [CHTf2]− anion, Fig. 2a, is known as an intermediate in the synthesis of [CTf3]−, which is used as ligand in catalysis.62,63 We have previously investigated ionic liquids of [CHTf2]− paired with ammonium and phosphonium cations.45 Compared with the imide anion [CHTf2]−, the methanide central group in [CHTf2]− leads to a much more rigid anion.39 Thus, the barriers in the PES, Fig. 3b, are much higher for [CHTf2]− compared to [NTf2]−, and changes in the properties of the corresponding ionic liquids can be traced back to their different conformational flexibility.
The two anions [NTfAc]− and [NMsTFA]−, Fig. 2b, have the same sum formula and thus identical molecular weight. The different relative position of the CH3 and CF3 groups alone lead to a difference in conformational flexibility, see the PES in Fig. 3c and d. Thus, these two anions are ideally suited as targeted modifications to experimentally investigate the effects of conformational flexibility.
Fig. 2c shows a systematic series of anions with increasing degree of fluorination, from the non-fluorinated [NMs2]− over the asymmetric, half fluorinated [NTfMs]− to the fully fluorinated [NTf2]−. Fluorination changes several characteristics of the anions, the most obvious change is the increase in mass and volume. More subtly, the conformational flexibility increases with fluorination as well, see the PES in Fig. 3a, e and f.
Finally, we also investigate a series of fully fluorinated anions, Fig. 2d. The three acyclic anions [NFs2]−, [NTf2]−, and [NPf2]− have similar conformational flexibility, the main difference is again mass and volume. In contrast, the 6-membered cyclic perfluoroalkylbis(sulfonyl)imide anion [6cPFSI]− is covalently locked into the cis conformer.64 Hence, this anion serves as a reference without conformational flexibility, as no conversion into the trans conformer is possible.
The corresponding ionic liquids with the 1-butyl-3-methylimidazolium ([C4C1im]+) cation have been prepared as part of this work. Where necessary, the required anion precursors have been synthesised as well; details can be found in the ESI.† Specifically, we developed improved procedures for the synthesis of H[NTfAc] and H[NMsTFA]. [C4C1im]+ was chosen as one of the most widely used cations in ionic liquids research to date. The ionic liquid [C4C1im][NTf2] is particularly well characterised and has been the subject of numerous diverse studies.27,37,65–69 A comparison of our physicochemical data for [C4C1im][NTf2] to the literature is provided in the ESI† to demonstrate reliability and reproducibility of our experimental setup.
The anions in Fig. 2 are very similar. Hence, we decided to include [C4C1im][B(CN)4] for comparison. This ionic liquid (with the tetracyanoborate anion) is similar to [C4C1im][NTf2] in the sense that both ionic liquids are hydrophobic (but hygroscopic) and show comparable behaviour experimentally, including in their syntheses. The volume of the [B(CN)4]− anion is in between those for [NFs2]− and [NTf2]−, and all three anions are weakly coordinating.45 The crucial difference is that [B(CN)4]− only possesses one conformer, which will be valuable to discuss this work in a larger setting.
Crystals suitable for X-ray crystallography were grown for several of the anions and their corresponding free acids, details are provided in the ESI.† Crucially, the crystal structures provide experimental values for the conformation of the anions. The corresponding experimental dihedral angles extracted from the crystal structures are shown as circled crosses in Fig. 3. The agreement between theory and experiment is excellent; see also the ESI† for a numerical comparison. This shows that our gas phase ab initio calculations indeed provide reliable predictions. In addition, the solid state is in general more affected by specific intermolecular interactions and packing effects than the liquid state. Hence, it is likely that the ab initio predictions are relevant for the liquid, where thermal sampling of the PES is less restricted than in the solid.
The non-fluorinated ionic liquid [C4C1im][NMs2] showed remarkable supercooling, and remained liquid for months at room temperature, approximately 30 °C below the melting point. Physicochemical characterisation in the supercooled state was also possible without encountering solidification. However, once crystallised, the solid could be used as a seed to initiate nucleation in an independently synthesised sample of [C4C1im][NMs2] which was also obtained as supercooled liquid. A crystal structure of [C4C1im][NMs2] could thus be recorded. The [NMs2]− anion is known to form stronger hydrogen bonds than its fluorinated counterpart, [NTf2]−.29 Nevertheless, only weak hydrogen bonds were observed in the crystal structure, see ESI.†
Factors affecting the viscosity
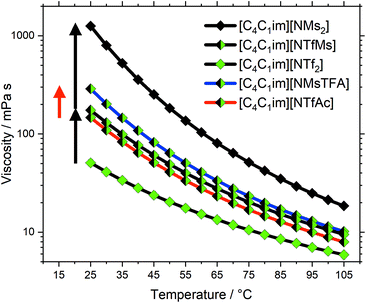
The transport properties are not independent; low viscosities correlate with fast diffusion and high conductivity. A detailed discussion of all our available physicochemical data would by far exceed the scope of this work. Hence, we will focus on viscosities as the central transport property. Diffusion coefficients and electrical conductivities are given in the ESI† and will be discussed in a separate publication. We have furthermore recorded 1H and 19F NMR relaxation profiles via Fast Field Cycling (FFC) at different temperatures (which give access to rotational and translational relaxation times) and pressure dependent diffusion coefficients; these results are far beyond the scope of this work and will also be published separately.An overview of the ionic liquids in this work, their characteristics and experimental viscosities is given in Table 1. The flexibility of the anion was judged qualitatively based on their PES. Here, an anion is considered flexible if its conformers are not separated by barriers larger than 15 kJ mol−1.39 The anion volumes were calculated from the electron density in the gas phase, which is sufficient as relative measure. In the following, the ionic liquids will be discussed according to their group, see also Fig. 2.
| Group | Ionic liquid | CAS | Anion flexibility | M(anion)/g mol−1 | V(anion)/Å3 | η 25 °C/mPa s |
|---|---|---|---|---|---|---|
| (a) | [C4C1im][NTf2] | 174899-83-3 | Flexible | 280 | 210 | 51 |
| [C4C1im][CHTf2] | 1005735-46-5 | Rigid | 279 | 217 | 153 | |
| (b) | [C4C1im][NTfAc] | 2486007-65-0 | Flexible | 190 | 174 | 147 |
| [C4C1im][NMsTFA] | 2486007-63-8 | Rigid | 190 | 175 | 288 | |
| (c) | [C4C1im][NMs2] | 945611-32-5 | Rigid | 172 | 178 | 1256 |
| [C4C1im][NTfMs] | — | Intermediate | 226 | 194 | 175 | |
| [C4C1im][NTf2] | 174899-83-3 | Flexible | 280 | 210 | 51 | |
| (d) | [C4C1im][NFs2] | 1235234-58-8 | Flexible | 180 | 143 | 33 |
| [C4C1im][NTf2] | 174899-83-3 | Flexible | 280 | 210 | 51 | |
| [C4C1im][6cPFSI] | 1201362-14-2 | Rigid | 292 | 213 | 172 | |
| [C4C1im][NPf2] | 254731-29-8 | Flexible | 380 | 274 | 116 | |
| [C4C1im][B(CN)4] | 742099-78-1 | Rigid | 115 | 156 | 31 |
We have previously observed that the viscosities of ionic liquids with the rigid [CHTf2]− anion are significantly higher than those with the flexible [NTf2]− anion. Specifically, across different phosphonium and ammonium ionic liquids, the relative increase in viscosity at room temperature was between 2 and 3.45 For the imidazolium ionic liquids in this work, the viscosity increased by a factor of 3, from 51 mPa s for [C4C1im][NTf2] to 153 mPa s for [C4C1im][CHTf2]. Hence, the dynamics of these two systems are clearly affected by conformational flexibility. The well-known [C4C1im][NTf2] ionic liquid has the additional advantage that carefully parameterised classical force fields are available.55–57 Hence, group (a) was chosen to further investigate the structural relaxation by means of MD simulation, which will be presented further below.
The ionic liquids in group (b), [C4C1im][NTfAc] and [C4C1im][NMsTFA], have already been discussed in our preliminary work on conformational design concepts.39 Briefly, the viscosity increases by a factor of two from the ionic liquid with the flexible anion to that with the rigid anion. It is worth noting that we independently synthesised new samples using our improved synthesis route and repeated the physicochemical measurements. The values in Table 1 differ from those previously reported by less than 2%, thus our measurements on these novel ionic liquids are reproducible.
The ionic liquids in group (c) vary in their degree of anion fluorination, which has three major implications. First, the size (i.e. volume and mass) increases with the fluorine content. Second, the conformational flexibility increases with the fluorine content. Third, fluorination helps to delocalise the negative charge over the anion, thus decreasing its basicity and coordination tendency. The increase in size is expected to increase viscosity. However, this contribution is small, as the discussion of group (d) will show. Thus, we will neglect the influence of size and focus on flexibility and basicity.
The viscosity at room temperature increases by a factor of 3.4 from [C4C1im][NTf2] to [C4C1im][NTfMs], and by a factor of 7.2 from [C4C1im][NTfMs] to [C4C1im][NMs2], see the black arrows in Fig. 4. Both higher flexibility and lower basicity are expected to contribute to low viscosities, which explains the great changes in viscosity within group (c). For comparison, Fig. 4 also shows the two half-fluorinated ionic liquids [C4C1im][NTfAc] (red curve) and [C4C1im][NMsTFA] (blue curve) from group (b). These two ionic liquids only differ in conformational flexibility, see the red arrow in Fig. 4. In contrast, the changes in viscosity corresponding to the black arrows contain contributions from both flexibility and basicity. A quantitative comparison is not meaningful due to the relatively crude approximations, however Fig. 4 shows that conformational flexibility and basicity are equally important.
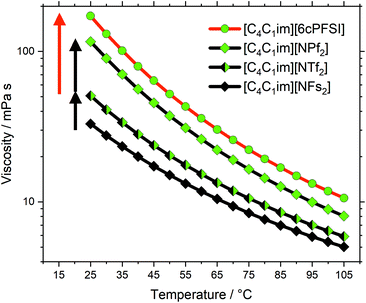
The changes in size are much larger in group (d) compared to group (c). From [C4C1im][NFs2] to [C4C1im][NTf2], the anion molecular weight increases from 180 g mol−1 to 280 g mol−1, which leads to an increase in viscosity by a factor of 1.5. The increase in anion molecular weight is similar from [C4C1im][NMs2] (172 g mol−1) to [C4C1im][NTf2], but the viscosity decreases 25-fold, hence we have previously neglected the influence of size. However, since basicity and conformational flexibility do not change considerably in the series [NFs2]−–[NTf2]−–[NPf2]−, size becomes more important in comparison. The increase in viscosity from [C4C1im][NTf2] to [C4C1im][NPf2] (by a factor of 2.3) is larger than that from [C4C1im][NFs2] to [C4C1im][NTf2] (by a factor of 1.5), which might be due to the onset of fluorous domain formation.70–74
The cyclic anion [6cPFSI]− (M = 292 g mol−1) is only marginally heavier than the acyclic [NTf2]− (anion M = 280 g mol−1). Yet, the viscosity of [C4C1im][6cPFSI] is 3.4 times higher than that of [C4C1im][NTf2], exceeding even the viscosity of [C4C1im][NPf2], Fig. 5. The higher viscosity arises due to the cyclic, rigid structure of [6cPFSI]−. This observation shows the relative importance of conformational flexibility in this anion class (red arrow in Fig. 5), which has a larger impact on the viscosity than the change in size (black arrows in Fig. 5) when two CF2 groups are introduced to the side chain.
The experimental evidence clearly shows the importance of conformational flexibility, on a par with the direct effects of anion fluorination. It is thus interesting to consider the [C4C1im][B(CN)4] ionic liquid which we included to discuss our results in the broader frame of ionic liquids in general. The viscosities of [C4C1im][B(CN)4] and [C4C1im][NFs2] are very similar, the [B(CN)4]− anion has a slightly larger volume and slightly lower mass than the [NFs2]− anion. This similarity is surprising, given the very different structures of the two anions, especially with the [B(CN)4]− anion only having one conformer. Two explanations appear viable. First, the [NFs2]− anion is so small that its (high) conformational flexibility loses relevance – in line with the sweep volume and slithering hypotheses.35,36,39 Second, specific pathways of structural relaxation might be present with the [B(CN)4]− anion.
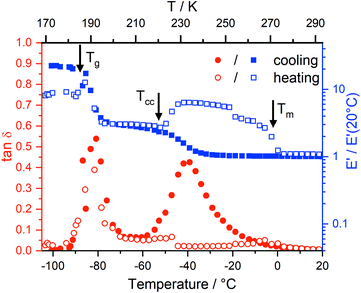
DMTA measurements
Dynamic mechanical thermal analysis (DMTA) is a well known technique to study the structural relaxation behaviour of bulk materials,38,75–77 see the ESI† for more details of the technique, analysis, and results. Fig. 6 shows the DMTA spectrum of [C4C1im][NTf2] as a prototypical example. The observed thermal transitions showed excellent agreement between DMTA and DSC measurements. The relative variation of the storage modulus E′ on cooling increases significantly during vitrification (around −90 °C) while on heating back it increases at the cold crystallisation (around −50 °C), and decreases on further heating during melting (around 0 °C).Two peaks are visible in the cooling curve of the loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, see Fig. 7 for measurements at different frequencies. The narrow peak around −90 °C does not change with frequency and corresponds to the glass transition. The signatures of glass transition, cold crystallisation, and melting transition were indeed frequency independent as expected. Critically, dynamic relaxation leads to a thermally activated peak in the loss tangent which shifts to higher temperature with increasing frequency, f, of the oscillating deformation. Thus, the broad peaks in Fig. 7 are the signature of a thermally activated relaxation process similar to those already reported, including components related to viscous flow.38,78 Furthermore, the intensity is higher for those peaks at higher temperature/larger f, suggesting the occurrence of relaxation is dominated by a two state process whose energy difference ΔE must be larger than zero in this case.38
δ, see Fig. 7 for measurements at different frequencies. The narrow peak around −90 °C does not change with frequency and corresponds to the glass transition. The signatures of glass transition, cold crystallisation, and melting transition were indeed frequency independent as expected. Critically, dynamic relaxation leads to a thermally activated peak in the loss tangent which shifts to higher temperature with increasing frequency, f, of the oscillating deformation. Thus, the broad peaks in Fig. 7 are the signature of a thermally activated relaxation process similar to those already reported, including components related to viscous flow.38,78 Furthermore, the intensity is higher for those peaks at higher temperature/larger f, suggesting the occurrence of relaxation is dominated by a two state process whose energy difference ΔE must be larger than zero in this case.38
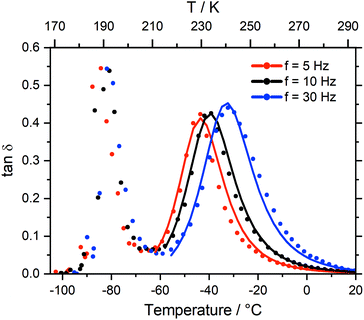 | ||
| Fig. 7 Loss tangent from the DMTA spectrum of [C4C1im][NTf2], measured at different frequencies. Solid lines are a concomitant fit, see ESI.† | ||
Viscous flow is a complex, collective process which involves transitions between minimum energy configurations on the global PES of the liquid. The observed relaxation can be described using a simplified, two state model; i.e. the rate-limiting ‘elementary reaction’ is the thermally activated transition between two states. Such a state may be a well-defined minimum energy configuration, or a collection of minimum energy configurations separated by small energy barriers. Many configurations – and even more transitions between them – are accessible in a liquid, and conformational flexibility is not the only pathway to viscous flow and structural relaxation. However, the simple model works well where other contributions are negligible compared to conformational flexibility. In this case, conformational flexibility becomes the main contribution to the height of the energy barrier between the two states. Accordingly, the two ionic liquids with rigid anions – [C4C1im][CHTf2] and [C4C1im][6cPFSI] – showed complex DMTA spectra with overlapping transitions which could not be analysed. The ionic liquid [C4C1im][NMsTFA] showed at least two dominant relaxation mechanisms, which could be fitted separately. Details of the fits are given in the ESI,† the key results are summarised in Table 2 for those systems where the two state model could be applied. For comparison, the ab initio energy differences between relevant conformers are given in italics.
| Ionic liquid | ΔE/kJ mol−1 | τ 0/s | W/kJ mol−1 | |
|---|---|---|---|---|
| a Additional GS at 12.4 kJ mol−1. | ||||
| [C4C1im][NTf2] | 2.6(3) | 3.5 | 1.6(2) × 10−13 | 31(1) |
| [C4C1im][NTfAc] | 1.6(2) | 1.7 | 1.7(2) × 10−13 | 40(1) |
| [C4C1im][NMsTFA] | 12(4) | 12.0 | 4.0(1) × 10−13 | 41(1) |
| [C4C1im][NMsTFA] | 4.1(5) | — | 4.0(1) × 10−13 | 47(1) |
| [C4C1im][NMs2] | ≈15 | 22.2 | 1.0(1) × 10−13 | 35(4) |
| [C4C1im][NTfMs] | 4.7(2) | 1.5 | 2.3(5) × 10−13 | 46(1) |
| [C4C1im][B(CN)4] | 0 | — | 2.4(9) × 10−6 | 2.3(1) |
The DMTA spectra of the two ionic liquids in group (b), [C4C1im][NTfAc] and [C4C1im][NMsTFA], were qualitatively different, with the [C4C1im][NMsTFA] showing an additional thermally activated peak. This can be attributed to conformational flexibility, with the [NMsTFA]− anion being more rigid than [NTfAc]−. We thus propose transitions between thermally accessible basins in the PES as the rate-limiting step for viscous flow at low temperatures, see the red arrows in Fig. 8. The four relevant minima on the PES of [NTfAc]− are grouped together in two basins. The ab initio calculations show that the lowest energy conformers in these two basins are separated by 1.7 kJ mol−1, in good agreement with the 1.6 kJ mol−1 observed in the DMTA measurement.
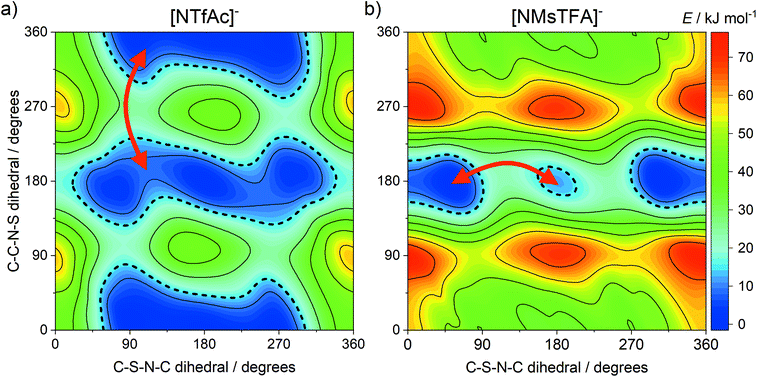 | ||
| Fig. 8 Potential energy surfaces of (a) [NTfAc]− and (b) [NMsTFA]−, red arrows indicate plausible transitions between basins in line with the DMTA measurements. | ||
The two thermally accessible basins in the ab initio PES of the [NMsTFA]− anion are separated by 12.0 kJ mol−1, almost at the threshold of 15 kJ mol−1 used here, again in agreement with the energy difference obtained from the DMTA measurement. This transition is represented by the red arrow in Fig. 8b and corresponds to the two geometries shown in Fig. 9. Critically, the observation of a second thermally activated peak shows that conformational flexibility of the [NMsTFA]− anion is not high enough to be the predominant mechanism for viscous flow.
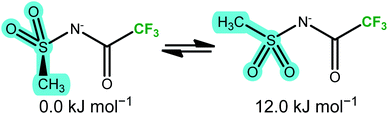 | ||
| Fig. 9 The two unique minimum energy geometries in [NMsTFA]−, cf.Fig. 8b. | ||
The anion conformational flexibility increases within group (c) from [NMs2]− over [NTfMs]− to [NTf2]−, the experimental energy difference obtained decreased in the same order. The ΔE obtained from the DMTA measurements were slightly smaller than those obtained ab initio for the two symmetric anions, [NMs2]− and [NTf2]−. This observation can be explained with the cis conformer being favoured by entropic contributions, which are not included in the ab initio simulation. For [NTfMs]− two geometrically very similar pathways are plausible, Fig. 10, and likely contribute to the experimentally observed energy difference of 4.7 kJ mol−1.
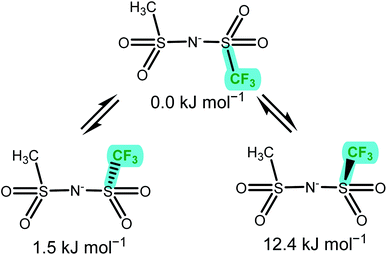 | ||
| Fig. 10 The three unique minimum energy geometries in [NTfMs]−. The nitrogen atom points out the back of the paper plane. The two cis conformers are geometrically very similar, but not enantiomers. | ||
All five ionic liquids with imide anions showed nonzero energy differences within the two state model, with comparable relaxation time parameters, τ0, between 1 × 10−13 s and 4 × 10−13 s. The activation energies, W, were also similar, between 31 kJ mol−1 and 47 kJ mol−1. The experimental activation energies were consistently higher than the activation energies for conformational changes from the ab initio simulations. This was anticipated since conformational reorganisation in the bulk ionic liquid is associated with an energy penalty for the creation of free volume, which is not the case in the gas phase. The experimental activation energies were furthermore obtained from the fit of the DMTA spectra which makes use of the VFT equation, eqn (1). For comparison, the Arrhenius model is given in eqn (2), with the Arrhenius activation energy, EA. The activation energy W in the VFT equation is equivalent to a temperature dependent Arrhenius activation energy. Hence a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence between the theoretical and experimental activation energies is not expected.
1 correspondence between the theoretical and experimental activation energies is not expected.
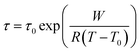 | (1) |
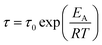 | (2) |
The DMTA analysis of [C4C1im][B(CN)4] revealed a behaviour fundamentally different to the other ionic liquids. The relaxation time for [C4C1im][B(CN)4] was seven orders of magnitude higher than for the other ionic liquids. For [C4C1im][B(CN)4], τ0 was on the order of microseconds, which is roughly the timescale of diffusive processes, see ESI.† For the imide ionic liquids, τ0 was on the order of tenths of picoseconds, which is roughly the timescale of the fast intramolecular conformational dynamics, cf.Fig. 13. In general, τ0 ≈ 10−14 s are typical for viscous liquids near the glass transition.38,78,79 Furthermore, the analysis of the DMTA spectrum revealed that the relaxation in [C4C1im][B(CN)4] involved two sites of identical energy, separated by a very small barrier of 2.3 kJ mol−1. Hence, the mechanism dominating the dynamics in [C4C1im][B(CN)4] is likely intermolecular in nature.
We have previously highlighted the similarities of [C4C1im][B(CN)4] and [C4C1im][NFs2]. Indeed, we were unable to analyse the DMTA spectrum of [C4C1im][NFs2] with the same model as used for the other ionic liquids with flexible anions. In contrast to [C4C1im][NTf2], no clear thermally activated peak could be observed for [C4C1im][NFs2]. The fluorine and oxygen atoms in the [NFs2]− anion are of comparable size, thus there is little possibility for coupling between structural relaxation and conformational reorganisation. This finding further corroborates the sweep volume and slithering hypotheses.35,36,39 Thus, it becomes clear why some anions such as [B(CN)4]−, but also [BF4]− or [PF6]− lead to ionic liquids with reasonably fast transport properties, despite the absence of conformational dynamics. These ions are by themselves comparable in size to the triflate groups in [NTf2]−. Similarly, it can be expected that the impact on transport properties would be small if the [NFs2]− anion were rigid, since its sweep volume is small as well.
MD simulations: [C4C1im][NTf2] vs. [C4C1im][CHTf2]
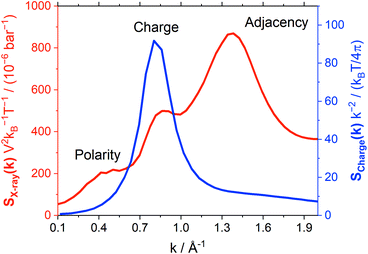
Atomistic MD simulations offer further, molecular-level insight into dynamics. Hence, we decided to investigate the impact of conformational flexibility in imide ionic liquids on key dynamic quantities obtained from statistical mechanics. We will use (auto)correlation functions which statistically quantify how fast an ensemble of molecules transitions from an initial state (such as a certain orientation) to a random distribution. The faster this transition, the lower the corresponding lifetime. The two ionic liquids from group (a), [C4C1im][NTf2] and [C4C1im][CHTf2], were chosen for this purpose as reliable force fields to current standards were readily available.A common approach to probe liquid structure is Small Angle X-ray Scattering (SAXS). The simulated SAXS pattern is shown in Fig. 11, black curve. Three features are generally observed.80–85 The peak at 1.36 Å−1 corresponds to adjacency correlations, i.e. neighbouring atoms, and is present in molecular liquids as well.86 The shoulder at 0.49 Å−1 corresponds to long-range correlations, e.g. due to nanosegregation into polar and apolar domains.80,83,85 Within this work, the intermediate peak at 0.86 Å−1 is most relevant. This ‘charge peak’ is a signature of the characteristic charge network in ionic liquids, though it might be suppressed due to systematic cancellations even if a charge network is present.81,86,87 Recent work has shown that the relaxation of the charge network is closely related to viscous flow.87–91
The charge network of ionic liquids is better characterised by the charge correlation structure factor Scharge, which is related (through linear response theory) to the dielectric properties of the electrolyte.92 Such charge correlation is often difficult to infer from SAXS patterns, as the X-ray scattering cross section of an atom/molecule is dictated by the total electron density rather than net charge. It has been previously shown that peaks in Scharge are distinctly different for ILs that exhibit different properties.93 In this work, we use a simplified charge correlation structure factor which is calculated using only the positions of the centre of charge for each molecular ion, rather than atomic charges. Thus, we obtain Scharge in a way which is characteristic for the intermolecular charge network. Fig. 11 compares the charge correlation structure factor Scharge to the X-ray scattering structure factor SX-ray for [C4C1im][NTf2]. There are clear differences between the two types of structure factors, with Scharge primarily reflecting the ‘charge peak’ at 0.86 Å−1 that is a signature of the characteristic charge network.
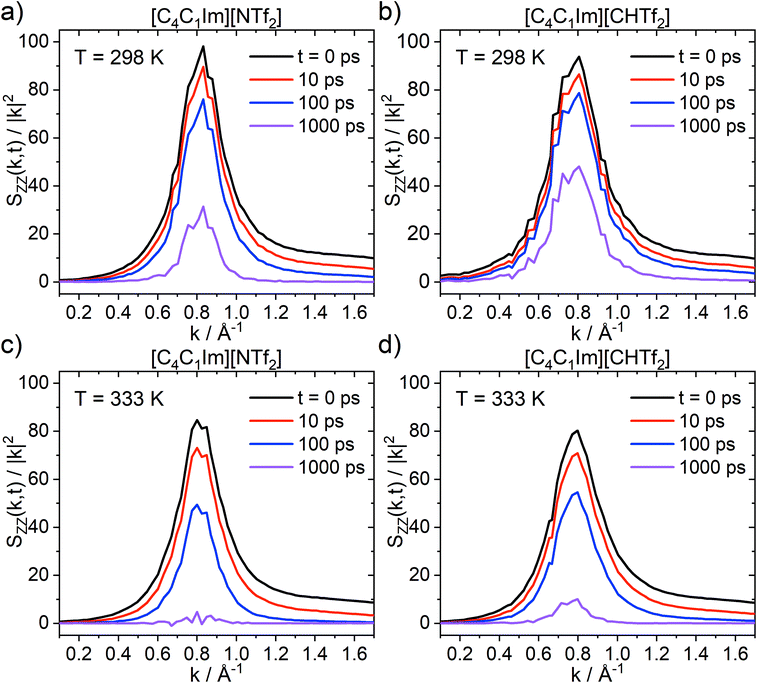
The charge network relaxation is characterised by the decorrelation of the dynamic charge–charge correlation structure factor Scharge(k,t), Fig. 12. Note that Scharge(k,t) is the central property reporting on the charge relaxation dynamics; ionic systems typically exhibit the slowest dynamical relaxation at length scales corresponding to the peak in Scharge.94,95 An exception are those systems which show a polarity peak with even slower relaxation, however this is not relevant for the ionic liquids in this work. The reason for the slow charge relaxation dynamics is that the long-range coulombic interactions impose restrictions on the movement of ions, for example electroneutrality conditions, which must be fulfilled. In general, the charge network relaxation is faster at higher temperatures and for the ionic liquid with the more flexible anion, [C4C1im][NTf2]; see ESI† for numerical values of the corresponding charge network relaxation times. At the higher temperature (333 K), Scharge(k,t) at 1 ns is decorrelated for [C4C1im][NTf2], but not for [C4C1im][CHTf2]. This behaviour is expected, given that the different transport properties and dynamics are interrelated and show similar trends with increasing temperature.
The relative ratios by which charge network relaxation times increase from 333 K to 298 K are virtually identical for [C4C1im][NTf2] (3.579) and [C4C1im][CHTf2] (3.586). Comparing the charge network relaxation times across the two ionic liquids, it is evident that the relaxation is faster in [C4C1im][NTf2] compared to [C4C1im][CHTf2] by a factor of 1.59 at both temperatures. This is an interesting observation which shows the stability of the quantity Scharge(k,t) introduced here. Furthermore, higher temperatures and higher conformational flexibility have a similar effect on structural relaxation, in line with the potential energy landscape picture.26,96–98 Thus, conformational flexibility as a design element is especially important for applications at low temperatures.
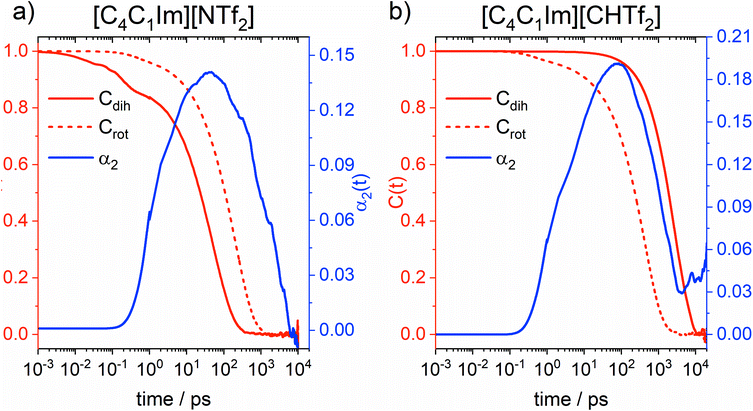
Information on intramolecular reorganisation – and thus conformational flexibility – can also be obtained from the fully atomistic MD simulations. To this end, we employ the intermittent dihedral autocorrelation function Cdih(t), which describes how fast the anions transition from a given initial state (Cdih = 1) to a final, random state in which the conformations of the anions show no correlation to the initial state (Cdih = 0). The process of changing from Cdih = 1 to Cdih = 0 is called decorrelation. In addition, we will use the rotational correlation function Crot(t) of the sulphur–sulphur vector in the anion to describe orientational reorganisation of the molecular anion as a whole. The decorrelation is formally similar to that of Cdih, only that the monitored quantity is a vector rather than a conformation. Finally, we also calculated the α2 parameter, commonly called the non-Gaussian parameter. This parameter is used to identify deviations from a Gaussian diffusion profile, for example due to dynamical heterogeneity. These three functions are shown in Fig. 13, details on the theory behind them is given in the ESI.†
The α2 parameter at 333 K shows a maximum at 47 ps for [C4C1im][NTf2] and at 77 ps for [C4C1im][CHTf2]. The timescale of non-Gaussian behaviour shifts to longer times at lower temperature, at 298 K the maxima are located at 61 ps for [C4C1im][NTf2] and 286 ps for [C4C1im][CHTf2]. Rotational decorrelation also takes place on this intermediate timescale, which is between (fast) intramolecular dynamics and (slow) diffusive dynamics. It is this intermediate timescale which dominates the dynamics of structural relaxation and viscous flow.
By design, the [CHTf2]− anion is rigid, as opposed to the much more flexible [NTf2]− anion. This is reflected in the intermittent dihedral autocorrelation functions, which probe the cis–trans interconversion. Importantly, the conformational reorganisation (=decorrelation) in [C4C1im][NTf2] occurs on a shorter timescale than that of structural relaxation. Thus, the [NTf2]− anion can adjust its shape to the surroundings quickly enough to provide additional pathways for structural relaxation. These pathways are not available in the [C4C1im][CHTf2] ionic liquid, where cis–trans interconversion is too slow; hence rotation of the rigid [CHTf2]− anion as a whole is faster than this and thus the more likely response to changes in the environment.
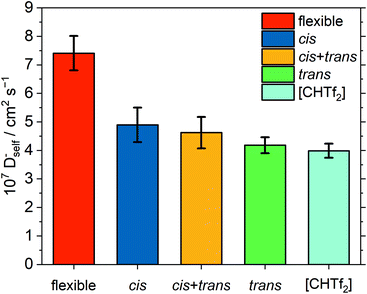
It is often impossible for targeted modifications to be ‘perfect’, and some confounding variables are unavoidable. This is also the case for [C4C1im][NTf2] and [C4C1im][CHTf2]. For example, the equilibrium in the [CHTf2]− anion is shifted towards the trans conformer. This shift might impact the dynamics due to their different charge arm lengths, see ESI.† Briefly, the charge arm is the distance between the centre of mass and the centre of charge of an ion and is equivalent to the dipole moment. The charge arm length influences rotational–translational coupling between the ion and its environment and thus the dynamics in the ionic liquid.21,26,99,100 Hence, we also performed simulations of [C4C1im][NTf2] where the flexibility of the anion was removed artificially. To this end, harmonic biases were added to the two dihedral angles, every other aspect of the [C4C1im][NTf2] simulation was kept unchanged. Three separate simulations were run: (1) all anions were restricted to the cis conformer, (2) 317 anions in cis and 195 anions in trans, mimicking the native conformer ratio, and (3) all anions were restricted to the trans conformer. The resulting anion diffusion coefficients are shown in Fig. 14. Cation diffusion coefficients show the same trend, see ESI.†
All four simulations with rigid anions showed significantly slower diffusion than the simulation of the native [C4C1im][NTf2] with flexible anion. As expected, a very small influence of the anion conformation – as opposed to the anion conformational flexibility – is visible. Specifically, rigid anions in cis conformation show a tendency to slightly faster diffusion than rigid anions in trans conformation, however the difference is within the error bars. This is in line with previous studies on the influence of charge asymmetry, see ESI.† However, the effect is very small compared to that of conformational flexibility.
Conclusions
In this work, we studied ionic liquids with targeted modifications of the widely used [NTf2]− anion. We used targeted modifications to isolate the effects of conformational flexibility, fluorination, and mass. We took care to address confounding variables, which required the use of several complementary methods. Importantly, only complementary experimental and computational techniques together gave a complete and consistent picture. For example, ab initio potential energy surfaces (PES) showed excellent agreement with experimental crystal structures.The ab initio PES provide insight into conformational flexibility of the anions, which in turn has a profound influence on macroscopic properties. Our results show that conformational flexibility of imide anions is a versatile design element to lower viscosities, lower thermal transition temperatures, and accelerate transport properties. Conformational flexibility of the anions furthermore leaves a clear signature in the DMTA spectra. The analysis of the DMTA spectra in combination with the ab initio PES revealed the possible rate-limiting steps underlying the structural relaxation.
Fluorination is another common design element for anions to improve the properties of the corresponding ionic liquids. Highly fluorinated anions have long been a preferred choice for ionic liquids with fast dynamics. However, fluorination has several knock-on effects, for example by changing size and flexibility. In this work, we demonstrated how to separate these knock-on effects. Thus, we show that conformational flexibility plays an important role in the fluidity of [C4C1im][imide] ionic liquids, while the impact of size is small.
The holistic picture developed in this work is crucial for the design of new ionic liquids. An excellent example are the two ionic liquids [C4C1im][6cPFSI] and [C4C1im][NTfMs]. The first ionic liquid has a fully fluorinated, but conformationally locked anion, the anion of the second ionic liquid is only half-fluorinated but more flexible. Both ionic liquids have virtually identical viscosities to within a few percent. This demonstrates that a higher degree of fluorination is not always the optimal choice in terms of resulting properties of the ionic liquids, and that conformational flexibility of the anions should always be considered where transport properties are important.
MD simulations were used to compare the timescales of relaxation between ionic liquids with rigid and flexible anions. Conformational flexibility provides alternative pathways for relaxation on an intermediate timescale (≈100 ps). Structural relaxation, especially relaxation of the charge network, occurs on this timescale, which is critical for viscous flow. If the interconversion between conformers is slower than this intermediate timescale, then rotation of the rigid anion as a whole becomes the dominant pathway instead, so resulting in a more viscous liquid.
Finally, MD simulations allow for targeted modifications beyond what is accessible experimentally. The native conformer ratios are not the same in [NTf2]− and [CHTf2]−, and the [6cPFSI]− anion is even fully locked in the cis conformer. Hence, several performed MD simulations of [C4C1im][NTf2] with the anions being restrained to well defined conformers. These simulations showed that the effect of the conformer ratio is small compared to conformational flexibility, thus validating the use of [CHTf2]− and [6cPFSI]− as targeted modifications of the [NTf2]− anion.
Data availability
Experimental and computational data is deposited in the ESI associated with this publication as well as on the Github pages given in the methodology.Author contributions
Frederik Philippi: conceptualisation, data curation (simulation data, ESI†), formal analysis (statistical mechanics), investigation (syntheses, ab initio and MD simulations, force field development), methodology, project administration, software (prealpha), validation, visualisation, writing – original draft, writing – review and editing. Daniel Dauber: formal analysis (physicochemical data), investigation (syntheses, physicochemical characterisation), visualisation, writing – review and editing. Oriele Palumbo: formal analysis (DMTA), funding acquisition, investigation (DMTA measurements), methodology, writing – review and editing. Kateryna Goloviznina: methodology, software (fftool), writing – review and editing. Jesse McDaniel: data curation, software (structure factors), writing – review and editing. David Pugh: data curation (XRD), formal analysis (XRD). Sophia Suarez: formal analysis (FFC), investigation (FFC), supervision. Carla C. Fraenza: formal analysis (FFC), investigation (FFC). Agilio Padua: software (fftool), supervision. Christopher W. M. Kay: resources (physicochemical characterisation equipment), supervision, writing – review and editing. Tom Welton: funding acquisition, resources (facilities for syntheses), supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the Joint Bilateral Agreement CNR (Italy)/Royal Society (UK) – Biennial Programme 2022–2023 – prot. number 0082091-2021. We thank Nicholas Carboni for preparing our samples for DMTA in the glovebox. We would like to thank Lisa Haigh, Imperial College London, for mass spectrometry. Computational resources provided by the Imperial College Research Computing Service are gratefully acknowledged https://doi.org/10.14469/hpc/2232. This work is based on the PhD thesis of FP. FP acknowledges funding by the President's PhD scholarships. KG thanks IDEX Lyon Fellowship (ANR-16-IDEX-005) for the financial support.Notes and references
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- M. B. Shiflett, Commercial Applications of Ionic Liquids, Springer International Publishing, Cham, 2020 Search PubMed.
- K. E. Gutowski, Phys. Sci. Rev., 2018, 3, 1–10 CrossRef.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- A. J. Greer, J. Jacquemin and C. Hardacre, Molecules, 2020, 25, 5207 CrossRef CAS PubMed.
- H. Niu, L. Wang, P. Guan, N. Zhang, C. Yan, M. Ding, X. Guo, T. Huang and X. Hu, J. Energy Storage, 2021, 40, 102659 CrossRef.
- W. Kunz and K. Häckl, Chem. Phys. Lett., 2016, 661, 6–12 CrossRef CAS.
- P. J. Scammells, J. L. Scott and R. D. Singer, Aust. J. Chem., 2005, 58, 155 CrossRef CAS.
- G. Chatel, E. Naffrechoux and M. Draye, J. Hazard. Mater., 2017, 324, 773–780 CrossRef CAS PubMed.
- S. Magina, A. Barros-Timmons, S. P. M. Ventura and D. V. Evtuguin, J. Hazard. Mater., 2021, 412, 125215 CrossRef CAS PubMed.
- S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843 RSC.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32–37 CrossRef.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- K. N. Marsh, A. Deev, A. C. T. Wu, E. Tran and A. Klamt, Korean J. Chem. Eng., 2002, 19, 357–362 CrossRef CAS.
- I. Newington, J. M. Perez-Arlandis and T. Welton, Org. Lett., 2007, 9, 5247–5250 CrossRef CAS PubMed.
- H. Ohno, M. Yoshizawa-Fujita and Y. Kohno, Bull. Chem. Soc. Jpn., 2019, 92, 852–868 CrossRef CAS.
- G. Yu, D. Zhao, L. Wen, S. Yang and X. Chen, AIChE J., 2012, 58, 2885–2899 CrossRef CAS.
- S. Jiang, Y. Hu, Y. Wang and X. Wang, J. Phys. Chem. Ref. Data, 2019, 48, 033101 CrossRef.
- R. Shi and Y. Wang, Sci. Rep., 2016, 6, 1–12 CrossRef PubMed.
- Q. Berrod, F. Ferdeghini, J.-M. Zanotti, P. Judeinstein, D. Lairez, V. G. Sakai, O. Czakkel, P. Fouquet and D. Constantin, Sci. Rep., 2017, 7, 2241 CrossRef PubMed.
- M. N. Kobrak, ECS Proc. Vol., 2004, 2004-24, 417–425 CrossRef.
- S. A. Mirkhani and F. Gharagheizi, Ind. Eng. Chem. Res., 2012, 51, 2470–2477 CrossRef CAS.
- D. H. Zaitsau, A. V Yermalayeu, S. P. Verevkin, J. E. Bara and A. D. Stanton, Ind. Eng. Chem. Res., 2013, 52, 16615–16621 CrossRef CAS.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef CAS PubMed.
- W. Silva, M. Zanatta, A. S. Ferreira, M. C. Corvo and E. J. Cabrita, Int. J. Mol. Sci., 2020, 21, 7745 CrossRef CAS PubMed.
- F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021 RSC.
- P. Bonhôte, A.-P. Dias, M. Armand, N. Papageorgiou, K. Kalyanasundaram and M. Grätzel, Inorg. Chem., 1996, 35, 1168–1178 CrossRef PubMed.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- J. M. Pringle, J. Golding, K. Baranyai, C. M. Forsyth, G. B. Deacon, J. L. Scott and D. R. MacFarlane, New J. Chem., 2003, 27, 1504–1510 RSC.
- K. Tsunashima and M. Sugiya, Electrochem. Commun., 2007, 9, 2353–2358 CrossRef CAS.
- A. Vallée, S. Besner and J. Prud'Homme, Electrochim. Acta, 1992, 37, 1579–1583 CrossRef.
- P. Johansson, S. P. Gejji, J. Tegenfeldt and J. Lindgren, Electrochim. Acta, 1998, 43, 1375–1379 CrossRef CAS.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- J. N. Canongia Lopes, K. Shimizu, A. A. H. Pádua, Y. Umebayashi, S. Fukuda, K. Fujii and S. Ishiguro, J. Phys. Chem. B, 2008, 112, 1465–1472 CrossRef CAS PubMed.
- O. Borodin, W. Gorecki, G. D. Smith and M. Armand, J. Phys. Chem. B, 2010, 114, 6786–6798 CrossRef CAS PubMed.
- S. N. Suarez, A. Rúa, D. Cuffari, K. Pilar, J. L. Hatcher, S. Ramati and J. F. Wishart, J. Phys. Chem. B, 2015, 119, 14756–14765 CrossRef CAS PubMed.
- K. Pilar, A. Rua, S. N. Suarez, C. Mallia, S. Lai, J. R. P. Jayakody, J. L. Hatcher, J. F. Wishart and S. Greenbaum, J. Electrochem. Soc., 2017, 164, H5189–H5196 CrossRef CAS PubMed.
- O. Palumbo, F. Trequattrini, F. M. Vitucci and A. Paolone, J. Phys. Chem. B, 2015, 119, 12905–12911 CrossRef CAS PubMed.
- F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, Chem. Sci., 2020, 11, 6405–6422 RSC.
- K. R. Harris and M. Kanakubo, Phys. Chem. Chem. Phys., 2022, 24, 14430–14439 RSC.
- I. J. Neuwald, D. Zahn and T. P. Knepper, Anal. Bioanal. Chem., 2020, 412, 4881–4892 CrossRef CAS PubMed.
- T. P. T. Pham, C.-W. Cho and Y. Yun, Water Res., 2010, 44, 352–372 CrossRef CAS PubMed.
- A. Jordan and N. Gathergood, Chem. Soc. Rev., 2015, 44, 8200–8237 RSC.
- N. S. M. Vieira, S. Stolte, J. M. M. Araújo, L. P. N. Rebelo, A. B. Pereiro and M. Markiewicz, ACS Sustainable Chem. Eng., 2019, 7, 3733–3741 CrossRef CAS.
- F. Philippi, D. Rauber, B. Kuttich, T. Kraus, C. W. M. Kay, R. Hempelmann, P. A. Hunt and T. Welton, Phys. Chem. Chem. Phys., 2020, 22, 23038–23056 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Dequidt, J. Devémy and A. A. H. Pádua, J. Chem. Inf. Model., 2016, 56, 260–268 CrossRef CAS PubMed.
- K. Goloviznina, Z. Gong, M. F. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2021, 17, 1606–1617 CrossRef CAS PubMed.
- K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2019, 15, 5858–5871 CrossRef CAS PubMed.
- F. Philippi, K. Goloviznina, Z. Gong, S. Gehrke, B. Kirchner, A. A. H. Pádua and P. A. Hunt, Phys. Chem. Chem. Phys., 2022, 24, 3144–3162 RSC.
- K. Goloviznina, Z. Gong and A. A. H. Pádua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 1–16 Search PubMed.
- J. N. C. Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef CAS.
- J. N. C. Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef CAS.
- A. S. L. Gouveia, C. E. S. Bernardes, L. C. Tomé, E. I. Lozinskaya, Y. S. Vygodskii, A. S. Shaplov, J. N. C. Lopes and I. M. Marrucho, Phys. Chem. Chem. Phys., 2017, 19, 29617–29624 RSC.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS PubMed.
- O. Hollóczki, M. Macchiagodena, H. Weber, M. Thomas, M. Brehm, A. Stark, O. Russina, A. Triolo and B. Kirchner, ChemPhysChem, 2015, 16, 3325–3333 CrossRef PubMed.
- F. J. Waller, A. G. M. Barrett, D. C. Braddock, D. Ramprasad, R. M. McKinnell, A. J. P. White, D. J. Williams and R. Ducray, J. Org. Chem., 1999, 64, 2910–2913 CrossRef CAS PubMed.
- A. G. M. Barrett, N. Bouloc, D. C. Braddock, D. Catterick, D. Chadwick, A. J. P. White and D. J. Williams, Tetrahedron, 2002, 58, 3835–3840 CrossRef CAS.
- S. Kakinuma, T. Ishida and H. Shirota, J. Phys. Chem. B, 2017, 121, 250–264 CrossRef CAS PubMed.
- R. S. Anaredy and S. K. Shaw, Langmuir, 2016, 32, 5147–5154 CrossRef CAS PubMed.
- J. G. McDaniel, C. Y. Son and A. Yethiraj, J. Phys. Chem. B, 2018, 122, 4101–4114 CrossRef CAS PubMed.
- K. R. Harris and M. Kanakubo, Phys. Chem. Chem. Phys., 2015, 17, 23977–23993 RSC.
- B. Brunetti, A. Ciccioli, G. Gigli, A. Lapi, N. Misceo, L. Tanzi and S. Vecchio Ciprioti, Phys. Chem. Chem. Phys., 2014, 16, 15653 RSC.
- R. Clark, M. A. Nawawi, A. Dobre, D. Pugh, Q. Liu, A. P. Ivanov, A. J. P. White, J. B. Edel, M. K. Kuimova, A. J. S. McIntosh and T. Welton, Chem. Sci., 2020, 112, 103–112 Search PubMed.
- F. Lo Celso, Y. Yoshida, F. Castiglione, M. Ferro, A. Mele, C. J. Jafta, A. Triolo and O. Russina, Phys. Chem. Chem. Phys., 2017, 19, 13101–13110 RSC.
- F. Lo Celso, Y. Yoshida, R. Lombardo, C. Jafta, L. Gontrani, A. Triolo and O. Russina, C. R. Chim., 2018, 21, 757–770 CrossRef CAS.
- F. Lo Celso, G. B. Appetecchi, E. Simonetti, M. Zhao, E. W. Castner, U. Keiderling, L. Gontrani, A. Triolo and O. Russina, Front. Chem., 2019, 7, 1–14 CrossRef PubMed.
- F. Lo Celso, G. B. Appetecchi, E. Simonetti, U. Keiderling, L. Gontrani, A. Triolo and O. Russina, J. Mol. Liq., 2019, 289, 111110 CrossRef.
- M. Brehm, H. Weber, M. Thomas, O. Hollóczki and B. Kirchner, ChemPhysChem, 2015, 16, 3271–3277 CrossRef CAS PubMed.
- A. S. Nowick, B. S. Berry and J. L. Katz, Anelastic Relaxation in Crystalline Solids, Academic Press, New York and London, 1972 Search PubMed.
- O. Palumbo, A. Paolone, R. Cantelli, C. M. Jensen and M. Sulic, J. Phys. Chem. B, 2006, 110, 9105–9111 CrossRef CAS PubMed.
- R. Cantelli, O. Palumbo, A. Paolone, C. M. Jensen, M. T. Kuba and R. Ayabe, J. Alloys Compd., 2007, 446–447, 260–263 CrossRef CAS.
- O. Palumbo, F. Trequattrini, G. B. Appetecchi, L. Conte and A. Paolone, J. Mol. Liq., 2017, 243, 9–13 CrossRef CAS.
- F. Trequattrini, A. Paolone, O. Palumbo, F. M. Vitucci, M. A. Navarra and S. Panero, Arch. Metall. Mater., 2015, 60, 385–390 CAS.
- H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838–16846 CrossRef CAS PubMed.
- J. J. Hettige, H. K. Kashyap, H. V. R. Annapureddy and C. J. Margulis, J. Phys. Chem. Lett., 2013, 4, 105–110 CrossRef CAS PubMed.
- M. A. A. Rocha, C. M. S. S. Neves, M. G. Freire, O. Russina, A. Triolo, J. A. P. Coutinho and L. M. N. B. F. Santos, J. Phys. Chem. B, 2013, 117, 10889–10897 CrossRef CAS PubMed.
- A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641–4644 CrossRef CAS PubMed.
- D. Pontoni, M. DiMichiel and M. Deutsch, ChemPhysChem, 2020, 21, 1887–1897 CrossRef CAS PubMed.
- C. E. S. Bernardes, K. Shimizu, A. I. M. C. Lobo Ferreira, L. M. N. B. F. Santos and J. N. Canongia Lopes, J. Phys. Chem. B, 2014, 118, 6885–6895 CrossRef CAS PubMed.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. Lett., 2020, 11, 2062–2066 CrossRef CAS PubMed.
- J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 7015–7029 CrossRef CAS PubMed.
- T. Yamaguchi, J. Chem. Phys., 2016, 145, 194505 CrossRef PubMed.
- T. Yamaguchi, J. Chem. Phys., 2016, 144, 124514 CrossRef PubMed.
- T. Yamaguchi, Phys. Chem. Chem. Phys., 2018, 20, 17809–17817 RSC.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, 4th edn, 2013 Search PubMed.
- J. G. McDaniel and A. Yethiraj, J. Phys. Chem. B, 2019, 123, 3499–3512 CrossRef CAS PubMed.
- S. Okazaki, Y. Miyamoto and I. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 2055–2062 CrossRef CAS PubMed.
- J. P. Hansen and I. R. McDonald, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 2111–2123 CrossRef.
- M. Goldstein, J. Chem. Phys., 1969, 51, 3728–3739 CrossRef CAS.
- J. C. Dyre and N. B. Olsen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 042501 CrossRef PubMed.
- C. Maggi, B. Jakobsen, T. Christensen, N. B. Olsen and J. C. Dyre, J. Phys. Chem. B, 2008, 112, 16320–16325 CrossRef CAS PubMed.
- H. Li, M. Ibrahim, I. Agberemi and M. N. Kobrak, J. Chem. Phys., 2008, 129, 124507 CrossRef PubMed.
- M. N. Kobrak and H. Li, Phys. Chem. Chem. Phys., 2010, 12, 1922 RSC.
- J. D. Holbrey, W. M. Reichert and R. D. Rogers, Dalton Trans., 2004, 2267–2271 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Ab initio simulation results, synthetic details and procedures, single crystal XRD data, hydrogen bond geometries, thermal transitions, experimental data as a function of temperature (density, viscosity, conductivity and fits thereof), self-diffusion coefficients, theoretical background and experimental data for DMTA measurements, MD simulation details and force field development, theoretical background on statistical mechanics (structure, diffusion, heterogeneity, time correlation functions, conformational space, charge arm, charge network relaxation), input and example output files for the prealpha software package, Gaussian log files, MULTIWFN analysis results, fftool force field files, representative LAMMPS input files and data files and additional code. See https://doi.org/10.1039/d2sc03074h |
| ‡ Current address: Sorbonne Université, CNRS, Physico-chimie des Électrolytes et Nanosystèmes Interfaciaux, PHENIX, F-75005 Paris, France. |
| This journal is © The Royal Society of Chemistry 2022 |