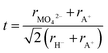Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Expanding the hydride chemistry: antiperovskites A3MO4H (A = Rb, Cs; M = Mo, W) introducing the transition oxometalate hydrides†
Alexander
Mutschke
 *a,
Annika
Schulz
a,
Marko
Bertmer
*a,
Annika
Schulz
a,
Marko
Bertmer
 b,
Clemens
Ritter
c,
Antti J.
Karttunen
b,
Clemens
Ritter
c,
Antti J.
Karttunen
 d,
Gregor
Kieslich
d,
Gregor
Kieslich
 e and
Nathalie
Kunkel
e and
Nathalie
Kunkel
 *a
*a
aChair of Inorganic Chemistry with Focus on Novel Materials, Technical University of Munich, Lichtenbergstrasse 4, 85748 Garching, Germany. E-mail: Alex.Mutschke@tum.de; ga74lud@mytum.de
bFelix Bloch Institute for Solid State Physics Leipzig University, Linnéstrasse 5, 04103 Leipzig, Germany
cInstitut Laue-Langevin, 71 Avenue des Martyrs, 38042 Grenoble Cedex 9, France
dDepartment of Chemistry and Materials Science, Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland
eChair of Inorganic and Metal-Organic Chemistry, Technical University of Munich, Lichtenbergstrasse 4, 85748 Garching, Germany
First published on 25th May 2022
Abstract
The four compounds A3MO4H (A = Rb, Cs; M = Mo, W) are introduced as the first members of the new material class of the transition oxometalate hydrides. The compounds are accessible via a thermal synthesis route with carefully controlled conditions. Their crystal structures were solved by neutron diffraction of the deuterated analogues. Rb3MoO4D, Cs3MoO4D and Cs3WO4D crystallize in the antiperovskite-like K3SO4F-structure type, while Rb3WO4D adopts a different orthorhombic structure. 2H MAS NMR, Raman spectroscopy and elemental analysis prove the abundance of hydride ions next to oxometalate ions and experimental findings are supported by quantum chemical calculations. The tetragonal phases are direct and wide band gap semiconductors arising from hydride states, whereas Rb3WO4H shows a unique, peculiar valence band structure dominated by hydride states.
Introduction
Mixed anionic hydrides as a subclass of mixed anionic compounds1 have recently raised a lot of attention due to a variety of academically interesting and technological relevant properties such as fast hydride ion conduction,2 tunable optical properties3 and superconductivity4 amongst others. In addition, the number of mixed anionic hydrides with acceptable air and moisture stability is steadily increasing which facilitates their application in the future.5–8 To date, oxy hydrides with isolated oxide ions represent the largest group of this materials class which includes a variety of transition metal based oxy hydrides.9–11 The latter are typically synthesized by high pressure synthesis or reductive topotactic reaction which often leads to materials with disordered anions such as AECrO2H (AE = Sr, Ba)10,11 or BaTiO3−xHx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12,13 as archetypical examples. Undoubtedly, transition metal-based oxy hydrides show fascinating characteristics on their own such as magnetic ordering at elevated temperatures10,11,14 diffusional dynamics,15 good electronic13,16 or ionic17 conductivities. However, yet no single hydridic compound containing complex transition orthooxometalate anions such as tetrahedral MoO42− or WO42− anions has been reported. The reductive nature of hydrogenation reactions often requires carefully designed synthetic routes to keep the complex anions intact. In turn, only a handful mixed anionic hydrides with complex (oxo-)anions, such as aluminate hydrides18,19 or borate hydrides7 are reported to date. The combination of complex oxoanions of transition metals with hydrides has not yet been realized to date. Expanding the field of mixed anionic hydrides to complex transition metalate anions, by binding the oxygen covalently to the metal center, is expected to uncover different and potentially unforeseen and desirable material properties.
12,13 as archetypical examples. Undoubtedly, transition metal-based oxy hydrides show fascinating characteristics on their own such as magnetic ordering at elevated temperatures10,11,14 diffusional dynamics,15 good electronic13,16 or ionic17 conductivities. However, yet no single hydridic compound containing complex transition orthooxometalate anions such as tetrahedral MoO42− or WO42− anions has been reported. The reductive nature of hydrogenation reactions often requires carefully designed synthetic routes to keep the complex anions intact. In turn, only a handful mixed anionic hydrides with complex (oxo-)anions, such as aluminate hydrides18,19 or borate hydrides7 are reported to date. The combination of complex oxoanions of transition metals with hydrides has not yet been realized to date. Expanding the field of mixed anionic hydrides to complex transition metalate anions, by binding the oxygen covalently to the metal center, is expected to uncover different and potentially unforeseen and desirable material properties.
Here we report the direct synthesis, structure and electronic properties of the compounds A3MO4H (A = Rb, Cs; M = Mo, W) which are the first four representatives of the transition oxometalate hydrides. These are also the first oxide-based hydrides containing molybdenum and tungsten as transition metal. Reduction of the transition metal is avoided by an exploratory optimized synthesis route which allows to keep the transition metal with high oxidation number and the complex metalate ions intact. Moreover, covalent or coordinative interactions between the hydride and the transition metal center can be excluded in the presented compounds.
Results and discussion
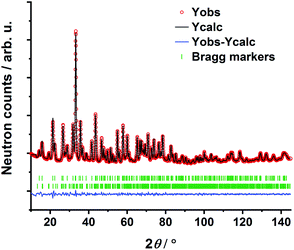
The transition oxometalate hydrides are synthetically accessible by a solid-state reaction under hydrogen pressure with controlled conditions. As inspired by a recent study about a novel sulfate hydride,20 a thermal synthesis route is applied to synthesize the herein presented compounds. In a typical synthesis, the alkaline metal A (A = Rb, Cs) is reacted with the quasi-binary oxometalate salts (A2MoO4, A2WO4) at 528 K for the molybdate hydrides and 600 K for the tungstate hydrides under an applied hydrogen pressure of 10 bar. The hydrogen pressure is required to hydrogenate the alkaline metal to form the alkaline hydride which readily reacts with the quasi-binary molybdate or tungstate salts to form the respective transition oxometalate hydrides. Mild conditions are required to avoid reduction of the transition metalate ion to the elemental transition metal or different bronzes thereof; however, too mild conditions drastically prolong the reaction time and impede phase pure synthesis or prevent the reaction as a whole. The molybdate hydrides are only accessible in a temperature window of approximately 15 K as the reduction of the molybdate ions is beginning above 535 K. The formation of the tungstate analogues occurs over a range of up to 60 K. A mechanochemical activation route as demonstrated in previous studies about new mixed anionic hydrides7,21 resulted in the reduction of the oxometalate ions into several different valent transition metal oxides. Short scan powder X-ray diffraction measurements of the obtained polycrystalline powders revealed diffraction patterns of new, unknown phases. Indexing of reflections from the X-ray diffraction patterns return tetragonal structures for Rb3MoO4H, Cs3MoO4H and Cs3WO4H and an orthorhombic structure for Rb3WO4H. Initial structural models were obtained by using superflip22 as implemented in Jana2006.23 Due to the very weak X-ray scattering power of hydrogen and the abundance of heavy metal atoms, we applied powder neutron diffraction of the deuterated analogues to obtain complete structural models of the newly formed phases. Due to the large bound coherent scattering length (6.671 barn) of deuterium (2H),24 the deuteride and the corresponding equal hydride positions were determined reliably, completing and enhancing the initial structural models obtained by X-ray diffraction. Subsequently, structure solution has been carried out by Rietveld-refinement of neutron diffraction data at room temperature with Fullprof.25 An exemplary neutron refinement plot of Cs3MoO4D is shown in Fig. 1. Structural data and all further Rietveld refinement plots obtained from X-ray and neutron diffraction data can be found in the ESI.†The compounds Rb3MoO4D, Cs3MoO4D and Cs3WO4D crystallize isostructural in the tetragonal K3SO4F-structure type with the space group I4/mcm (140),26 while Rb3WO4D presumably adopts a different structure-type. The corresponding cell parameters are listed in Table 1. The building principle of all compounds is related to an A3BX antiperovskite-like structure. The hydride (X) occupies the octahedral site and is octahedrally coordinated by the alkaline metal (A). The larger complex anions (B) occupy the cuboctahedral voids within the [A3B]+ ReO3-type network. The tetragonal phases belong to the K3SO4F-structure type and show activated octahedral tilts along the c-direction when compared to the ideal cubic perovskite structure in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The assigned glazer tilt notation is a0a0c−.27 In addition to the prototype K3SO4F,26 several compounds with tetrahedral complex anions are known to crystallize in this structure-type such as the selenate fluoride K3SeO4F,28 the oxonitrodosilicates Ln3[SiN3O]O (Ln = La, Ce, Pr),29 or the aluminate hydride Sr3AlO4H.19 A schematic of the crystal structure of the tetragonal phases can be found in the ESI in Fig. S9.†
m. The assigned glazer tilt notation is a0a0c−.27 In addition to the prototype K3SO4F,26 several compounds with tetrahedral complex anions are known to crystallize in this structure-type such as the selenate fluoride K3SeO4F,28 the oxonitrodosilicates Ln3[SiN3O]O (Ln = La, Ce, Pr),29 or the aluminate hydride Sr3AlO4H.19 A schematic of the crystal structure of the tetragonal phases can be found in the ESI in Fig. S9.†
| Rb3MoO4D | Cs3MoO4D | Cs3WO4D | Rb3WO4D | |
|---|---|---|---|---|
| a Due to distortions of the octahedra, the application of the Glazer-notation is not straightforwardly applicable; however, when neglecting these distortions, the same tilt-system as for the other compounds is obtained. | ||||
| Space group | I4/mcm (140) | I4/mcm (140) | I4/mcm (140) | Pbca (61) |
| Phase prototype | K3SO4F | K3SO4F | K3SO4F | Own structure type |
| Lattice parameter (Å) | a = 7.8620(3) | a = 8.2113(2) | a = 8.2331(2) | a = 11.9262(3) |
| c = 12.2998(5) | c = 12.7893(4) | c = 12.8289(3) | b = 11.3972(5) | |
| c = 11.4492(5) | ||||
| Formular units (Z) | 4 | 4 | 4 | 8 |
| M–O dist. (Å) | 1.766(1) | 1.767(1) | 1.775(1) | 1.735(10)–1.784(7) |
| ∠ (Ø): O–M–O, (M = Mo, W) | 109.32° | 109.17° | 109.17° | 109.42° |
| Glazer tilt notation | a0a0c− | a0a0c− | a0a0c− | |
The Mo–O bond lengths are found to be in average 1.766 Å, while the W–O bond lengths are found to be 1.775 Å. Both agree with typical Mo–O bond lengths within the orthomolybdate ion (1.70 Å)30 and W–O bond lengths (1.79 Å) of orthotungstate ions.31 The tetrahedron angles within the complex orthometalate ions are found to have mean values in the range of 109.17–109.32° which fit closely to the ideal tetrahedron angle of 109.47°.
Solely Rb3WO4H could not be solved in I4/mcm. Careful structural analysis based on neutron and X-ray diffraction data, delivers a new orthorhombic structure type with the space group Pbca (61). In this presented structure model, the Rb-built octahedrons surrounding the hydrides are distorted and tilted towards each other, most notably in the c-direction (Fig. 2). Also, the tungstate ions located in the cuboctahedral voids between the corner-sharing Rb6D octahedrons are tilted slightly towards each other in all three crystallographic directions. Overall, these slight distortions result in an antiperovskite-like structure with a pseudo tetragonal setup (a/b = 1.0464, b/c = 0.9955, c/a = 0.9600). Notably, such a distorted (anti)perovskite-like variant has not been observed this far and differs from other orthorhombic perovskite variants in the GdFeO3-structure type and derivatives thereof. As the Rb6D octahedra are unusual with Rb-positions close to special positions, several different structure solutions with varying space-groups were tested; however, no other obtained solution sufficiently converged or enhanced the herein presented model. We thus conclude the reported structural model to be the most fitting hitherto. In average the W–O bond lengths are found to be 1.77 Å, again fitting the typical W–O bond length of orthooxotungstate ions of 1.79 Å.31 The tetrahedron angles are found to be in average 109.42° which fits very closely to the ideal tetrahedron angle of 109.47° The Rb–D distances are found to be between 2.8529 Å and 3.0040 Å corresponding to the typical bond lengths found in ionic metal hydrides.7,20,21,32 Further details on the crystal structure investigations are given in the ESI,† on quoting the depository numbers CSD 2127403 (Rb3MoO4D), CSD 2127400 (Cs3MoO4D), CSD 2127401 (Cs3WO4D), CSD 2127405 (Rb3WO4D). As already stated, the cesium compounds Cs3MoO4H and Cs3WO4H are isostructural and rather unexpectedly, the structures of the rubidium based phases Rb3MoO4H and Rb3WO4H differ from one another. Due to the lanthanide contraction, molybdenum and tungsten have equal ionic radii, therefore it is expected for both compounds to be isostructural; however, when considering M–O bond lengths, the Mo–O bond length is in average about 0.01 Å shorter than the W–O bond length and thus, the molybdate ions overall have a marginal smaller total ionic radius compared to the tungstate ions. This results in slightly different packing factors which might cause the formation of different structural distortions. Interestingly, Schmitz-Dumont and Weeg observed an identical trend of the corresponding fluoride molybdates and fluoride tungstates. Even though they did not report any structural data, laboratory powder diffraction data revealed two different crystallographic set-ups for Rb3MoO4F and Rb3WO4F.33
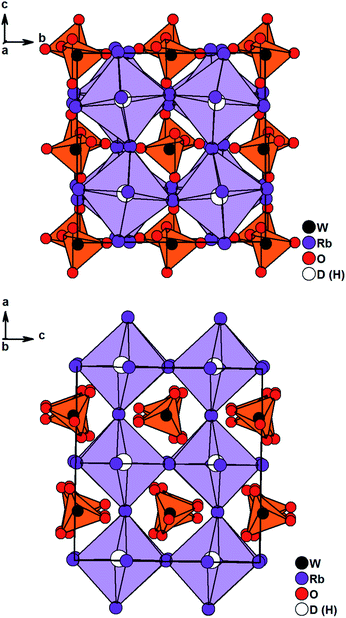 | ||
| Fig. 2 Crystal structure of Rb3WO4D along the c-axis (top) and the a-axis (bottom). Tungstate anions are depicted as orange tetrahedrons, Rb6D octahedrons are lilac. | ||
To further understand the structural modifications of the antiperovskite-like structures, we calculated the Goldschmidt-tolerance factor of all four compounds. According to Goldschmidt, a compound with the general formula ABX3 forms the ideal cubic (anti)perovskite structure when the ionic radii have a certain ratio or simply when t ≈ 1.34 Such compounds usually adopt distorted variants if t differs too far from the ideal value of 1, often if t < 0.9 or t > 1.1.34–36 While many deviations from this trend are known, the tolerance factor is a powerful approach for rationalizing the crystal chemistry especially when applied to material series. For the here investigated systems, the tolerance factors can be calculated by considering the molybdates and tungstates as complex ions, applying the formula below:35–37
For details on the determination of ionic radii of MO42− and H− see ESI.†
As seen in Table 2, the determined tolerance factors all deviate from the ideal value of t ≈ 1; however, they fit closely to the determined value of the phase prototype K3SO4F, with Cs3MoO4H having the best fitting value of 1.11. By a further look at the tolerance factors, it is recognizable that Rb3WO4H deviates the most from the phase prototype and the related tetragonal phases, with a calculated tolerance factor of 1.14. As suggested by the Goldschmidt-factor, the Rb+ ion in this structure might be just too small in relation to the large complex WO42− anion to stabilize Rb3WO4H in a less distorted structure when compared to the other compounds reported in this work. The tolerance factor deviates even more from 1 in Na3SO4H which represents a further antiperovskite-like hydride (P4/nmm, Ag3CrO4Cl-type).20 Compared to the structure types presented in this work, the assembly is different in Na3SO4H as the alkaline (Na+) ions are now considerably smaller than the hydride ions. In turn, the sulfate anions demand less space within the cuboctrahedral voids in relation to the larger oxometalate anions. This overall results in another tetragonal structure with only distorted but not tilted (Na6D) octahedra.
| Compound | Tolerance factor t |
|---|---|
| Rb3MoO4H | 1.12 |
| Cs3MoO4H | 1.11 |
| Rb3WO4H | 1.14 |
| Cs3WO4H | 1.12 |
| K3SO4F | 1.09 |
| Na3SO4H | 1.15 |
MAS NMR spectroscopy
Structure analysis based on X-ray and neutron diffraction is complemented by magic angle spinning nuclear magnetic resonance (MAS NMR) to obtain information on the atomic level. Especially 1H and 2H MAS NMR have proven to be a powerful tool to confirm the presence of hydride ions.7,8,20,21,381H is the most receptive nuclear spin, however, the 2H spin is superior as the spectra are not affected by any other present hydrogen containing material like impurities from the probe background or from synthesis.
The 2H MAS spectra of the four samples are summarized in Fig. 3. Corresponding 1H spectra show the same signals with quasi identical shifts, yet contain additionally other signals originating from the rotor cap or other external impurities. All obtained 2H MAS NMR spectra contain one dominant signal that is assigned to the parent material. Additionally, in all samples a minor signal with a small linewidth at negative chemical shift is present. This signal originates from hydrides covalently bound to transition elements, typically showing negative shifts.39 In the case of Rb3WO4D and Cs3MoO4D a quadrupolar pattern indicative of a covalent bond is seen. Since these signals contribute only to a minor amount besides the main signal, a more detailed analysis was not done.
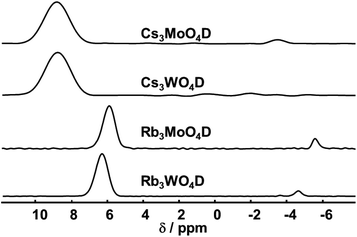 | ||
| Fig. 3 2H MAS NMR spectra of the four compounds (isotropic region only). The spectra were acquired at room temperature with a spinning frequency of 5 kHz and a magnetic field B0 = 17.6 T. | ||
Both rubidium and both cesium containing samples show each very similar shifts, about 6.0–6.4 ppm for rubidium and 9.8 ppm for cesium. The higher shift for cesium is expected following the trend of the size of alkali metal hydrides and corresponding shifts in the simple hydrides (LiH: 2.9 ppm, NaH: 3.6 ppm, KH: 4.7 ppm).40 DFT-PBE calculations of the chemical shift of the 1H nucleus support the experimental findings. The shifts were calculated to be 6.4 ppm for Cs3MoO4H, 6.2 ppm for Cs3WO4H and 5.5 ppm for both rubidium compounds in reference to SiMe4. While the calculated shifts of the cesium compounds differ compared to the experimental findings, the trend of the higher homologues to be downfield shifted is reproduced. In the case of cesium, the mismatching downfield shift might be due to the spin–orbit heavy-atom effect on the light-atom, where the heavy cesium atom has a deshielding effect of on the neighbouring H atom.41 Spin–orbit coupling effects have not been taken into account in the present calculations.
Overall, the chemical shifts were found to be in the region typical for inorganic salt-like hydrides.7,8,20,21,38,40 In combination with DFT calculations, 2H MAS NMR proves the abundance of hydrides within the crystal lattice.
Further evidence of the hydride abundance is provided by simple elemental analysis. Here, the experimental determined weight percentage of hydrogen is determined to be close to the theoretical values in all four compounds. The simultaneous abundance of either tungsten or molybdenum is additionally determined and underlines the abundance of both hydride anions next to tungstate and molybdate ions. The elemental analysis reports can be seen in the ESI.†
Raman spectroscopy is used to verify the abundance of complex tetrahedral (ortho)anions through the presence of their typical stretching and bending modes. The experimental spectra were additionally compared to simulated spectra obtained by density functional theory (DFT-PBE0) calculations of the hydridic species (see ESI† for the computational details). As can be seen in Fig. 4 and S25–S27† the obtained Raman spectra are in good agreement with the simulated spectra. All Raman-active vibrational modes, ν1 to ν4, are observed in the expected wavenumber regions with the predicted intensity, confirming the abundance of the complex orthometalate anions and supporting in overall the structural models. The Raman spectra also differ from the corresponding Raman spectra of the binary oxometalate salts. The respective spectra, due to the lower orthorhombic symmetry of the starting materials, show a splitting of the ν3 mode and overlapping ν2 and ν4 modes. This deviates from the spectra of the newly formed phases where the ν2 and ν4 modes appear noticeable distant to each other and the ν3 mode does not show splitting.42 As the structure of Rb3WO4H differs from the structure of the tetragonal phases, its Raman spectrum shows a slightly different Raman spectrum (Fig. 4). In addition to the vibrational modes of the tungstate anions, vibrational modes of the tungstate anions coupled to hydride modes (ν3H) are seen at about 850–900 cm−1 as predicted in the simulated spectrum. This again confirms the abundance of hydride ions and supports the structural model obtained by neutron diffraction. By comparison with the Raman spectrum of Rb2WO4, it is apparent that in this case the ν3 modes are more distinctly split and the ν3H modes are missing. Similarly for the ν2 and ν4 modes that show more recognizable and pronounced bending modes, not seen in the Raman spectrum of Rb3WO4H.43 This overall affirms the successful formation of a new phase.
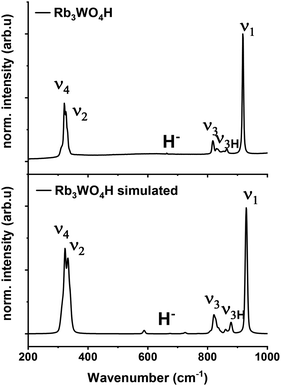 | ||
| Fig. 4 Experimental Raman spectrum of Rb3WO4H (top) and simulated Raman spectrum of Rb3WO4H (bottom, DFT-PBE0 method). | ||
Fig. S19, S21 and S23† show the calculated electronic band structures and density of states of the tetragonal phases crystallizing in the K3SO4F-structure. All three compounds can be classified as wide band gap semiconductors with direct band gaps of approximately 3.2 eV (Cs3MoO4H), 3.4 eV (Rb3MoO4H) and 3.8 eV (Cs3WO4H). All three calculated band structures show similar features where hydride is dominating the topmost valence band with only minor contributions from rubidium or cesium. Due to the polarizability of hydride and the strong covalent character of the hydride ion, the topology of the band structure is directly influenced by the hydride ion and is directly responsible for the direct band gap and thus the semiconducting character of the tetragonal compounds. These findings reflect and are in line with previous studies of inorganic salt like hydrides where hydride is always predicted to dominate the topmost valence band.6–8,20,44 UV/Vis absorption spectroscopy and the resulting Tauc-plots confirm the direct band gaps and are close to the estimated band gap value which underlines the direct influence of the hydride ion regarding the direct band gap. As the compounds are isostructural, a band gap tuning might be possible by the synthesis of mixed cationic or mixed tungstate/molybdate solid-solutions.
The calculated band structure of Rb3WO4H (Fig. 5) is very peculiar and the valence bands are dominated by the hydride states. At the Γ-point, all eight hydride bands are non-degenerate, while at the R-point all states are degenerate. In this crystal structure, the hydrides form a quasi-cubic arrangement, resulting in slightly unequal paths within the reciprocal space. Even though a relatively large band gap of approx. 4.6 eV is estimated, again a direct transition is predicted.
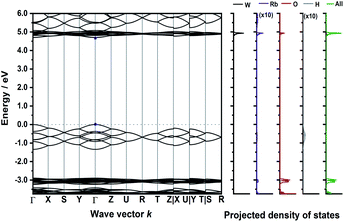 | ||
| Fig. 5 Electronic band structure of Rb3WO4H and projected density of states (DFT-PBE0). The band paths in the reciprocal space have been determined by the Seek-path webservice.45 The DOS of Rb and H are enhanced by a factor of ten for better visibility. | ||
Interestingly, in all four calculated band structures the states arising from the hydride ions are located between states arising from the complex transition metalate ion. An initial approach for the design of direct semiconductors might target a modification of this band structure.
Conclusions
In summary, we hereby provide the groundwork for a potentially broad class of materials: the transition oxometalate hydrides. The four compounds A3MO4H (A = Rb, Cs; M = Mo, W) are accessible via a sophisticated thermal synthesis route and are introduced as the first representatives of this new class. To the best of our knowledge, such a combination of transition metal anions with hydride ions has not been realized this far. The unprecedented abundance of hydrides next to complex oxoanions within single structures is proven by several analytical methods including neutron diffraction, Raman spectroscopy, MAS NMR spectroscopy, elemental analysis and beyond that supported by quantum chemical calculations. The four compounds show interesting electronic and structural features. While the compounds of the tetrahedral class are direct and wide band gap semiconductors, Rb3WO4H shows a very dispersive, peculiar valence band structure dominated by hydride states arising from the pseudo cubic arrangement of the hydride ions within the orthorhombic crystal structure. Overall, these findings demonstrate a pathway to hitherto unexplored anion combinations and open the door for further anion combinations containing other complex transition metalate ions like e.g. (di)chromates or orthovanadates. Likewise, these compounds may act as chemical templates for new, more complex structures such as combinations of hydrides with polymetalate ions.Data availability
Full experimental details and further data supporting the research are provided in the ESI.†Author contributions
A. M., G. K. and N. K. coordinated the research and wrote the main parts of the manuscript, A. M. and A. S. performed the syntheses, M. B. performed the NMR experiments, A. M. and A. J. K. performed DFT calculations, C. R. collected the neutron diffraction data, N. K. acquired funding and administrated the project. All authors commented on the paper.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank Christoph Wallach for Raman measurements and Sabine Zeitz for UV/Vis absorption spectroscopy. A. M. and M. B. thank Leonhard Dorsch for packing of the MAS rotors. Bircan Dilki is thanked gratefully for conducting the elemental analysis. We would like to thank the Institut Laue-Langevin for beam time allocated on D2B; https://doi.org/10.5291/ILL-DATA.5-21-1170 and https://doi.org/10.5291/ILL-DATA.EASY-725. A. M. and N. K. thank the DFG for funding (project number 245845833) within International Research Training Group IRTG 2022—Alberta Technical University of Munich School for Functional Hybrid Materials (ATUMS). A. M. thanks the International Graduate School for Science and Engineering (IGSSE) for support. A. J. K. thanks Academy of Finland for funding (grant 324973) and CSC, the Finnish IT Center for Science for computational resources.References
- (a) H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772 CrossRef PubMed; (b) T. Yajima, F. Takeiri, K. Aidzu, H. Akamatsu, K. Fujita, W. Yoshimune, M. Ohkura, S. Lei, V. Gopalan, K. Tanaka, C. M. Brown, M. A. Green, T. Yamamoto, Y. Kobayashi and H. Kageyama, Nat. Chem., 2015, 7, 1017 CrossRef CAS PubMed.
- (a) H. Ubukata, F. Takeiri, K. Shitara, C. Tassel, T. Saito, T. Kamiyama, T. Broux, A. Kuwabara, G. Kobayashi and H. Kageyama, Sci. Adv., 2021, 7, eabf7883 CrossRef CAS PubMed; (b) G. Kobayashi, Y. Hinuma, S. Matsuoka, A. Watanabe, M. Iqbal, M. Hirayama, M. Yonemura, T. Kamiyama, I. Tanaka and R. Kanno, Science, 2016, 351, 1314 CrossRef CAS PubMed.
- (a) A. Mutschke, T. Wylezich, A. D. Sontakke, A. Meijerink, M. Hoelzel and N. Kunkel, Adv. Opt. Mater., 2021, 9, 2002052 CrossRef CAS; (b) T. Wylezich, S. Welinski, M. Hoelzel, P. Goldner and N. Kunkel, J. Mater. Chem. C, 2018, 6, 13006 RSC.
- K. Kobayashi, J.-i. Yamaura, S. Iimura, S. Maki, H. Sagayama, R. Kumai, Y. Murakami, H. Takahashi, S. Matsuishi and H. Hosono, Sci. Rep., 2016, 6, 39646 CrossRef CAS PubMed.
- N. Zapp, D. Sheptyakov, A. Franz and H. Kohlmann, Inorg. Chem., 2021, 60, 3972 CrossRef CAS PubMed.
- N. Zapp, H. Auer and H. Kohlmann, Inorg. Chem., 2019, 58, 14635 CrossRef CAS PubMed.
- T. Wylezich, R. Valois, M. Suta, A. Mutschke, C. Ritter, A. Meijerink, A. J. Karttunen and N. Kunkel, Chem.–Eur. J., 2020, 26, 11742 CrossRef CAS PubMed.
- F. Gehlhaar, R. Finger, N. Zapp, M. Bertmer and H. Kohlmann, Inorg. Chem., 2018, 57, 11851 CrossRef CAS PubMed.
- (a) J. Bang, S. Matsuishi, H. Hiraka, F. Fujisaki, T. Otomo, S. Maki, J.-i. Yamaura, R. Kumai, Y. Murakami and H. Hosono, J. Am. Chem. Soc., 2014, 136, 7221 CrossRef CAS PubMed; (b) F. Denis Romero, A. Leach, J. S. Möller, F. Foronda, S. J. Blundell and M. A. Hayward, Angew. Chem., Int. Ed., 2014, 53, 7556 CrossRef CAS PubMed; (c) Y. Goto, C. Tassel, Y. Noda, O. Hernandez, C. J. Pickard, M. A. Green, H. Sakaebe, N. Taguchi, Y. Uchimoto, Y. Kobayashi and H. Kageyama, Inorg. Chem., 2017, 56, 4840 CrossRef CAS PubMed; (d) L. Jin, M. Lane, D. Zeng, F. K. K. Kirschner, F. Lang, P. Manuel, S. J. Blundell, J. E. McGrady and M. A. Hayward, Angew. Chem., Int. Ed., 2018, 130, 5119 CrossRef; (e) C. Tassel, Y. Goto, D. Watabe, Y. Tang, H. Lu, Y. Kuno, F. Takeiri, T. Yamamoto, C. M. Brown, J. Hester, Y. Kobayashi and H. Kageyama, Angew. Chem., Int. Ed., 2016, 55, 9667 CrossRef CAS PubMed; (f) M. A. Hayward, E. J. Cussen, J. B. Claridge, M. Bieringer, M. J. Rosseinsky, C. J. Kiely, S. J. Blundell, I. M. Marshall and F. L. Pratt, Science, 2002, 295, 1882 CrossRef CAS PubMed.
- K. Higashi, M. Ochi, Y. Nambu, T. Yamamoto, T. Murakami, N. Yamashina, C. Tassel, Y. Matsumoto, H. Takatsu, C. M. Brown and H. Kageyama, Inorg. Chem., 2021, 60, 11957 CrossRef CAS PubMed.
- C. Tassel, Y. Goto, Y. Kuno, J. Hester, M. Green, Y. Kobayashi and H. Kageyama, Angew. Chem., Int. Ed., 2014, 53, 10377 CrossRef CAS PubMed.
- X. Liu, T. S. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2017, 5, 1050 RSC.
- T. Uchimura, F. Takeiri, K. Okamoto, T. Saito, T. Kamiyama and G. Kobayashi, J. Mater. Chem. A, 2021, 9, 20371–20374 RSC.
- (a) J. Bang, S. Matsuishi, S. Maki, J.-i. Yamaura, M. Hiraishi, S. Takeshita, I. Yamauchi, K. M. Kojima and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 064414 CrossRef; (b) T. Yamamoto, R. Yoshii, G. Bouilly, Y. Kobayashi, K. Fujita, Y. Kususe, Y. Matsushita, K. Tanaka and H. Kageyama, Inorg. Chem., 2015, 54, 1501 CrossRef CAS PubMed; (c) L. Jin and M. A. Hayward, Angew. Chem., Int. Ed., 2020, 59, 2076 CrossRef CAS PubMed; (d) Y. Wei, H. Gui, X. Li, Z. Zhao, Y.-H. Zhao and W. Xie, J. Phys.: Condens. Matter, 2015, 27, 206001 CrossRef PubMed; (e) C. A. Bridges, G. R. Darling, M. A. Hayward and M. J. Rosseinsky, J. Am. Chem. Soc., 2005, 127, 5996 CrossRef CAS PubMed.
- R. Lavén, U. Häussermann, A. Perrichon, M. S. Andersson, M. S. Targama, F. Demmel and M. Karlsson, Chem. Mater., 2021, 33, 2967 CrossRef PubMed.
- T. Yajima, A. Kitada, Y. Kobayashi, T. Sakaguchi, G. Bouilly, S. Kasahara, T. Terashima, M. Takano and H. Kageyama, J. Am. Chem. Soc., 2012, 134, 8782 CrossRef CAS PubMed.
- K. Fukui, S. Iimura, A. Iskandarov, T. Tada and H. Hosono, J. Am. Chem. Soc., 2022, 144, 1523 CrossRef CAS PubMed.
- B. Huang and J. D. Corbett, J. Solid State Chem., 1998, 141, 570 CrossRef CAS.
- T. Wu, K. Fujii, T. Murakami, M. Yashima and S. Matsuishi, Inorg. Chem., 2020, 59, 15384 CrossRef CAS PubMed.
- A. Mutschke, G. M. Bernard, M. Bertmer, A. J. Karttunen, C. Ritter, V. K. Michaelis and N. Kunkel, Angew. Chem., Int. Ed., 2021, 60, 5683 CrossRef CAS PubMed.
- A. Mutschke, T. Wylezich, C. Ritter, A. J. Karttunen and N. Kunkel, Eur. J. Inorg. Chem., 2019, 2019, 5073 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345 CrossRef.
- V. F. Sears, Neutron News, 1992, 3, 26 CrossRef.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55 CrossRef.
- J. M. S. Skakle, J. G. Fletcher and A. R. West, J. Chem. Soc., Dalton Trans., 1996, 2497 RSC.
- A. M. Glazer, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 756 CrossRef.
- J. M. S. Skakle, J. G. Fletcher and A. R. West, An. Quim., 1996, 92, 358 CAS.
- (a) D. Durach and W. Schnick, Eur. J. Inorg. Chem., 2015, 2015, 4095 CrossRef CAS; (b) J. A. Kechele, C. Schmolke, S. Lupart and W. Schnick, Z. Anorg. Allg. Chem., 2010, 636, 176 CrossRef CAS.
- P. A. Williams, in Encyclopedia of Geology, Elsevier, 2005, pp. 551–552 Search PubMed.
- F. D. Hardcastle and I. E. Wachs, J. Raman Spectrosc., 1995, 26, 397 CrossRef CAS.
- N. Zapp, D. Sheptyakov and H. Kohlmann, Crystals, 2021, 11, 750 CrossRef CAS.
- O. Schmitz-Dumont and A. Weeg, Z. Anorg. Allg. Chem., 1951, 265, 139 CrossRef CAS.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477 CrossRef CAS.
- H. Fang and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11046 CrossRef CAS PubMed.
- W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099 CrossRef.
- S. Fujii, S. Gao, C. Tassel, T. Zhu, T. Broux, K. Okada, Y. Miyahara, A. Kuwabara and H. Kageyama, J. Am. Chem. Soc., 2021, 143, 10668 CrossRef CAS PubMed.
- K. Hayashi, P. V. Sushko, Y. Hashimoto, A. L. Shluger and H. Hosono, Nat. Commun., 2014, 5, 3515 CrossRef PubMed.
- (a) P. Hrobárik, V. Hrobáriková, F. Meier, M. Repiský, S. Komorovský and M. Kaupp, J. Mater. Chem. A, 2011, 115, 5654 Search PubMed; (b) Y. Ruiz-Morales, G. Schreckenbach and T. Ziegler, Organometallics, 1996, 15, 3920 CrossRef CAS.
- F. Gehlhhar, Master's thesis, Universität Leipzig, 2019.
- (a) J. Vícha, S. Komorovsky, M. Repisky, R. Marek and M. Straka, J. Chem. Theory Comput., 2018, 14, 3025 CrossRef PubMed; (b) J. Vı Cha, J. Novotný, S. Komorovsky, M. Straka, M. Kaupp and R. Marek, Chem. Rev., 2020, 120, 7065 CrossRef PubMed.
- (a) A. Erdőhelyi, K. Fodor, R. Németh, A. Hancz and A. Oszkó, J. Catal., 2001, 199, 328 CrossRef; (b) M. Naji, F. Di Lemma, A. Kovács, O. Beneš, D. Manara, J.-Y. Colle, G. Pagliosa, P. Raison and R. J. M. Konings, J. Raman Spectrosc., 2015, 46, 661 CrossRef CAS PubMed.
- A. Jorio, P. Saint-Grégoire and M. A. Pimenta, J. Phys.: Condens. Matter, 2000, 12, 9307 CrossRef CAS.
- T. Wu, A. Ishikawa, T. Honda, H. Tamatsukuri, K. Ikeda, T. Otomo and S. Matsuishi, RSC Adv., 2019, 9, 5282 RSC.
- (a) Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Band Structure Diagram Paths Based on Crystallography, 2016 Search PubMed; (b) A. Togo and I. Tanaka, 2018, arXiv:1808.01590v1; (c) Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01861f. |
| This journal is © The Royal Society of Chemistry 2022 |