Open Access Article
Open Access ArticleMechanoresistive single-molecule junctions
Andrea
Vezzoli
 *ab
*ab
aDepartment of Chemistry, University of Liverpool, Crown Street, Liverpool L69 7ZD, UK. E-mail: andrea.vezzoli@liverpool.ac.uk
bStephenson Institute for Renewable Energy, University of Liverpool, Peach Streat, Liverpool L69 7ZF, UK
First published on 7th February 2022
Abstract
Single-molecule junctions – devices fabricated by electrically connecting a single molecule to two electrodes – can respond to a variety of stimuli, that include electrostatic/electrochemical gating, light, other chemical species, and mechanical forces. When the latter is used, the device becomes mechanoresistive which means that its electrical resistance/conductance changes upon application of a mechanical stress. The mechanoresistive phenomenon can arise at the metal-molecule interface or it can be embedded in the molecular backbone, and several strategies to attain high reproducibility, high sensitivity and reversible behaviour have been developed over the years. These devices offer a unique insight on the process of charge transfer/transport at the metal/molecule interface, and have potential for applications as nanoelectromechanical systems, integrating electrical and mechanical functionality at the nanoscale. In this review, the status of the field is presented, with a focus on those systems that proved to have reversible behaviour, along with a discussion on the techniques used to fabricate and characterise mechanoresistive devices.
Introduction
The concept of single molecules as active components in electronic devices has been around since the 1970s, when Aviram and Ratner designed a “unimolecular diode” based on a donor–spacer–acceptor structure sandwiched between two metallic electrodes.1 This device would represent a significant scale-down of electronic components, allowing current rectification at the nanoscale: Aviram and Ratner's calculations predicted that their system would conduct significant amounts of current only in one direction, when electrons are injected from the source into the acceptor, flow through the spacer and are ultimately ejected from the donor into the drain electrode. Attempts at injecting electrons into the donor would encounter a larger potential barrier with resulting minimal current through the device. Since this first conceptualisation of unimolecular electronics, progress in the field has been made on many fronts, from experimental techniques that allow reliable and reproducible fabrication of single-molecule junctions,2,3 to sophisticated in silico methods for the prediction of their charge-transport properties.4–7 These experimental and theoretical advances aided the development of functional single-molecule diodes8–10 (thus fulfilling Aviram and Ratner's predictions), insulators,11–13 transistors and switches,14–16 electroluminescent devices17,18 and other types of electronic and spintronic components.19–21 Another subset of single-molecule devices that is becoming increasingly more studied in the field are those that show mechanoresistive (or piezoesistive) behaviour. These devices are subject to changes in their charge transport efficiency upon mechanical stimulus, the latter being generally compression/stretching of the molecular wire obtained by moving the electrodes closer together or farther apart. They have been proposed in the literature as single-molecule potentiometers or, more accurately as they are two-terminal devices, single-molecule rheostats, but there is great promise for their applications as nanoelectromechanical systems (NEMS) and as analytical tools to probe metal–molecule interfaces.Charge transport in molecular wires
The vast majority of single-molecule devices operates at such length-scales that a quantum tunnelling mechanism of charge transport is dominant. Within this mechanism, the efficiency of charge transport is given by the transmission coefficient T(E), which is the ratio of the electron current density emerging from a potential barrier divided by the incident electron current density. In a zero-temperature, zero-bias approximation, the conductance G of a single molecule (a single quantum channel) attached to two electrodes via two chemisorbed termini (contact groups, Fig. 1a) can be described by the Landauer–Büttiker transmission model| G = G0T(EF) | (1) |
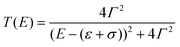 | (2) |
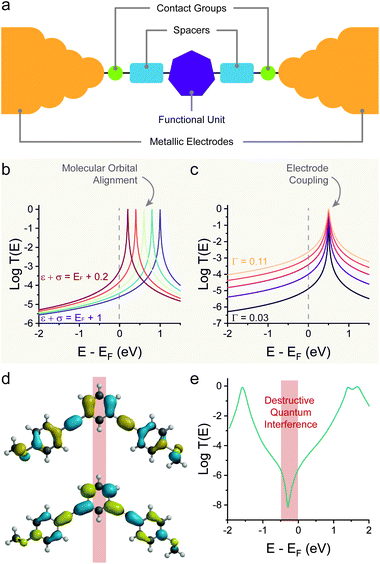 | ||
| Fig. 1 Fundamental concept of charge transport in molecular wires. (a) Anatomy of a molecular junction, showing the electrodes “chemically soldered” to a functional unit by the use of contact groups (with or without the use of spacers). (b) Example of T(E) as the orbital energy is moved closer to the Fermi level of the electrodes. (c) Example of T(E) as the coupling parameter Γ is increased. (d) Molecular orbitals (HOMO = top; LUMO = bottom) for a meta-connected molecular wire (1,3-bis((4-(methylthio)phenyl)ethynyl)benzene) and (e) resulting DFT-calculated T(E) for its Au–molecule–Au junction. Panels (b) and (c) calculated with eqn (2). Molecular orbitals in (d) calculated with Wavefunction Inc. Spartan 18, DFT ωB97X-d/6-31G*. Data in panel (e) digitised from Jiang et al.22 and replotted. | ||
The interaction of a molecular orbital with the electrodes and the subsequent formation of a conducting quantum channel is an example of constructive quantum interference.23 The opposite case, where destructive quantum interference phenomena arise, is also possible.24–27 The standing waves generated by charge carriers propagating through the molecular wire will create a pattern of nodes, and if one of these nodes is located on the molecular charge transport pathway then an antiresonance will arise in the T(E) curve. The position in energy of this antiresonance is key, and the closer it is to the Fermi energy of the electrodes, the greater the resulting conductance suppression will be. A common example of destructive interference of significant magnitude is observed in meta (1,3)-connected phenyl rings, as there are nodes in both the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) (Fig. 1d). The simple single-level model presented earlier cannot capture destructive interference phenomena, and more detailed analytical or density functional theory (DFT) calculations are needed to obtain an accurate T(E) spectrum (Fig. 1e).23,28–30
Single-molecule junction fabrication techniques
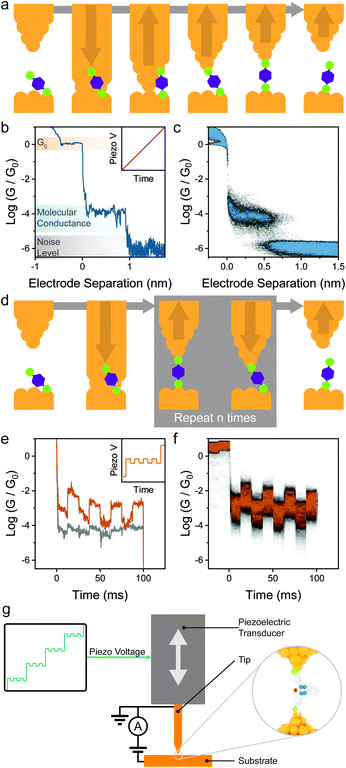
Several techniques for the fabrication and characterisation of single-molecule junctions have been introduced in the last 25 years but the most widely used (as of 2021) is the break-junction31 technique, whether in its mechanically-controlled (MCBJ),2 scanning tunnelling microscope-based (STMBJ)3 or conductive probe atomic force microscope-based (CP-AFMBJ)32–34 implementation. In both cases, a piezo stack is responsible for the movement of the electrodes, the only difference between the two methods being their geometry: two electrodes immobilised on a flexible substrate in MCBJ,35–37 and a tip and substrate pair in STMBJ/CP-AFMBJ.38–40 The electrodes, under bias V, are first pushed together to form a nanocontact, and then pulled apart while following the electrical current I (or electrical conductance G = I/V) through the device, as a function of the movement z (Fig. 2a). As the electrodes are pulled apart, the nanocontact is thinned to an atomic point contact, and the conductance signal settles into consecutive plateaux having conductance of multiple integers of the quantum of conductance G0, indicative of transport through integer numbers of metallic atoms.41 Further movement results in rupture of the atomic point contact, and a small (0.3–0.7 nm) nanogap is created by electrode snapback. Molecules, either present as a chemisorbed sub-monolayer or in solution, can assemble in the gap to create a single-molecule junction. In a linear-ramp break-junction experiment, routinely used for the determination of molecular conductance, the electrodes are continuously pulled apart at a rate of a few nm s−1 to stretch the junction to its most extended state, followed by junction break-off. Plateaux at values of conductance ≪G0 appear in the MCBJ/STMBJ traces (Fig. 2b), and those are attributed to charge transport through the molecular wire. After rupture of the junction, the metal–metal contact is rapidly reformed, and the break-junction process repeated. Thousands of traces are consecutively acquired, and these are compiled in conductance histograms and conductance vs. electrode separation density plots (Fig. 2c) to determine the most probable value of conductance and to correlate it with the junction size.The linear-ramp break-junction experiment allows direct characterisation of mechanoresistive phenomena during junction stretching, but it does not give any information on the behaviour of the junctions under compression and, as such, about the repeatability/cyclability of the mechanoresistive phenomena. Analysis of the break-junction closing traces would allow the characterisation of molecule under the compression cycle, and such experiments have been routinely used42 for the fabrication and subsequent manipulation of atomic junctions (i.e. where a single atom bridges the nanoelectrode gap), allowing minute electromechanical characterisation of one-dimensional conductors.43 In order to obtain repeatability and cyclability details of single-molecule mechanoresistivity, piezo-modulation experiments44 are necessary. In these experiments custom voltage waveforms are imposed to the piezoelectric transducer of the break-junction apparatus, in lieu of a linear ramp (sawtooth) one. The custom waveform is designed so that it first creates a gap where the molecule of interest can assemble in its fully elongated state, and the position of the two electrodes is modulated to continuously compress the junction by a few Å, to then stretch it again to its relaxed state. A final pull is performed to rupture the molecular bridge. The process is shown in Fig. 2d, and example single-molecule conductance traces under modulation are shown in Fig. 2e, with the piezo signal shown in the inset. Thousands of individual traces are usually acquired and compiled in conductance vs. time density plots (Fig. 2f) that allow the observation of the overall conductance modulation under the imposed signal. While piezo-modulation experiments are indeed challenging and require modification of commercial STMs (Fig. 2g), they allow a vastly superior level of characterisation, and since their introduction they have been used extensively to study the behaviour of mechanoresistive molecular junctions.
It is worth stressing here that break-junction methods can also go beyond the statistical determination of molecular conductance at fixed bias described so far. Once the nanogap between the two electrodes has been opened and the molecular wire has self-assembled, the electrode separation process can be halted, to “freeze” the junction in place and perform further experiments.31,45 These include, for instance, bias modulations to measure I–V characteristics and directly extrapolate numerical values for level alignment and coupling coefficient (ε + σ and Γ of eqn (2)),46 or further experiments towards the determination of thermoelectric47–49 and emissive17 properties of single-molecule junctions. These methods, which highlight the versatility of break-junction measurements beyond the determination of charge transport efficiency have been extensively reviewed elsewhere.31,35,45,50
Mechanically-induced changes at the metal–molecule interface
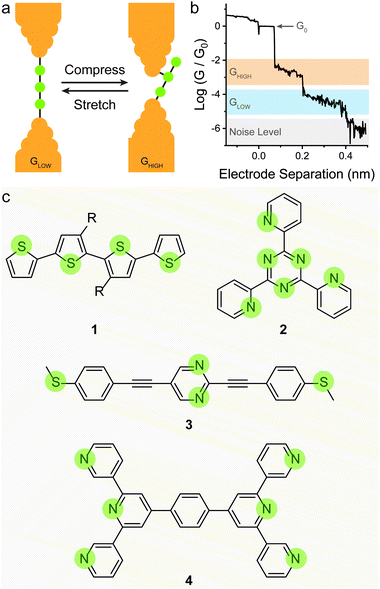
The most straightforward way to introduce mechanoresistive effects in a molecular junction is to design molecular components with multiple contact groups. In a conceptual example, a molecular wire of structure A–B–C (where A, B and C are three moieties capable of coordinating to the metallic electrodes) the molecule will be metal–A–B–metal connected to the electrodes at low separation, and as the junction is stretched, it will switch to a metal–A–B–C–metal configuration with an associated lower conductance due to the increased tunnelling pathway length and lower molecule–electrode coupling (the parameter Γ in eqn (2)) as pictured in Fig. 3a and b.This strategy has been shown to work efficiently in oligothiophenes, where the individual thienyl sulfurs act as (weak) aurophilic groups. Kiguchi et al. studied an α-quaterthiophene (1 in Fig. 3c) molecular wire and obtained staircase-like traces during STMBJ experiments, each bearing multiple plateaux with roughly one order of magnitude spacing between them (∼5 × 10−2, ∼5 × 10−3, and ∼5 × 10−4G0) that contributed to three distinct peaks in the conductance histogram.51 The highest conductance value was attributed to transport through two neighbouring thienyl units (equivalent to an α-bithiophene), the middle value to transport through three units (equivalent to an α-terthiophene) and the lowest value to transport through the entire length of the α-quaterthiophene wire. The authors also proceeded with piezo-modulation experiments and found that the switch between different molecular configuration was not regular and reproducible, but rather abrupt and stochastic in nature. It is of topical interest that only a single, broad conductance peak in the conductance histogram and no evident staircase in the STM-BJ traces was found using α-quaterthiophene functionalised with stronger contacts, such as thiols32 or methyl sulfides52 on the two termini. This specific case is described later in the text. Other devices designed on the same concept of multiple contact groups spaced along the molecular backbone have been proposed in the literature, and the examples include tri(pyrid-2-yl)triazine compounds (2 in Fig. 3c),53 substituted p-(phenylene)ethynylene oligomers (3 in Fig. 3c),54,55 bis(terpyridyl) molecular breadboards (4 in Fig. 3c),56 and fullerene dumbbells.57 While this strategy towards functional single-molecule mechanoresistive devices is indeed attractive and easy to implement, it has shown to suffer from poor reproducibility and cyclability. While most junctions fabricated with this class of compound clearly show the GHIGH → GLOW transition as the electrodes are pulled apart, the GLOW → GHIGH transition is less clearly defined in the piezo-modulation experiments. The only notable exception is the C60 dumbbell where GLOW → GHIGH transitions can be observed in the approach traces, but no extended modulation experiments have been performed.57
Reducing the distance between the anchoring points on the molecular wire can yield higher sensitivity to mechanical modulations. The carbodithioate group (OPE-style wire shown as 5 in Fig. 4a) bears a S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–S− atomic configuration, and has been introduced by Xing et al. as a superior contact for Au electrodes. Its bidentate coordinative/covalent nature grants stronger electronic coupling of the molecule to the electrodes, and higher electronic transmission.58 It was later demonstrated that as the junction evolves during an STMBJ experiment (i.e. as the molecule is stretched), there is reorganisation at the molecule–metal interface, with a bidentate → monodentate transition that results in a drastic drop in conductance.59 The opposite monodentate → bidentate transition upon junction compression was however not studied. We demonstrated a different system containing S–C–S termini to be fully cyclable, with reproducible bidentate ⇌ monodentate transitions even at high piezo-modulation speed (up to 10 kHz). As discussed earlier in the text, thiol- or thioether-terminated oligothiophenes show exceptionally wide conductance spread during break-junction experiments. While this can be partially attributed to symmetry,60 thiophenes themselves have been demonstrated to be efficient contact groups,61,62 and when a thiomethyl group is added in the 2-position, the system behaves like a functional hemilabile terminus. Hemilabile ligands63,64 are heterobifunctonal units with one strong binding site and a second weaker (reversible) one, and as such they are ideal for mechanoresistive purposes with clear and easy to attain bidentate ⇌ monodentate transition at the molecule–electrode interface (Fig. 4b). Molecules terminated with 2-(methylthio)thiophenes such as 6 and 7 in Fig. 4a, in fact, showed exquisite sensitivity to small changes in junction size (Fig. 4c), and no apparent signal distortion even at high modulation speed.65 DFT calculations show that junction compression and stretching cause significant distortion of the transmission curves near the Fermi level of the electrodes, with a shift in the energy of the transport orbital (σ in eqn (2)) and a mechanically-induced change in the molecule–electrode coupling (Γ in eqn (2)).
C–S− atomic configuration, and has been introduced by Xing et al. as a superior contact for Au electrodes. Its bidentate coordinative/covalent nature grants stronger electronic coupling of the molecule to the electrodes, and higher electronic transmission.58 It was later demonstrated that as the junction evolves during an STMBJ experiment (i.e. as the molecule is stretched), there is reorganisation at the molecule–metal interface, with a bidentate → monodentate transition that results in a drastic drop in conductance.59 The opposite monodentate → bidentate transition upon junction compression was however not studied. We demonstrated a different system containing S–C–S termini to be fully cyclable, with reproducible bidentate ⇌ monodentate transitions even at high piezo-modulation speed (up to 10 kHz). As discussed earlier in the text, thiol- or thioether-terminated oligothiophenes show exceptionally wide conductance spread during break-junction experiments. While this can be partially attributed to symmetry,60 thiophenes themselves have been demonstrated to be efficient contact groups,61,62 and when a thiomethyl group is added in the 2-position, the system behaves like a functional hemilabile terminus. Hemilabile ligands63,64 are heterobifunctonal units with one strong binding site and a second weaker (reversible) one, and as such they are ideal for mechanoresistive purposes with clear and easy to attain bidentate ⇌ monodentate transition at the molecule–electrode interface (Fig. 4b). Molecules terminated with 2-(methylthio)thiophenes such as 6 and 7 in Fig. 4a, in fact, showed exquisite sensitivity to small changes in junction size (Fig. 4c), and no apparent signal distortion even at high modulation speed.65 DFT calculations show that junction compression and stretching cause significant distortion of the transmission curves near the Fermi level of the electrodes, with a shift in the energy of the transport orbital (σ in eqn (2)) and a mechanically-induced change in the molecule–electrode coupling (Γ in eqn (2)).
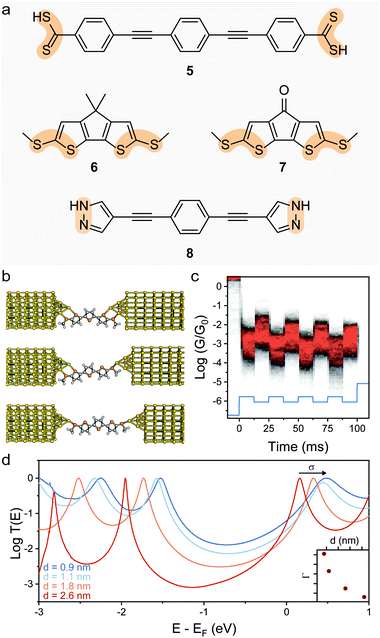 | ||
| Fig. 4 Switch between denticity at multifunctional electrode contacts. (a) Structures of the bifunctional molecular wire termini discussed in this review. The bidentate system is highlighted in orange. (b) Evolution of a junction fabricated with (methylthio)thienyl contacts as the electrodes are driven apart. The molecule–electrode interface evolves from a bidentate–bidentate configuration to bidentate–monodentate and finally monodentate–monodentate before junction rupture. (c) Example conductance vs. time density map for compound 7, with the 0.3 nm modulation piezo signal superimposed in light blue. Conductance is modulated in phase by approximately one order of magnitude, as the molecule is cycled between different configurations. (d) Transmission curves for the α-terthienyl derivative shown in (b), where the effect of the junction size on the parameters σ and Γ of eqn (2) can be appreciated. The evolution of Γ as a function of junction stretching is shown in the inset. Panels (b)–(e) replotted from data publicly available in Ferri et al.65 | ||
The pyrazolyl contact group, bearing a N–N unit, also results in an interface to the electrodes that undergoes reorganisation as the molecule is stretched.66 In this case conductance increases as the molecule is stretched, and Herrer et al. demonstrated that this is due to deprotonation of the pyrazolyl N–H, happening during junction evolution in an OPE-style wire terminated with pyrazolyl contacts (8 in Fig. 4a). Further confirmation of the conductance increase mechanism was obtained in experiments performed on monolayer devices.67 After deprotonation, a covalent N–Au bond is formed, granting higher electronic coupling and higher conductance. Mechanosensitive behaviour of these junctions was only assessed for the stretching process, and no information on the reversibility of the deprotonation process is available in the literature.
Another way of introducing mechanosensitive behaviour to a molecular junction is to exploit the different configurations that some contact groups can adopt when chemisorbed on the electrodes. Thiols, for instance, have been proposed to be able to interact with Au in a “top” conformation, covalently bonded to an apex atom or in a “bridge” (or “hollow”) conformation, sitting at the site between multiple Au atoms, with both covalent and coordinative (donor–acceptor) bonds (Fig. 5a).68 These different configurations contribute to a large conductance spread in thiols, as each configuration is associated with a different molecule–electrode coupling coefficient Γ (see eqn (2)) and, therefore, a different charge transport efficiency.69 There is evidence that thiol-terminated molecules can undergo a mechanically-induced transition between the more conductive “bridge/hollow” and the less conductive “top” configuration as the molecular junctions are stretched,70 but the process has been shown to be poorly reproducible (even under strict piezo-modulation), and largely stochastic in nature71 unless performed at cryogenic conditions.72 The most common outcome of this phenomenon is a large spread of conductance values found in junctions fabricated with molecules terminated with thiol contacts at room temperature, that result in poorly resolved peaks in the STMBJ conductance histograms if no data filtering or data selection process is applied.73
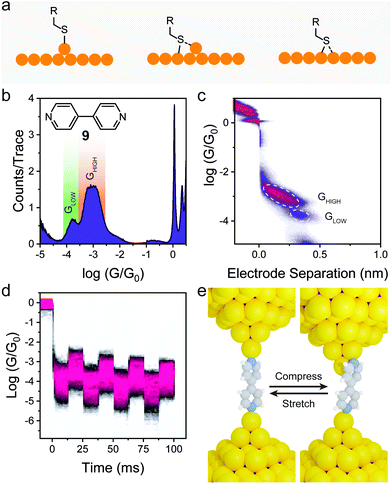 | ||
| Fig. 5 Switch between different contact configurations at the molecule–electrode interface. (a) Possible thiol binding configurations on Au surfaces. (b) Conductance histogram for 4,4′-dipyridyl (structure shown as inset) and (c) its 2D conductance vs. electrode separation density map. A bimodal conductance can be observed, with the GLOW feature associated with a longer electrode-electrode distance. (d) Conductance vs. time density map under piezo modulation for 4,4′-dipyridyl. Data in (b–d) acquired by the author, by reproducing the experiments originally performed in Quek et al.44 (e) Conductance modulation model for 4,4′-dipyridyl developed by Quek et al.44 | ||
4-Pyridyl electrode contacts, on the other hand, show a well-defined bimodal spread of conductance values even in unfiltered STMBJ histograms (Fig. 5b), and analysis of the individual traces demonstrates that in most cases there is a clear GHIGH → GLOW transition, with GHIGH ≅ 10 × GLOW and a difference in molecular extension Δz between the two states of approximately 2 Å (Fig. 5c). Quek et al. studied this phenomenon in detail, performing piezo-modulation experiment on 4,4′-dipyridyl (9 in Fig. 5b), and demonstrating the complete reversibility and cyclability of the GHIGH ⇌ GLOW switching, upon applying a mechanical modulation of the junction size with an amplitude Δz = 2 Å (Fig. 5d). DFT calculations were then used to demonstrate that the bimodal conductance is due to a change in the molecule–electrode interface. In a compressed junction (of size too small to accommodate the molecule in its extended state) 4,4′-dipyridyl is forced to adopt a conformation where the N–Au bond is tilted out of the plane of the heteroaromatic ring. In this conformation, however, the LUMO π* orbital is ideally positioned to interact with the Au orbitals, giving a higher electronic coupling Γ (see eqn (2)) and relatively high charge transport efficiency. As the junction is extended, the N–Au bond becomes coplanar with the pyridyl ring, reducing the extent of the π-Au interaction and causing a decrease in the electronic coupling Γ and molecular conductance (Fig. 5e). This phenomenon of lateral coupling between the π-system of a tilted molecular junction and the metallic electrodes has been indeed reported several times.74–78 In a particularly comprehensive study, Diez-Perez et al. measured the single-molecule conductance of a thiol-terminated, fused oligoindene as a function of junction size, and confirmed the interaction of the extended π-system with the electrodes by applying an AC modulation to the x and y piezoelectric transducers of the STM.79 Lateral coupling of the π-system alone is however a less prominent phenomenon than what is observed in 4-pyridyl contacts, with a much lower GHIGH/GLOW ratio at similar values of Δz. The uniqueness of 4-pyridyl as interface to the electrodes can be explained in terms of the geometry of the lone pair on the N atoms (responsible coordination to the electrode) being perfectly orthogonal to the heteroaromatic π-system. This orthogonality grants poor conjugation of the lone pair into the HOMO and the LUMO of the molecule and maximises the effect of small changes in the tilt angle on molecular conductance. The mechanoresistive effect is not limited to 4,4′-dipyridyl studied by Quek et al.44 but is a general phenomenon of the 4-pyridyl electrode contact.80,81
We also provided further confirmation of the mechanism of mechanical switching in these compounds, by synthesising a series of substituted 4,4′-dipyridyls bearing bulky alkyl substituents and measuring their mechanoresistive behaviour with piezo-modulation experiments.82 We found that the presence of the alkyl substituents reduces the extent of the π-Au interactions, resulting in a loss of sensitivity of the coupling coefficient Γ on molecular compression and effectively suppressing the mechanoresistive behaviour. Providing the substituents with a π-system (in the form of a pendant phenyl ring) reinstated the mechanical switching of conductance, albeit with a reduced magnitude compared to pristine 4,4′-bipyridyl.
Mechanically-induced changes in the molecular backbone
The mechanoresistive effect can also arise from mechanically-induced changes in the molecular backbone itself. One of the first examples of such behaviour was found in a bis(terpyridyl) Fe(II) spin-crossover organometallic complex (10 in Fig. 6a), that showed conductance increasing by approximately one order of magnitude as the junctions were stretched.83 The authors attributed this behaviour to a switch between a low-spin state for the relaxed molecule to a high-spin state for the stretched junction (Fig. 6b), with a resulting increase in conductance confirmed by DFT transport calculations. The spin transition is caused by a mechanically induced deformation in the coordination sphere that reduces the ligand field energy and allows the spin transition. The effect was shown to be reasonably robust, happening in approximately half of the fabricated junctions, and comparison with Ru(II) complexes where spin crossover is not expected confirmed the proposed mechanism, but the reverse high → low transition upon junction relaxation was not characterised.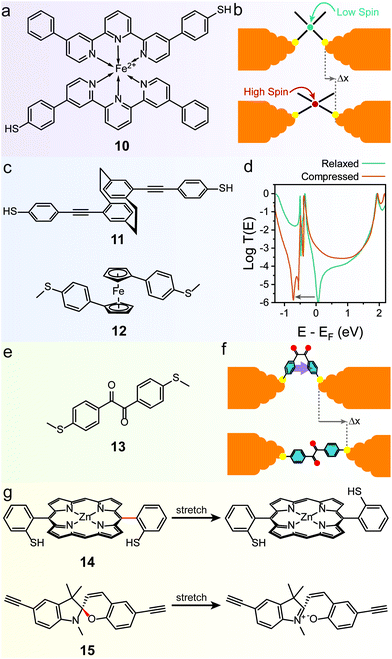 | ||
| Fig. 6 Mechanically-induced changes in the molecular backbone. (a) Structure of the spin-crossover Fe(II) complex 10 and (b) mechanism of its mechanoresistive behaviour. (c) Structures of the quantum interference based mechanosensitive compounds discussed in this review. (d) T(E) curves for 12, in the relaxed and compressed state. The QI feature is moved at energies below that of the LUMO in the compressed configuration, effectively lifting conductance suppression at EF. (e) Structure of the conformationally-flexible benzil analogue discussed in the text and (f) model for its mechanoresistive behaviour. In the compressed structure the two phenyl rings rotate to a cofacial arrangement, allowing efficient through-space transport. (g) Structures for the mechanochemical switches discussed in the text. The mechanosensitive bond in the structure is highlighted in red. T(E) curves in (d) digitised from Camarasa-Gómez et al.86 and replotted. | ||
Mechanoresistivity in a molecular junction can also be introduced by quantum interference effects. Stefani et al. demonstrated this in a substituted [2.2]paracyclophane (11 in Fig. 6c), where strong conductance oscillations were observed during linear-ramp STMBJ experiments.84 These oscillations were attributed to changes in the overlap between the frontier orbitals of the two intramolecularly π-stacked phenyl rings. In the relaxed state, the orbital symmetry introduces a destructive quantum interference feature in the transmission spectrum near the Fermi level of the electrodes, thus suppressing charge transport. As the [2.2]paracyclophane system is compressed or stretched, orbital symmetry is changed and quantum interference is lifted (i.e. moved to energies far from the electrodes EF), leading to higher charge transport efficiency. The effect was demonstrated to be completely reversible and cyclable for long periods of time with no fatigue or loss of functionality through piezo-modulation experiments, which also highlighted an exquisite sensitivity to small changes in electrode separation. A later study on the substitution pattern in [2.2]paracyclophanes further confirmed the quantum interference origin of mechanoresistivity.85 Similar effects have also been observed in the 1,1′-(thioanisolyl)ferrocene (12 in Fig. 6c) studied by Camarasa-Gómez et al.86 A sharp destructive interference feature near the Fermi level of Au suppresses charge transport in the fully-extended state, but its energy is dependent on the angle between the two cyclopentadienyl (Cp) rings of ferrocene (Fig. 6d). As the junction is compressed, the ferrocene core acts like a hinge and the two Cp rings rotate relative to each other, lifting the interference feature and allowing more transparent charge transport. Again, piezo-modulation experiments confirmed reversibility and full cyclability of the mechanoresistive behaviour.
A further strategy towards molecular mechanoresistivity is to exploit flexible fragments in the molecular backbone. Permethyloligo-silanes87 and -germanes,88 for instance, undergo stereoelectronic switching as they are stretched in the junction, with the fully extended structure being higher in conductance due to some unique properties of the Si and Ge σ-bonding system. In both cases, complete reversibility was assessed with piezo-modulation experiments, and some “junction training” was found to be required in order to attain a modest switching factor. Conformational effects can be maximised by designing molecules with intramolecular interactions that stabilise the molecule in the different configurations. A pentaphenylene foldamer, for instance, has been demonstrated to be able to adopt a “parallel” folded configuration in the early stages of an STM-BJ experiments, and evolve to the more stable “antiparallel” configuration as the electrodes are driven apart.89 In both cases charge transport is made efficient by the presence of multiple π-stacked channels, as evidenced by flicker noise90 measurements. The antiparallel → parallel configuration switch upon junction compression was however not characterised in this study. Completely reversible behaviour was instead found in compounds that can transition from a folded conformation to an extended one. This class of devices was originally proposed in a theoretical study by Franco et al.91 and we later confirmed their feasibility. In our study, we employed a conformationally-flexible benzil derivative (13 in Fig. 6e), where the dicarbonyl bridge grants a low energy barrier between the folded (syn) and the extended (anti) conformations. The low energy barrier enables the molecule to freely adapt its configuration to the size of the junction, therefore folding itself along the dicarbonyl axis to a syn conformer at low electrode separation and unfolding to the less-conductive anti conformer as the electrodes are driven apart (Fig. 6f).92 Flicker noise measurements and DFT calculations were then used to rationalise the findings. In the syn state the two phenyl rings turn to a co-planar, π-stacked configuration, thereby opening a new through-space transport channel that grants higher charge transport efficiency. In the extended state, on the other hand, the additional π–π channel is lost and conductance is purely through-bond, further suppressed by a quantum interference feature introduced by the dicarbonyl bridge.
Mechanical forces can also be used to break or rearrange chemical bonds (mechanochemistry93), and particularly labile chemical interactions are ideal for exploitation in molecular mechanoresistive devices. Mechanically-induced atropisomerization, for instance, has been observed in 5,15-diaryl phorphyrin molecular wires (14 in Fig. 6g),94 while ring-opening reactions have been observed in single-molecule junctions fabricated with functionalised spiropyrans (15 in Fig. 6g).95 Both these phenomena, however, could be driven in one direction only (cis → trans atropisomerization / spiropyran → merocyanine ring opening) by mechanical means.
Conclusions and outlook
Mechanoresistive molecular devices have emerged as an attractive application of single-molecule electronics. As an analytical tool, they can provide valuable physical insights on the nature of the molecule–metal interface, especially when combined with CP-AFM techniques that allow single-molecule force spectroscopy. This approach has been valuable in understanding the variety of configurations that chemisorbed species can adopt in contact with the electrodes. Metal–molecule interfaces are of paramount importance for heterogeneous catalysis,96 while interfacial electron transfer phenomena97 are fundamental in fields such as electrochemistry, organic light-emitting devices,98 photochemistry and dye-sensitised solar cells,99 and any kind of information on their nature and properties can therefore be highly beneficial to the wider chemical community.The study of mechanoresistive phenomena at the single-molecule level is however in need of some characterisation and reporting standards. The linear-ramp break-junction experiments used routinely to measure single-molecule conductance only show phenomena occurring in one direction (e.g. molecular stretching) and only measurements under piezo-modulation can verify reversibility of the mechanical switching and repeatability of the observed phenomena. Furthermore, some molecular junctions require a degree of “training” to achieve their best electromechanical performance,88 a phenomenon that would not be captured without piezo-modulation measurements. It would therefore be beneficial to the field to include modulation experiments in every report on molecular mechanoresistivity, possibly performed with a range of different waveforms. The 50% duty cycle square/trapezoidal wave routinely employed in the field (see inset of Fig. 2e for reference) does not allow a detailed characterisation of the switching between high/low conductance states. Sinusoidal65 or triangular85 waveforms have been used to capture these details, and they also allow for calculation of mechanoresistive parameters such as gauge factors84 and mechanoresistive sensitivity.78
From a technological point of view, the development of nanoelectromechanical devices (integrating mechanical and electrical functionality) has been so far focussed on materials such as carbon nanotubes100–102 and graphene,103,104 but the work described in this review is ideally suited to be developed into functional devices. While single-molecule junctions are indeed far from ready to be deployed in real-life applications, monolayer-type molecular electronic devices are available on the market,105,106 and some of the molecular systems described in this review are expected to retain the mechanoresistive behaviour when assembled into one-molecule thick films. Here, mechanoresistive molecular junctions have already shown their potential for improved thermoelectric harvesting, by allowing optimisation of the Seebeck coefficient by adjusting the pressure applied on a self-assembled monolayer, and therefore tuning the coupling coefficient Γ.107
Conflicts of interest
There are no conflicts to declare.References
- A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283 CrossRef CAS.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- B. Xu and N. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029 CrossRef.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- I. Díez-Pérez, J. Hihath, Y. Lee, L. Yu, L. Adamska, M. A. Kozhushner, I. I. Oleynik and N. Tao, Nat. Chem., 2009, 1, 635–641 CrossRef PubMed.
- B. Capozzi, J. Xia, O. Adak, E. J. Dell, Z.-F. Liu, J. C. Taylor, J. B. Neaton, L. M. Campos and L. Venkataraman, Nat. Nanotechnol., 2015, 10, 522–527 CrossRef CAS PubMed.
- M. L. Perrin, E. Galan, R. Eelkema, F. C. Grozema, J. M. Thijssen and H. S. J. van der Zant, J. Phys. Chem. C, 2015, 119, 5697–5702 CrossRef CAS.
- H. Li, M. H. Garner, T. A. Su, A. Jensen, M. S. Inkpen, M. L. Steigerwald, L. Venkataraman, G. C. Solomon and C. Nuckolls, J. Am. Chem. Soc., 2017, 139, 10212–10215 CrossRef CAS PubMed.
- M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419 CrossRef CAS PubMed.
- M. Mayor, C. von Hänisch, H. B. Weber, J. Reichert and D. Beckmann, Angew. Chem., Int. Ed., 2002, 41, 1183–1186 CrossRef CAS PubMed.
- J. A. Mol, C. S. Lau, W. J. M. Lewis, H. Sadeghi, C. Roche, A. Cnossen, J. H. Warner, C. J. Lambert, H. L. Anderson and G. A. D. Briggs, Nanoscale, 2015, 7, 13181–13185 RSC.
- R. J. Brooke, C. Jin, D. S. Szumski, R. J. Nichols, B. Mao, K. S. Thygesen and W. Schwarzacher, Nano Lett., 2015, 15, 275–280 CrossRef CAS PubMed.
- C. Wu, X. Qiao, C. M. Robertson, S. J. Higgins, C. Cai, R. J. Nichols and A. Vezzoli, Angew. Chem., Int. Ed., 2020, 59, 12029–12034 CrossRef CAS PubMed.
- G. Reecht, F. Scheurer, V. Speisser, Y. J. Dappe, F. Mathevet and G. Schull, Phys. Rev. Lett., 2014, 112, 047403 CrossRef PubMed.
- M. C. Chong, L. Sosa-Vargas, H. Bulou, A. Boeglin, F. Scheurer, F. Mathevet and G. Schull, Nano Lett., 2016, 16, 6480–6484 CrossRef CAS PubMed.
- J. de Bruijckere, P. Gehring, M. Palacios-Corella, M. Clemente-León, E. Coronado, J. Paaske, P. Hedegård and H. S. J. van der Zant, Phys. Rev. Lett., 2019, 122, 197701 CrossRef CAS PubMed.
- S. Schmaus, A. Bagrets, Y. Nahas, T. K. Yamada, A. Bork, M. Bowen, E. Beaurepaire, F. Evers and W. Wulfhekel, Nat. Nanotechnol., 2011, 6, 185–189 CrossRef CAS PubMed.
- R. Hayakawa, M. A. Karimi, J. Wolf, T. Huhn, M. S. Zöllner, C. Herrmann and E. Scheer, Nano Lett., 2016, 16, 4960–4967 CrossRef CAS PubMed.
- F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., Int. Ed., 2019, 58, 18987–18993 CrossRef CAS PubMed.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265 CrossRef CAS PubMed.
- J. Bai, A. Daaoub, S. Sangtarash, X. Li, Y. Tang, Q. Zou, H. Sadeghi, S. Liu, X. Huang, Z. Tan, J. Liu, Y. Yang, J. Shi, G. Mészáros, W. Chen, C. Lambert and W. Hong, Nat. Mater., 2019, 18, 364–369 CrossRef CAS PubMed.
- S. Gunasekaran, J. E. Greenwald and L. Venkataraman, Nano Lett., 2020, 20, 2843–2848 CrossRef CAS PubMed.
- S. Naghibi, A. K. Ismael, A. Vezzoli, M. K. Al-Khaykanee, X. Zheng, I. M. Grace, D. Bethell, S. J. Higgins, C. J. Lambert and R. J. Nichols, J. Phys. Chem. Lett., 2019, 10, 6419–6424 CrossRef CAS PubMed.
- M. H. Garner, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2016, 120, 9097–9103 CrossRef CAS.
- L. A. Zotti, E. Leary, M. Soriano, J. C. Cuevas and J. J. Palacios, J. Am. Chem. Soc., 2013, 135, 2052–2055 CrossRef CAS PubMed.
- T. Markussen, R. Stadler and K. S. Thygesen, Phys. Chem. Chem. Phys., 2011, 13, 14311–14317 RSC.
- P. Gehring, J. M. Thijssen and H. S. J. van der Zant, Nat. Rev. Phys., 2019, 1, 381–396 CrossRef.
- B. Q. Xu, X. L. Li, X. Y. Xiao, H. Sakaguchi and N. J. Tao, Nano Lett., 2005, 5, 1491–1495 CrossRef CAS PubMed.
- S. V. Aradhya, M. Frei, M. S. Hybertsen and L. Venkataraman, Nat. Mater., 2012, 11, 872–876 CrossRef CAS PubMed.
- Y. Zhu, Z. Tan and W. Hong, ACS Omega, 2021, 6, 30873–30888 CrossRef CAS PubMed.
- C. A. Martin, D. Ding, H. S. J. van der Zant and J. M. van Ruitenbeek, New J. Phys., 2008, 10, 065008 CrossRef.
- N. Muthusubramanian, E. Galan, C. Maity, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Appl. Phys. Lett., 2016, 109, 013102 CrossRef.
- J. M. Van Ruitenbeek, A. Alvarez, I. Piñeyro, C. Grahmann, P. Joyez, M. H. Devoret, D. Esteve and C. Urbina, Rev. Sci. Instrum., 1996, 67, 108–111 CrossRef CAS.
- C. Huang, A. V. Rudnev, W. Hong and T. Wandlowski, Chem. Soc. Rev., 2015, 44, 889–901 RSC.
- F. Schwarz and E. Lörtscher, J. Phys.: Condens. Matter, 2014, 26, 474201 CrossRef PubMed.
- K. Wang and B. Xu, Top. Curr. Chem., 2017, 375, 17 CrossRef PubMed.
- J. I. Pascual, J. Mendez, J. Gomez-Herrero, A. M. Baro, N. Garcia, U. Landman, W. D. Luedtke, E. N. Bogachek and H. P. Cheng, Science, 1995, 267, 1793–1795 CrossRef CAS PubMed.
- A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agraït and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785 CrossRef CAS.
- N. Agraït, A. L. Yeyati and J. M. van Ruitenbeek, Phys. Rep., 2003, 377, 81–279 CrossRef.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- R. Frisenda and H. S. J. van der Zant, Phys. Rev. Lett., 2016, 117, 126804 CrossRef CAS PubMed.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571 CrossRef CAS PubMed.
- L. Cui, R. Miao, C. Jiang, E. Meyhofer and P. Reddy, J. Chem. Phys., 2017, 146, 092201 CrossRef.
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306 RSC.
- D. Xiang, H. Jeong, T. Lee and D. Mayer, Adv. Mater., 2013, 25, 4845–4867 CrossRef CAS PubMed.
- M. Kiguchi, T. Ohto, S. Fujii, K. Sugiyasu, S. Nakajima, M. Takeuchi and H. Nakamura, J. Am. Chem. Soc., 2014, 136, 7327–7332 CrossRef CAS PubMed.
- B. Capozzi, E. J. Dell, T. C. Berkelbach, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2014, 136, 10486–10492 CrossRef CAS PubMed.
- M. Iwane, S. Fujii, T. Nishino and M. Kiguchi, J. Phys. Chem. C, 2016, 120, 8936–8940 CrossRef CAS.
- L. Palomino-Ruiz, P. Reiné, I. R. Márquez, L. Álvarez de Cienfuegos, N. Agraït, J. M. Cuerva, A. G. Campaña, E. Leary, D. Miguel, A. Millán, L. A. Zotti and M. T. González, J. Mater. Chem. C, 2021, 9, 16282–16289 RSC.
- D. Miguel, L. Álvarez De Cienfuegos, A. Martín-Lasanta, S. P. Morcillo, L. A. Zotti, E. Leary, M. Bürkle, Y. Asai, R. Jurado, D. J. Cárdenas, G. Rubio-Bollinger, N. Agraït, J. M. Cuerva and M. T. González, J. Am. Chem. Soc., 2015, 137, 13818–13826 CrossRef CAS PubMed.
- C. Seth, V. Kaliginedi, S. Suravarapu, D. Reber, W. Hong, T. Wandlowski, F. Lafolet, P. Broekmann, G. Royal and R. Venkatramani, Chem. Sci., 2017, 8, 1576–1591 RSC.
- P. Moreno-García, A. La Rosa, V. Kolivoška, D. Bermejo, W. Hong, K. Yoshida, M. Baghernejad, S. Filippone, P. Broekmann, T. Wandlowski and N. Martín, J. Am. Chem. Soc., 2015, 137, 2318–2327 CrossRef PubMed.
- Y. Xing, T. H. Park, R. Venkatramani, S. Keinan, D. N. Beratan, M. J. Therien and E. Borguet, J. Am. Chem. Soc., 2010, 132, 7946–7956 CrossRef CAS PubMed.
- Z. Li, M. Smeu, T.-H. Park, J. Rawson, Y. Xing, M. J. Therien, M. A. Ratner and E. Borguet, Nano Lett., 2014, 14, 5493–5499 CrossRef CAS PubMed.
- E. J. Dell, B. Capozzi, K. H. DuBay, T. C. Berkelbach, J. R. Moreno, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2013, 135, 11724–11727 CrossRef CAS PubMed.
- R. Frisenda, R. Gaudenzi, C. Franco, M. Mas-Torrent, C. Rovira, J. Veciana, I. Alcon, S. T. Bromley, E. Burzurí and H. S. J. van der Zant, Nano Lett., 2015, 15, 3109–3114 CrossRef CAS PubMed.
- S. Bock, O. A. Al-Owaedi, S. G. Eaves, D. C. Milan, M. Lemmer, B. W. Skelton, H. M. Osorio, R. J. Nichols, S. J. Higgins, P. Cea, N. J. Long, T. Albrecht, S. Martín, C. J. Lambert and P. J. Low, Chem. – Eur. J., 2017, 23, 2133–2143 CrossRef CAS PubMed.
- A. Bader and E. Lindner, Coord. Chem. Rev., 1991, 108, 27–110 CrossRef CAS.
- S. E. Angell, C. W. Rogers, Y. Zhang, M. O. Wolf and W. E. Jones, Coord. Chem. Rev., 2006, 250, 1829–1841 CrossRef CAS.
- N. Ferri, N. Algethami, A. Vezzoli, S. Sangtarash, M. McLaughlin, H. Sadeghi, C. J. Lambert, R. J. Nichols and S. J. Higgins, Angew. Chem., Int. Ed., 2019, 58, 16583–16589 CrossRef CAS PubMed.
- I. L. Herrer, A. K. Ismael, D. C. Milán, A. Vezzoli, S. Martín, A. González-Orive, I. Grace, C. Lambert, J. L. Serrano, R. J. Nichols and P. Cea, J. Phys. Chem. Lett., 2018, 9, 5364–5372 CrossRef CAS PubMed.
- L. Herrer, S. Martín, A. González-Orive, D. C. Milan, A. Vezzoli, R. J. Nichols, J. L. Serrano and P. Cea, J. Mater. Chem. C, 2021, 9, 2882–2889 RSC.
- C. Li, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, J. Am. Chem. Soc., 2008, 130, 318–326 CrossRef CAS PubMed.
- Z. Li, L. Mejía, J. Marrs, H. Jeong, J. Hihath and I. Franco, J. Phys. Chem. C, 2021, 125, 3406–3414 CrossRef CAS.
- A. Mishchenko, D. Vonlanthen, V. Meded, M. Bürkle, C. Li, I. V. Pobelov, A. Bagrets, J. K. Viljas, F. Pauly, F. Evers, M. Mayor and T. Wandlowski, Nano Lett., 2010, 10, 156–163 CrossRef CAS PubMed.
- K. Wang, J. M. Hamill, J. Zhou and B. Xu, J. Am. Chem. Soc., 2014, 136, 17406–17409 CrossRef CAS PubMed.
- M. Taniguchi, M. Tsutsui, K. Yokota and T. Kawai, Chem. Sci., 2010, 1, 247–253 RSC.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6, 458–462 CrossRef CAS PubMed.
- L. Lafferentz, F. Ample, H. Yu, S. Hecht, C. Joachim and L. Grill, Science, 2009, 323, 1193–1197 CrossRef CAS PubMed.
- W. Haiss, C. Wang, I. Grace, A. S. Batsanov, D. J. Schiffrin, S. J. Higgins, M. R. Bryce, C. J. Lambert and R. J. Nichols, Nat. Mater., 2006, 5, 995–1002 CrossRef CAS PubMed.
- W. Haiss, C. Wang, R. Jitchati, I. Grace, S. Martín, A. S. Batsanov, S. J. Higgins, M. R. Bryce, C. J. Lambert, P. S. Jensen and R. J. Nichols, J. Phys.: Condens. Matter, 2008, 20, 374119 CrossRef PubMed.
- R. Ramachandran, H. B. Li, W.-Y. Lo, A. Neshchadin, L. Yu and J. Hihath, Nano Lett., 2018, 18, 6638–6644 CrossRef CAS PubMed.
- J. S. Meisner, M. Kamenetska, M. Krikorian, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nano Lett., 2011, 11, 1575–1579 CrossRef CAS PubMed.
- I. Diez-Perez, J. Hihath, T. Hines, Z.-S. Wang, G. Zhou, K. Müllen and N. Tao, Nat. Nanotechnol., 2011, 6, 226–231 CrossRef CAS PubMed.
- R. J. Brooke, D. S. Szumski, A. Vezzoli, S. J. Higgins, R. J. Nichols and W. Schwarzacher, Nano Lett., 2018, 18, 1317–1322 CrossRef CAS PubMed.
- K. Yoshida, I. V. Pobelov, D. Z. Manrique, T. Pope, G. Mészáros, M. Gulcur, M. R. Bryce, C. J. Lambert and T. Wandlowski, Sci. Rep., 2015, 5, 9002 CrossRef CAS PubMed.
- A. K. Ismael, K. Wang, A. Vezzoli, M. K. Al-Khaykanee, H. E. Gallagher, I. M. Grace, C. J. Lambert, B. Xu, R. J. Nichols and S. J. Higgins, Angew. Chem., Int. Ed., 2017, 56, 15378–15382 CrossRef CAS PubMed.
- R. Frisenda, G. D. Harzmann, J. A. Celis Gil, J. M. Thijssen, M. Mayor and H. S. J. van der Zant, Nano Lett., 2016, 16, 4733–4737 CrossRef CAS PubMed.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988 CrossRef CAS PubMed.
- K. Reznikova, C. Hsu, W. M. Schosser, A. Gallego, K. Beltako, F. Pauly, H. S. J. van der Zant and M. Mayor, J. Am. Chem. Soc., 2021, 143, 13944–13951 CrossRef CAS PubMed.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. Inkpen, G. Lovat, E.-D. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7, 215–220 CrossRef CAS PubMed.
- T. A. Su, H. Li, V. Zhang, M. Neupane, A. Batra, R. S. Klausen, B. Kumar, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, J. Am. Chem. Soc., 2015, 137, 12400–12405 CrossRef CAS PubMed.
- J. Li, P. Shen, S. Zhen, C. Tang, Y. Ye, D. Zhou, W. Hong, Z. Zhao and B. Z. Tang, Nat. Commun., 2021, 12, 167 CrossRef CAS PubMed.
- O. Adak, E. Rosenthal, J. Meisner, E. F. Andrade, A. N. Pasupathy, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2015, 15, 4143–4149 CrossRef CAS PubMed.
- I. Franco, C. B. George, G. C. Solomon, G. C. Schatz and M. A. Ratner, J. Am. Chem. Soc., 2011, 133, 2242–2249 CrossRef CAS PubMed.
- C. Wu, D. Bates, S. Sangtarash, N. Ferri, A. Thomas, S. J. Higgins, C. M. Robertson, R. J. Nichols, H. Sadeghi and A. Vezzoli, Nano Lett., 2020, 20, 7980–7986 CrossRef CAS PubMed.
- R. T. O'Neill and R. Boulatov, Nat. Rev. Chem., 2021, 5, 148–167 CrossRef.
- E. Leary, C. Roche, H.-W. Jiang, I. Grace, M. T. González, G. Rubio-Bollinger, C. Romero-Muñiz, Y. Xiong, Q. Al-Galiby, M. Noori, M. A. Lebedeva, K. Porfyrakis, N. Agrait, A. Hodgson, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, J. Am. Chem. Soc., 2018, 140, 710–718 CrossRef CAS PubMed.
- M. C. Walkey, C. R. Peiris, S. Ciampi, A. C. Aragonès, R. B. Domínguez-Espíndola, D. Jago, T. Pulbrook, B. W. Skelton, A. N. Sobolev, I. Díez Pérez, M. J. Piggott, G. A. Koutsantonis and N. Darwish, ACS Appl. Mater. Interfaces, 2019, 11, 36886–36894 CrossRef CAS PubMed.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- X. Y. Zhu, J. Phys. Chem. B, 2004, 108, 8778–8793 CrossRef CAS.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- A. Hagfeldt and M. Grätzel, Chem. Rev., 1995, 95, 49–68 CrossRef CAS.
- A. Kis and A. Zettl, Philos. Trans. R. Soc., A, 2008, 366, 1591–1611 CrossRef CAS PubMed.
- J. O. Island, V. Tayari, A. C. McRae and A. R. Champagne, Nano Lett., 2012, 12, 4564–4569 CrossRef CAS PubMed.
- S. Bauerdick, A. Linden, C. Stampfer, T. Helbling and C. Hierold, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2006, 24, 3144 CrossRef CAS.
- A. Reserbat-Plantey, K. G. Schädler, L. Gaudreau, G. Navickaite, J. Güttinger, D. Chang, C. Toninelli, A. Bachtold and F. H. L. Koppens, Nat. Commun., 2016, 7, 10218 CrossRef CAS PubMed.
- J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315, 490–493 CrossRef CAS PubMed.
- A. J. Bergren, L. Zeer-Wanklyn, M. Semple, N. Pekas, B. Szeto and R. L. McCreery, J. Phys.: Condens. Matter, 2016, 28, 94011 CrossRef PubMed.
- M. Peplow, ACS Cent. Sci., 2016, 2, 874–877 CrossRef CAS PubMed.
- X. Wang, A. Ismael, A. Almutlg, M. Alshammari, A. Al-Jobory, A. Alshehab, T. L. R. Bennett, L. A. Wilkinson, L. F. Cohen, N. J. Long, B. J. Robinson and C. Lambert, Chem. Sci., 2021, 12, 5230–5235 RSC.
| This journal is © The Royal Society of Chemistry 2022 |