Deep learning for the automation of particle analysis in catalyst layers for polymer electrolyte fuel cells

Abstract

The rapidly growing use of imaging infrastructure in the energy materials domain drives significant data accumulation in terms of their amount and complexity. The applications of routine techniques for image processing in materials research are often ad hoc, indiscriminate, and empirical, which renders the crucial task of obtaining reliable metrics for quantifications obscure. Moreover, these techniques are expensive, slow, and often involve several preprocessing steps. This paper presents a novel deep learning-based approach for the high-throughput analysis of the particle size distributions from transmission electron microscopy (TEM) images of carbon-supported catalysts for polymer electrolyte fuel cells. A dataset of 40 high-resolution TEM images at different magnification levels, from 10 to 100 nm scales, was annotated manually. This dataset was used to train the U-Net model, with the StarDist formulation for the loss function, for the nanoparticle segmentation task. StarDist reached a precision of 86%, recall of 85%, and an F1-score of 85% by training on datasets as small as thirty images. The segmentation maps outperform models reported in the literature for a similar problem, and the results on particle size analyses agree well with manual particle size measurements, albeit at a significantly lower cost.

---

1. Introduction

Relentless exhaustion of non-renewable resources in combination with ever-rising environmental concerns demand escalating efforts to develop and improve clean energy technology.^1–3 As one of the leading candidates for clean energy applications, especially in the automotive sector, polymer electrolyte membrane fuel cells (PEMFCs) demonstrate remarkable technical characteristics such as high power density, high energy conversion efficiency, instant start-up/shut-down and zero-emission operation.^4–6 Despite numerous advantages, PEMFC technology suffers from a significant drawback in terms of high costs and insufficient performance of the catalyst layer (CL). The latter is fabricated using expensive Platinum (Pt) nanoparticles (NPs), which are supported on a high-surface area carbon material (Pt/C).^7,8 Therefore, further advances in performance and cost reduction of the Pt-based catalyst layer are vital to ensure the widespread deployment of PEMFCs.^9–11

In the past three decades, a plethora of research activities have focused on developing and evaluating novel alternatives to improve the performance of Pt-based CL through experimental methods, computational studies, and comprehensive characterization.^12–22 High-resolution X-ray and electron microscopy (in situ/ex situ) characterization methods are increasingly used for the evaluation of the catalytic activity and stability of the catalyst layer. Examples include ultra-small angle X-ray scattering (u-SAXS), focussed ion beam scanning electron microscopy (FIB-SEM), transmission electron microscopy (TEM), scanning transmission electron microscopy (STEM), or scanning transmission X-ray microscopy (STXM).^23–26

To unravel the connection between microstructure properties and performance, it becomes essential to quantify certain features of the imaging data correctly, e.g., the particle size distribution (PSD), pore size, pore network, or aggregate size – with less reliance on human intervention and interpretation.^27,28 This quantification usually requires additional analyses, which can be done either manually by the operator or automatically via processing the images through a set of specialized algorithms to extract the pertinent structural features.^29,30

The type of post-processing analysis of materials characterization data alluded to be beneficial as numerous studies suggested that the electrochemical performance of CL is strongly dependent on the surface area, size, shape, and distribution of Pt NPs.^31–34 For example, an increase in mean Pt particle size in an aged cathode and subsequent reduction at anode, associated with Pt²⁺ ion crossover, could indicate degradation of the carbon support.^35–37 In another study the larger particle size and agglomeration after potential loading was attributed to the dissolution and re-deposition of Pt in the catalyst layer.³⁸ Smaller Pt particles are not favorable either because of the stronger adsorption of reaction intermediates at the edges and corners of NPs; the latter results in blockage of oxygen reduction reaction path and makes the Pt more susceptible to dissolution.³⁹

The widely employed technique for particle size analysis entails measuring a set of manually drawn straight lines from the edges of individual particles in the image.⁴⁰ This approach employs standard image processing tools like ImageJ⁴¹ and may require thresholding the image and applying filters for denoising, to segment the particles from the support material or background. Notwithstanding, this essential thresholding step becomes tricky in capturing small particles or when the contrast between particle and support material is not strong. In addition, in a one-at-a-time inspection of particles, the operator usually considers only a subset of the particles for each image, resulting in the loss of information. The long, tedious, and detailed manual procedure makes this approach ineffective for high-throughput or real-time analysis. Moreover, identifying the overlapping particles is strongly dependent on the operator's bias and judgment. These issues generate an unreliable metric for the quantification and can slow down or even falsify the analysis.

Semi-automated approaches for the analysis of well-separated and monodisperse NPs have been developed. For example, for magnetite NPs, classical approaches using Otsu's binarization with Canny edge detection and edge linking algorithms were employed.⁴⁵ For the population analysis of Pt NPs on glassy Carbon, an earlier report has introduced the local adaptive threshold (LAT) in the image processing steps.⁴⁶ This step improved the segmentation of particles by thresholding the smaller patches of the image, but at the cost of additional computing time.⁴⁶ Ponti and co-workers developed PEBBLES,⁴⁷ the software program for the size measurement and morphological analysis of nanoparticles in TEM micrographs. PEBBLES applies fitting 3D intensity models to relate the contrast of the image and the depth of the dip in the intensity surface to the NP size, making the automatic measurement and analysis of the distribution of morphological parameters passible. However, as pointed out by the authors, the software is limited in accurately fitting the overlapping NPs or the heterostructured NPs (e.g., core–shell NPs).⁴⁷

Over the last decade, deep learning (DL) methods based on the convolutional neural networks (ConvNets) have transformed the field of computer vision by outperforming the conventional methods in various image and video recognition tasks such as in verification/identification, classification, object detection, and segmentation, as well in other applications including image reconstruction, denoising, image synthesis, colorization, style transfer and other tasks.^48,49 To leverage the advancements in DL-based approaches in microscopy image processing, more recently, the ConvNets algorithms have been deployed to several platforms for various analysis tasks like segmentation, object detection, denoising, or super-resolution microscopy. The most exciting example is the recently developed ZeroCostDL4Mic⁵⁰ platform that provides the advantage of free computational resources on GoogleColab for training the deep neural network models. Unlike the conventional procedures requiring several preprocessing steps for particle analysis to construct suitable features, DL models utilize the information content directly from the raw TEM micrographs;⁵¹ once a suitable model is trained on a representative dataset, they can predict swiftly and accurately without the necessity for the human-based alteration of parameters. Moreover, the robustness of DL models is validated with various metrics like precision, recall, or accuracy, which introduces well-defined quantification metrics for particle analysis.

Image segmentation is a topic of unfading interest in various domains. Table 1 summarizes a few use cases from the recent literature, with information about the dataset used (to the best of our knowledge).^52–61 Specifically in materials science, more recently, Yao et al. implemented the popular U-Net model⁴⁴ for real-time nanoparticle segmentation in liquid-phase TEM videos.⁶² This novel approach enabled the statistical analysis of the diffusion, reaction, and assembly kinetics of the rod-, prism- and cube-shaped colloidal NPs.⁶² Cole and co-workers introduced ImageDataExtractor,^63,64 a novel tool to automate the extraction and analysis of microscopy imaging data from the scientific literature. The main feature of the ImageDataExtractor is its capability in segmentation and quantification of NPs via Bayesian DL for a diverse set of morphologies.⁶⁴ However, as will be discussed, ImageDataExtractor is limited in the accurate localization of overlapping NPs, as is the case for Pt NPs on a carbon support material.

Table 1 Few examples of the recent literature employing deep learning-based segmentation models in various domains

Ref.	Dataset size	Public availability	Application
Haugland Johansen et al. (2021)^52	104	No	Microscopic foraminifera segmentation
Velesaca et al. (2020)^53	523	Yes	Corn kernel classification
Gené-Mola et al. (2020)^54	582	Yes	Fruit detection
Kim et al. (2021)^55	2592	No	Bubble detection
Zhou et al. (2020)^56	1109	No	Cervical cell segmentation
Jayakody et al. (2021)^57	3065	Yes	Stomata detection
Chen et al. (2020)^58	500	No	Aluminum alloy microstructure segmentation
Toda et al. (2020)^59	1200	Yes	Seed phenotyping segmentation
Poletaev et al. (2020)^60	30 000	Yes	Gas bubble size distribution
Zhiming Cheng et al. (2020)^61	871	Yes	Cell nuclei segmentation

---

This paper presents a novel DL-based approach to automate the PSD analysis from TEM micrographs of catalyst layers in PEMFCs. We trained the StarDist model⁴³ on our annotated imaging dataset for the instance segmentation of Pt NPs on the high surface area Carbon support. The model largely resolved the localization of overlapping particles. Unlike the conventional procedure, this approach adopts definite quantification metrics for evaluating the segmentation.

2. Materials and methods

This work employs historical imaging data of catalyst layer materials. Samples for TEM imaging were either catalyst powders directly dispersed on the TEM grid or thin sections of the fuel cell electrodes. The catalyst powders were prepared by dispersing catalyst powders in 50 vol% isopropyl alcohol in water and dropped on the 200 lacey carbon TEM grid. Thin sections of the electrodes were prepared by embedding the electrode in a 1 : 1 mixture of trimethylolpropane triglycidyl ether resin (Sigma-Aldrich, USA) and 4,4′-methylenebis (2-methylcyclohexylamine, Sigma-Aldrich, USA) hardener, and sectioning thin slices (≈100 nm) using Leica UCT ultramicrotome and Ultra 45° DiATOME knife, USA. The sections were placed on 200 mesh Cu TEM grids. Images for particle size distribution were obtained using Talos F200X scanning transmission electron microscope (Thermo Fisher Scientific, USA) with electron accelerating voltage of 200 kV.

Our approach for the PSD analysis involves the four steps shown in Fig. 1(a): (1) manual annotation of Pt NPs, (2) supervised learning for particle segmentation, (3) programmed diameter measurement on the predicted region-of-interest (ROI), and (4) statistics and visualization. The quality of the trained model largely depends on the quality of the labeled data; therefore, it is important to choose an efficient and accurate tool for the first step. For this purpose, we used QuPath,⁶⁵ a user-friendly open-source software initially developed for quantitative pathology and bioimage analysis. Forty high-resolution TEM images (1024 × 1024 and 2048 × 2048 pixels) of Pt NPs on Carbon support were manually annotated. The image set comprised four different magnification levels, at 10, 20, 50, and 100 nm scales, providing a generalization of the scale range to train more robust models. An expert performed the annotations considering visual evidence for the overlapping particles while eluding the strongly crowded Pt aggregates. We will make this dataset publicly available.

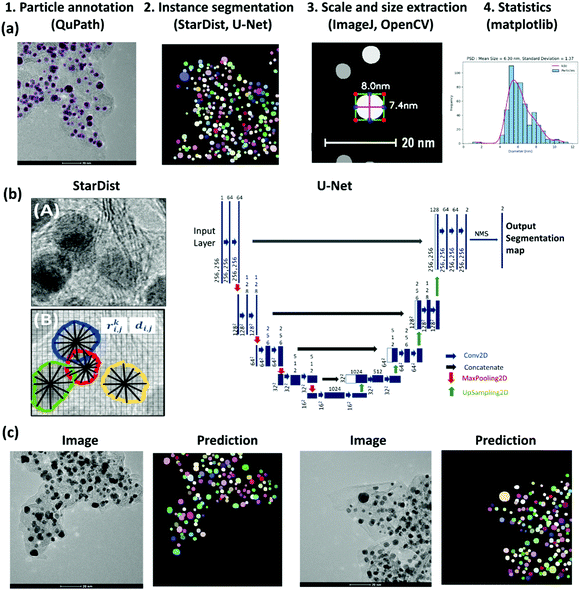Fig. 1 (a) Methodical pipeline for deep learning-based analysis of particle size distribution involving 1. Particle annotation, 2. Supervised learning for the instance segmentation of particles, 3. Setting scale for image calibration and programmed particle size extraction, using OpenCV library,⁴² 4. Obtaining particle size statistics with visualization libraries. (b) The left panel shows a TEM image with overlapped Pt particles supported on a carbon agglomerate; the StarDist method used in this work predicts star-convex polygons parameterized by the radial distances r_i,j, and object probabilities d_i,j. for the pixel i,j.⁴³ The right panel shows the U-Net architecture.⁴⁴ (c) Example TEM images and their corresponding predicted instance segmentation of Pt particles using U-Net with StarDist formulation for the loss function.

Given the images and corresponding labeled masks as ground truth, for the pixel-level localization of individual Pt particles, we trained the StarDist model.⁴³ StarDist employs the U-Net architecture⁴⁴ and overcomes the typical segmentation errors for the dense prediction of merged bordering particles by localizing them as star-convex polygons (Fig. 1(b)). StarDist was initially developed for the segmentation of biological systems to differentiate the overlapping cells in crowded images. In this model, each pixel is parameterized by two values, the radial distances and the object probabilities. For the former, a star-convex polygon is fitted from the pixel position to the edges of the ROI. The latter is represented by the normalized shortest distance from the edge which increases with decreasing the distance from the particle center.

Standard architectures for image segmentation usually involve fully convolutional networks that first perform convolution and down-sampling operations to extract essential features from the image (encoding into a latent space), followed by up-sampling and transpose convolution operations that make the activation maps larger until it reaches the input image size (decoding from a latent space). In the U-Net architecture,⁴⁴ in addition to this data stream, the up-sampled decoder features are concatenated with the exact corresponding resolution from encoder feature maps (as shown by the gray arrows in Fig. 1(b)). Concatenating encoder and decoder feature maps enables recognizing object boundaries or edges by combining features across all levels, from low to high, leading to more accurate output segmentation maps (Fig. 1(c)). The StarDist implementation of U-Net employs data augmentation to expand the size of the training set by generating modified versions of images in the dataset, where the images are cropped in patches and augmented by rotation, changing intensity, and Gaussian blurring. In this model, the non-maximum suppression (NMS) technique is further used to suppress the multiple detections of individual objects. This way, the predicted box with higher object probability suppresses the overlapped boxes with lower probabilities. For training, the number of epochs and the number of steps per epoch were chosen as 400 and 100, respectively.

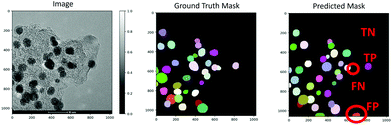
The performance of the trained model was analyzed by plotting standard metrics concerning the Intersection over Union (IoU) threshold. The IoU measures the number of pixels common between the ground truth and prediction masks divided by the total number of existing pixels in both masks. Conventionally, reliable predictions correspond to an IoU value ≥ 0.5. In our case, a true-positive (TP) represents the case if a prediction-target mask pair for nanoparticles has an IoU score that exceeds 0.5; likewise, a true-negative (TN) is that for support or background. On the other hand, a false-positive (FP) indicates a predicted NP mask with no associated ground truth mask, and a false-negative (FN) indicates a ground truth NP mask with no associated predicted mask. Examples of TP, TN, FP, and FN are demonstrated in Fig. 2. This way, the metrics of accuracy, precision, recall, and F1 score are defined as,

Accuracy = (TP + TN)/(TP + FP + TN + FN);

Precision = (TP)/(TP + FP);

Recall = (TP)/(TP + FN);

F1 = 2 × precision × recall/(precision + recall)

Fig. 2 Demonstration of a TEM image along with the ground truth and predicted masks. Examples of true-positive (TP), true-negative (TN), false-positive (FP), and false-negative (FN) predictions are shown on the predicted mask.

For an image with many NPs, it is not a severe problem to have a few FN predictions because it does not significantly affect the statistical analysis. However, a model with high precision indicates that false particles are not introduced to the particle size distribution analysis. Therefore, precision is a reliable measure for the evaluation of the model performance. The accuracy, on the other hand, can be a misleading metric for the images with a small number of NPs as it becomes biased in mainly relating how well the model predicts the background.

Given the model's prediction in segmentation maps, the ROI for each particle was white-filled, cropped, and saved into a JPEG file. Next, using the contrasted contours, we used the OpenCV library⁴² to place a bounding box around the predicted masks and measured the number of pixels along with the X or Y directions (step 3 in Fig. 1(a)). Here, manual image calibration was used for a pixel-to-real-distance conversion. Lastly, the particle size can be estimated as the average values along with the X and Y directions, and the corresponding histogram can be generated for the PSD analysis (step 4 in Fig. 1(a)).

3. Results and discussion

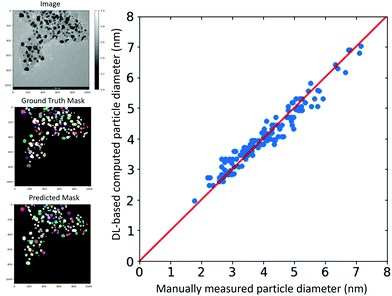
Fig. 3 compares the manually measured particle diameter performed by an expert as a reference and the computed particle diameter values for a test TEM image according to the approach presented. The image is shown in the left panel along with the ground truth and predicted segmentation masks. The strong correlation between the values indicates the effectiveness of our deep learning-based approach for the high-throughput particle size analysis with minimal human interventions. For this image, the trained StarDist model on our annotated dataset could localize a total of 134 particles out of the 150 particles in the ground truth mask. Interestingly enough, the model captured most of the overlapping particles.

Fig. 3 The left panel shows the TEM image, ground truth mask, and predicted mask. The right panel compares the manually measured particle diameter with the deep learning-based computed particle diameter.

Table 2 summarizes the performance of the segmentation model in terms of precision, recall, and F1-score for varying split ratios between the training and validation sets at the IoU threshold of 0.5. The model's performance becomes saturated with training sets as small as ten annotated images. We obtained a precision, recall, and F1-score as high as 0.86%, 0.85%, 0.85%, respectively, at a 3 : 1 ratio of training to the validation set. Further in-depth error sensitivity analysis of the model in terms of the AUC–ROC metric is shown in Fig. 4. The model is robust against the Gaussian blur with standard deviations as large as 8. The performance was also not affected concerning rotation and zoom-in transformations to extract the largest area from the center of the image. Even though the performance of the model may be further improved by expanding the training set, the main origin of discrepancies is for the non-rounded shape particles. This can be explained by general difficulty to predict non-convex shapes that is rooted in StarDist radial model for contour representation. As can also be seen from the predicted map, most of the localized particles are round-shaped or have a convex contour. This would suggest further room for improvements in the correct shape predictions using for example algorithms that use a more flexible contour representation for learning like the SplineDist,⁶⁶ Contour Proposal Networks,⁶⁷ or PolarMask++.⁶⁸

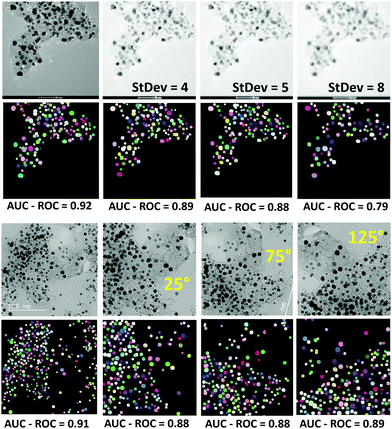Fig. 4 Sensitivity of the model in terms of AUC–ROC to Gaussian blur with varying standard deviation values (upper panel), and rotation transformations (lower panel).

Table 2 Performance of the segmentation model on the validation data for several train : validation split ratios at an IoU threshold of 0.5

Train : validation ratio	Precision	Recall	F1
34 : 6	0.86	0.81	0.83
30 : 10	0.86	0.85	0.85
26 : 14	0.85	0.86	0.86
22 : 18	0.85	0.84	0.84
16 : 24	0.84	0.83	0.84
10 : 30	0.87	0.8	0.83
5 : 35	0.81	0.77	0.79
2 : 38	0.67	0.42	0.52

---

As shown in Fig. 5(a), the ROI data makes it possible to count the particles in the image. Likewise, the area of individual particles can be calculated. These abilities can be in particular helpful in estimating the Pt/C ratio or the Pt mass loading from the image. Fig. 5(b) compares the segmentation maps obtained in this study with those from the recently developed ImageDataExtractor 2.0 software.⁶⁴ ImageDataExtractor also uses a deep learning approach for particle segmentation. On our dataset, the StarDist model significantly outperforms the software in both predicting the number of particles and localizing the overlapping particles. As shown in Fig. 5(b), for the test TEM images at 10, 20, 50, and 100 nm scales, the StarDist predicted 27, 144, 628, and 286 particles, respectively, while ImageDataExtractor 2.0 found 14, 67, 29, and 133 particles. Notably, StarDist's capability to separate the overlapping ROIs avoids the fusion of the near particles, increasing the total number of detections in comparison to the software.

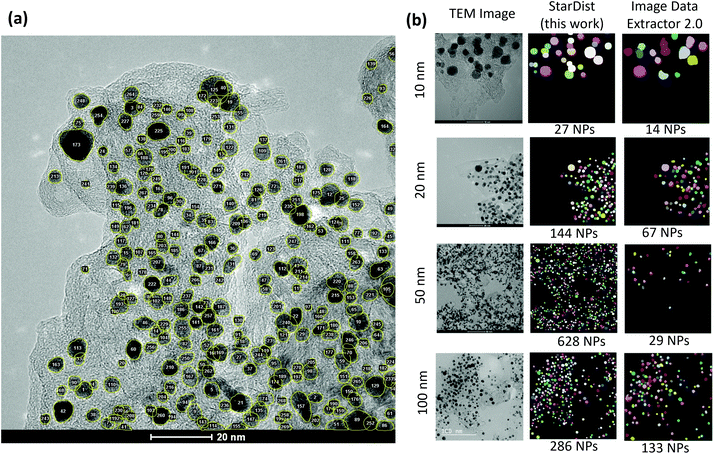Fig. 5 (a) Localization and counting the particles made available by the instance segmentation approach. (b) Comparison between the predicted segmentation maps of test images at different scales using the StarDist model employed in this work and the ImageDataExtractor 2.0.⁶⁴

Lastly, with the computed particle sizes the histograms for particle size distributions can be generated using typical visualization packages available in various programming languages. An example is shown in Fig. 6. Here, we used a bin size of 0.5 nm and the kernel density estimation (KDE) function for fitting the histogram. Binning can also be accomplished by using conventional statistical methods and expressions including Sturge's rule, Doane's rule, Scott's rule, Rice's rule or Freedman and Diaconis's rule.^69–71,72 Fitting for particle size distribution histogram can be performed using algorithms based on a variety of distribution functions such as polynomial distribution, Gaussian distribution, Weibull probability distribution, lognormal distribution, or Rayleigh distribution.^73,74,75

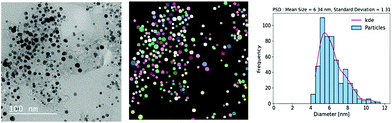Fig. 6 Particle size distribution was obtained using the deep learning-based approach of the instance segmentation of nanoparticles in the TEM images of Pt/C catalyst layers.

4. Conclusions

In conclusion, this paper presented a deep learning-based approach to automating particle size analysis in the TEM images of catalyst layers for polymer electrolyte fuel cells. The StarDist model trained on our annotated imaging dataset, could segment round-shaped overlapping nanoparticle instances. Minimizing the human intervention in the imaging-based characterization of catalyst layers in PEFCs enables the high-throughput screening required in the accelerated design and fabrication of novel materials. Unlike the manual approach, the deep learning-based approach introduces a well-defined metric for particle analysis: the model's precision for the segmentation of nanoparticles. Future research will focus on developing algorithms for the segmentation of nanoparticles with diverse, non-convex shapes enabling the morphological analyses. While we specifically discussed the particle size analyses, the deep learning algorithms are generic and can learn to automate the pore size or network analyses in the catalyst layers. Advanced characterization can also be achieved via auxiliary-task learning in an end-to-end training pipeline. The latter allows finding the structure–property relationships directly as the output of the model towards a full automation. A pivotal application of this approach is in autonomous materials fabrication using lab-scale stationary or mobile robotic systems^76–80 which demands a bidirectional and rapid data flow from catalyst fabrication to ink preparation, catalyst coated membrane fabrication, membrane electrode assembly, and a half or complete cell design, including testing and in situ/ex situ characterization steps.

Author contributions

André Colliard-Granero: Conceptualization, methodology, software, visualization, writing – original draft, writing – review & editing. Mariah Batool: Visualization, writing – original draft, writing – review & editing. Jasna Jankovic: Methodology, visualization, writing – original draft, writing – review & editing. Jenia Jitsev: Conceptualization, methodology, writing – review & editing. Michael H. Eikerling: Conceptualization, supervision, writing – original draft, writing – review & editing. Kourosh Malek: Conceptualization, supervision, writing – original draft, writing – review & editing. Mohammad J. Eslamibidgoli: Conceptualization, methodology, supervision, visualization, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the Federal Ministry of Science and Education (BMBF) under the German–Canadian Materials Acceleration Centre (GC-MAC) grant number 01DM21001A. The authors also gratefully acknowledge the Gauss Centre for Supercomputing e.V. (http://www.gauss-centre.eu) for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS⁸¹ at Jülich Supercomputing Centre (JSC).

References

1. J. Nowotny, J. Dodson, S. Fiechter, T. M. Gür, B. Kennedy, W. Macyk, T. Bak, W. Sigmund, M. Yamawaki and K. A. Rahman, Renewable Sustainable Energy Rev., 2018, 81, 2541–2551.
2. I. Staffell, D. Scamman, A. V. Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491.
3. D. K. Niakolas, M. Daletou, S. G. Neophytides and C. G. Vayenas, Ambio, 2016, 45, 32–37.
4. J. Zhang, H. Zhang, J. Wu and J. Zhang, PEM Fuel Cell Testing and Diagnosis, 2013, pp. 1–42.
5. F. T. Wagner, B. Lakshmanan and M. F. Mathias, J. Phys. Chem. Lett., 2010, 1, 2204–2219.
6. A. Ajanovic and R. Haas, Int. J. Hydrogen Energy, 2021, 46, 10049–10058.
7. K. Sopian and W. R. W. Daud, Renewable Energy, 2006, 31, 719–727.
8. J. Zhang, PEM fuel cell electrocatalysts and catalyst layers: fundamentals and applications, Springer Science & Business Media, 2008.
9. J. Chen, Z. Ou, H. Chen, S. Song, K. Wang and Y. Wang, Chin. J. Catal., 2021, 42, 1297–1326.
10. M. K. Debe, Nature, 2012, 486, 43–51.
11. M. J. Eslamibidgoli, J. Huang, T. Kadyk, A. Malek and M. Eikerling, Nano Energy, 2016, 29, 334–361.
12. M. Eikerling, A. A. Kornyshev and A. A. Kulikovsky, Physical modeling of fuel cells and their components, Wiley Online Library, 2007.
13. Y. He, Q. Tan, L. Lu, J. Sokolowski and G. Wu, Electrochem. Energy Rev., 2019, 2, 231–251.
14. P. Spinelli, C. Francia, E. Ambrosio and M. Lucariello, J. Power Sources, 2008, 178, 517–524.
15. M. Sabharwal, L. M. Pant, N. Patel and M. Secanell, J. Electrochem. Soc., 2019, 166, F3065.
16. S. Jomori, K. Komatsubara, N. Nonoyama, M. Kato and T. Yoshida, J. Electrochem. Soc., 2013, 160, F1067.
17. Q. Wang, M. Eikerling, D. Song, Z. Liu, T. Navessin, Z. Xie and S. Holdcroft, J. Electrochem. Soc., 2004, 151, A950.
18. K. Malek, T. Mashio and M. Eikerling, Electrocatalysis, 2011, 2, 141–157.
19. M. Eikerling and A. Kulikovsky, Polymer electrolyte fuel cells: physical principles of materials and operation, CRC Press, 2014.
20. E. Sadeghi, A. Putz and M. Eikerling, J. Electrochem. Soc., 2013, 160, F1159.
21. T. Muzaffar, T. Kadyk and M. Eikerling, Sustainable Energy Fuels, 2018, 2, 1189–1196.
22. J. P. Owejan, J. E. Owejan and W. Gu, J. Electrochem. Soc., 2013, 160, F824.
23. W. Li, Z. Wang, F. Zhao, M. Li, X. Gao, Y. Zhao, J. Wang, J. Zhou, Y. Hu and Q. Xiao, et al. , Chem. Mater., 2020, 32, 1272–1280.
24. A. P. Hitchcock, V. Lee, J. Wu, M. M. West, G. Cooper, V. Berejnov, T. Soboleva, D. Susac and J. Stumper, AIP Conf. Proc., 2016, 020012.
25. K. Karan, Curr. Opin. Electrochem., 2017, 5, 27–35.
26. R. Singh, A. Akhgar, P. Sui, K. Lange and N. Djilali, J. Electrochem. Soc., 2014, 161, F415.
27. J.-N. Rouzaud and C. Clinard, Fuel Process. Technol., 2002, 77, 229–235.
28. A. Abbas, G. Fathifazl, B. Fournier, O. B. Isgor, R. Zavadil, A. G. Razaqpur and S. Foo, Mater. Charact., 2009, 60, 716–728.
29. L. Wojnar, Image analysis: applications in materials engineering, Crc Press, 2019.
30. K. M. Halsall, V. M. Ellingsen, J. Asplund, R. H. Bradshaw and M. Ohlson, Holocene, 2018, 28, 1345–1353.
31. R. L. Borup, A. Kusoglu, K. C. Neyerlin, R. Mukundan, R. K. Ahluwalia, D. A. Cullen, K. L. More, A. Z. Weber and D. J. Myers, Curr. Opin. Electrochem., 2020, 21, 192–200.
32. P. Jovanovič, A. Pavlišič, V. S. Šelih, M. Šala, N. Hodnik, M. Bele, S. Hočevar and M. Gaberšček, ChemCatChem, 2014, 6, 449–453.
33. A. Pavlišič, P. Jovanovič, V. S. Šelih, M. Šala, N. Hodnik and M. Gaberšček, J. Electrochem. Soc., 2018, 165, F3161.
34. D. J. Myers, X. Wang, M. C. Smith and K. L. More, J. Electrochem. Soc., 2018, 165, F3178.
35. E. Guilminot, A. Corcella, F. Charlot, F. Maillard and M. Chatenet, J. Electrochem. Soc., 2006, 154, B96.
36. M. J. Eslamibidgoli, P.-É. A. Melchy and M. H. Eikerling, Phys. Chem. Chem. Phys., 2015, 17, 9802–9811.
37. S. Helmly, M. Eslamibidgoli, K. A. Friedrich and M. Eikerling, Electrocatalysis, 2017, 8, 501–508.
38. Z.-M. Zhou, Z.-G. Shao, X.-P. Qin, X.-G. Chen, Z.-D. Wei and B.-L. Yi, Int. J. Hydrogen Energy, 2010, 35, 1719–1726.
39. M. Maciá, J. Campina, E. Herrero and J. Feliu, J. Electroanal. Chem., 2004, 564, 141–150.
40. ASTM E112-13, Standard Test Methods for Determining Average Grain Size, https://www.astm.org/e0112-13.html.
41. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
42. G. Bradski, Dr. Dobb's Journal: Software Tools for the Professional Programmer, 2000, 25, 120–123.
43. U. Schmidt, M. Weigert, C. Broaddus and G. Myers, International Conference on Medical Image Computing and Computer-Assisted Intervention, 2018, pp. 265–273.
44. O. Ronneberger, P. Fischer and T. Brox, International Conference on Medical image computing and computer-assisted intervention, 2015, pp. 234–241.
45. U. Phromsuwan, C. Sirisathitkul, Y. Sirisathitkul, B. Uyyanonvara and P. Muneesawang, J. Magn., 2013, 18, 311–316.
46. P. Bele, F. Jager and U. Stimming, Microsc. Anal., 2007, 122, S5.
47. S. Mondini, A. M. Ferretti, A. Puglisi and A. Ponti, Nanoscale, 2012, 4, 5356–5372.
48. K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
49. Y. Guo, Y. Liu, A. Oerlemans, S. Lao, S. Wu and M. S. Lew, Neurocomputing, 2016, 187, 27–48.
50. L. von Chamier, R. F. Laine, J. Jukkala, C. Spahn, D. Krentzel, E. Nehme, M. Lerche, S. Hernández-Pérez, P. K. Mattila and E. Karinou, et al. , Nat. Commun., 2021, 12, 1–18.
51. M. J. Eslamibidgoli, F. Tipp, J. Jitsev, M. Jankovic, J. Eikerling and K. Malek, RSC Adv., 2021, 11, 32126–32134.
52. T. H. Johansen, S. A. Sørensen, K. Møllersen and F. Godtliebsen, arXiv preprint arXiv:2105.14191, 2021.
53. H. O. Velesaca, R. Mira, P. L. Suárez, C. X. Larrea and A. D. Sappa, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 2020, pp. 66–67.
54. J. Gené-Mola, R. Sanz-Cortiella, J. R. Rosell-Polo, J.-R. Morros, J. Ruiz-Hidalgo, V. Vilaplana and E. Gregorio, Comput. Electron. Agric., 2020, 169, 105165.
55. Y. Kim and H. Park, Sci. Rep., 2021, 11, 1–11.
56. Y. Zhou, H. Chen, H. Lin and P.-A. Heng, International Conference on Medical Image Computing and Computer-Assisted Intervention, 2020, pp. 521–531.
57. H. Jayakody, P. Petrie, H. J. de Boer and M. Whitty, Plant Methods, 2021, 17, 1–13.
58. D. Chen, D. Guo, S. Liu and F. Liu, Symmetry, 2020, 12, 639.
59. Y. Toda, F. Okura, J. Ito, S. Okada, T. Kinoshita, H. Tsuji and D. Saisho, Commun. Biol., 2020, 3, 1–12.
60. I. Poletaev, M. P. Tokarev and K. S. Pervunin, Int. J. Multiphase Flow, 2020, 126, 103194.
61. Z. Cheng and A. Qu, IEEE Access, 2020, 8, 158679–158689.
62. L. Yao, Z. Ou, B. Luo, C. Xu and Q. Chen, ACS Cent. Sci., 2020, 6, 1421–1430.
63. K. T. Mukaddem, E. J. Beard, B. Yildirim and J. M. Cole, J. Chem. Inf. Model., 2019, 60, 2492–2509.
64. B. Yildirim and J. M. Cole, J. Chem. Inf. Model., 2021, 61, 1136–1149.
65. P. Bankhead, M. B. Loughrey, J. A. Fernández, Y. Dombrowski, D. G. McArt, P. D. Dunne, S. McQuaid, R. T. Gray, L. J. Murray and H. G. Coleman, et al. , Sci. Rep., 2017, 7, 1–7.
66. S. Mandal and V. Uhlmann, 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), 2021, pp. 1082–1086.
67. E. Upschulte, S. Harmeling, K. Amunts and T. Dickscheid, arXiv preprint arXiv:2104.03393v1, 2021.
68. E. Xie, W. Wang, M. Ding, R. Zhang and P. Luo, IEEE Trans. Pattern Anal. Mach. Intell., 2021 DOI:10.1109/TPAMI.2021.3080324.
69. D. W. Scott, Wiley Interdiscip. Rev.: Comput. Stat., 2009, 1, 303–306.
70. D. W. Scott, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 497–502.
71. R. Sahann, T. Möller and J. Schmidt, arXiv preprint arXiv:2109.06612, 2021.
72. M. Wand, Am. Stat., 1997, 51, 59–64.
73. Z. Fang, B. R. Patterson and M. E. Turner, Mater. Charact., 1993, 31, 177–182.
74. S. Baker and R. D. Cousins, Nucl. Instrum. Methods Phys. Res., 1984, 221, 437–442.
75. A. Abd-Elfattah, J. Stat. Comput. Simul., 2011, 81, 357–366.
76. B. P. MacLeod, F. G. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. Yunker, M. B. Rooney and J. R. Deeth, et al. , Sci. Adv., 2020, 6, eaaz8867.
77. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li and R. Clowes, et al. , Nature, 2020, 583, 237–241.
78. R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, APL Mater., 2020, 8, 111110.
79. C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 22858–22893.
80. A. Malek, M. J. Eslamibidgoli, M. Mokhtari, Q. Wang, M. H. Eikerling and K. Malek, ChemPhysChem, 2019, 20, 2946–2955.
81. D. Krause, J. Large-scale Res. Facil., 2019, 5, 135.

---