Kinetic square scheme in oxygen-redox battery electrodes

Abstract

Integrating an anionic-redox (or oxygen-redox) capacity with a conventional cationic-redox capacity is a promising strategy for large-capacity battery cathodes exceeding present technical limits. However, most oxygen-redox cathodes exhibit a large charge/discharge voltage hysteresis (>0.5 V), resulting in poor energy efficiency and impractical implementation. Here, we show that nonpolarizing O⁻ ↔ O²⁻ (4.4 V vs. Li/Li⁺) and polarizing O₂²⁻ → O²⁻ (3.3 V vs. Li/Li⁺) coexist and kinetically compete in O2-type Li_1.12–yNi_0.17Mn_0.71O₂. The oxygen-redox reaction is described as a square scheme, involving bond-forming 2O⁻ → O₂²⁻ and bond-cleaving O₂⁴⁻ → 2O²⁻ processes, where preventing the formation of O₂²⁻ is essential to realize non-polarizing and energy-efficient oxygen-redox reactions.

---

Broader context

Development of high-performance energy storage systems is of vital importance for realizing a sustainable society. Although lithium-ion batteries (LIBs) are the state-of-the-art energy storage technology, a modest cathode capacity relying solely on transition-metal redox severely limits their energy density. An additional oxygen-redox capacity, which possesses a high promise to enhance the energy density, normally causes an unacceptably large voltage hysteresis during charge/discharge, rendering their use impractical. This work identifies the origin of the voltage hysteresis as a ‘square scheme’ involving both thermodynamic and kinetic issues, providing a standard landscape for extra oxygen redox in battery electrodes.

Introduction

The rapid market growth of electric vehicles (EVs) has significantly increased the industrial demands for their improved performance, such as longer driving distance, longer calendar life, and lower cost.^1–3 For example, the driving distance of an EV is determined by the energy density of in-vehicle lithium-ion batteries (LIBs). However, current LIBs possess an unsatisfactory gravimetric energy density of 200–250 W h kg⁻¹, powering typical EVs for 300–400 km per charge, which is below most consumers’ requirements.^4,5 Thus, increasing the energy density of LIBs is crucial for the widespread use of EVs.

The energy density of LIBs is limited in part by the specific capacity of the positive electrode (cathode) material. Conventional cathode materials, i.e., layered transition-metal oxides LiMO₂ (M = transition metal), deliver a modest capacity of approximately 160 mA h g⁻¹, where the dominant mechanism of charge compensation for lithium-ion (de)intercalation is the valence change of the transition metal.^6–8 Further increase in the cathode capacity requires an additional redox center. To activate redox reactions of oxide ions (oxygen redox), lithium-rich transition-metal oxides (Li_1+xM_1−xO₂) have been extensively studied for over a decade as they deliver much larger reversible capacities (> 200 mA h g⁻¹).^9–12

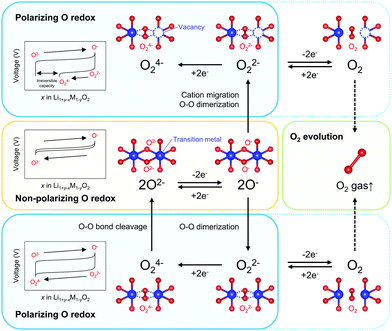
Redox-active oxygen is generated by specific Li–O–Li and Li–O–□ (□; vacancy) local configurations in Li_1+xM_1−xO₂, where non-bonding O 2p states just below the Fermi level undergo oxidation to increase the charge capacity.^13–15 When oxidized oxide ions O⁻ are stabilized through an M–O bond, a nonpolarizing discharge capacity of an O⁻/O²⁻ redox couple is obtained, as reported for Na₂Mn₃O₇ (Scheme 1).¹⁶ However, most Li_1+xM_1−xO₂ electrodes exhibit polarizing reduction of peroxo-like O₂²⁻ (e.g., Li₂Ru_0.5Sn_0.5O₃) or trapped O₂ molecules (e.g., Li_1.2Ni_0.13Co_0.13Mn_0.54O₂) to deliver the discharge capacity at a lower voltage.^{11,15,17–25} Considering immediate electron transfer (O²⁻ → O⁻ + e⁻) against subsequent structural deformation (O–O dimerization), the overall hypothetical mechanism of the oxygen-redox reactions is described as a square scheme (Scheme 1): if an oxidized oxide ion (O⁻) is stable, it directly contributes to a non-polarizing discharge capacity (non-polarizing O redox). Meanwhile, unstable O⁻ dimerize to form stable peroxo-like O₂²⁻, which may be accelerated by cation migration. The O₂²⁻ dimers provide a polarizing discharge capacity (polarizing O redox) and an unstable reduced dimer (e.g., O₂⁴⁻) decomposes to O²⁻. The O–O dimerization is prone to result in release of O₂ gas (O₂ evolution) by their excessive oxidation. This sequential square-type mechanism explains the fragmental experimental observations such as a large voltage hysteresis during charge/discharge, spectroscopic detection of O₂²⁻ or O₂ in bulk after the charging process, O₂ gas release upon charge, and different enthalpies on charge versus discharge.^18–30 However, experimental verification of the square scheme is limited in part due to complicated structural changes during the oxygen-redox reactions.^31–36 For example, O3-Li_1.2Ni_0.2Mn_0.6O₂ (O3: lithium ions occupy octahedral sites between the MO₂ layers, and the packing arrangement of the oxide ions is ABCABC) exhibits irreversible structural degradation such as layered-to-spinel transformation and surface cation densification upon cycling.^31,32 For reliable analysis, electrode materials that possess structural integrity against the oxygen-redox reactions should be considered.

Scheme 1 Reaction paths of an oxygen-redox reaction. ‘Non-polarizing’ and ‘polarizing’ correspond to reversible and irreversible processes, respectively.

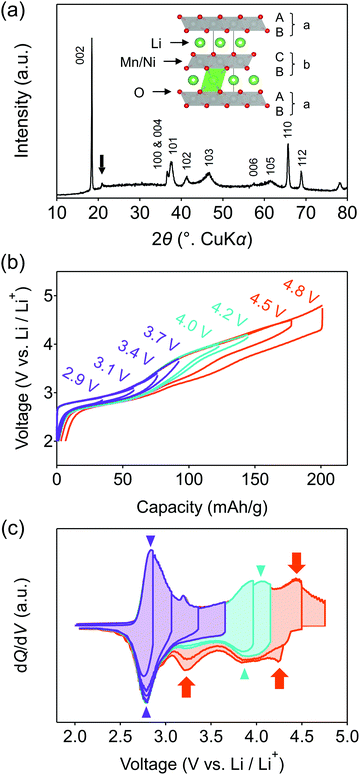
This work focuses on O2-type lithium-rich layered transition-metal oxides as cathode materials with structural integrity (Fig. 1a inset, O2: lithium ions occupy octahedral sites between the MO₂ layers and the packing arrangement of the oxide ions is ABCBA), which is an emerging class of oxygen-redox electrode materials.^37–41 In the O2-type oxides, the structural degradation upon cycling is suppressed because migration of M to the Li⁺ layers is unfavorable: M in a Li⁺ layer suffers from strong Coulombic repulsion from face-sharing Mⁿ⁺ in an adjacent MO₂ layer.³⁹ Moreover, O2-type Li-rich layered oxides exhibit negligible O₂ gas release.⁴⁰ As a consequence, O2-Li_1.12−yNi_0.17Mn_0.71O₂ provides a large reversible capacity greater than 200 mA h g⁻¹ with minimal voltage decay and capacity fading upon cycling.³⁸

Fig. 1 Structural characterization and electrochemical properties of O2-Li_1.12−yNi_0.17Mn_0.71O₂. (a) Powder X-ray diffraction pattern and crystal structure of O2-Li_1.12−yNi_0.17Mn_0.71O₂. The black arrow highlights a superstructure peak arising from in-plane cation ordering. The inset depicts the structure of O2-Li_1.12−yNi_0.17Mn_0.71O₂ with an ‘abcba’-type oxide-ion packing arrangement. (b) Galvanostatic charge/discharge curves and their (c) dQ/dV plots at C/20 with increasing the upper cut-off voltage from 2.0 to 4.8 V vs. Li/Li⁺. The triangles indicate reversible redox couples, while the arrows indicate the coexistence of non-polarizable and polarizable redox couples.

Taking advantage of the structural integrity of O2-Li_1.12−yNi_0.17Mn_0.71O₂, multi-angle analyses were performed to identify the chemical states of oxygen (O²⁻, O⁻, O₂²⁻, O₂⁴⁻) and their inter-state transformation, using X-ray absorption/emission spectroscopy, magnetic susceptibility measurements, and density functional theory calculations. Based on the electrochemical kinetic analysis, particularly for the 2O²⁻ → O₂²⁻ transformation, technical strategies to realize non-polarizing and energy-efficient oxygen redox will be discussed.

Results and discussion

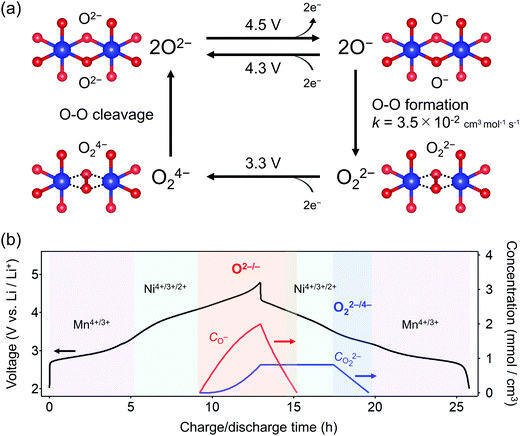
O2-Li_1.12−yNi_0.17Mn_0.71O₂ was synthesized by the Na⁺/Li⁺ ion-exchange method using P2-Na_0.71[Li_0.12Ni_0.17Mn_0.71]O₂ (Fig. S1, ESI†) as a precursor.³⁸ The powder X-ray diffraction pattern of O2-Li_1.12−yNi_0.17Mn_0.71O₂ (Fig. 1a) shows Bragg peaks indexed to a hexagonal system (space group: P6₂mc, typical of the O2 phase^37,42,43), indicating the successful transformation of the P2-type sodium layered oxide to the O2-type lithium layered oxide (i.e., ‘aba’ stacking of the transition-metal layers in an ‘ABCBA’ oxide-ion packing arrangement, Fig. 1a inset). Indeed, a high-angle annular dark-field scanning transmission electron microscopy image confirms the ‘aba’ stacking of the transition–metal layers (Fig. S2, ESI†). The elemental analyses (inductively coupled plasma atomic emission and absorption spectroscopy) for the pristine compound determined the chemical composition of Li_0.78Mn_0.72Ni_0.13O₂. Galvanostatic charge/discharge measurements show that O2-Li_1.12−yNi_0.17Mn_0.71O₂ delivers a large discharge capacity of approximately 210 mA h g⁻¹, exceeding the M-redox capacity (193 mA h g⁻¹) (Fig. S3a, ESI†). After 80 cycles, 98% of the discharge capacity in the second cycle is retained, while the decay of the average discharge voltage is negligibly small (<5 mV) (Fig. S3b and c, ESI†). Typically, conventional O3-type oxygen-redox layered oxides exhibit structural degradation initiated by the migration of M to Li⁺ layers.^33,34 In contrast, in O2-type layered oxides, Mⁿ⁺ ions migrated to Li⁺ layers would be subjected to strong Coulombic repulsion from face-sharing Mⁿ⁺ ions in the adjacent MO₂ layers, such that the migration of M would be energetically unfavorable to mitigate both capacity fading and voltage decay during the charge/discharge cycles.³⁹ These observations are consistent with those reported previously, i.e., O2-Li_1.12−yNi_0.17Mn_0.71O₂ exhibits a stable oxygen-redox reaction.³⁸

This stable oxygen-redox reaction was further investigated by measuring the charge/discharge curves under incremental upper cut-off voltages from 2.9 to 4.8 V vs. Li/Li⁺ (Fig. 1b). Under the cut-off voltages below 4.2 V vs. Li/Li⁺, dQ/dV plots (Fig. 1c) show two reversible redox reactions occurring at approximately 2.8 and 3.9 V vs. Li/Li⁺ with small polarizations of 0.05 and 0.13 V (purple and cyan triangles in Fig. 1c), respectively. These two nonpolarizing dQ/dV peaks should be attributed to the conventional redox reactions of Mn and Ni. With an increase in the cut-off voltage above 4.2 V vs. Li/Li⁺, a new anodic dQ/dV peak emerges at 4.5 V vs. Li/Li⁺. Correspondingly, two additional cathodic dQ/dV peaks emerge at 4.3 and 3.3 V vs. Li/Li⁺ (orange arrows in Fig. 1c), with the emergence of this anodic peak, which can be attributed to the oxygen-redox reactions. For most O3-type oxides, the oxygen-redox reaction proceeds simultaneously with the cationic-redox reactions such as Mn⁴⁺/Mn³⁺ and Ru⁵⁺/Ru⁴⁺.^27,44 In contrast, the cathodic reaction at 3.3 V vs. Li/Li⁺ in O2-Li_1.12−yNi_0.17Mn_0.71O₂ can be ascribed solely to the polarizing oxygen reduction coupled with oxygen oxidation at 4.5 V vs. Li/Li⁺, allowing its systematic investigation.

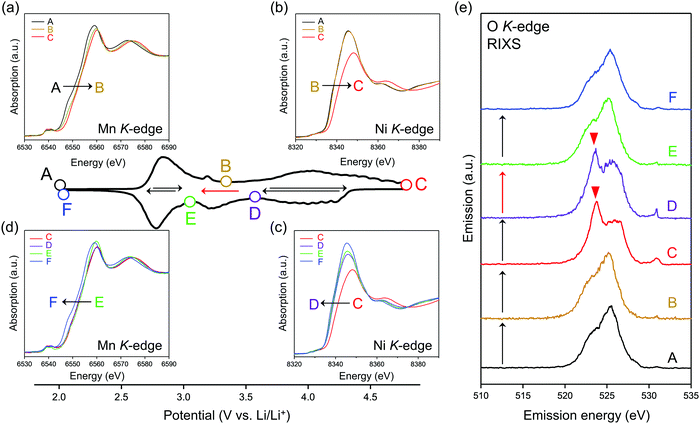
To identify the redox center for each dQ/dV peak, ex situ X-ray absorption/emission spectroscopy measurements were conducted. Fig. 2a–d shows Mn and Ni K-edge X-ray absorption near-edge structure (XANES) spectra during the second cycle. The redox reaction at 2.8 V vs. Li/Li⁺ causes a reversible shift of the Mn K-edge XANES spectra (Fig. 2a and d), indicating that the oxidation and reduction of Mn occur at the dQ/dV peaks of A → B and E → F, respectively. As the Ni K-edge XANES spectra show a reversible shift at 3.9 V vs. Li/Li⁺ (Fig. 2b and c), the dQ/dV peaks of B → C and C → D can be attributed to the oxidation and reduction of Ni, respectively. These attributions (Mn and Ni redox reactions at 2.8 and 3.9 V vs. Li/Li⁺, respectively) are double-confirmed by Mn and Ni L_2,3-edge absorption spectra. (Fig. S4 and S5, ESI†).

Fig. 2 Redox couples in O2-Li_1.12−yNi_0.17Mn_0.71O₂. dQ/dV plot during the second cycle at a charge/discharge rate of C/20. (a–d) Ex situ Mn and Ni K-edge X-ray absorption spectra upon charge and discharge. (e) Ex situ O K-edge resonant inelastic X-ray scattering (RIXS) spectra excited by an incident photon energy of 531 eV.

After charging to 4.8 V vs. Li/Li⁺, O K-edge X-ray absorption spectroscopy shows the emergence of new absorption at approximately 531 eV (Fig. S6, ESI†), while resonant inelastic X-ray scattering (RIXS) spectrum with the incident photon energy of 531 eV shows intense emission at 524 eV (spectrum C in Fig. 2e), both of which are characteristic features of charged oxygen-redox electrode materials.^{14,15,19–21,33,39,45–47} Thus, the anodic dQ/dV peak at 4.5 V vs. Li/Li⁺ corresponds to the oxidation of oxide ions. These signals for oxidized oxygen do not completely disappear even after discharging to 3.6 V vs. Li/Li⁺. Instead, the disappearance is confirmed after discharging to 3.1 V vs. Li/Li⁺. Considering the similar emission peaks observed for Li₂O₂, CaO₂, and O₂ molecule,^19,28,48 dimerized oxygen species O₂ⁿ⁻ (n = 0 or 2) exists in charged O2-Li_1.12−yNi_0.17Mn_0.71O₂ at 4.5 V. It is noteworthy that an enhancement in the elastic peak region was observed after charge (spectrum C and D in Fig. 2e). A possible explanation is the Raman scattering arising from the vibrational transition of O–O bond^19–21 although its origin is still under debates.^49,50

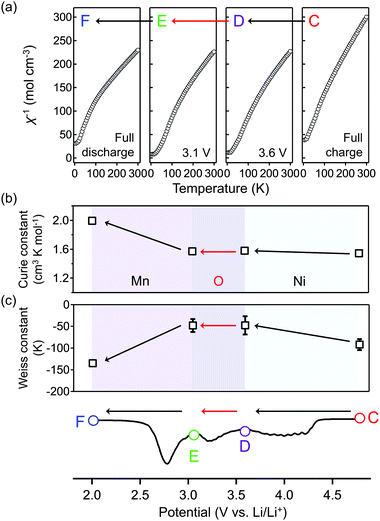
To obtain firm evidence of the above-mentioned sequential chemical states of oxygen during the oxygen-redox reaction, the magnetic properties of O2-Li_1.12−yNi_0.17Mn_0.71O₂ were measured along the C → D → E → F discharging process (Fig. 3). Analyses of the temperature dependence of magnetic susceptibility (χ) at high temperature (T > 200 K) (Fig. 3a and Fig. S7, ESI†) provide two important physical quantities, the Curie constant (C) and Weiss temperature (Θ), for each state of discharge (C: 4.8 V, D: 3.6 V, E: 3.1 V, and F: 2.0 V vs. Li/Li⁺, Fig. 3b and 3c) according to the Curie–Weiss law (χ = C(T − Θ)⁻¹). Upon discharging from 4.8 to 3.6 V (C → D in the dQ/dV plot) and from 3.1 to 2.0 V vs. Li/Li⁺ (E → F), the value of C increases (observed ΔC = 0.04 and 0.42 cm³ K mol⁻¹) mainly due to the reduction of Ni⁴⁺ to Ni²⁺ (S = 0 → 1, calculated ΔC = 0.13 cm³ K mol⁻¹) and Mn⁴⁺ to Mn³⁺ (S =3/2 → 2, calculated ΔC = 0.37 cm³ K mol⁻¹), respectively. A small difference between the observed and calculated ΔC at the C–D region is owing to the nonpolarizing reduction of O⁻ to O²⁻ (S = 1/2 → 0, ΔC < 0). The spin-state changes of the transition metals from 4.8 to 3.6 V (C → D) and from 3.1 to 2.0 V (E → F) vs. Li/Li⁺ induce a large change in Θ (Fig. 3c) through the drastic modulation of super-exchange interactions. Contrarily, both C and Θ remain almost unchanged from 3.6 to 3.1 V (D → E) vs. Li/Li⁺, indicating the redox reaction of diamagnetic species, i.e., the reduction of O₂²⁻ to O²⁻ (S = 0 → 0, ΔC = 0), verifying the square scheme of the oxygen-redox reaction, including the polarizing reduction of O₂²⁻ (Scheme 1). No signature is identified to support the existence of paramagnetic O₂ molecules in the bulk. Therefore, the cathodic dQ/dV peaks at 4.3 and 3.3 V (Fig. 1c) are ascribed to the existence of two types of reduction processes: (i) the nonpolarizing reduction of O⁻ (4.3 V) and (ii) the polarizing reduction of O₂²⁻ (3.3 V), respectively.

Fig. 3 Spin-state variation during discharge. (a) Inverse of magnetic susceptibility (χ) as a function of temperature, (b) the Curie constant (C), and (c) the Weiss temperature (Θ) of O2-Li_1.12−yNi_0.17Mn_0.71O₂ during the second discharge. The dQ/dV plot is provided as a voltage region reference. The Curie constant and Weiss temperature at each state-of-discharge are the average values for the three samples. The error bars represent standard errors.

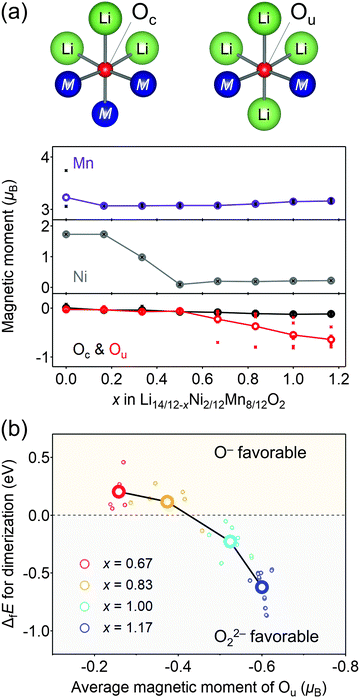
Considering that O₂²⁻ formation is the origin of the voltage hysteresis, it is crucial to minimize the polarizing discharge capacity of O₂²⁻ by decelerating the dimerization process of 2O⁻ → O₂²⁻ to maximize the energy efficiency of a battery cell. To quantify and visualize the energetic competition for the formation of O⁻versus O₂²⁻, density functional theory (DFT) calculations were conducted, where the model structures of O2-Li_14/12−xNi_2/12Mn_8/12O₂ were obtained using the genetic algorithm (GA; Fig. S8–S11, ESI†). Fig. 4a shows the plots of the magnetic moments of Mn, Ni, and O in hypothetical model structures without O–O dimerization. The oxygen atom coordinated by two transition metals is labelled as O_u, which possesses non-bonding O 2p state, while those coordinated by three transition metals are labelled as O_c. The magnetic moment of O_u changes from 0μ_B to −0.64μ_B at x = 0.50 → 1.17 (O²⁻ → O⁻ (S = 0 → 1/2)), whereas that of O_c remains constant during the entire process (x = 0 → 1.17), which is consistent with the other oxygen-redox cathode materials.^13,15,51 In contrast, the magnetic moments of Mn and Ni increase at x = 0 → 0.50 (Ni²⁺ → Ni⁴⁺ (S = 1 → 0) and Mn³⁺ → Mn⁴⁺ (S = 2 → 3/2)). These calculation results are consistent with the attributions of redox centers for the dQ/dV plots, and emphasis should be placed on the conclusion that the non-polarizing redox reaction of O²⁻/O⁻ occurs only above the potential of the M redox reactions.

Fig. 4 Computational investigation of O–O dimerization. (a) Variation of a magnetic moment as a function of the composition x in Li_14/12−xNi_2/12Mn_8/12O₂. Integration radius of the ion core is 1.2 Å for all the atoms. The large, colored circles are the averaged magnetic moments. Oxygen coordinated by three transition metals is denoted as O_c, while oxygen coordinated by two transition metals is denoted as O_u. (b) Formation energy of O_u–O_u dimers (Δ_fE) as a function of the averaged magnetic moment, representing an extent of oxidation, of the dimerizing O_u atoms. The bold circles correspond to the average of the formation energy and magnetic moment of each delithiated state (x = 0.67, 0.83, 1.00, and 1.17). All the hypothetical O_c–O_u dimers exhibit immediate bond cleavage and can be excluded from possible local structures.

The formation of O₂²⁻ (2O⁻ → O₂²⁻) was then simulated by decreasing the distances of several oxygen pairs in the model structure. For the model structures with x < 0.67, the O–O bonds immediately cleave during structural optimization owing to their thermodynamic instability. In contrast, the O–O dimers survive in the optimized structures of x ≥ 0.67 with the bond lengths of 1.4–1.5 Å, close to the typical experimental values of O₂²⁻ (1.56 Å) observed in Li₂O₂.⁵² In addition, these bond lengths are in good agreement with those obtained by the DFT calculations for Li₂MnO₃.⁵³ Importantly, O₂²⁻ formation energy (Δ_fE) is negative (O₂²⁻ favorable) for the oxygen pairs with average magnetic moments below −0.5μ_B at highly oxidized states (Fig. 4b). Bader charge analysis (Fig. S12, ESI†) also indicates that over-oxidized oxide ions (<−0.5μ_B) are thermodynamically prone to undergo the dimerization of 2O⁻ → O₂²⁻.

Overall, the O–O dimerization in O2-Li_1.12−yNi_0.17Mn_0.71O₂ can be summarized by the square scheme in Fig. 5a. Upon charge, O_u²⁻ with non-bonding 2p states is oxidized to O⁻ above 4.2 V vs. Li/Li⁺. At the early stage of oxygen oxidation, O⁻ is thermodynamically more favorable than O₂²⁻. However, with further oxygen oxidation, the over-oxidized oxide ions dimerize to form O₂²⁻. If a constant voltage is applied for a time duration, Δt, after galvanostatic charge (float mode) and the dimerization proceeds with a rate constant, k, the corresponding discharge capacity (Q, in region D–E in Fig. 2) of O₂²⁻ is expected to increase according to the additional dimerization during constant-voltage application as Q = jt₁ − FC_r(t₁)ρ⁻¹{1 + kΔtC_r(t₁)}⁻¹, where j is the specific current density, t = t₁ is the time to start applying the constant voltage, F is the Faraday constant, ρ is the density of the electrode material, and C_r(t₁) is the concentration of O⁻ after charge (t = t₁). The kinetic analysis of this float-time dependence successfully provides the dimerization rate constant as k = 3.5 × 10⁻² cm³ mol⁻¹ s⁻¹ (‘Rate constant for dimerization of O⁻ under a CCCV (float) mode’, Fig. S13–S18, ESI†). Indeed, DFT calculations using a climbing image nudged elastic band (CI-NEB) method provide an energy barrier of 0.2–0.4 eV for O–O dimerization in the delithiated structures, implying the possible occurrence of the dimerization process (Fig. S19, ESI†). Fig. 5b depicts the calculated concentrations of O⁻ and O₂²⁻ in O2-Li_1.12−yNi_0.17Mn_0.71O₂ during the charge/discharge at C/20 using the square scheme shown in Fig. 5a. The chemical state at the end of charge is estimated as O2-Li_1.12−yNi_0.17Mn_0.71O_1.75(O⁻)_0.13(O₂²⁻)_0.06. Upon discharge, the sequential reduction of O⁻, Ni, O₂²⁻, and Mn occurs, where the reduction of O₂²⁻ induces immediate O–O bond cleavage to regenerate O²⁻.

Fig. 5 Square scheme of oxygen-redox reaction in O2-Li_1.12−yNi_0.17Mn_0.71O₂. (a) Square scheme for polarizing oxygen-redox reaction. The oxidation of O²⁻ to unstable O⁻ above 4.3 V vs. Li/Li⁺ leads to stable peroxide O₂²⁻ formation with a rate constant of k = 3.5 × 10⁻² cm³ mol⁻¹ s⁻¹, while the reduction of O₂²⁻ to unstable O₂⁴⁻ at 3.3 V vs. Li/Li⁺ induces immediate bond cleavage to O²⁻. (b) Time dependence of O⁻ and O₂²⁻ concentration upon charge/discharge at C/20 calculated using the kinetic model based on the square scheme.

It is widely accepted that O–O dimerization is accelerated by transition-metal migration to alkali-ion layers.^20,29 This is clearly not the case for O2-Li_1.12−yNi_0.17Mn_0.71O₂ because the MO₆ octahedra share a face with the LiO₆ octahedra in adjacent Li layers, which prohibits M migration. However, as demonstrated through the DFT calculations (Fig. 4b), the suppression of M migration alone cannot completely mitigate O–O dimerization. As shown in Fig. 5b, 12.5% of the oxide ions (0.25 oxide ions per 2 oxide ions) are oxidized at the end of charge, corresponding to an oxygen-redox capacity of 42 mA h g⁻¹, and then the O–O dimerization of the 48% oxidized oxide ions (0.12 oxide ions per 0.25 oxidized oxide ions) occurs even without M migration. Recently, Na₂Mn₃O₇ was reported to exhibit nonpolarizing oxygen-redox reaction (O⁻/O²⁻), where 14% of the oxide ions (1 oxide ion per 7 oxide ions) are oxidized but stably exist as O⁻ without dimerization.¹⁶ One possible explanation is the effect of large Na⁺ to significantly mitigate the M migration to the alkaline-metal layers and hence the formation of peroxo-like O₂²⁻, where large prismatic sites of Na⁺ layers are unfavorable for much smaller Mⁿ⁺ (radii ratio Na⁺/Mⁿ⁺ ∼ 1.6 vs. Li⁺/Mⁿ⁺ ∼ 1.2).^54,55 Alternatively, or in parallel, covalent Ni⁴⁺–O₂²⁻ interaction (strong ligand-to-metal charge transfer) promotes the O–O dimerization as compared to ionic Mn⁴⁺–O₂²⁻ interaction. Indeed, average O₂²⁻ formation energy (Δ_fE) for the O pairs coordinated to Ni is lower than that for the O pairs coordinated to Mn (Fig. S20, ESI†). Therefore, in addition to mitigating the M migration, selecting less electronegative transition metals (e.g., Ti, Mn), which can suppress O–O dimerization is crucial to maximize the non-polarizing oxygen-redox capacity.

Conclusions

Kinetic formation of the peroxo-like O₂²⁻ dimer was identified as the origin of a voltage hysteresis in O2-type Li_1.12–yNi_0.17Mn_0.71O₂. Even in O2-type layered oxides that prohibit M migration, O₂²⁻ is thermodynamically favorable under certain high-voltage conditions where the oxide ions are over-oxidized. Multiple experimental and theoretical investigations have revealed that (i) O²⁻ → O⁻ is dominant at an early stage of oxygen oxidation, while (ii) 2O⁻ → O₂²⁻ becomes energetically favorable at over oxidation. However, (iii) 2O⁻ → O₂²⁻ requires O–O bond formation, causing (iv) coexistence of O⁻ and O₂²⁻ at charged states, followed by simultaneous emergence of non-polarizing direct O⁻ → O²⁻ reduction at 4.3 V and polarizing O₂²⁻ → O₂⁴⁻ reduction at 3.2 V upon discharge, where (v) the O₂²⁻ → O₂⁴⁻ reduction capacity at 3.2 V is pronounced by prolonged float charging at 4.8 V. However, as O–O dimerization is a kinetic process that occurs after oxidation of O²⁻ to O⁻, a part of O⁻ survives to contribute to the nonpolarizing discharge capacity through reversible O²⁻/O⁻ redox reaction. These insights emphasize the importance of suppressing the formation of O₂²⁻ and maximizing the contribution of the nonpolarizing O²⁻/O⁻ redox couple to develop energy-efficient oxygen-redox battery electrodes. The square scheme confirmed in this work, involving both thermodynamic and kinetic issues, encompasses all the reaction models proposed thus far in the literature and provides a standard landscape for extra oxygen redox in battery electrodes.

Methods

Materials

O2-type Li_1.12−yNi_0.17Mn_0.71O₂ was synthesized by the Na⁺/Li⁺ ion-exchange method.³² Stoichiometric amounts of NiSO₄·6H₂O (Wako Pure Chemical Industries, Ltd, min. 98.0%) and MnSO₄·5H₂O (Wako Pure Chemical Industries, Ltd, min. 99.9%) were dissolved in distilled water with a total metal concentration of 0.5 mol dm⁻³. In parallel, a 0.5 mol dm⁻³ Na₂CO₃ (Wako Pure Chemical Industries, Ltd, min. 99.8%) aqueous solution was prepared. The two solutions were slowly dropped into a beaker of distilled water at 70 °C and stirred continuously. After 1 h, the precipitate was filtered and washed with distilled water and ethanol to remove sodium. The product was dried overnight in vacuum at 120 °C. The resulting metal carbonate was mixed with stoichiometric amounts of Na₂CO₃ and Li₂CO₃ (Wako Pure Chemical Industries, Ltd., min. 99.0%) to obtain an intermediate P2-Na_0.71[Li_0.12Ni_0.17Mn_0.71]O₂ phase. The mixture was pressed into a pellet and heated at 800 °C for 8 h under dry air. Ion-exchange from Na⁺ to Li⁺ was conducted using the molten-salt method.³⁸ The P2-Na_0.71[Li_0.12Ni_0.17Mn_0.71]O₂ powder was mixed with LiNO₃ (Wako Pure Chemical Industries, Ltd) and LiCl (Wako Pure Chemical Industries, Ltd, min. 99.0%) in a molar ratio of 82 : 18 to obtain a Na : Li ratio of 1 : 10 in an Ar-filled glovebox. This mixture was heated at 280 °C for 4 h in air. The final product was filtered and washed with distilled water and ethanol. The powder was dried overnight in vacuum at 120 °C.

Materials characterization

Powder X-ray diffraction patterns were measured using Rigaku RINT-TTR III (Cu Kα radiation) in 0.02° steps over a 2θ range of 10°–80°. The P2 and O2 phases were analyzed under an Ar atmosphere using an airtight sample holder. The crystal structures were drawn by VESTA.⁵⁶ A high-angle annular dark-field scanning transmission electron microscope image was recorded using Themis Z (Thermo Fisher Scientific) with an acceleration voltage of 300 kV. A thin specimen was prepared using a focused ion beam of Ga using JIB-4501 (JEOL) at −180 °C. The elemental analyses were carried out using the inductively coupled plasma atomic emission spectroscopy (ICP-AES) (Seiko SPS4000) and ICP atomic absorption spectroscopy (ICP-AAS) (Hitachi Z-2300).

Electrochemical measurements

Electrochemical measurements were performed using 2032-type coin cells assembled in an Ar-filled glovebox. To prepare the working electrodes, a slurry composed of active material (80 wt%), acetylene black (10 wt%) (Li-400, DENKA) and poly(vinylidene fluoride) (10 wt%) (KUREHA) mixed in N-methyl pyrrolidone (Kanto Chemical Co., Inc., min. 99.0%) was coated onto an Al foil and then dried overnight at 65 °C in air. The counter electrodes were Li foil (Honjo Metal Co., Ltd). The electrolyte was 1 mol dm⁻³ LiPF₆ in a 1 : 1 (v/v) mixture of ethylene carbonate and dimethyl carbonate (battery grade, Kishida Chemical Co., Ltd). The separators used were glass fibers (GB-100R, Advantec) dried overnight at 180 °C in vacuum. Galvanostatic charge/discharge measurements were performed using a potentio-galvanostat, TOSCAT (TOYO Corporation). For ex situ analyses, the cells were disassembled in the Ar-filled glovebox. The electrodes were rinsed with dimethyl carbonate (Kishida Chemical) three times and dried in vacuum at 25 °C.

Hard X-ray spectroscopy

Ex situ Mn and Ni K-edge X-ray absorption near edge structure (XANES) spectra were collected at room temperature in a transmission mode at BL-9C in Photon Factory, High Energy Accelerator Research Organization (KEK), Tsukuba, Japan. For Mn K-edge XAFS measurements, initial and final energy were 6502.6 and 6607.6 eV with an energy step of 0.3 eV. Photon energy was calibrated by setting a peak top of first derivative of K-edge XANES spectrum for Mn foil at 6539 eV. For Ni K-edge XAFS measurements, initial and final energy were 8296.7 and 8401.7 eV with an energy step of 0.3 eV. Photon energy was calibrated by setting a peak top of first derivative of K-edge XANES spectrum for Ni foil at 8333 eV. The electrodes after charging/discharging were wrapped with a Kapton tape to prevent exposure to air. Thereafter, data analysis was performed using Athena software.⁵⁷

Soft X-ray spectroscopy

Ex situ soft X-ray absorption spectra (XAS) and resonant inelastic X-ray scattering (RIXS) spectra were measured at room temperature in vacuum at BL07LSU and BL27SU in Spring-8, Hyogo, Japan.⁵⁸ All the samples were transferred from an Ar-filled glovebox into a vacuum chamber using a transfer vessel without air exposure. A partial fluorescence yield (PFY) mode was adopted for the O K-edge and Ni L_2,3-edge XAS and inverse PFY mode for the Mn L_2,3-edge XAS using inversed intensity of O Kα emission to prevent the distortion of spectra due to self-absorption and saturation effect.^59,60 The RIXS spectra were collected for the O K-edge. A silicon-drift detector was used for Mn and Ni L_2,3-egdge XAS and O K-edge XAS measurements. The total energy resolution of the RIXS measurement at BL07LSU was ΔE ∼ 160 meV at 530 eV. Mass loading of electrodes was 1.06 mg cm⁻² and thickness of electrode was approximately 15 μm for soft XAS/RIXS measurements.

Magnetic measurements

Magnetic susceptibility measurements were performed using an MPMS-5S SQUID magnetometer (Quantum Design) in the temperature range of 5–300 K under an applied field of 0.1 T. All the samples were packed into capsules to prevent exposure to air. The obtained data were corrected considering the core diamagnetism based on Pascal's constants.

Ab initio calculations

Ab initio calculations were performed using the Vienna ab initio simulation package with the projected augmented-wave method.^61–65 To model O2-type Li_1.12–yNi_0.17Mn_0.71O₂, Li₁₄Ni₂Mn₈O₂₄ (Z = 12) was prepared as a unit cell. The arrangements of Li/Ni/Mn in the transition-metal layers were determined using the genetic algorithm (GA) approach. The GA calculation details are introduced in the next section. The total energies were calculated based on density functional theory (DFT) using the generalized gradient approximation of Perdew–Burke–Ernzerhof exchange–correlation functional with Hubbard U = 5.04 and 5.10 eV for Ni and Mn, respectively, to correct the self-interaction error of correlated d electrons.⁶⁶ The energy cut-off and the number of k-points in the reciprocal cell were 300 eV and unity (Γ-point sampling), respectively. All the calculations were performed considering the initial ferromagnetic ordering of the Ni and Mn atoms. The lattice parameters and atomic positions were relaxed until the forces on each atom were less than 0.01 eV Å⁻¹. After the GA procedure, the five lowest-energy structures were recalculated with an energy cut-off of 520 eV and a k-point mesh of 4 × 3 × 3. Similarly, the Li/vacancy arrangements in the delithiated phases of Li_14–zNi₂Mn₈O₂₄ (4 ≤ z ≤ 10 at intervals of 2) were also determined using the GA approach, and the total energies of the five lowest-energy structures were recalculated for each Li composition. In the case of z = 2 and 12, the total energies for all the Li/vacancy arrangements were calculated for possible structures. For electronic structure analysis, the hybrid functional introduced by Heyd–Scuseria–Ernzerhof (HSE) was used with the exact exchange fraction in the Hartree–Fock/DFT hybrid functional and range-separation parameter of 0.25 and 0.2, respectively (HSE06).⁶⁷ The Bader charge was calculated using the script provided by Henkelman's group.^68–71 Dimerization energy (Δ_fE) is defined as follows:

Δ_fE = E(Li_14–zNi₂Mn₈O₂₂(O₂ⁿ⁻)) − E(Li_14–zNi₂Mn₈O₂₄)

where E(Li_14–zNi₂Mn₈O₂₂(O₂ⁿ⁻)) and E(Li_14–zNi₂Mn₈O₂₄) are the total energies of the unit cells with and without peroxo-like O₂ⁿ⁻, respectively. CI-NEB calculation⁷² was performed using a supercell of 2 × 1 × 1 (96 atoms).

Details of genetic algorithm

The arrangements of Li/vacancy/Ni/Mn in O2-type Li_14–zNi₂Mn₈O₂₄ were optimized by the genetic algorithm (GA). A molar ratio of Li/Ni/Mn in a fully lithiated phase was set to reproduce the experimental composition (Li_1.12Ni_0.17Mn_0.71O₂). Layered O2-type LiCoO₂ in a hexagonal structure (a space group of P6₃mc, 8 atoms) was used to prepare a supercell (48 atoms). Six cationic octahedral sites in each transition-metal layer contain one Li, one Ni, and four Mn atoms, while twelve octahedral sites in the Li layers were occupied by only Li atoms. In the GA procedure, a Li/Ni/Mn arrangement is regarded as a tertiary string consisting of four labels, 0 (Li), 1 (Ni), and 2, (Mn) and each cationic site was assigned to a specific string index. We prepared 20 configurations with random Li/Ni/Mn arrangements in the cationic sites and calculated the total electron energies based on DFT with a low energy cut-off (300 eV) and single k-point mesh to accelerate the calculations. Twelve lowest-energy structures among twenty candidates (60%) were selected as survivors and their structural features were inherited to the next generation by following the four points. First, the three best structures survived without any changes. Second, eight new structures were produced using the two-point crossover technique. Third, eight structures were produced by the half-uniform crossover technique. Fourth, four structures were produced by the mutation technique. The algorithm for the travelling salesman problem was adopted to maintain the molar ratio of Li/Ni/Mn during the above four genetic manipulations. The generated structures were selected to be inconsistent with the previously calculated configuration (a random cation arrangement is chosen if the above genetic operation cannot produce a new structure). Repeating this procedure determines the lowest-energy structure heuristically. The Li/vacancy arrangements in the delithiated phases of Li_14-zNi₂Mn₈O₂₄ (4 ≤ z ≤ 10 at intervals of 2) were also determined with the secondary strings in the GA approach but the number of structures per generation was reduced to 10 for z = 4 and 10.

Author contributions

M. O. and A. Y. conceived and directed the project. K. K., J. J., and B. M. B. synthesized and characterized Li_1.12−yNi_0.17Mn_0.71O₂. K. K., X. M. S., N. T., and M. N. conducted theoretical calculations. K. K. and J. K. measured TEM images. K. K., A. T., and D. A. conducted synchrotron X-ray absorption/emission spectroscopy. All authors wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan; Grant-in-Aid for Specially Promoted Research No. 15H05701 and Grant-in-Aid for Scientific Research (S) No. 20H05673. This work was also supported by “Elements Strategy Initiative for Catalysts and Batteries (ESICB)”. M. O. was financially supported by JPSP KAKENHI (Grant Number: 19H05816, 18K19124, and 18H03924), and the Asahi Glass Foundation. M. N. was financially supported by Grant-in-Aid for Scientific Research on Innovative Areas “Interface Ionics” (Grant Number: 19H05815). K. K. was financially supported by JPSP KAKENHI (Grant Number: 20J14291). Soft X-ray absorption/emission spectroscopy at BL07LSU of SPring-8 was performed by joint research in SRRO and ISSP, the University of Tokyo (Proposal No. 2020A7474, 2019B7456, 2019A7452, 2018B7590, 2018A7560, 2018B1514, 2017B1328, and 2016B1503). Soft X-ray absorption/emission spectroscopy at BL27SU of SPring-8 was performed under the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2018A1359). XAFS was performed under the approval of the Photon Factory Program Advisory Committee (Proposal No. 2018G082). Magnetic measurements were performed using facilities of the Cryogenic Research Center, the University of Tokyo. The computations partly conducted in this study have been partly pursued by using the facilities of the Supercomputer Center at the Institute for Solid State Physics at the University of Tokyo. The authors are grateful to J. Miyawaki and Y. Harada at the University of Tokyo and K. Tsuruta and Y. Tamenori at JASRI for their support on the X-ray absorption/emission experiments.

Notes and references

1. D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29.
2. P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 6710–6711.
3. G. Crabtree, Science, 2019, 366, 422–424.
4. R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278.
5. M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561.
6. K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789.
7. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
8. A. Manthiram, Nat. Commun., 2020, 11, 1550.
9. Z. Lu, L. Y. Beaulieu, R. A. Donaberger, C. L. Thomas and J. R. Dahn, J. Electrochem. Soc., 2002, 149, A778–A791.
10. H. Koga, L. Croguennec, M. Ménétrier, K. Douhil, S. Belin, L. Bourgeois, E. Suard, F. Weill and C. Delmas, J. Electrochem. Soc., 2013, 160, A786–A792.
11. M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J.-M. Tarascon, Nat. Mater., 2013, 12, 827–835.
12. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814.
13. D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Y. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697.
14. K. Luo, M. R. Robert, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691.
15. T. Sudayama, K. Uehara, T. Mukai, D. Asakura, X.-M. Shi, A. Tsuchimoto, B. Mortemard de Boisse, T. Shimada, E. Watanabe, Y. Harada, M. Nakayama, M. Okubo and A. Yamada, Energy Environ. Sci., 2020, 13, 1492–1500.
16. A. Tsuchimoto, X.-M. Shi, K. Kawai, B. Mortemard de Boisse, J. Kikkawa, D. Asakura, M. Okubo and A. Yamada, Nat. Commun., 2021, 12, 631.
17. E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák, G. V. Tendeloo, R. Dominiko and J.-M. Tarascon, Science, 2015, 350, 1516–1521.
18. Z. N. Taylor, A. J. Perez, J. A. Coca-Clemente, F. Braga, N. E. Drewett, M. J. Pitcher, W. J. Thomas, M. S. Dyer, C. Collins, M. Zanella, T. Johnson, S. Day, C. Tang, V. R. Dhanak, J. B. Claridge, L. J. Hardwick and M. J. Rosseinsky, J. Am. Chem. Soc., 2019, 141, 7333–7346.
19. R. A. House, U. Maitra, M. A. Pérez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K.-J. Zhou, M. R. Roberts and P. G. Bruce, Nature, 2020, 577, 502–508.
20. R. A. House, G. J. Rees, M. A. Pérez-Osorio, J.-J. Marie, E. Boivin, A. W. Robertson, A. Nag, M. Garcia-Fernandez, K.-J. Zhou and P. G. Bruce, Nat. Energy, 2020, 5, 777–785.
21. R. Sharpe, R. A. House, M. J. Clarke, D. Förstermann, J.-J. Marie, G. Cibin, K.-J. Zhou, H. Y. Playford, P. G. Bruce and M. S. Islam, J. Am. Chem. Soc., 2020, 142, 21799–21809.
22. C. Zhao, C. Li, H. Liu, Q. Qiu, F. Geng, M. Shen, W. Tong, J. Li and B. Hu, J. Am. Chem. Soc., 2021, 143, 18652–18664.
23. R. A. House, H. Y. Playford, R. I. Smith, J. Holter, I. Griffiths, K.-J. Zhou and P. G. Bruce, Energy Environ. Sci., 2022, 15, 376–383.
24. H. Umeno, K. Kawai, D. Asakura, M. Okubo and A. Yamada, Adv. Sci., 2022, 9, 2104907.
25. M. Okubo, K. Kawai, Z. Ma and A. Yamada, Acc. Mater. Res., 2022, 3, 33–41.
26. J. R. Croy, K. G. Gallagher, M. Balasubramanian, B. R. Long and M. M. Thackeray, J. Electrochem. Soc., 2014, 161, A318–A325.
27. G. Assat, D. Foix, C. Delacourt, A. Iadecola, R. Dedryvère and J.-M. Tarascon, Nat. Commun., 2017, 8, 2219.
28. W. E. Gent, I. I. Abate, W. Yang, L. F. Nazar and W. C. Chueh, Joule, 2020, 4, 1369–1397.
29. A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694–8698.
30. G. Assat, S. L. Glazier, C. Delacourt and J.-M. Tarascon, Nat. Energy, 2019, 4, 647–656.
31. J. Hong, D.-H. Seo, S.-W. Kim, H. Gwon, S.-T. Oh and K. Kang, J. Mater. Chem., 2010, 20, 10179–10186.
32. B. Xu, C. R. Fell, M. F. Chi and Y. S. Meng, Energy Environ. Sci., 2011, 4, 2223–2233.
33. J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund, C.-J. Sun, K. H. Stone, D. Passarello, W. Yang, D. Prendergast, G. Ceder, M. F. Toney and W. C. Chueh, Nat. Mater., 2019, 18, 256–265.
34. K. Ku, B. Kim, S.-K. Jung, Y. Gong, D. Eum, G. Yoon, K.-Y. Park, J. Hong, S.-P. Cho, D.-H. Kim, H. Kim, E. Jeong, L. Gu and K. Kang, Energy Environ. Sci., 2020, 13, 1269–1278.
35. P. M. Csernica, S. S. Kalirai, W. E. Gent, K. Lim, Y.-S. Yu, Y. Liu, S.-J. Ahn, E. Kaeli, X. Xu, K. H. Stone, A. F. Marshall, R. Sinclair, D. A. Shapiro, M. F. Toney and W. C. Chueh, Nat. Energy, 2021, 6, 642–652.
36. Y. Yu, P. Karayaylali, D. Sokaras, L. Giordano, R. Kou, C. J. Sun, F. Maglia, R. Jung, F. Gittleson and Y. Shao-Horn, Energy Environ. Sci., 2021, 14, 2322–2334.
37. N. Yabuuchi, R. Hara, M. Kajiyama, K. Kubota, T. Ishigaki, A. Hoshikawa and S. Komaba, Adv. Energy Mater., 2014, 4, 1301453.
38. B. Mortemard de Boisse, J. Jang, M. Okubo and A. Yamada, J. Electrochem. Soc., 2018, 165, A3630–A3633.
39. D. Eum, B. Kim, S. J. Kim, H. Park, J. Wu, S. P. Cho, G. Yoon, M. H. Lee, S. K. Jung, W. Yang, W. M. Seong, K. Ku, O. Tamwattana, S. K. Park, I. Hwang and K. Kang, Nat. Mater., 2020, 19, 419–427.
40. H. Shang, Y. Zuo, F. Shen, J. Song, F. Ning, K. Zhang, L. He and D. Xia, Nano Lett., 2020, 20, 5779–5785.
41. C. Cui, X. Fan, X. Zhou, J. Chen, Q. Wang, L. Ma, C. Yang, E. Hu, X.-Q. Yang and C. Wang, J. Am. Chem. Soc., 2020, 142, 8918–8927.
42. J. M. Paulsen and J. R. Dahn, Solid State Ionics, 1999, 126, 3–24.
43. D. Carlier, I. Saadoune, L. Croguennec, M. Ménétrier, E. Suard and C. Delmas, Solid State Ionics, 2001, 144, 263–276.
44. G. Assat, C. Delacourt, D. A. Dalla Corte and J.-M. Tarascon, J. Electrochem. Soc., 2016, 163, A2965–A2976.
45. R. A. House, L. Jun, U. Maitra, K. Tsuruta, J. W. Somerville, D. P. Förstermann, F. Messel, L. Duda, M. R. Robert and P. G. Bruce, Energy Environ. Sci., 2018, 11, 926–932.
46. U. Maitra, R. A. House, J. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Y. Jin, M. A. Perez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Y. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295.
47. J. Xu, M. Sun, R. Qiao, S. E. Renfrew, L. Ma, T. Wu, S. Hwang, D. Nordlund, D. Su, K. Amine, J. Lu, B. D. Mccloskey, W. Yang and W. Tong, Nat. Commun., 2018, 9, 947.
48. Z. Zhuo, C. D. Pemmaraju, J. Vinson, C. Jia, B. Moritz, I. Lee, S. Sallies, Q. Li, J. Wu, K. Dai, Y.-D. Chuang, Z. Hussain, F. Pan, T. P. Devereaux and W. Yang, J. Phys. Chem. Lett., 2018, 9, 6378–6384.
49. Q. Li, Z. W. Lebens-Higgins, Y. Li, Y. S. Meng, Y. Chuang, L. F. J. Piper, Z. Liu and W. Yang, J. Phys. Chem. Lett., 2021, 12, 1138–1143.
50. M. J. Zuba, A. Grenier, Z. Lebens-Higgins, G. J. Paez Fajardo, Y. Li, Y. Ha, H. Zhou, M. S. Whittingham, W. Yang, Y. S. Meng, K. W. Chapman and L. F. J. Piper, ACS Energy Lett., 2021, 6, 1055–1064.
51. M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502.
52. L. G. Cota and P. de la Mora, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 133–136.
53. Z. Chen, J. Li and X. C. Zeng, J. Am. Chem. Soc., 2019, 141, 10751–10759.
54. X. Rong, J. Liu, E. Hu, Y. Liu, Y. Wang, J. Wu, X. Yu, K. Page, Y.-S. Hu, W. Yang, H. Li, X.-Q. Yang, L. Chen and X. Huang, Joule, 2018, 17, 125–140.
55. B. Song, M. Tang, E. Hu, O. J. Borkiewicz, K. M. Wiaderek, Y. Zhang, N. D. Phillip, X. Liu, Z. Shadike, C. Li, L. Song, Y.-Y. Hu, M. Chi, G. M. Veith, X.-Q. Yang, J. Liu, J. Nanda, K. Page and A. Huq, Chem. Mater., 2019, 31, 3756–3765.
56. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
57. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
58. Y. Harada, M. Kobayashi, H. Niwa, Y. Senba, H. Ohashi, T. Tokushima, Y. Horikawa, S. Shin and M. Oshima, Rev. Sci. Instrum., 2012, 83, 013116.
59. A. J. Achkar, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 2–5.
60. H. Wadati, et al. , Appl. Phys. Lett., 2012, 100, 193906.
61. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
62. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
63. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
64. D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
65. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
66. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121.
67. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
68. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
69. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
70. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
71. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.
72. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03503g

‡ Present address: Department of Electrical Engineering and Bioscience, School of Advanced Science and Engineering, Waseda University, Okubo 3-4-1, Shinjuku-ku, Tokyo 169-0555, Japan.

---