Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of metallocene catalyst activation: alignment of theory and experiment†
Mikko
Linnolahti
 * and
Scott
Collins‡
* and
Scott
Collins‡

Department of Chemistry, University of Eastern Finland, Joensuu Campus, Yliopistokatu 7, FI-80100, Joensuu, Finland. E-mail: mikko.linnolahti@uef.fi
First published on 5th July 2022
Abstract
Three equilibria involved in metallocene catalyst activation, including dissociation of R6Al2 (R = Me, Et or i-Bu) and related species such as [L2ZrMe2AlMe2][B(C6F5)4] (L2 = Cp2, 1,2-ethylenebis(η5-indenyl), Me2C(η5-C5H4)2) or [(L2ZrMe)2μ-Me][MePBB] (L2 = (h5-1,2-Me2C5H3)2, [MePBB]− = [MeB(ArF)3]− with ArF = o-C6F5-C6F4) are studied by DFT using various approaches to account for the enthalpy and entropy changes in gas and condensed phases. These studies reveal that both low energy vibrations and translational entropy conspire to cause significant deviations between theory and experiment when it comes to the free energy change in condensed or even gas phase. Alignment of theory with experiment requires in addition, consideration of specific solvation of reactants and products.
Introduction
Over the past several years there has been renewed study of the structure and reactivity of large aluminoxane structures with formulae (MeAlO)n (Me3Al)m.1 These are thought to be models for methylaluminoxane (MAO), and in particular for the active components of that mixture, as MAO is commonly used to activate group 4 metallocene and other single site catalysts for olefin polymerization.2Previous computational studies have focused on systematic evaluation of the structure of MAO,3 including following its formation via hydrolysis of Me3Al.4 The growth of MAO oligomers has been demonstrated to start out as linear aggregates, rings and sheet structures with tetrahedral Al and trigonal O.5 Hydrolysis studies of the initial steps have employed MP2 level of theory, while in subsequent work, approaching the experimentally relevant size-domain,6 we adopted the more cost-effective M06-2X DFT method,7 combined with a basis set of triple zeta quality,8 since this functional is well known to treat dispersion forces in the Al-μ-Me-Al or (μ4-O)Al4 bonding found in the structures.9
Transition from sheets to cages was initially proposed at ca. n ∼ 13, and a stable cage was located with n = 16 and m = 6,6 which corresponds to the composition of the most intense anion detected by ESI MS upon reaction of hydrolytic MAO with Lewis bases, including metallocene complexes.10 However, some of the Me3Al was incorporated as structural Me3Al1d,e,11 – i.e. as linear but aggregated Me2Al(OAlMe)xMe moieties in this unstrained cage rather than terminal OAl2Me5 groups. Based on the number of readily exchangeable Al-Me groups as detected using e.g. Et3Al and ESI-MS,12 the cage structure did not seem reasonable. This guided us toward a more detailed investigation of the structural motifs, revealing that transition from sheets to cages does not take place at n ≤ 18. The reason for the preference of sheets over isomeric cages lies in significantly higher entropy, and hence lower free energy, of the sheets. An especially stable sheet anion [(MeAlO)16(Me3Al)6Me]− (hereinafter [16,6]−) along with its neutral 16,6 precursor does possess the requisite number of exchangeable Al-Me groups.13
Accurate calculation of entropy, and thus free energy, requires special attention. As systems get large, the number of low energy normal modes increase dramatically and to the point where it is difficult to estimate their energy, and thus the vibrational entropy using a harmonic oscillator approximation. This is a general and well-known problem, for which quasi-harmonic entropy corrections have been proposed, e.g. by raising the problematic low energy vibrations to a cut-off frequency of 100 cm−1.14
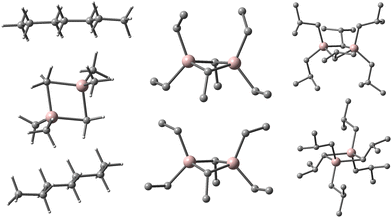
We noticed the importance of this particularly for isomeric structures differing little in the arrangement of the constituent atoms (i.e., conformers) as in recently proposed contact ion-pairs (CIP) between Cp2ZrMe2 and our new sheet model for 16,6 (Fig. 1).15
 | ||
| Fig. 1 Equilibria involving contact ion-pair to form outer-sphere ion-pairs detected spectroscopically.15 Zr in blue, Al in pink, O in red, C in grey, H omitted for clarity. | ||
The calculated TS values of these isomers had a variation of σ = ±6.1 kJ mol−1 at 298 K. Though the standard deviation is small compared with the total entropy for these large systems (ca. 0.75%), in free energy terms this corresponds to a significant amount and might overwhelm attempts to characterize the reactivity of these large structures in gas phase but also importantly in solution. For example, outer-sphere ion-pairs (OSIP) that have been detected spectroscopically in the case of the Cp2ZrMe2-MAO system include [Cp2ZrMe2AlMe2][16,6] and [(Cp2ZrMe)2μ-Me][16,6]15 and yet the equilibria between these species and any contact ion-pairs present are not as well-documented, in contrast to other ion-pairs featuring well-defined counter-anions.2
Accurate computation of thermodynamic quantities in solution is a topic of great difficulty and debate – we cannot provide here an in-depth discussion but refer the reader to recent literature.16 We begin by noting that movements become more restricted when moving from gas-phase to solution, thereby reducing the total entropy. Hence, an approximate estimate for the solution Gibbs energy can obtained by simply scaling the gas-phase entropy, where a ⅔TS scaling factor has been previously employed in the context of metallocenium ion-pair complexes.17 A more accurate description of specific solvents effects can be obtained by using quantum mechanical continuum solvation models,18 although these generally do not account for specific solvation of reactants vs. products nor effects arising from solvation such as perturbation to the thermodynamically most stable gas phase conformation. Furthermore, the continuum models do not generally account for the restricted movements in solution, and hence the entropies determined in continuum need to be further corrected, particularly for the sake of proper estimation of translational entropy.19
This prompted us to investigate this issue in more detail and for relevant catalyst activation or other reactions for which thermodynamic data was available, ideally in both gas and condensed phases. In this paper, we discuss three different reversible reactions involving both neutral species and metallocenium ion-pairs that have been studied experimentally.
Results and discussion
Dissociation of R6Al2
The first equilibrium involving dissociation of R6Al2 (R = Me, Et or i-Bu) in gas or condensed phases has been studied in detail.20 For R = Me, there is general agreement as to the energetics of this process in gas phase with ΔH = 84.2 to 85.4 kJ mol−1, ΔS = 177(2) J mol−1 K−1 and ΔG = 31.6(0.3) kJ mol−1 at 298 K (Table 1, entries 1 and 2).21 The enthalpy change is accurately estimated at the M06-2X/TZVP level of theory with ΔH = 84.9 kJ mol−1. In the case of entropy, consideration of symmetry is required for technical correctness, because of its effect on rotational entropy.9,22 However, constraining Me3Al to C3h-symmetry increases the gas-phase ΔS from 244 to 282 J mol−1 K−1.| Entry | R | T (K) | ΔH | ΔS | ΔG | ΔH-qhb | ΔS-qhb | ΔG-qhb | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a ΔG and ΔH in kJ mol−1, ΔS in J mol−1 K−1 with estimated standard deviation in parentheses for experimental data (entries 1–4). b Corrected for low energy vibrations using a quasi-harmonic approach. | |||||||||
| 1 | Me | 298 | 85(1) | — | — | — | — | — | 21a |
| 2 | Me | 298 | 84.2(7) | 177(2) | 31.6(3) | — | — | — | 21b |
| 3 | Me | 418 | 84.2(7) | 177(2) | 10.4(1) | — | — | — | 21b |
| 4 | Et | 418 | 76(1) | 190(3) | 1.3(2) | — | — | — | 25 |
| 5 | Me | 298 | 84.9 | 282.5 | 0.6 | 82.7 | 187.8 | 26.7 | This work |
| 6 | Me | 418 | 83.5 | 278.7 | −33.0 | 80.3 | 183.8 | 3.4 | This work |
| 7 | Et | 418 | 87.8 | 231.1 | −8.8 | 86.0 | 203.6 | 0.8 | This work |
The calculated reaction entropy is thus significantly larger than measured, and even more so in C3h-symmetry. The origin of the increase lies in the low energy normal modes, which gain significant population at T = 298 K.
While the rotational entropy of Me3Al decreases, as it should, on constraining to C3h (108.9 to 99.7 J mol−1 K−1), it is over-compensated by an increase in vibrational entropy (112.6 to 141.0 J mol−1 K−1) due to minute changes in low energy normal modes, which cannot be calculated to precision using a harmonic oscillator approximation.
We tested Truhlar's quasi-harmonic (qh) entropy correction14 as a potential remedy for this problem, using a cut-off frequency of 100 cm−1. The correction has a marked effect, reducing the reaction entropy from ΔS = 282 J mol−1 K−1 to ΔS-qh = 188 J mol−1 K−1, thus bringing it close to the experimental value of 177 J mol−1 K−1.
The low energy modes also influence the zero-point correction to the electronic energy. Using a similar correction,23 ΔH = 84.9 kJ mol−1 reduces to ΔH-qh = 82.7 kJ mol−1, indicating that the M06-2X/TZVP level of theory underestimates ΔH by 2–3 kJ mol−1. Thus, our best estimate for the free energy change in gas phase is ΔG-qh = 26.7 kJ mol−1 at 298 K which is within 5 kJ mol−1 of the experimental value extrapolated from studies at higher T. For greater certainly we estimated ΔG-qh at 418 K in the range covered by experiment, and reasonable agreement is observed (Table 1, entry 6 vs. entry 3).
For R = Et, the dissociation equilibrium has been studied in condensed phase by several techniques (vide infra), though some data obtained in gas phase reported in a thesis24 were disseminated in a paper by Smith.25 A plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdvs. 1/T was non-linear for Et3Al over the temperature range studied, consistent with decomposition at higher temperatures. Thus, gas phase values of ΔH and ΔS over the T range studied are not available. At the lowest T examined (418 K) ΔG = 1.3(2) kJ mol−1 with estimates of ΔH = 76(1) kJ mol−1 and ΔS = 190(3) J mol−1 K−1 based on studies of the liquid phase (vide infra).
Kdvs. 1/T was non-linear for Et3Al over the temperature range studied, consistent with decomposition at higher temperatures. Thus, gas phase values of ΔH and ΔS over the T range studied are not available. At the lowest T examined (418 K) ΔG = 1.3(2) kJ mol−1 with estimates of ΔH = 76(1) kJ mol−1 and ΔS = 190(3) J mol−1 K−1 based on studies of the liquid phase (vide infra).
We calculated using the quasi-harmonic correction for both H and S that ΔG-qh = 0.8 kJ mol−1, which is in almost precise, though probably fortuitous agreement with the experimental value, as indicated by the larger deviations from experiment for ΔH-qh = 86.0 kJ mol−1 and ΔS-qh = 203.6 J mol−1 K−1 at 418 K (Table 1, entries 7 vs. 4).
However, the experimental estimates are not based on the T dependence of Kd so we cannot attach too much significance to these discrepancies, except to state that we did not consider more than one conformer when calculating thermodynamic properties.26
In condensed phase, experimental thermodynamic data for dissociation of liquid R6Al2 and solutions in aromatic or aliphatic hydrocarbons differ significantly (Table 2). Beginning with iBu3Al, it is widely known that this compound is appreciably dissociated in condensed phase, and the accepted values in the liquid phase or hydrocarbon solution are reported in Table 2, entry 1.27
| Entry | R | ΔT (°C) | ΔH | ΔS | ΔGb | ΔGc | Solvent | Ref. |
|---|---|---|---|---|---|---|---|---|
| a ΔG and ΔH in kJ mol−1, ΔS in J mol−1 K−1 with estimated standard deviation in parentheses. b Estimated from data obtained at 298 K. c Extrapolated from data at higher T to 298 K. d Liquid or hydrocarbon solution. e Mesitylene. f Heptane. g Xylenes. | ||||||||
| 1 | iBu | 10–45 | 34.1(5) | 128(1) | −3.92(4) | — | 27 | |
| 2 | Et | 60–150 | 71(1) | 135(3) | — | 30.5(6) | 25 | |
| 3 | Et | 60–150 | 55.7(5) | 100(2) | — | 25.9(5) | 28 | |
| 4 | Et | 60–100 | 44(5) | 69(26) | 23(0) | 23(9) | 29a | |
| 5 | Et | 60–100 | 40(2) | 65(12) | 20(7) | 20(4) | 29a | |
| 6 | Me | 40–100 | 54(2) | 74(6) | 32(2) | 32(3) | 29b | |
| 7 | Me | 40–100 | 55(6) | 81(16) | 30(5) | 31(6) | 29b | |
| 8 | Me | — | 81(1) | 122(1) | — | 45(1) | 25 | |
| 9 | Me | — | 63.8(4) | — | — | — | 28 | |
The situation with Et3Al is complicated by the technique used to determine the dissociation constants, and the temperature range over which the data was collected. The most widely cited values were reported by Smith in papers where calorimetry was used to measure the heat of dilution of this material in both hydrocarbon25 and aromatic hydrocarbon28 solution over a wide temperature range. His data are summarized in entries 2 and 3 where the enthalpy of dissociation is significantly lower in aromatic vs. saturated hydrocarbon media. Later work by Černý and co-workers utilized 27Al NMR spectroscopy to study this equilibrium.29 Despite collecting data over a similar temperature range (25–100 °C) these workers only analyzed their data between 60–100 °C. Their estimates of ΔG based on this data (entries 4 and 5) differ significantly from those reported by Smith.
Finally, the situation for Me3Al in condensed phase is the most confusing. Černý and co-workers also studied this equilibrium using 27Al NMR spectroscopy.29b The quality of the data, particularly in mesitylene solution, is not as high as that reported for Et3Al and moreover these authors concluded that there was little difference in either the enthalpy or entropy of dissociation in comparing aromatic vs. saturated hydrocarbon solution, despite the fact that Et3Al is more dissociated under the former conditions with a significant difference in ΔG at 298 K according to Smith.
In earlier work, Smith could not use calorimetry to study this equilibrium as Me3Al is less dissociated than Et3Al under all conditions.25 He provided estimates based on a number of reasonable assumptions but none of the estimates are based on actual measurement of the equilibrium in question. The available data are summarized in Table 2, entries 6–9.
If we focus on the entropy change for these reactions in hydrocarbon media, those values reported by Smith for iBu3Al (ΔS = 128(1) J mol−1 K−1), Et3Al (135(3)) and that estimated for Me3Al (122(1)) compared with gas phase values of 177(2) and 190(3) for Me3Al and Et3Al, or theoretical estimates (vide infra) appear reasonable. The much lower values reported by Černý and co-workers (entries 4–5 and 6–7) do not, and suggest an insufficiently large temperature range was used or other sources of error are involved. Certainly, the error in some reported values for ΔS is unacceptably large (e.g. entries 4 and 7).
On the other hand, in the case of Me3Al, ΔG = 45(1) kJ mol−1 at 298 K extrapolated by Smith corresponds to an equilibrium constant of 1.3 × 10−8 M in hydrocarbon solution. Based on the work of Černý et al. no change in 27Al chemical shift would be expected over the concentration range they studied, while the measured equilibrium constant is 3.1(1.6) × 10−6 M, admittedly with a large error involved.
Concerning calculations, approximating solution Gibbs energy for dissociation of Me6Al2 by the ⅔TS scaling factor17 leads to good agreement (ΔG-c = 28.8 kJ mol−1) seen in the more recent experimental work (Table 2, entries 6 or 7). However, this approach has limited applicability for large systems, where the total entropy is dominated by vibrations, whilst translations are primarily affected when moving from gas-phase to solution.
The thermodynamic functions calculated for dissociation of R6Al2 by polarizable continuum method (PCM)30 in a variety of media are given in the ESI (Table S-1†). Though a slight decrease is predicted for ΔH or ΔH-qh relative to gas phase, we do not reproduce the much lower values seen experimentally. To account for specific solvation of reactants and products, we looked at solvent–solute interactions, subtracting the difference in ΔH-qh between R3Al-solvent and R6Al2-solvent interactions (ΔΔH in Table 3) from the PCM results for the thermodynamic functions. The lower reaction enthalpies seen in both hydrocarbon and especially in aromatic hydrocarbon solution are related to this phenomenon.
| R | Solvent | ΔH | ΔH-qh | ΔΔHb | ΔG (ΔS) | ΔG-qh (ΔS-qh) | ΔG-qh-trc (ΔS-qh-tr) |
|---|---|---|---|---|---|---|---|
| a ΔG and ΔH in kJ mol−1, ΔS in J mol−1 K−1. Additional data are reported as ESI.† b Difference in ΔH-qh due to specific solvation of reactant vs. product, calculated as the difference between ΔH-qh in R3Al-solvent and R6Al2-solvent interactions. c Corrected for both low energy vibrations and reduced translational entropy in solution. See text for discussion. d 313 K cf.Table 5. e C 2 symmetry adopted in solution in the presence of specific Et6Al2-solute interactions; Cs symmetry in gas phase (see Fig. 2). f C 2 symmetry in solution; gas-phase Ci symmetry (see Fig. 2). | |||||||
| Me | Mesitylene | 58.3 | 60.5 | 19.1 | −9.5 (228) | 4.6 (188) | 18.6 (141) |
| Me | Heptane | 70.9 | 71.4 | 7.8 | −6.3 (259) | 15.1 (189) | 27.9 (146) |
| Me | Benzened | 63.2 | 63.5 | 14.6 | −7.7 (227) | 4.6 (188) | 19.2 (142) |
| Ete | Mesitylene | 59.1 | 55.3 | 22.3 | −28.5 (264) | −12.9 (229) | 1.1 (182) |
| Ete | Heptane | 73.3 | 72.0 | 6.5 | −9.2 (276) | 4.2 (228) | 17.0 (184) |
| i-Buf | Heptane | 36.9 | 37.5 | 0.2 | −31.9 (231) | −35.8 (246) | −23.0 (203) |
The final data are summarized in Table 3, and Fig. 2 illustrates the molecular structures of the R6Al2 dimers in both gas-phase and under specific interactions with two heptane molecules, one for each half of the dimer.
If we focus on the data for Et3Al, the theoretical estimates of ΔH-qh in mesitylene (55.3 kJ mol−1), heptane (72.0) or for i-Bu3Al in heptane (37.5) are within a few kJ mol−1 of the corresponding experimental values reported by Smith (Table 2, entries 1–3). We cannot confirm the experimental findings of Černý and coworkers, who reported much lower values for the enthalpy changes for Et3Al (and Me3Al) and quite similar values in hydrocarbon and aromatic hydrocarbon solution. As will be shown below, the interaction energies between Me3Al and itself or other molecules at the M062-X/TZVP level of theory are accurate within 4–5 kJ mol−1 of the values obtained by the CCSD(T) method.
The experimental values provided by Černý and coworkers lie well outside this limit of theoretical error. We conclude that our theoretical estimates for ΔH-qh for Me3Al in both solvents (Table 3, entries 1 and 2) should be considered reliable. While the value in mesitylene (60.5 kJ mol−1) is in reasonable agreement with Smith's estimate (63.8 kJ mol−1), our theoretical estimate in hydrocarbon (71.4 kJ mol−1) is significantly lower than Smith's (81 kJ mol−1). This may account for his estimate for Kd and ΔG at 298 K being inconsistent with the measurements of Černý and coworkers at that temperature.
Alignment of theory vs. experiment cannot rely solely on accurate estimation of ΔH and thus ΔS requires attention. The PCM model as such cannot account for the observed reduced entropy in solution, as is clear from the calculated ΔS-qh ≈ 188 J mol−1 K−1 for Me6Al2 dissociation at T = 298K in both gas-phase (Table 1, entry 4) and in any of the solvents (Table 3), while the range of the measured entropies is lower, 74–122 J mol−1 K−1 (Table 2). Therefore, to account for the restricted movements in solution, the entropies determined in continuum were corrected for the reduced accessible space due to the volume occupied by the solvent, resulting in reduced translational entropy, as describes by Whitesides and co-workers.19
The translational entropy correction (tr) combined with the harmonic entropy correction (qh) provides our best estimates of the free energy change, labeled ΔG-qh-tr in Table 3. These combined corrections take us towards the experimentally measured entropies (Table 2). Still, the ΔG-qh-tr values are not in quantitative agreement with experiment though we predict the ease of dissociation correctly (Me < Et ≪ i-Bu) and in the different solvents (i.e. more dissociated in aromatic hydrocarbon due to lower ΔH).
There are several potential reasons for the remaining discrepancy in ΔS between theory and experiment. The experimental values suggest that motion is more restricted in solution than indicated by the approximation in use. The approximation based on free volume indicates an entropy lowering of ΔS-qh-tr − ΔS-qh = ΔΔS = 43–47 J mol−1 K−1 for the various solvents at 298 K. We note that another approximation based on the increased density and thus pressure of the liquid state16c leads to ΔΔS values of almost identical magnitude. If we were to further restrict translation using densities typical for organic glasses (ca. 1300 kg m−3) we estimate ΔΔS = 46–50 J mol−1 K−1 suggesting either approach has limits of this magnitude.
Neither approximation leads to limiting values of ΔS-qh-tr that match experiment. It is possible that rotations are also constrained in the liquid state but the rotational entropy (S-r) of the products (2 × 99.7 J mol−1 K−1 in the case of Me3Al) might be expected to decrease in proportion to that of the reactant (119.1 J mol−1 K−1), where the difference is ΔS-r = 80.3 J mol−1 K−1 in gas phase at 298 K. A reduction similar to that seen for translations, which we don't think is justified here,31 would lead to a further lowering of perhaps no more than 20 J mol−1 K−1. This would bring us into quantitative agreement with the results of Smith in hydrocarbon media.
Besides being systematically higher, the calculated entropies (for R = Me, ΔS-qh-tr = 141 or 146 J mol−1 K−1 in aromatic or aliphatic hydrocarbon solution) are insignificantly different in the two different media compared to experiment (cf.Table 2, entries 2 and 3). We suspect this also reflects that both products and reactants are specifically solvated, which would have the effect of reducing the entropy further and may account for the significant difference between aromatic vs. aliphatic solvents seen experimentally but not theoretically.
We end this section with a discussion of the energetic consequences of specific solvation as studied using the M06-2X and MN15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 functionals, def2-TZVP33 and def2-TZVPD34 basis sets and CCSD(T) method. The data are summarized in Table 4.
32 functionals, def2-TZVP33 and def2-TZVPD34 basis sets and CCSD(T) method. The data are summarized in Table 4.
| Adduct | M06-2Xa | M06-2Xb | MN15b | MN15c | CCSD(T)d |
|---|---|---|---|---|---|
| a TZVP. b def2-TZVP.33 c def2-TZVPD.34 d CCSD(T)/def2-TZVPD single-point energy in MP2/def2-TZVPD optimized geometry. | |||||
| Me3Al-AlMe3 | −92.1 | −98.2 | −103.7 | −104.5 | −96.5 |
| Me3Al-C7H16 | −23.8 | −23.8 | −33.0 | −34.2 | −25.7 |
| Me3Al-C6H5CH3 | −40.5 | −40.8 | −48.8 | −49.3 | −43.4 |
| Me3Al-C6H3(CH3)3 | −48.2 | −48.1 | −58.0 | −58.6 | −51.4 |
| Me3Al-C6H6 | −36.1 | −36.6 | −44.0 | −44.4 | −39.0 |
| Me6Al2-C6H6 | −19.7 | −19.5 | −25.1 | −25.5 | −25.4 |
The first entry corresponds to the energy change for dimerization of Me3Al, which can be thought of as an interaction energy as Me6Al2 is energetically the most stable adduct of Me3Al with itself. The single-point CCSD(T)/def2-TZVPD energies calculated for the MP2/def2-TZVPD optimized geometries provide an instructive reference. At this sophisticated level of theory, the Me3Al dimerization energy is calculated as −96.5 kJ mol−1, which when combined with the quasi-harmonic enthalpy correction calculated at MP2/def2-TZVPD level of theory, gives ΔH-qh = −84.2 kJ mol−1, i.e. in precise match with the experimental enthalpy of 84.2 kJ mol−1 for the reverse reaction, quoted from Table 1.
Our method of choice, M06-2X/TZVP underestimates the Me3Al dimerization energy by ca. 4 kJ mol−1 (which we already saw in the discussion of Me3Al dissociation enthalpies, Table 1). While improving the basis set to def2-TZVP might be justified, it has very little effect on the solvent interactions (Table 4, second column), based on which, the effect of specific solvation on dissociation was calculated (Table 3). As for dimerization of Me3Al, M06-2X is more accurate than MN15, which is consistent with previous evaluations of X3Al dimerization energies in general.35 However, when it comes to noncovalent interactions, MN15 is better suited to describe those as the Me6Al2-benzene interaction energies are very closely aligned to the CCSD(T) results.
If we consider the specific case of dissociation of Me6Al2 in benzene, the dissociation energy is within 4.4 kJ mol−1 of the theoretical limiting value, while we underestimate solvation of the Me3Al product by 2.9 kJ mol−1 and of Me6Al2 by 5.7 kJ mol−1 with respect to the CCSD(T) results. So, overall, our M06-2X/TZVP results are about 7.2 kJ mol−1 lower in electronic energy for this reaction than predicted at the CCSD(T) level of theory. This provides some indication of the errors involved when it comes to equilibria involved in larger systems featuring non-covalent interactions, as in the section dealing with metallocenium ion pairs (vide infra).
Dissociation of R6Al2vs. kinetics of alkyl exchange
The continuing study of the dissociation equilibrium has been motivated by kinetic work focused on the mechanism of exchange of bridging and terminal Al-R groups in these compounds,36 which can be studied by dynamic NMR spectroscopy. There is consensus from this work that the enthalpy of activation decreases in the order Me > Et > higher alkyls and the exchange process is significantly faster in aromatic vs. aliphatic media at the same temperature.37 Accepted values for ΔH‡ vary between 63–67 kJ mol−1 for R = Me in hydrocarbon media between 263 and 213 K with ΔG‡ = 46.0 kJ mol−1 at 223 K. An early study featuring the widest temperature range provides an estimate of 84 J mol−1 K−1 for ΔS‡ with ΔH‡ = 65.2 kJ mol−1.37eIn earlier work we examined the dissociation of Me6Al2 at the M06-2X/TZVP level of theory, and observed a continuous decrease in enthalpy with increasing Al–Al separation, partially offset by a concomitant increase in entropy such that a maximum in ΔG‡ = 40.4 kJ mol−1 was observed at 298 K.10a This is in excellent agreement (±1 kJ mol−1) with experimental values extrapolated from the low temperature NMR data.37 It should be noted that this value is significantly higher than the experimental estimates of ΔG for the dissociation equilibrium at 298 K determined by Černý and coworkers (Table 2, entries 6 and 7) but lower than the value extrapolated by Smith (entry 8) which is inconsistent with their NMR results.
Though there has been a predictable focus on the enthalpy change when discussing the thermodynamics vs. kinetics of the exchange process, and thus its mechanism, it should be noted that the important criterion at any given temperature is that ΔG‡ > ΔG and we find this to be the case here.
In comparing e.g., R = Me with Et it can be seen in aliphatic media, the principal reason for Et3Al being more dissociated than Me3Al at any given temperature is the more favourable entropy increase for the former (Table 3).
Dissociation of [L2ZrMe2AlMe2]+
The solution structure and dynamics of zirconocenium ion-pairs featuring discrete counter-anions has seen intensive experimental and theoretical study.2c,d,38 These studies reveal that alkylzirconocenium cations partnered with [B(C6F5)4]− or related weakly coordinating anions39 typically form CIP in apolar media featuring Zr–F interactions due to the 14 e− alkylzirconocenium cation. In contrast, 16 e− cations typically form OSIP in sufficiently dilute solution.38 Also, the CIP can adopt two or more structures featuring different Zr–F interactions,38,40 and any equilibrium will thus be weighted by their relative contributions. Finally, specific solvation of the cation in the CIP to form a solvent-separated species has recently been confirmed in toluene solution at least for some complexes of this type.41 Our particular example involves dissociation of Me3Al from [L2ZrMe2AlMe2][B(C6F5)4]42 in benzene at T = 313 K with L2 = Cp2, rac-1,2-ethylenebis(η5-1-indenyl) (EBI) and Me2C(η5-C5H4)2 (Me2CCp2) (Table 5).43| Entry | L2 | ΔH | ΔH-qh | ΔG (ΔS) | ΔG-qh (ΔS-qh) | ΔG-qh-tr (ΔS-qh-tr) |
|---|---|---|---|---|---|---|
| a ΔG and ΔH in kJ mol−1, ΔS in J mol−1 K−1 with estimated standard deviation in parentheses where applicable. b Includes specific solvation of the reactant ion-pair by two benzene molecules. | ||||||
| [L2ZrMe2AlMe2][B(C6F5)4] ⇌ Me3Al + [L2ZrMe][B(C6F5)4] (benzene solution, 313 K) | ||||||
| 1 | Cp2 | — | — | 20.0(3) | 20.0(3) | 20.0(3) |
| 2 | Cp2 | 75.9 | 76.9 | 10.0 (210) | 9.7 (215) | 24.2 (168) |
| 3 | EBI | — | — | 23.8(4) | 23.8(4) | 23.8(4) |
| 4 | EBI | 81.0 | 82.3 | 15.8 (208) | 17.0 (209) | 31.6 (162) |
| 5 | Me2CCp2 | — | — | 18.7(3) | 18.7(3) | 18.7(3) |
| 6 | Me2CCp2 | 59.8 | 61.4 | 0.1 (191) | −3.5 (207) | 11.1 (161) |
| [L2ZrMe2AlMe2][B(C6F5)4]·C6H6 + C6H6 ⇌ Me3Al·C6H6 + [L2ZrMe(C6H6)] [B(C6F5)4] (benzene solution, 313 K) | ||||||
| 7 | Cp2 | 64.0 | 67.5 | 10.2 (172) | 3.7 (204) | 18.2 (157) |
| 8b | Cp2 | 64.2 | 68.2 | 12.4 (166) | 4.3 (204) | 18.9 (157) |
| 9 | EBI | 47.8 | 48.3 | 30.0 (57.0) | 27.3 (67.1) | 27.3 (67.1) |
| 10 | Me2CCp2 | 36.3 | 36.2 | 16.8 (62.2) | 14.1 (70.5) | 14.1 (70.5) |
We should note that the experimental values for Kd and thus ΔG were derived from Dixon plots of the carboalumination rate constants vs. [Me3Al] with the concentration of monomeric Me3Al being derived from the results of Černý et al. at 313 K in mesitylene. Since the two solvents benzene and mesitylene feature different interaction energies with Me3Al (Table 4), there may be systematic errors involved in this assumption but, not so as to affect the differences in ΔG for the three different ion-pairs (entries 1, 3 and 5).
While the correct order in ΔG-qh-tr is predicted in condensed phase (entries 2, 4 and 6), theory strongly accentuates the differences with ΔG-qh-tr = 11.1 to 31.6 kJ mol−1 such that the equilibrium constants would span three orders of magnitude, instead of the experimental results – which do not vary by even one order of magnitude.43 We did investigate using the Boltzmann distribution to weight the theoretical ΔG-qh-tr values according to the stability of isomeric product vs. reactant ion-pairs located by theory but the results did not change significantly (see ESI†).
DFT calculations predict these equilibria involve dissociation of Me3Al from an OSIP to form a CIP in all three cases (see Fig. 3). For the EBI system where the ligand can adopt forward vs. backward conformations,44 we note that the thermodynamically most stable OSIP and CIP adopt the backward conformation. The CIP differ significantly in their geometry about Zr in the three different complexes, reflecting differing interactions with the counter-anion. Only in the case of the Cp2 system can the anion be considered mono-dentate with a short Zr–F distance of 2.313 Å. There are two other quite long Zr–F contacts of 3.456 and 3.644 Å though both lie within the sum of the crystallographic van der Waals radii of the two elements (∼3.98 Å).46 In the case of the Me2CCp2 system, the anion can be considered bidentate with two short Zr-o-F distances of 2.349 and 2.739 Å involving different C6F5 rings. The longest Zr–F distance involves the central coordination site for an idealized Cp2ZrL3 geometry.47 The EBI system is intermediate between these extremes with one short (Zr-o-F = 2.335 Å) and one longer (Zr-m-F = 3.117 Å) contact involving the same C6F5 ring. We should note that similar structures have been detected in simulations involving [Me2SiCp2ZrMe][B(C6F5)4] at a lower level of theory.40 We suspect these different interactions between anion and cation lead to the larger spread in free energy differences for the different ligands, while the experimental results suggest the involvement of species in which the effect of the anion has been mitigated to some extent.
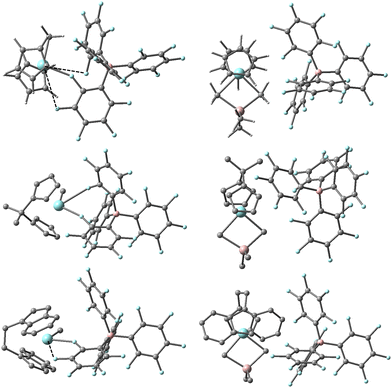 | ||
| Fig. 3 Most stable structures of [L2ZrMe][B(C6F5)4] (L2 = Cp2,45 Me2CCp2 and EBI, left) and [L2ZrMe2AlMe2][B(C6F5)4] (right) based on Gibbs energy (ΔG-qh-tr) at the M062-X/TZVP level of theory. Zr and F in blue, Al and B in pink, C in grey, H omitted from lower two structures for clarity. Long Zr–F contacts are shown as dashed lines. | ||
We thus considered specific solvation of reactant vs. product ion-pairs by benzene. We found that both the Zr cation and the anion were susceptible to specific solvation, though inclusion of two benzene moieties led to results that were not significantly different compared to just one (Table 5, entry 7 vs. 8). In some CIP structures the coordinated benzene was also involved in arene-perfluoroarene interactions with the anion48 (see ESI,†e.g. [Cp2ZrMe][B(C6F5)4]-benzene isomer 2). Inclusion of specific solvation has the desired effect as we move closer to experiment in all three cases, where the differences now result in Kd values that differ by less than 160 at 313 K. We should temper this positive result by stating that binding of benzene to the thermodynamically most stable CIP (and also OSIP) is endergonic with ΔG-qh-tr = 6.7 to 16.1 kJ mol−1 for the equilibrium:
| [L2ZrMe][B(C6F5)4] + C6H6 ⇌ [L2ZrMe(C6H6)] [B(C6F5)4] |
However, since we underestimate the Me6Al2-C6H6 interaction energy at the M06-2X/TZVP level of theory by 5.7 kJ mol−1 (Table 4), it is probable that we underestimate enthalpy changes at least by the same amount for equilibria of this type. We hesitate to apply any quantitative correction and conclude that specific solvation is undoubtedly important.
Dissociation of [(L2ZrMe)2Me]+
Our third and final test equilibrium is dissociation of Cp′′2ZrMe2 from [(Cp′′2ZrMe)2μ-Me][MePBB] (Cp′′ = 1,2-Me2C5H3, PBB = tris-(perfluorobiphenyl)borane) in toluene.49 This dinuclear ion-pair was fully characterized in solution and the solid state. The dinuclear cation features an s-gauche geometry15 with a dihedral angle Me–Zr⋯Zr–Me angle φ = 108.5° and a near linear geometry for the μ-Me bridge (∠ZrMeZr = 170.9°). However, we find in the presence of the counter-anion in gas phase and toluene continuum that a syn isomer with ∠ZrMeZr = 171.0° and φ = 37.7° (Fig. 4) is most stable electronically, compared to two anti stereoisomers with ΔE = 7.4 and 9.0 kJ mol−1. The higher energy of these corresponded to the X-ray structure.In comparing the two structures, it is obvious that the theoretical structure has a much closer contact of the anion with the cation, as would be expected for an isolated ion-pair in gas or condensed phase in a low dielectric medium.
In earlier work, several limiting conformers were located for dinuclear cations of this type with the stability of the syn isomers (φ < 90°) vs. the anti conformers (φ > 90°) being dependent on ligand structure in gas phase.15,50 Thus, the X-ray structure more closely resembles the situation in gas or condensed phase of an isolated cation, while our DFT results suggest that close contact of anion and cation induces a conformational change in the latter.
In discussing the dissociation equilibrium we considered three anti and syn [(Cp′′2ZrMe)2μ-Me][MePBB] stereoisomers located by theory. The results are summarized in Table 6.
| syn or anti-[(Cp′′2ZrMe)2μ-Me][MePBB] ⇌ Cp′′2ZrMe2 + [Cp′′2ZrMe][Me(PBB)] (Cp′′ = η5-1,2-Me2C5H3, toluene solution, 298 K) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Entry | Isomer | ΔH | ΔH-qh | ΔS | ΔS-qh | ΔS-tr | ΔS-qh-tr | ΔG | ΔG-qh | ΔG-tr | ΔG-qh-tr |
| a ΔG and ΔH in kJ mol−1, ΔS in J mol−1 K−1 with estimated standard deviation in parentheses where applicable. b Geometry corresponds to the X-ray structure.49 | |||||||||||
| 1 | syn | 53.4 | 59.3 | 173 | 236 | 126 | 190 | 1.3 | −11.1 | 15.1 | 2.7 |
| 2 | anti | 46.3 | 50.7 | 198 | 245 | 151 | 198 | −13.2 | −22.3 | 0.6 | −8.4 |
| 3 | anti | 42.9 | 48.5 | 154 | 247 | 107 | 200 | 2.9 | −25.0 | 10.9 | −11.2 |
| Experiment | 42.9(8) | 42.9(8) | 110(17) | 110(17) | 110(17) | 110(17) | 10.1(2) | 10.1(2) | 10.1(2) | 10.1(2) | |
When it comes to ΔH the experimental result is significantly lower than theory would indicate for the syn stereoisomer, while better agreement is seen for either anti stereoisomer, especially that corresponding to the X-ray structure. We thus hypothesize that rotamers of both types are present in toluene solution, and to the extent that anti isomers contribute to the dissociation equilibrium, one can expect the ΔH to decrease. We do note that correction for low energy vibrations in all cases moves ΔH-qh away from experiment.
Similarly, ΔS-qh also moves in the wrong direction, away from both experiment when lower energy vibrations are approximated for in this case. The poor agreement between calculated and experimental entropy may be related to the somewhat arbitrary cut-off frequency of 100 cm−1. For example, using 50 and 150 cm−1 cut-offs for the syn stereoisomer, ΔS-qh = 180 and 218 J mol−1 K−1, respectively. Based on these numbers, it is clear how sensitive the vibrational entropy really is for systems of this size and complexity. In fact, if we just correct for the translational entropy, we obtain estimates of ΔS-tr that are in reasonable agreement with experiment, while inclusion of both translation and vibrational entropy corrections moves us further away.
We did locate six low energy isomers of the product ion-pair [Cp′′2ZrMe][Me(PBB)] within 10 kJ mol−1 of the minimum and also the neutral Cp′′2ZrMe2 by-product can adopt two low energy conformations in toluene continuum, both involving rotations about the Cp′ rings. In this case, use of the ΔG-tr values, which seem especially close to experiment, weighted by the Boltzmann distribution leads to an averaged value ΔG-tr = 15.3 kJ mol−1. However, it was prohibitive to locate all low energy isomers of the dinuclear ion-pair, due to the presence of many low energy conformations available to the 1,2-Me2C5H3 rings (with each a five-fold rotor there are 54 = 625 unique conformers in the presence of the anion). Similarly, treatment of specific solvation by toluene is much more complicated in this case given these distinguishing features. Hence, a more exact treatment is not possible.
Conclusions
Taking this all together, we have shown that experimental reaction enthalpies are well produced by the M06-2X/TZVP method, both in gas-phase and in solution, provided in the latter case that specific solvent interactions are taken into consideration. However, entropy and hence free energy poses a great challenge for theory, and even more so in solution.To understand the difficulty in accurate calculation of entropy, the vibrational, translational, and rotational contributions must be studied separately. Concerning vibrations, low-energy (<100 cm−1) normal modes make a significant contribution to entropy at room temperature, but since they cannot be calculated to precision using a harmonic oscillator approximation, the resulting entropies vary widely even within different conformers without genuine physical significance. A partial remedy for this general problem is to get rid of the low-energy normal modes using a quasi-harmonic entropy correction, e.g., by raising each of them to the same energy (e.g., 100 cm−1). This approach improves accuracy for small systems such as those involved in R6Al2 dissociation equilibrium (Table 1). However, as demonstrated for dissociation of [(Cp′′2ZrMe)2μ-Me][MePBB] (Table 6), it is troublesome for complicated systems, such as reactions involving ion pairs, because the number of low-energy vibrations is so large (for the reactant there are >30 normal modes below the arbitrary threshold of 100 cm−1) that the quasi-harmonic correction leads to significant artificial lowering of the total entropy, and as consequence, to significant increase in the reaction entropy in this specific case.
Entropy is reduced on moving from gas-phase to solution, which mostly originates from suppression of translations. Since this is neglected by the polarizable continuum model calculations, it needs to be considered separately. We evaluated two previously proposed approaches, which produced consistent entropy reductions, though not quite large enough to quantitatively match with the experimental observations.
Finally, we note that although the primary motivation of this work was to set up the path for detailed computational investigation of metallocene-MAO catalyst activation, the expressed concerns regarding entropy computations should be considered universal. The arbitrariness of vibrational entropy and its consequences on free energy of large systems need to be recognized, and methodologies for reliable calculation of solution entropy require further consideration.
Experimental section
DFT calculations
Geometry optimizations and electronic energy calculations were employed by the M06-2X density functional,7 in conjunction with the TZVP basis set.8 Interaction energies summarized in Table 4 employed in addition the MN15 density functional32 in combination with a def2-TZVP33 or def2-TZVPD34 basis set, and frozen-core CCSD(T)/def2-TZVPD single point calculations carried out at MP2/def2-TZVPD optimized geometries. Relativistic effective core potential of 28 electrons was used to describe the core electrons of Zr.55 Polarizable continuum model calculations were employed by the integral equation formalism variant (IEFPCM).30 We also tested the SMD variation of IEFPCM,51 with similar results, but decided to abandon it due to significant convergence issues. Stationary points were confirmed as minima by harmonic vibrational frequency calculations. All calculations were carried out using Gaussian 16.52Quasi-harmonic corrections to the entropy14 and enthalpy23 were employed using cut-off frequency of 100 cm−1 and corrections to reduced translational entropy in solution were calculated by the method described by Whitesides et al.19 All the corrections were employed using the Goodvibes script,53 modified to include molarities and molecular volumes of the solvents, which were required for calculation of free accessible space.54
Author contributions
M. L. carried out the quantum chemical calculations. M. L. and S. C. jointly aligned theory with experiments and co-wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. L. acknowledges the Academy of Finland Flagship Programme, Photonics Research and Innovation (PREIN), decision 320166. Computations were made possible by use of the Finnish Grid and Cloud Infrastructure resources (urn:nbn:fi:research-infras-2016072533).Notes and references
- Recent aluminoxane literature: (a) A. F. R. Kilpatrick, H. S. Geddes, Z. R. Turner, J.-C. Buffet, A. L. Goodwin and D. O'Hare, Catal. Sci. Technol., 2021, 11, 5472–5483 RSC; (b) R. Tanaka, M. Nishizono, Y. Nakayama and T. Shiono, Polym. J., 2021, 53, 1187–1193 CrossRef CAS; (c) T. V. Tyumkina, D. N. Islamov, P. V. Kovyazin and L. V. Parfenova, Mol. Catal., 2021, 512, 111768 CrossRef CAS; (d) F. Zaccaria, C. Zuccaccia, R. Cipullo, P. H. M. Budzelaar, A. Macchioni, V. Busico and C. Ehm, Eur. J. Inorg. Chem., 2020, 1088–1095 CrossRef CAS; (e) F. Zaccaria, P. H. M. Budzelaar, R. Cipullo, C. Zuccaccia, A. Macchioni, V. Busico and C. Ehm, Inorg. Chem., 2020, 59, 5751–5759 CrossRef CAS PubMed; (f) J. V. Lamb, J.-C. Buffet, Z. R. Turner and D. O'Hare, Macromolecules, 2020, 53, 929–935 CrossRef CAS; (g) A. F. R. Kilpatrick, N. H. Rees, Z. R. Turner, J. C. Buffet and D. O'Hare, Physicochemical surface-structure studies of highly active zirconocene polymerisation catalysts on solid polymethylaluminoxane activating supports, Mater. Chem. Front., 2020, 4, 3226–3233 RSC; (h) V. E. Teixeira and P. R. Livotto, J. Mol. Graphics Modell., 2020, 99, 107626 CrossRef CAS PubMed; (i) M. E. Z. Velthoen, J. M. Boereboom, R. E. Bulo and B. M. Weckhuysen, Catal. Today, 2019, 334, 223–230 CrossRef CAS; (j) M. E. Z. Velthoen, A. Muñoz-Murillo, A. Bouhmadi, M. Cecius, S. Diefenbach and B. M. Weckhuysen, Macromolecules, 2018, 51, 343–355 CrossRef CAS PubMed; (k) Z. Falls, E. Zurek and J. Autschbach, Phys. Chem. Chem. Phys., 2016, 18, 24106–24118 RSC.
- Reviews: (a) H. S. Zijlstra and S. Harder, Eur. J. Inorg. Chem., 2015, 19–43 CrossRef CAS; (b) W. Kaminsky, Macromolecules, 2012, 45, 3289–3297 CrossRef CAS; (c) M. Bochmann, Organometallics, 2010, 29, 4711–4740 CrossRef CAS; (d) E. Y.-X. Chen and T. J. Marks, Chem. Rev., 2000, 100, 1391–1434 CrossRef CAS PubMed.
- See e.g. (a) E. Zurek and T. Ziegler, Prog. Polym. Sci., 2004, 29, 107–148 CrossRef CAS; (b) Z. Boudene, T. De Bruin, H. Toulhoat and P. Raybaud, Organometallics, 2012, 31, 8312–8322 CrossRef CAS; (c) Z. Falls, N. Tymińska and E. Zurek, Macromolecules, 2014, 47, 8556–8569 CrossRef CAS.
- (a) L. Negureanu, R. W. Hall, L. G. Butler and L. A. Simeral, J. Am. Chem. Soc., 2006, 128, 16816–16826 CrossRef CAS PubMed; (b) M. Linnolahti, J. R. Severn and T. A. Pakkanen, Angew. Chem., Int. Ed., 2008, 47, 9279–9283 CrossRef CAS PubMed; (c) R. Glaser and X. Sun, J. Am. Chem. Soc., 2011, 133, 13323–13336 CrossRef CAS PubMed; (d) M. Linnolahti, A. Laine and T. A. Pakkanen, Chem. – Eur. J., 2013, 19, 7133–7142 CrossRef CAS PubMed; (e) J. T. Hirvi, M. Bochmann, J. R. Severn and M. Linnolahti, ChemPhysChem, 2014, 15, 2732–2742 CrossRef CAS PubMed.
- S. Collins, A. Joshi and M. Linnolahti, Chem. – Eur. J., 2021, 27, 15460–15471 CrossRef CAS PubMed.
- M. Linnolahti and S. Collins, ChemPhysChem, 2017, 18, 3369–3374 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- C. Ehm, G. Antinucci, P. H. M. Budzelaar and V. Busico, J. Organomet. Chem., 2014, 772–773, 161–171 CrossRef CAS.
- (a) H. S. Zijlstra, A. Joshi, M. Linnolahti, S. Collins and J. S. McIndoe, Eur. J. Inorg. Chem., 2019, 2346–2355 CrossRef CAS; (b) H. S. Zijlstra, M. Linnolahti, S. Collins and J. S. McIndoe, Organometallics, 2017, 36, 1803–1809 CrossRef CAS; (c) S. Collins, M. Linnolahti, M. G. Zamora, H. S. Zijlstra, M. T. R. Hernández and O. Perez-Camacho, Macromolecules, 2017, 50, 8871–8884 CrossRef CAS; (d) T. K. Trefz, M. A. Henderson, M. Linnolahti, S. Collins and J. S. McIndoe, Chem. – Eur. J., 2015, 21, 2980–2991 CrossRef CAS PubMed; (e) T. K. Trefz, M. A. Henderson, M. Wang, S. Collins and J. S. McIndoe, Organometallics, 2013, 32, 3149–3152 CrossRef CAS.
- (a) D. E. Babushkin, N. V. Semikolenova, V. N. Panchenko, A. P. Sobolev, V. A. Zakharov and E. P. Talsi, Macromol. Chem. Phys., 1997, 198, 3845–3854 CrossRef CAS; (b) I. Tritto, C. Méalares, M. C. Sacchi and P. Locatelli, Macromol. Chem. Phys., 1997, 198, 3963–3977 CrossRef CAS.
- H. S. Zijlstra, A. Joshi, M. Linnolahti, S. Collins and J. S. McIndoe, Dalton Trans., 2018, 47, 17291–17298 RSC.
- (a) A. Joshi, S. Collins, M. Linnolahti, H. S. Zijlstra, E. Liles and J. S. McIndoe, Chem. – Eur. J., 2021, 27, 8753–8763 CrossRef CAS PubMed; (b) S. Collins, G. Hasan, A. Joshi, J. S. McIndoe and M. Linnolahti, ChemPhysChem, 2021, 22, 1326–1335 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- S. Collins and M. Linnolahti, ChemCatChem, 2022, 14, e202101918 CrossRef CAS and references therein.
- See e.g. (a) J. N. Harvey, F. Himo, F. Maseras and L. Perrin, ACS Catal., 2019, 9, 6803–6813 CrossRef CAS; (b) M. Besora, P. Vidossich, A. Lledós, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392–1399 CrossRef CAS PubMed; (c) L. Falivene, V. Barone and G. Talarico, Mol. Catal., 2018, 452, 138–144 CrossRef CAS.
- (a) S. Tobisch and T. Ziegler, J. Am. Chem. Soc., 2004, 126, 9059–9071 CrossRef CAS PubMed; (b) F. Zaccaria, C. Ehm, P. H. M. Budzelaar and V. Busico, ACS Catal., 2017, 7, 1512–1519 CrossRef CAS; (c) F. Zaccaria, R. Cipullo, P. H. M. Budzelaar, V. Busico and C. Ehm, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 2807–2814 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- M. Mammen, E. I. Shakhnovich, J. M. Deutch and G. M. Whitesides, J. Org. Chem., 1998, 63, 3821–3830 CrossRef CAS.
- See. J. J. Eisch, in Comprehensive Organometallic Chemistry, ed. G. Wilkinson, F. G. A. Stone and E. W. Abel, Pergamon Press, London, 1982, vol. 1, ch. 6, pp. 555–682 Search PubMed.
- (a) C. H. Henrickson and D. P. Eyman, Inorg. Chem., 1967, 6, 1461–1465 CrossRef CAS; (b) A. W. Laubengayer and W. F. Gilliam, J. Am. Chem. Soc., 1941, 63, 477–479 CrossRef CAS.
- L. A. Watson and O. Eisenstein, J. Chem. Educ., 2002, 79, 1269–1277 CrossRef CAS.
- Y.-P. Li, J. Gomes, S. M. Sharada, A. T. Bell and M. Head-Gordon, J. Phys. Chem. C, 2015, 119, 1840–1850 CrossRef CAS.
- W. F. Gilliam, PhD thesis, Cornell University, 1939.
- M. B. Smith, J. Organomet. Chem., 1972, 46, 31–49 CrossRef CAS.
- In terms of G-qh, we calculated the C2h-symmetric minimum 4.5 kJ mol−1 higher, and two C1-symmetric minima 4.6 and 6.6 kJ mol−1 higher than the Cs-symmetric minimum, see: L. Verrieux, J. Thuilliez, F. Jean-Baptiste-dit-Dominique, C. Boisson, M.-N. Poradowski and L. Perrin, ACS Catal., 2020, 10, 12359–12369 CrossRef CAS.
- M. B. Smith, J. Organomet. Chem., 1970, 22, 273–281 CrossRef CAS.
- M. B. Smith, J. Organomet. Chem., 1972, 46, 211–217 CrossRef CAS.
- (a) Z. Černý, S. Heřmánek, J. Fusek, O. Kříẑ and B. Čásenský, J. Organomet. Chem., 1988, 345, 1–9 CrossRef; (b) Z. Černý, J. Fusek, O. Kříẑ, S. Heřmánek, M. Šolc and B. Čásenský, J. Organomet. Chem., 1990, 386, 157–165 CrossRef.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- M. S. Searle and D. H. Williams, J. Am. Chem. Soc., 1992, 114, 10690–10697 CrossRef CAS.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- (a) Y. Wang, P. Verma, X. Jin, D. G. Truhlar and X. He, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10257–10262 CrossRef CAS PubMed; (b) L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- D. S. Matteson, Organometallic Reaction Mechanisms of the Non-transition Elements, Academic Press, New York, 1974, ch. 2, pp. 34–58 Search PubMed.
- (a) O. Yamamoto, R. Hayamizu and M. Yanagisawa, J. Organomet. Chem., 1974, 73, 17–25 CrossRef CAS; (b) E. A. Jeffery and T. Mole, Aust. J. Chem., 1973, 26, 739–748 CrossRef CAS; (c) T. L. Brown and L. L. Murrell, J. Am. Chem. Soc., 1972, 94, 378–384 CrossRef CAS; (d) D. S. Matteson, Inorg. Chem., 1971, 10, 1555 CrossRef CAS; (e) C. Ramey, J. F. O'Brien, I. Hasegawa and A. E. Borchert, J. Phys. Chem., 1965, 69, 3418–3423 CrossRef.
- Review: F. Zaccaria, L. Sian, C. Zuccaccia and A. Macchioni, in Advances in Organometallic Chemistry, ed. P. J. Perez, Academic Press, 2020, vol. 73, ch. 1, pp. 1–78 Search PubMed.
- For recent examples see e.g. (a) S. O. Gunther, Q. Lai, T. Senecal, R. Huacuja, S. Bremer, D. M. Pearson, J. C. DeMott, N. Bhuvanesh, O. V. Ozerov and J. Klosin, ACS Catal., 2021, 11, 3335–3342 CrossRef CAS; (b) T. Nakashima, Y. Nakayama, T. Shiono and R. Tanaka, ACS Catal., 2021, 11, 865–870 CrossRef CAS.
- A. Correa and L. Cavallo, J. Am. Chem. Soc., 2006, 128, 10952–10959 CrossRef CAS PubMed.
- L. Sian, A. Dall'Anese, A. Macchioni, L. Tensi, V. Busico, R. Cipullo, G. P. Goryunov, D. Uborsky, A. Z. Voskoboynikov, C. Ehm, L. Rocchigiani and C. Zuccaccia, Organometallics, 2022, 41, 547–560 CrossRef CAS and references therein.
- M. Bochmann and S. J. Lancaster, Angew. Chem., Int. Ed. Engl., 1994, 33, 1634–1637 CrossRef.
- J. M. Camara, R. A. Petros and J. R. Norton, J. Am. Chem. Soc., 2011, 133, 5263–5273 CrossRef CAS PubMed.
- Theory: (a) M. Linnolahti, T. A. Pakkanen, R. Leino, H. J. G. Luttikhedde, C.-E. Wilén and J. H. Näsman, Eur. J. Inorg. Chem., 2001, 2033–2040 CrossRef CAS and references therein; Experiment: (b) F. Piemontesi, I. Camurati, L. Resconi, D. Balboni, A. Sironi, M. Moret, R. Zeigler and N. Piccolrovazzi, Organometallics, 1995, 14, 1256–1266 CrossRef CAS.
- A. Laine, B. B. Coussens, J. T. Hirvi, A. Berthoud, N. Friederichs, J. R. Severn and M. Linnolahti, Organometallics, 2015, 34, 2415–2421 CrossRef CAS.
- S. Alvarez, Dalton Trans., 2013, 42, 8617–8636 RSC.
- J. W. Lauher and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1729–1742 CrossRef CAS.
- C. E. Smith, P. S. Smith, R. Ll. Thomas, E. G. Robins, J. C. Collings, C. Dai, A. J. Scott, S. Borwick, A. S. Batsanov, S. W. Watt, S. J. Clark, C. Viney, J. A. K. Howard, W. Clegg and T. B. Marder, J. Mater. Chem., 2004, 14, 413–420 RSC.
- (a) Y.-X. Chen, M. V. Metz, C. L. Stern and T. J. Marks, J. Am. Chem. Soc., 1998, 120, 6287–6305 CrossRef CAS For earlier work see ref. 42 and. S. Beck, M.-H. Prosenc, H.-H. Brintzinger, R. Goretzki, N. Herfert and G. Fink, J. Mol. Catal. A: Chem., 1996, 111, 67–79 CrossRef CAS.
- W. Meelua, N. Keawkla, J. Oláh and J. Jitonnom, J. Organomet. Chem., 2020, 905, 121024 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- G. Luchini, J. V. Alegre-Requena, Y. Guan, I. Funes-Ardoiz and R. S. Paton, GoodVibes, Version 3.0.1, 2019, DOI:10.5281/zenodo.595246.
- The following molarities (mol dm−3)/molecular volumes (Å3) were used: toluene: 9.4/138.4; benzene: 11.2/116.4; mesitylene: 7.19/181.9; heptane: 6.82/184.1. Volumes were calculated by Gaussian 16 using tight option and an average of ten volume calculations was used.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt01711c |
| ‡ Former address: Department of Chemistry, University of Victoria, 3800 Finnerty Rd. Victoria, BC. |
| This journal is © The Royal Society of Chemistry 2022 |