Water formation on interstellar silicates: the role of Fe2+/H2 interactions in the O + H2 → H2O reaction†
Marc
Serra-Peralta
 ,
Christian
Domínguez-Dalmases
,
Christian
Domínguez-Dalmases
 and
Albert
Rimola
and
Albert
Rimola
 *
*
Departament de Química, Universitat Autònoma de Barcelona, 08193 Bellaterra, Catalonia, Spain. E-mail: albert.rimola@uab.cat
First published on 1st November 2022
Abstract
Water is the most abundant molecule in the solid state of the interstellar medium, and its presence is critically important for life in space. Interstellar water is thought to be effectively synthesised by reactions occurring on the surfaces of interstellar grains, as gas-phase reactions are not efficient enough to justify its high abundance. In the present work, DFT simulations have been performed to investigate the formation of interstellar water through the O + H2 → H2O reaction on olivinic silicate surfaces that contain Fe2+ cations. The surfaces have been modeled adopting both periodic and cluster approaches. This study focuses on: (i) the stability of the surface models as a function of the electronic states (i.e., quintuplet, triplet and singlet) arising from the presence of the Fe2+ centers, (ii) the adsorption of H2 on the silicate surfaces and its likely activation due to the Fe2+/H2 interactions, and (iii) characterising the energy profiles of the H2O formation reaction complemented with kinetics that include tunneling effects. The results indicate that quintuplet is the most stable electronic state in all the bare surface models. H2 adsorption, however, does not show a clear trend on the relative stabilities of the H2/surface complexes with the electronic states, which is in general more favourable on singlet state surfaces. Finally, reactions simulated on the periodic surfaces show elementary high energy barriers but the reaction is kinetically feasible (considering the long lifetime of interstellar clouds) due to the dominance of tunnelling. In contrast, in the nanocluster models, tunneling effects cannot contribute due to the presence of endoenergetic elementary steps. It is predicted that the reactions on the nanoclusters are only possible if the energy released during the adsorption of the O atom is used to overcome the energy barriers.
1 Introduction
The interstellar medium (ISM) is the dilute matter and radiation that fill the space between stars. It plays a central role in the formation of stellar systems and galaxies because it is involved in different phases of their life cycles.1,2 As a result, these astrophysical regions are inhomogeneous, with temperatures ranging from 10 to more than 106 K, and atomic densities from 10−4 to 108 cm−3.3The matter of the ISM, which aggregates forming the so-called interstellar clouds, is found in the gas-phase state and in the form of solid-state dust grains. In the gas phase, more than 240 species have been detected through rovibrational and IR emission observations,4 of which the H2 molecule is the most abundant. Depending on the C/O ratio at which they form, the dust grains are built up by refractory materials of carbonaceous materials or silicates. The main families of interstellar silicates are pyroxenes and olivines,5 with general compositions of MgxFe(1−x)SiO3 and Mg2xFe(2−2x)SiO4 (with x = 0–1). These dust particles lock up nearly 100% of the silicon, magnesium and iron, and around 30% of the oxygen.6 Although their mean size is about 0.1 μm, the majority of the surface available for heterogeneous reactions comes from the 0.001 μm-sized grains.7 Commonly, interstellar grain silicates are structurally amorphous (although crystalline silicates have also been identified8,9) and, thus, the outer surface morphology and composition of the grains depend on the type of the interstellar cloud where they are found. Most of the surface sites are suited for physisorption, but there is also space for chemisorption, depending on the nature of the interactions between the adsorbate species and the surface binding sites.10–12
Interstellar clouds can be divided into several types, depending on their size, temperature, density and chemical composition.13,14 Diffuse clouds are characterized to have temperatures ≤80 K and atomic densities ∼102 cm−3. In contrast, dense molecular clouds are colder (10 K) and denser (∼104 cm−3) regions, which are created by the accumulation of mass in the center of a diffuse cloud, known as the pre-stellar phase in a star's life cycle.1 In diffuse clouds, the dust particles are usually referred to as core grains as they are composed of naked refractory materials. In contrast, in the dense clouds, the refractory materials are covered by ices, primarily of H2O, which forms and grows in situ through reactions occurring on the grains surfaces.15,16 In addition to H2O, icy mantles can also contain other volatile molecules,17 like CO, CO2, NH3, CH4, and CH3OH, which are predicted to be the result of hydrogenation and oxidation of the dominant atoms and molecules in the gas phase (O, C, N and CO).18,19 It has been estimated that a typical 0.1 μm-sized silicate grain core is surrounded by about 100–250 monolayers of water ice,3 hence creating a mantle of ∼0.02 μm.1 However, recent findings indicate that, due to the porous and inhomogeneous surfaces of the core grains, ices do not fully cover the refractory cores, hence being partly exposed to the environmental gas, also in dense clouds.20
Water is the most abundant solid-state component in the ISM17,21–23 and, as aforementioned, it is mostly found covering the core grains in the form of ice. The abundance of interstellar gas-phase water is different depending on the regions of the ISM, as the rate of ice sublimation and desorption varies with temperature, leading to densities <10−8 to >10−4 with respect to H2.22,24,25 As solid and gas, water takes out most of the elemental oxygen, in which the chemical composition of these regions is governed by how the available oxygen is used to form other species.6,26,27 The importance of interstellar water is also due to its crucial role in life: its presence is considered a mandatory criterion for the habitability of exoplanets.28,29 Therefore, studying the evolution of the dust grains in protoplanetary discs (prior to planet formation) including the presence of water ice is of paramount importance,30 and the formation of water in astrophysical environments is a research subject of fundamental interest.
Interstellar water can be produced through gas-phase and surface chemical reactions.6 In the gas phase, two main synthetic routes are considered: (1) low-temperature ion-neutral, and (2) high-temperature neutral–neutral31 reactions. However, it has been long recognized that the large abundances of interstellar water cannot properly be explained by only gas-phase reactions and, therefore, it is considered to be efficiently synthesized by reactions occurring on the surfaces of grains.6,18
The different proposed paths through which water can be produced are summarized in Fig. 1. In general, they can be based on: (i) reaction of H (the most abundant gas-phase atomic species in ISM), mostly to O, O2, and O3 (although as yet there is no evidence of the presence of interstellar ozone4), and (ii) reaction of H2 (the most abundant gas-phase molecular species in ISM), mostly with O and OH. Different experimental studies have investigated these possible pathways in interstellar clouds (see Table 1). Most of them are centered on the reaction of O2 + H, which leads to mainly H2O through H2O2 as the intermediate. In addition, for some of these reactions, the effective rate constants have been estimated32 and analyzed via astrochemical modeling.33
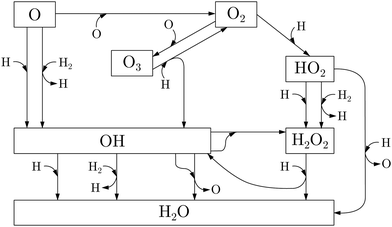 | ||
| Fig. 1 Scheme of the chemical reaction network relative to the H2O formation on interstellar grain surfaces. Adapted from.1,2,6 | ||
| Reaction | Method | T surface (K) | Observed products | Ref. |
|---|---|---|---|---|
| O + H | Sequential deposition of plasma-activated N2O and D2 | 12 | D2O | 34 |
| Co-deposition of microwave-discharged O2 and D2 | 10 | HDO, D2O | 35 | |
| Co-deposition of microwave-discharged 18O2 and D2 | 15–25 | D2O, D2O2, O3 | 36 | |
| O2 + H | Exposure of microwave-discharged H2 to solid O2 | 20 | 37 | |
| Exposure of microwave-discharged H2 (D2) to solid O2 | 10 | H2O2, H2O (D2O2, D2O) | 38 | |
| Exposure of microwave-discharged H2 (D2) to solid O2 | 12–28 | H2O2, H2O (D2O2, D2O) | 39 | |
| Exposure of microwave-discharged H2 to solid O2 | 15–27 | H2O2, H2O, O3 | 40 | |
| Co-deposition of microwave-discharged H2 and molecular O2 gas | 10–40 | H2O2, H2O | 41 | |
| Co-deposition of microwave-discharged H2 and molecular O2 gas | 15–25 | H2O2, H2O, O3, HO2 | 42 | |
| Co-deposition of microwave-discharged D2 and molecular O2 gas | 10 | D2O2, D2O | 43 | |
| O3 + H | Exposure of microwave-discharged H2 to solid O3 | 10 | H2O, H2O2 | 44 |
| Exposure of microwave-discharged H2 (D2) to solid O3 | 25–50 | H2O, H2O2 (D2O, D2O2) | 45 | |
| OH + H2 | Co-deposition of H2 gas and microwave-discharged H2O | 10 | H2O, H2O2, O3 | 46 |
| OH + OH | Deposition of microwave-discharged H2O | 40–60 | H2O, H2O2, O3 | 47 |
| Deposition of microwave-discharged H2O with rare gases | 3.5–30 | OH, HO2, H2O | 48 |
At variance with the extensive experimental work, theoretical studies are practically missing, the available works mainly addressing the adsorption of water on silicate surfaces by means of classical potential or quantum chemical methods.49–54 An interesting study on water formation was published by Goumans et al.55 The authors investigated the hydrogenation of atomic O by means of QM/MM simulations using a cluster model of 34 atoms mimicking a Mg2SiO4 (010) silicate surface. Results indicated that the reaction steps are exoergonic with low activation energies (below 7 kcal mol−1). Another similar study was done by Molpeceres et al.,12 which characterized the potential energy surfaces of the hydrogenation of atomic O using a periodic model for the (010) Mg2SiO4 surface, including a kinetic study, showing the relevance of tunneling effects. Other theoretical studies investigated the formation of H2O on the surfaces of water ice mantles,56,57 instead of silicate surfaces. The authors also included a kinetic study to evaluate the tunneling effect, which was also shown to be of great importance.
In view of the lack of theoretical studies addressing the interstellar H2O formation, the scope of this work is to investigate the formation of interstellar water adopting the reaction of
| H2(surf) + O(surf) → H2O(surf) |
2 Methods
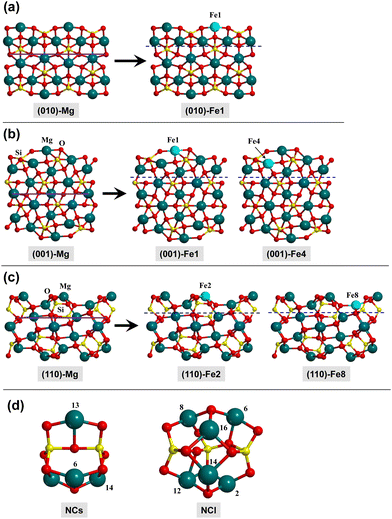
In this work, the olivine surfaces have been modelled adopting both periodic and cluster approaches.The periodic surfaces were based on the crystalline (010), (001), and (110) Mg2SiO4 surfaces, previously used by some of us.10,12,58 For each surface, the Mg2+ cations placed at the outermost positions of the surfaces were replaced by Fe2+, thus generating olivine surfaces containing one Fe center in the unit cell. This procedure has given rise to five different Fe-containing olivine surfaces, hereafter referred to as: (010)-Fe1, (001)-Fe1, (001)-Fe4, (110)-Fe2, and (110)-Fe8. All the periodic surfaces contain 56 atoms in the unit cell. Fig. 2(a)–(c) show the original Mg2SiO4 surfaces and the resulting Fe-containing slab models.
The periodic surfaces have been computed using the CRYSTAL17 code,59 an all electron program that performs full periodic simulations adopting Gaussian-type orbitals centered to the atoms. Periodic calculations were performed using the hybrid B3LYP60,61 density functional in combination with the D3(BJ)62,63 empirical correction for dispersion interactions. In previous works by some of us12,64 as well as in others dealing with silicates theoretically,65–68 it is shown that B3LYP performs pretty well for the modeling of this kind of systems and simulation of their physico-chemical properties. Moreover, the inclusion of dispersion forces is of fundamental importance to properly describe the interaction of H2 with silicate surfaces.10,58
The lattice parameters of the optimized surfaces (both the Mg2SiO4 and the Fe-substituted analogues) are summarized in the ESI.† Geometry optimizations of the H2/surface complexes and of the stationary points of the H2O formation reaction were carried out keeping the optimized cell parameters of the bare surfaces fixed and, accordingly, only the positions of the internal atoms were optimized through the analytic and energy gradients. The shrinking factor for the net of the reciprocal space was set to 3, requiring diagonalizing the Hamiltonian matrix in 5 k points. The SCF convergence was set to 10−7 Hartree, and the overlap integrals that control the Coulomb and exchange series to 10−6 and 10−16. Zero-point energy (ZPE) and thermal corrections to the calculated energetics were computed through the application of standard statistical thermodynamics formulae within the harmonic approximation. Frequencies were computed at the Γ point by diagonalizing the mass-weighted matrix. In CRYSTAL, this is done by numerical differentiation of the first-energy derivatives, in which for a given equilibrium geometry, the nuclear positions are displaced by 0.003 Å. To save computational cost, and considering that surface regions not involved in the adsorption/reactions remain unperturbed along the processes, this has been done considering a fragment of the surfaces (defined by the blue dashed lines in Fig. 2).
The cluster models are based on two nanoclusters previously described by Zamirri et al.:69 Mg4Si2O8 and Mg6Si3O12 (see Fig. 2(d)), hereafter referred to as NCs (small nanocluster) and NCl (large nanocluster), respectively. To generate Fe-containing nanoclusters, a Mg atom was replaced by a Fe one. The resulting structures have been named NCs-FeX and NCl-FeX, where X is the label of the substituted Mg atom (see Fig. 2(d) for these labels). Accordingly, the substitution in NCs leads to three different nanoclusters (NCs-Fe6, NCs-Fe13 and NCs-Fe14), and substitution in NCl leads to six nanoclusters (NCl-Fe2, NCl-Fe6, NCl-Fe8, NCl-Fe12, NCl-Fe14 and NCl-Fe16).
Calculations for the nanoclusters have been done with the Gaussian 16 programs package.70 Since Fe-containing nanoclusters have not been reported yet in the literature (and accordingly no methodological benchmark is available), in this work, the B3LYP-D3(BJ) method has been used, alongside the meta-hybrid M06-2X71 complemented with the D3 dispersion correction (M06-2X-D3). The employed basis set has been the 6-311++G(d,p) one. For the sake of accuracy, in some selected cases, single point energy calculations on the optimized-B3LYP-D3(BJ) geometries have been performed at the CCSD(T) level72 using an aug-cc-VTZ basis set (see below, in the Nanoclusters Section, the details on these selected cases). Nanocluster-based structures were characterized by the analytical calculation of the harmonic frequencies. ZPE-corrected values were obtained including thermochemical corrections computed at the B3LYP-D3(BJ) level resulting from the standard rigid-rotor/harmonic-oscillator treatment.
Due to the very low temperatures at which the reactions under study take place (namely, 80–100 K, in the diffuse clouds), and the fact that in the reactions H atoms participate, tunneling effects are expected to be of paramount importance. Accordingly, rate constants accounting for tunneling adopting a semi-classical approach, kSC (T), have been computed through the Eyring equation:73
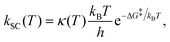 | (1) |
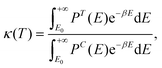 | (2) |
3 Results and discussion
Results of this work are centered on the following aspects, for both the periodic surfaces and the nanocluster systems. First, the relative stabilities of the bare Fe-containing silicates as a function of the electronic state (which arise from the presence of one Fe2+ cation on at the surface) are studied. Then, the adsorption of H2 on the Fe2+ center is performed, calculating the adsorption energies and considering the different electronic states. Finally, for one periodic surface and one nanocluster model, the reactivity towards H2O formation is simulated, including the calculation of semi-classical rate constants associated with the different elementary steps. This section starts with the results for the periodic surfaces and then is followed by the results for the nanoclusters.3.1 Periodic surfaces
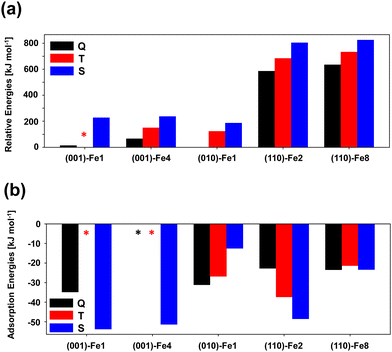
The presence of one Fe2+ metal center in the unit cell of the slab surfaces gives rise to the following different electronic states: quintuplet (Q), triplet (T), and singlet (S). In a previous study by some of us,10 it was found that, for the crystalline (010) olivine surface containing a Fe2+ cation in the outermost positions, the electronic states follow the relative trend of (from more to less stable): Q > T > S. In the present work, we have performed the same stability study with the other Fe-containing surfaces. The obtained results are shown in Fig. 3. Unfortunately, the (001)-Fe1 T surface has not been possible to compute due to convergence energy problems, and cannot be reported in the graphs (labelled by an asterisk). As for the (010) olivine surface, the overall trend is the same: the Q high spin states are more stable than the T states, which in turn are more stable than the S states. This is in agreement with the fact that transition-metal unsaturated coordinations stabilize high spins versus low spins (or what is the same, saturated coordinated environments stabilize low spin states due to the large splitting of the 3d orbitals). For a given electronic state, the relative surface stabilities are in the following order (from more to less stable): (010) > (001) > (110), the same trend as for the Mg-pure analogue surfaces.58 This is because the (010) surface presents less unstable point defects (in this case, less unsaturated metal centers placed on the top of the surface) with respect to the other surfaces, which present more unsaturated metal centers and/or metal centers with less coordination numbers.H2 adsorption on Fe-containing olivine surfaces has been studied. Fig. 4 presents the structures of the optimized complexes, Table 2 reports the computed adsorption energies alongside interesting structural and vibrational parameters, and Fig. 3(b) is the trend of the adsorption energies as a function of the surface type and the electronic state.
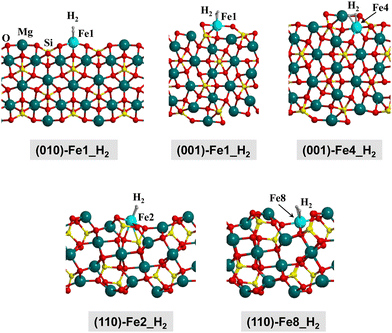 | ||
| Fig. 4 B3LYP-D3(BJ)-optimized complexes for the H2 adsorption on the Fe-containing olivine surfaces. Since the complexes in the Q, T and S electronic states do not present significant structural changes, here we only show the complexes at the S state for a qualitative view. Energetic, structural and vibrational parameters of all the complexes are reported in Table 2. | ||
| Surface | State | d(H–H) | d(Fe–H) | ν(H–H) | ΔEads |
|---|---|---|---|---|---|
| (010)-Fe1 | Q | 0.786 | 1.844/1.829 | 3698 | −31.2 |
| T | 0.783 | 1.777/1.758 | 3796 | −26.9 | |
| S | 0.791 | 1.716/1.722 | 3592 | −12.5 | |
| (001)-Fe1 | Q | 0.772 | 1.915/1.897 | 3925 | −34.9 |
| T | — | — | — | — | |
| S | 0.792 | 1.672/1.730 | 3608 | −53.8 | |
| (001)-Fe4 | Q | — | — | — | — |
| T | — | — | — | — | |
| S | 0.816 | 1.686/1.626 | 3294 | −51.4 | |
| (110)-Fe2 | Q | 0.769 | 1.972/1.989 | 3953 | −22.8 |
| T | 0.783 | 1.982/2.004 | 3828 | −37.4 | |
| S | 0.799 | 1.657/1.647 | 3556 | −48.6 | |
| (110)-Fe8 | Q | 0.756 | 2.189/2.279 | 4117 | −23.5 |
| T | 0.776 | 1.916/1.867 | 3898 | −21.4 | |
| S | 0.793 | 1.703/1.672 | 3600 | −23.3 |
In relation to the adsorption energies, there is no clear trend here with the electronic state. For the most stable (010)-Fe1 surface, the relative stability of the electronic states when an H2 molecule adsorbs on the Fe2+ center is kept with respect to the bare surface (Q > T > S). In contrast, for (110)-Fe2 and (001)-Fe1, the trend is the opposite (Q < T < S), while for (001)-Fe8, the three electronic states present similar stabilities (the S state being the most stable one). Thus, it seems that the adsorption of H2 exerts important changes in the electronic structure of the olivine surfaces. It is worth mentioning that, in the (001)-Fe4 Q and T surfaces, the H2 adsorption was not possible because the H2 molecule, during the geometry optimization, moves towards a nearby Mg2+ metal center. In this surface, the Fe2+ cation is somewhat buried and, since the H2 interaction with Fe2+ in these electronic states are weak (by analogy with the (001)-Fe1 surface), H2 prefers to interact with the outermost Mg2+ cation. This does not happen on the (001)-Fe4 S surface because the Fe2+/H2 interactions in this electronic state are strong enough (ca. 50 kJ mol−1) to retain H2 on the Fe2+ center.
For the set of computed adsorption complexes, the Fe2+/H2 interaction has also been assessed by analysing the H–H and Fe–H distances, and the ν(H–H) frequency (reported in Table 2). In general, the S state induces the strongest bathochromic shifts on the ν(H–H) vibration, the largest enlargement of the H–H bond length, and the shortest Fe–H distances. The average values for Q, T and S, respectively, are: ν(H–H) of 3923, 3817 and 3347 cm−1; H–H distances of 0.77, 0.78 and 0.80 Å; and Fe–H distances of 1.99, 1.88 and 1.68 Å.
From the optimized H2/olivine adsorption complexes, we have studied the water formation through the H2 + O → H2O reaction. However, instead of characterising the full potential energy surfaces (PESs) for all the adsorption complexes, we have performed a preliminary energetic assessment. That is, we have computed all the minima stationary points (i.e., reactants, products and intermediates) of the PESs to elucidate if the reactive paths are feasible, at least from a thermodynamic standpoint. This has been useful to rule out those paths that are unfavourable energetically and focus on the most favourable ones. This preliminary energetic assessment, moreover, has been done by taking as pre-reactants the most stable H2/olivine complexes (considering the surface type and the electronic states). That is: (001)-Fe1 S, (001)-Fe4 S, (010)-Fe1 Q, (110)-Fe2 S, and (110)-Fe8 S. The minima stationary points have been computed considering two different mechanisms (Mech1 and Mech2), as represented in Fig. 5. The main difference among the two mechanisms is that, in Mech1, the H2 dissociation occurs before the O adsorption, while in Mech2 it takes place after the O adsorption. A priori, Mech2 has an advantage over Mech1 in that the energy released by the O adsorption can be used to dissociate the H2 on the Fe2+ center.
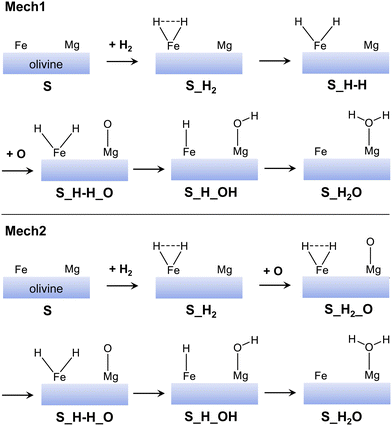 | ||
| Fig. 5 Sketch of the mechanisms adopted in this work for the water formation. In mechanism 1 (Mech1), the H2 dissociation takes place before the O adsorption, while in mechanism 2 (Mech2) after. | ||
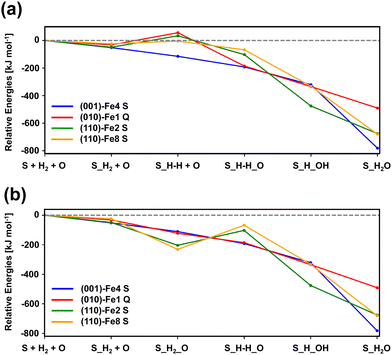
Fig. 6(a) and (b) show the relative stabilities of the computed minima for Mech1 and Mech2, respectively, taking as the 0th reference the “surface + H2 + O(3P)” point (i.e., the asymptote). Computed results indicate that Mech2 is overall energetically more favourable than Mech1: all the computed minima stationary points of Mech2 have negative relative energies, while this is not the case in Mech1 (some of them are positive). Indeed, in the later mechanism, the minima stationary points involving the dissociation of H2, in most of the cases have positive relative energies (they are more unstable than the asymptote), while those in Mech2 are negative. This difference is due to what we anticipated above: the adsorption of atomic O before the dissociation (here adopted in Mech2) is very favorable in such a way that the subsequent H2 dissociation leaves the dissociated complex submerged in energy with respect to the asymptote. For the adsorption of atomic O, it is worth mentioning that, although gas-phase O atom has a 3P electronic state, its adsorption on silicate surfaces renders the singlet state as the most stable one.12 Accordingly, we assume that, in the O adsorption, an inter-system crossing from the triplet (gas-phase) to the singlet (adsorbed) states takes place.
Focusing on the different profiles based on Mech2 (Fig. 6(b)), although all the minima structures are lower than the asymptote, two types of paths can be distinguished: (i) those in which all the elementary steps are exoenergetic (namely, (001)-Fe4 S and (010)-Fe1 Q) and (ii) those in which the H2 dissociation is endoenergetic (namely, (110)-Fe2 S and (110)-Fe8 S). Thus, the first two are more favourable than the latter two. Accordingly, and by considering this preliminary energetic assessment, we decided to compute the full PES towards H2O formation considering the path on the (010)-Fe1 Q surface. The choice is based on (i) all the elementary steps are exoenergetic, and (ii) it is the most stable surface (also considering the spin multiplicity) among the investigated ones (and hence excluding the (001)-Fe4 S one).
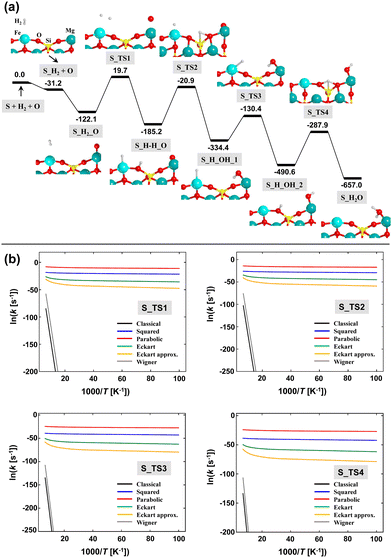
The computed PES (corrected for ZPE) of the O + H2 → H2O reaction adopting Mech2 on the (010)-Fe1 Q surface is shown in Fig. 7(a). According to this mechanism, the first and second steps correspond to the adsorption of H2 on the Fe2+ metal center (structure S_H2) and to the adsorption of the atomic O (Oads) on the Mg2+ cation (structure S_H2_O), respectively. Both steps are barrierless and largely exoenergetic, specially the O adsorption (−90.0 kJ mol−1). These values are similar to those reported in the literature.11,12 The next, crucial step is the dissociation of H2, in which one resulting H atom lies on the Fe2+ center and the other forms a silanol (SiOH) surface group (see structure S_H–H_O). This dissociation presents a very high energy barrier (141.8 kJ mol−1 with respect to S_H2_O) and is +19.7 kJ mol−1 above the asymptote. Despite these values, the resulting structure (i.e., with the H2 dissociated) is more stable than the undissociated complex. The next steps concern the diffusion of the generated H atoms towards Oads to form H2O. To this end, three elementary steps have been identified, the sequence of which is S_H–H_O → S_H_OH_1 → S_H_OH_2 → S_H2O. Calculations indicate that all these elementary steps present very high intrinsic energy barriers, between 160 and 200 kJ mol−1.
These computed energy barriers are impractical to classically overcome under the interstellar conditions. However, all the steps involve H atoms and, accordingly, tunneling effects can be dominant. Because of this, we have computed the rate constants taking into account tunneling in a semi-classical way (see the Methods section above). The Arrhenius plots for each elementary step is shown in Fig. 7(b). It can be clearly seen that tunneling dominates the kinetics of the processes at the considered range of temperatures (10–100 K), since the slope of the plots is almost null, rendering the rate constants independent of T and with similar values at these temperatures (at variance with the plots without tunneling). Among the different models used, the parabolic barrier model exhibits the largest tunneling effects, providing semi-classical rate constants of very few negative orders of magnitude (in s−1) at the considered interstellar temperatures. Thus, considering the long lifetimes of interstellar clouds (between 10–50 Myrs), formation of H2O through the simulated mechanism on Fe-containing olivines seems to be feasible.
3.2 Nanoclusters
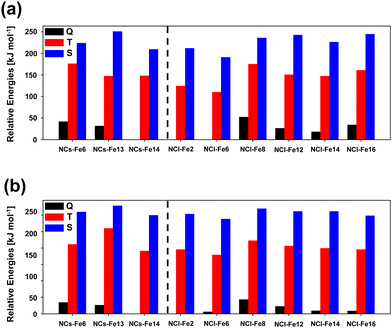
A similar study to that done for the periodic surfaces is here presented for the nanocluster systems, that is, their relative stability as a function of the electronic spin state, the H2 adsorption energies, and the reactivity towards H2O formation. As mentioned in the Methods section, for the nanoclusters, calculations have been performed at the B3LYP-D3(BJ) and M06-2X-D3 levels. Moreover, for the sake of accuracy, for the small nanoclusters, single point energy calculations at CCSD(T) have also been performed when (i) calculating the different electronic states of the bare nanoclusters, and (ii) calculating the energetics of the water formation reaction. The reason for point (i) is because, to the best of our knowledge and at variance with the crystalline surfaces, no methodological benchmarking studies are available for Fe-containing silicate nanoclusters, in such a way that we here present a calibration study relative to these systems. The reason for point (ii) stands for accuracy reasons, that is, to obtain highly accurate values in relation to the energetics of the reaction. It is worth mentioning that these single point energy CCSD(T) calculations have only been done on small nanoclusters because, due to their size, calculations are computationally affordable, which is not the case in large nanoclusters (they are extremely expensive).Fig. 8 presents bar graphs representing the relative stabilities of the bare Fe-containing nanoclusters, considering the different electronic spin states (Q, T and S) computed at the two DFT theory levels. The observed trends are very similar irrespective of the method, indicating that both DFT functionals are robust as far as the electronic structure of the bare nanoclusters is concerned. Moreover, the stability trend as a function of the electronic state found in the periodic surfaces is kept in the nanoclusters, i.e., from more to less stable, Q > T > S. Both methods give as the most stable Fe-containing nanocluster NCs-Fe14 and NCl-Fe2 for the small and large nanocluster sets, respectively, the latter one followed by NCl-Fe6, in which Fe occupies a similar position in the nanocluster structure (see Fig. 2(d)).
H2 adsorption on all the Fe positions for all the nanoclusters in their different electronic states have been computed. Fig. 9 presents the structures of the optimized complexes. The calculated adsorption energies are represented in the bar graphs of Fig. 10(a) and (b)) (B3LYP-D3(BJ) and M06-2X-D3, respectively).
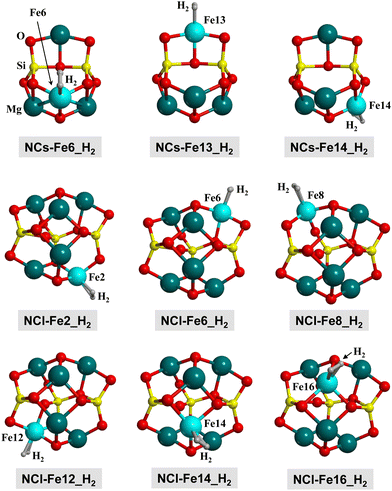 | ||
| Fig. 9 B3LYP-D3(BJ)-optimized complexes for the H2 adsorption on the nanocluster models. Since the complexes in the Q, T and S electronic states do not present significant structural changes, here we only show the complexes at the S state for a qualitative view. Energetic, structural and vibrational parameters of all the complexes are reported in Table 4. | ||
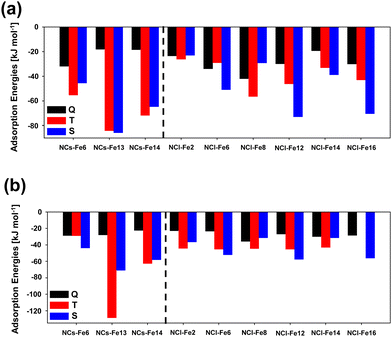
According to these results, it is clear that the electronic states providing the most favourable adsorption complexes are either S or T, but not Q. This was also observed for the periodic surfaces. In general, both DFT methods agree in the most stable complexes as a function of the electronic state for each nanocluster system. That is, both methods gives NCs-Fe14 T as the most stable H2 adsorption complex for this nanocluster type, and NCl-Fe2 T, NCl-Fe6 S, NCl-Fe8 T, NCl-Fe12 S and NCl-Fe16 S as the most stable complexes of the corresponding nanocluster families. However, discrepancies are also found among the two methods. This is particularly the case of the small nanocluster set: M06-2X-D3 gives NCs-Fe6 S and NCs-Fe13 T as the most stable complexes, while, at the B3LYP-D3(BJ) level, NCs-Fe6 T is the most stable structure, and for NCs-Fe13, the T and S states are nearly degenerate. Similarly, there is a swap in stability between the T and S states in the NCl-Fe14 nanocluster. With the aim to shed light onto the accuracy of the DFT methods in the energetics of the adsorption complexes, we performed single point energy calculations at the CCSD(T) theory level for the NC set, and compared the results with the DFT ones. Results are reported in Table 3. According to these data, B3LYP-D3(BJ) provides more comparable H2 adsorption energies to the CCSD(T) ones. Indeed, for all the nanocluster sets, the stability trend as a function of the electronic state is the same for B3LYP-D3(BJ) and CCSD(T) (see the NCs-Fe6 and NCs-Fe13 families). Moreover, for NCs-Fe6 T and NCs-Fe13 T, calculated adsorption energies are in better agreement between these methods, while at the M06-2X-D3 level the values are dramatically different.
| Nanocluster | State | B3LYP-D3(BJ) | M06-2X-D3 | CCSD(T) |
|---|---|---|---|---|
| NCs-Fe6 | Q | −31.9 | −28.7 | −29.6 |
| T | −55.3 | −29.1 | −49.4 | |
| S | −45.6 | −43.9 | −42.2 | |
| NCs-Fe13 | Q | −18.2 | −28.0 | −16.9 |
| T | −84.3 | −128.5 | −70.6 | |
| S | −86.0 | −70.9 | −80.3 | |
| NCs-Fe14 | Q | −18.5 | −22.6 | −16.7 |
| T | −71.9 | −62.7 | −66.2 | |
| S | −64.8 | −58.1 | −60.5 |
Focusing, then, on the B3LYP-D3(BJ) results, the likely perturbation of H2 due to its interaction with the Fe2+ center has been quantified by the H–H and Fe–H distances and the vibrational ν(H–H) frequency. The values are reported in Table 4. In general (and by averaging the values for all the nanocluster sets), one can identify the following trends: (i) for the H–H distance, d(H–H)S > d(H–H)T > d(H–H)Q; (ii) for the Fe–H distance, d(Fe–H)S < d(Fe–H)T < d(Fe–H)Q; and (iii) for the the H–H frequency, ν(H–H)S < ν(H–H)T < ν(H–H)Q. All these trends indicate that the singlet state is that in which the H2 molecule is more activated than the other spin states. The interaction with Fe2+ is stronger in the S state (the Fe–H distances are the shortest ones), inducing the largest weakening of the H–H bond, which is reflected by the largest H–H distances and the largest bathochromic shifts of the H–H frequency.
| Surface | State | d(H–H) | d(Fe–H) | ν(H–H) | ΔEads |
|---|---|---|---|---|---|
| NCs-Fe6 | Q | 0.785 | 1.830/1.861 | 3784 | −31.9 |
| T | 0.803 | 1.670/1.679 | 3448 | −55.3 | |
| S | 0.803 | 1.666/1.663 | 3467 | −45.6 | |
| NCs-Fe13 | Q | 0.753 | 2.199/2.198 | 4253 | −18.2 |
| T | 0.796 | 1.717/1.717 | 3611 | −84.3 | |
| S | 0.813 | 1.639/1.626 | 3341 | −86.0 | |
| NCs-Fe14 | Q | 0.763 | 1.971/1.993 | 4049 | −18.5 |
| T | 0.802 | 1.677/1.677 | 3476 | −71.9 | |
| S | 0.810 | 1.637/1.646 | 3371 | −64.8 | |
| NCl-Fe2 | Q | 0.771 | 1.910/1.904 | 3938 | −23.5 |
| T | 0.773 | 1.870/1.866 | 3904 | −26.3 | |
| S | 0.792 | 1.679/1.680 | 3626 | −23.1 | |
| NCl-Fe6 | Q | 0.777 | 1.861/1.865 | 3835 | −34.1 |
| T | 0.791 | 1.706/1.707 | 3653 | −29.2 | |
| S | 0.801 | 1.660/1.653 | 3494 | −51.0 | |
| NCl-Fe8 | Q | 0.776 | 1.880/1.873 | 3857 | −42.1 |
| T | 0.778 | 1.810/1.814 | 3910 | −56.6 | |
| S | 0.781 | 1.784/1.769 | 4125 | −29.3 | |
| NCl-Fe12 | Q | 0.780 | 1.853/1.848 | 3800 | −30.0 |
| T | 0.777 | 1.846/1.846 | 4012 | −46.3 | |
| S | 0.804 | 1.649/1.661 | 3467 | −73.1 | |
| NCl-Fe14 | Q | 0.772 | 1.910/1.899 | 3933 | −19.3 |
| T | 0.776 | 1.817/1.810 | 3887 | −33.1 | |
| S | 0.799 | 1.657/1.663 | 3557 | −38.9 | |
| NCl-Fe16 | Q | 0.768 | 1.948/1.926 | 3988 | −30.1 |
| T | 0.775 | 1.799/1.793 | 3904 | −43.2 | |
| S | 0.797 | 1.662/1.668 | 3571 | −70.6 |
As the H2 interaction with the Fe2+-containing nanoclusters is more favorable when the complexes have a singlet state, this electronic state has been chosen to study the H2O formation. In particular, we have chosen the NCs-Fe13 S nanocluster because it is the one presenting the largest H2 adsorption and perturbation with respect to its discrete, gas-phase state. Moreover, by choosing this electronic state, the present work takes into account two different limit cases: the less H2/surface activated complex (quintuplet state, adopting a periodic surface) and the most H2/surface activated complex (singlet state adopting a nanocluster structure).
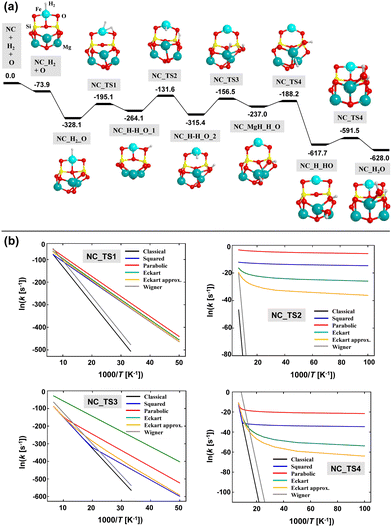
The calculated energy profile adopting Mech2 is shown in Fig. 11(a). Taking advantage of the small size of the NCs-Fe13 nanocluster, the relative energies of this reaction profile are based on single point energy calculations at CCSD(T) on the B3LYP-D3(BJ)-optimized geometries and including the ZPE corrections obtained at this DFT theory level. Interestingly, the linear regression ECCSD(T) = 1.02EB3LYP-D3(BJ) + 64.65 (r2 = 0.997) indicates that the B3LYP-D3(BJ) energy values are accurate enough.
The resulting path follows, in general, the steps of Mech2 represented in Fig. 5, but particular differences have been found. After the H2 adsorption on the Fe2+ center, the adsorption of atomic O (Oads) takes place on Mg6 (which is the most stable Mg site among the available ones). As occurring for the periodic case, O adsorption is more stable in the singlet state than in the triplet one. Thus, along the reaction, the former electronic state has been considered. Interestingly, the Oads atom forms a peroxo group with a nearby O atom of the nanocluster. This phenomenon was already observed and described by Molpeceres et al.12 The next step is the H2 dissociation, which results in the formation of Fe–H and SiOH groups. The following steps involve the diffusion of the H atoms to form finally H2O. The diffusion of the H atom of the SiOH group occurs through jumps on different surface O atoms, forming different SiOH groups, towards reaching Oads. In contrast, the H atom attached to the Fe2+ center jumps first to the Mg atoms where the Oads is, and then couples with this atom.
As far as the reaction energetics is concerned, all the stationary points after the O adsorption (i.e., after the NC_H2_O structure) lie below in energy with respect to the stationary point before the O adsorption (i.e., the “NC_H2 + O” point). Since the reaction is occurring on a nanocluster silicate, to assess the feasibility of the reaction, two different scenarios can be considered: (i) the energy gain due to the O adsorption is not fully transferred to the nanocluster and dissipated, or, in contrast, (ii) the O adsorption energy is released and dissipated among the nanocluster through the silicate phonon modes. For the reaction occurring on the periodic surface, scenario (ii) was considered to be the operating one because the silicate surface is a model of interstellar grains of nm–μm sizes, in such a way that the energy released by Oads is dissipated among the grains. On the nanoclusters, in contrast, due to their ultrasmall sizes, the O adsorption energy might not be fully dissipated (scenario (i)) in such a way that the extra energy can be used for the progress of the reaction. If this scenario (i) is operating, all the elementary steps can be achieved because the excess of energy retained by the system allows overcoming all the energy barriers, which are submerged below the “NC_H2 + O” stationary point. In contrast, if scenario (ii) is dominant, some elementary steps present high energy barriers (particularly the first four). However, since H atoms are involved in the processes, tunneling effects can significantly contribute. Thus, a kinetic study as that done for the periodic surface has been performed. The resulting Arrhenius plots for the first four steps (the ones presenting the highest energy barriers) are shown in Fig. 11(b). Ruling out the Wigner model (which cannot be applied because the requirement of high temperatures is not satisfied in the ISM), the other tunneling schemes show similar trends. Taking the Eckart potential model, and considering a T of 90 K, the calculated semi-classical rate constants are (in Myear−1): 1.8 × 10−28, 7.3 × 1011, 2.3 × 10−26, and 5.4 × 105, for the first four steps. These values clearly indicate that, under the scenario (ii), the reaction presents bottlenecks in the first and third steps. Interestingly, the reason is not because the energy barriers are too high, but because they are endoenergetic steps. That is, as the interstellar temperatures are extremely low, the reactants are not thermally promoted to rotational and vibrational excited states, which is a compulsory condition to be converted into products. For the second and fourth steps, tunneling effects are shown to be of great importance for their evolution.
Finally, to study the role of the Fe2+/H2 interactions in the silicate nanocluster, the H2 dissociation step has been computed considering a Mg-pure nanocluster. Results indicate an energy barrier of 61.9 kJ mol−1, significantly lower than on Fe2+ (145.9 kJ mol−1). A possible explanation of this difference lies on the adsorption energy of H2 when on Mg2+ (computed to be −22.3 kJ mol−1) or on Fe2+ (−85.9 kJ mol−1). Since the H2 adsorption on Fe2+ is stronger than on Mg2+, H2 dissociation on Fe2+ presents higher energy because of this enhanced stability of the H2 adsorption complex with respect to the Mg-pure nanocluster. In this sense, our results point out that Fe-containing silicates can act as reservoirs of interstellar H2 molecules.
4 Conclusions
In this work, the interstellar H2O formation adopting the reaction of O + H2 → H2O on Fe-containing silicate surfaces has been investigated by means of quantum chemical simulations. Two different types of surface models have been adopted: one based on periodic crystalline slabs arising from the (010), (001), and (110) Mg2SiO4 surfaces, the other based on nanocluster systems of Mg4Si2O8 and Mg6Si3O12 stoichiometries, in which for both approaches a Mg2+ cation is replaced by one Fe2+ metal center. Periodic surfaces have been computed at the DFT B3LYP-D3(BJ) level, while nanoclusters at the B3LYP-D3(BJ) and M06-2X-D3 levels, complemented by single point CCSD(T) calculations, since no benchmarking studies are available for these systems.The electronic structure of the bare surfaces, including the different electronic states arising from the presence of the Fe2+ cation, i.e., spin multiplicities of quintuplet (Q), triplet (T) and singlet (S), and of the resulting complexes upon H2 adsorption has been investigated, alongside the structural and vibrational features of the H2/surface adsorption complexes. The potential energy surfaces (PESs) corrected for the zero-point energies (ZPEs) of the mechanisms for the H2O formation have been characterized, which are based on the adsorption of atomic O, dissociation of H2 and diffusion of the resulting H atoms to the adsorbed O atom. A kinetic study based on the calculation of semi-classical rate constants accounting for tunneling through different schemes has been performed.
From the present calculations, the following concluding points emerge:
• For both the periodic surfaces and the nanocluster systems, the stability of the bare Fe-containing silicates as a function of their electronic spin state is (from more to less stable): Q > T > S.
• The H2 adsorption on the Fe2+ centers is favourable in all the electronic states. However, at variance with the bare models, a robust trend relative to the adsorption energies as a function of the surface spin state is not found. On average, the most stable adsorption is for the S state, which is accompanied by significant H–H bond enlargements and ν(H–H) bathochromic shifts, and the shortest Fe–H bond distances.
• Among the proposed mechanisms, the most energetically favourable one is that in which the H2 dissociation occurs after the adsorption of the O atom because the energy released due to the O adsorption can be used to dissociate the H2 molecules.
• On the periodic surfaces, the H2O formation has been studied on the most stable bare slab model, the (010) Q one. The computed ZPE-corrected PES indicate that the reaction presents high energy barriers insurmountable from a classical perspective at the very low interstellar temperatures. However, tunneling effects have been found to be very important and allow the occurrence of the reaction in diffuse interstellar clouds.
• On the nanocluster systems, the H2O formation has been studied on the most stable H2/surface complex, the NCs-Fe13 S one. The computed ZPE-corrected PES presents very high energy barriers and tunneling effects do not allow the evolution of the reaction due to presenting elementary endoenergetic steps. However, the reaction is predicted to be possible if the energy released by the O adsorption is not dissipated throughout the nanocluster (a plausible scenario due to the ultrasmall size of the silicate cluster). If this was the case, the extra energy retained by the system can be used to overcome the energy barriers.
• For the nanocluster system, a comparison of the reaction in the presence and absence of Fe2+ cations has been done. Results indicate that the reaction is energetically more favourable on Mg2+-pure nanoclusters. This is because the Fe2+/H2 interactions are stronger than the Mg2+/H2 ones, thus increasing the H2 dissociation energy barriers. Accordingly, Fe-containing silicates can represent reservoirs of interstellar H2 molecules.
The results of the present work give an overview of the H2O formation through the reaction of atomic O with H2 on Fe-containing silicates, a reaction that has not been investigated experimentally. In this respect, new experimental astrochemical measurements stimulated by our promising results would be welcome to validate the present results, and in the case to be positive, to include this reaction channel in the chemical network of the H2O formation on interstellar grains.
Author contributions
M. S.-P.: data curation (lead); formal analysis (equal); investigation (equal); software (lead); visualization (equal); and writing – review and editing (supporting). C. D.-D.: data curation (lead); formal analysis (equal); investigation (equal); validation (lead); visualization (equal); and writing – review and editing (supporting). A. R.: conceptualization (lead); formal analysis (equal); funding acquisition (lead); investigation (equal); project administration (lead); resources (lead); supervision (lead); visualization (equal); writing – original draft (lead); and writing – review and editing (lead).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Unions Horizon 2020 research and innovation programme from the European Research Council (ERC) for the project “Quantum Chemistry on Interstellar Grains” (Quantumgrain), grant agreement no. 865657, and from the Marie Sklodowska-Curie for the project “Astro-Chemical Origins” (ACO), grant agreement no. 811312. A. R. is indebted to the “Ramón y Cajal” program. M. S.-P. is indebted to the Spanish “Ministerio de Educación y Formación Profesional” for a collaboration grant.Notes and references
- P. Caselli and C. Ceccarelli, Astron. Astrophys Rev., 2012, 20, 56 CrossRef.
- A. G. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- E. F. Van Dishoeck, Faraday Discuss., 2014, 168, 9–47 RSC.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- T. Henning, Annu. Rev. Astron. Astrophys., 2010, 48, 21–46 CrossRef CAS.
- E. F. Van Dishoeck, E. Herbst and D. A. Neufeld, Chem. Rev., 2013, 113, 9043–9085 CrossRef CAS PubMed.
- I. Oliveira, J. Olofsson, K. M. Pontoppidan, E. F. van Dishoeck, J.-C. Augereau and B. Merín, Astrophys. J., 2011, 734, 51 CrossRef.
- F. Molster and C. Kemper, Space Sci. Rev., 2005, 119, 3–28 CrossRef CAS.
- H. W. W. Spoon, A. Hernán Caballero, D. Rupke, L. B. F. M. Waters, V. Lebouteiller, A. G. G. M. Tielens, T. Loredo, Y. Su and V. Viola, arXiv e-prints, 2022, arXiv:2203.03071.
- J. Navarro-Ruiz, M. Sodupe, P. Ugliengo and A. Rimola, Phys. Chem. Chem. Phys., 2014, 16, 17447–17457 RSC.
- J. Navarro-Ruiz, P. Ugliengo, M. Sodupe and A. Rimola, Chem. Commun., 2016, 52, 6873–6876 RSC.
- G. Molpeceres, A. Rimola, C. Ceccarelli, J. Kästner, P. Ugliengo and B. Maté, Mon. Not. R. Astron. Soc., 2019, 482, 5389–5400 CrossRef CAS PubMed.
- E. Herbst, J. Phys. Chem. A, 2005, 109, 4017–4029 CrossRef CAS PubMed.
- E. A. Bergin and M. Tafalla, Annu. Rev. Astron. Astrophys., 2007, 45, 339–396 CrossRef CAS.
- D. Hudgins, S. Sandford, L. Allamandola and A. Tielens, Astrophys. J., Suppl. Ser., 1993, 86, 713–870 CrossRef CAS PubMed.
- H. Linnartz, J.-B. Bossa, J. Bouwman, H. M. Cuppen, S. H. Cuylle, E. F. Van Dishoeck, E. C. Fayolle, G. Fedoseev, G. W. Fuchs and S. Ioppolo, et al. , Proc. Int. Astron. Union, 2011, 7, 390–404 CrossRef.
- A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581 CrossRef CAS.
- A. Tielens and W. Hagen, Astron. Astrophys., 1982, 114, 245–260 CAS.
- T. Hama and N. Watanabe, Chem. Rev., 2013, 113, 8783–8839 CrossRef CAS PubMed.
- A. Potapov, C. Jäger and T. Henning, Phys. Rev. Lett., 2020, 124, 221103 CrossRef CAS PubMed.
- F. Gillett and W. Forrest, Astrophys. J., 1973, 179, 483–491 CrossRef.
- E. Gibb, D. Whittet, A. Boogert and A. Tielens, Astrophys. J., Suppl. Ser., 2004, 151, 35 CrossRef CAS.
- A. C. Boogert, K. M. Pontoppidan, C. Knez, F. Lahuis, J. Kessler-Silacci, E. F. van Dishoeck, G. A. Blake, J.-C. Augereau, S. Bisschop and S. Bottinelli, et al. , Astrophys. J., 2008, 678, 985 CrossRef CAS.
- P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427–483 CrossRef CAS.
- V. Taquet, P. S. Peters, C. Kahane, C. Ceccarelli, A. Lòpez-Sepulcre, C. Toubin, D. Duflot and L. Wiesenfeld, Astron. Astrophys., 2013, 550, A127 CrossRef.
- D. Hollenbach, M. J. Kaufman, E. A. Bergin and G. J. Melnick, Astrophys. J., 2008, 690, 1497 CrossRef.
- E. F. van Dishoeck, L. Kristensen, A. Benz, E. Bergin, P. Caselli, J. Cernicharo, F. Herpin, M. Hogerheijde, D. Johnstone and R. Liseau, et al. , Publ. Astron. Soc. Pac., 2011, 123, 138 CrossRef.
- L. Testi, H. Beuther, R. Klessen, C. Dullemond and T. Henning, Protostars and Planets VI, 2014 Search PubMed.
- L. Silva, G. Vladilo, G. Murante and A. Provenzale, Mon. Not. R. Astron. Soc., 2017, 470, 2270–2282 CrossRef CAS.
- L. Testi, T. Birnstiel, L. Ricci, S. Andrews, J. Blum, J. Carpenter, C. Dominik, A. Isella, A. Natta and J. P. Williams, et al., Protostars and Planets VI, 2014, vol. 914, pp. 339–61 Search PubMed.
- D. Hollenbach and C. F. McKee, Astrophys. J., 1989, 342, 306–336 CrossRef CAS.
- N. Watanabe and A. Kouchi, Prog. Surf. Sci., 2008, 83, 439–489 CrossRef CAS.
- F. Du, B. Parise and P. Bergman, Astron. Astrophys., 2012, 538, A91 CrossRef.
- K. Hiraoka, T. Miyagoshi, T. Takayama, K. Yamamoto and Y. Kihara, Astrophys. J., 1998, 498, 710 CrossRef CAS.
- F. Dulieu, L. Amiaud, E. Congiu, J.-H. Fillion, E. Matar, A. Momeni, V. Pirronello and J. Lemaire, Astron. Astrophys., 2010, 512, A30 CrossRef.
- D. Jing, J. He, J. Brucato, A. De Sio, L. Tozzetti and G. Vidali, Astrophys. J. Lett., 2011, 741, L9 CrossRef.
- R. Klein and M. D. Scheer, J. Chem. Phys., 1959, 31, 278–279 CrossRef CAS.
- N. Miyauchi, H. Hidaka, T. Chigai, A. Nagaoka, N. Watanabe and A. Kouchi, Chem. Phys. Lett., 2008, 456, 27–30 CrossRef CAS.
- S. Ioppolo, H. Cuppen, C. Romanzin, E. Van Dishoeck and H. Linnartz, Astrophys. J., 2008, 686, 1474 CrossRef CAS.
- S. Ioppolo, H. M. Cuppen, C. Romanzin, E. F. van Dishoeck and H. Linnartz, Phys. Chem. Chem. Phys., 2010, 12, 12065–12076 RSC.
- Y. Oba, N. Miyauchi, H. Hidaka, T. Chigai, N. Watanabe and A. Kouchi, Astrophys. J., 2009, 701, 464 CrossRef CAS.
- H. Cuppen, S. Ioppolo, C. Romanzin and H. Linnartz, Phys. Chem. Chem. Phys., 2010, 12, 12077–12088 RSC.
- H. Chaabouni, M. Minissale, G. Manicò, E. Congiu, J. Noble, S. Baouche, M. Accolla, J. Lemaire, V. Pirronello and F. Dulieu, J. Chem. Phys., 2012, 137, 234706 CrossRef CAS PubMed.
- H. Mokrane, H. Chaabouni, M. Accolla, E. Congiu, F. Dulieu, M. Chehrouri and J. Lemaire, Astrophys. J., Lett., 2009, 705, L195 CrossRef CAS.
- C. Romanzin, S. Ioppolo, H. Cuppen, E. Van Dishoeck and H. Linnartz, J. Chem. Phys., 2011, 134, 084504 CrossRef CAS PubMed.
- Y. Oba, N. Watanabe, T. Hama, K. Kuwahata, H. Hidaka and A. Kouchi, Astrophys. J., 2012, 749, 67 CrossRef.
- Y. Oba, N. Watanabe, A. Kouchi, T. Hama and V. Pirronello, Phys. Chem. Chem. Phys., 2011, 13, 15792–15797 RSC.
- E.-L. Zins, P. R. Joshi and L. Krim, Mon. Not. R. Astron. Soc., 2011, 415, 3107–3112 CrossRef CAS.
- N. De Leeuw, S. Parker, C. Catlow and G. Price, Phys. Chem. Miner., 2000, 27, 332–341 CrossRef CAS.
- C. Richard A áCatlow and E. Helen, et al. , Chem. Commun., 2010, 46, 8923–8925 RSC.
- K. Muralidharan, P. Deymier, M. Stimpfl, N. H. de Leeuw and M. J. Drake, Icarus, 2008, 198, 400–407 CrossRef.
- H. King, M. Stimpfl, P. Deymier, M. Drake, C. Catlow, A. Putnis and N. de Leeuw, Earth Planet. Sci. Lett., 2010, 300, 11–18 CrossRef CAS.
- A. M. Asaduzzaman, S. Laref, P. A. Deymier, K. Runge, H.-P. Cheng, K. Muralidharan and M. Drake, Philos. Trans. R. Soc., A, 2013, 371, 20110582 CrossRef PubMed.
- V. Prigiobbe, A. Suarez Negreira and J. Wilcox, J. Phys. Chem. C, 2013, 117, 21203–21216 CrossRef CAS.
- T. P. M. Goumans, C. R. A. Catlow, W. A. Brown, J. Kästner and P. Sherwood, Phys. Chem. Chem. Phys., 2009, 11, 5431 RSC.
- T. Lamberts, P. K. Samanta, A. Köhn and J. Kästner, Phys. Chem. Chem. Phys., 2016, 18, 33021–33030 RSC.
- J. Meisner, T. Lamberts and J. Kästner, ACS Earth Space Chem., 2017, 1, 399–410 CrossRef CAS.
- J. Navarro-Ruiz, J. Á. Martínez-González, M. Sodupe, P. Ugliengo and A. Rimola, Mon. Not. R. Astron. Soc., 2015, 453, 914–924 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Navarro-Ruiz, P. Ugliengo, A. Rimola and M. Sodupe, J. Phys. Chem. A, 2014, 118, 5866–5875 CrossRef CAS PubMed.
- Y. Noël, M. De La Pierre, L. Maschio, M. Rérat, C. M. Zicovich-Wilson and R. Dovesi, Int. J. Quantum Chem., 2012, 112, 2098–2108 CrossRef.
- M. De La Pierre, C. Carteret, R. Orlando and R. Dovesi, J. Comput. Chem., 2013, 34, 1476–1485 CrossRef CAS PubMed.
- M. Bruno, F. R. Massaro, M. Prencipe, R. Demichelis, M. De La Pierre and F. Nestola, J. Phys. Chem. C, 2014, 118, 2498–2506 CrossRef CAS.
- R. Demichelis, M. Bruno, F. R. Massaro, M. Prencipe, M. De La Pierre and F. Nestola, J. Comput. Chem., 2015, 36, 1439–1445 CrossRef CAS PubMed.
- L. Zamirri, P. Ugliengo, C. Ceccarelli and A. Rimola, ACS Earth Space Chem., 2019, 3, 1499–1523 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Table with the lattice parameters of the optimized periodic Mg-pure (forsterite, Mg2SiO4) and Fe-containing (olivine, (Mg,Fe)SiO4) surfaces; description of the calculation of rate constants and of tunneling correction schemes adopting a semi-classical approach; optimized fractionary coordinates of the periodic surfaces; and optimized Cartesian coordinates of the nanocluster systems. See DOI: https://doi.org/10.1039/d2cp04051d |
| This journal is © the Owner Societies 2022 |