Open Access Article
Open Access ArticleCryogenic IR and UV spectroscopy of isomer-selected cytosine radical cation†
Franco
Molina
abcd,
Jordan
Dezalay
a,
Satchin
Soorkia
 a,
Michel
Broquier
a,
Majdi
Hochlaf
a,
Michel
Broquier
a,
Majdi
Hochlaf
 e,
Gustavo Ariel
Pino
e,
Gustavo Ariel
Pino
 bc and
Gilles
Grégoire
bc and
Gilles
Grégoire
 *a
*a
aUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d’Orsay, F-91405 Orsay, France. E-mail: gilles.gregoire@universite-paris-saclay.fr
bINFIQC (CONICET-UNC), Ciudad Universitaria, Pabellón Argentina, 5000 Córdoba, Argentina. E-mail: gpino@unc.edu.ar
cDepartamento de Fisicoquímica, Fac. de Ciencias Químicas, Universidad Nacional de Córdoba, Ciudad Universitaria, Pabellón Argentina, X5000HUA Córdoba, Argentina
dCentro Láser de Ciencias Moleculares, Universidad Nacional de Córdoba, Ciudad Universitaria, Pabellón Argentina, X5000HUA Córdoba, Argentina
eUniversité Gustave Eiffel, COSYS/IMSE, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
First published on 11th October 2022
Abstract
Oxidation of the nucleobases is of great concern for the stability of DNA strands and is considered as a source of mutagenesis and cancer. However, precise spectroscopy data, in particular in their electronic excited states are scarce if not missing. We here report an original way to produce isomer-selected radical cations of DNA bases, exemplified in the case of cytosine, through the photodissociation of cold cytosine–silver (C–Ag+) complex. IR–UV dip spectroscopy of C–Ag+ features fingerprint bands for the two keto-amino cytosine tautomers. UV photodissociation (UVPD) of the isomer-selected C–Ag+ complexes produces the cytosine radical cation (C˙+) without isomerization. IR–UV cryogenic ion spectroscopy of C˙+ allows for the unambiguous structural assignment of the two keto-amino isomers of C˙+. UVPD spectroscopy of the isomer-selected C˙+ species is recorded at a unique spectral resolution. These benchmark spectroscopic data of the electronic excited states of C˙+ are used to assess the quantum chemistry calculations performed at the TD-DFT, CASSCF/CASPT2 and CASSCF/MRCI-F12 levels.
1 Introduction
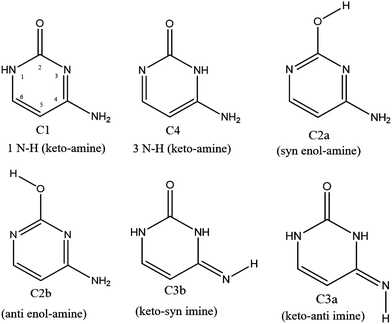
Understanding the detailed mechanisms responsible for DNA damage derived from endogenous and exogenous sources is of great importance because they can lead to genomic instability and carcinogenesis if the DNA reparation mechanisms fail. Among the exogenous sources of DNA damage, ionizing radiation plays a relevant role since the electron hole produced upon ionization migrates along the double helix followed by proton transfer (PT) reactions.1 The intermolecular PT reactions between complementary bases Adenine–Thymine (A–T) or Guanine–Cytosine (G–C) are facilitated upon ionization of one of the bases by lowering the energy barrier for the reaction.2 This PT reaction leads to tautomerization of the bases, which disrupts the Watson–Crick (WC) hydrogen bonding pattern established for the A–T and G–C pairs, and the subsequent strand scission and mutagenesis. Ionizing radiation may lead to the formation of the radical cations of the DNA bases in their electronic excited states. Therefore, to have a complete knowledge of the effect of ionizing radiation on DNA, it is important to understand the underlying molecular mechanisms when light interacts with DNA bases, its building-blocks, as well as their spectroscopic and molecular properties.Gas phase studies offer the possibility to access information of the intrinsic physical and chemical properties of DNA bases. From an experimental point of view, the main problem arises from the large number of isomers/tautomers of each DNA base that can be populated even at low temperature as achieved in molecular beams. Microwave spectroscopy is particularly suitable to assign the tautomers of DNA bases through the analysis of the corresponding rotational spectrum. Previous works showed that complexity increases in the following order: thymine,3 then adenine,4 followed by cytosine5 and finally guanine.6 While a single isomer of thymine is observed, a mixture of at least 3 and 4 tautomers of cytosine and guanine have been identified, respectively. In principle, double resonance IR–UV and UV–UV laser spectroscopies allow recording isomer-selected spectra.7 However, such technique could not be used for molecular species that have ultrashort excited state lifetime, as in the case of the canonical tautomer of guanine.8–10
In the specific case of cytosine (C), there is at least 6 low lying energy tautomers as shown in Scheme 1. The keto-amino (C1) tautomer, the two enol-amino isomers (C2a and C2b) and the keto-imine tautomer (C3a) have been identified by IR and UV spectroscopies of the neutral molecule in the gas phase11,12 and in low-temperature rare gas matrix.13 Besides, Lapinski et al. showed that a second keto-imine isomer (C3a) can be formed following the photo isomerization of the C3b form.14 However, the second keto-amino (C4) isomer, predicted at much higher energy, has never been experimentally observed in isolated conditions. It should be stressed out that in water solution, the keto tautomers (C1 and C4) are the most stable structures due to their larger dipole moments than the other enol and imine tautomers.15,16 Finally, while protonated keto and enol cytosine have been experimentally assigned by cold ion spectroscopy,17 only the keto tautomer C1 was observed for alkali metal cations containing cytosine complexes.18
Although neutral cytosine can be found in several tautomeric forms in the gas phase, only the C1 tautomer and its radical cation C1˙+ are canonical structures in the nucleic acids. The other tautomers are non-canonical and could be involved in mutation processes. While neutral cytosine has been extensively characterized by different isomer-selective spectroscopies, the works on its radical cation (C˙+) are rather scarce. Therefore, detailed studies with isomer-selectivity are needed to reach a better understanding of their intrinsic properties. Most of the experimental results have been obtained at synchrotron facilities. Not only the ground cationic state but also the corresponding excited states of the DNA bases can be reached upon excitation of the neutral base with VUV (vacuum ultraviolet) photons. Extensive experimental19–21 and theoretical works22,23 dealing with the determination of fundamental properties such as the vertical and adiabatic ionization energies (Ev and Ead, respectively) of the DNA bases have been performed in the past. Despite the large number of studies on this topic, the Ead of all tautomers/isomers of the DNA bases are not completely established yet because of the lack of isomer selectivity in the VUV photoionization process. Besides, the relative population of the different tautomers/isomers in the gas phase may vary upon the vaporization method used (thermal heating, laser desorption, helium droplet…).24,25
Spectroscopy information of the cytosine radical cation (C˙+) is rather scarce. To the best of our knowledge, there are a few experimental works dealing with the excited states of C˙+. In two of them,26,27 a mixture of keto, enol and imine tautomers of C˙+ was produced with a tunable synchrotron source by single VUV photon ionization of a molecular beam of C vaporized at high temperature. However, the lack of isomer selectivity renders the assignment elusive. The experimental results were interpreted with the help of high-level ab initio calculations. For the analysis of these experimental spectra, a further complication is that the radical cations possess low lying excited electronic states. This results on their mutual interactions by vibronic couplings and the subsequent mixing of their electronic wave functions, which are thus of multiconfigutational nature. This means that from a theoretical point of view, the approach to tackle the problem implies dealing with excited states of open shell species, which is a great challenge for such relatively large molecular system.
In 2017, Lesslie et al.28 probed a mixture of different isomers of C˙+, which were produced by collision induced dissociation (CID) of ternary copper complexes containing C in an ion trap at room temperature. This mixture of C˙+ isomers at room temperature was analyzed by infrared multiphoton dissociation (IRMPD) spectroscopy with a free electron laser and by low resolution UV photofragmentation spectroscopy (UV-PD) and complemented with theoretical calculations. At least four isomers of C˙+ (C2a˙+, C2b˙+, C1˙+ and C4˙+) were proposed and several electronic bands were reported in the UV-PD spectrum. Here again, the lack of isomer selectivity in the reported spectroscopy and the low spectral resolution renders the comparison with calculations even more difficult. Reader are referred to a recent review by Turecek on the generation and action spectroscopy of DNA cation radicals.29
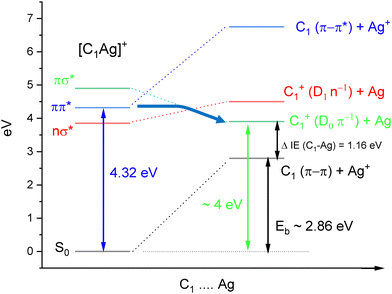
Former studies obviously showed that different tautomers of cytosine can be produced depending on the experimental conditions (gas phase, matrix, solution, metal complexes). Here, we report an original way to produce isomer-selected and cold radical cations of C˙+ that can be extended to other DNA bases. The method is based on our recent studies on the UV-PD spectroscopy of cold Cytosine–Ag+ (C–Ag+) complexes.30,31 The excitation of cold C–Ag+ complexes in the spectral range 3.9–4.60 eV leads to the photochemical production of the radical cation C˙+, through a weakly bound charge transfer state (CT). Scheme 2 illustrates the energy diagram of C1–Ag+ leading to the dissociation into C1˙+ cation. The onset of the π−π* transition of C1–Ag+ is observed at 4.32 eV, the binding energy (Eb) of the complex was calculated at 2.86 eV at the B3LYP/6-31+G* level.30 The dissociation limit resulting in the formation of C1˙+ can be roughly estimated, taken into account the binding energy of the complex plus the difference of ionization energies between cytosine C1 (IEC = 8.73 eV)32 and silver atom (IEAg = 7.57 eV).33 A dissociation energy of about 4 eV is thus needed to produce C1˙+.
As compared to the aforementioned methods to produce the radical cations, the main improvement of the photodissociation scheme is to take advantage of the isomer selectivity offered by the laser spectroscopy of the C–Ag+ complex. Besides, by applying cryogenic ion spectroscopy of isomer-selected species, well-resolved vibrational spectra can be recorded and directly compared to quantum chemistry calculations.34 Indeed, we performed IR and UV cryogenic ion spectroscopy on the C–Ag+ complex and on the photochemical product C˙+. Ground state vibrational (3 μm region) and vibronic spectra (from 2 to 3.5 eV) are recorded with an unprecedented high spectral resolution. The isomer selectivity allows for unambiguous structural assignments through comparison with DFT based calculations and post Hartree–Fock computations. The accurate treatment of the nature of the electronic excited states of the radical cation species remains challenging.
2 Experimental and computational methods
2.1 Experimental
The experimental setup in Orsay has already been described in detail.35 It is based on an electrospray ion source, a cryogenic cooled 3D quadrupole ion trap (QIT, Jordan TOF Inc) and a home-made linear time-of-flight mass spectrometer. A water/methanol solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of cytosine (200 μM) and AgNO3 (100 μM) is electrosprayed in front of a heated capillary, the produced ions are then transferred into an octopole through a skimmer and stored for 100 ms. A bunch of ions is extracted from the octopole by a pulsed electrode and accelerated at 200 V. C–Ag+ ions are mass-selected by a pulsed mass gate located in front of the QIT biased at 200 V and mounted on a cold head of a compressed helium cryostat (CH-204S, Sumitomo) that maintains the temperature around 15 K. The mass-selected complexes (m/z 218 and m/z 220, comprising the two main silver isotopes) are stored and thermalized through collisions with helium buffer gas injected by a pulsed valve (Parker, general valve) a few ms before the entering of the ions. Parent ions and photofragments, produced as described below, are mass-analyzed in a linear TOF-MS and detected by microchannel plates (Z-Gap, Jordan TOF Inc.).
1) of cytosine (200 μM) and AgNO3 (100 μM) is electrosprayed in front of a heated capillary, the produced ions are then transferred into an octopole through a skimmer and stored for 100 ms. A bunch of ions is extracted from the octopole by a pulsed electrode and accelerated at 200 V. C–Ag+ ions are mass-selected by a pulsed mass gate located in front of the QIT biased at 200 V and mounted on a cold head of a compressed helium cryostat (CH-204S, Sumitomo) that maintains the temperature around 15 K. The mass-selected complexes (m/z 218 and m/z 220, comprising the two main silver isotopes) are stored and thermalized through collisions with helium buffer gas injected by a pulsed valve (Parker, general valve) a few ms before the entering of the ions. Parent ions and photofragments, produced as described below, are mass-analyzed in a linear TOF-MS and detected by microchannel plates (Z-Gap, Jordan TOF Inc.).
Vis/UV lasers and an IR-OPO laser were used for the photodissociation spectroscopy. UV photodissociation of C–Ag+ complexes is performed by shining the output of a ps OPA laser (EKSPLA PG 411, 8–10 cm−1 bandwidth) and detecting the cytosine radical cation fragment (C˙+) which is the most intense photofragment of this complex (see Fig. SI1, ESI†). To record the spectroscopy of C˙+, a first photodissociation laser is shined at the early beginning of the trapping sequence (3 ms) when C–Ag+ complexes are already cooled and the relative pressure of the helium in the QIT is still high enough to efficiently cool the nascent C˙+ photofragment. An auxiliary RF (1–2 V during 2 ms after the photodissociation laser) whose frequency is tuned in resonance with the mass of the C–Ag+ complex is sent to the entrance endcap of the QIT to eject the remaining complex to ensure the mass-selection of the C˙+. A second UV laser is then shined about 40 ms later to record the photodissociation spectroscopy of the cooled radical cation.
To record the IR signature of isomer-selected species, two kinds of IR–UV double resonance spectroscopy have been performed depending on the vibronic pattern of the UV spectrum. For species that show sharp vibronic transitions, IR–UV dip spectroscopy is used, i.e. a tunable OPO IR laser (Laserspec) excites the ions a few μs before the UV photodissociation laser whose frequency is set on the band origin of the UV spectrum. When the ions are selectively excited by the IR laser, the UV photofragmentation yield is reduced by the depletion of its ground vibrational state. When the UV spectroscopy exhibits a broad absorption band, IR–UV gain spectroscopy is chosen,36i.e. the tunable IR laser is still shined a few μs before the UV laser whose frequency is, in this case, set off-resonance in the red of the onset of the absorption band (red shifted by a few nm). In that case, the resonant absorption of the IR photon heats the molecules which can now absorb the UV photon and triggers the photofragmentation. It is noteworthy that this latter method is very sensitive since it allows detecting the IR absorption on a background free UV signal.
2.2 Computational
The main aim of the present computations is to identify the isomers/tautomers of the C˙+ radical cation produced after photodissociation of C–Ag+ complex. Therefore, two types of computations were carried out dealing with the ground state (D0) of these species and of their four lowest electronic excited states (D1–D4). These computations consist of the geometry optimizations of these electronic states followed by frequency computations, where all internal coordinates were relaxed (C1 point group). Specifically, the ground state equilibrium geometries and frequencies of C–Ag+ complexes and C˙+ radical cation were calculated at the restricted and unrestricted DFT CAM-B3LYP/aug-cc-pVDZ level, respectively, as implemented in Gaussian16.37 Stuttgart effective core potential is used for the silver atom.38 The harmonic frequencies were corrected with a global scaling factor of 0.953.39 Excited state optimizations and frequency calculations of the different isomers of C˙+ were performed at the TD-DFT level with the same functional and basis set as for the ground state of the six lowest energy isomers (two keto-amino, two enol-amino and two keto-imine tautomers) as specified in Scheme 1.Alternatively, we used a multi-configurational approach as implemented in MOLPRO,40 which consists on geometry optimizations of the specific electronic cationic states at the state-averaged complete active space – self consistent field (SA-CASSCF) level41,42 and frequency computations, followed by a single point computations of the D0–Dn (n = 1–4) excitation energy using the explicitly correlated internally contracted multi reference configuration interaction (MRCI-F12) approach.43–45
At CASSCF, the active space was constructed after considering as active 9 molecular orbitals (MOs) ranging from HOMO−4 to LUMO+3 whereas the core orbitals and the valence orbitals up to HOMO−5 were considered as closed. At MRCI-F12, we took into account all configurations having a weight ≥0.05 in the CI expansion of the CASSCF wavefunctions. This results on more than 3.2 × 109 (1.2 × 108) uncontracted (contracted) configuration state functions (CSFs) to be treated. In these computations, all valence electrons were correlated in the valence molecular orbitals space. The atoms were described by the aug-cc-pVDZ basis set of Dunning and co-workers.46,47 The CASSCF/MRCI-F12/aug-cc-pVDZ scheme should lead to excitation energies as accurate (i.e. to within 0.1 eV) as those that may be obtained using the standard CASSCF/MRCI/aug-cc-pVQZ level but with a strongly reduced computational cost (both CPU and Disks occupancy).45 Also, CASPT2 calculations have been performed with a standard IPEA shift of 0.25 a.u., and a level shift of 0.3 a.u. on the same active space as for the CASSCF method48,49 by means of the OpenMolcas suite of program.50
3 Results and discussion
3.1 Reassignment of the C–Ag+ conformations through IR–UV double resonance spectroscopy.
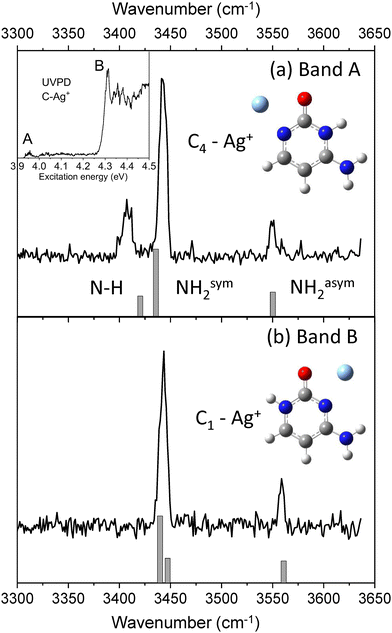
UV photodissociation of C–Ag+ (m/z 218 and m/z 220) was shown to generate C˙+ (m/z 111) as the main fragmentation channel.30,31 Such specific photofragment emphasizes the role of excited state charge transfer following excitation of C–Ag+ over internal conversion to the complex ground state. Conversely, silver cation (m/z 107 and m/z 109) and HNCO loses (m/z 175 and m/z 177) are minor fragmentation channels accounting for less than 10% of the total fragmentation yield (Fig. SI1a, ESI†). The HNCO loss is the signature of the dissociation in the ground state of the complex since it is the only fragmentation channel observed upon IRMPD or CID.51,52 The UV photodissociation spectrum of cold C–Ag+ complex has already been reported30,31 and is composed of a set of two absorption bands, the most intense one (band B) peaked at 4.32 eV along with a weak signal (band A) starting at about 3.95 eV (see insert in Fig. 1). These bands were previously assigned to the π–π* and n–σ* excitation transitions of the lowest energy isomer C1–Ag+ of the complex, respectively, by comparison with adiabatic excitation energies calculated at the SCS-CC2/def2-SVPD level.31 The new experimental and theoretical results reported here lead to a reassignment of the band A at 3.95 eV.The IR–UV gain spectra with the UV laser set to the red of each band are shown in Fig. 1. These two IR spectra are clearly distinct, revealing that two isomers contribute to the UV spectrum of C–Ag+. In particular, a transition at 3408 cm−1 (Fig. 1b) is only detected when the UV is set on the first weak band A of the UV spectrum (3.95 eV).
The experimental IR–UV gain spectra are compared in Fig. 1 to the calculated vibrational spectra of the two lowest energy minima of C–Ag+ (keto-amino tautomer). C1–Ag+ is the global minimum, while C4–Ag+ is calculated 0.18 eV above (see Table 1). The calculated vibrational spectrum of the C1–Ag+ isomer shows a very good agreement with the IR spectrum for which the UV is probing the intense band A at 4.32 eV. As already reported,31 SCS-CC2 excited state calculation predicts the adiabatic excitation energy of the π–π* transition of the C1–Ag+ complex at 4.39 eV. However, the distinct IR spectrum recorded when the UV laser is set on the band A at 3.95 eV reveals that a second isomer contributes to the UVPD spectrum in this spectral region instead of the n–π* transition of the C1–Ag+ complex as previously assigned.30,31 The predicted vibrational spectrum of the C4–Ag+ isomer satisfyingly reproduces the experimental IR spectrum, in particular the agreement with the slight splitting of the NH and symmetric NH2 stretches observed at 3408 cm−1 and 3441 cm−1, respectively. Besides, the adiabatic excitation energy of the π−π* transition of the C4–Ag+ isomer, corrected by the difference in the zero-point energies between the ground and excited states, is calculated at 3.86 eV (SCS-CC2/def2-SVPD), which equals the experimental band origin within 10 meV. Finally, the predicted IR spectra of the 4 others isomers of the C–Ag+ complex containing the cytosine enol (C2a and C2b) and keto-imine (C3a and C3b) are reported in Fig. SI2 (ESI†). These isomers can readily be excluded from the discussion because of the poor match with the present experimental spectra, in particular because of the presence of the extra OH vibrational stretch calculated at 3617 cm−1 and 3604 cm−1 for the enol tautomers and the missing asymmetric NH2 stretch for the keto-imine tautomers.
3.2 UV spectroscopy of C˙+ produced from the photodissociation of the C–Ag+ complexes
Cytosine radical cation is produced from the UV photodissociation of two isomers of the cytosine–silver complex, C1–Ag+ and C4–Ag+. However, as reported in Table 1, the lowest energy isomers of C˙+ are the enol C2b˙+ and C2a˙+ forms, so one can wonder whether these two keto tautomers will be preserved in the cationic form after photodissociation or intramolecular isomerization occurs upon photodissociation of the C–Ag+ complexes.The electronic spectroscopies of C˙+ produced upon excitation of the two complexes, C4–Ag+ (band A) and C1–Ag+ (band B) are shown in Fig. 2a and b, respectively, from 2 eV up to 3.3 eV. As it can be readily seen, the spectroscopy of C˙+ strongly depends on the C–Ag+ isomer excited to produce it. In Fig. 2a, the spectrum of C˙+ issued from the photodissociation of the sole C4–Ag+ consists of a set of broadened vibronic transitions with a band origin at 2.2 eV. In that case, m/z 83 signal (loss of CO) corresponds to the unique photofragment (Fig. SI1b, ESI†). The absorption band extends further to the blue and almost vanishes at about 3 eV (Fig. SI3, ESI†). Although the amount of C˙+, issued from the excitation of the low-intensity transition of the C4–Ag+ complex remains weak, the high fragmentation yield (i.e. 40% of the radical cation signal) leads to a good signal-to-noise ratio in this spectral region.
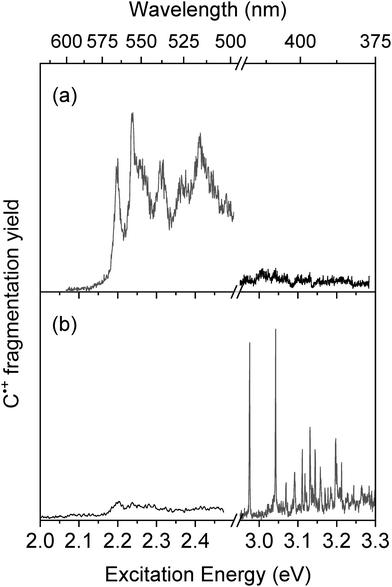 | ||
| Fig. 2 Photodissociation spectroscopy of C˙+ issued from the photodissociation of C–Ag+ at (a) band A at 3.95 eV and (b) band B at 4.32 eV. | ||
Exciting the band B of C–Ag+ complex leads to a 10-fold increase of the C˙+ signal, which is mostly due to the contribution of the intense π–π* transition of the lowest energy isomer C1–Ag+. Interestingly, the electronic spectroscopy of C˙+ drastically changes (Fig. 2b). First, sharp vibronic transitions are now detected in the 3 eV region, with a first transition at 2.97 eV and a vibronic progression up to 3.2 eV. Second, the fragmentation yield of C˙+ falls off in the visible region from 2.2 eV to 3 eV. This weak intensity band reminiscent of the signal reported in Fig. 2a underlines the overlapping of the blue tail band of the C4–Ag+ complex with the onset of the excitation band of the C1–Ag+ complex at 4.32 eV. Finally, three main photofragments are now detected at m/z 68, m/z 69 and m/z 83, corresponding to HNCO, NCO and CO loss, respectively (Fig. SI1c, ESI†). These fragments were also produced under low-energy CID conditions53,54 and through photofragmentation of neutral cytosine up to 3 eV above the adiabatic ionization energy.55 A similar result was reported in a low resolution room temperature UV-photofragmentation spectrum of the C˙+,28m/z 83 being the only photofragment at low excitation energy while m/z 69 being observed in the near UV region.
The sharp (10 cm−1 limited by the laser bandwidth) vibronic transitions observed in the 3 eV region clearly reveal the efficient cooling of C˙+ issued from the photodissociation of C–Ag+. This well-resolved spectrum also suggests that the broadening of the vibronic bands observed in the other spectral region around 2.2 eV is not due to temperature effect. The two different electronic spectroscopies observed for C˙+ depending on which of the two isomers of C–Ag+ is excited suggest that at least two C˙+ isomers contribute to the experimental spectra. Then, IR–UV dip spectroscopy has been performed to record the IR signature of UV selected species.
3.3 IR–UV hole-burning spectroscopy of C˙+
The IR–UV dip spectra of C˙+ probed at 2.2 eV and 2.97 eV are reported in Fig. 3a and b, respectively, along with the predicted vibrational spectra of the lowest energy isomers of C˙+. The two experimental IR spectra share similarities yet being different. They comprise a transition around 3500–3550 cm−1 along with two others in the 3350–3400 cm−1 spectral region. As it can be seen from the comparison with the predicted spectra of the enol-amino tautomers (C2b˙+ and C2a˙+), the two lowest energy isomers of C˙+ (Table 1), have two calculated vibrational frequencies in the 3500–3600 cm−1 region assigned to the OH stretch and NH2 asymmetric stretch, respectively, and one frequency at about 3375 cm−1 (NH2 symmetric stretch) at odds with the experimental spectra. So these two enol tautomers are excluded from the assignment. Accordingly, the two imine tautomers can be excluded because of the missing transitions in the spectral region above 3450 cm−1. In fine, solely the two keto-amino forms (C1˙+ and C4˙+) of the radical cation provide a satisfactory agreement with experiments, with a single frequency above 3500 cm−1 (NH2 asymmetric stretch) and two close lying frequency modes at about 3400 cm−1 (NH2 symmetric stretch) and 3350 cm−1 (NH stretch). The NH2 asymmetric stretch of the C1˙+ isomer is predicted at 3548 cm−1, significantly blue-shifted as compared to the one of C4˙+ calculated at 3519 cm−1. The frequency difference between the NH2 symmetric stretch and NH stretch is larger for C1˙+ than for the C4˙+ isomer. This suggests that the IR spectra of Fig. 3a and b can be assigned to the C4˙+ and C1˙+ isomers, respectively. Finally, another IR–UV dip spectroscopy has been performed. The IR–UV dip signal with the IR wavelength set at 3350 cm−1 (NH stretch, Fig. 3b) while scanning the UV in the 2.95–3.22 eV region is reported in Fig. 4. All vibronic transitions are depleted (Fig. 4), so it can be firmly concluded that C1˙+ is the only isomer which contributes to the vibronic spectrum recorded in the 3 eV region.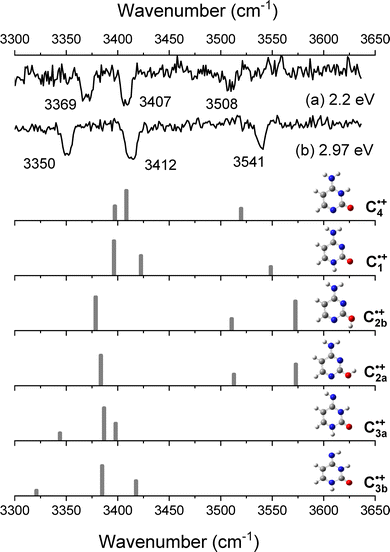 | ||
| Fig. 3 IR–UV dip spectra of C˙+ recorded when probing the UV transition at (a) 2.2 eV and (b) at 2.97 eV. Below, the calculated vibrational spectra of the six isomers of C˙+. | ||
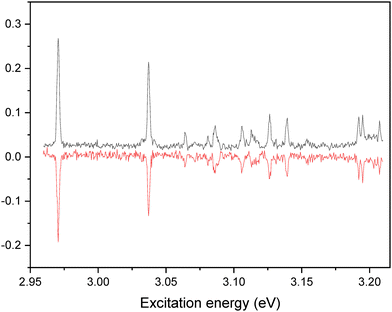 | ||
| Fig. 4 IR–UV dip signal of C˙+ with the IR wavelength set at 3350 cm−1 compared to the vibronic spectrum recorded in the 2.95–3.22 eV. | ||
These spectroscopic results unambiguously demonstrate the lack of isomerization of C˙+ formed through photodissociation of C–Ag+ complexes. Excitation of C1–Ag+ produces exclusively the C1˙+ isomer and the excitation of the C4–Ag+ complex forms solely the C4˙+ isomer. As reported in Table 1, these two keto-amino tautomers are not the lowest energy isomers of C˙+ but are calculated slightly above (at 0.03–0.1 eV) the lowest energy isomer C2b˙+. While the energies of the different isomers of C˙+ are close, barriers to isomerization from the keto-amino to the enol-amino tautomers are relatively large, around 1.3–1.5 eV, as calculated by Wolken et al.54 In our experiment, the cytosine radical cation is produced with the energy released during the dissociation of the complex. For instance, the maximum internal energy imparted in the nascent C1˙+ radical cation is about 0.3 eV, according to Scheme 2. Whatever the excitation energy of the C–Ag+ complex used in our experiment, the low internal energy released in C˙+ will preclude any isomerization process.
3.4 Excited state calculations of the keto-amino C1˙+ and C4˙+ isomers
Geometry optimizations and harmonic vibrational frequencies calculations for the excited states of the two experimentally observed C4˙+ and C1˙+ isomers were carried out at the TD-DFT level of theory using the UCAM-B3LYP/aug-cc-pVDZ method, and the results are shown in Table 2. The optimization and adiabatic excitation energy (Ead) calculations were only achieved for those states whose vertical excitation energies were calculated above the first experimental band (2.20 eV) and whose oscillator strengths (f) are large enough. Indeed, the first three vertical excitation energies for the C1˙+ isomer lie below 1.5 eV, so only the D0–D4 cationic transition that has a sizable oscillator strength could be experimentally observed. Its adiabatic excitation energy is calculated at 3.22 eV (0.25 eV above the experimental band origin at 2.97 eV). For the C4˙+ isomer, the D0–D3 and D0–D4 transitions that have vertical excitation energies in between 2.75 eV and 3.33 eV could be eventually observed because of their large oscillator strengths. The adiabatic D0–D3 transition energy is calculated at 2.33 eV, so less than 0.15 eV above the onset of the experimental transition. Finally, the D0–D4 transition energy is calculated at 3.12 eV. There is no experimental evidence of such transition in the experimental spectrum of the C4˙+, which would appear in the blue tail of the intense D0–D3 transition (see Fig. SI3, ESI†).| Keto amino isomers | Electronic state | E v | E ad + ΔZPE | f |
|---|---|---|---|---|
| a Not optimized because Ev is lower than the first transition experimentally observed (2.20 eV). | ||||
|
D1 (Ã, A′) | 0.83 | 0.00 | |
D2 (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) , A′′) , A′′) |
1.06 | 1.6 × 10−2 | ||
D3 (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) , A′) , A′) |
1.44 | 1.0 × 10−4 | ||
D
4
(![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) , A′′) , A′′)
|
3.40 | 3.22 | 6.5 × 10 −2 | |
|
D1 (Ã, A′) | 1.35 | 2.0 × 10−4 | |
D2 (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) , A′) , A′) |
1.89 | 1.0 × 10−4 | ||
D
3
(![[C with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0043_0303.gif) , A′′) , A′′)
|
2.75 | 2.31 | 5.7 × 10 −2 | |
D4 (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , A′′) , A′′) |
3.33 | 3.12 | 1.9 × 10−2 | |
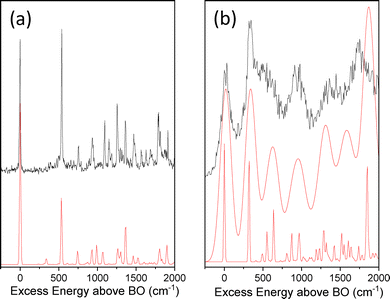
Franck-Condon (FC) simulations for the D0–D4 transition of the C1˙+ isomer and for the D0–D3 transition of the C4˙+ isomer reported in Fig. 5a and b, respectively, are in very good agreement with the experimental spectra. For both isomers, geometry optimizations of the ground and excited states kept the planar Cs symmetry of cytosine. This leads to rather simple calculated FC spectra in which only in-plane modes or out-of-plane modes with even number of quanta are active. The main difference between both experimental spectra is the broadening of the spectrum of C4˙+ in the 2.20 eV region (Fig. 5b) as compared to the calculated one convoluted by a Gaussian of 10 cm−1 as for the D0–D4 transition of C1˙+ (Fig. 5a). The lack of predicted low frequency modes (below 300 cm−1) close to the band origin of the D0–D3 transition of the C4˙+ isomer emphasizes a homogeneous broadening of the experimental spectrum that cannot be due to vibrational congestion. In Fig. 5b, the calculated FC spectrum convoluted with a Gaussian function of 70 cm−1 provides a fair agreement with the experimental spectrum. The D4 state of C1˙+ lies significantly higher than the D3 state by more than 2 eV, so electronic couplings are not thought to be effective in such a case. However, for C4˙+, the energy gaps between D3 and D2 or D4 at the optimized geometry of the D3 and D4 states, respectively, are within 0.5 eV. In the former case, efficient internal conversion from the D3 state to the D2 state would be prone to occur, leading to the broadened excitation spectrum as experimentally observed. Besides, the excitation transition to the D4 state may also be buried in the blue tail of the strong absorption band of the D0–D3 transition.
The comparison between the experimental excitation energies of C1˙+ and C4˙+ and the ones calculated at the TD-DFT level is surprisingly good with absolute errors within 0.25 eV. This is may be due to error compensation that one needs to be aware of. Alternatively, costly CASPT2 and MRCI-F12 on top of CASSCF calculations have been also performed, either for the optimized structures obtained at the UCAM-B3LYP level or after geometry optimizations of the corresponding states at the CASSCF level with the same basis set (cf.Table 3). Interestingly, such high level calculations do not significantly improve the agreement with the experiment. Only for the C1˙+ isomers, the PT2 correction at the CASSCF optimized geometry leads to Ead = 3.14 eV, which is slightly closer to the experimental excitation energy than those calculated with the other methods. For all other calculated excitation energies, the TD-DFT energies match better, in particular for the D0–D3 transition of the C4˙+ isomer. These findings are somehow contradictory with the expected better description of the excited states of the radical cation at the CASSCF level compared to the DFT level. It is clear that our experimental results provide benchmark results at an unprecedented spectral resolution that challenges theoretical predictions.
| Electronic transition | Exp | TD-DFT optimization | CASSCF optimization | |||
|---|---|---|---|---|---|---|
| DFT | CASPT2a | MRCI-F12a | CASPT2 | MRCI-F12 | ||
| a CASPT2 and MRCI-F12 energies correction of the CASSCF energies calculated with the same active space as for the CASSCF optimization. | ||||||
| C1˙+ D0–D4 | 2.97 | 3.22 | 3.24 | 3.60 | 3.14 | 3.42 |
| C4˙+ D0–D3 | 2.2 | 2.31 | 2.88 | 3.30 | 2.64 | 2.89 |
4. Conclusion
The IR and UV photodissociation spectroscopies of isomer-selected cytosine radical cations have been recorded in a cryogenic ion trap. Cytosine radical cations are produced from the photodissociation of cytosine silver complexes (C–Ag+) that are formed in an electrospray source and transferred in a cryogenic ion trap. In the silver complex, the cytosine is found in its two keto-amine tautomers (C1 and C4) that have distinct UV absorption bands, thus allowing conformer selection. UV photodissociation of isomer-selected C1–Ag+ and C4–Ag+ leads to the formation of the corresponding cytosine radical cation without isomerization, assigned through the comparison of their IR spectra with the corresponding DFT calculations. UV photodissociation of the two keto-amine cytosine radical cations reveals a more complex vibronic spectroscopy that still represents a challenge for theoretical predictions even at the CASPT2 and MRCI-F12 levels. Cryogenic ion spectroscopy of radical cations of DNA bases formed through photodissociation of isomer-selected DNA-silver complexes provides a unique method to get precise insights into the structure and electronic properties of DNA radical cations. These benchmark experimental data should be used for the assessment of high-level theoretical calculations of open shell species.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been conducted within the International Associated Laboratory LEMIR (CNRS/CONICET) and was supported in part by CNRS, CONICET, FONCyT, SeCyT-UNC and by the “ADI 2019” project funded by the IDEX Paris-Saclay, ANR-11-IDEX-0003-02. The computations were performed at the HPC resources from the ‘‘Mésocentre’’ computing center of CentraleSupelec and Ecole Normale Supérieure Paris-Saclay supported by CNRS and Région Ile-de-France (https://mesocentre.centralesupelec.fr/) and the HPC resources Méso-LUM from ISMO and MAGI from University Paris 13.References
- S. Kanvah, J. Joseph, G. B. Schuster, R. N. Barnett, C. L. Cleveland and U. Z. I. Landman, Acc. Chem. Res., 2010, 43, 280–287 CrossRef CAS PubMed.
- J. Bertran, L. Blancafort, M. Noguera and M. Sodupe, Computational Studies of RNA and DNA, Springer, Netherlands, 2006, pp. 411–432 Search PubMed.
- R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, J. Chem. Soc., Chem. Commun., 1989, 0, 37–38 RSC.
- R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, Chem. Phys. Lett., 1989, 156, 61–63 CrossRef CAS.
- R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, J. Am. Chem. Soc., 1989, 111, 2308–2310 CrossRef CAS.
- J. L. Alonso, I. Peña, J. C. López and V. Vaquero, Angew. Chem., Int. Ed., 2009, 48, 6141–6143 CrossRef CAS PubMed.
- M. S. De Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612 CrossRef CAS PubMed.
- M. Mons, I. Dimicoli, F. Piuzzi, B. Tardivel and M. Elhanine, J. Phys. Chem. A, 2002, 106, 5088–5094 CrossRef CAS.
- E. Nir, C. Plützer, K. Kleinermanns and M. de Vries, Eur. Phys. J. D, 2002, 20, 317–329 CrossRef CAS.
- M. Y. Choi and R. E. Miller, J. Am. Chem. Soc., 2006, 128, 7320–7328 CrossRef CAS PubMed.
- E. Nir, M. Müller, L. I. Grace and M. S. de Vries, Chem. Phys. Lett., 2002, 355, 59–64 CrossRef CAS.
- E. Nir, I. Hünig, K. Kleinermanns and M. S. de Vries, Phys. Chem. Chem. Phys., 2003, 5, 4780 RSC.
- G. Bazsó, G. Tarczay, G. Fogarasi and P. G. Szalay, Phys. Chem. Chem. Phys., 2011, 13, 6799–6807 RSC.
- L. Lapinski, I. Reva, M. J. Nowak and R. Fausto, Phys. Chem. Chem. Phys., 2011, 13, 9676 RSC.
- S. A. Trygubenko, T. V. Bogdan, M. Rueda, M. Orozco, F. J. Luque, J. Šponer, P. Slavíček and P. Hobza, Phys. Chem. Chem. Phys., 2002, 4, 4192–4203 RSC.
- H. Ai, J. Liu and K. Chan, J. Mol. Model., 2013, 19, 3447–3461 CrossRef CAS PubMed.
- M. Broquier, S. Soorkia, G. Pino, C. Dedonder-Lardeux, C. Jouvet and G. Grégoire, J. Phys. Chem. A, 2017, 121, 6429–6439 CrossRef CAS PubMed.
- B. Yang, R. R. Wu, N. C. Polfer, G. Berden, J. Oomens and M. T. Rodgers, J. Am. Soc. Mass Spectrom., 2013, 24, 1523–1533 CrossRef CAS PubMed.
- A. B. Trofimov, J. Schirmer, V. B. Kobychev, A. W. Potts, D. M. P. Holland and L. Karlsson, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 305–329 CrossRef CAS.
- L. Belau, K. R. Wilson, S. R. Leone and M. Ahmed, J. Phys. Chem. A, 2007, 111, 7562–7568 CrossRef CAS PubMed.
- M. Schwell and M. Hochlaf, Photoinduced Processes in Nucleic Acids, 2014, pp. 155–208 Search PubMed.
- D. Roca-Sanjuán, M. Rubio, M. Merchán and L. Serrano-Andrés, J. Chem. Phys., 2006, 125, 084302 CrossRef PubMed.
- K. B. Bravaya, O. Kostko, S. Dolgikh, A. Landau, M. Ahmed and A. I. Krylov, J. Phys. Chem. A, 2010, 114, 12305–12317 CrossRef CAS PubMed.
- J. Zhou, C. Nicolas, X. Tang, L. Belau, M. S. De Vries and M. Ahmed, J. Phys. Chem. A, 2009, 113, 4829–4832 CrossRef CAS PubMed.
- D. Touboul, F. Gaie-Levrel, G. A. Garcia, L. Nahon, L. Poisson, M. Schwell and M. Hochlaf, J. Chem. Phys., 2013, 138, 094203 CrossRef CAS PubMed.
- O. Kostko, K. Bravaya, A. Krylov and M. Ahmed, Phys. Chem. Chem. Phys., 2010, 12, 2860–2872 RSC.
- Z. Chen, K. C. Lau, G. A. Garcia, L. Nahon, D. K. Božanić, L. Poisson, M. M. Al-Mogren, M. Schwell, J. S. Francisco, A. Bellili and M. Hochlaf, J. Am. Chem. Soc., 2016, 138, 16596–16599 CrossRef CAS PubMed.
- M. Lesslie, J. T. Lawler, A. Dang, J. A. Korn, D. Bím, V. Steinmetz, P. Maître, F. Tureček and V. Ryzhov, ChemPhysChem, 2017, 18, 1293–1301 CrossRef CAS PubMed.
- F. Tureček, J. Phys. Chem. B, 2021, 125, 7090–7100 CrossRef PubMed.
- M. I. Taccone, G. Féraud, M. Berdakin, C. Dedonder-Lardeux, C. Jouvet and G. A. Pino, J. Chem. Phys., 2015, 143, 041103 CrossRef PubMed.
- M. I. Taccone, A. F. Cruz-Ortiz, J. Dezalay, S. Soorkia, M. Broquier, G. Grégoire, C. G. Sánchez and G. A. Pino, J. Phys. Chem. A, 2019, 123, 7744–7750 CrossRef CAS PubMed.
- S. Lobsiger and S. Leutwyler, J. Phys. Chem. Lett., 2012, 3, 3576–3580 CrossRef CAS PubMed.
- NIST, available at http://webbook.nist.gov/chemistry/.
- S. Soorkia, C. Jouvet and G. Grégoire, Chem. Rev., 2020, 120, 3296–3327 CrossRef CAS PubMed.
- M. Broquier, S. Soorkia and G. Grégoire, Phys. Chem. Chem. Phys., 2015, 17, 25854–25862 RSC.
- A. Y. Pereverzev, X. Cheng, N. S. Nagornova, D. L. Reese, R. P. Steele and O. V. Boyarkin, J. Phys. Chem. A, 2016, 120, 5598–5608 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- D. O. Kashinski, G. M. Chase, R. G. Nelson, O. E. Di Nallo, A. N. Scales, D. L. Vanderley and E. F. C. Byrd, J. Phys. Chem. A, 2017, 121, 2265–2273 CrossRef CAS PubMed.
- MOLPRO, version 2015, a package of ab initio programs written by H.-J. Werner, P. J. Knowles, et al. See https://www.molpro.net.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- T. Shiozaki, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 134, 034113 CrossRef PubMed.
- T. Shiozaki and H. J. Werner, J. Chem. Phys., 2011, 134, 184104 CrossRef PubMed.
- T. Shiozaki and H. J. Werner, Mol. Phys., 2013, 111, 607–630 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- G. Ghigo, B. O. Roos and P. Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- J. P. Zobel, J. J. Nogueira and L. González, Chem. Sci., 2017, 8, 1482–1499 RSC.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- Z. Yang and M. T. Rodgers, Phys. Chem. Chem. Phys., 2012, 14, 4517–4526 RSC.
- M. Berdakin, V. Steinmetz, P. Maitre and G. A. Pino, Phys. Chem. Chem. Phys., 2015, 17, 25915–25924 RSC.
- J. M. Rice, G. O. Dudek and M. Barber, J. Am. Chem. Soc., 1965, 87, 4569–4576 CrossRef CAS PubMed.
- J. K. Wolken, C. Yao, F. Tureček, M. J. Polce and C. Wesdemiotis, Int. J. Mass Spectrom., 2007, 267, 30–42 CrossRef CAS.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone and K. C. Prince, Chem. Phys., 2007, 334, 53–63 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03953b |
| This journal is © the Owner Societies 2022 |