Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coincidence ion pair production (cipp) spectroscopy of diiodine†
Kristján
Matthíasson
 a,
Ágúst
Kvaran
a,
Ágúst
Kvaran
 *a,
Gustavo A.
Garcia
*a,
Gustavo A.
Garcia
 b,
Peter
Weidner
b,
Peter
Weidner
 c and
Bálint
Sztáray
c and
Bálint
Sztáray
 *c
*c
aScience Institute, University of Iceland, Dunhagi 3, 107 Reykjavík, Iceland. E-mail: agust@hi.is
bSynchrotron SOLEIL, L’Orme des Merisiers, St, Aubin BP 48, 91192 Gif sur Yvette, France
cDepartment of Chemistry, University of the Pacific, Stockton, CA-95211, USA. E-mail: bsztaray@pacific.edu
First published on 29th June 2022
Abstract
Coincidence ion pair production (I+ + I−) (cipp) spectra of I2 were recorded in a double imaging coincidence experiment in the one-photon excitation region of 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600–74
600–74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The I+ + I− coincidence signal shows vibrational band head structure corresponding to iodine molecule Rydberg states
000 cm−1. The I+ + I− coincidence signal shows vibrational band head structure corresponding to iodine molecule Rydberg states 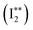 crossing over to ion-pair (I+I−) potential curves above the dissociation limit. The band origin (ν0), vibrational wavenumber (ωe) and anharmonicity constants (ωexe) were determined for the identified Rydberg states. The analysis revealed a number of previously unidentified states and a reassignment of others following a discrepancy in previous assignments. Since the ion pair production threshold is well established, the electric field-dependent spectral intensities were used to derive the cutoff energy in the transitions to the rotational levels of the 7pσ(1/2) (v′ = 3) state.
crossing over to ion-pair (I+I−) potential curves above the dissociation limit. The band origin (ν0), vibrational wavenumber (ωe) and anharmonicity constants (ωexe) were determined for the identified Rydberg states. The analysis revealed a number of previously unidentified states and a reassignment of others following a discrepancy in previous assignments. Since the ion pair production threshold is well established, the electric field-dependent spectral intensities were used to derive the cutoff energy in the transitions to the rotational levels of the 7pσ(1/2) (v′ = 3) state.
I. Introduction
A large number of Rydberg states have been identified for the iodine molecule (I2) by standard absorption spectroscopy1 and by REMPI.2–4 Interactions between Rydberg and ion-pair states are well known for the halogens5–9 as well as for the interhalogens.10–12 These have been found to occur either above or below7,8,12,13 the dissociation energy thresholds for ion-pair states. In the former case, ion pairs (AB → A+ + B−) are formed by bound Rydberg-to-free ion-pair state transitions, whereas in the latter case bound-to-bound (Rydberg to ion-pair state) state transfer occurs. Exciting I2 into a bound high energy Rydberg state which interacts with an ion-pair state should simultaneously form positive and negative ions, I+ and I− at discreet energies once the excitation energy goes above the respective ion-pair dissociation energy threshold.14,15 Kvaran et al. demonstrated this by vibrationally resolved excitation of I2, where both I+ and I− were formed above the dissociation threshold of about 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 cm−1.6 They observed virtually identical ion yield spectra for both atomic ions (I+ and I−) in the excitation region above the ion pair threshold. Spectral analysis revealed series of overlapping Rydberg states converging to the molecular ion ground state.
150 cm−1.6 They observed virtually identical ion yield spectra for both atomic ions (I+ and I−) in the excitation region above the ion pair threshold. Spectral analysis revealed series of overlapping Rydberg states converging to the molecular ion ground state.
Recently, we have used the new experimental technique of coincidence ion pair production (cipp) spectroscopy, which is based on the coincident detection of the positive and negative ions that are formed together. Experimentally, the cipp setup is identical to the well-established technique of photoelectron photoion coincidence (pepico) spectroscopy (bar some trivial wiring details). In the first such work, we have measured molecular fluorine (F2) and shown that cipp signal shows rotational band head structure, corresponding to F2 Rydberg states crossing over to the ion pair production potential surface. Spectral simulation and quantum defect analysis allowed characterization of five new molecular Rydberg states. The lowest-energy observed Rydberg state lacked some of the predicted rotational structure, which allowed an accurate determination of the ion pair production threshold which, together with pepico experiments carried out on the same apparatus, allowed us to determine the previously disputed F2 dissociation energy with unprecedented accuracy.16
In this paper, we present coincidence ion pair production (cipp) spectra for I2, which allowed identification of a large number of Rydberg states. Detailed analyses of the spectra and reanalysis of older absorption data1 revealed a number of new states and complete reassignment of some I2 molecule Rydberg states. Furthermore, detailed spectral simulations revealed how the cipp spectral intensities vary with the electric field near the ion pair formation energy threshold.
II. Experimental
The experiments were carried out with the DELICIOUS III double-imaging photoelectron photoion coincidence (i2PEPICO) spectrometer on the DESIRS undulator beamline17 of Synchrotron Soleil, in France. The instrument has been described in detail elsewhere18 and only a brief summary of the relevant parts is given here. Briefly, crystals of iodine were sublimated in an oven kept at 80 °C in a stream of helium bath gas. The iodine gas entered the ionization chamber through a supersonic expansion of an I2/He mixture, through a 200 μm heated nozzle, kept at 90 °C. The supersonic beam was collimated with a double skimmer setup of the SAPHIRS molecular beam endstation.19 Typical pressures were 1.5 × 10−3 mbar in the expansion, 3.5 × 10−6 mbar in the differential pumping, and less than 9 × 10−8 mbar in the ionization regions. Photons from the variable polarization undulator OPHELIE2 were dispersed by a 6.65 m normal-incidence monochromator with a 2400 lines per mm grating and focused onto a 200/300 μm (H/V) spot in the ionization region. The entrance and exit slits of the monochromator were set to 100 μm and 300 μm, respectively, providing an energy resolution of 9.7 cm−1 (1.2 meV) at 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (16 eV). To block out high-order harmonics, a gas filter located upstream of the beamline was filled with neon. For absolute energy calibration, the same gas filter was filled with krypton and its well-known absorption lines, corresponding to dips in the cation signal, because of the diminished photon intensity due to absorption by krypton in the gas filter, were used for calibration. Specifically, the 4p5(2P°3/2)5s–4p6(1S) (80 916.75 cm−1) and 4p5(2P°1/2)5s′–4p6(1S) (85 846.71 cm−1) absorption lines were used for calibration as reported by Yoshino and Tanaka and later deposited into the NIST Atomic Spectra Database.20,21 To validate the accuracy of this calibration, the cipp spectral lines were cross-referenced against the Venkateswarlu spectra,1vide infra.
000 cm−1 (16 eV). To block out high-order harmonics, a gas filter located upstream of the beamline was filled with neon. For absolute energy calibration, the same gas filter was filled with krypton and its well-known absorption lines, corresponding to dips in the cation signal, because of the diminished photon intensity due to absorption by krypton in the gas filter, were used for calibration. Specifically, the 4p5(2P°3/2)5s–4p6(1S) (80 916.75 cm−1) and 4p5(2P°1/2)5s′–4p6(1S) (85 846.71 cm−1) absorption lines were used for calibration as reported by Yoshino and Tanaka and later deposited into the NIST Atomic Spectra Database.20,21 To validate the accuracy of this calibration, the cipp spectral lines were cross-referenced against the Venkateswarlu spectra,1vide infra.
The DELICIOUS III spectrometer is composed of an electron velocity map imaging setup and a modified Wiley–McLaren time-of-flight 3D momentum imaging ion mass analyzer in a multistart–multistop coincidence detection mode. This setup produces a multi-dimensional coincidence data set, two cross sections of which yield photoion mass-selected photoelectron spectra, as well as mass spectra of internal energy-selected photoions. In the recently pioneered coincidence ion pair production (cipp) experiments, the same physical setup was utilized, except that anions were detected on the imaging electron detector, in coincidence with cations from the same ion pair production events, as explained in more detail in the first cipp publication.16 Ion pair production coincidences were registered at the calculated and experimentally confirmed time delay between the I+ and I− ions, using raytracing simulations of the DELICIOUS III coincidence setup.
III. Results and analysis
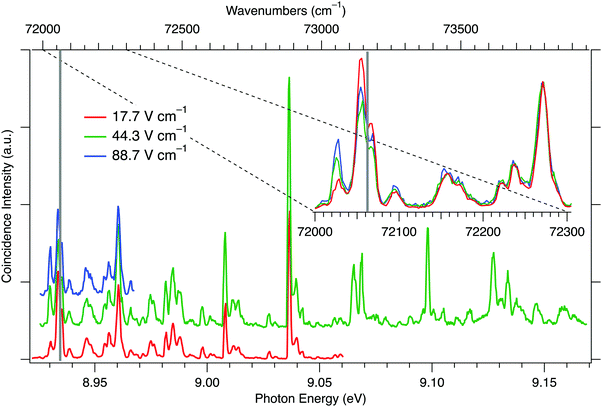
The coincidence ion pair production experiments were carried out in an electric field and, as previously noted,16 the cipp spectral lines may be susceptible to Stark shifts. Therefore, the experiments were carried out at three different extraction fields: 17.7, 44.3, and 88.7 V cm−1. Due to limitations on the available synchrotron beamtime, the whole spectral range (8.92–9.17 eV) was only covered in the 44.3 V cm−1 measurements. The 17.7 V cm−1 measurements were carried out in the 8.92–9.06 eV range. In order to assess the effect of higher electric field near the ion pair production threshold, we have also collected data with 88.7 V cm−1 field for the first 40 meV of the spectra. Fig. 1 shows the collected cipp spectra at the three extraction fields and a cursory comparison shows that, unlike the F2 cipp spectra,16 the peaks do not shift significantly with the extraction field strengths. However, close to the ion pair production threshold, the peak intensities and peak shapes do exhibit field-dependence. The inset in Fig. 1 shows that the first major peak between 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020–72
020–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 cm−1 is diminished at low field, while the next peak and its shoulder between 72
030 cm−1 is diminished at low field, while the next peak and its shoulder between 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045–72
045–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065 cm−1 is somewhat enhanced, when the spectra are normalized for matching peak intensities above 72
065 cm−1 is somewhat enhanced, when the spectra are normalized for matching peak intensities above 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1.
100 cm−1.
Spectral analysis
The mid-field (44.3 V cm−1) spectrum was used for spectral analysis. It is shown in Fig. 1 and 2 for the excitation region of 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600–74
600–74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. These show vibrational spectral bands due to transitions from the ground state I2, X1Σ+(v′′ = 0) to Rydberg vibrational states
000 cm−1. These show vibrational spectral bands due to transitions from the ground state I2, X1Σ+(v′′ = 0) to Rydberg vibrational states 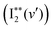 followed by a transfer to an ion-pair state (I+I−) above its dissociation limit to form I+ and I−, i.e.,
followed by a transfer to an ion-pair state (I+I−) above its dissociation limit to form I+ and I−, i.e.,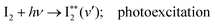 | (1a) |
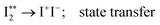 | (1b) |
| I+I− → I+ + I−; dissociation | (1c) |
No signal was detected below 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 cm−1 and the weak spectral bands in the region of 71
730 cm−1 and the weak spectral bands in the region of 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730–71
730–71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 cm−1 are “hot bands” due to transitions from ν′′ = 1 (see Fig. 2). This is in agreement with expectations, since the threshold for atom ion pair (I+/I−) formation is predicted to be 72
930 cm−1 are “hot bands” due to transitions from ν′′ = 1 (see Fig. 2). This is in agreement with expectations, since the threshold for atom ion pair (I+/I−) formation is predicted to be 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062.4 ± 0.5 cm−1.22 These spectral bands show close correspondence to peak positions observed in the absorption spectra by Venkateswarlu.1 The published peak assignment therein, however, needed a revision based on a quantum defect analysis in combination with a spectral simulation.
062.4 ± 0.5 cm−1.22 These spectral bands show close correspondence to peak positions observed in the absorption spectra by Venkateswarlu.1 The published peak assignment therein, however, needed a revision based on a quantum defect analysis in combination with a spectral simulation.
The band origin (ν00) of a Rydberg vibrational state 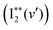 spectrum due to transitions to the lowest vibrational level, v′ = 0 can, to a first approximation, be expressed as,
spectrum due to transitions to the lowest vibrational level, v′ = 0 can, to a first approximation, be expressed as,
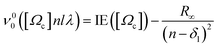 | (2) |
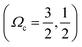 of the ground ionic state I2+(X2Πg) in vibrational level v+ = 0, for a Rydberg electron with principal quantum number n, in a molecular orbital λ, corresponding to an atomic orbital l. IE([Ωc]) is the ionization energy of I2(X1Σg+(v′′ = 0, J′′ = 0)) to form I2+([Ωc]) for v+ = 0. R∞ is the Rydberg constant (109 735.85 cm−1) and δl is an l-dependent quantum defect value, which is a measure of how much a Rydberg series diverges from the corresponding hydrogen atom Rydberg series. The I2 molecule is best described by Hunds case (c)23 in which case the total spin is not a good quantum number and singlet and triplet states are not distinguishable. Accepted values for the ionization energies of I2 to form I2+
of the ground ionic state I2+(X2Πg) in vibrational level v+ = 0, for a Rydberg electron with principal quantum number n, in a molecular orbital λ, corresponding to an atomic orbital l. IE([Ωc]) is the ionization energy of I2(X1Σg+(v′′ = 0, J′′ = 0)) to form I2+([Ωc]) for v+ = 0. R∞ is the Rydberg constant (109 735.85 cm−1) and δl is an l-dependent quantum defect value, which is a measure of how much a Rydberg series diverges from the corresponding hydrogen atom Rydberg series. The I2 molecule is best described by Hunds case (c)23 in which case the total spin is not a good quantum number and singlet and triplet states are not distinguishable. Accepted values for the ionization energies of I2 to form I2+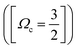 of 9.3074 ± 0.0002 eV (75
of 9.3074 ± 0.0002 eV (75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069 cm−1) and to form I2+
069 cm−1) and to form I2+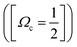 of 9.950 ± 0.002 eV (80 252 cm−1)22,24 were used. These differ significantly from the 9.3995 eV (75 814 cm−1) and 10.0297 eV (80 895 cm−1) values, respectively, used by Venkateswarlu,1 which explains why the overall Rydberg state assignments needed to be revised. δl values of about 3.5 ± 0.1 and 0.93 ± 0.12 were reported by Venkateswarlu for p(l = 1) and f(l = 3) Rydberg series of I21 and judging from atomic energy levels25δl values of about 4.01, 3.57, 2.50 and 0.04 are expected for s(l = 0), p(1), d(2) and f(3) Rydberg electron iodine atom orbitals, respectively.
of 9.950 ± 0.002 eV (80 252 cm−1)22,24 were used. These differ significantly from the 9.3995 eV (75 814 cm−1) and 10.0297 eV (80 895 cm−1) values, respectively, used by Venkateswarlu,1 which explains why the overall Rydberg state assignments needed to be revised. δl values of about 3.5 ± 0.1 and 0.93 ± 0.12 were reported by Venkateswarlu for p(l = 1) and f(l = 3) Rydberg series of I21 and judging from atomic energy levels25δl values of about 4.01, 3.57, 2.50 and 0.04 are expected for s(l = 0), p(1), d(2) and f(3) Rydberg electron iodine atom orbitals, respectively.
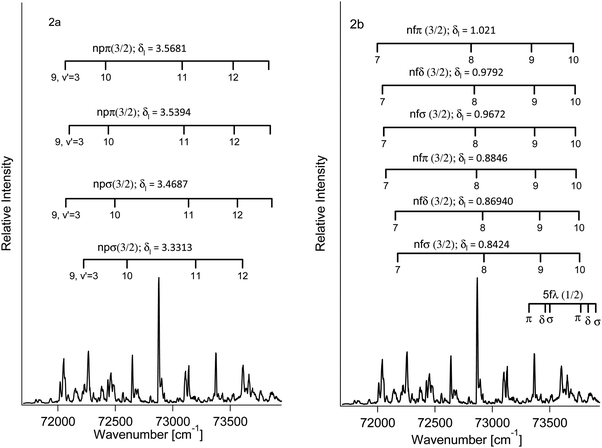
Determination of the band origins (ν00) was based on a search of band/peak series observed in our spectra as well as the absorption spectra1 for consistent and realistic values of δl (i.e. a quantum defect analysis). The experimental band/peak maxima were assumed to correspond to the band origin. This could be justified for our observed spectral bands by analysis of band shapes (see Fig. S1 and S2 in the ESI†). A total of 20 Rydberg state series were identified (see Table 1 and Fig. 2). Eight Rydberg series were found to correspond to transitions to np Rydberg orbitals (δl in the range of 3.33–3.57), for which four converge to the Ωc = 3/2 spin–orbit molecular ion state and four converge to the Ωc = 1/2 spin–orbit excited state. Further 12 Rydberg series were found to correspond to transitions to nf Rydberg orbitals (δl in the range of 0.84–1.03), with six series converging to each of the two spin–orbit ion states.
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| n | np (3/2); δl = 3.3313 | np (3/2); δl = 3.4687 | np (3/2); δl = 3.5394 | np (3/2); δl = 3.56812 | ||||
| Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | |
| 6 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 662 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 942 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 958 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 613 613 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 519 519 |
| 7 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 916 |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 948 948 |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906 906 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 752 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
| 8 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 034 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028 028 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 725 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717 717 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 554 554 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 482 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
| 9 | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 482 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 485 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389 389 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389 389 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
| 10 | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602* 602* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497 497 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496* 496* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440* 440* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 416 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416* 416* |
| 11 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203 203 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200* 200* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138* 138* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098* 098* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082 082 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085* 085* |
| 12 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608* 608* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 562 562 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563* 563* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535* 535* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 526 526 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525* 525* |
| 13 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 895 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 893 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 861 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863 863 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 843 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849 849 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 836 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 835 |
| 14 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 106 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081 081 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066 066 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 061 |
— |
| 15 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263 263 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 244 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 230 |
— |
| 16 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 367 367 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363 363 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364 364 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359 359 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
| 17 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481 481 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 464 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461 461 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
|
| 18 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 559 559 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 550 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 544 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 542 |
— | |
| 19 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
— | |
| 20 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 674 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 672 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 664 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 663 663 |
— | |
| 21 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717 717 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079 079 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
|
| 22 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754 754 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 747 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746 746 |
||
| n | np (1/2); δl = 3.3313 | np (1/2); δl = 3.4687 | np (1/2); δl = 3.5394 | np (1/2); δl = 3.56812 | ||||
|---|---|---|---|---|---|---|---|---|
| Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | |
| 6 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 841 841 |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803 803 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 122 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 122 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 124 124 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
| 7 | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096* 096* |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449 449 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449 449 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 085 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932 932 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
| 8 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 215 |
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 904 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906 906 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 662 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 672 |
| (b) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | nf (3/2); δl = 0.84243 | nf (3/2); δl = 0.8636 | nf (3/2); δl = 0.8846 | nf (3/2); δl = 0.9672 | nf (3/2); δl = 0.9861 | nf (3/2); δl = 1.021 | ||||||
| Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | |
| 4 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063 |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074 074 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 914 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763 763 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754 754 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 138 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 122 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 988 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 004 004 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 696 |
| 5 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 721 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 656 656 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652 652 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322 322 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258 258 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 179 179 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139 139 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
| 6 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 955 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 910 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 918 918 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876 876 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 883 883 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737 737 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 704 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 702 702 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 643 643 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 637 |
| 7 | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 175 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175* 175* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 155 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155* 155* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135* 135* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054* 054* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035* 035* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 8 | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 927 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930* 930* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 915 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914* 914* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902 902 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901* 901* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850* 850* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839 839 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839* 839* |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816 816 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815* 815* |
| 9 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422* 422* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412 412 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411* 411* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 403 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403* 403* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368* 368* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 361 361 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360* 360* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 346 346 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341* 341* |
| 10 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762* 762* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750* 750* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749 749 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748* 748* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 724 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724* 724* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 719 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719* 719* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705* 705* |
| 11 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 001 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999 999 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997 997 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999 999 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979 979 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 984 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
| 12 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188 188 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 184 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 181 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 167 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165 165 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 167 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 157 |
| 13 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 328 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 324 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322 322 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309 309 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
— |
| 14 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 435 435 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 433 433 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 423 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 423 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421 421 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 423 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 414 |
| 15 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 522 522 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 521 |
7452 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 521 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 518 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 508 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
| 16 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 592 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 577 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 582 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 577 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 580 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 577 |
| 17 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649 649 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 646 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 648 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676 676 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 647 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 646 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 641 641 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
| 18 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 696 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 697 697 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 696 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 695 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 691 691 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 690 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689 689 |
— |
| 19 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
— | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 732 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 731 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723 723 |
| 20 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 769 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 766 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 766 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 762 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 765 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
| 21 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 799 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 799 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798 798 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 795 795 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 794 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
| 22 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 824 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 824 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 821 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 821 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 820 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
| n | nf (1/2); δl = 0.84243 | nf (1/2); δl = 0.8636 | nf (1/2); δl = 0.8846 | nf (1/2); δl = 0.9672 | nf (1/2); δl = 0.9861 | nf (1/2); δl = 1.021 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | Calculated | Observed | |
| 4 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243 243 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 256 256 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052 052 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943 943 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 845 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 318 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165 165 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139 139 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
| 5 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 901 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904* 904* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 818 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814* 814* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 769 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769* 769* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501* 501* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438 438 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438* 438* |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 319 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319* 319* |
The λ(σ, π, or δ) configurations of the Rydberg states were further specified by energetic considerations based on,
(i) that the energy progression of Rydberg molecular states is analogous to that of the corresponding Rydberg atomic states, for s < p < d < f.
(ii) that the energies change as π < δ < σ for the f Rydberg series and as π < σ for the p series.23
Thus, series of f(σ, π, δ) and p(σ, π) states were identified as listed in Table 1. Two series for each set of quantum numbers were identified due to the two possible spin states of the excited electron. Energy differences corresponding to the spin–orbit coupling for the p and f Rydberg electrons were found to be about 330 cm−1 and 1000 cm−1, respectively, virtually independent of λ(σ, π, δ) for the same l (f or p). Judging from our observations the trends in (i)–(ii) are independent of the molecular ion core spin–orbit configuration ([1/2], [3/2]).
In combination with the quantum defect analysis of the band origins for v′ = 0(ν00), search for vibrational bands due to transitions to higher Rydberg vibrational states (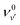 ; v′ > 0) was made (Fig. 3). This was guided by the assumption that the vibrational frequencies/wavenumbers are comparable to that of the ground neutral (
; v′ > 0) was made (Fig. 3). This was guided by the assumption that the vibrational frequencies/wavenumbers are comparable to that of the ground neutral (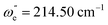
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22) and ionic (ωe+ = 220–240 cm−1
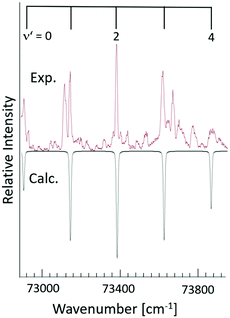
22) and ionic (ωe+ = 220–240 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22) molecular states. Finally, the observed spectrum was simulated by using the PGOPHER program.26 The simulation was performed by optimizing a fit of calculated and experimental spectra for the total spectral range. The calculated spectra were based on Franck–Condon factors for the absorption transition, using known vibrational constants for the ground state of I2 and vibrational constants for the excited states as fit parameters. Voigt (a combination of Gaussian width contribution of 8 cm−1 and Lorentzian width contribution of 2 cm−1) line profiles were used to represent the vibrational bands profiles (see Fig. 3 and 4). The fit analysis resulted in vibrational temperature (Tvib) of about 40 K. In some cases, significant difference in peak intensities was observed between the experimental and calculated spectra. This is not a surprise, since the cipp detection depends on the crossover from the Rydberg states to ion-pair states, in addition to absorption, whereas the simulation is based on the absorption cross-sections only. In particular we were unable to fit/explain an unusually high intensity peak which appears at 72
22) molecular states. Finally, the observed spectrum was simulated by using the PGOPHER program.26 The simulation was performed by optimizing a fit of calculated and experimental spectra for the total spectral range. The calculated spectra were based on Franck–Condon factors for the absorption transition, using known vibrational constants for the ground state of I2 and vibrational constants for the excited states as fit parameters. Voigt (a combination of Gaussian width contribution of 8 cm−1 and Lorentzian width contribution of 2 cm−1) line profiles were used to represent the vibrational bands profiles (see Fig. 3 and 4). The fit analysis resulted in vibrational temperature (Tvib) of about 40 K. In some cases, significant difference in peak intensities was observed between the experimental and calculated spectra. This is not a surprise, since the cipp detection depends on the crossover from the Rydberg states to ion-pair states, in addition to absorption, whereas the simulation is based on the absorption cross-sections only. In particular we were unable to fit/explain an unusually high intensity peak which appears at 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874 cm−1 (see Fig. 4).
874 cm−1 (see Fig. 4).
All in all, the analyses allowed assignment of the Rydberg state spectra with respect to n, l, λ and v′ as well as determination of band origin (ν00), vibrational wavenumber (ωe), and in some cases anharmonicity constants (ωexe) for the Rydberg states (see Tables 1 and 2).
| Configuration | ν 00 [cm−1] | ω e′ [cm−1] | ω e x e′ [cm−1] | Relative intensity |
|---|---|---|---|---|
| a Based on simulation of spectra. | ||||
| (a) | ||||
| [σg2πu4πg3σu, 2Π3/2u] nlλ | ||||
| 9pπu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350a 350a |
241 | 0.8 | 0.50 |
| 10pπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 416 |
240 | 0.6 | 0.10 |
| 11pπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086 |
240 | 0.6 | 0.10 |
| 12pπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 525 |
240 | 0.6 | 0.30 |
| 9pπu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389a 389a |
239 | 0.4 | 0.25 |
| 10pπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
239 | 0.8 | 0.50 |
| 11pπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
241 | 0.6 | 0.20 |
| 12pπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 535 |
241 | 0.6 | 0.20 |
| 9pσu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485a 485a |
196 | 0.1 | 0.70 |
| 10pσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 496 |
206 | 0.2 | 0.40 |
| 11pσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 138 |
199 | 0.6 | 0.35 |
| 12pσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
205 | 0.6 | 0.4 |
| 9pσu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654a 654a |
190 | 0.4 | 0.20 |
| 10pσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602 602 |
190 | 0.2 | 0.25 |
| 11pσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
190 | 0.4 | 0.2 |
| 12pσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
190 | 0.6 | 0.2 |
| (b) | ||||
| [σg2πu4πg3σu, 2Π3/2u] nlλ | ||||
| 7fπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000a 000a |
242 | 0.6 | 0.3 |
| 8fπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 815 |
239 | 0.6 | 0.25 |
| 9fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 341 |
240 | 0.6 | 0.1 |
| 10fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
— | — | — |
| 7fδu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035 |
230 | 0.2 | 0.8 |
| 8fδu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839 839 |
231 | 0.6 | 0.4 |
| 9fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
231 | 0.6 | 0.2 |
| 10fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 719 |
— | — | — |
| 7fσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
217 | 0.5 | 0.8 |
| 8fσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
215 | 0.6 | 0.4 |
| 9fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 368 |
216 | 0.6 | 0.2 |
| 10fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 724 |
— | — | — |
| 7fπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
224 | 0.8 | 0.23 |
| 8fπu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 901 |
223 | 0.8 | 0.2 |
| 9fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 403 |
222 | 0.6 | 0.5 |
| 10fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748 748 |
— | — | — |
| 7fδu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 155 |
237 | 0.2 | 0.8 |
| 8fδu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 914 |
238 | 0.2 | 0.4 |
| 9fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 409 |
239 | 0.6 | 0.3 |
| 10fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
— | — | — |
| 7fσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 175 |
214 | 0.5 | 0.4 |
| 8fσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
216 | 0.6 | 0.35 |
| 9fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422 422 |
218 | 0.3 | 0.2 |
| 10fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 766 |
— | — | — |
| (c) | ||||
| [σg2πu4πg3σu, 2Π1/2u] nlλ | ||||
| 7pπu | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930a 930a |
238 | 0.9 | 0.50 |
| 7pπu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085a 085a |
237 | 0.8 | 0.35 |
| 7pσu | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449a 449a |
196 | 0.4 | 0.40 |
| 7pσu | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
190 | 0.8 | 0.25 |
| 5fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 319 |
238 | 0.6 | 0.2 |
| 5fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438 438 |
231 | 0.6 | 0.5 |
| 5fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
216 | 0.6 | 0.2 |
| 5fπu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 773 773 |
— | — | — |
| 5fδu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 901 |
— | — | — |
| 5fσu | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912 |
— | — | — |
Ion pair threshold energetics
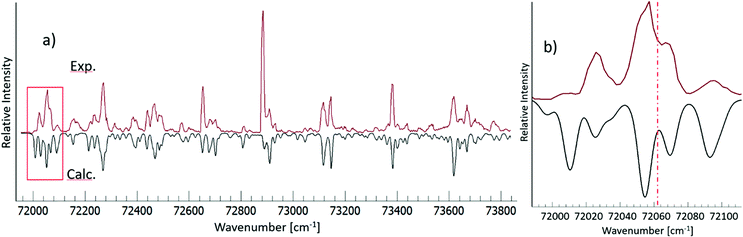
Close-up figure in the threshold energy region reveals missing vibrational bands below 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 cm−1 (Fig. 4b). The lack of observable lines in that region must correspond to transitions with energy levels below the ion pair dissociation energy threshold for I2. The Active Thermochemical Tables (ATcT) value of the ion pair production threshold is 862.0575 ± 0.0061 kJ mol−1 or 72062.4 ± 0.5 cm−1,27 which is significantly larger than the observed cut off in our cipp spectra (≤72
020 cm−1 (Fig. 4b). The lack of observable lines in that region must correspond to transitions with energy levels below the ion pair dissociation energy threshold for I2. The Active Thermochemical Tables (ATcT) value of the ion pair production threshold is 862.0575 ± 0.0061 kJ mol−1 or 72062.4 ± 0.5 cm−1,27 which is significantly larger than the observed cut off in our cipp spectra (≤72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 cm−1). This must be due to a shifting of the ion pair production threshold by the applied electric field in the extraction region of the spectrometer. The ion pair production threshold is known to red-shift in energy (ΔE) proportionally to the square root of the electric field (F) as,
030 cm−1). This must be due to a shifting of the ion pair production threshold by the applied electric field in the extraction region of the spectrometer. The ion pair production threshold is known to red-shift in energy (ΔE) proportionally to the square root of the electric field (F) as,were α is the shift constant.28–31 Typical measured values of α range from −3.9 to −6.11 cm−1, when F is given in V cm−1.32
The relative intensity of the spectral band at 72 025 cm−1 is found to increase with the electric field (F) (see Fig. 1 and 5). This can be attributed to a different cutoff of the rotational energy levels of the 7pσ(1/2) (v′ = 3) vibrational Rydberg state, as the ion pair energy threshold decreases with increasing F. A good fit to the experimentally determined relative intensities in the 44.3 V cm−1 and 17.7 V cm−1 cipp spectra in the 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015–72
015–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 cm−1 region was achieved when the spectral simulations were carried out with or without including transitions to the lowest 20 J′ rotational energy levels, as shown in Fig. 5. Thus, by assigning the cutoff energy in the 17.7 V cm−1 cipp spectrum to the energy of the J′ = 20 levels of the 7pσ(1/2) (v′ = 3) state, a value of α = −5.5 ± 0.2 cm−1 was obtained for the I2 cipp process.
080 cm−1 region was achieved when the spectral simulations were carried out with or without including transitions to the lowest 20 J′ rotational energy levels, as shown in Fig. 5. Thus, by assigning the cutoff energy in the 17.7 V cm−1 cipp spectrum to the energy of the J′ = 20 levels of the 7pσ(1/2) (v′ = 3) state, a value of α = −5.5 ± 0.2 cm−1 was obtained for the I2 cipp process.
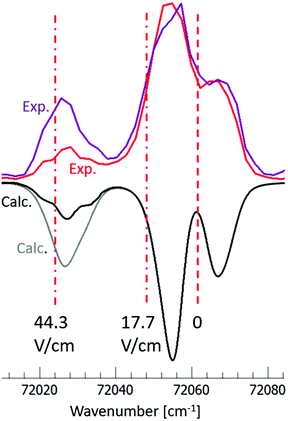 | ||
Fig. 5 Simulation of the I2 coincidence ion pair production spectra in the excitation region of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015–72 015–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 cm−1, recorded at 17.7 V cm−1 (red) and 44.3 V cm−1 (purple) electric fields; experimental spectra on top, calculated spectra inverted below. Calculated spectra are obtained without (black) and with (grey) transitions to J′ < 20 in the 7pσ(1/2), (v′ = 3) vibrational Rydberg state. The ion pair thresholds are marked by vertical broken lines for no electric field, for electric field 17.7 V cm−1 and for electric field 44.3 V cm−1. Note that the normalization of spectral intensities is different from the inset in Fig. 1. See main text. 080 cm−1, recorded at 17.7 V cm−1 (red) and 44.3 V cm−1 (purple) electric fields; experimental spectra on top, calculated spectra inverted below. Calculated spectra are obtained without (black) and with (grey) transitions to J′ < 20 in the 7pσ(1/2), (v′ = 3) vibrational Rydberg state. The ion pair thresholds are marked by vertical broken lines for no electric field, for electric field 17.7 V cm−1 and for electric field 44.3 V cm−1. Note that the normalization of spectral intensities is different from the inset in Fig. 1. See main text. | ||
This observed field dependence is markedly different from what we saw in the F2 cipp experiments, where the rotational energy resolution allowed us to directly observe how the individual rotational lines exhibited energy-dependent Stark shift, with the α value ranging from −0.96 cm−1 at threshold to −1.7 cm−1 at the high end of the studied photon energy range.
IV. Discussion
As the excitation energy closes in on the ionization potential of molecules, discreet rotational and vibrational spectra structures can be difficult to obtain by spectroscopic means. This can be partly due to increasing overlap of spectral features in association with larger density of states as the energy increases, and partly due to enhanced line broadening in association with shorter lifetime of states as the number of decay pathways increase with energy. The nature of the coincidence ion pair detection using high-resolution synchrotron radiation in conjunction with a supersonic molecular beam source bypasses some of these problems. First, the technique allows a distinction between direct ion and ion pair formation and offers very low background noise, due to the coincidence detection. Second, the jet-cooling reduces the number of observable rotational and vibrational excitations and therefore lowers overlap of spectral features. Third, in addition to a photon absorption, a crossing from the excited states to ion-pair states is involved. Thus, the latter step acts selectively to detect only spectra of Rydberg states with non-zero probabilities for transfer to the ion-pair states.Comparison of our results with an earlier work on excitation functions for I+ and I− formed from photodissociation of I2 is of particular interest.6 The coincident ion pair detection method combined with a supersonic molecular beam inlet and a high-resolution photon source is found to greatly improve sensitivity, selectivity, and spectral resolution, allowing for detection of a many more Rydberg state transitions. The low-resolution excitation spectra in the observation region of concern were attributed to a minimum of 5 overlapping Rydberg state spectra. Three of these spectra were assigned to transitions to [σg2πu4πg3σu, 2Π3/2u] npπ Rydberg states for n = 9, 10, and 11 whereas others were left unassigned. Those analyses were based on quantum defect calculations and spectral simulations as well as on an analogy to corresponding spectra derived for Br2.5 In contrast, our analysis reveals the involvement of a total of fifty Rydberg states in that spectral region.
All Rydberg states observed are of ungerade symmetry and either Ω = 0 or 1 according to selection rules. Therefore, assuming that homogeneous state interactions (ΔΩ = 0) and conservation of the symmetry (u ↔ u) hold for the Rydberg to ion-pair state transfer process, only two (D(0u+) and γ(1u)) of six possible ion-pair states (D(0u+), γ(1u), δ(2u), E(0g+), β(1g), and D′(2g)) are involved.33 The Voigt profile line widths derived from our simulation calculations of about 9.1 cm−1 (see above) is close to the expected fwhm of cipp spectral peaks of about 1.2 meV/9.7 cm−1, suggesting that the lifetime of the Rydberg state is not shorter than about 0.6 ps.
V. Summary and conclusions
Coincidence ion pair detection was used for photoexcitation of jet cooled I2 molecular beam in the 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940–74
940–74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 photon energy region. The observed peak structures were attributed to vibrational bands due to transitions from the ground state (I2 X1Σ+(v′′ = 0, 1)) to a number of Rydberg states, followed by transfer to ion-pair states above the dissociation threshold to form the atom ion pair (I+/I−). Simulations of the peak structures revealed a total of fifty Rydberg states in this region and allowed the determination of spectroscopic constants (band origin, vibrational wavenumber and anharmonicity constants) for the excited states.
000 cm−1 photon energy region. The observed peak structures were attributed to vibrational bands due to transitions from the ground state (I2 X1Σ+(v′′ = 0, 1)) to a number of Rydberg states, followed by transfer to ion-pair states above the dissociation threshold to form the atom ion pair (I+/I−). Simulations of the peak structures revealed a total of fifty Rydberg states in this region and allowed the determination of spectroscopic constants (band origin, vibrational wavenumber and anharmonicity constants) for the excited states.
Transfer from Rydberg states to ion-pair states analogous to those reported here is well known for many other molecules, such as other diatomic halogens,5–9 hydrogen halides,34,35 and small polyatomic molecules.36,37 In this respect, the method of coincidence ion pair detection has only been applied to the fluorine molecule.16 Based on the present work on I2 and our work on F2 there is a reason to believe that coincidence ion pair production spectroscopy could be a valuable tool to explore relevant state transfer mechanisms as well as to characterize the Rydberg states involved for many other systems. Indeed, the method could be applied to number of intriguing molecular systems where Rydberg to ion-pair interactions are known to be involved. We hope that the data and interpretations presented here will produce further experimental and theoretical studies along those lines in the near future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. Sz. gratefully acknowledges the support of the National Science Foundation (grant no. CHE-1665464). Experiments were performed at the DESIRS VUV beamline of the Soleil Synchrotron under proposal number 20190866 and we thank the beamline staff for their support, in particular Dr Laurent Nahon for helpful discussions in the design and preparation of the experiment. The financial support of the University Research Fund, University of Iceland and the Icelandic Research Fund (Grant No. 184693-053) is gratefully acknowledged. We are grateful to Ms Jessica De La Cruz for her help with the cipp experiments.References
- P. Venkateswarlu, Can. J. Phys., 1970, 48, 1055–1080 CrossRef CAS.
- R. J. Donovan, R. V. Flood, K. P. Lawley, A. J. Yencha and T. Ridley, Chem. Phys., 1992, 164, 439–450 CrossRef CAS.
- W. Huasheng, J. Ásgeirsson, Á. Kvaran, R. J. Donovan, R. V. Flood, K. P. Lawley, T. Ridley and A. J. Yencha, J. Mol. Struct., 1993, 293, 217–222 CrossRef.
- Á. Kvaran, H. Wang and J. Ásgeirsson, J. Mol. Spec., 1994, 163, 541–558 CrossRef.
- A. J. Yencha, D. K. Kela, R. J. Donovan, A. Hopkirk and Á. Kvaran, Chem. Phys. Lett., 1990, 165, 283–288 CrossRef CAS.
- Á. Kvaran, A. J. Yencha, D. K. Kela, R. J. Donovan and A. Hopkirk, Chem. Phys. Lett., 1991, 179, 263–267 CrossRef.
- Á. Kvaran, H. Wang, G. H. Jóhannesson and A. J. Yencha, Chem. Phys. Lett., 1994, 222, 436–442 CrossRef.
- Á. Kvaran, G. H. Jóhannesson and H. Wang, Chem. Phys., 1996, 204, 65–75 CrossRef.
- K. P. Lawley, T. Ridley, Z. Min, P. J. Wilson, M. S. N. Alkahali and R. J. Donovan, Chem. Phys., 1995, 197, 37–50 CrossRef CAS.
- A. J. Yencha, T. Ridley, R. Maier, R. V. Flood, K. P. Lawley, R. J. Donovan and A. Hopkirk, J. Phys. Chem., 1993, 97, 4582–4588 CrossRef CAS.
- D. Kaur, A. J. Yencha, R. J. Donovan, Á. Kvaran and A. Hopkirk, Org. Mass Spec., 1993, 28, 327–334 CrossRef CAS.
- Á. Kvaran, H. Wang and G. H. Jóhannesson, J. Phys. Chem., 1995, 99, 4451–4457 CrossRef.
- K. P. Lawley, T. Ridley, Z. Min, P. J. Wilson, M. S. N. Al-Kahali and R. J. Donovan, Chem. Phys., 1995, 197, 37–50 CrossRef CAS.
- J. Yang, Y. S. Hao, J. Li, C. Zhou and Y. X. Mo, J. Chem. Phys., 2005, 122, 134308 CrossRef PubMed.
- J. Yang, Y. S. Hao, J. Li, C. Zhou and Y. X. Mo, J. Chem. Phys., 2007, 127, 209901 CrossRef.
- K. Matthiasson, A. Kvaran, G. A. Garcia, P. Weidner and B. Sztaray, Phys. Chem. Chem. Phys., 2021, 23, 8292–8299 RSC.
- L. Nahon, N. de Oliveira, G. A. Garcia, J. F. Gil, B. Pilette, O. Marcouille, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef CAS PubMed.
- G. A. Garcia, B. K. C. de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef CAS PubMed.
- X. F. Tang, G. A. Garcia, J. F. Gil and L. Nahon, Rev. Sci. Instrum., 2015, 86, 123108 CrossRef PubMed.
- K. Yoshino and Y. Tanaka, J. Opt. Soc. Am., 1979, 69, 159–165 CrossRef CAS.
- D. C. Morton, Astrophys. J. Suppl. Ser., 2000, 130, 403–436 CrossRef CAS.
- K. P. Huber, G. H. Herzberg, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899 Search PubMed.
- G. Herzberg, Molecular Spectra and Molecular Structure; I. Spectra of Diatomic Molecules, Van Nostrand Reinhold Company, New York, 2nd edn, 1950, ch. VI Search PubMed.
- M. C. R. Cockett, J. G. Goode, K. P. Lawley and R. J. Donovan, J. Chem. Phys., 1995, 102, 5226–5234 CrossRef CAS.
- A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (version 5.9), National Institute of Standards and Technology, Gaithersburg, MD, 20899 Search PubMed.
- PGOPHER, A Program for Simulating Rotational, Vibrational and Electronic Spectra, C. M. Western, University of Bristol, https://pgopher.chm.bris.ac.uk.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122r of the Thermochemical Network (2021); available at http://ATcT.anl.gov.
- M. G. Littman, M. M. Kash and D. Kleppner, Phys. Rev. Lett., 1978, 41, 103–107 CrossRef CAS.
- E. Y. Xu, H. Helm and R. Kachru, Phys. Rev. Lett., 1987, 59, 1096–1099 CrossRef CAS PubMed.
- W. L. Glab and J. P. Hessler, Phys. Rev. Lett., 1989, 62, 1472–1475 CrossRef CAS PubMed.
- E. D. Poliakoff, J. L. Dehmer, A. C. Parr and G. E. Leroi, Chem. Phys. Lett., 1984, 111, 128–132 CrossRef CAS.
- S. T. Pratt, E. F. McCormack, J. L. Dehmer and P. M. Dehmer, Phys. Rev. Lett., 1992, 68, 584–587 CrossRef CAS PubMed.
- Á. Kvaran, S. Ó. Jónsdóttir and T. E. Thorgeirsson, Proc. Indian Acad. Sci. (Chem. Sci.), 1991, 103, 417–428 CrossRef.
- A. Kvaran, K. Matthiasson and H. S. Wang, J. Chem. Phys., 2009, 131, 044324 CrossRef PubMed.
- Á. Kvaran, K. Matthíasson, H. Wang, A. Bodi and E. Jonsson, J. Chem. Phys., 2008, 129, 164313 CrossRef PubMed.
- K. Matthiasson, G. Koumarianou, M. X. Jiang, P. Glodic, P. C. Samartzis and A. Kvaran, Phys. Chem. Chem. Phys., 2020, 22, 4984–4992 RSC.
- A. Kvaran, H. Wang, K. Matthiasson and A. Bodi, J. Phys. Chem. A, 2010, 114, 9991–9998 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01684b |
| This journal is © the Owner Societies 2022 |