Nucleophilic catalysis of p-substituted aniline derivatives in acylhydrazone formation and exchange

Abstract

Hydrazone bond formation is a versatile reaction employed in several research fields. It is one of the most popular reversible reactions in dynamic combinatorial chemistry. Under physiological conditions, hydrazone exchange benefits from the addition of a nucleophilic catalyst. We report a mechanistic study and superior performance of electron-rich p-substituted aniline derivatives as catalysts for efficient hydrazone formation and exchange in both protic and aprotic solvents. Rigorous kinetic analyses demonstrate that imine formation with 3-hydroxy-4-nitrobenzaldehyde and aniline derivatives proceeds with unprecedented third-order kinetics in which the aldehyde consistently shows a partial order of two. Computational investigations provide insights into the mechanisms of these transformations.

---

Introduction

Hydrazone bond formation is a versatile reaction employed in bioconjugation, polymer functionalization, peptide ligation, metal sensing, dyes, and medicinal and supramolecular chemistry amongst others.^1–12 The hydrazone group's popularity has been attributed to its easy synthesis and distinctive structural properties such as (i) the isomerism of the C=N bond, (ii) the stability to hydrolysis of the C=N bond under neutral conditions due to its mesomeric effect, (iii) an imine carbon that has both electrophilic and nucleophilic characters; and (iv) an acidic NH proton used in anion sensing, metal coordination or intramolecular H-bonding.¹³

However, despite the appealing hydrazone bond properties, the relatively slow rate of its formation under physiological conditions has limited its applications (Fig. 1).

Fig. 1 Acylhydrazone formation for DCC at physiological pH (a) in the absence and (b) in the presence of aniline as a catalyst.

Over the last fifteen years, several groups have used nucleophilic catalysts to speed up this reaction, including aniline as a catalyst.^14–16

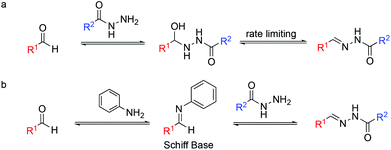
Early comparative polarimetric studies of kinetics and mechanisms regarding hydrazone, semicarbazone and oxime formation were reported by Stempel et al. in the 1940s.¹⁷ Mechanistic studies on semicarbazone and oxime formation provided by Jencks in the 1960s¹⁸ showed that the rate-limiting reaction was the condensation of the substrate with the catalyst to form the activated imine, prior to the transimination reaction. Studies showing how the structural features of aldehydes and hydrazines influence the hydrazone reaction^19,20 and the hydrolytic stability of the hydrazone bond²¹ have been reported.

On the other hand, hydrazone exchange has been extensively used in dynamic combinatorial chemistry (DCC), being one of the most popular reversible chemistries.^22,23 DCC is based on adaptive molecular networks, named dynamic combinatorial libraries (DCLs), which under thermodynamic control and through reversible bonds respond to external stimuli. Protein-directed DCC has been proven to be an excellent tool to speed up the drug discovery process allowing the protein target to find its best ligand in situ.²⁴ We are interested in the application of hydrazone exchange under physiological conditions to protein-directed dynamic combinatorial systems. Acidic conditions were used to speed up bond formation and cleavage until the addition of aniline as a nucleophilic catalyst for acylhydrazone DCC at physiological pH was reported.^25,26 Mechanistically, aniline reacts with the aldehyde as a nucleophilic catalyst to form an aromatic Schiff base intermediate (Fig. 1b). This intermediate acts as an electrophile. The higher reactivity of Schiff bases compared to that of their parent aldehydes toward nitrogen nucleophiles enables the transimination step to achieve the hydrazone/acylhydrazone exchange. Nevertheless, the requirement of a high concentration of aniline and its toxicity reported in cells prompted the search for alternative catalysts.^27–30 Note that in catalyzed DCC, unlike in conventional catalysis, the amount of catalyst used is not limited to substoichiometric concentrations.³¹

Recently, modelling studies on hydrazone exchange in the absence of a catalyst supported the hypothesis that the rate-limiting step in hydrazone exchange is the nucleophilic attack on the protonated hydrazone,^32,33 whereas in hydrazone formation the rate-limiting step in water at neutral pH was the cleavage of the carbinolamine intermediate to eliminate water.^18c

Studies regarding the effectiveness of nucleophilic catalysts in aqueous solvents have been reported and the reaction rate of the global process is described, assuming that the imine formation is always the rate-limiting step.^18c,34 Nonetheless, the acylhydrazone formation mechanism has been rarely studied as a multistep process.

Here we present a detailed study of three different p-substituted aniline derivatives compared to aniline in acylhydrazone formation. We performed kinetic studies by NMR spectroscopy on imine and acylhydrazone formation as separate reactions in a polar aprotic solvent (acetonitrile) in analogy to previous reports.³⁵ Furthermore, the acylhydrazone reaction was performed in water in the absence and presence of the catalysts, and in a dynamic combinatorial chemistry system which confirmed the efficiency of p-toluidine and p-anisidine in acylhydrazone exchange at physiological pH and low temperatures.

Results and discussion

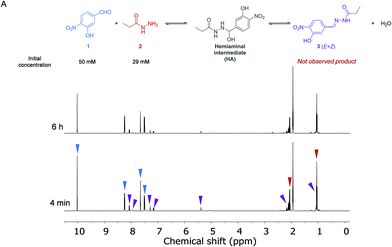
The kinetics of the reaction between aldehyde 1 (50 mM) and acylhydrazide 2 (29 mM) in the absence of a catalyst was first analyzed by ¹H NMR spectroscopy in anhydrous CD₃CN at 288 K (Fig. 2 and the ESI†). Acetonitrile was selected as a convenient aprotic and anhydrous solvent to ensure complete solubilization of the reagents and avoid hydrolysis of the formed hydrazone.

Fig. 2 (A) Reaction between aldehyde 1 and acylhydrazide 2 in CD₃CN to form acylhydrazone 3. ¹H NMR (500 MHz, 288 K) spectra at different reaction times. Blue, red and purple arrows indicate the signals of compounds 1, 2 and HA, respectively.

A dynamic equilibrium between both reagents and the corresponding hemiaminal intermediate (HA) was reached before the first experiment was performed, yielding a ratio of around 4 : 2 : 1 of compounds 1 : 2 : HA, respectively. This ratio was maintained, and no new signals appeared after more than 5 h, indicating that the subsequent dehydration reaction to form the final acylhydrazone 3 did not take place at a measurable rate. From these data, the equilibrium constant for the first step of the imine formation reaction and, thus the ratio between the forward (k₁) and reverse (k₋₁) reaction rates was found to be: K_eq = k₁/k₋₁ = 12.7 M⁻¹.

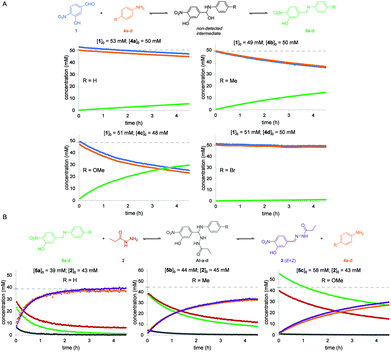
The same reaction between aldehyde 1 and acylhydrazide 2 was then analyzed in the presence of different aniline derivatives 4a–d as catalysts, namely 4a: aniline, 4b: p-toluidine, 4c: p-anisidine and 4d: p-bromoaniline. For a better understanding of the global process the two consecutive reactions, namely imine formation between aldehyde 1 and aniline derivatives 4a–d and subsequent imine exchange with acylhydrazide 2 to yield acylhydrazone 3, were studied separately (Fig. 3). The estimated reaction rate constants for all the studied reactions are summarized in Table 1.

Fig. 3 (A) Reaction between aldehyde 1 and anilines 4a–d in CD₃CN to form imines 5a–d. Plots show the concentrations (mM) of compounds 1, 4a–d and 5a–d at different reaction times using approximately equal initial concentrations of reagents 1 and 4a–d. Grey dashed lines indicate the initial concentrations of the limiting reagents for each reaction. (B) Reaction between imines 5a–d and acylhydrazide 2 in CD₃CN to form acylhydrazone 3 as a mixture of Z/E isomers. Plots show the concentrations (mM) of compounds 4a–c, 3 and 5a–c at different reaction times using approximately equal initial concentrations of reagents 5a–c and 3. Grey dashed lines indicate the initial concentrations of the limiting reagents for each reaction. Imine 5d was discarded due to its poor solubility in CD₃CN at the concentrations required for NMR analysis.

Table 1 Estimated reaction rate constants (k_obs) for the reactions between aldehyde 1 and anilines 4a–d to form imines 5a–d, and the subsequent reactions of these imines with acylhydrazide 2 to form acylhydrazone 3. n.d.: not determined. For experimental and theoretical details on the derivation of these parameters, see the ESI†

Aniline	R	Reaction 1 + 4a–d	Reaction 5a–d + 2
		k obs (M^−2 s^−1)	k obs (M^−2 s^−1)
4a	H	0.0030 ± 0.0026	0.5795 ± 0.3887
4b	Me	0.0107 ± 0.0020	0.0686 ± 0.0476
4c	OMe	0.0365 ± 0.0093	0.0521 ± 0.0252
4d	Br	0.0006 ± 0.0013	n.d.

---

For the first reaction (i.e. imine formation), compounds 5a–d formed smoothly at measurable reaction rates, and no signals corresponding to the hemiaminal intermediates (HA) were observed in the NMR spectra. This suggests that a fast-dynamic equilibrium between reagents 1 and 4a–d and the corresponding hemiaminal intermediates is reached in which the reverse nucleophilic addition reaction is much faster than the forward process, and that elimination of water from intermediates is also fast.

By performing the reactions using different sets of initial concentrations for the reagents and using the initial rate method, an unexpected partial order of 2 for aldehyde 1 and an expected order of 1 for anilines 4a–d were determined. To the best of our knowledge, such a second-order character in aldehydes has been only reported for processes involving nucleophilically activated aromatic aldehydes such as the Cannizaro³⁶ and benzoin condensation³⁷ reactions. Possible mechanistic explanations for this behavior, including catalysis by a benzoic derivative of aldehyde 1 (labelled as 1′, see below) are summarized in the ESI.† Third-order integrated rate laws for reactions in which the initial concentrations were either different or equal were derived, which allowed the estimation of the observed reaction rate constants; k_obs (see the ESI†). As expected, the reaction with p-anisidine 4c was observed to be the fastest process due to its higher nucleophilic character (k_obs = 0.0365 M⁻² s⁻¹), while the reactions with the other aniline derivatives were 3 to 61 times slower (Table 1).

Identical analyses were performed for the second reaction in the global aniline-catalyzed process, namely the reaction between acylhydrazide 2 and freshly synthesized and purified imines 5a–c. Imine 5d was discarded due to its poor solubility in CD₃CN at the concentrations required for NMR analysis, which precluded obtaining reliable and reproducible initial concentration values. Before the first experiment was performed, a fast-dynamic equilibrium was reached between both reagents and the corresponding aminal intermediates (AI-a–c), which could be detected by ¹H NMR in nearly all cases (Fig. 3 and the ESI†). The final acylhydrazone 3 was then steadily formed as a mixture of Z/E isomers from the corresponding intermediates. This reaction mechanism was also found to be second-order in the imine and first-order in the acylhydrazide, although the deviation from integer partial orders was quite significant in some cases such as with imine 5a. As a consequence, the resulting third-order integrated rate laws provided quite different k_obs values depending on the initial concentrations of the reagents and thus such values must be taken with caution. As expected, the reaction with the imine derived from p-anisidine 5c was observed to be the slowest one due to its poor electrophilic character (k_obs = 0.0521 M⁻² s⁻¹) (Table 1). Nevertheless, as can be seen in Fig. 3, when nearly equimolecular concentrations of reactants were used, it was clear that this second reaction (i.e. acylhydrazone formation) was always faster than the first reaction (i.e. imine formation), which is rate-limiting in all cases.

Anilines para-substituted with electron-donating groups 4b (R = Me) and 4c (R = OMe) were determined to be the most effective catalysts for the global reaction between aldehyde 1 and acylhydrazide 2 in acetonitrile solution. In fact, predicting the consequences of varying the electronic properties of the substituents at the para position of aniline catalysts is not trivial in this type of multi-step reaction. On one hand, for the first reaction (imine formation) electron-donating substituents (p-OMe and p-Me) are expected to lower the activation barriers for the initial nucleophilic attack on the aldehyde and, to a lower extent, for water elimination (i.e. the lone electron pairs of the nitrogen atom are more localized and thus more available for forming the double C=N bond). On the other hand, for the second reaction (hydrazone formation), electron-donating substituents (p-OMe and p-Me) are expected to increase the activation barriers for the nucleophilic attack of the acylhydrazide on the imine (i.e. imines are less electrophilic) and aniline elimination (i.e. the anilines are worse leaving groups). Thus, since so many equilibria and microkinetic steps are involved in the global reaction, the effects of the aniline substituents on the global reaction rate will be determined by the rate-limiting step (i.e. the step with the highest activation barrier). The observation that electron-rich anilines (p-OMe and p-Me) accelerate the global reaction indicates that the rate-limiting steps occur at the first reaction (i.e. formation of the imine), either in the initial nucleophilic attack on the aldehyde or water elimination steps. Performing the reaction in different solvents (i.e. aqueous or not aqueous) can affect the relative rates of each step, water elimination being expected to be unfavored in aqueous solvents as previously reported. Our results stress the importance of studying the accelerating properties of a given catalyst in the different sequential reaction steps, and are in good agreement with the results observed in aqueous solvents with similar reagents (vide infra).

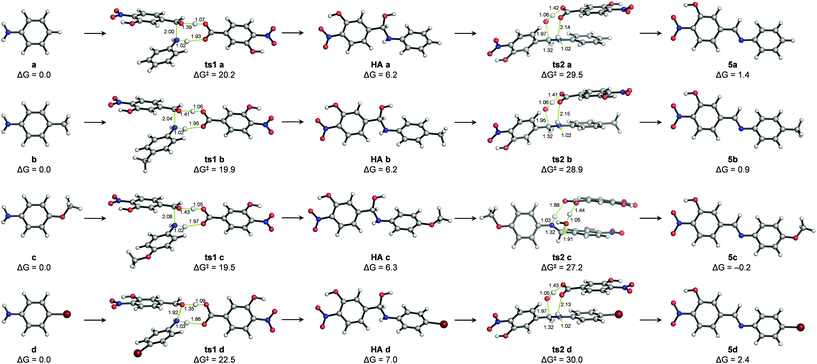
The mechanism of hydrazone exchange in the presence of aniline catalysts was further studied through quantum mechanical calculations in an implicit solvent (acetonitrile) at the SMD(CH₃CN)/M06-2X/6-311++G(2d,p)//PCM(CH₃CN)/M06-2X/6-31+G(d,p) level (see Computational details and the ESI†). For the initial imine formation reaction (i.e. condensation of aldehyde 1 with anilines) no transition structures describing the direct nucleophilic addition to the aldehyde carbonyl group – either in its protonated or neutral forms – could be located. However, assisting the nucleophilic attack with protic molecules acting as proton shuttles, such as water, the ortho-nitrophenol moiety of aldehyde 1 or a benzoic acid derivative generated from or present as an impurity of aldehyde 1 not detected by ¹H NMR (labelled as 1′),^38–40 did allow locating feasible transition structures for both the nucleophilic addition (ts1 a–d) and water elimination (ts2 a–d) elementary steps (see the ESI†). Hence, catalysis by the benzoic acid derivative 1′ yielded the lowest activation barriers (ΔG^‡) for these processes and, more importantly, suggested that water elimination is the rate-limiting step to yield imines 5a–d in agreement with previous reports^17,18 and reproduced the experimental reactivity trends: ΔG^‡ (ts2c) < ΔG^‡ (ts2 b) < ΔG^‡ (ts2 a) < ΔG^‡ (ts2 d) (Fig. 4).

Fig. 4 Lowest-energy structures calculated with SMD(CH₃CN)/M06-2X/6-311++G(2d,p)//PCM(CH₃CN)/M06-2X/6-31+G(d,p) for the nucleophilic addition of anilines a–d to aldehyde 1 (ts1 a–d), the corresponding hemiaminal intermediates (HA a–d) and subsequent water elimination (ts2 a–d) to yield imines 5a–d. Both elementary steps are catalyzed with the benzoic acid derivative 1′ (see the main text). Relative free energies (ΔG) from the separated reactants are given in kcal·mol⁻¹ and distances are given in Angstrom.

Such a catalytic effect of acid 1′ would provide a plausible explanation for the experimentally observed partial order of 2 for aldehyde 1. Assuming that the concentration of acid 1′ at a given reaction time is a fraction (χ) of the concentration of aldehyde 1 ([1′] = χ [1]), third-order reaction rate equations could be written as: rate = k [1′][1][a–d] = k·χ [1]²[a–d].

Thermodynamics is also well represented by this model, indicating that (a) the hemiaminal intermediate formation is an endergonic process (and thus not experimentally detectable) and (b) the formation of the stable imine products (the E isomers being much more stable) is either thermoneutral or slightly endergonic, suggesting microscopic reversibility.

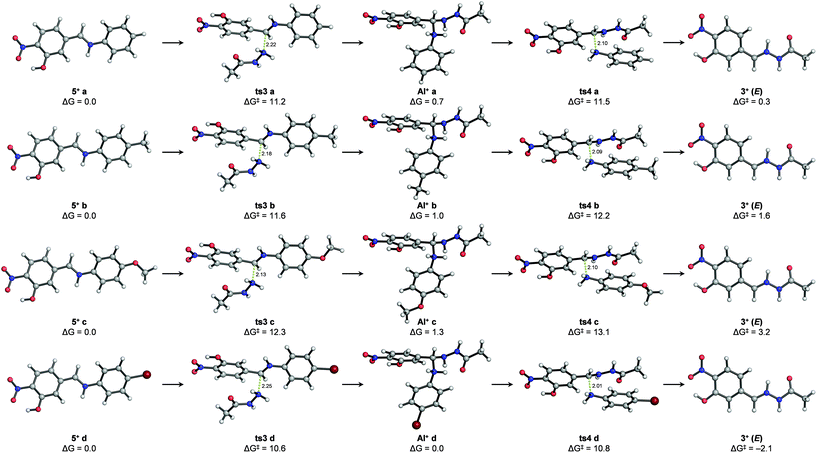
Stationary points (i.e. transition structures and energy minima) could also be located for the second reaction (i.e. nucleophilic attack of an abbreviated model of acylhydrazide (2′) followed by aniline cleavage) starting from protonated iminium intermediates (5⁺ a–d) (Fig. 5 and the ESI†). It is noteworthy that the transition states of none of the elementary steps were involved in this reaction (i.e. nucleophilic attack of acylhydrazide and aniline cleavage could be computed unless the C=N bonds of the reacting imines were protonated as iminium ions (C=NH⁺)). Given the lack of experimental pK_b values for imines 5a–d or similar compounds, the energy penalty associated with the formation of such iminium species (5⁺ a–d) in acetonitrile was estimated indirectly using combinations of machine learning approaches and experimental data^41–44 (see the ESI†). However, considering the insufficient accuracy of these estimations, we were more interested in the intrinsic activation energies involved in the process. Although the transition states for the nucleophilic addition (ts3a–d) and aniline cleavage (ts4a–d) were calculated to be very close in energy, the activation barriers for the latter step were rate-limiting in all cases, with values following the trend observed experimentally: ΔG^‡ (ts4c) > ΔG^‡ (ts4 b) > ΔG^‡ (ts4 a) > ΔG^‡ (ts4 d). In agreement with the NMR experiments described above that allowed the detection of transient species, stable protonated aminal intermediates (AI⁺ a–d) after the addition of a model acylhydrazide were calculated for all studied cases involving derivatives from aniline, p-toluidine, p-anisidine and p-bromoaniline. Also in agreement with the experimental observations, both the Z and E isomers of the protonated hydrazone (3⁺) were calculated to have similar energies, the latter being slightly more stable. As in the imine formation reaction, hydrazone formation is also either thermoneutral or slightly endergonic, suggesting microscopic reversibility. Calculations in implicit water yielded virtually identical results, with differences in the relative energies of the calculated stationary points smaller than 1 kcal mol⁻¹ (see the ESI†). As a referee noted, water and protic solvents could change the reaction mechanism acting as a proton shuttle and/or favoring the elimination of hydroxide ions from carbinolamine intermediates,⁴⁵ although such theoretical predictions have not been confirmed experimentally.^46,47

Fig. 5 Lowest-energy structures calculated with SMD(CH₃CN)/M06-2X/6-311++G(2d,p)//PCM(CH₃CN)/M06-2X/6-31+G(d,p) for the nucleophilic addition of acylhydrazide to iminium derivatives im a–d (ts3 a–d), the corresponding protonated aminal intermediates (AI⁺ a–d) and subsequent water elimination (ts4 a–d) to yield hydrazone 3 (only the E isomer is shown). Relative free energies (ΔG) from the separated reactants are given in kcal·mol⁻¹ and distances are given in Angstrom.

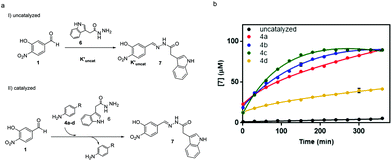
To study the performance of the catalysts at physiological pH, the reaction between aldehyde 1 (0.09 mM) and acylhydrazide 6 (0.9 mM) to yield acylhydrazone 7 was performed according to our previous work in a Tris buffer solution, using an excess of acylhydrazide to achieve fast conversion at reasonable reaction times.³⁰ To monitor the reaction progress by HPLC-MS, an acylhydrazide with a chromophore group, like compound 6, was selected (Fig. 6).

Fig. 6 Acylhydrazone formation in the absence and presence of a nucleophilic catalyst in aqueous buffer solution. Reaction conditions: aldehyde 1 (0.09 mM), acylhydrazide 6 (0.9 mM), 20 mM Tris buffer (pH 7.8), T = 6 °C, 5% DMSO. (a) Acylhydrazone reaction mechanism. (b) Time course formation of acylhydrazone 7 in the absence of the catalyst (black dots), and in the presence of 15 mM aniline (red dots), p-toluidine (green dots), p-anisidine (blue dots) and p-bromoaniline (yellow dots). Experiments were performed in triplicate and the mean ± SD values are represented in the plot.

The performance of amines 4a–d as catalysts was monitored for 1 week and compared to the uncatalyzed reaction (Fig. 6a). The time-course of the reaction during the first 6 h is shown in Fig. 6b. The reaction in the presence of the catalyst was completed between 3 hours and 4 days depending on the catalyst (5.5 h for 4a, 4 h for 4b, 3 h for 4c, and 4 days for 4d). It is noteworthy that the two best catalysts in aqueous buffer solutions, namely, 4b (R = Me) and 4c (R = OMe), also exhibited the fastest kinetics in acetonitrile, thus validating the initial predictions and mechanistic studies despite the different reaction conditions used.

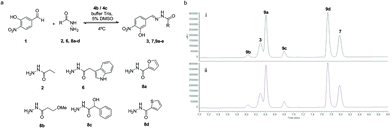
In a dynamic combinatorial library, a particular challenge of hydrazone chemistry at physiological pH lies in the efficiency of achieving the exchange process. After establishing p-toluidine (4b) and p-anisidine (4c) as the most efficient catalysts for acylhydrazone formation in water, the DCC approach was attempted by mixing aldehyde 1 (Fig. 7) with six acylhydrazides (2, 6, and 8a–d). Structurally diverse building blocks were chosen for the DCL composition. The equilibration was completed in the presence of 4b (2 h 30 min) and 4c (3 h), whereas the same system in the absence of the catalyst took more than 2 days to equilibrate (>16-fold acceleration). Aldehyde 1 could not be detected in the reaction mixture, indicating that it was continuously being sequestered as an acylhydrazone component. The acylhydrazones were identified by HPLC-MS (see the ESI†). The reversibility of the DCL was confirmed by setting up consecutive DCLs where a new acylhydrazide was added once the DCL reached its equilibration point. The DCL started with mixing aldehyde 1 and four acylhydrazides 6, 8a, 8c and 8d. This was followed by the addition of acylhydrazide 2 and finally, acylhydrazide 8b was added, showing an identical distribution to that in Fig. 7, either in the presence of catalyst 4b or 4c (see the ESI†).

Fig. 7 DCL catalyzed by 4b and 4c in an aqueous buffer solution. (a) Aldehyde 1 and acylhydrazides 2, 6 and 8a–d as building blocks. (b) DCLs in the presence of 4b (i) and 4c (ii). Reaction conditions: aldehyde 1 (90 μM), acylhydrazide 2, 6, and 8a–d (6 × 270 μM), 4b or 4c (15 mM), 20 mM Tris buffer (pH 7.8), T = 6 °C, 5% (v/v) DMSO.

Conclusions

We have reported the study of aniline and three p-aniline derivatives as nucleophilic catalysts for acylhydrazone formation in a polar, aprotic solvent, CD₃CN. Kinetic studies by NMR spectroscopy provided the relative rates for each of the two reactions occurring in the catalytic process, with support from quantum mechanical calculations. Comparison of imine and acylhydrazone formation separately showed that the rate-limiting process was always imine formation. para-Substituted anilines 4b (p-toluidine, R = Me) and 4c (p-anisidine, R = OMe) were the most effective catalysts for the reaction between aldehyde 1 and acylhydrazide 2 in acetonitrile solution. The results from the catalytic performance in water at physiological pH further supported our mechanistic and predictive studies in acetonitrile.

Furthermore, a dynamic combinatorial library with the best performing aniline derivatives, p-toluidine (4b) and p-anisidine (4c), was set up at physiological pH and low temperatures. The DCL achieved the required equilibrium composition in 3 h and 2.5 h, respectively, considerably improving the reported results in the absence of both catalysts. Additionally, taking into account the performance and properties of p-anisidine such as water solubility, affordability, and low toxicity, it proves to be an interesting alternative to aniline in systems where biological targets are present.

These efficient catalysts could expand the application of hydrazone-based chemistry, contributing to the development of DCC in biological environments and its use as a hit identification tool in drug discovery.

Experimental section

Materials and methods

The chemical reagents 1, 2, and 4a–d and solvents were obtained from commercial sources such as Sigma-Aldrich, Fluorochem and TCI Europe. Microwave-assisted reactions were performed with a Biotage Initiator classic model reactor using sealed vessel tubes with a maximum capacity of 20 mL. The melting point was measured using a Büchi Melting Point M-560 device. ¹H-NMR and ¹³C-NMR spectra were recorded using a Bruker NanoBay AVIII 300 MHz spectrometer equipped with a 5 mm probe BOF and an automation system BACS-60 operated at 300 MHz and 75 MHz. Chemical shifts are reported in ppm (δ), using the corresponding deuterated solvent. Shift multiplicity is denoted as s: single, d: double, and m: multiplet, and coupling constant values (J) were measured in Hz, acquired in the Nuclear Magnetic Resonance Centre of Complutense University of Madrid. Elemental analysis was performed using a LECO CHNS-932 elemental analyzer of Universidad Complutense de Madrid. HPLC-MS assays were performed by high-performance liquid chromatography-mass spectroscopy (HPLC-MS) using an HPLC Surveyor and a Thermo Mod. Finnigan TM LXQ TM ion trap mass spectrometry system (Thermo Mod. Finnigan TM LXQ TM). HPLC solvents and formic acid were obtained from J.T. Baker and Sigma-Aldrich, respectively. Analyses were performed using a reversed phase HPLC column (ACE Excel 3 C18-PFP 4.6 × 100 mm, 3 μm) using an injection volume of 25 μL, a flow rate of 1 mL min⁻¹ and a gradient (15–85%) in 15 min of acetonitrile in water, both containing 0.1% formic acid at 15 °C. Positive ion mass spectra were obtained using electrospray ionization (drying temperature: 300 °C, sheath gas flow: 60, HV capillary: 6000 V, source voltage: 5.50 kV, and source current: 100 μA).

Synthesis of (E/Z)-N′-(3-hydroxy-4-nitrobenzylidene)propionohydrazide (3). Over a solution of 3-hydroxy-4-nitrobenzaldehyde (629 mg, 3.77 mmol) in MeOH (60 mL) as a solvent, propanoic acid hydrazide (300 μL, 2.90 mmol) was added. The reaction mixture was stirred at 85 °C using a heating plate and a DrySyn heating block for 16 h. The crude product was cooled down at room temperature and a yellow amorphous solid precipitated (0.50 g, 65%) (E : Z = 40 : 60). M.p: 179–180 °C. ¹H-NMR (300 MHz, DMSO-d₆) δ 11.59 (s, 1H, E), 11.44 (s, 1H, Z), 11.14 (s, 1H, E/Z), 8.70 (s, 1H, E), 8.13 (s, 1H, Z), 7.93–7.86 (m, 1H, E/Z), 7.39 (s, 1H, E/Z), 7.27–7.24 (m, 1H, E/Z), 2.65 (q, J = 7.5 Hz, 2H, Z), 2.23 (q, J = 7.5 Hz, 2H, E), 1.08 (t, J = 7.5 Hz, 3H, E/Z). ¹³C-NMR {¹H} (75 MHz, DMSO-d₆): δ 176.0, 152.8, 143.7, 141.4, 140.3, 126.4, 117.8, 116.7, 25.7, 9.1. Anal. calcd for C₁₀H₁₁N₃O₄: C, 50.63%; H, 4.67%; N, 17.71%. Found: C, 50.36%; H, 4.60%; N, 17.59%. HPLC-MS: t_R: 7.06 min, [M + H]⁺ = 238 m/z.

General procedure for synthesis of imines 5 (a–d)

A solution of 3-hydroxy-4-nitrobenzaldehyde 1 (1 eq.) and the corresponding amines 4a–d (1 eq.) was stirred under microwave irradiation at 115 °C for 30 min in anhydrous THF (12 mL) in a sealed 20 mL vial. The solvent was removed under reduced pressure and the compounds were afforded as a yellow solid (90–98%). No further purification was performed.

(E)-2-Nitro-5-((phenylimino)methyl)phenol (5a). 3-Hydroxy-4-nitrobenzaldehyde 1 (174 mg, 1.00 mmol), aniline (95 μL, 1.00 mmol), and THF (12 mL) were used. Yellow amorphous solid. Yield: 240 mg, 95%, (E > 99). M.p: 99–100 °C. ¹H-NMR (500 MHz, DMSO-d₆): δ 11.02 (s, 1H), 8.67 (s, 1H), 8.03–7.99 (m, 1H), 7.70–7.68 (m, 1H), 7.57–7.38 (m, 2H), 7.40–7.24 (m, 3H). ¹³C-NMR {¹H} (75 MHz, DMSO-d₆): δ 159.4, 152.5, 151.0, 141.9, 138.9, 129.7 (2C), 129.2, 127.2 (2C), 126.2, 121.7, 119.7. Anal. calcd for C₁₃H₁₀N₂O₃: C, 64.46%; H, 4.16%; N, 11.56%. Found: C, 64.63%; H, 4.27%; N, 11.42%.

(E)-2-Nitro-5-((p-tolylimino)methyl)phenol (5b). 3-Hydroxy-4-nitrobenzaldehyde (162 mg, 0.9 mmol), p-toluidine (100 mg, 0.9 mmol), and THF (12 mL) were used. Yellow amorphous solid. Yield: 220 mg, 90%, (E > 99). M.p: 144–145 °C. ¹H-NMR (500 MHz, DMSO-d₆): δ 11.20 (s, 1H), 8.68 (s, 1H), 8.00 (d, J = 8.5 Hz, 1H), 7.68 (d, J = 1.6 Hz, 1H), 7.51 (dd, J = 8.5, 1.6 Hz, 1H), 7.26 (s, 4H), 2.34 (s, 3H). ¹³C-NMR {¹H} (75 MHz, DMSO-d₆): δ 158.3, 152.5, 148.3, 142.1, 138.7, 136.9, 130.2 (2C), 126.2, 121.8 (2C), 119.6, 118.6, 21.1. Anal. calcd for C₁₄H₁₂N₂O₃: C, 65.62%; H, 4.72%; N, 10.93%. Found: C, 65.37%; H, 4.69%; N, 10.85%.

(E)-5-(((4-Methoxyphenyl)imino)methyl)-2-nitrophenol (5c). 3-Hydroxy-4-nitrobenzaldehyde (124 mg, 0.70 mmol), p-anisidine (93 mg, 0.70 mmol), and THF (12 mL) were used. Yellow amorphous solid. Yield: 190 mg, 95%, (E > 99). M.p: 143–144 °C. ¹H-NMR (500 MHz, DMSO-d₆): δ 11.14 (s, 1H), 8.69 (s, 1H), 8.00 (d, J = 8.6 Hz, 1H), 7.66 (d, J = 1.6 Hz, 1H), 7.50 (dd, J = 8.6, 1.6 Hz, 1H), 7.44–7.32 (m, 2H), 7.07–6.95 (m, 2H), 3.80 (s, 3H). ¹³C-NMR {¹H} (75 MHz, DMSO-d₆): δ 159.1, 156.6, 152.6, 143.6, 142.4, 138.4, 126.2, 123.4 (2C), 119.4, 118.4 (2C), 115.0, 55.8. Anal. calcd. for C₁₄H₁₂N₂O₄: C, 61.76%; H, 4.44%; N, 10.29%. Found: C, 61.88%; H, 4.49%; N, 10.25%.

(E)-5-(((4-Bromophenyl)imino)methyl)-2-nitrophenol (5d). 3-Hydroxy-4-nitrobenzaldehyde (102 mg, 0.60 mmol), 4-bromoaniline (98 mg, 0.60 mmol), and THF (12 mL) were used. Yellow amorphous solid. Yield: 160 mg, 98%, (E > 99). M.p: 158–159 °C. ¹H-NMR (500 MHz, CDCl₃): δ 10.56 (s, 1H), 8.39 (m, 1H), 8.12 (m, 1H), 7.63–7.55 (m, 1H), 7. 53–7.49 (m, 1H), 7.48–7.45 (m, 2H), 7.09–7.06 (m, 2H). ¹³C-NMR {¹H} (75 MHz, CDCl₃): δ 155.5, 152.9, 147.5, 141.6, 132.9, 130.3 (2C), 123.6, 120.7 (2C), 118.6, 118.4, 117.4. Anal. calcd for C₁₃H₉BrN₂O₃: C, 48.62%; H, 2.83%; N, 8.72%; found: C, 48.76%; H, 2.89%; N, 8.67%.

Catalytic study by ¹H-NMR

The pure amine or imine and the aldehyde were dissolved in 500 μL of cooled deuterated acetonitrile (CD₃CN) in a 5 mm tube. The final concentrations of the reagents were different for each case (from 16.7 mM to 50 mM, each). NMR spectra were obtained on a Bruker AV 500 MHz spectrometer operating at a ¹H frequency of 500.13 MHz equipped with a 5 mm probe head of direct detection. The temperature stability was controlled via a Bruker BCU05 unit and set up to 288 K. The spectrometer was previously stabilized with a sample of similar characteristics (deuterated solvent and sample volume) and shims, tune and match were adjusted. They were not changed during the experiment. All ¹H spectra were obtained and processed using the program TOPSPIN 2.1. Once the sample was placed inside the magnet, the reaction was monitored by a ¹H spectrum array (600 experiments recorded) for 4.5 h. The acquisition parameters are: number of scans (NS): 8, time domain (TD): 32 K, spectral window (SW): 15 ppm, O1: 3000.78 Hz and relaxation delay (d1): 1s.

Computational details

Full geometry optimizations and transition structure (TS) searches were carried out with Gaussian 16 ⁴⁸ using the M06-2X hybrid functional⁴⁹ and 6-31+G(d,p) basis set with ultrafine integration grids. Bulk solvent effects in acetonitrile and water were considered implicitly using the IEF-PCM polarizable continuum model.⁵⁰ The possibility of different conformations was taken into account for all structures. All stationary points were characterized by a frequency analysis performed at the same level used in the geometry optimizations from which thermal corrections were obtained at 298.15 K. The quasiharmonic approximation reported by Truhlar et al. was used to replace the harmonic oscillator approximation for the calculation of the vibrational contribution to enthalpy and entropy.⁵¹ Scaled frequencies were not considered. Mass-weighted intrinsic reaction coordinate (IRC) calculations were carried out using the Gonzalez and Schlegel scheme^52,53 in order to ensure that the TSs indeed connected the appropriate reactants and products. Single point energies were calculated at the M06-2X/6-311++G(2d,p) level using the SMD polarizable continuum model.⁵⁴ Zero-point energy, enthalpy and Truhlar's entropy corrections, obtained from the frequency calculation at the PCM(CH₃CN)/M06-2X/6-31G(d,p) level, were added to the single point energy calculated at the SMD(CH₃CN/H₂O)/M06-2X/6-311++G(2d,p) level to give the final reported enthalpy and Gibbs free energy. Relative Gibbs free energies (ΔG) were used for the discussion on the stabilities of the considered structures. The lowest energy conformer for each calculated stationary point was considered in the discussion; all the computed structures can be obtained from authors upon request. Cartesian coordinates, electronic energies, entropies, enthalpies, Gibbs free energies, and lowest frequencies of the calculated structures are summarized in the ESI.†

Hydrazone reaction monitored by HPLC

The absorbances of aldehyde 1 and acylhydrazone 7 were measured. Their concentrations were determined using a calibration curve equation. The reaction in the presence of the catalyst was completed between 3 hours and 4 days depending on the catalyst (4a-5.5 h, 4b-4 h, 4c-3 h, and 4d-4 days). The experiment was performed by the addition of the aldehyde 1 (1.8 μL, 50 mM, 9.0 × 10⁻⁸ mol, in DMSO) after preparing the solution of the acylhydrazide 6 (18 μL, 50 mM, 9.0 × 10⁻⁷ mol, in DMSO), the catalyst (1.5 μL, 10 M in DMSO) or in the absence of the catalyst, 1.5 μL of DMSO, buffer 20 mM Tris, 0.5 M NaCl, 1 mM CaCl₂, and 1 mM DTT pH 7.4 (950 μL) using 5% v/v DMSO (28.7 μL) at 6 °C. Four p-substituent anilines were studied: aniline, p-toluidine, p-anisidine, and p-bromoaniline.

DCL preparation

The DCL was set up by mixing Aldehyde 1 (1.2 μL, 50 mM, 6.0 × 10⁻⁸ mol in DMSO), 6 acylhydrazides (2, 6, and 8a–d) (6 × 3.6 μL, 50 mM, 1.8 × 10⁻⁷ mol each in DMSO), p-anisidine or p-toluidine (1.0 μL, 12 M, 1.2 × 10⁻⁵ mol in DMSO), DMSO (10 μL), buffer 20 mM Tris, 0.5 M NaCl, 1 mM CaCl₂, and 1 m M DTT pH 7.4 (632 μL) with 5% DMSO at 6 °C. Both DCLs were analyzed by HPLC at 3, 4 and 5 hours. Each peak corresponding to acylhydrazones 3, 7, and 9a–d was identified by HPLC-MS and compared to previously synthesized compounds (7 and 9a–d).³⁰

Reversibility study

The addition of each acylhydrazide was performed after the stabilization of the previous mixture. Firstly, aldehyde 1 (1.2 μL, 50 mM, 6.0 × 10⁻⁸ mol, DMSO), four acylhydrazides 6, 8a, 8c and 8d (4 × 3.6 μL, 50 mM, 4 × 1.8 × 10⁻⁷ mol, DMSO), catalyst 4b or 4c (1.0 μL, 10 M, 1.0 × 10⁻⁵ mol, DMSO) and DMSO (6.2 μL) were mixed in buffer 20 mM Tris, 0.5 M NaCl and 1 mM CaCl₂, and 1 mM DTT pH 7.4 (574 μL) using 5% v/v DMSO at 6 °C. The DCL was analyzed by HPLC-MS to check the stabilization. Then, acylhydrazide 2 was added (3.6 μL, 50 mM, 1.8 × 10⁻⁷ mol, DMSO), and the DCL was analyzed again after 3 hours. Finally, acylhydrazide 8b (3.6 μL, 50 mM, 1.8 × 10⁻⁷ mol, DMSO) was added and analyzed three hours later, affording the same result.

Author contributions

R. P. F. and G. J. O. conceptualized and supervised the research. A. C. M. performed the chemical experiments. C. D. N. performed the theoretical calculations and analyzed kinetics. E. S. and D. M. performed NMR experiments. R. P. F. and G. J. O. wrote the manuscript with contributions from all authors.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank Prof. J. Elguero (IQM-CSIC) for useful discussions. This work was supported by grants from the Spanish Ministry of Science and Innovation (MCI) co-financed with the FEDER funds (PID2019-108587RB-I00 to R. P. F. and RTI2018-099592-B-C22 to G. J. O.).

Notes and references

1. E. M. Sletten and C. R. Bertozzi, Angew. Chem., Int. Ed., 2009, 48, 6974.
2. D. K. Kölmel and E. T. Kool, Chem. Rev., 2017, 117, 10358.
3. W. R. Algar, D. E. Prasuhn, M. H. Stewart, T. L. Jennings, J. B. Blanco-Canosa, P. E. Dawson and I. L. Medintz, Bioconjugate Chem., 2011, 22, 825.
4. X.-G. Li, M. Haaparanta and O. Solin, J. Fluorine Chem., 2012, 143, 49.
5. L. A. Tatum, X. Su and I. Aprahamian, Acc. Chem. Res., 2014, 47, 2141.
6. T. T. Dang, T. T. Dang and P. Langer, Synlett, 2011, 2633.
7. L. H. Yuen, N. S. Saxena, H. S. Park, K. Weinberg and E. T. Kool, ACS Chem. Biol., 2016, 11, 2312.
8. K. Larsen, M. B. Thygesen, F. Guillaumie, W. G. T. Willats and K. J. Jensen, Carbohydr. Res., 2006, 341, 1209.
9. R. Raue, A. Brack and K. Lange, Angew. Chem., Int. Ed. Engl., 1991, 30, 1643.
10. C. Serbutoviez, C. Bosshard, G. Knopfle, P. Wyss, P. Pretre, P. Gunter, K. Schenk, E. Solari and G. Chapuis, Chem. Mater., 1995, 7, 1198.
11. J.-M. Lehn, Angew. Chem., Int. Ed., 2013, 52, 2836.
12. P. Vicini, F. Zani, P. Cozzini and I. Doytchinova, Eur. J. Med. Chem., 2002, 37, 553.
13. X. Su and I. Aprahamian, Chem. Soc. Rev., 2014, 43, 1963.
14. A. Dirksen and P. E. Dawson, Bioconjugate Chem., 2008, 19, 2543.
15. J. Y. Byeon, F. T. Limpoco and R. C. Bailey, Langmuir, 2010, 26(19), 15430.
16. Y. Zeng, T. N. C. Ramya, A. Dirksen, P. E. Dawson and J. C. Paulson, Nat. Methods, 2009, 6, 207.
17. G. H. Stempel and G. S. Schaffel, J. Am. Chem. Soc., 1944, 66(7), 1158.
18. (a) W. P. Jencks, J. Am. Chem. Soc., 1959, 81, 475; (b) E. H. Cordes and W. P. Jencks, J. Am. Chem. Soc., 1962, 84, 827; (c) E. H. Cordes and W. P. Jencks, J. Am. Chem. Soc., 1962, 84, 4319; (d) W. P. Jencks, Prog. Phys. Org. Chem., 1964, 2, 63.
19. E. T. Kool, D. H. Park and P. Crisalli, J. Am. Chem. Soc., 2013, 47, 17663.
20. J. M. Sayer, M. Peskin and W. P. Jencks, J. Am. Chem. Soc., 1973, 95, 4277.
21. J. Kalia and R. T. Raines, Angew. Chem., Int. Ed., 2008, 47, 7523.
22. S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 898.
23. O. Ramström and J.-M. Lehn, Nat. Rev. Drug Discovery, 2002, 1, 26.
24. A. Canal-Martín and R. Pérez-Fernández, ACS Omega, 2020, 5, 26307.
25. A. Dirksen, S. Dirksen, T. M. Hackeng and P. E. Dawson, J. Am. Chem. Soc., 2006, 128, 15602.
26. V. T. Bhat, A. M. Caniard, T. Luksch, R. Brenk, D. J. Campopiano and M. F. Greaney, Nat. Chem., 2010, 2, 490.
27. A. R. Blanden, K. Mukherjee, O. Dilek and S. L. Bane, Bioconjugate Chem., 2011, 22, 1954.
28. P. Crisalli and E. T. Kool, J. Org. Chem., 2013, 78, 1184.
29. P. Crisalli and E. T. Kool, Org. Lett., 2013, 15, 11646.
30. A. Canal-Martín, J. Sastre, M. J. Sanchez-Barrena, A. Canales, S. Baldominos, N. Pascual, L. Martínez-González, D. Molero, M. E. Fernández-Valle, E. Sáez, P. Blanco, E. Gomez, S. Martín-Santamaría, A. Sáiz, A. Mansilla, F. J. Cañada, J. Jiménez-Barbero, A. Martínez and R. Pérez-Fernández, Nat. Commun., 2019, 10, 2798.
31. I. N. Levine, Physical Chemistry, Mc Graw Hill, USA, 5th edn, 2004, ch. 17, vol. (II).
32. P. L. Higgs, A. Ruiz-Sanchez, M. Dalmina, B. R. Horrocks, A. G. Leach and D. A. Fulton, Org. Biomol. Chem., 2019, 17, 3218.
33. R. Nguyen and I. Huc, Chem. Commun., 2003, 942.
34. D. W. Domaille and J. N. Cha, Chem. Commun., 2014, 50, 3831.
35. S. Kulchat, M. N. Chaur and J.-M. Lehn, Chem. – Eur. J., 2017, 23, 11108.
36. C. G. Swain, A. L. Powell, W. A. Sheppard and C. R. Morgan, J. Am. Chem. Soc., 1979, 101(13), 3576.
37. F. López-Calahorra and R. A. Rubires, Tetrahedron, 1995, 51, 9713.
38. V. C. Rufino and J. R. Pliego, Comput. Theor. Chem., 2020, 1191, 113053.
39. V. C. Rufino and J. R. Pliego, Asian J. Org. Chem., 2021, 10, 1472.
40. L. Hong, W. Sun, D. Yang, G. Li and R. Wang, Chem. Rev., 2016, 116, 4006–4123.
41. Q. Yang, Y. Li, Y. Liu, L. Zhang, S. Luo and J.-P. Cheng, Angew. Chem., Int. Ed., 2020, 59, 19282–19291.
42. J.-D. Yang, X.-S. Xue, P. Ji, X. Li and J.-P. Cheng, Internet Bond-energy Databank (pK_a and BDE):/BonD Home Page http://ibond.chem.tsinghua.edu.cnor http://ibond.nankai.edu.cn.
43. J. F. Coetzee and G. R. Padmanabhan, J. Phys. Chem., 1965, 69, 3193–3196.
44. J. Jover, R. Bosque and J. Sales, QSAR Comb. Sci., 2008, 27, 563–581.
45. V. C. Rufino and J. R. Pliego, ARKIVOC, 2020, part ii, 34–52.
46. M. Ciaccia and S. Di Stefano, Org. Biomol. Chem., 2015, 13, 646–654.
47. M. Ciaccia, R. Cacciapaglia, P. Mencarelli, L. Mandolini and S. Di Stefano, Chem. Sci., 2013, 4, 2253–2261.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
49. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
50. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
51. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556.
52. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
53. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
54. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.

---

Footnotes

† Electronic supplementary information (ESI) available: NMR spectra, MS, computational data, kinetic experiments and equations. See DOI: 10.1039/d1ob00871d

‡ These authors contributed equally to the work.

---