Tailoring the multistability of origami-inspired, buckled magnetic structures via compression and creasing†
Yi
Li‡
a,
Samuel J.
Avis‡
 b,
Teng
Zhang
b,
Teng
Zhang
 *c,
Halim
Kusumaatmaja
*c,
Halim
Kusumaatmaja
 *b and
Xueju
Wang
*b and
Xueju
Wang
 *ad
*ad
aDepartment of Materials Science and Engineering, University of Connecticut, Storrs, CT 06269, USA. E-mail: xueju.wang@uconn.edu
bDepartment of Physics, Durham University, Durham, DH1 3LE, UK. E-mail: halim.kusumaatmaja@durham.ac.uk
cDepartment of Mechanical and Aerospace Engineering, BioInspired Syracuse, Syracuse University, Syracuse, NY 13244, USA. E-mail: tzhang48@syr.edu
dPolymer program, Institute of Materials Science, University of Connecticut, Storrs, CT 06269, USA
First published on 9th September 2021
Abstract
Origami-inspired multistable structures are gaining increasing interest because of their potential applications in fields ranging from deployable structures to reconfigurable microelectronics. The multistability of such structures is critical for their applications but is challenging to manipulate due to the highly nonlinear deformations and complex configurations of the structures. Here, a comprehensive experimental and computational study is reported to tailor the multistable states of origami-inspired, buckled ferromagnetic structures and their reconfiguration paths. Using ribbon structures as an example, a design phase diagram is constructed as a function of the crease number and compressive strain. As the crease number increases from 0 to 7, the number of distinct stable states first increases and then decreases. The multistability is also shown to be actively tuned by varying the strain from 0% to 40%. Furthermore, analyzing energy barriers for reconfiguration among the stable states reveals dynamic changes in reconfiguration paths with increasing strains. Guided by studies above, diverse examples are designed and demonstrated, from programmable structure arrays to a soft robot. These studies lay out the foundation for the rational design of functional, multistable structures.
New conceptsAn outstanding challenge in the field of origami-inspired multistable structures is to actively control the number of possible stable states and their reconfiguration paths. In this work, we present an integrated experimental and computational study on how they can be systematically tailored and controlled via two effective and easy-to-control parameters, creasing and compressive strains. Computationally, we construct a detailed design phase diagram for a representative ribbon structure showing how the number of stable states can be varied. Furthermore, we predict the reconfiguration paths and their corresponding energy barriers to transition between stable states. Experimentally, we realize origami-inspired structures composed of ferromagnetic composite thin films under various creasing and compressive strain conditions, where fast, remote reconfigurations are achieved using a portable magnet. The computational and experimental results are in excellent agreement. We believe the new insights generated from our work are valuable for diverse applications exploiting origami-inspired structures. For instance, here we design and demonstrate programmable structure arrays, a biomimetic insect, and an origami robot that can be actuated by remote magnetic forces. |
1. Introduction
Origami, the ancient art of folding two-dimensional (2D) thin sheets along predefined creases to create three-dimensional (3D) objects,1–3 has inspired the design of many engineering structures for a wide range of applications, including deployable systems,4–6 self-folding machines,7 reconfigurable metamaterials,8–10 and DNA origami.11 For those applications, a key design feature of the structures is their ability to have multiple stable states as well as the tailoring of those states for tunability and adaptability. Existing works so far have primarily focused on bistable systems for rigid origami patterns (like the Miura folding12 and its derivates13) and deformable origami (like the twisted square pattern14). For example, Sadeghi and Li realized rapid and reversible folding by harnessing the asymmetric bistability of designed origami structures.15 Liu et al. demonstrated that a folded hyper origami, obtained by folding a piece of paper along concentric squares and their diagonals to arrive at a seemingly smooth saddle shape, exhibits bistability between two symmetric configurations.16 More recently, Melancon et al. realized pressure-deployable origami structures characterized by two stable configurations – one compact and one expanded – at the meter scale.5 Furthermore, Fang et al. showed that the potential energy landscapes of stacked Miura-ori and Kresling-ori structures, and therefore their stability profiles and constitutive force–displacement relations, can be effectively tuned by embedded magnets.17In addition to multistability, reconfiguration among the different stable states of origami-inspired structures in a well-controlled manner is demanded in many engineering devices and structures. Theoretical and experimental studies have been performed on reconfiguration paths in origami-inspired structures. For example, Zhai et al. created an origami-inspired mechanical metamaterial that can be deployed and collapsed along different configuration paths.18 Silverberg et al. showed that hidden degrees of freedom in square twist origami structures give rise to a critical transition from mono- to bi-stability.14 Moreover, significant advances have been made to improve the tunability and adaptability of origami-inspired structures by incorporating stimuli-responsive materials, such as shape memory polymers,19–22 hydrogels,23,24 liquid crystal elastomers,25,26 and magnetic composites,27 into origami-inspired structures to achieve self-folding and on-demand shape morphing under external actuations (i.e., variations in temperature, light, pH, and magnetic fields). Such self-actuating materials have also enabled the assembly of origami structures at the microscale to provide opportunities for micro robotics, biomedical devices, and many others.28–32
Previous studies have laid solid foundations for the design and development of origami-inspired structures with bistability and tunability. One of the remaining challenges in the field of origami-inspired multistable structures is to actively control the number of possible stable states and their reconfiguration paths. Here, we demonstrate how the multistability of origami-inspired structures that are buckled from ferromagnetic composite thin films19,33 can be tailored via creasing and compressive strains. Ribbon structures are chosen as an example for the study because of their very rich nonlinear buckling behavior while having a simple geometry and their potential as basic building blocks for more complicated structures, thereby providing an ideal platform to explore our design strategy. The two key control parameters, compression strains and creasing in the ribbon, are selected because they are easy to tune and very effective in altering the multistable behaviors of the structure for real applications. In this work, the experiments are thoroughly complemented with systematic simulations. A computationally efficient discrete shell model,34,35 which is used to simulate nonlinear deformations in thin films, is combined with a random search algorithm for energy minimization36–38 to construct phase diagrams showing how the available stable states sensitively depend on the compressive assembly strain and the creases of structures. The predictions from the phase diagram are experimentally verified for cases at a representative constant strain (15%) and varying crease numbers, as well as those at a given crease number (3 creases) and varying strains. In addition, reconfiguration paths between the stable states are identified using energy landscape exploration algorithms,39,40 where the transition states connecting the minima are first located with a double-ended search method, then the full pathways are computed using the downhill routes to each stable state. Our approach allows the computation of reconfiguration paths with the lowest energy barriers systematically without the need to assume a predefined path for structure morphing.41 Fast, remote reconfigurations among the multistable states of the ferromagnetic structures are performed experimentally with a portable magnet, the pathways of which are shown to be consistent with those from computational predictions. Finally, guided by tightly integrated numerical and experimental analysis, we demonstrate diverse complex origami-inspired structures, including structure arrays that can display various patterns based on the multistability of the structural unit, a biomimetic insect, and a soft robot.
2. Results and discussions
2.1 Concept of origami-inspired, multistable 3D ferromagnetic structures
Fig. 1 schematically illustrates the assembly process and reconfiguration of origami-inspired structures compressively buckled from ferromagnetic composites.19,42,43 Ferromagnetic composites are used as the constitutional material for the origami-inspired structures in this study to enable fast, remote reconfiguration among their mutistable states.44–46 The scheme begins with the fabrication of soft ferromagnetic composite films (130 μm thick) made from polydimethylsiloxane (PDMS) embedded with magnetic NdFeB (neodymium–iron–boron) microparticles (∼5 μm in diameter). Laser patterning (VLS 2.30, Universal Laser System, Ansonia, CT) of the film defines the geometry and the crease of the 2D precursor with a thickness ratio of 46.15% between the crease- and non-crease regions. The location of the crease region and the reduced thickness of the corresponding segments (2.5 mm of unit length) determine the location of hinges that affect potential multistable reconfigurations.47 To assemble origami-inspired structures, the 2D precursor is laminated onto a pre-stretched silicone elastomer substrate (Dragon skin; Smooth-on, Easton, PA), followed by the release of the pre-strain to geometrically transform the 2D precursor into the corresponding 3D structure. Under an external magnetic field generated by a manually manipulated magnet, the assembled origami-inspired structure can be reconfigured into up to four distinct stable states: state 1 (S1, one center peak), state 2 (S2, one side peak), state 3 (S3, two peaks), and state 4 (S4, twisted two peaks). Remarkably, due to their mechanical stability, the reconfigured states remain stable after the removal of the applied magnetic field.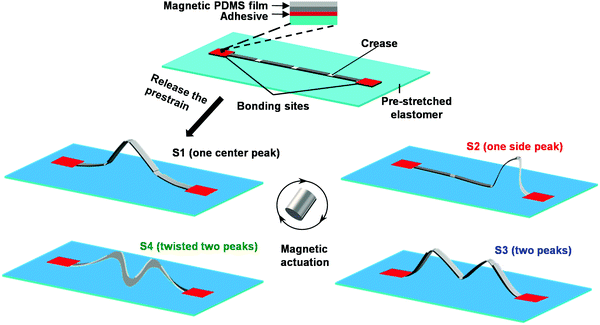 | ||
| Fig. 1 Schematic illustration of the assembly and magnetic reconfiguration schemes of origami-inspired multistable ribbon structures. | ||
2.2 Design phase diagram of multistable states of magnetically reconfigurable, origami-inspired structures
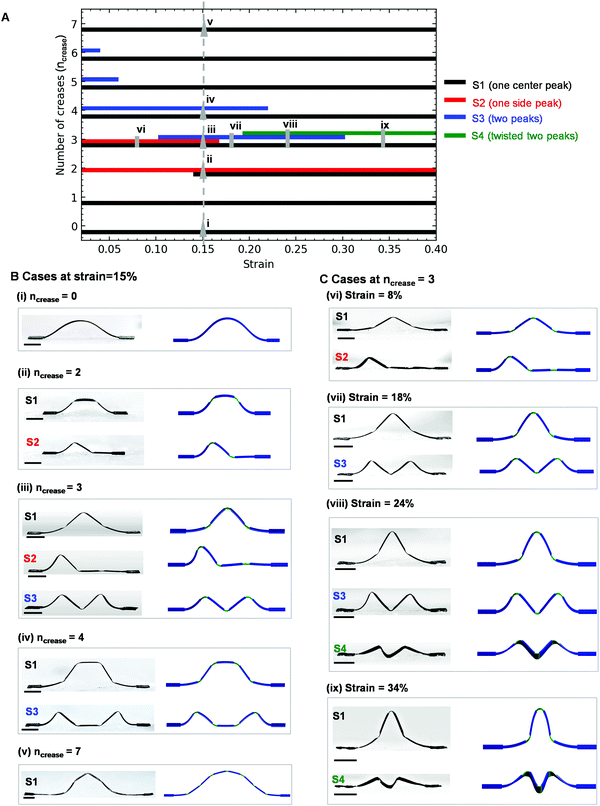
We first study the effect of two essential parameters, the number of creases and compressive strains, on the number and configurations of stable states by using a ribbon structure as an example. A design phase diagram, indicating the stable states of the structure with up to seven creases and at strain levels of 0–40%, is shown in Fig. 2A and serves as a theoretical foundation for the multistability design. The design phase diagram is constructed computationally by identifying the local minima in the energy landscape of the structure under various conditions of strain levels and crease numbers. To obtain these minima, we use a discrete model combined with a random search algorithm for energy minimization (see the Experimental section for full details). The discrete model has been widely used to simulate nonlinear deformation in thin films and shells, and it has been shown to be in good agreement with the more accurate but computationally more expensive finite element method.39,48 In our computational strategy, at selected points (typically 5 different strain levels for each crease number) across the design phase diagram, the structure is randomly initialized several hundreds of times, after which it is relaxed to the minima. Once the qualitatively distinct configurations are identified, we systematically vary the compressive strain to observe the full range over which each state is stable. It is worth noting that while it is difficult to guarantee that all possible stable states are obtained, we do not find additional states when more points in the design phase diagram are sampled. Hence, we consider the identified stable states to be representative in this study.As shown in Fig. 2A, the number of creases (ncrease) has notable effects on the number and configurations of stable states. To better illustrate this point, we demonstrate the available states of the structures as ncrease is increased from 0 to 7 under a constant compressive strain of 15% in Fig. 2B, with the computational and experimental results shown side by side. When ncrease is zero, i.e., a continuous ribbon structure, only S1 (one center peak) exists at all strain levels (e.g., point i). An additional asymmetric state S2 becomes available when ncrease rises to two at a compressive strain of 15% (point ii). A further increase to three creases causes the structure to admit state S3 (two peaks) at a strain of 15% (point iii) and S4 (twisted two peaks) at a higher strain level. As ncrease increases above three, the number of stable states begins to decline, with S2 becoming unstable for structures with four creases (point iv). For structures with five creases and above, only S1 remains stable at a compressive strain of 15%, although S3 is still stable under lower strains for ncrease = 5 and 6. This can be expected because we are approaching the continuous case when the number of creases is large.
The available stable states also depend strongly on the magnitude of the applied compressive strain used in the assembly process of the structure. We illustrate this using a structure with three creases due to its rich phenomena that will be discussed in the following. Based on the number and configurations of stable states, five regimes are identified: (a) two distinct stable states (S1 and S2; 0–10% strain), (b) three distinct stable states (S1, S2, and S3; 10–17% strain), (c) two distinct stable states (S1 and S3; 17–19% strain), (d) three distinct stable states (S1, S3, and S4; 19–30% strain), and (e) two distinct stable states (S1 and S4; 30–40% strain). Fig. 2C shows experimental and computational results of distinct stable states at representative strain levels for the five regimes. Under a relatively low compressive strain of 8% (point vi), states S1 (one center peak) and S2 (one side peak) exist, which can be reversibly reconfigured into each other via manually controlling the magnetic force and direction. Increasing the strain to 15% (point iii) leads to the appearance of a third state, S3 with two peaks, which increases the number of stable states to three. However, when the strain is further increased to 18% (point vii), S2 with one side peak disappears. Further increasing the strain to 24% (point viii) causes the formation of an interesting twisted state (S4) and therefore increases the number of stable states to three (S1, S3, and S4). As the strain becomes even larger, S3 disappears and only S1 and S4 exist at the strain of 34% (point ix). The experimental and computational results shown above agree reasonably well. The discrepancy in the configuration of some stable states (e.g., state S1 at point v in Fig. 2B) between experiments and modeling likely results from the friction between the structure and the substrate in experiments, which is neglected in computational modeling. The effect of friction will be further discussed in Section 2.3. Furthermore, by continuously changing the strain levels from 0% to 40% using the 3-crease structure, we record the dynamic progression of the five regimes and the fast, remote magnetic reconfiguration among the stable states within each regime in Movie S1 (ESI†), which is highly consistent with the predictions of the design phase diagram in Fig. 2A. We also show that the states are stable under perturbations perpendicular to the vertical surface (along the height direction) of the ribbon, except in cases where S4 (twisted two peaks) is present. By using S1 as an example, the structure is shown to maintain its S1 configuration after the perturbations caused by a tweezer-induced external mechanical force (Fig. S1, ESI†).
The studies above provide important guidelines for tailoring the number and configurations of stable states in origami-inspired structures by tuning the number of creases and the assembly strain. For example, for applications like in digital logic devices where multiple stable states are desired, structures with three creases may offer more design space and tunability, while structures with a lower or higher number of creases are preferred for applications where a single stable state is needed. Furthermore, from the design phase diagram, we observe that structures with two and three creases have multistable states under a wide range of strain (15–40% strain for the case of two creases and 0–40% strain for the case of three creases), which can be used for applications of multistable structures that demand a wide working strain range. It is also worth emphasizing that a major advantage of employing the assembly strain as a control parameter is that varying strain levels and therefore tunable multistability can be repeatedly achieved by using a simple mechanical stage, as we will demonstrate later in Section 2.4.
We also study the effects of the crease thickness ratio and the crease length ratio (defined in Fig. S2, ESI†) on the multistability by using the 3-crease ribbon under a strain level of 14% as an example. Tables S1 and S2 (ESI†) show that both ratios have a significant effect on the multistability of the ribbon structure. In this work, we focus on the study of how the multistability can be tuned by the crease number and the strain levels. More detailed studies on the effects of the crease thickness ratio and the crease length ratio will be pursued elsewhere.
2.3 Reconfiguration paths among distinct stable states of origami-inspired ferromagnetic structures
In addition to locating the stable configurations, we also investigate available pathways that the structure can be reconfigured among its stable states, which is important for many applications. The pathways are computationally identified by first locating the saddle points that connect the local minima on the energy landscape, also known as the transition states, using the so-called Binary Image Transition State Search model (see the Experimental section for the description of the algorithm). A full pathway is then given by the steepest-descent paths from the transition state to the energy minima, which are found by tracing the route of a minimization from each downhill side of the transition state.Here we use the three-crease structure as a representative case for study because of its complexity in the configurations and the number of stable states, which results in a large number of reconfiguration paths. As illustrated in Fig. 3A, we identify four distinct pathways among the stable states of the structure: P1–2 for the transition path between S1 and S2, P1–3 between S1 and S3, P2–3 between S2 and S3, and P3–4 between S3 and S4. It is worth noting that in cases where one or more of those states are not stable, the corresponding individual paths may merge into one, as we will detail below.
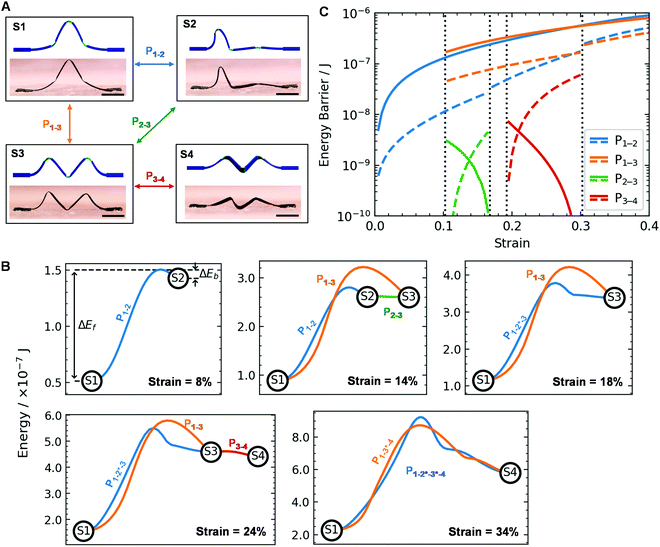 | ||
| Fig. 3 Reconfiguration paths among distinct stable states of origami-inspired ferromagnetic ribbon structures. (A) Possible pathways between the stable states. Scale bars, 2 mm. (B) Energy profiles of pathways for the 3-crease ribbon structure at various strain levels. (C) Minimum energy barriers for pathways in Fig. 3B as a function of the strain. The solid lines indicate the energy barriers from the lower numbered states to the higher numbered states (illustrated by ΔEf in (B)), and the dashed lines are the barriers from the higher numbered states to the lowered numbered states (illustrated by ΔEb in (B)). Here, the line colors follow those of the pathways labelled in (A). The blue and orange lines also encompass the extended pathways P1–2*–3, P1–2*–3*–4, and P1–3*–4. | ||
Fig. 3B shows the available pathways and the associated energy profiles for a representative case in each of the five regimes for a 3-crease ribbon (identified in Fig. 2A) as the strain is increased from 0% to 40%. In the first regime (0–10% strain), only states S1 and S2 exist, with a single pathway (P1–2) to reconfigure between them, as shown in Movie S2 (ESI†). In the second regime (10–17% strain), state S3 appears, so two additional pathways, P1–3 and P2–3, become accessible (Movie S3, ESI†). Our analysis also highlights that there are not only multiple stable states existing in the structure but also multiple available paths for transforming the structure from one state to another. For example, we can observe that there are two main pathways that can be taken from state S1 to S3. The first path, initially following P1–2 to reconfigure S1 to S2, subsequently involves the creation of an asymmetric peak at one side of the structure to form state S3 from S2 (P2–3). Due to symmetry, there are two equivalent scenarios depending on which side the peak is created to form S3. The second path, P1–3, directly reconfigures S1 to S3 by forming two edge peaks simultaneously while maintaining symmetry. As the strain increases to the regime of 17–19%, state S2 becomes unstable, so P1–2 and P2–3 merge into a single path P1–2*–3 (Movie S4, ESI†), where 2* denotes that state 2 is no longer stable. Above the strain of 19%, pathway P3–4 appears between state S3 and twisted state S4, while the two pathways from S1 to S3 still exist (Movie S5, ESI†). Finally, at the strain of 30% and above, S3 is no longer stable leaving just two merged paths P1–2*–3*–4 and P1–3*–4 between S1 and S4 (Movie S6, ESI†), where 3* denotes that state S3 is no longer stable.
We further investigate the energy barriers of each pathway as a function of strain. For each pathway, there are two relevant energy barriers, as illustrated in Fig. 3B using P1–2 in the case of 8% strain as an example. We label ΔEf for the energy required to transition from a lowered numbered state to a higher numbered state in each pathway (here, S1 to S2), while ΔEb is the energy required for the opposite transition (here, S2 to S1). We summarize the values of the energy barriers for all the available pathways in Fig. 3C, where ΔEf and ΔEb for each pathway are represented by solid and dotted lines, respectively. We can see that the energy barriers for pathways reconfiguring from S1 to other states including S2, S3 and S4 depending on the strain levels (P1–2, P1–2*–3, P1–2*–3*–4, P1–3, P1–3*–4; solid blue and orange lines) is much larger than their corresponding reverse barriers (dotted blue and orange lines, respectively). Such difference suggests that state S1 is more stable than the other states (S2, S3 and S4), which is consistent with the design phase diagram in Fig. 2A, where S1 is almost always stable for wide-ranging strains under all crease numbers. It is also seen that the energy barriers of paths P2–3 (green lines, transition between S2 and S3) and P3–4 (red lines, transition between S3 and S4) are significantly lower than those of pathways involving state S1 represented by solid blue and orange lines. This suggests that reconfigurations among states S2, S3, and S4 are much easier than those between S1 and S2/S3/S4. Correspondingly, the required forces to disturb the reconfiguration paths or trap locally stable states are low. Hence, forces like friction between the structure and the substrate (assembly platform) in experiments may be sufficient to trap the structure along these paths for states S2, S3, and S4. This may explain why experimentally the structure appears to get trapped in some states which are shown to be unstable in computational results (Movies S4–S6, ESI†). For example, in Movie S4 (ESI†), when the structure is reconfigured from S2 to S3, the 2nd edge peak is not fully formed due to possible friction between the structure and the substrate, causing the slight asymmetric configuration of S3.
From Fig. 3C, we can also see that the energy barriers for the majority of the reconfiguration paths increase monotonically with the strain, implying that it becomes more difficult to reconfigure the states at larger strains. Exceptions occur for reconfiguration paths P2–3 (solid green line, transition from S2 to S3) and P3–4 (solid red line, transition from S3 to S4), the energy barriers of which decrease with increasing strain levels. Here, the cases when the energy barriers tend to be zero correspond to the instances where S2 and S3 become unstable, i.e., the instability modes of these states. Overall, the energy barrier analysis reinforces the previous observation that, as the strain is varied from 0% to 40%, state S1 always exists for ncrease = 3 while the availability of states S2, S3 and S4 strongly depends on the strain imposed.
2.4 Origami-inspired multistable ferromagnetic structures of multi-ribbon configurations
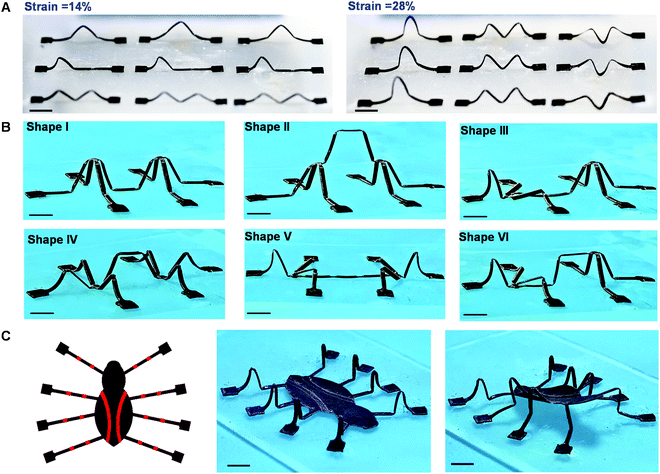
The multistable ribbon configurations studied above can serve as building blocks for complicated geometries and diverse types of origami-inspired structures. Fig. 4A and Fig. S3 (ESI†) show a 3 × 3 array of ribbons with three creases at different strain levels, which is consistent with the prediction of the design phase diagram in Fig. 2A and demonstrates the scalability and versatility of the technique. Particularly, as predicted by the design phase diagram, three distinct stable states exist at the strain levels of 14% (S1, S2, and S3) and 28% (S1, S3, and S4), respectively. In experiments, each individual ribbon unit is separately addressable and therefore the structure array can be magnetically tuned in a sequential manner to display all the three stable states (S1 in row 1, S2 in row 2, and S3 in row 3 at a strain of 14%; S1 in column 1, S3 in column 2, and S4 in column 3 at a strain of 28%). Such capability of dynamically and reversibly tuning the patterns in a structure array represents an important option for applications including digital coding and smart switches,9 especially when integrated with other functional materials or elements. In addition, the complexity of origami-inspired structures and the number of stable states can be increased by incorporating a larger number of interconnected structural units, like ribbons with two creases. Fig. 4B presents a structure consisting of two creased table structures connected by a creased ribbon, which can be magnetically reconfigured into six distinct stable states that are enabled by the multistability of the ribbon units. Furthermore, the multistable origami-inspired structures can be extended to diverse geometries. Fig. 4C and Fig. S4 (ESI†) demonstrate structures that mimic insect flexion, standing states, and a series of biomimetic movements. More examples including those that resemble two stable states of a butterfly, a cage, and a drug-release system are shown in Fig. S5 (ESI†).2.5 Application in soft robotics
Based on the multistability of origami-inspired structures and the flexibility of magnetic actuation, we further assemble two 3-crease ribbon structures (side by side) into a 3D origami robot to achieve a fast, remote response to an external magnetic field. Fig. 5A shows the design concept and assembly process, which begins with two buckled ferromagnetic ribbon structures of 3 creases (150 μm thick) attached to an elastomer substrate (400 μm thick). Each center peak of the two structures acts as the “foot” of the robot, which can drive the robot to move forward under magnetic actuation. To actuate the robot, a portable magnet is placed directly underneath the structure to bring the front “foot” forward, while the other one serves as a fulcrum at the back. Once the magnet is removed, the hinge on the front “foot” recovers its original shape, driving the robot forward. The actuation process above is recorded in Fig. 5B and Movie S7 (ESI†). Future opportunities include the fabrication and actuation of freestanding biomimetic structures by using the shape fixing effect of shape memory polymers,19,49 or liquid crystal elastomers50 for applications including remotely controlled soft robotics.3. Conclusion
To sum up, we show from experiments and simulations that the multistability and the associated transition paths of origami-inspired, compressively buckled ferromagnetic structures can be tailored by controlling the number of creases and assembly strain. Our constructed design phase diagram of a representative creased ribbon structure from the energy landscape analysis is validated by our experiments and provides important guidelines for the targeted number of stable states by varying the two control factors. In addition, transition pathways among the distinct stable states are computed, and they illustrate how the structure can be manipulated to be reconfigured along different pathways. The experimental results of our origami-inspired ferromagnetic structures show targeted multistable states following designed pathways, which highly agrees with those from modeling. The fundamental understanding of the multistability of creased ribbon structures provides important guidelines for the design and application of complex classes of origami-inspired systems that are capable of multiple shape reconfigurations. Demonstrated examples include the arrays of creased ribbon units, a series of biomimetic states of a developed “insect” structure, and a soft robot based on a double-ribbon structure. These results highlight potential opportunities in the future to exploit multistable, origami-inspired ferromagnetic structures for intelligent and adaptive systems such as programmable digital logic arrays by integrating complex structure design and functional materials like stimuli-responsive polymers and electronics. It will also be interesting to explore the concept of actively manipulating the number of stable states and their reconfiguration paths in the design of other types of functional structures by using alternative control parameters.4. Experimental section
Fabrication of 2D ferromagnetic composite precursors
The fabrication of ferromagnetic composite films began with using a planetary mixer (AR-100, Thinky) to homogeneously mix (2000 rpm for 2 min, then defoaming at 2000 rpm for 1 min) NdFeB (neodymium iron boron) microparticles (average diameter: 5 μm, Neo Magneuench) into uncured PDMS (polydimethylsiloxane, made with a volume ratio of part A over part B of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) resin at a volume ratio of 1
1) resin at a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. Then the obtained ferromagnetic PDMS composite was spin coated onto a Petri-dish at 500 rpm for 15 s. The completely cured ferromagnetic film (thickness = 180–200 μm) was obtained after 2 days and laser cut into desired 2D patterns. The raster mode of the laser (VLS 2.30, Universal Laser System, Ansonia, CT) was used to create the crease segment of origami structures.
5. Then the obtained ferromagnetic PDMS composite was spin coated onto a Petri-dish at 500 rpm for 15 s. The completely cured ferromagnetic film (thickness = 180–200 μm) was obtained after 2 days and laser cut into desired 2D patterns. The raster mode of the laser (VLS 2.30, Universal Laser System, Ansonia, CT) was used to create the crease segment of origami structures.
3D assembly
The assembly of origami-inspired structures was conducted using the previously introduced 3D buckling technique.42 The 2D precursor was transferred onto a prestreched elastomer substrate (1 mm thick, Dragon Skin; Smooth-On, Easton, PA). Strong adhesion was formed at bonding sites by applying a thin layer of superglue. More specifically, a needle tip was used to apply a tiny drop of the superglue to the center of the bonding site, followed by physical lamination of the film onto the elastomer substrate to spread the superglue into a very thin layer. Releasing the prestrain in the assembly platform transformed the 2D pattern into a 3D structure and completed the assembly process.Magnetic actuation
A cylinder magnet (D8Y0, K&J magnetics) was used to actuate the origami-inspired structures, and the ferromagnetic field was generated from the circular surface (diameter: 1.27 cm) of the cylinder magnet. The working distance of the magnet for effective actuation was identified to be 3–22 mm for this specific magnet. By adjusting the distance within this range and the angle (0–180°) between the circular surface and the targeted part of the structure, the strength and the direction of the applied ferromagnetic field were controlled to address the needs of reconfigurations.Assembly of a soft robot
The 3D buckling technique was used for the assembly of a soft robot. 2D precursors of two ribbon structures with 3 creases were patterned from ferromagnetic composite films by using a laser (VLS 2.30, Universal Laser System, Ansonia, CT), which were then transferred onto a prestreched elastomer substrate (400 μm thick, Dragon Skin; Smooth-On, Easton, PA). Strong adhesion was formed at bonding sites by applying a thin layer of superglue. Releasing the prestrain in the assembly platform transformed the 2D patterns into origami structures (in a form of a 2 × 1 array) in their symmetric one-peak state (state S1). Then a laser was used to cut the substrate around the structure into a rectangle of 16 mm × 5 mm. The entire system was then turned upside-down.Modeling
The structures were discretized as a 2D triangular mesh using a Delaunay refinement with an optimal mesh size equal to an eighth of the ribbon width. The energy of the structure was calculated by considering contributions from the stretching and bending of the mesh, as well as a repulsive potential with the substrate. A bar-and-hinge model was used for the stretching and bending components. This involved treating the bonds in the triangulation as elastic springs and with elastic hinges connecting adjacent triangular faces. The resulting expression for the energy is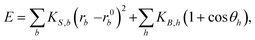 | (1) |
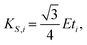 | (2) |
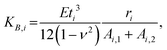 | (3) |
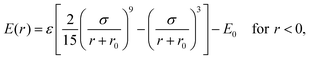 | (4) |
Finding stable states
The stable states correspond to configurations that lie at the local minima in the energy landscape, so they were found by minimizing the energy of the system. The L-BFGS algorithm was used for this because it is efficient for large numbers of degrees of freedom. To enable different states to be obtained, we carefully sampled the available states at selected points in the design phase diagram, typically at 5 different strain levels for each crease number. At such a point, random forces were applied to each of the creases and the structure was buckled by moving the binding sites according to the strain over the first 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, after which the structure was allowed to relax. This process was repeated several hundred times. Once the qualitatively distinct configurations were identified, the strain was then varied for each configuration to observe the range over which they were stable. To ensure our procedure is robust, we increased the sampling frequency of each configuration and we reliably found the same states.
000 iterations, after which the structure was allowed to relax. This process was repeated several hundred times. Once the qualitatively distinct configurations were identified, the strain was then varied for each configuration to observe the range over which they were stable. To ensure our procedure is robust, we increased the sampling frequency of each configuration and we reliably found the same states.
Finding transition states
To identify the transition states for use in locating the pathways, the binary-image transition state search (BITSS) method was used. Briefly, this method used two states, denoted by x1 and x2, which were initialized at the two minima. The energy of this pair of states was then minimized subject to two constraints. Firstly, the distance between the two states was set as a value d0, which was steadily reduced to zero such that the states converged at the transition state. The second constraint required the energies of the individual states, E1 and E2, to be equal. This prevented one state from passing over the saddle point, which would result in the convergence occurring at one of the minima instead. These two constraints were applied as penalty terms in the total energy to be minimized:| Etot(x1,x2) = E1 + E2 + Ke(E1 − E2)2 + Kd(d(x1,x2) − d0)2, | (5) |
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We acknowledge the support of the following grants: NSF-CMMI-2103012 (X. W.), NSF-CMMI-2020476 (T. Z.). S. J. A. is supported by a studentship from the Engineering and Physical Sciences Research Council (EPSRC, grant no. 2210196). Simulations were performed at the facilities of the Hamilton HPC Service of Durham University and the Comet cluster (Award TG-MSS170004 to T. Z.) in The Extreme Science and Engineering Discovery Environment.References
- Y. Chen, R. Peng and Z. You, Science, 2015, 349, 396 CrossRef CAS PubMed.
- L. H. Dudte, E. Vouga, T. Tachi and L. Mahadevan, Nat. Mater., 2016, 15, 583–588 CrossRef CAS PubMed.
- X. Ning, X. Wang, Y. Zhang, X. Yu, D. Choi, N. Zheng, D. S. Kim, Y. Huang, Y. Zhang and J. A. Rogers, Adv. Mater. Interfaces, 2018, 5, 1800284 CrossRef.
- D. Thesiya, A. Srinivas and P. Shukla, J. Astron. Instrum., 2015, 4, 1550006 CrossRef.
- D. Melancon, B. Gorissen, C. J. García-Mora, C. Hoberman and K. Bertoldi, Nature, 2021, 592, 545–550 CrossRef CAS PubMed.
- M. Liu, L. Domino and D. Vella, Soft Matter, 2020, 16, 7739–7750 RSC.
- S. Felton, M. Tolley, E. Demaine, D. Rus and R. Wood, Science, 2014, 345, 644–646 CrossRef CAS PubMed.
- J. L. Silverberg, A. A. Evans, L. McLeod, R. C. Hayward, T. Hull, C. D. Santangelo and I. Cohen, Science, 2014, 345, 647–650 CrossRef CAS PubMed.
- T. Chen, M. Pauly and P. M. Reis, Nature, 2021, 589, 386–390 CrossRef CAS PubMed.
- C. Yang, M. Boorugu, A. Dopp, J. Ren, R. Martin, D. Han, W. Choi and H. Lee, Mater. Horiz., 2019, 6, 1244–1250 RSC.
- J. Hellmeier, R. Platzer, A. S. Eklund, T. Schlichthaerle, A. Karner, V. Motsch, M. C. Schneider, E. Kurz, V. Bamieh, M. Brameshuber, J. Preiner, R. Jungmann, H. Stockinger, G. J. Schutz, J. B. Huppa and E. Sevcsik, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(4) DOI:10.1073/pnas.2016857118.
- K. Miura, Inst. Space Astronaut. Sci. Rep., 1985, 1–9 Search PubMed.
- E. T. Filipov, T. Tachi and G. H. Paulino, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12321–12326 CrossRef CAS PubMed.
- J. L. Silverberg, J. H. Na, A. A. Evans, B. Liu, T. C. Hull, C. D. Santangelo, R. J. Lang, R. C. Hayward and I. Cohen, Nat. Mater., 2015, 14, 389–393 CrossRef CAS PubMed.
- S. Sadeghi and S. Li, Extreme Mech. Lett., 2020, 40, 100958 CrossRef.
- K. Liu, T. Tachi and G. H. Paulino, Nat. Commun., 2019, 10, 4238 CrossRef PubMed.
- H. Fang, T.-S. Chang and K. W. Wang, Smart Mater. Struct., 2019, 29, 015026 CrossRef.
- Z. R. Zhai, Y. Wang and H. Q. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2032–2037 CrossRef CAS PubMed.
- X. Wang, X. Guo, J. Ye, N. Zheng, P. Kohli, D. Choi, Y. Zhang, Z. Xie, Q. Zhang, H. Luan, K. Nan, B. H. Kim, Y. Xu, X. Shan, W. Bai, R. Sun, Z. Wang, H. Jang, F. Zhang, Y. Ma, Z. Xu, X. Feng, T. Xie, Y. Huang, Y. Zhang and J. A. Rogers, Adv. Mater., 2019, 31, e1805615 CrossRef PubMed.
- Y. Liu, B. Shaw, M. D. Dickey and J. Genzer, Sci. Adv., 2017, 3, e1602417 CrossRef PubMed.
- Q. Ge, C. K. Dunn, H. Qi and M. Dunn, Smart Mater. Struct., 2014, 23, 094007 CrossRef.
- S. Janbaz, R. Hedayati and A. A. Zadpoor, Mater. Horiz., 2016, 3, 536–547 RSC.
- A. S. Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–418 CrossRef PubMed.
- Y. Zhang, X. Le, Y. Jian, W. Lu, J. Zhang and T. Chen, Adv. Funct. Mater., 2019, 29, 1905514 CrossRef CAS.
- A. Kotikian, C. McMahan, E. C. Davidson, J. M. Muhammad, R. D. Weeks, C. Daraio and J. A. Lewis, Sci. Robot., 2019, 4(33) DOI:10.1126/scirobotics.aax7044.
- Y. Li, H. Yu, K. Yu, X. Guo and X. Wang, Adv. Funct. Mater., 2021, 2100338 CrossRef CAS.
- Y. Kim, H. Yuk, R. Zhao, S. A. Chester and X. Zhao, Nature, 2018, 558, 274–279 CrossRef CAS PubMed.
- M. Jamal, S. S. Kadam, R. Xiao, F. Jivan, T.-M. Onn, R. Fernandes, T. D. Nguyen and D. H. Gracias, Adv. Healthcare Mater., 2013, 2, 1142–1150 CrossRef CAS PubMed.
- S. Chen, J. Chen, X. Zhang, Z.-Y. Li and J. Li, Light: Sci. Appl., 2020, 9, 75 CrossRef CAS PubMed.
- L. Xu, T. C. Shyu and N. A. Kotov, ACS Nano, 2017, 11, 7587–7599 CrossRef CAS PubMed.
- L. S. Novelino, Q. Ze, S. Wu, G. H. Paulino and R. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 24096 CrossRef CAS PubMed.
- W. Xu, Z. Qin, C. T. Chen, H. R. Kwag, Q. Ma, A. Sarkar, M. J. Buehler and D. H. Gracias, Sci. Adv., 2017, 3, e1701084 CrossRef PubMed.
- S. Xu, Z. Yan, K.-I. Jang, W. Huang, H. Fu, J. Kim, Z. Wei, M. Flavin, J. McCracken and R. J. S. Wang, Science, 2015, 347, 154–159 CrossRef CAS PubMed.
- H. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005 CrossRef PubMed.
- E. Grinspun, A. N. Hirani, M. Desbrun and P. Schröder, ACM/Eurographics Symposium on Computer Animation, 2003, pp. 62–67 Search PubMed.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- J. Chen, G. Schusteritsch, C. J. Pickard, C. G. Salzmann and A. Michaelides, Phys. Rev. Lett., 2016, 116, 025501 CrossRef PubMed.
- H. Zhang, X. Cheng, D. Yan, Y. Zhang and D. Fang, Compos. Sci. Technol., 2019, 183, 107822 CrossRef CAS.
- J. Panter, J. Chen, T. Zhang and H. Kusumaatmaja, Commun. Phys., 2019, 2, 1–9 Search PubMed.
- E. Weinan, W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103 CrossRef PubMed.
- Y. Li, S. Avis, J. Chen, G. Wu, T. Zhang, H. Kusumaatmaja and X. Wang, Extreme Mech. Lett., 2021, 48, 101428 CrossRef.
- Y. H. Zhang, Z. Yan, K. W. Nan, D. Q. Xiao, Y. H. Liu, H. W. Luan, H. R. Fu, X. Z. Wang, Q. L. Yang, J. C. Wang, W. Ren, H. Z. Si, F. Liu, L. H. Yang, H. J. Li, J. T. Wang, X. L. Guo, H. Y. Luo, L. Wang, Y. G. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11757–11764 CrossRef CAS PubMed.
- Y. Liu, X. Wang, Y. Xu, Z. Xue, Y. Zhang, X. Ning, X. Cheng, Y. Xue, D. Lu, Q. Zhang, F. Zhang, J. Liu, X. Guo, K. C. Hwang, Y. Huang, J. A. Rogers and Y. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15368–15377 CrossRef CAS PubMed.
- W. Hu, G. Z. Lum, M. Mastrangeli and M. Sitti, Nature, 2018, 554, 81–85 CrossRef CAS PubMed.
- S. Wu, W. Hu, Q. Ze, M. Sitti and R. Zhao, Multifunct. Mater., 2020, 3, 042003 CrossRef CAS PubMed.
- D. Yan, M. Pezzulla, L. Cruveiller, A. Abbasi and P. M. Reis, Nat. Commun., 2021, 12, 2831 CrossRef CAS PubMed.
- Y. Tang, Y. Li, Y. Hong, S. Yang and J. Yin, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(52), 26407–26413 CrossRef CAS PubMed.
- W. Huang, Y. Wang, X. Li and M. K. Jawed, J. Mech. Phys. Solids, 2020, 145, 104168 CrossRef.
- Y. Li, C. Luo, K. Yu and X. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 8929–8939 CrossRef CAS PubMed.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- Y. Kim, G. A. Parada, S. Liu and X. Zhao, Sci. Robot., 2019, 4(33) DOI:10.1126/scirobotics.aax7329.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh01152a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |