Single-cell microfluidic impedance cytometry: from raw signals to cell phenotypes using data analytics†
Carlos
Honrado
 a,
Paolo
Bisegna
a,
Paolo
Bisegna
 b,
Nathan S.
Swami
b,
Nathan S.
Swami
 *a and
Federica
Caselli
*a and
Federica
Caselli
 *b
*b
aDepartment of Electrical and Computer Engineering, University of Virginia, Charlottesville, VA 22904, USA. E-mail: nswami@virginia.edu
bDepartment of Civil Engineering and Computer Science, University of Rome Tor Vergata, Via del Politecnico 1, 00133 Rome, Italy. E-mail: caselli@ing.uniroma2.it
First published on 23rd November 2020
Abstract
The biophysical analysis of single-cells by microfluidic impedance cytometry is emerging as a label-free and high-throughput means to stratify the heterogeneity of cellular systems based on their electrophysiology. Emerging applications range from fundamental life-science and drug assessment research to point-of-care diagnostics and precision medicine. Recently, novel chip designs and data analytic strategies are laying the foundation for multiparametric cell characterization and subpopulation distinction, which are essential to understand biological function, follow disease progression and monitor cell behaviour in microsystems. In this tutorial review, we present a comparative survey of the approaches to elucidate cellular and subcellular features from impedance cytometry data, covering the related subjects of device design, data analytics (i.e., signal processing, dielectric modelling, population clustering), and phenotyping applications. We give special emphasis to the exciting recent developments of the technique (timeframe 2017–2020) and provide our perspective on future challenges and directions. Its synergistic application with microfluidic separation, sensor science and machine learning can form an essential toolkit for label-free quantification and isolation of subpopulations to stratify heterogeneous biosystems.
1 Introduction
Cellular systems exhibit a wide degree of heterogeneity,1,2 likely due to temporal fluctuations in the levels of regulatory proteins, position in the cell cycle and the activation of cell death mechanisms. These heterogeneous subpopulations can fundamentally affect biological function and determine disease presentation, progression and treatment response.3 Quantifying phenotypic heterogeneity is particularly important, since it represents active changes to the cell under external interventions or micro-environment alterations.The state-of-the-art method for quantifying phenotypic heterogeneity is by fluorescence-based flow cytometry, wherein the characteristic surface proteins expressed by cells are labelled using fluorescent antibody receptors and measured at high throughput (103–104 cells per s) under laser excitation to obtain multi-dimensional data. However, quantification by this technique is infeasible in several scenarios, such as when the expressed cell surface proteins may not reliably identify cells of interest (e.g. stem cells4–7); when the measured phenotype exhibits spatial complexity (e.g. mitochondrial features8) or unknown intensity thresholds (e.g. metabolism9). Other limiting scenarios include the need to repeatedly analyse the same set of cells (e.g. kinetic monitoring under drug interventions10); or when cell labelling affects its functionality or the staining process involves costly chemicals and time-consuming tasks. In these cases, which are forming an increasing proportion of cell phenotypic studies of relevance to diseases, there is much interest in complementary methods for biophysical analysis of single-cells,11 preferably using label-free metrics that are based on inherent cell properties, to enable phenotypic quantification from heterogeneous samples and to trigger downstream cell isolation strategies.
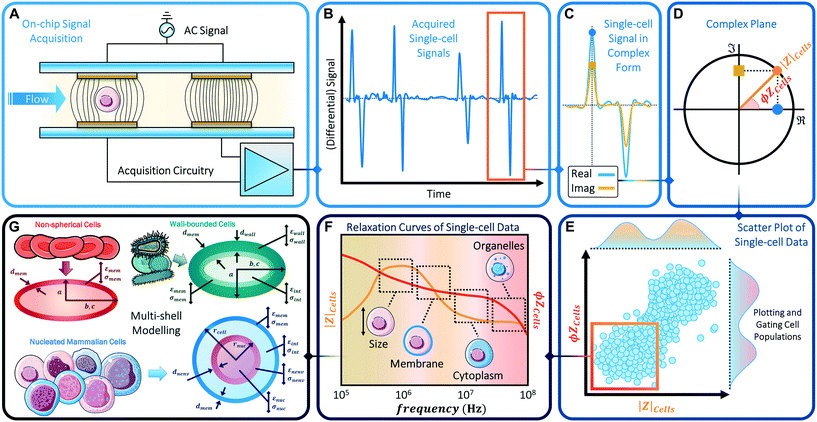
Phenotypic heterogeneity is often assessed based on measurable differences in biophysical properties, such as cell size, shape, deformability and subcellular characteristics, including membrane composition and morphology, mitochondrial network, organelles in cytoplasm, ion pile-up in endoplasmic reticulum and nucleus size. Such cell phenotype changes can be influenced by genetic and/or proteomic factors, as well as by the extracellular matrix and by active environmental cues. Fluorescence cytometry, while highly sensitive to biochemical phenotypes, is not well suited to discern biophysical phenotypes. On the other hand, the emerging frontier of cell biophysical characterization can be achieved by means of impedance cytometry (Fig. 1). In fact, biophysical phenotypes can be assessed by fitting single-cell impedance cytometry data to appropriate dielectric models, thereby enabling the quantification and stratification of complex samples in a label-free multi-parametric manner.
Microfluidic impedance cytometry involves the measurement of the electric field screening of individual cells passing over patterned electrodes in a microchannel, as accomplished by electric current variation under an applied AC voltage (Fig. 1A). The measured current exhibits a characteristic temporal signal shape (Fig. 1B and C) whose features depend on: the applied potential, the system impedance, and cell properties, i.e. volume and dielectric properties.12 The measured impedance is frequency dependent and exhibits characteristic dispersions for each subcellular region13 (Fig. 1F). While the electrical double-layer around the electrodes screens the field at frequencies <100 kHz, the signal is chiefly determined by the cellular electrical size in the 0.1–1 MHz range due to complete membrane-induced screening. Polarization of the plasma membrane in the 2–10 MHz range offers information on membrane morphology based on measured capacitance. In the 10–30 MHz range, the membrane is minimally polarized, so that the cytoplasmic conductivity and permittivity provide information on the organelles, while at higher frequencies, the response is dependent on nucleus properties. It is noteworthy that the exact frequency range values are dependent on cell size, media conductivity and the complex conductivity of the respective subcellular layer (see also Scheme 2 in section 3). Using superimposed voltage sinusoids the impedance magnitude and phase (Fig. 1D) can be obtained simultaneously over multiple frequencies for each cell, paving the way for multiparametric analysis by fitting impedance spectra to the appropriate shell model14,15 (Fig. 1G) for characterization of subcellular electrophysiology. However, while cell recognition by fluorescence cytometry can simply be determined based on pre-set thresholds, recognition based on impedance metrics requires the analysis of temporal signal trains of single cells at each frequency and population-level analysis of the scatter plots (Fig. 1E) to identify characteristic frequency dispersions (Fig. 1F).
A number of reviews with broad scope include a discussion on microfluidic impedance cytometry (e.g., ref. 16–24). For a comprehensive description of the basic principles of microfluidic impedance cytometry and the relevant literature from early works to 2010, the reader is referred to the review papers by Cheung et al.25 and Sun and Morgan.13 Subsequent developments were reviewed by Chen et al.26 in 2015 and by Petchakup et al.27 in 2017. In particular, Chen et al. discussed systems with enhanced sensitivity, systems coupled with optical flow cytometry, and point-of-care systems, whereas Petchakup et al. reviewed common designs and provided an overview of biomedical applications of the technique. The specific topic of positional dependence and position detection of particles and cells has been recently reviewed by Daguerre et al.28
The present review covers the exciting developments that have been achieved in recent years (2017–2020), with a focus on phenotypic elucidation based on signal processing, cell modelling and population-level data analysis. Microfluidic impedance cytometry has evolved from the standard approaches towards novel designs and strategies that greatly enhance the sensitivity and accuracy of the measurements, as well as the information content embedded in the electrical fingerprints, thus enabling multiparametric cell characterization. Furthermore, hybrid platforms combining microfluidic impedance cytometry with other sensing or manipulation modalities have been developed, and device portability has been pursued via system integration, simplified fabrication and real-time processing. Overall, this opens up new opportunities in fundamental and applied research, with biophysical cell phenotyping of complex samples becoming increasingly important. It is our intention to provide the reader with an overview of such current research efforts.
On the other hand, the evolution from classical analysis based on signal amplitude at limited bandwidth, towards accurate multiparametric characterization at high-throughput, calls for tailored strategies of signal processing and data analysis to elucidate cell phenotypes from impedance cytometry data. Accordingly, this review has two main tutorial goals: i) to provide a cohesive overview of how high-content single-cell electrical fingerprints are collected and processed; ii) to elucidate the strategies to identify sub-populations of cells based on dielectric modelling and population-level analytics on the collected data to enable statistically relevant inferences on cell phenotype. We provide a systematic review on the emerging approaches to impedance-based cell phenotyping, so that future studies can focus on its standardization and make it more amenable to inline cell recognition for triggering of downstream sorting.
The overall structure of the paper is as follows: section 2 focuses on device designs for high content signal acquisition, section 3 deals with data analytics tools to extract the information embedded in the electrical fingerprints, and section 4 presents a survey of recent cell phenotyping applications. Finally, in section 5 we draw our view on the perspectives of the technique.
2 Device designs for high-content measurement of single-cell electrical fingerprints
After general guidelines, we briefly review the classic electrode configurations. Then we describe innovative chip designs to obtain increased accuracy and multiparametric cell characterization, as well as platforms with multiple electrical sensing zones and hybrid platforms.2.1 General considerations
In order to achieve real-time analysis at high throughput, which is needed for active particle sorting47,48 or selective enrichment, a high processing throughput is also required (i.e., the number of analysed single-particle signals per unit time), thus calling for tailored signal-processing approaches.
2.2 Electrode configurations
 | ||
| Fig. 2 (A) and (B) Classic coplanar and facing electrodes designs, respectively, along with relevant idealized signals. (C) Liquid electrodes concept. (D) Design based on three-dimensional electrodes. (E–G) Designs enabling compensation of position blurring, along with simulated impedance traces for different particle trajectories. See sections 2.2 and 2.3 for details. Images were adapted with permission from (A) ref. 57, copyright The Royal Society of Chemistry 2001, (B) ref. 36, copyright 2005 Wiley-Liss, Inc. (C) ref. 75, copyright The Royal Society of Chemistry 2010 (D) ref. 79, copyright 2017 Elsevier B.V. (E) ref. 58, copyright 2017 The Author(s), (F) ref. 94, copyright 2017 The Author(s), (G) ref. 90, copyright The Royal Society of Chemistry 2016. | ||
2.3 Cytometer designs for increased accuracy
Due to non-homogeneous electric field distribution, nominally identical particles flowing along different trajectories experience different electric field strengths, thereby generating different impedance signals.25,28,57,68 This introduces blurring of the estimated particle properties, thereby limiting accuracy and reproducibility. To overcome this issue, several approaches have been developed.While optimal sample focusing strategies remains elusive, it should be noted86 that active focusing adds complexity to fabrication; sheath flow systems cause dilution; the high flow rates required for inertial focusing place an inordinate demand on electrical sampling; and viscoelastic focusing is sensitive to rheology of the carrier fluid.
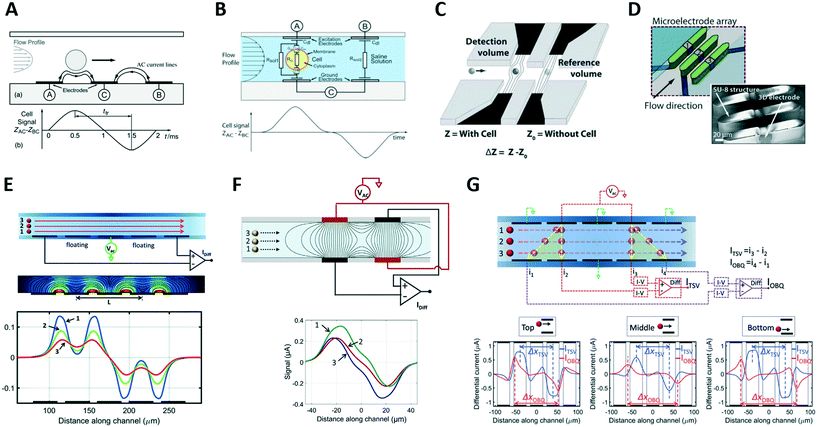
In the typical coplanar electrode chip with the three-electrode differential measurement scheme (Fig. 2A), the pulse width normalized by the peak-to-peak transit time correlates with the vertical position of the particle.58 By introducing a floating electrode between the stimulating and sensing electrodes (Fig. 2E), a bipolar double-Gaussian signal is obtained, and the relative prominence of the peaks with respect to the saddle in between them, can be correlated with the particle's vertical position.91 Those metrics were used to achieve accurate sizing of yeasts58,91 and human blood cells.92,93
Rewiring the standard facing electrode design by applying voltage and ground to the pairs of diagonally opposite electrodes (Fig. 2F) generates an asymmetric bipolar Gaussian signal due to flowing particles, with the relative difference in peak heights of positive versus negative pulse offering information on vertical position of the particle.94 This results from the interplay between transverse and longitudinal electric fields established in the sensing zone. Alternatively, by using five pairs of facing electrodes (Fig. 2G), the particle vertical position is encoded by the ratio between transit times relevant to oblique and transverse current paths.90 The designs in Fig. 2F and G can also be implemented in a liquid electrode configuration, thereby enabling mitigation of measurement sensitivity to particle lateral position.
2.4 Cytometer designs for multiparametric characterization
Typical impedance measurements are focused on the characterization of cell size, membrane capacitance and interior conductivity, but design solutions that are tailored to enrich the information content of electrical fingerprints have emerged. These designs can be used to provide additional information valuable for monitoring cell position, cell shape and cell mechanical properties, as discussed in this section (see Table 1A and B for an overview).| A. Designs for electrical position detection | |||
|---|---|---|---|
| Electrode layout | Direction (and principle) of detection | Application | Ref. |
| Single pair of non-parallel coplanar electrodes | Channel width (transit time) | Discrimination of five different transverse bead positions | Wang et al. 2017 (ref. 95) (Fig. 3A) |
| 3 N-shaped coplanar electrodes | Channel width (measured electrical signal and geometric relationships) | RBC/bead position detection, monitoring bead hydrodynamic focusing | Yang et al. 2019 (ref. 96) (Fig. 3B) |
| 2 facing electrode arrays | Channel width (gradient in electric field) | Bead tracking | Solsona et al. 2019 (ref. 97) (Fig. 3C) |
| 2 coplanar electrodes with non classical shape + DEP-focusing electrode array | Channel length (impedance variation) | Bead tracking (potentially real-time) | Brazey et al. 2018 (ref. 98) (Fig. 3D) |
| Network of 10 code-multiplexed Coulter sensors | Location across 10 parallel channels (recognition of signal patterns) | Position detection of cells from different cell lines | Wang et al. 2019 (ref. 46) (Fig. 3E) |
| 5 coplanar L-electrode pairs + 5 coplanar electrodes | Channel width (ratio of transit times) + channel height (relative prominence) | Monitoring bead inertial focusing | Reale et al. 2018 (ref. 99) |
| 2 coplanar L-electrode pairs + 5 coplanar electrodes | Channel width (peak relative difference) + channel height (relative prominence) | Monitoring RBC/bead hydrodynamic focusing | Reale et al. 2019 (ref. 93) (Fig. 3F) |
| 2 coplanar L-electrode pairs + 2 facing electrode pairs | Channel width (peak relative difference) + channel height (peak relative difference) | RBC/yeast position detection | Honrado et al. 2020 (ref. 100) (Fig. 3G) |
| B. Designs sensitive to cell shape or cell mechanical properties | |||
|---|---|---|---|
| Electrode and fluidic layouts | Impedance-based metrics | Application | Ref. |
| 1 coplanar electrode pair, 1 constriction structure | Pulse width, amplitude and width-to-amplitude ratio | Morphology-based yeast buddying analysis | Xie et al. 2019* (ref. 88) (Fig. 4B) |
| 1 coplanar electrode pair, straight channel | Baseline-to-plateau current magnitude | Identification of developmental stages of C. elegans with variable morphology | Zhu et al. 2018* (ref. 108) |
| 4 coplanar electrode pairs, 1 constriction channel | 3 passage times, impedance magnitude | Simultaneous electrical and mechanical cell characterization | Zhou et al. 2018* (ref. 116) (Fig. 4E) |
| 1 coplanar electrode pair, 2 (or 5) constriction regions separated by 1 (or 4) relaxation region(s) | Signal features (transit times, rise times ratio, rise slope, impedance and phase drops) | Simultaneous electrical and mechanical cell characterization | Ren et al. 2019 (ref.117) (Fig. 4F), and Ghassemi et al. 2020 (ref. 118) |
| 4 three-dimensional electrodes, differential multiconstriction channel | 4 transit times, relaxation index (i.e., transit times ratio), average impedance magnitude | Simultaneous electrical and mechanical cell characterization | Yang et al. 2019* (ref. 115) (Fig. 4G) |
| C. Platforms with multiple electrical sensing zones | |||
|---|---|---|---|
| MIC sensing zone (#, layout, wiring) | Separating region(s) | Application | Ref. |
| 2 zones, 1 coplanar electrode pair each, absolute measurement | Hypertonic stimulation | Quantification of cell survival rate | Zi et al. 2020* (ref. 119) (Fig. 5A) |
| 2 zones, 2 coplanar L-electrode pairs each, crossed differential wiring scheme | Dielectrophoresis | Monitoring dielectrophoretic focusing | Reale et al. 2019 (ref. 120) (Fig. 5B) |
| 2 zones, 3 coplanar electrodes each, differential measurement | Hyperbolic constriction | Coincidence arbitration | Caselli et al. 2020 (ref. 44) (Fig. 5C) |
| 2 zones, 2 coplanar electrodes each (1 in common), absolute measurement | N/A | Automated antischistosomal drug screening | Chawla et al. 2018 (ref. 121) |
| 2 zones, 3 coplanar electrodes each, differential measurement | Antigen specific capture chamber | Protein detection in undiluted plasma samples | Valera et al. 2018 (ref. 59) |
| 6 zones, 3 coplanar electrodes overall, shaped to create coded Coulter counters | Antigen specific capture chambers (4 overall) | Immunophenotyping against multiple antigens | Liu et al. 2019 (ref. 125) (Fig. 5D) |
| D. Hybrid platforms | |||
|---|---|---|---|
| MIC sensing zone (layout, wiring) | Other sensing/manipulation modality | Application | Ref. |
| 2 coplanar L-electrode pairs, crossed differential wiring scheme | High-speed optical imaging of individual flowing cells | Multimodal analysis of pollen grains | Reale et al. 2019 (ref. 126) |
| 2 coplanar electrodes, absolute measurement | High-speed optical imaging of travelling single cell invading into a side constriction channel | Multiparametric cell characterization | Liu et al. 2020 (ref. 127) (Fig. 5E) |
| 2 coplanar electrodes, absolute measurement | Time-lapse microscopy of growing cells | Long-term monitoring of cell growth rates | Chawla et al. 2018 (ref. 128) (Fig. 5F) |
| 2 coplanar electrodes, absolute measurement | Impedance spectroscopy of individual trapped cells | Electrical property measurement of single cells | Feng et al. 2019* (ref. 129) (Fig. 5G) |
| 2 coplanar electrodes, absolute measurement | Contactless dielectrophoretic particle manipulation | Increase robustness against chip-to-chip variability due to microfabrication errors | Farmehini et al. 2019 (ref. 130) |
| 2 coplanar electrodes, absolute measurement | Vortex chip | Isolation and enumeration of circulating tumour cells | Raillon et al. 2019 (ref. 52) (Fig. 5H) |
| 3 coplanar electrodes, differential measurement | Dean flow fractionation and flow rate reduction based on inertial focusing | Leukocyte isolation | Petchakup et al. 2019* (ref. 63) (Fig. 5I) |
| Interdigital electrodes (5 fingers) | Encapsulation of cells in droplets | Monitoring osteogenic differentiation | Fan et al. 2019 (ref. 131) |
Wang et al.95 reported a system using a single pair of non-parallel microelectrodes to detect the lateral position of particles flowing in a microchannel on the basis of pulse width (Fig. 3A), however non-uniformity of velocity profile can be a confounding effect. Yang et al.96 presented a system based on N-shaped electrodes (Fig. 3B) that also accounts for particle velocity. Using simple geometric relationships, they derived an analytical expression yielding the particle's lateral position from the measured electrical signal. Particle size characterization was also reported. Solsona et al.97 exploited a gradient in the electric field to detect the particle lateral position (Fig. 3C). Brazey et al.98 presented an impedance based real-time sensor for the detection of the longitudinal particle position (Fig. 3D), which also provided particle velocity. Wang et al.46 predicted the location of particles across ten parallel channels, along with particle velocity and size, by using a code-multiplexed Coulter sensor network (Fig. 3E).
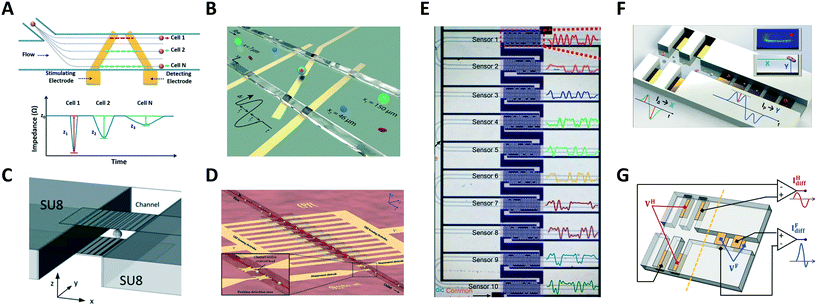 | ||
| Fig. 3 (A–E) Systems for electrical position detection along one spatial coordinate. (F) and (G) Designs for cross-sectional position detection. See section 2.3 and Table 1A for details. Images were adapted with permission from (A) ref. 95, copyright The Royal Society of Chemistry 2017, (B) ref. 96, copyright The Royal Society of Chemistry 2019 (C) ref. 97, copyright The Royal Society of Chemistry 2019 (D) ref. 98, copyright The Royal Society of Chemistry 2018 (E) ref. 46, copyright The Royal Society of Chemistry 2019 (F) ref. 93, copyright The Royal Society of Chemistry 2019, (G) ref. 100, copyright Springer-Verlag GmbH Germany, part of Springer Nature 2020. | ||
The previous systems were limited to position detection along one axis. The first high-throughput system for electrical detection of cross-sectional (i.e., lateral and vertical) position of individual particles flowing through a rectangular microchannel was presented by Reale et al.,99 combining the design in Fig. 2E (for vertical position detection) with the design in Fig. 2G (in liquid electrode configuration, for lateral position detection). The system was used to investigate inertial particle focusing at different particle Reynolds numbers. More compact design solutions93,100 (Fig. 3F and G) were subsequently developed and used to monitor hydrodynamic focusing of red blood cells. Impedance-based characterization of cell velocity, size and opacity was simultaneously performed.93
A microfluidic impedance cytometer capable of single cell morphology discrimination under continuous sample flow was presented by Shaker et al.107 The device, based on liquid electrodes, is fabricated in a cross configuration around a sensing zone (Fig. 4A). This arrangement allows measurement of cell impedance along orthogonal orientations and enables extraction of an index describing cell shape anisotropy. The system was used to monitor shape changes experienced by budding yeasts. A dielectrophoretic focusing and orientation region was introduced before the shape sensing region, to avoid blurring introduced by randomization of particle trajectory and orientation. An impedance cytometer based on particle self-alignment for enabling single-cell morphology discrimination was reported by Xie et al.88 A constriction structure is introduced to focus the particle stream and a pair of coplanar electrodes are used to record the impedance signal (Fig. 4B). Typical late-budding, early-budding, and unbudded yeast cells were distinguished based on width, amplitude and width-to-amplitude ratio of impedance pulses.
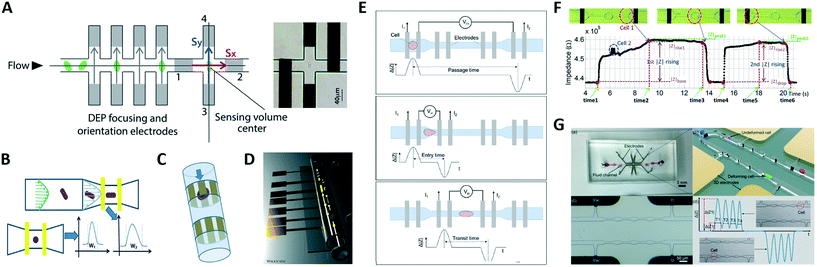 | ||
| Fig. 4 (A–C) Shape-sensitive designs. (D) Microtubular channel with integrated electrodes. (E–G) Designs for mechanical characterization. See section 2.4 and Table 1B for details. Images were adapted with permission from (A) ref. 107, copyright The Royal Society of Chemistry 2014, (B) ref. 88, copyright 2019 American Chemical Society, (C) ref. 109, copyright 2010 IEEE, (D) ref. 111, 2018 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, (E) ref. 116, copyright 2017 American Chemical Society, (F) ref. 117, copyright 2019 Author(s), (G) ref. 115, copyright 2019 Elsevier B.V. | ||
Differential impedance measurements were used by de Wagenaar et al.48 to detect a particular morphological anomaly on the sperm due to presence of cytoplasmic droplets on their flagella. A droplet induced a characteristic bump in the impedance signal and droplet content was quantified by calculating the area under the curve. This area was suitably corrected to mitigate confounding effects due to cell orientation, location and velocity. Zhu et al.108 developed an optimized platform to identify Caenorhabditis elegans (C. elegans) developmental stages, eliminating the influence of worm variable morphology.
A microfluidic cytometer for electrical impedance tomography of single flowing cells was proposed by Caselli et al.109 While progress on this in silico proof of concept design was limited by fabrication challenges (Fig. 4C), recent developments towards three-dimensional microtubular devices for lab-on-a-chip sensing applications (Fig. 4D) may alter the landscape of microcytometer designs.110,111
Zhou et al.116 used four pairs of coplanar electrodes to investigate the time required by cells to pass through a constriction (Fig. 4E). The total passage time was divided into two components: the entry time required for a cell to deform and enter a constriction, which is dominated by cell deformability, and the transit time required for the fully deformed cell to travel inside the constriction, which mainly relies on surface interaction of the cell with channel walls. Cells were simultaneously characterized via electrical impedance spectroscopy. Constriction channels separated by relaxation regions have been proposed to improve the discrimination capability, since the relaxation regions provide extra time stamps in the impedance trace. Ren et al.117 designed a chip containing four parallel sensing channels, each one including two constriction regions separated by a relaxation region (Fig. 4F). The ratio of the rise times of the impedance signal magnitude recorded during cell entrance at each of the two constriction regions was used to characterize cell mechanical properties. Bioelectrical parameters were simultaneously collected. A subsequent version of that chip features five sequential constriction channels separated by relaxation regions118 and was successfully used to distinguish between four different prostate cancer cell lines. Yang et al.115 developed a differential multi-constriction microfluidic device with self-aligned 3D electrodes (Fig. 4G) to simultaneously measure cell deformability, electrical impedance and relaxation index. The total transit time is taken as an indicator of cell deformability. The ratio of the cell transit times through last and first constrictions is used to define an index to quantify the cell relaxation capacity.
2.5 Multizone electrical sensing and other hybrid platforms
Given the versatility of integrating electrical sensing within microfluidic channels, several designs have been proposed, as reviewed below (see Table 1C and D for an overview).A few reports present systems wherein two (or more) electrical sensing zones are present, typically separated by an intermediate region that is devoted to particle stimulation, manipulation or selective capture. Zi et al.119 investigated cell survival rate by using two electrode pairs separated by a region where cells were exposed to a hypertonic stimulus (Fig. 5A). Reale et al.120 monitored the lateral displacement induced by a dielectrophoretic (DEP) force on cell/particle by electrical sensing in the pre-DEP and post-DEP zones (Fig. 5B). Caselli et al.44 performed coincidence arbitration of particles flowing in close proximity to each other, by exploiting nonuniformity of particle velocity distribution and comparing the electrical snapshots from two sensing regions that are separated by a hyperbolic constriction (Fig. 5C). Chawla et al.121 proposed a microfluidic analysis unit consisting of two sets of electrodes and a channel of variable geometry to enable counting and size detection of single Schistosoma mansoni parasite larvae, and the collective evaluation of the motility of the larvae as an unbiased estimator for their viability. An improved version of that microfluidic unit, featuring simpler operation and higher analysis throughput, has been recently reported.122
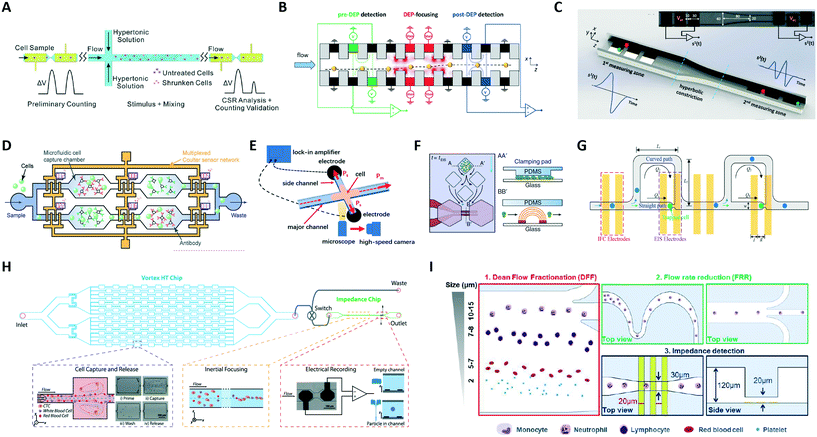 | ||
| Fig. 5 (A–D) Platforms with two or more electrical sensing zones, which are separated by: (A) a region of hypertonic stimulation, (B) a region of dielectrophoretic focusing, (C) a hyperbolic constriction, and (D) antigen specific capture chambers. (E–I) Hybrid platforms combining impedance cytometry with: (E) high-speed optical imaging, (F) time-lapse microscopy of growing cells, (G) impedance spectroscopy of individual trapped cells, (H) a Vortex chip for selective enrichment, and (I) two inertial focusing stages for Dean flow fractionation and flow rate reduction, respectively. See section 2.5 and Table 1C and D for details. Images were adapted with permission from (A) ref. 119, copyright 2019 Elsevier B.V, (B) ref. 120, copyright 2019 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, (C) ref. 44, copyright 2020 IEEE, (D) ref. 125, 2019 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, (E) ref. 127, copyright Springer-Verlag GmbH Germany, part of Springer Nature 2020, (F) ref. 128, copyright The Author(s) 2018, (G) ref. 129, copyright 2019 American Chemical Society, (H) ref. 52, copyright 2019 International Society for Advancement of Cytometry, (I) ref. 63, copyright The Royal Society of Chemistry 2019. | ||
Leveraging on the idea of antigen-based electrical labelling,123,124 Valera et al.59 presented a platform to detect proteins in undiluted human plasma samples. The device uses a differential enumeration platform that integrates two electrical counting zones, antigen specific capture chambers, and bead-based immunodetection to quantify cytokines. Similarly, Liu et al.125 used multiple electrical sensors for cell immunophenotyping against multiple antigens. The microfluidic device (Fig. 5D) consists of an array of microfluidic cell capture chambers, each functionalized with a different antibody to recognize a target antigen, and a network of code-multiplexed Coulter counters placed at strategic nodes across the device to quantify the fraction of cell population captured in each microfluidic chamber.
Other works used electrical impedance sensing of flowing cells in combination with other sensing modalities, like high-speed imaging of flowing cells126 or of cells invading into side constriction channels127 (Fig. 5E), time-lapse microscopy of growing cells128 (Fig. 5F), or impedance spectroscopy of trapped cells129 (Fig. 5G).
Platforms combining impedance sensing with dielectrophoretic manipulation,130 or with inertial microfluidics for sample enrichment52 or sample fractionation,63 have also been recently developed. Farmehini et al.130 used the voltage drops determined from impedance measurements to compute the fraction of applied voltage used for contactless dielectrophoretic particle manipulation at each frequency of interest. In this manner, they envisioned the integration of impedance measurements on the dielectrophoresis chip to account for chip-to-chip variability due to microfabrication errors. Raillon et al.52 developed a label-free high-throughput platform to isolate, enumerate, and size circulating tumour cells (CTCs) on two coupled microfluidic devices (Fig. 5H). Cancer cells were purified through a Vortex chip (Vortex Biosciences) and subsequently introduced in-line to an impedance chip, where a pair of electrodes measured fluctuations of an applied electric field generated by the passing cells. Petchakup et al.63 presented a multi-staged platform that enables isolation of neutrophils and monocytes from diluted or lysed blood samples directly within minutes, based on Dean flow fractionation (DFF) (Fig. 5I). DFF-purified leukocytes are inertially focused in serpentine channels into single stream prior to impedance detection.
Fan et al.131 combined impedance cytometry and droplet microfluidics to monitor the osteogenic differentiation of single bone marrow mesenchymal stem cells in droplets. The device enabled single-cell trapping, positioning, and impedance measurements of individual cells.
It is noticed that many platforms (e.g., ref. 121, 128, 131 and 132) also allow for parallelization of the analysis units, resulting in increased throughput.
2.6 Portable platforms
One of the current challenges in the development and commercialization of lab-on-a-chip microsystems is the integration and miniaturization of all the components that are required for chip operation at the point of care facility, spanning from sample preparation to detection.133,134 To this aim, integrated impedance-based devices have been developed. Credit-card-sized cell counters have been implemented, based on modular microfluidics65 or based on a CMOS lock-in application-specific integrated circuit, combined with an event counter that is embedded in a field-programmable gate array.133 Smartphone-based cytometers are also being developed, where the smartphones function to replace benchtop computers or laptops for the purpose of receiving and analysing the collected data.135 Furniturewalla et al.51 presented a wearable microfluidic impedance cytometer implemented on a flexible circuit wristband with on-line smartphone readout. Moreover, in order to reduce the costs related to electrode microfabrication, devices with integrated micro-needles,136 devices with integrated Field's metal microelectrodes,137 and PCB-based solutions have been proposed.138 Finally, the use of electronically barcoded particles50,56,139 is being explored as a tool for point-of-care diagnostic applications.3 Data analytics
In this section, we review the tools for data analytics that are used in microfluidic impedance cytometry. First, we discuss the signal-processing strategies adopted to extract single-cell features from the raw impedance signals (section 3.1). Then we present an overview of the available modelling approaches (section 3.2), which are used for the interpretation of the device response and for in silico design, or to correlate raw impedance features to biophysical cell properties (section 3.3). Finally, we review population-level data analysis that enables cell phenotyping (section 3.4).3.1 Signal-processing of raw data streams
The analysis of raw signals for parameter extraction to enable recognition of phenotypes at the single-cell level requires sturdy signal processing. Herein we provide a description of the signal processing techniques that may be implemented to extract the information embedded in the raw impedance signals. Even though the particular chosen approach may depend on the specific system design utilized, the following steps can be generally identified: signal conditioning, segmentation, feature extraction, and feature processing, which are discussed below. A typical workflow is presented in Scheme 1.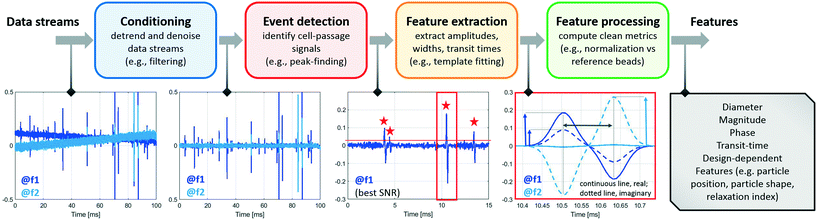 | ||
| Scheme 1 Signal processing steps: from the raw data streams (electrical currents demodulated at different frequencies) to the electrical features of individual flowing cells. | ||
Segmentation is usually performed by means of thresholding and peak-finding. This can be done on the conditioned signal (e.g., ref. 48 and 65), in the wavelet-domain,33 or after correlation with a suitable template (e.g., ref. 29 and 140). Derivative-based approaches have also been implemented to detect local maxima (e.g., ref. 86).
An alternative approach is the identification of idle time frames (i.e., data stream portions not containing events). As an example, Liu et al.141 used the zero crossing rate (ZCR) as the discrimination parameter, since ZCR of the noise is greater than that of signal recorded during cell passage.
In order to achieve robust feature extraction, or when the electrical fingerprints have peculiar shapes, approaches based on correlation with design-tailored templates can be used.29,91,94,142 As an example, a bipolar Gaussian template can be used for the differential current in case of classic designs29 (Fig. 1A and B). Moreover, inter-channel correlations can be exploited. As an example, although the peak amplitude varies significantly among the different frequency channels and between the real and imaginary signal parts, the peak-width and the peak-to-peak time of the measured signals are quite similar. Accordingly, a unique bipolar Gaussian template characterized by a complex frequency-dependent amplitude may be used to process all frequency channels at the same time.64 Generally, template-fitting strategies have higher computational cost than peak-finding strategies. An emerging alternative that potentially enables both, accuracy and real-time processing, is given by neural network-based approaches (cf. also Table S2 of the ESI†). By using a recurrent neural network, Honrado et al.100 showed the characterization of red blood cells and yeasts with a unitary prediction time of 0.4 ms. Wang et al.46 trained a convolutional neural network to analyse waveforms from a network of ten code-multiplexed Coulter counters (Fig. 3E) at high processing speed. Their network was also capable of resolving interferences generated by coinciding particles.
In fact, multiple particles may reach the sensing zone in close proximity, generating a plethora of possible signal shapes from which single particle features cannot be reliably extracted, unless joint system design and custom signal processing algorithms are implemented. Kellman et al.45 presented a method to perform individual particle coincidence correction in a Coulter counter, inspired by multiple-user communication theory. They modulated the channel response, introducing wider and narrower regions to give each particle a binary Barker sequence signature, and applied a successive interference cancellation method to separate coinciding particles. Caselli et al.44 proposed a model of the signals generated by coinciding particles in a microchannel comprising two electrical sensing zones (Fig. 5C) and used maximum a posteriori probability estimation to characterize individual particle properties, thus enabling accurate RBC counting at 2500 cell per s. In a following work,143 in order to reduce the computational time, a machine-learning based approach was developed (cf. Table S2†).
Besides coinciding particles, other application-specific or design-specific situations may give rise to peculiar signal shapes that call for tailored signal processing algorithms. Zhu et al.108 measured C. elegans worms and employed Gaussian kernel density estimation to efficiently extract the baseline-to-plateau current magnitude, in presence of drastic spikes generated by motion of the worms. Zhang et al.87 used kernel density estimation and binarization to identify the time duration of three subsequent pulses generated in the signal waveform as the cell passed through an asymmetric constriction channel (cf. Fig. S2†). Brazey et al.98 used an extended Kalman filter for real-time detection in a noisy environment. Saateh et al.62 developed a user-friendly software for real-time impedimetric droplet measurement.
3.2 Modelling approaches for microfluidic impedance cytometry
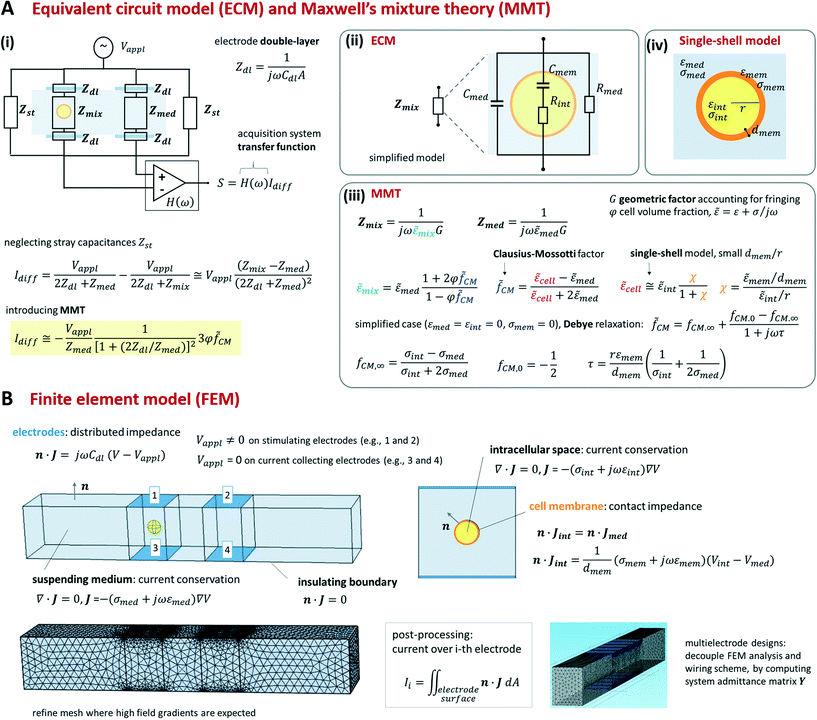
Foundational analytical and numerical modelling approaches for microfluidic impedance cytometry were described in Gawad et al.12 and Sun et al.144 They include equivalent circuit models (ECM), Maxwell's mixture theory (MMT), and finite element method (FEM). While we refer the reader to the previous literature for an extensive presentation of the relevant theory, we provide a synthetic view of those approaches in Scheme 2 (cf. also section S1 and Table S1 of the ESI†).As shown in Scheme 2A(iii) the impedance Zmix can be directly related to the geometric and dielectric properties of the system by using Maxwell's mixture theory (cf. e.g. Sun et al.144). Under the assumption of small volume fraction φ (defined as the volume ratio of the cell to the detection area), the complex permittivity of the cell-medium mixture (![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) mix) is given in terms of the complex permittivity of the medium (
mix) is given in terms of the complex permittivity of the medium (![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) med), the volume fraction, and the complex Clausius–Mossotti factor (
med), the volume fraction, and the complex Clausius–Mossotti factor (![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) CM). The latter accounts for the complex permittivity of the cell (
CM). The latter accounts for the complex permittivity of the cell (![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) cell) that is generally computed by using suitable shell models.14,15 As an example, we report a single-shell spherical model (Scheme 2A(iv)) assuming that the cell membrane thickness (dmem) is much smaller than the cell radius (r). Since Maxwell's mixture theory assumes uniform field, a geometric correction factor G has to be included in Zmix to account for fringing fields.12,68
cell) that is generally computed by using suitable shell models.14,15 As an example, we report a single-shell spherical model (Scheme 2A(iv)) assuming that the cell membrane thickness (dmem) is much smaller than the cell radius (r). Since Maxwell's mixture theory assumes uniform field, a geometric correction factor G has to be included in Zmix to account for fringing fields.12,68
By using MMT and neglecting stray capacitances, the following approximate expression for the differential current is obtained (Scheme 2A(i)):
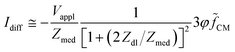 | (1) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) CM. The sensitivity of the differential current Idiff to cell properties (φ
CM. The sensitivity of the differential current Idiff to cell properties (φ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) CM) depends on the current flowing in the empty cytometer (Vappl/Zmed). At low frequency, the double-layer impedance Zdl may significantly reduce this sensitivity. The current Idiff multiplied by the transfer function of the acquisition system (H(ω)) provides the amplitude of the measured signal S. Therefore, S also depends on frequency-dependent phase and gain of the acquisition system.
CM) depends on the current flowing in the empty cytometer (Vappl/Zmed). At low frequency, the double-layer impedance Zdl may significantly reduce this sensitivity. The current Idiff multiplied by the transfer function of the acquisition system (H(ω)) provides the amplitude of the measured signal S. Therefore, S also depends on frequency-dependent phase and gain of the acquisition system.
As summarized in Scheme 2B, FEM model equations include the conservation of the electric current density J in the intracellular space and in the suspending medium, the insulating boundary condition over the channel walls, and the equation accounting for the electrode double-layer capacitance. To optimize mesh quality, the cell membrane is preferably modelled as an interface with a contact impedance between the intracellular space and the medium, rather than a very thin three-dimensional domain. Accordingly, the electric current flux is continuous across the interface, whereas the electric potential is discontinuous, with a jump depending on membrane conductance and capacitance per unit surface, σmem/dmem and εmem/dmem, respectively. Any geometric structure with small thickness-to-surface ratio is better modelled as an interface, as shown for cell membrane. The model can be easily modified to account for additional features, like for instance the presence of cell nucleus or cell wall.82 For prescribed applied potentials over the electrodes, the distribution of the electric potential V in the device is solved and the electric currents through the electrodes are computed by integration.
In order to find an optimal compromise between computational cost and solution accuracy, the mesh should be wisely designed. In particular, it should be finer near the electrodes and around the cell membrane, wherein higher field gradients are expected, and coarser elsewhere.
Simulating the signal produced by a flowing particle requires a series of FEM analyses, involving different meshes for different particle locations. However, rather noisy simulated signals are generally obtained due to mesh variations, unless extremely fine meshes are used. As a matter of fact, smooth, accurate signals can be obtained, using even relatively coarse meshes, as long as two sets of FEM analyses with the same mesh are performed for each particle location, one with the particle inside the measuring zone and another one with the particle replaced by the suspending medium. By subtracting the results of the two simulations, the mesh-generated numerical noise can be effectively cancelled out.
Moreover, sometimes it can be convenient to model the device as a network of admittances. The admittance matrix of the network (depending on cell properties and location) is computed by performing a suitable single set of finite element analyses.109 Based on this, different wiring schemes can be readily modelled, solved and compared.
3.3 Cell biophysical characterization by model fitting
Equivalent circuit models, Maxwell's mixture theory, and shell-models have been widely used to compute cell dielectric properties by fitting simulated impedance spectra to measured ones (e.g.ref. 69 and 89). To this aim, the signal associated with each cell (Scell) is usually normalized with respect to the signal measured using reference beads (Sbead), to cancel the transfer function of the acquisition system. In particular, normalization enables comparison of cells based on their impedance frequency response, since field penetration through the reference bead is invariant versus frequency. In order to differentiate cells from beads, a reference high frequency channel (e.g., 18 MHz) is typically used, wherein there is no field penetration through beads (e.g., ref. 151). Assuming the experimental setup described in Scheme 2, the normalization is computed as follows:89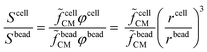 | (2) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) cellCM), along with its size can be found by multiplying the experimentally measured quantity (Scell/Sbead) by a calibration factor (
cellCM), along with its size can be found by multiplying the experimentally measured quantity (Scell/Sbead) by a calibration factor (![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) beadCM):
beadCM):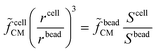 | (3) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) cellCM can be estimated – refer to section S1 of the ESI† for further details. As an example, in case of a single-shell model, it is possible to estimate (cf.Scheme 2): permittivity and conductivity of the intracellular space (εint and σint, respectively), membrane capacitance (εmem/dmem), and membrane conductance (σmem/dmem). By using multi-shell models additional parameters can be estimated, such as conductivity and permittivity of the cell wall, as in case of yeasts or bacteria,152,153 or the dielectric properties of intraerythrocytic parasites.69 The inclusion of multiple shells, however, comes at the cost of model complexity, processing time and overall confidence in the fitted data. By increasing the number of modelled shells, more parameters must then be considered and iterated, resulting in longer modelling/fitting times. Furthermore, initial values and boundaries for each modelled parameter need to be defined, with the risk of biasing the modelling outcome. Commonly accepted values from previous literature are often used. This not only permits certain parameters to be fixed at a specific reference value but also allows for other parameters to be further varied and/or to include additional shells, without compromising complexity and processing time.
cellCM can be estimated – refer to section S1 of the ESI† for further details. As an example, in case of a single-shell model, it is possible to estimate (cf.Scheme 2): permittivity and conductivity of the intracellular space (εint and σint, respectively), membrane capacitance (εmem/dmem), and membrane conductance (σmem/dmem). By using multi-shell models additional parameters can be estimated, such as conductivity and permittivity of the cell wall, as in case of yeasts or bacteria,152,153 or the dielectric properties of intraerythrocytic parasites.69 The inclusion of multiple shells, however, comes at the cost of model complexity, processing time and overall confidence in the fitted data. By increasing the number of modelled shells, more parameters must then be considered and iterated, resulting in longer modelling/fitting times. Furthermore, initial values and boundaries for each modelled parameter need to be defined, with the risk of biasing the modelling outcome. Commonly accepted values from previous literature are often used. This not only permits certain parameters to be fixed at a specific reference value but also allows for other parameters to be further varied and/or to include additional shells, without compromising complexity and processing time.
Typically, the mean dielectric properties of a homogeneous population of cells are determined.69,71 As an example, experimentally measured impedance spectra of malaria parasite infected-RBCs69 are shown in Fig. S1A,† along with their best fit (double-shell oblate spheroid model). In that figure, each data point is the average impedance over at least 150 cells. In Spencer et al.,89 the impedance spectra of single flowing RBC ghosts were reported (Fig. S1B†). The latter were obtained by simultaneously applying eight frequencies to the stimulation electrodes. Accordingly, the electrical properties of thousands of single cells at high throughput were determined.
Although fitting of impedance spectra generally requires measurements at several frequencies, Chen's group87,127,154 developed a high-throughput approach to quantify single-cell intrinsic bioelectrical markers by simultaneous application of just two frequencies. In a recent work,87 they introduced a microfluidic platform composed of an asymmetrical constriction channel through which single-cells are forced to squeeze, while capturing impedance profiles (amplitude and phase waveforms) (Fig. S2†). A number of features are extracted from the raw impedance signals and then translated into values of specific membrane capacitance, cytoplasm conductivity and cell diameter, by using an equivalent circuit model and channel geometrical parameters. Mahesh et al.155 proposed an approach to estimate cell size and cell membrane capacitance with a single frequency, by exploiting a fine feature of the reactive current.
While modelling approaches to obtain cell dielectric properties are well-established and widely used, models capable of translating impedance-based measurements (e.g., cell transit time through a constriction channel) into biomechanical cell properties are in their infancy. This is mainly due to the complexity of the cell deformation process, including: non-linear mechanical constitutive behaviour, large deformations, contact and friction, fluid–structure interactions. These features require complex, computationally-demanding numerical integration schemes. Accordingly, phenomenological parameters (e.g., relaxation indices computed as transit time ratios), rather than biophysical parameters, are generally used in impedance-based deformability cytometry. Simple viscoelastic cell-models were used to characterize the instantaneous Young modulus156 or the cytoplasmic viscosity127 of cells in a microfluidic impedance chip, wherein optical measurements of cell aspiration length, rather than electrical metrics, were used as input for the analysis. There is a need for tailored device designs and coupled modelling approaches to bring impedance-based deformability cytometry to its full maturity.
3.4 Cell population data analysis: clustering into phenotypes
Investigations on a multitude of sample types using impedance cytometry have been performed in recent literature (see section 4 for an in-depth exploration of recently published work). The analysis of impedance cytometry data invariably relies on the visualization of data in terms of specific features (e.g. impedance magnitude and phase, transit-time) represented as scatter-plots, histograms, frequency relaxation spectra or other methods to discern clusters of specific phenotype(s) present in the data. Scheme 3 provides a broad suggestive guideline on how to perform data visualization and analysis.An examination of published material shows that a common practice in cell population data analysis is to acquire impedance data using low frequencies (≤1 MHz). Impedance data at low frequencies allows for inferences on cell size to be drawn, either based purely on signal magnitude or on estimated electrical diameter (using reference particles). Differences in cell size are the most frequently used biophysical parameters to distinguish cell types and even perform separation.157–159 Thus, when performing impedance cytometry measurements of heterogeneous populations, it is valuable to gather data at the low frequency range, so that subpopulations of varying size can be distinguished and properly gated (e.g. RBCs versus WBCs versus cancer cells).
Signals from multiple frequencies are also commonplace in recent literature, since specific frequency ranges supply information about different cell properties (Fig. 1). Thus, impedance data in the form of magnitude (sometimes referred to as amplitude) and phase at different frequencies are regularly used to plot and analyse data. Moreover, these different variables can also be used to calculate metrics that further probe cell properties and can give qualitative estimations of certain dielectric properties, with the best known example being magnitude opacity.40,55,57,60,63,71,160,161 Being the result of the ratio of impedance magnitude at mid-range frequency (i.e., 1–10 MHz) over impedance magnitude at low frequency (i.e., 0.1–1 MHz), this metric effectively probes membrane properties and is inversely related to membrane capacitance.36,160 It has been widely used in recent literature to profile different cell types40,60,63,71 or assess alterations to membrane properties due to different interventions.55,161
Quantitative electrophysiological cell properties derived from dielectric modelling can also be used to plot and analyse cell populations (as explored in section 3.3). However, only recently have these models been able to do so at a single-cell level,89,154,156,162,163 thereby making these properties (e.g. Cmem or σcyt) available as another component of the overall data analysis process, while unveiling the presence of subpopulations and different phenotypes in the analysed samples.
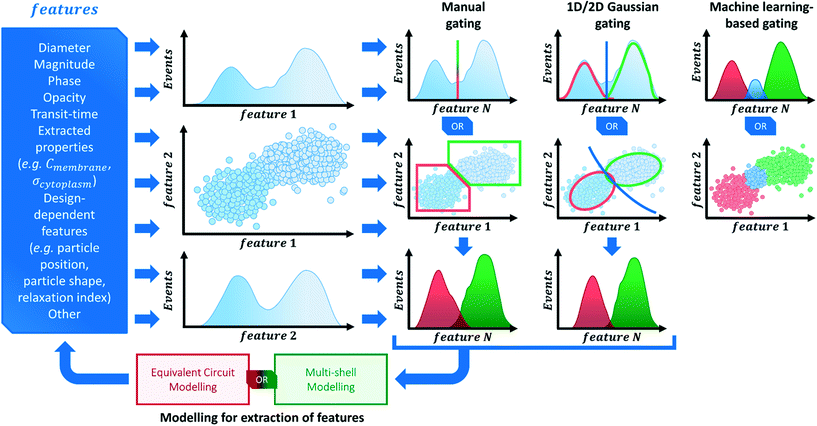
Contingent on the homogeneity/heterogeneity of samples, the clustering of data and gating process can be rather involved, with different approaches being available (Scheme 3). The simplest method relies on “manually” gating clusters of data that are evident on the data plot. This approach is easily implementable and probably satisfactory to many sample types. However, by its nature, this method can be unreliable and skew the perception of the data, as it often depends on familiarity with the subpopulations expected to be found in the data. Other methods rely on the fitting of normal distributions to the data, be it 1-dimensional Gaussian fits to histograms or 2-dimensional Gaussian fits to scatter plots, for example. By identifying normal distributions in the data, gates can be generated to cluster the data into subpopulations. However, such approaches are not easily implemented (specially for 2D distributions) and rely on the presence of normally distributed populations, which need not be the case for all sample types.
Another analysis method that has gathered much interest in recent literature focuses on machine learning-based classification of different cell subpopulations (cf. also Table S2 of the ESI†). In particular, support vector machines53 and neural networks115,154 have been used as supervised classifiers based on impedance cytometry data. These methods allow for a quasi-real-time analysis of data, limiting human interference into the gating strategy, but these need to be trained with a representative dataset.
4 Phenotyping cell populations
The juxtaposition of single-cell versus large population-level analysis has presented itself as a recurrent topic of debate within the microfluidics community at large,164 and is the manifestation of a crucial question regarding any cell population analysis: how homogeneous can a given sample be? Bulk analysis techniques are generally simple to use and readily available (e.g., PCR or Raman spectroscopy), however, cells exposed to seemingly identical environmental stimuli will often display a distribution of heterogeneous behaviours. A collective averaging of results could thus cause the loss of crucial information regarding the population makeup, potentially giving rise to misleading results. In contrast, high throughput single-cell analysis offers the capability to, not only analyse large quantities of individual cells, but also to identify the distribution of responses, along with measuring statistically relevant numbers to make inferences from the data. Consequently, it is advantageous for the analysis of impedance cytometry data to be performed at a single-cell population level, be it in the form of electrical features (e.g. impedance phase or magnitude) or extracted biophysical parameters (e.g. electrical size or dielectric properties), so that the single-cell data can be analysed for the presence of various subpopulations in the heterogeneous sample. It is by this process that different phenotypes can be identified for cells under specific external stimuli (e.g. modifications during differentiation, stages of infection, activation processes, or differences in drug resistance or therapeutic potential, to name a few examples).Table 2 offers an extensive list of literature focused on cell population analysis. Recent literature has focused on investigating a wide variety of cell types to identify and characterize specific phenotype(s) present in the samples of interest. The following section will focus on highlighting some of those approaches. Table 3 presents a broader view on the key phenotypical findings. With the interest in studying cell samples originating from tumour xenografts or model cancer cell lines increasing in the recent years, we divide the scope of the work performed with cancer cells into three independent sub-sections. These sub-sections cover the studies probing the role of electrophysiological phenotypes to understand disease presentation and single-cell dielectric properties (section 4.1); biomechanical phenotyping studies (section 4.2); and the application of electrophysiological phenotypes as a metric to assess cell viability and drug sensitivity (section 4.3). The remainder of this section covers the works focused on a variety of sample types: mammalian cells (section 4.4), human pathogens (section 4.5), yeast cells (section 4.6) and others (section 4.7).
| Sample type | Focus | Sample composition | Sample concentration, flow-rate & cell throughput | Frequencies, voltage & channel cross-section | Characterization metrics & methods | Ref. |
|---|---|---|---|---|---|---|
| a PS = polystyrene. b NCCD = no cell concentration declared. c NFRD = no flow-rate declared. d NSVD = no signal voltage declared. | ||||||
| Algae | Viability assessment of bacterium-sized green algae | Picochlorum SE3 algae (∼2–3 μm cell diameter); (ref. particles: aPS beads) | NCCD | 500 kHz to 30 MHz (8 simultaneous frequencies) | Magnitude & opacity (magnitude 20 MHz/magnitude 500 kHz) | Sui et al. 2020 (ref. 55) |
| NFRD | NSVD | |||||
| 30 μm × 8 μm | ||||||
| C. elegans | Identification of C. elegans developmental stages | C. elegans (∼200 μm–1.2 mm length) | NCCD | 300 kHz | Transit time & magnitude | Zhu et al. 2018 (ref. 108) |
| 30 μL per min | 1.5 V amplitude | |||||
| 160 μm × 130 μm | ||||||
| Cancer cells | Discrimination of dissociated tumour cell lines from major cancer types | Lung, thyroid, breast, ovarian, and kidney normal and cancer cells (∼10–20 μm cell diameter); (testing particles: peripheral blood mononucleated cells, RBCs) | NCCD | 250 kHz | Transit-time & signal peak-to-peak voltage | Desai et al. 2019 (ref. 194) |
| 50 μL per min | NSVD | |||||
| 25 μm × 25 μm | ||||||
| Cancer cells | Characterization of phenotypical properties of circulating tumour cells | Lung cancer cell lines A549 and MLO-Y4; isolated CTCs from hepatic, oral and lung cancer (∼10–20 μm cell diameter) | 2 × 104 cells per mL | 1 kHz & 100 kHz | Transit-time, magnitude, phase & dielectric properties (Cmem & σcyt); equivalent circuit models | Chiu et al. 2017 (ref. 162) |
| 50, 100 and 150 μL per h | NSVD | |||||
| 6–10 μm × 6–10 μm | ||||||
| Cancer cells | Characterization of phenotypical properties of tumour cell lines | Lung cancer cell line A549, adenoid carcinoma cell line SACC-83 and lung metastasis cell line SACC-LM (∼10–20 μm cell diameter) | 5 × 106 cells per mL | 100 kHz & 250 kHz | Transit-time, magnitude, phase & dielectric properties (Cmem & σcyt); equivalent circuit models | Zhang et al. 2019 (ref. 163) |
| NFRD | NSVD | |||||
| 11 μm × 9 μm | ||||||
| Cancer cells | Characterization of phenotypical properties of single-nuclei | Nuclei from cancer cell lines A549 and SW620 | 1 × 106 nuclei per mL | 1 kHz to 250 kHz | Magnitude, phase & dielectric properties (Cne, Rne, & Rnp); equivalent circuit models | Liang et al. 2019 (ref. 165) |
| NFRD | 0.2 V amplitude | |||||
| 5–8 μm × 5–7 μm | ||||||
| Cancer cells | Characterization of pancreatic tumourigenicity phenotypes | Pancreatic tumour xenografts from metastatic (T366 and T608) vs. primary cancer of mutant genotype (T449 and T395) and wild type (T738 and T188) (∼12–20 μm cell diameter); (ref. particles: 7 μm aPS beads) | 2 × 105 cells per mL | 500 kHz, 18.3 MHz & 250 kHz to 50 MHz (24 frequencies) | Real, imaginary, magnitude, phase, electrical diameter, opacity (magnitude 2 MHz/magnitude 500 kHz) & contrast (phase 50 MHz/phase 500 kHz); 2D Gaussian gating | McGrath et al. 2019 (ref. 71) |
| 1.2 × 105 beads per mL | 6 V amplitude | |||||
| 100 μL per min | 60 μm × 30 μm | |||||
| Cancer cells | Characterization of phenotypical properties of tumour cell lines with epithelial–mesenchymal transitions | Lung cancer cell lines A549 & H1299; (testing particles: HeLa model cell line) (∼10–40 μm cell diameter) | 3–5 × 106 cells per mL | 100 kHz & 250 kHz | Transit-time, magnitude, phase & dielectric properties (Cmem & σcyt); equivalent circuit models & neural network pattern recognition (two-layer feed forward) | Zhao et al. 2018 (ref. 154) |
| NFRD | NSVD | |||||
| 10 μm × 12 μm | ||||||
| Human pathogens | Detection and enumeration of Gram-positive and Gram-negative bacteria | Gram-positive Staphylococcus aureus and Gram-negative Escherichia coli (∼1 μm cell diameter and 2–3 μm × 0.5 μm, respectively); (ref. particles: 1 and 2 μm aPS beads) | 2–2.5 × 106 particles per mL | 200 kHz, 7 MHz & 8 MHz | Magnitude, phase & opacity (magnitude 7 MHz/magnitude 200 kHz) | Clausen et al. 2018 (ref. 40) |
| 0.01 μL per min | 3 V amplitude | |||||
| 10 μm × 10 μm | ||||||
| Human pathogens | Viability assessment and species discrimination of water-borne pathogens | Cryptosporidium parvum, Cryptosporidium muris and Giardia lamblia (∼4 μm, ∼6 μm and 9 μm cell diameter, respectively); (ref. particles: 7 μm aPS beads) | 1 × 105 cells per mL | 18.3 MHz & 250 kHz to 50 MHz (24 frequencies) | Real, imaginary, magnitude & phase; 2D Gaussian gating & multi-shell modelling | McGrath et al. 2017 (ref. 151) |
| 1 × 105 beads per mL | 1 to 10 V amplitude | |||||
| 40 μL per min | 40 μm × 30 μm | |||||
| Human pathogens | Characterization of phenotypical properties of Plasmodium falciparum-infected RBCs | Plasmodium falciparum-infected RBCs and uninfected RBCs (∼7.5 μm × 2 μm); (ref. particles: 7 μm aPS beads) | 5 × 105 cells per mL | 18.3 MHz & 250 kHz to 50 MHz (24 frequencies) | Real, imaginary, magnitude, phase & fluorescence; multi-shell modelling | Honrado et al. 2018 (ref. 69) |
| 1 × 105 beads per mL | NSVD | |||||
| 40 μL per min | 40 μm × 30 μm | |||||
| Human pathogens | Detection of susceptibility of host microbiota to bacterial spore germination | Clostridioides difficile in spore and vegetative form (∼0.5 μm diameter and ∼2–5 μm × 0.5 μm, respectively); (ref. particles: 2 μm aPS beads) | NCCD | 0.5, 2 & 10 MHz | Magnitude & phase | Moore et al. 2020 (ref. 153) |
| 10 μL per min | 0.5 V amplitude | |||||
| 30 μm × 30 μm | ||||||
| HUVECs | Viability assessment of hypertonic stimulated cells | Human umbilical vein endothelial cells – HUVECs, human colon cancer (HT-29) cells and immature bone-marrow-derived macrophages (iBMDM) (∼10–20 μm cell diameter); (testing particles: 5, 10 and 15 μm aPS beads) | 1 × 105 cells per mL | 450 kHz | Magnitude | Zi et al. 2020 (ref. 119) |
| 0.3–1.7 × 105 beads per mL | 5 V amplitude | |||||
| 20 μL per min | 20 μm × 20 μm | |||||
| Model cell lines | Discrimination of live, necrotic and apoptotic cells | HeLa and Jurkat model cell lines (∼10–40 μm cell diameter); (ref. particles: 3, 5, 7 and 10 μm aPS beads) | 1–10 × 106 particles per mL | 1 MHz | Conductance, susceptance, magnitude & phase | Xie et al. 2017 (ref. 49) |
| −200 μL per min | 0.3 V amplitude | |||||
| 25 μm × 12 μm | ||||||
| Model cell lines | Combined impedance flow cytometry (IFC) and electrical impedance spectroscopy (EIS) for cell analysis | HeLa, HepG2 and A549 model cell lines (∼10–40 μm cell diameter); (ref. particles: 6 μm aPS beads) | 1 × 106 cells per mL | IFC: 1 MHz | Magnitude; equivalent circuit models | Feng et al. 2019 (ref. 129) |
| 10 nL per min | EIS: 1–103 kHz | |||||
| 1 V amplitude | ||||||
| 30 μm × 20 μm | ||||||
| Model cell lines | Discrimination of live, necrotic and apoptotic cells | Lymphoma model cell line U937 (∼13 μm cell diameter); (ref. particles: 10 μm aPS beads) | NCCD | 500 kHz, 2 MHz, 6 MHz & 12 MHz | Magnitude & phase | Ostermann et al. 2020 (ref. 41) |
| NFRD | NSVD | |||||
| 50 μm × 50 μm | ||||||
| Model cell lines | Discrimination of live, necrotic and apoptotic cells | Lymphoma model cell line U937 (∼13 μm cell diameter); (ref. particles: 6 μm aPS beads) | 10 μL per min | 500 kHz & 10 MHz | Electrical diameter & phase; multi-shell modelling | De Ninno et al. 2020 (ref. 64) |
| 200 cells per s | 5 V amplitude | |||||
| 40 μm × 21 μm | ||||||
| Model cell lines | Characterization of deformability and impedance phenotypes of cancer cells | Normal, fixed and PMA-modified model MCF-7 cells (∼15–25 μm cell diameter); (ref. particles: RBCs) | 0.5–1 × 106 cells per mL | 1 MHz | Time metrics & magnitude | Zhou et al. 2018 (ref. 116) |
| 1000 cells per min | 0.5 V amplitude | |||||
| 10 μm × 20 μm | ||||||
| Model cell lines | Characterization of biophysical and impedance phenotypes of cancer cells | Model cell lines (H460, H446, A549, 95D and 95C) (∼10–20 μm cell diameter) | 1 × 106 cells per mL | 1 kHz & 100 kHz | Extracted properties (Young's modulus, electrical diameter, Cmem & σcyt); equivalent circuit models | Wang et al. 2017 (ref. 156) |
| NFRD | NSVD | |||||
| 10 μm × 10 μm | ||||||
| Model cell lines | Characterization of deformability and impedance phenotypes of cancer cells | Model MCF-7 cell line (∼15–25 μm cell diameter) | >430 cells per min | 50 kHz | Transit-time, magnitude; neural network pattern recognition (three-layer back propagation) | Yang et al. 2019 (ref. 115) |
| 2 V amplitude | ||||||
| 10 μm × 20 μm | ||||||
| Model cell lines | Viability assessment of drug-treated cancer cells | Model T47D cell line (∼10–20 μm cell diameter) | 4 × 105 cells per mL | 500 kHz & 300 kHz to 30 MHz (4 simultaneous frequencies) | Magnitude, phase; neural network pattern recognition (support vector machines) | Ahuja et al. 2019 (ref. 53) |
| NFRD | NSVD | |||||
| 100 μm × 30 μm | ||||||
| Pollen | Viability assessment of pollen | Tobacco (Nicotiana tabacum), tomato (Solanum lycopersicum), cucumber (Cucumis sativus) and pepper (Capsicum annuum) pollen (∼15–150 μm cell diameter) (testing particles: 10, 20, 30, 60 and 100 μm aPS beads) | 5 × 104–5 cells per mL | 500 kHz, 3 MHz & 12 MHz | Magnitude & phase | Heidmann et al. 2016 (ref. 169) |
| 1–5 × 104 beads per mL | NSVD | |||||
| NFRD | 120–250 μm × 120–250 μm | |||||
| Red blood cells | Characterization of phenotypical properties of individual RBCs | RBCs, sphericallized RBCs, RBCs ghosts (∼7.5 μm × 2 μm) (ref. particles: 7 μm aPS beads) | 5 × 105 cells per mL | 18 MHz & 250 kHz to 80 MHz (8 simultaneous frequencies) | Real, imaginary, magnitude, phase & dielectric properties (electrical radius, Cmem, εcyt & σcyt); multi-shell modelling | Spencer and Morgan 2020 (ref. 89) |
| 40 μL per min | 4 V amplitude | |||||
| 40 μm × 30 μm | ||||||
| Stem cells | Characterization of phenotypical properties of skeletal stem cells after enrichment and expansion | Patient-derived skeletal stem cells & human bone marrow mononuclear cells – hBMMNCs (∼5–30 μm cell diameter); (ref. particles: 7 μm aPS beads) | 2–2.5 × 105 cells per mL | 500 kHz & 2 MHz | Electrical diameter, opacity (magnitude 2 MHz/magnitude 500 kHz) & fluorescence | Xavier et al. 2017 (ref. 161) |
| 0.5–1 × 105 beads per mL | 4 V amplitude | |||||
| 40 μL per min | 40 μm × 30 μm | |||||
| White blood cells | Detection and profiling of activated T-lymphocytes | Unstimulated CD8+ T-lymphocytes, activated CD8+–CD69+ T-lymphocytes, non-activated CD8+–CD69− T-lymphocytes (∼5–15 μm cell diameter); (ref. and testing particles: 8, 10 and 15 μm aPS beads) | 3–5 × 105 cells per mL | 100 kHz to 27 MHz (6 simultaneous frequencies) | Real & imaginary | Rollo et al. 2017 (ref. 79) |
| 5 × 105 beads per mL | 0.4 V amplitude | |||||
| 1 μL per min | 30 μm × 50 μm | |||||
| 400 cells per min | ||||||
| White blood cells | Detection and profiling of white blood cells post inertial-based separation | Lymphocytes, monocytes and neutrophils (∼5–20 μm cell diameter); (testing particles: diluted whole blood and peripheral blood mononucleated cells) | 1 × 106 cells per mL | 300 kHz & 1.7 MHz | Magnitude & opacity (magnitude 1.7 MHz/magnitude 300 kHz) | Petchakup et al. 2018 (ref. 60) |
| 5 μL per min | 3 V amplitude | |||||
| 30 μm × 20 μm | ||||||
| White blood cells | Detection and profiling of neutrophils post integrated inertial-based separation of white blood cells | Lymphocytes, monocytes and neutrophils (testing particles: peripheral blood mononucleated cells) (∼5–20 μm cell diameter); (ref. particles: 10 μm aPS beads) | 1–5 × 105 cells per mL | 300 kHz & 1.7 MHz | Electrical diameter & opacity (magnitude 1.7 MHz/magnitude 300 kHz) | Petchakup et al. 2019 (ref. 63) |
| 1–2.5 × 104 beads per mL | NSVD | |||||
| ∼800 cells per min | 30 μm × 20 μm | |||||
| White blood cells | Characterization of deformability and impedance phenotypes of diabetic lymphocytes | Normal and diabetic-activated lymphocytes (∼5–15 μm cell diameter); (testing particles: normal and fixed RBCs) | 4 × 106 cells per mL | 800 kHz | Transit-time & magnitude | Mahesh et al. 2019 (ref. 145) |
| 50 μL per h | 0.1 V amplitude | |||||
| 10 μm × 5–15 μm | ||||||
| Yeast cells | Viability assessment of drug-treated yeast cells and insect cells | Yeast cells (Saccharomyces cerevisiae carlsbergensis) (∼4–40 μm cell diameter); normal and baculovirus-infected Sf9 insect cell | 1 × 105–7 cells per mL | 500 kHz, 10 MHz & 12 MHz | Magnitude & phase | Opitz et al. 2019 (ref. 72) |
| 500 to 1000 cells per s | NSVD | |||||
| 30–50 μm × 30–50 μm | ||||||
| Yeast cells | Detection and cell shape phenotyping of single buddying yeast cells | Buddying yeast cells (Saccharomyces cerevisiae) (∼4–40 μm cell diameter); (testing particles: 5 and 8 μm aPS beads; 8 and 15 μm by 4 μm SU-8 rods) | 107 cells per mL | 1 MHz | Particle shape metrics & magnitude; | Xie et al.2019 (ref. 88) |
| 40 μL per min | 0.2 V amplitude | |||||
| ∼3–6 cells per s | 17 μm × 12 μm | |||||
| Yeast cells | Dielectrophoretic trapping and determination of cell size | Buddying yeast cells (Saccharomyces cerevisiae) (∼4–40 μm cell diameter); (testing particles: 6, 8 and 10 μm aPS beads) | 1 × 106 cells per mL | 300 kHz to 10 MHz | Magnitude | Geng et al. 2019 (ref. 132) |
| 1 × 105–6 beads per mL | NSVD | |||||
| 0.5 μL per min | 150 μm × 15 μm | |||||
| Cell phenotype of interest | Dielectric property | Sub-cellular properties |
|---|---|---|
| Cell death: viable, necrotic and apoptotic | C mem | Loss of viability, e.g. induced by heat-inactivation, causes increased cell membrane permeability with break-down of the membrane integrity, rendering cells non-viable. These result in a decreased Cmem, as the cell loses the ability to function as a perfect insulator at low frequencies. Such phenomena have been observed in literature: heat-treated non-viable MCF7 cells show higher magnitude opacity (i.e. lower Cmem) than viable cells in 1× PBS;160 heat-treated non-viable lymphoma cells show a decrease in absolute impedance phase at 500 kHz in 1× PBS;64 heat-treated non-viable algae cells show a decrease in magnitude opacity (based on 20 MHz/500 kHz data) in 1× PBS;55 cytotoxic nanomaterials-induced non-viable lymphoma cells show lower impedance phase at 6 MHZ in a 0.25× PBS + sucrose buffer41 hypertonic stimulus-induced non-viable HUVECs show increased impedance magnitude at low frequency (450 kHz)119 |
| σ int & εint | Increased permeability in non-viable cells causes increased ion exchange between the cell interior and medium, together with internal degradation of cell organelles. These result in alterations of the cell interior properties, such as σint & εint, which can be qualitatively observed with changes to impedance at higher frequencies, as reported in literature: heat-treated non-viable yeast cells show a decrease in impedance phase at 10 MHz in 0.5× PBS;72 heat-treated non-viable pollen particles show a decrease in impedance phase at 12 MHz;169 apoptosis causes shedding of smaller-sized apoptotic bodies from cells, identifiable based on their size and greater impedance phase at high frequency (≥10 MHz) in 1× PBS64 | |
| Immune cells: cell activation, differentiation and diabetic response | Size & Cmem | Monocytes, lymphocytes and neutrophils are distinguishable based on impedance magnitude and opacity.60,195,196 When processes such as activation or differentiation occur in these cell types, alterations to cell membrane permeability and conformation can result in alterations to Cmem. Various phenomena have been reported in literature: monocyte differentiation into macrophages results in size increase but no impedance magnitude alteration;60 inflammatory stimulus induces an increase in impedance magnitude opacity (i.e. lower Cmem);60 NETosis neutrophils have higher cell size and magnitude opacity (i.e. lower Cmem) than unstimulated neutrophils;63 diabetic lymphocytes present loss of deformability and higher impedance magnitude at 800 kHz than normal lymphocytes;145 diabetic neutrophils show higher magnitude opacity (i.e. lower Cmem) than monocytes in 1× PBS;60 glucose-stimulated neutrophils show larger size than unstimulated neutrophils at 120 min post-stimulus63 |
| Cancer cells: measuring drug sensitivity & metastasis | C mem & σcyt | Cancer cells are known for an increased cell membrane roughness and folding, which affects the surface area dependent metric of Cmem, and higher nucleus-to-cytoplasm ratios and cell cycle turnover, which in turn affects estimations of σcyt. Differences in the phenotypes of various cancer cells tied to these specific characteristics have been reported in literature: EpCAM+ CTCs have lower Cmem and higher σcyt than EpCAM− CTCs;162 epithelial–mesenchymal transitions (EMT) on lung tumour cells causes lower Cmem and σcyt;154 lung metastasis adenoid carcinoma cells present a lower Cmem and higher σcyt than non-metastatic adenoid carcinoma cells;163 more tumourigenic pancreatic cancer cells show higher impedance phase at high frequencies (>10 MHz) and lowered σint71 |
| Bacteria: detection, viability, germination and antibiotic susceptibility | σ int & εint | Gram-negative E. coli and Gram-positive S. aureus are detectable and discriminated using impedance phase at 8 MHz with a buffer of low conductivity (0.085 S m−1)40 |
| Heat-treated C. difficile bacteria show lower impedance phase at 10 MHz than untreated bacteria153 | ||
| Germinated vegetative C. difficile bacteria have higher impedance phase at 10 MHz than C. difficile in spore form153 | ||
| Stem cells: alterations with cell expansion and passage | Size & Cmem | Unexpanded skeletal stem cells are larger than other bone marrow cell populations,161 while the expansion of skeletal stem cells and following passages cause an increase in size and Cmem (assessed by magnitude opacity)161 |
4.1 Cancer cells – phenotypical characterization
The majority of recently published literature utilize cancer cell lines, either from long-standing established model cell lines or from patient derived xenografts, with a focus on phenotypical characterization of various cancer cell types. The Chen group87,127,154,156,162,163,165 used a narrow microfluidic constriction channel (e.g., Fig. 5E and S2†) for extraction of single-cell specific dielectric properties using equivalent circuit models (sections 3.2 and 3.3). It is noteworthy that this squeezed state of the cell may alter the measured electrical activity due to its effects on the cell membrane.166 This system was applied to the phenotypical characterization of CTCs from hepatic, oral and lung and the identification of EpCAM+ CTCs after their isolation.162 (Fig. 6A). For hepatic and oral cancer samples, EpCAM+ CTCs had an estimated lower Cmem and higher σcyt than EpCAM− CTCs. Furthermore, significant differences in Cmem and σcyt were observed between the studied cancer cell types. In an updated system,154 microchannels defining a crossing constriction were capable of measuring >100 cells per s, allowing acquisition of >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per sample type analysed. To evaluate the updated system, H1299 and HeLa model cell lines were compared, with significant differences in Cmem and σcyt being observed between these cells (Fig. 6B). A neural network-based pattern recognition tool was used to classify cell types based on their estimated dielectric properties (cf. Table S2†), with classification success rates above 90% and 75% for the distinctions of H1299 versus HeLa cell lines and A549 versus EMT-activated A549, respectively.
000 cells per sample type analysed. To evaluate the updated system, H1299 and HeLa model cell lines were compared, with significant differences in Cmem and σcyt being observed between these cells (Fig. 6B). A neural network-based pattern recognition tool was used to classify cell types based on their estimated dielectric properties (cf. Table S2†), with classification success rates above 90% and 75% for the distinctions of H1299 versus HeLa cell lines and A549 versus EMT-activated A549, respectively.
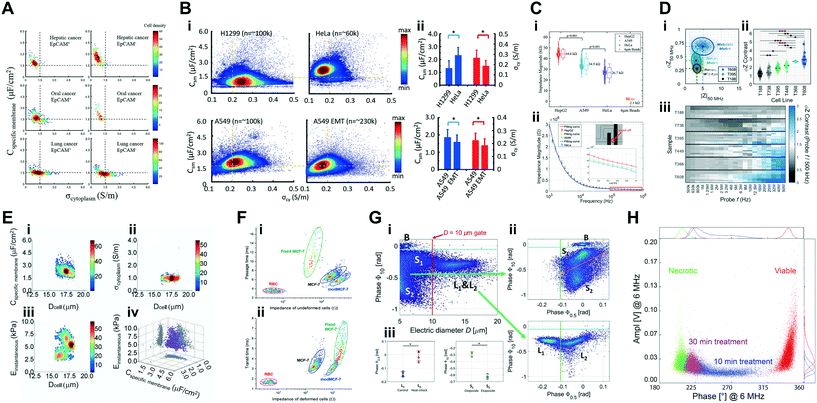 | ||
| Fig. 6 Collection of phenotyping results on cancer cells and model cell lines from literature. See sections 4.1, 4.2 and 4.3 for further details. (A) Measurements of estimated σcytvs. Cmem of CTCs, with and without EpCAM expression, from hepatic, oral and lung cancers. (B) i – Measurements of estimated σcytvs. Cmem of H1299, HeLa, A549 and A549 undergoing EMT (epithelial mesenchymal transition); ii – comparison between cell lines, where significant differences were observed (*p < 0.001). (C) i – Impedance magnitude distributions for three cancer types and reference beads; ii – EIS magnitude measurements of the three cancer types with corresponding MMT model fitting curves. (D) i – Measurements of impedance magnitude vs. phase at 50 MHz for various PDAC cell lines; ii – comparison of impedance phase contrast between cell lines, where significant differences were observed (*p < 0.003, **p < 0.0007, ***p < 0.00007); iii – phase contrast range for PDAC samples along the frequency spectra measured. (E) Measurements of 95D model cells in terms of their estimated: i – Dcellvs. Cmem; ii – Dcellvs. σcyt; iii – Dcellvs. Einstantaneous; iv – Cmemvs. σcytvs. Einstantaneous. (F) Measurements of impedance vs. transit time for cells before (i) and after (ii) passing the channel constriction. (G) i – Measurements of electric diameter vs. impedance phase at 10 MHz for U937 model cells containing untreated and heat-treated cells; ii – measurements of impedance phase at 0.5 MHz vs. impedance phase at 10 MHz for gated sub-populations of smaller (top) and bigger (bottom) size; iii – comparison of impedance phase at 0.5 MHz (left) and 10 MHz (right) between the identified subpopulations, where significant differences were observed (*p < 0.001). (H) Measurement of impedance phase vs. magnitude at 6 MHz of U937 model cells undergoing a NM-300k treatment. Images were adapted with permission from (A) ref. 162, copyright 2017 Elsevier B.V., (B) ref. 154, copyright 2018 Elsevier B.V., (C) ref. 129, copyright 2019 American Chemical Society, (D) ref. 71, copyright 2020 Elsevier B.V., (E) ref. 156, copyright The Author(s) 2017, (F) ref. 116, copyright 2018 American Chemical Society, (G) ref. 64, copyright 2020 Elsevier B.V., (H) ref. 41, copyright The Author(s) 2020. | ||
A follow-up work163 presented the capability of distinguishing between adenoid carcinoma cell line SACC-83 and lung metastasis cell line SACC-LM, with metastatic cells presenting a lower Cmem and higher σcyt. Liang et al. followed with the characterization of the dielectric properties of single-nuclei from cancer cell lines A549 and SW620.165 By varying the constriction device to allow for trapping of individual isolated nucleus, the extracted dielectric properties (nuclear envelope capacitance (Cne) and resistance (Rne) and nucleoplasm resistance (Rnp)) were used to show significant differences in Rne, between the tested cell types. In another approach129 based on integration of hydrodynamic constrictions to passively trap single cancer model cells (HeLa, HepG2 and A549), temporal analysis of cells was possible using electrical impedance spectroscopy (EIS), where significant differences were observed between cell lines for impedance magnitude data at 1 MHz (Fig. 6C); while non-trapped flowing cells were analysed by standard impedance flow cytometry (IFC) (Fig. 5G). Such strategy, combining both IFC and EIS in a single system, could thus yield more data-rich results, improving the phenotypical characterization.
More recently, McGrath et al.71 presented a comprehensive study aiming at the phenotypical stratification of patient-derived, pancreatic tumour xenografts based on their tumourigenicity. Using a high-throughput system (>300 cells per s), single cells derived from primary pancreatic tumours versus those from liver metastasis were analysed with a novel impedance phase contrast metric, which is based on impedance phase variations in the high and low frequency range. Variations in this metric were found to be related to electrophysiology of the cell interior and to be systematically altered as a function of tumourigenicity (Fig. 6D). Moreover, dielectrophoresis was performed in parallel and confirmed that cancer cells of higher tumourigenicity exhibited lowered interior conductivity and enhanced permittivity. Genetic analysis also confirmed that dysregulation of Na+ transport and Ca2+ removal from the cytoplasm is present in more tumourigenic cell lines, further validating the phenotypical characterization.
4.2 Cancer cells – biomechanical phenotyping
Another topic of emerging research interest in recent literature is the integration of methods to determine biomechanical phenotypes of cells based on impedance cytometry. The measurement of mechanical and electrical properties of single cells can yield useful information on the physiological and pathological state of cells. Based on the constriction channel device, the Chen group,156 estimated the dielectric (Cmem and σcyt) and mechanical properties of single-cells from model cell lines (H460, H446, A549, 95D and 95C), with the latter measured through instantaneous estimation of Young's modulus (Einst) using a numerical mechanical model applied to high-speed camera images. (Fig. 6E).In another constriction-based system (Fig. 4E), four pairs of electrodes were included for the acquisition of impedance magnitude data and different time metrics (i.e. entry, transit and passage times) of individual cells, to characterize the deformability of MCF-7 model cells.116 The system was used to characterize the deformability and impedance phenotypes of normal, fixed and (phorbol 12-myristate 13-acetate) PMA-modified MCF-7 cells, while RBCs were used as highly deformable reference particles. Alterations to cell deformability by fixation (decrease) and PMA modification (increase) were confirmed based on time metrics and presented together with differences in impedance magnitude (Fig. 6F).
A system comprised of multiple constriction regions was presented by Yang et al. to characterize the biophysical phenotypes of model MCF-7 cells.115 Using 3D electrodes, impedance and deformability measurements of single cells based on the transit-time through the constrictions (Fig. 4G) were used to distinguish biophysical properties of untreated, nethylmaleimide-treated and cytochalasin B-treated MCF-7 cells. A back propagation neural network (cf. Table S2†) yielded a classification accuracy of more than 90%, when impedance and deformability metrics were considered together, demonstrating its applicability to the analysis of concurrent biophysical and impedimetric data.
4.3 Cancer cells – viability assessment
Another area of interest when studying various cancer cells is the determination of cell viability and the phenotypic alterations observed due to loss of viability by apoptosis or necrosis, specifically under chemotherapeutic drug treatments. Xie et al. proposed non-traditional parameters based on admittance (i.e. the reciprocal of impedance) as new metrics to discriminate live, necrotic and apoptotic cells.49 Specifically, conductance (G, the real part of admittance) and susceptance (B, the imaginary part of admittance) were used. Proof-of-concept demonstration was performed using HeLa and Jurkat cells treated with an apoptosis-inducing drug actinomycin D (AD). Higher concentrations of AD represented smaller G and B. Comparison between the phenotyping of cells using the novel G and B metrics versus standard flow cytometry was performed, with the ratios for viable, early apoptotic and necrotic/non-viable cells showing good correlation.De Ninno et al.64 presented a three-electrode coplanar device capable of discrimination between live, necrotic and apoptotic cells at high-throughput (∼200 cells per s). Cells from lymphoma model cell line U937 were either treated with etoposide (an apoptosis-inducing drug) or subjected to a heat-shock (to induce loss of viability and mimic natural necrosis). Results suggest that using electrical diameter (estimated using 500 kHz impedance magnitude) it was possible to discriminate between intact cells and smaller cell debris (possibly apoptotic bodies and/or necrotic cell fragments; Fig. 6G). Within the cell population, viable and necrotic cells were discriminated based on clear differences in impedance phase data at 500 kHz. Impedance phase at 10 MHz was used to identify two subpopulations of cell debris of differing phenotype, possibly due to capacitance and conductivity differences between apoptotic bodies and other cell fragments present.
In another work using the same lymphoma cell line,41 the viability of cells was found to be compromised by exposure to toxic nanomaterials (NMs) at various concentrations and time-points. After optimization steps for the acquisition conditions (e.g. frequency and buffer composition), a clear discrimination between viable and necrotic cells was obtained at 6 MHz using a buffer comprised of PBS and 0.28 M sucrose solution at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio (Fig. 6H). In fact, the effect of NMs on cell viability could not be assessed using trypan blue dye exclusion and flow cytometry, due to interference of NMs on the staining process using Annexin-V/7-AAD. This highlights the utility of impedance-based viability assessment systems for cases wherein labelling cannot identify functional alterations.
4 ratio (Fig. 6H). In fact, the effect of NMs on cell viability could not be assessed using trypan blue dye exclusion and flow cytometry, due to interference of NMs on the staining process using Annexin-V/7-AAD. This highlights the utility of impedance-based viability assessment systems for cases wherein labelling cannot identify functional alterations.
Supervised machine learning was implemented to perform viability assessment of drug-treated cancer cells (model T47D cell line) in a different approach.53 Since activated matriptase (a membrane-bound protease), is overexpressed in various epithelial cancers, cells were subject to an anti-matriptase-conjugated drug, inducing apoptosis and loss of viability. Cells sensitive to the drug presented changes in impedance magnitude and phase data with respect to drug insensitive cells (in the 500 kHz–30 MHz range). Support vector machines, using an 8-feature matrix (impedance magnitude and phase at 4 different frequencies), had an overall accuracy of >95% in predicting the viability of analysed cells (cf. Table S2†). These results highlight the value in implementing machine learning protocols (such as neural networks) to streamline cell viability assessment, without the need for staining or labelling.
4.4 Mammalian cells
Considering other mammalian cells, studies on various leukocytes populations in human blood has been a major focus. These cells play important roles in immune response, infections, cancer and other diseases. However, immune systems can become compromised as a consequence of certain diseases, with an example being diabetes, wherein key metabolic pathways are altered, thereby dysregulating many components of both the innate and adaptive immune systems. This effect was studied by Mahesh et al. using a system for biomechanical and electrical phenotyping of lymphocytes from diabetic patients.145 The device was comprised of a constriction channel wherein alterations to the mechanical properties of single cells was estimated based on differences in the transit-time of cells through the narrowing region, with pairs of electrodes at the entrance and exit of the constriction measuring single-cell signals. Results showed a significant increase in the transit-times of diabetic versus normal lymphocytes, indicating a loss of deformability by lymphocytes from diabetic patients (Fig. 7A). Significantly higher signal amplitude differences were also observed for the altered lymphocytes, indicating overall changes to the electrophysiology of diabetic lymphocytes, likely connected to alterations in the cytoskeleton of cells.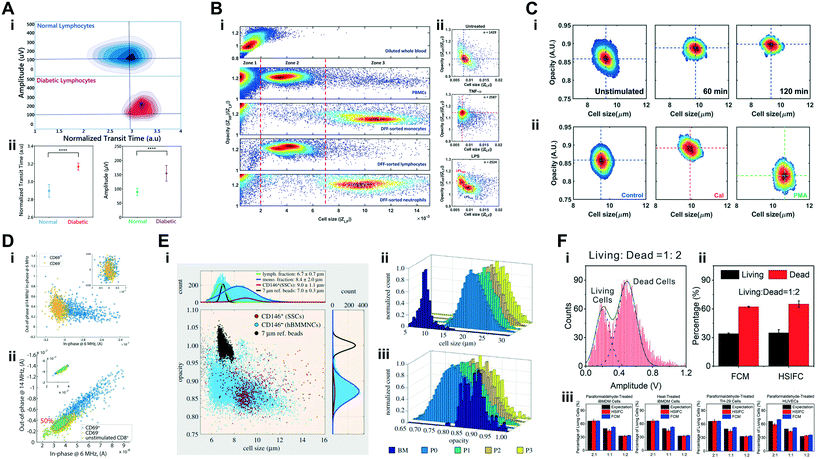 | ||
| Fig. 7 Collection of phenotyping results on mammalian cells from literature. See sections 4.4 for further details. (A) i – Measurements of transit time vs. signal amplitude for normal and diabetic lymphocytes; ii – comparison of transit time (left) and signal amplitude (right) between normal and diabetic lymphocytes, where significant differences were observed (****p < 0.0001). (B) Measurements of impedance magnitude at 300 kHz vs. opacity (impedance magnitude at 1.7 MHz/300 kHz) for various cell populations; ii – measurements of impedance magnitude at 300 kHz vs. opacity (impedance magnitude at 1.7 MHz/300 kHz) for untreated, TNF-α and LPS treated monocytes. (C) Measurements of electrical size vs. opacity (impedance magnitude at 1.7 MHz/300 kHz) for: i – neutrophils undergoing NETosis at different time points; ii – neutrophils undergoing NETosis induced via Cal and PMA. (D) Measurements of in-phase vs. out-of-phase signals at 6 MHz (i) and 14 MHz (ii) for CD69+ and CD69− T-lymphocytes (i) and unstimulated CD8+, CD69+ and CD69− T-lymphocytes (ii). (E) i – Measurements of electrical size vs. opacity (impedance magnitude at 2 MHz/500 kHz) for CD146+ and CD146− hBMMNCs; and distributions of electrical size (ii) and opacity (ii) for SSCs along passage number for one individual patient. (F) i – Distribution of signal amplitude at 450 kHz for a population of live an dead iBMDM cells; ii – comparison between viability estimations by flow cytometry (FCM) and impedance cytometry (HSIFC); iii – comparison between viability estimations by FCM and HSIFC for various cell types and treatments. Images were adapted with permission from (A) ref. 145, copyright 2019 IOP publishing, (B) ref. 60, copyright 2018 Elsevier B.V., (C) ref. 63 copyright 2019 The Royal Society of Chemistry, (D) ref. 79, copyright 2017 Elsevier B.V., (E) ref. 161, copyright 2017 The Royal Society, (F) ref. 119, copyright 2020 Elsevier B.V. | ||
Another work focused on the profiling of diabetic leukocytes was proposed by Petchakup et al.60 An innovation presented in this work was the utilization of a microfluidic device to perform a size-based, inertial cell sorting step (using Dean flow fractionation – DFF) to enrich for specific leukocyte populations prior to impedance cytometry (Fig. 5I). DFF-sorted leukocytes populations of monocytes, lymphocytes and neutrophils were clearly distinguishable from other blood cells on the basis of their impedance magnitude and magnitude opacity phenotypes (Fig. 7B). The activation of DFF-sorted monocytes with inflammatory stimulus from TNF-α induced alterations to the membrane as apparent by an increase in magnitude opacity, while LPS stimulation was used to pick out two subpopulations: activated monocytes and non-activated neutrophils within the expected homogeneous sample. Considering DFF-sorted samples from diabetic patients, the phenotypes of neutrophils presented significantly higher magnitude opacity versus that of monocytes, suggesting that diabetic patients would likely have neutrophils/monocytes expressing pro-inflammatory/activated phenotype, which can possibly serve as a novel biomarker for the inflammatory response.
In a follow-up work, impedance cytometry detection was integrated within the DFF sorting device.63 Focusing again on diabetes, the capability of healthy and glucose-treated neutrophils to form neutrophil extracellular traps (NETosis, an anti-inflammatory defense function, wherein web-like DNA structures are used to trap and kill pathogens) was assessed. Cells undergoing calcium ionophore (Cal) induced NETosis were measured, with NETosis neutrophils presenting a higher magnitude opacity and cell size than unstimulated neutrophils, especially at 120 min (Fig. 7C). These alterations could be related to cell membrane and cytoplasm conductivity alterations, together with the alteration of internal structure and degradation of the nucleus induced by NETosis. Moreover, a comparative study of NETosis induced by CaI and phorbol 12-myristate 13-acetate (PMA) revealed distinct phenotypes, with PMA-treated cells having significantly lower magnitude opacity and larger size than CaI-treated cells. The differential effects of each drug on the rates at which cells enlarge and exhibit altered membrane permeability due to NETosis may explain the differences. The results presented in both works by Petchakup et al. referred herein demonstrate the clear potential for integrating an analysis technique, such as impedance cytometry, with other relevant microfluidic sorting techniques, opening the door for truly point-of-care tools to be developed.
A different work also focusing on lymphocytes was presented by Rollo et al., aiming at the electrical profiling of activated T-lymphocytes.79 Adoptive T-cell immunotherapy is a promising approach in personalized medicine which requires the assessment of clonal antigen specificity followed by the label-free isolation of cells of interest. To assess if electrical phenotypes could indicate specific clonal antigen profiles, the authors analysed T-lymphocytes that were CD8+ unstimulated, CD8+ CD69+ activated, and CD8+ CD69-non-activated. Using a device comprised of 3D microelectrodes for signal acquisition (Fig. 2D), the impedance change associated with T-cell activation was measured using data at 6 and 14 MHz, where CD69+ cells presented a shift in the real component of impedance at both frequencies, possibly due to electrophysiology changes arising from activation processes, such as remodelling of actin cytoskeleton or the increment in nuclear volume (Fig. 7D).
Other mammalian cell types studied in recent literature include skeletal stem cells (SSCs) following enrichment and expansion.161 SSCs are a rare population found in bone marrow with high capacity for bone and cartilage regeneration. The phenotypical profiling of these rare cells has the potential for sorting and enrichment of this population. The system integrated fluorescence detection for the identification of CD146+ cells, a key SSC surface marker. Impedance measurements showed that unexpanded SSCs were on average larger than other cells found in the bone marrow. Furthermore, following the in vitro culturing of SSCs for expansion, both cell size and membrane capacitance (assessed by magnitude opacity) increased significantly, as early as by passage 0 (Fig. 7E). SSCs also showed an increased membrane capacitance with osteogenic differentiation. However, when compared to other bone marrow cells, no significant differences in magnitude opacity were found with primary SSCs, thereby limiting membrane capacitance-based DEP enrichment. Nonetheless, the observed phenotypical differences in size and stiffness could be harnessed by other microfluidic techniques for SSCs enrichment, as explored in a subsequent work.167
Another mammalian cell type studied recently was human umbilical vein endothelial cells (HUVECs), specifically utilized as model cells for the study of viability assessment after a hypertonic stimulus.119 Loss of viability was induced by either a paraformaldehyde treatment or a heat-shock. The hypertonic stimulus (Fig. 5A) was implemented to cause volumetric differences between viable and non-viable cells, making the loss of viability detectable based on difference in impedance magnitude at low frequency (450 kHz) (Fig. 7F). The system presented comparable sensitivity in the assessment of viability to that of flow cytometry results. The system was capable of determining loss of viability through both paraformaldehyde and heat-shock methods, not only for HUVECs cell type, but also human colon cancer (HT-29) cells and immature bone-marrow-derived macrophages (iBMDM).
4.5 Human pathogens
Recent literature in the realm of impedance cytometry has also focused on the detection and phenotypical characterization of different human pathogenic organisms. An example is the work by McGrath et al.151 focused on the analysis of waterborne parasitic protozoa, specifically from the Cryptosporidium and Giardia genus. Few techniques are capable of detecting and assessing the viability of single pathogens in a rapid manner,168 which is critical given that only 10 viable oocysts in a water sample can initiate a significant human infection. Measurements were performed comparing viable pathogens with heat-inactivated ones, which mimic naturally occurring non-viable oocysts. Due to the thick outer wall layer protecting oocysts, heat-inactivated cells undergo ion exchange with the suspending medium that causes a distinct electrophysiology difference versus untreated cells, as confirmed by the suspension of both sample types in a highly conductive medium (5× PBS) to optimize the discrimination (Fig. 8A). Using data at high frequency (50 MHz), 2D Gaussian confidence ellipses were defined for each population, with the gating strategy involving the definition of a line of equal probability (i.e., where detected events had equal probability of belonging to either population). This gating strategy resulted in the classification of the viability phenotype with over 90% certainty. Using the same strategy, discrimination between human pathogenic C. parvum and G. lamblia versus non-human pathogenic C. muris was also achieved with over 92% certainty, due to clear differences in cell size phenotypes (Fig. 8A).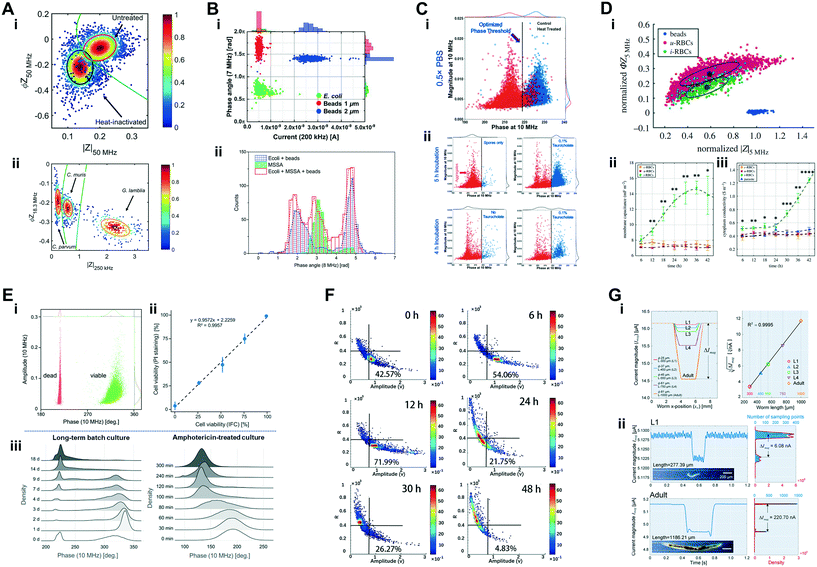 | ||
| Fig. 8 Collection of phenotyping results on various sample types from literature. See sections 4.5, 4.6 and 4.7 for further details. (A) i – Measurements of impedance magnitude vs. impedance phase at 50 MHz for untreated and heat-treated C. parvum oocysts; ii – measurements of impedance magnitude at 250 kHz vs. impedance phase at 18.3 MHz for different waterborne pathogens. (B) i – Measurements of current at 200 kHz vs. impedance phase at 7 MHz for E. coli and reference beads; ii – distribution of impedance phase at 8 MHz for populations of bacteria and reference beads. (C) Measurement of impedance phase vs. impedance magnitude at 10 MHz for: i – untreated and heat-treated C. difficile; ii – C. difficile cells under various conditions to quantify spore germination. (D) i – Measurement of impedance magnitude vs. impedance phase at 5 MHz for a mixed population of reference beads and uninfected and malaria parasite infected-RBCs; and estimated alterations to Cmem (ii) and σcyt (iii) for each cell population based on multi-shell modelling. (E) i – Measurement of impedance phase vs. impedance magnitude at 10 MHz for untreated (viable) and heat-treated (dead) yeast cells; ii – comparison between viability estimations by impedance cytometry vs. flow cytometry for various mixed samples of viable and dead yeast cells; iii – distributions of impedance phase at 10 MHz for yeast cells for long-term viability analysis. (F) Measurements of impedance magnitude at 1 MHz vs. a particle shape metric R for budding and single yeast cells along the culturing process. (G) i – Simulations of current magnitude for C. elegans worms at five developmental stages (L1–L4 and adult); ii – measurements of current magnitude for exemplary C. elegans worms at L1 and adult developmental stage. Images were adapted with permission from (A) ref. 151, copyright The Author(s) 2017, (B) ref. 40, copyright 2018 Multidisciplinary Digital Publishing Institute, (C) ref. 153, copyright 2020 Elsevier B.V., (D) ref. 69, copyright 2018 The Royal Society, (E) ref. 72, Springer-Verlag GmbH Germany, part of Springer Nature 2019. (F) Ref. 88, copyright 2019 American Chemical Society, (G) ref. 108, copyright 2018 Elsevier B.V. | ||
Another system focused on waterborne pathogens developed a system to detect micron-scale human pathogenic bacteria in water samples.40 Monitoring of bacterial concentrations is pivotal in water quality assessment, with 5 bacteria per mL being considered the permitted limit. Thus, the authors used impedance cytometry to identify bacteria suspended in tap water or an equivalent buffer of very low conductivity (0.085 S m−1). Using reference polystyrene beads of 1 and 2 μm mixed with an Escherichia coli bacteria sample to demonstrate discrimination based on size differences at 200 kHz and impedance phase phenotypes at 7 MHz (Fig. 8B), different bacterial types within a mixed sample were discriminated, with the Gram-positive Staphylococcus aureus presenting higher impedance phase at 8 MHz than the Gram-negative E. coli. These results,40,151 show the potential for an impedance-based system to be integrated in current water quality management for the detection of waterborne pathogens contaminations.
An additional work focused on the detection of bacterial phenotypes was recently presented by Moore et al.153 Gastrointestinal infections in hospital settings after antibiotic administration are widely attributed to the susceptibility of human microbiota to germination and colonization by Clostridium difficile (C. difficile). In this study, the metabolite conditions leading to germination of C. difficile spores was studied based on well separated high frequency (10 MHz) impedance phase signals from C. difficile in spore versus vegetative form (Fig. 8C), even though the impedance magnitude signal exhibited overlaps due to minimal size differences between spore aggregates and their vegetative form. In this manner, antibiotic-induced disruption of microbiota in a mouse model was shown to enhance susceptibility to spore germination.
Focusing on a different type of human pathogenic organisms, Honrado et al. performed the dielectric characterization of red blood cells infected by a malaria parasite.69 Since malaria is the world's most prevalent parasitic disease, there is a need to understand the electrophysiological alterations of cells during the malaria infection cycle. To investigate this, the infection of RBCs by malaria parasites (Plasmodium falciparum) was followed, with measurements performed every 6 h post-invasion along the 48 h intraerythrocytic life cycle of the parasite. To identify the subpopulation of infected cells, GFP emitting parasites were utilized for integrated fluorescence detection. Impedance data at 5 MHz revealed the differing phenotype of infected versus uninfected cell populations (Fig. 8D). To probe the origin of the observed phenotypes, multi-shell modelling was performed to determine the dielectric properties of the cell and parasite at each individual time-point post-invasion. Analysis showed a significant increase in Cmem and σcyt of infected RBCs along the infection time course (Fig. 8D). These alterations are probably related with known membrane alterations caused by the parasite starting at early stages, which also influence the extent of ionic exchange between the intra- and extra-cellular regions. Alterations include changes to membrane lipid and protein composition, the expression of new pathways and the formation of angular elevations that alter membrane structure. Furthermore, the volume ratio taken by the parasite within the host cell was estimated to vary from less than 10% at earlier stages of infection to more than 90% at later stages. These findings can be used in future microfluidic sorting techniques for the enrichment and detection of infected cells.
4.6 Yeast cells
A staple across the field of microfluidics is to utilize yeast cells (commonly from the Saccharomyces cerevisiae species) as a model sample type for testing of a variety of phenomena. Being easily accessible and culturable, yeast cells are optimal particles to investigate size-based methods or explore new methods for viability assessment. On the latter point, Opitz et al. explored the utilization of impedance cytometry as a new quality control tool for the determination of cell viability and to assess cell culture status.72 To mimic loss of viability, a heat-inactivation step was performed, with the estimated ratio of non-viable cells tracking well with standard flow cytometry methods, even in long-term batch cultures (Fig. 8E). By starving cells, the natural decay in viability was observed up to 18 days, with samples presenting a gradual decrease in impedance phase at 10 MHz. Cultures treated with the cytotoxic compound amphotericin showed a similar trend with increasing exposure times of up to 300 min. This phenotype of viability loss at 10 MHz is explained by the alterations in membrane properties upon death, resulting in changes to conductivity and capacitance for the cell membrane and internal structure.The phenomenon of budding yeast has also gathered some interest in recent publications, as it works as a model for phenotyping strategies focused on morphology and shape, which can provide information about cellular physiological and pathological conditions. An example can be found in a recent work where single-cell morphology was assessed based on particle self-alignment88 (Fig. 4B). Using signal width, amplitude and the ratio of width to amplitude (R) as metrics, unbudded yeast cells and early/late-budding cells were discriminated. By following the yeast proliferation process along 48 h (Fig. 8F), it was observed that most cells are in the budding stage for the first 12 h, however, from 24 h onward, the proportion of budding yeast is highly reduced, reaching a minimum at 48 h. This state is comparable to the inactive, non-budding stage that yeast cells are commonly found at.
In another example, dielectrophoretic forces were used to trap budding yeast cells and perform size estimations of the trapped cells.132 Eight trapping sites were defined to generate pressure differences capable of trapping the flowing particles. Electrical impedance spectroscopy was then performed on trapped particles. The size of trapped beads correlated well with impedance magnitude at 1 MHz. Hence, using the same metric, differences between single and budding yeast cells were observed, with the system being sensitive to variations in the size of the trapped particle. The capability to correctly identify the health and budding stage of cultures, presented in the herein highlighted literature, could possibly be applied in the fermentation industry as a rapid analysis technique.
4.7 Miscellaneous biosystems
Besides the more traditional lines of work and applications for impedance cytometry, there have been some recent works focusing on less usual sample types or procedures. In one example by Heidmann et al.,169 viability assessment of pollen from various species was studied: tobacco (Nicotiana tabacum), tomato (Solanum lycopersicum), cucumber (Cucumis sativus) and pepper (Capsicum annuum). Pollen quality control is important for plant breeding research, and for plant and food production processes. Pollen viability is typically determined by classical methods, such as staining, but also using more laborious processes, like in vitro pollen germination. Impedance cytometry was thus explored by the authors as an alternative method for pollen analysis and viability assessment. Due to the large size of pollen particles, samples were run in microchannels with cross-sections of 120 × 120 μm (tobacco, tomato and pepper) or 250 × 250 μm (cucumber). Results showed that different stages of developing, viable, germinating and non-viable pollen populations could be detected and quantified based on differences in impedance phase between 3 and 12 MHz, with high correlation to other standard benchmarking methods. Moreover, pollen with active germination potential were also discriminated against non-viable pollen and non-germinating viable populations. These results suggest that impedance cytometry could then be adopted as an effective label-free technique for pollen quality control.Another instance of an uncommon sample type is the green algae (Picochlorum SE3, Chlorophyta, 2 to 3 μm cell diameter), used for studies on viability assessment.55 Algae were rendered non-viable with a 1 h heat-treatment, with significant differences in magnitude opacity at 500 kHz and 20 MHz being observed. Non-viable cells presented smaller impedance magnitude at low and high frequencies, indicating a smaller size and altered cytoplasmic properties due to necrosis. Green algal cells were also cultured under different salinity conditions and analysed at different time points, with the magnitude opacity of cells being significantly reduced. Results suggest a capability by cells to adapt to the culturing conditions, which in turn suggests that this method could be implemented in situ to, not only analyse cell phenotype, but also assess the viability of cultures of varying media composition.
As a final example, while impedance cytometry has been widely used for label-free phenotyping of individual cells, it has yet to be used to detect larger biological systems or organisms. A recent case is the work by Zhu et al., which reported the study of C. elegans using impedance cytometry.108C. elegans is a well-characterized model organism which has been widely used in genetic studies on developmental biology, aging and neurobiology. In this work, the authors explored impedance cytometry as a tool to identify the developmental stage (larval L1, L2, L3 and L4 stages or adult stage) of individual C. elegans worms. Using impedance magnitude data at 300 kHz, worm-length related parameters were correlated to developmental stage, since worms present specific body morphology, size and behaviour at each stage (Fig. 8G). The accuracy of phenotyping and identification varied between 82% to 97%, with later stages (L4 and adult) presenting optimal accuracy. Furthermore, small (i.e., L1–L3) and large (i.e., L4 and adult) worms, from a mixed population, were separated to different outlets by first performing a size-based discrimination step using impedance cytometry data, and then re-directing individual C. elegans to the desired outlet using a system of individually addressable valves. The system was not only capable of identifying specific developmental-related phenotypes, but also for integrating impedance data within a decision step for particle separation. These results show that impedance cytometry could have a broader spectrum of interest and applications, by integration with separation technologies or by its application to sample types of larger scale.
5 Conclusions and outlook
The quantification of phenotypic heterogeneity is becoming increasingly significant to understand biological function and to address the needs of precision medicine. Over the last decade, microfluidic impedance cytometry has carved a niche within this broader need by enabling quantification of subpopulations based on their electrophysiology, especially for cell types that lack reliable biochemical markers to identify them. In recent years, novel design solutions have increased the accuracy of the technique and led to robust design-tailored tools to process the raw impedance signals. The capability of the technique to offer multiparametric information on the cells has also been enriched. It is now possible to acquire electrical fingerprints that convey biophysical information on cell size, shape, dielectric and mechanical properties, as well as on motion-related quantities such as cell velocity and position within the microchannel. Multifrequency measurements coupled with dielectric (multi-)shell models enable the quantification of conductivity and permittivity of subcellular features. Impedance spectroscopy of single flowing cells at up to eight simultaneous frequency has been demonstrated for identification by fitting of dielectric models, and microwave-based solutions are being developed to extend the frequency range, potentially enabling the identification of novel electrical biomarkers for the status of cell nucleus. Real-time processing of impedance data has also been shown, paving the way to inform sorting for downstream analysis of target sub-populations. Although cell sorting based on impedance-signature has been demonstrated,47,48,108 its great potential has not yet been fully exploited. Emerging microfabrication solutions, such as tubular microfluidics, are opening opportunities for electrical impedance tomography of flowing cells.Some novel emerging directions in cell analysis include the development of impedance cytometers for single-bacteria analysis, by overcoming the challenges of downscaling to enable early diagnosis of bacterial infections, such as through gauging host microbiota susceptibility to infection and for reducing the timeframes for antibiotic susceptibility analysis. Recent advances highlight the importance of biophysical properties determined by impedance-based single-cell analysis to complement the biochemical information obtained from fluorescence-based flow cytometry, thereby enabling a more holistic picture of the cell phenotype, which is essential for understanding cell death mechanisms, elucidating cancer metastasis, and predicting stem cell differentiation lineage. We envision enhanced impedance-based deformability cytometry protocols by novel device designs and coupled modelling approaches to translate impedance metrics into biomechanical properties. Impedance-based platforms to monitor dynamic changes at the single-cell level after drug interventions to the same sample are also very promising.
Electric fields represent an invaluable tool for single-cell analysis and manipulation in microfluidic devices. Electrical sensing has the key advantage of being label-free while electrical forces scale favourably with miniaturization.170 We envision the development of all-electrical integrated platforms wherein for instance: dielectrophoresis is used to manipulate cells171 and other analytes;172–174 impedance cytometry is used at multiple stations (e.g., pre and post-stimuli) for dynamic cell biophysical characterization and cell tracking; electro-actuated valves175 enable programmable flow control and sorting; selected cells undergo electrical lysis176 and the released intracellular material is analysed on chip by means of impedance-based nanopores.177,178 All-electrical systems show great promise for system integration and portability. The final goal is to design compact, modular and adaptive devices that use disposable chips and enable fast, user-friendly readout capabilities. This would enable the widespread use of the technology out-of-the-lab, within clinical settings, which is of central importance to validate newly discovered electrical biomarkers. A pivotal step in this direction would be the movement from cleanroom-based chip microfabrication to makerspace fabrication,179–181 which is getting closer thanks to developments in 3D printing, imprinting,182 flexible electronics and nanomaterials.
On the other hand, in order to stratify cell subpopulations in complex heterogeneous samples, novel hybrid microfluidic platforms could be developed, wherein electrical sensing is coupled e.g. with optical and fluorescence imaging,183,184 Raman185 and hyperspectral186 imaging, digital holography,187 and biochemical assays.188 In fact, probing complementary cell properties (e.g., morphological, biophysical, biochemical properties) enables multimodal sensing, which can significantly enhance the feature space used for cell characterization and discrimination. This comes with technical challenges in terms of device design and operation, as well as challenges in the combination of the acquired multimodal data.189,190 Data streams from heterogeneous sensor sources can have different noise level, information content and representation (e.g., structured vs. unstructured data, 1D or 2D signals), and multimodal information fusion still need to be improved in theories, methodologies and practical systems.191 Furthermore, as high-dimensional data become available, the identification of subpopulations by manual gating becomes impractical and automated data-driven clustering strategies are required.192,193 In particular, unsupervised clustering methods can enable the unbiased detection of novel subpopulations.
In this framework, synergistic research efforts involving microfluidics, sensor science and machine learning are expected to bring single-cell analysis to its next level, with a tremendous impact for life-science research, diagnostics and personalized medicine.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. C. and P. B. acknowledge support from MIUR Grant (SIR Programme): RBSI14TX20. N. S. and C. H. acknowledge support from NIH Grants 1R21AI130902-01 and NCATS UL1TR003015, and support from Office of the Secretary of Defense under Agreement Number W911NF-17-3-003 (Subcontract T0163). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Illustrations from SMART—Servier Medical Art, Servier, were used on Fig. 1 under the Creative Commons Attribution 3.0 Unported License.References
- S. Rubakhin, E. V. Romanova, P. Nemes and J. V. Sweedler, Nat. Methods, 2011, 8, S20–S29 CrossRef CAS PubMed.
- K. Klepárník and F. Foret, Anal. Chim. Acta, 2013, 800, 12–21 CrossRef PubMed.
- J. Cros, J. Raffenne, A. Couvelard and N. Poté, Pathobiology, 2018, 85, 64–71 CrossRef CAS PubMed.
- J. B. Mitchell, K. McIntosh, S. Zvonic, S. Garrett, Z. E. Floyd, A. Kloster, Y. Di Halvorsen, R. W. Storms, B. Goh, G. Kilroy, X. Wu and J. M. Gimble, Stem Cells, 2006, 24, 376–385 CrossRef PubMed.
- K. Yoshimura, T. Shigeura, D. Matsumoto, T. Sato, Y. Takaki, E. Aiba-Kojima, K. Sato, K. Inoue, T. Nagase, I. Koshima, K. Gonda, I. Koshima and K. Gonda, J. Cell. Physiol., 2006, 208, 64–76 CrossRef CAS PubMed.
- T. Jiang, W. Liu, X. Lv, H. Sun, L. Zhang, Y. Liu, W. J. Zhang, Y. Cao and G. Zhou, Biomaterials, 2010, 31, 3564–3571 CrossRef CAS PubMed.
- J. L. Nourse, J. L. Prieto, A. R. Dickson, J. Lu, M. M. Pathak, F. Tombola, M. Demetriou, A. P. Lee and L. A. Flanagan, Stem Cells, 2014, 32, 706–716 CrossRef CAS PubMed.
- A. Rohani, J. H. Moore, J. A. Kashatus, H. Sesaki, D. F. Kashatus and N. S. Swami, Anal. Chem., 2017, 89, 5757–5764 CrossRef CAS PubMed.
- Y. Liu and T. Ma, Biotechnol. Prog., 2015, 31, 468–481 CrossRef CAS PubMed.
- J. Skommer, T. Brittain and S. Raychaudhuri, Apoptosis, 2010, 15, 1223–1233 CrossRef CAS PubMed.
- W. C. Lee, H. Shi, Z. Poon, L. M. Nyan, T. Kaushik, G. V. Shivashankar, J. K. Y. Chan, C. T. Lim, J. Han and K. J. Van Vliet, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E4409–E4418 CrossRef CAS PubMed.
- S. Gawad, K. Cheung, U. Seger, A. Bertsch and P. Renaud, Lab Chip, 2004, 4, 241–251 RSC.
- T. Sun and H. Morgan, Microfluid. Nanofluid., 2010, 8, 423–443 CrossRef CAS.
- T. B. Jones, Electromechanics of Particles, Cambridge University Press, 1995 Search PubMed.
- H. Morgan and N. G. Green, AC Electrokinetics: Colloids and Nanoparticles, Research Studies Press, 2003 Search PubMed.
- A. Hedayatipour, S. Aslanzadeh and N. McFarlane, Biosens. Bioelectron., 2019, 143, 111600 CrossRef CAS PubMed.
- A. Vembadi, A. Menachery and M. A. Qasaimeh, Front. Bioeng. Biotechnol., 2019, 7, 147 CrossRef PubMed.
- D. Naranjo-Hernández, J. Reina-Tosina and M. Min, J. Sens., 2019, 2019, 9210258 Search PubMed.
- R. J. Yang, L. M. Fu and H. H. Hou, Sens. Actuators, B, 2018, 266, 26–45 CrossRef CAS.
- T. Vaclavek, J. Prikryl and F. Foret, J. Sep. Sci., 2019, 42, 445–457 CrossRef CAS PubMed.
- M. Carminati, J. Sens., 2017, 2017, 7638389 Search PubMed.
- Y. Xu, X. Xie, Y. Duan, L. Wang, Z. Cheng and J. Cheng, Biosens. Bioelectron., 2016, 77, 824–836 CrossRef CAS PubMed.
- K. Galler, K. Bräutigam, C. Große, J. Popp and U. Neugebauer, Analyst, 2014, 139, 1237–1273 RSC.
- K. Heileman, J. Daoud and M. Tabrizian, Biosens. Bioelectron., 2013, 49, 348–359 CrossRef CAS PubMed.
- K. C. Cheung, M. Di Berardino, G. Schade-Kampmann, M. Hebeisen, A. Pierzchalski, J. Bocsi, A. Mittag and A. Tárnok, Cytometry, Part A, 2010, 77, 648–666 CrossRef PubMed.
- J. Chen, C. Xue, Y. Zhao, D. Chen, M. H. Wu and J. Wang, Int. J. Mol. Sci., 2015, 16, 9804–9830 CrossRef CAS PubMed.
- C. Petchakup, K. H. H. Li and H. W. Hou, Micromachines, 2017, 8, 87 CrossRef.
- H. Daguerre, M. Solsona, J. Cottet, M. Gauthier, P. Renaud and A. Bolopion, Lab Chip, 2020, 20, 3665–3689 RSC.
- T. Sun, C. van Berkel, N. G. Green and H. Morgan, Microfluid. Nanofluid., 2009, 6, 179–187 CrossRef CAS.
- T. Sun, S. Gawad, C. Bernabini, N. G. Green and H. Morgan, Meas. Sci. Technol., 2007, 18, 2859–2868 CrossRef CAS.
- T. Sun, D. Holmes, S. Gawad, N. G. Green and H. Morgan, Lab Chip, 2007, 7, 1034–1040 RSC.
- C. Bernabini, D. Holmes and H. Morgan, Lab Chip, 2011, 11, 407–412 RSC.
- M. Evander, A. J. Ricco, J. Morser, G. T. A. Kovacs, L. L. K. Leung and L. Giovangrandi, Lab Chip, 2013, 13, 722–729 RSC.
- X. Zhu, K. W. Tung and P. Y. Chiou, Appl. Phys. Lett., 2017, 111, 143506 CrossRef.
- N. Haandbæk, S. C. Bürgel, F. Heer and A. Hierlemann, Lab Chip, 2014, 14, 369–377 RSC.
- K. Cheung, S. Gawad and P. Renaud, Cytometry, Part A, 2005, 65, 124–132 CrossRef PubMed.
- N. Haandbæk, O. With, S. C. Bürgel, F. Heer and A. Hierlemann, Lab Chip, 2014, 14, 3313–3324 RSC.
- M. Kelleci, H. Aydogmus, L. Aslanbas, S. O. Erbil and M. Selim Hanay, Lab Chip, 2018, 18, 463–472 RSC.
- J.-C. Chien, A. Ameri, E.-C. Yeh, A. N. Killilea, M. Anwar and A. M. Niknejad, Lab Chip, 2018, 18, 2065–2076 RSC.
- C. H. Clausen, M. Dimaki, C. V. Bertelsen, G. E. Skands, R. Rodriguez-Trujillo, J. D. Thomsen and W. E. Svendsen, Sensors, 2018, 18, 3496 CrossRef PubMed.
- M. Ostermann, A. Sauter, Y. Xue, E. Birkeland, J. Schoelermann, B. Holst and M. R. Cimpan, Sci. Rep., 2020, 10, 142 CrossRef CAS PubMed.
- E. J. W. Wynn and M. J. Hounslow, Powder Technol., 1997, 93, 163–175 CrossRef CAS.
- U. Hassan and R. Bashir, Lab Chip, 2014, 14, 4370–4381 RSC.
- F. Caselli, A. De Ninno, R. Reale, L. Businaro and P. Bisegna, IEEE Trans. Biomed. Eng., 2020 DOI:10.1109/TBME.2020.2995364.
- M. R. Kellman, F. R. Rivest, A. Pechacek, L. L. Sohn and M. Lustig, IEEE Sens. J., 2018, 18, 3068–3079 Search PubMed.
- N. Wang, R. Liu, N. Asmare, C. H. Chu and A. F. Sarioglu, Lab Chip, 2019, 19, 3292–3304 RSC.
- J. Schoendube, D. Wright, R. Zengerle and P. Koltay, Biomicrofluidics, 2015, 9, 14117 CrossRef CAS PubMed.
- B. de Wagenaar, S. Dekker, H. L. de Boer, J. G. Bomer, W. Olthuis, A. Van Den Berg and L. I. Segerink, Lab Chip, 2016, 16, 1514–1522 RSC.
- X. Xie, Z. Cheng, Y. Xu, R. Liu, Q. Q. Li and J. Cheng, Anal. Methods, 2017, 9, 1201–1212 RSC.
- G. Salles-Loustau, T. Le, L. Najafizadeh, S. Zonouz and M. Javanmard, Biomed. Microdevices, 2018, 20, 63 CrossRef PubMed.
- A. Furniturewalla, M. Chan, J. Sui, K. Ahuja and M. Javanmard, Microsyst. Nanoeng., 2018, 4, 20 CrossRef PubMed.
- C. Raillon, J. Che, S. Thill, M. Duchamp, B. X. E. Desbiolles, A. Millet, E. Sollier and P. Renaud, Cytometry, Part A, 2019, 95, 1085–1095 CrossRef CAS PubMed.
- K. Ahuja, G. M. Rather, Z. Lin, J. Sui, P. Xie, T. Le, J. R. Bertino and M. Javanmard, Microsyst. Nanoeng., 2019, 5, 34 CrossRef PubMed.
- Z. Lin, S. Y. Lin, P. Xie, C. Y. Lin, G. M. Rather, J. R. Bertino and M. Javanmard, Sci. Rep., 2020, 10, 3015 CrossRef CAS PubMed.
- J. Sui, F. Foflonker, D. Bhattacharya and M. Javanmard, Sci. Rep., 2020, 10, 1251 CrossRef CAS PubMed.
- J. Sui, P. Xie, Z. Lin and M. Javanmard, Talanta, 2020, 215, 120791 CrossRef CAS PubMed.
- S. Gawad, L. Schild and P. Renaud, Lab Chip, 2001, 1, 76–82 RSC.
- V. Errico, A. De Ninno, F. R. Bertani, L. Businaro, P. Bisegna and F. Caselli, Sens. Actuators, B, 2017, 247, 580–586 CrossRef CAS.
- E. Valera, J. Berger, U. Hassan, T. Ghonge, J. Liu, M. Rappleye, J. Winter, D. Abboud, Z. Haidry, R. Healey, K. White and R. Bashir, Lab Chip, 2018, 18, 1461–1470 RSC.
- C. Petchakup, H. M. Tay, W. H. Yeap, R. Dalan, S. C. Wong, K. H. H. Li and H. W. Hou, Biosens. Bioelectron., 2018, 118, 195–203 CrossRef CAS PubMed.
- M. Serhatlioglu, M. Asghari, M. Tahsin Guler and C. Elbuken, Electrophoresis, 2019, 40, 906–913 CrossRef CAS PubMed.
- A. Saateh, A. Kalantarifard, O. T. Celik, M. Asghari, M. Serhatlioglu and C. Elbuken, Lab Chip, 2019, 19, 3815–3824 RSC.
- C. Petchakup, H. M. Tay, K. H. H. Li and H. W. Hou, Lab Chip, 2019, 19, 1736–1746 RSC.
- A. De Ninno, R. Reale, A. Giovinazzo, F. R. Bertani, L. Businaro, P. Bisegna, C. Matteucci and F. Caselli, Biosens. Bioelectron., 2020, 150, 111887 CrossRef CAS PubMed.
- S. Dekker, P. K. Isgor, T. Feijten, L. I. Segerink and M. Odijk, Microsyst. Nanoeng., 2018, 4, 34 CrossRef PubMed.
- S. Emaminejad, S. Talebi, R. W. Davis and M. Javanmard, IEEE Sens. J., 2015, 15, 2715–2716 Search PubMed.
- P. Xie, X. Cao, Z. Lin, N. Talukder, S. Emaminejad and M. Javanmard, Sens. Actuators, B, 2017, 241, 672–680 CrossRef CAS.
- T. Sun, N. G. Green, S. Gawad and H. Morgan, IET Nanobiotechnol., 2007, 1, 69–79 CrossRef CAS PubMed.
- C. Honrado, L. Ciuffreda, D. Spencer, L. Ranford-Cartwright and H. Morgan, J. R. Soc., Interface, 2018, 15, 20180416 CrossRef PubMed.
- G. Arrabito, V. Errico, A. De Ninno, F. Cavaleri, V. Ferrara, B. Pignataro and F. Caselli, Langmuir, 2019, 35, 4936–4945 CrossRef CAS PubMed.
- J. S. McGrath, C. Honrado, J. H. Moore, S. J. Adair, W. B. Varhue, A. Salahi, V. Farmehini, B. J. Goudreau, S. Nagdas, E. M. Blais, T. W. Bauer and N. S. Swami, Anal. Chim. Acta, 2019, 1101, 90–98 CrossRef PubMed.
- C. Opitz, G. Schade, S. Kaufmann, M. Di Berardino, M. Ottiger and S. Grzesiek, Appl. Microbiol. Biotechnol., 2019, 103, 8619–8629 CrossRef CAS PubMed.
- D. Impe, J. Reitz, C. Köpnick, H. Rolletschek, A. Börner, A. Senula and M. Nagel, Front. Plant Sci., 2020, 10, 1588 CrossRef PubMed.
- N. Demierre, T. Braschler, P. Linderholm, U. Seger, H. Van Lintel and P. Renaud, Lab Chip, 2007, 7, 355–365 RSC.
- A. Valero, T. Braschler and P. Renaud, Lab Chip, 2010, 10, 2216–2225 RSC.
- N. Demierre, T. Braschler, R. Muller and P. Renaud, Sens. Actuators, B, 2008, 132, 388–396 CrossRef CAS.
- J. Cottet, A. Kehren, H. van Lintel, F. Buret, M. Frénéa-Robin and P. Renaud, Microfluid. Nanofluid., 2019, 23, 11 CrossRef.
- S. C. C. Kilchenmann, E. Rollo, E. Bianchi and C. Guiducci, Sens. Actuators, B, 2013, 185, 713–719 CrossRef CAS.
- E. Rollo, E. Tenaglia, R. Genolet, E. Bianchi, A. Harari, G. Coukos and C. Guiducci, Biosens. Bioelectron., 2017, 94, 193–199 CrossRef CAS PubMed.
- C. Grenvall, C. Antfolk, C. Z. Bisgaard and T. Laurell, Lab Chip, 2014, 14, 4629–4637 RSC.
- G. Mernier, E. Duqi and P. Renaud, Lab Chip, 2012, 12, 4344–4349 RSC.
- N. Haandbæk, S. C. Bürgel, F. Rudolf, F. Heer and A. Hierlemann, ACS Sens., 2016, 1, 1020–1027 CrossRef.
- M. Frankowski, J. Theisen, A. Kummrow, P. Simon, H. Ragusch, N. Bock, M. Schmidt and J. Neukammer, Sensors, 2013, 13, 4674–4693 CrossRef PubMed.
- Y. Song, T. Zhou, Q. Liu, Z. Liu and D. Li, Analyst, 2020, 145, 5466–5474 RSC.
- W. Tang, D. Tang, Z. Ni, N. Xiang and H. Yi, Anal. Chem., 2017, 89, 3154–3161 CrossRef CAS PubMed.
- I. Bilican, M. T. Guler, M. Serhatlioglu, T. Kirindi and C. Elbuken, Sens. Actuators, B, 2020, 307, 127531 CrossRef.
- Y. Zhang, H. Liang, H. Tan, D. Chen, Y. Wang, Y. Xu, J. Wang and J. Chen, Sens. Actuators, B, 2020, 317, 128231 CrossRef CAS.
- X. Xie, Z. Zhang, X. Ge, X. Zhao, L. Hao, Z. Cheng, W. Zhou, Y. Du, L. Wang, F. Tian, F. Tian and X. Xu, Anal. Chem., 2019, 91, 13398–13406 CrossRef PubMed.
- D. Spencer and H. Morgan, ACS Sens., 2020, 5, 423–430 CrossRef CAS PubMed.
- D. Spencer, F. Caselli, P. Bisegna and H. Morgan, Lab Chip, 2016, 16, 2467–2473 RSC.
- A. De Ninno, V. Errico, F. R. Bertani, L. Businaro, P. Bisegna and F. Caselli, Lab Chip, 2017, 17, 1158–1166 RSC.
- A. De Ninno, R. Reale, A. Giovinazzo, F. R. Bertani, L. Businaro, P. Bisegna, C. Matteucci and F. Caselli, Biosens. Bioelectron., 2019, 111887 Search PubMed.
- R. Reale, A. De Ninno, L. Businaro, P. Bisegna and F. Caselli, Lab Chip, 2019, 19, 1818–1827 RSC.
- F. Caselli, A. De Ninno, R. Reale, L. Businaro and P. Bisegna, Sens. Actuators, B, 2018, 256, 580–589 CrossRef CAS.
- H. Wang, N. Sobahi and A. Han, Lab Chip, 2017, 17, 1264 RSC.
- D. Yang and Y. Ai, Lab Chip, 2019, 19, 3609–3617 RSC.
- M. Solsona, E. Y. Westerbeek, J. G. Bomer, W. Olthuis and A. Van Den Berg, Lab Chip, 2019, 19, 1054–1059 RSC.
- B. Brazey, J. Cottet, A. Bolopion, H. Van Lintel, P. Renaud and M. Gauthier, Lab Chip, 2018, 18, 818–831 RSC.
- R. Reale, A. De Ninno, L. Businaro, P. Bisegna and F. Caselli, Microfluid. Nanofluid., 2018, 22, 1–13 CrossRef CAS.
- C. Honrado, J. S. McGrath, R. Reale, P. Bisegna, N. S. Swami and F. Caselli, Anal. Bioanal. Chem., 2020, 412, 3835–3845 CrossRef CAS PubMed.
- C.-C. Chung, I.-F. Cheng, H.-M. Chen, H.-C. Kan, W.-H. Yang and H.-C. Chang, Anal. Chem., 2012, 84, 3347–3354 CrossRef CAS.
- J. Choi, J. Yoo, M. Lee, E.-G. Kim, J. S. Lee, S. Lee, S. Joo, S. H. Song, E.-C. Kim, J. C. Lee, Y.-G. Jung and S. Kwon, Sci. Transl. Med., 2014, 6, 267ra174 CrossRef PubMed.
- A. Rohani, J. H. Moore, Y.-H. Su, V. Stagnaro, C. Warren and N. S. Swami, Sens. Actuators, B, 2018, 276, 472–480 CrossRef CAS.
- D. Porro, M. Vai, M. Vanoni, L. Alberghina and C. Hatzis, Cytometry, Part A, 2009, 75, 114–120 CrossRef.
- Z. Zhu, X. Xu, L. Fang, D. Pan and Q.-A. Huang, Sens. Actuators, B, 2016, 235, 515–524 CrossRef CAS.
- K. L. Chen, M. M. Crane and M. Kaeberlein, Mech. Ageing Dev., 2017, 161, 262–269 CrossRef CAS PubMed.
- M. Shaker, L. Colella, F. Caselli, P. Bisegna and P. Renaud, Lab Chip, 2014, 14, 2548–2555 RSC.
- Z. Zhu, W. Chen, B. Tian, Y. Luo, J. Lan, D. Wu, D. Chen, Z. Wang and D. Pan, Sens. Actuators, B, 2018, 275, 470–482 CrossRef CAS.
- F. Caselli, P. Bisegna and F. Maceri, J. Microelectromech. Syst., 2010, 19, 1029–1040 Search PubMed.
- J. Wang, D. Karnaushenko, M. Medina-Sánchez, Y. Yin, L. Ma and O. G. Schmidt, ACS Sens., 2019, 4, 1476–1496 CrossRef CAS PubMed.
- S. M. Weiz, M. Medina-Sánchez and O. G. Schmidt, Adv. Biosyst., 2018, 2, 1870011 CrossRef.
- D. Di Carlo, J. Lab. Autom., 2012, 17, 32–42 CrossRef CAS PubMed.
- Y. Zheng, J. Nguyen, C. Wang and Y. Sun, Lab Chip, 2013, 13, 3275–3283 RSC.
- M. Urbanska, H. E. Muñoz, J. Shaw Bagnall, O. Otto, S. R. Manalis, D. Di Carlo and J. Guck, Nat. Methods, 2020, 17, 587–593 CrossRef CAS PubMed.
- D. Yang, Y. Zhou, Y. Zhou, J. Han and Y. Ai, Biosens. Bioelectron., 2019, 133, 16–23 CrossRef CAS PubMed.
- Y. Zhou, D. Yang, Y. Zhou, B. L. Khoo, J. Han and Y. Ai, Anal. Chem., 2018, 90, 912–919 CrossRef CAS PubMed.
- X. Ren, P. Ghassemi, J. S. J. S. Strobl and M. Agah, Biomicrofluidics, 2019, 13, 044103 CrossRef PubMed.
- P. Ghassemi, K. S. Harris, X. Ren, B. M. Foster, C. D. Langefeld, B. A. Kerr and M. Agah, Sens. Actuators, B, 2020, 321, 128522 CrossRef CAS PubMed.
- Q. Zi, W. Ding, C. Sun, S. Li, D. Gao, L. He, J. Liu, L. Xu and B. Qiu, Biosens. Bioelectron., 2020, 148, 111820 CrossRef CAS PubMed.
- R. Reale, A. De Ninno, L. Businaro, P. Bisegna and F. Caselli, Electrophoresis, 2019, 40, 1400–1407 CrossRef CAS PubMed.
- K. Chawla, M. M. Modena, P. S. Ravaynia, F. C. Lombardo, M. Leonhardt, G. Panic, S. C. Bürgel, J. Keiser and A. Hierlemann, ACS Sens., 2018, 3, 2613–2620 CrossRef CAS.
- P. S. Ravaynia, F. C. Lombardo, S. Biendl, M. A. Dupuch, J. Keiser, A. Hierlemann and M. M. Modena, Adv. Biosyst., 2020, 4, 1900304 CrossRef CAS PubMed.
- D. Holmes and H. Morgan, Anal. Chem., 2010, 82, 1455–1461 CrossRef CAS PubMed.
- S. I. Han and K. H. Han, Anal. Chem., 2015, 87, 10585–10592 CrossRef CAS PubMed.
- R. Liu, C.-H. Chu, N. Wang, T. Ozkaya-Ahmadov, O. Civelekoglu, D. Lee, A. K. M. Arifuzzman and A. F. Sarioglu, Small, 2019, 15, 1904732 CrossRef CAS PubMed.
- R. Reale, A. De Ninno, M. A. Brighetti, L. Businaro, A. Travaglini, P. Bisegna and F. Caselli, in 23nd International Conference on Miniaturized Systems for Chemistry and Life Sciences (MicroTAS 2019), 2019 Search PubMed.
- Y. Liu, K. Wang, X. Sun, D. Chen, J. Wang and J. Chen, Microfluid. Nanofluid., 2020, 24, 45 CrossRef CAS.
- K. Chawla, S. C. Bürgel, G. W. Schmidt, H.-M. Kaltenbach, F. Rudolf, O. Frey and A. Hierlemann, Microsyst. Nanoeng., 2018, 4, 8 CrossRef PubMed.
- Y. Feng, L. Huang, P. Zhao, F. Liang and W. Wang, Anal. Chem., 2019, 91, 15204–15212 CrossRef CAS.
- V. Farmehini, W. Varhue, A. Salahi, A. R. Hyler, J. Čemažar, R. Davalos and N. S. Swami, IEEE Trans. Biomed. Eng., 2019, 1 Search PubMed.
- W. Fan, X. Chen, Y. Ge, Y. Jin, Q. Jin and J. Zhao, Biosens. Bioelectron., 2019, 145, 111730 CrossRef CAS PubMed.
- Y. Geng, Z. Zhu, Y. Wang, Y. Wang, S. Ouyang, K. Zheng, W. Ye, Y. Fan, Z. Wang and D. Pan, Electrophoresis, 2019, 40, 1436–1445 CrossRef CAS PubMed.
- M. Carminati, G. Ferrari, M. D. D. Vahey, J. Voldman and M. Sampietro, IEEE Trans. Biomed. Circuits Syst., 2017, 11, 1438–1449 Search PubMed.
- S. Dekker, W. Buesink, M. Blom, M. Alessio, N. Verplanck, M. Hihoud, C. Dehan, W. César, A. Le Nel, A. van den Berg and M. Odijk, Sens. Actuators, B, 2018, 272, 468–478 CrossRef CAS.
- S. Zhang, Z. Li and Q. Wei, Nami Jishu Yu Jingmi Gongcheng, 2020, 3, 32–42 Search PubMed.
- M. A. Mansor, M. Takeuchi, M. Nakajima, Y. Hasegawa and M. R. Ahmad, Appl. Sci., 2017, 7, 170 CrossRef.
- J. Panwar and R. Roy, Microelectron. Eng., 2019, 215, 111010 CrossRef.
- Y. Fu, Q. Yuan and J. Guo, Microfluid. Nanofluid., 2017, 21, 20 CrossRef.
- S. Prakash, B. K. Ashley, P. S. Doyle and U. Hassan, Sci. Rep., 2020, 10, 6109 CrossRef CAS.
- F. Caselli and P. Bisegna, IEEE Trans. Biomed. Eng., 2016, 63, 415–422 Search PubMed.
- R. Liu, N. Wang, N. Asmare and A. F. Sarioglu, Biosens. Bioelectron., 2018, 120, 30–39 CrossRef CAS PubMed.
- R. Liu, N. Wang, F. Kamili and A. F. Sarioglu, Lab Chip, 2016, 16, 1350–1357 RSC.
- F. Caselli, A. De Ninno, R. Reale, L. Businaro and P. Bisegna, in 24nd International Conference on Miniaturized Systems for Chemistry and Life Sciences (MicroTAS 2020), 2020 Search PubMed.
- T. Sun, N. G. Green and H. Morgan, NANO: Brief Reports and Reviews, 2008, 3, 55–63 CrossRef CAS.
- K. Mahesh, M. M. Varma and P. Sen, J. Micromech. Microeng., 2019, 29, 115001 CrossRef CAS.
- H. Li, C. Multari, C. Palego, X. Ma, X. Du, Y. Ning, J. Buceta, J. C. M. Hwang and X. Cheng, Sens. Actuators, B, 2018, 255, 1614–1622 CrossRef CAS.
- K. R. Foster and H. P. Schwan, Crit. Rev. Biomed. Eng., 1989, 17, 25–104 CAS.
- F. Caselli and P. Bisegna, Med. Eng. Phys., 2017, 48, 81–89 CrossRef PubMed.
- F. Caselli, R. Reale, N. A. Nodargi and P. Bisegna, Micromachines, 2017, 8, 283 CrossRef PubMed.
- J. Claudel, A. L. De Araujo and M. Nadi, Sensors, 2019, 19, 3366 CrossRef CAS PubMed.
- J. S. McGrath, C. Honrado, D. Spencer, B. Horton, H. L. Bridle and H. Morgan, Sci. Rep., 2017, 7, 2601 CrossRef CAS PubMed.
- J. H. Moore, C. Honrado, V. Stagnaro, G. Kolling, C. A. Warren and N. S. Swami, ACS Infect. Dis., 2020, 6, 1000–1007 CrossRef CAS PubMed.
- J. H. Moore, A. Salahi, C. Honrado, C. Warburton, C. A. Warren and N. S. Swami, Biosens. Bioelectron., 2020, 166, 112440 CrossRef CAS PubMed.
- Y. Zhao, K. Wang, D. Chen, B. Fan, Y. Xu, Y. Ye, J. Wang, J. Chen and C. Huang, Biosens. Bioelectron., 2018, 111, 138–143 CrossRef CAS PubMed.
- K. Mahesh, M. M. Varma and P. Sen, Lab Chip, 2020, 20, 4296–4309 RSC.
- K. Wang, Y. Zhao, D. Chen, B. Fan, Y. Lu, L. Chen, R. Long, J. Wang and J. Chen, Sci. Data, 2017, 4, 170015 CrossRef PubMed.
- D. R. Gossett, W. M. Weaver, A. J. MacH, S. C. Hur, H. T. K. Tse, W. Lee, H. Amini and D. Di Carlo, Anal. Bioanal. Chem., 2010, 397, 3249–3267 CrossRef CAS PubMed.
- A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2019, 144, 87–113 RSC.
- C. Wyatt Shields IV, C. D. C. D. Reyes, G. P. Lopez and G. P. López, Lab Chip, 2015, 15, 1230–1249 RSC.
- D. Spencer, V. Hollis and H. Morgan, Biomicrofluidics, 2014, 8, 64124 CrossRef PubMed.
- M. Xavier, M. C. De Andres, D. Spencer, R. O. C. Oreffo and H. Morgan, J. R. Soc., Interface, 2017, 14, 20170233 CrossRef PubMed.
- T.-K. Chiu, Y. Zhao, D. Chen, C.-H. Hsieh, K. Wang, W.-P. Chou, C.-J. Liao, H.-Y. Wang, B. Fan, J. Wang, J. Chen and M.-H. Wu, Sens. Actuators, B, 2017, 246, 29–37 CrossRef CAS.
- Y. Zhang, Y. Zhao, D. Chen, K. Wang, Y. Wei, Y. Xu, C. Huang, J. Wang and J. Chen, Analyst, 2019, 144, 1008–1015 RSC.
- H. A. Svahn and A. Van Den Berg, Lab Chip, 2007, 7, 544–546 RSC.
- H. Liang, Y. Zhang, D. Chen, H. Tan, Y. Zheng, J. Wang and J. Chen, Micromachines, 2019, 10, 740 CrossRef PubMed.
- J. M. Meacham, K. Durvasula, F. L. Degertekin and A. G. Fedorov, Sci. Rep., 2018, 8, 3727 CrossRef PubMed.
- M. Xavier, S. H. Holm, J. P. Beech, D. Spencer, J. O. Tegenfeldt, R. O. C. Oreffo and H. Morgan, Lab Chip, 2019, 19, 513–523 RSC.
- Y. H. Su, M. Tsegaye, W. Varhue, K. T. Liao, L. S. Abebe, J. A. Smith, R. L. Guerrant and N. S. Swami, Analyst, 2013, 139, 66–73 RSC.
- I. Heidmann, G. Schade-Kampmann, J. Lambalk, M. Ottiger and M. Di Berardino, PLoS One, 2016, 11, 1–15 CrossRef PubMed.
- R. Pethig, Dielectrophoresis: Theory, Methodology and Biological Applications, Wiley, 1st edn, 2017 Search PubMed.
- J. Cottet, A. Kehren, S. Lasli, H. van Lintel, F. Buret, M. Frénéa-Robin and P. Renaud, Electrophoresis, 2019, 40, 1498–1509 CrossRef CAS PubMed.
- R. E. Fernandez, B. J. Sanghavi, V. Farmehini, J. L. Chávez, J. Hagen, N. Kelley-Loughnane, C. F. Chou and N. S. Swami, Electrochem. Commun., 2016, 72, 144–147 CrossRef CAS.
- J. H. Moore, W. B. Varhue, Y. H. Su, S. S. Linton, V. Farmehini, T. E. Fox, G. L. Matters, M. Kester and N. S. Swami, Anal. Chem., 2019, 91, 10424–10431 CrossRef CAS PubMed.
- A. Rohani, B. J. Sanghavi, A. Salahi, K.-T. Liao, C.-F. Chou and N. S. Swami, Nanoscale, 2017, 9, 12124–12131 RSC.
- Y. Arango, Y. Temiz, O. Gökçe and E. Delamarche, Sci. Adv., 2020, 6, eaay8305 CrossRef.
- G. Mernier, W. Hasenkamp, N. Piacentini and P. Renaud, Procedia Eng., 2010, 5, 37–40 CrossRef CAS.
- K. Yokota, M. Tsutsui and M. Taniguchi, RSC Adv., 2014, 4, 15886–15899 RSC.
- Y. Jiang and W. Guo, Sci. Bull., 2015, 60, 491–502 CrossRef CAS.
- S. Emaminejad, M. Javanmard, R. W. Dutton and R. W. Davis, Lab Chip, 2012, 12, 4499–4507 RSC.
- A. Kundu, C. Nattoo, S. Fremgen, S. Springer, T. Ausaf and S. Rajaraman, RSC Adv., 2019, 9, 8949–8963 RSC.
- S. Hales, E. Tokita, R. Neupane, U. Ghosh, B. Elder, D. Wirthlin and Y. L. Kong, Nanotechnology, 2020, 31, 172001 CrossRef CAS PubMed.
- A. Salahi, W. B. Varhue, V. Farmehini, A. R. Hyler, E. M. Schmelz, R. V. Davalos and N. S. Swami, Anal. Bioanal. Chem., 2020, 412, 3881–3889 CrossRef CAS PubMed.
- A. Kleiber, A. Ramoji, G. Mayer, U. Neugebauer, J. Popp and T. Henkel, Lab Chip, 2020, 20, 1676–1686 RSC.
- N. Nitta, T. Sugimura, A. Isozaki, H. Mikami, K. Hiraki, S. Sakuma, T. Iino, F. Arai, T. Endo, Y. Fujiwaki, H. Fukuzawa, M. Hase, T. Hayakawa, K. Hiramatsu, Y. Hoshino, M. Inaba, T. Ito, H. Karakawa, Y. Kasai, K. Koizumi, S. Lee, C. Lei, M. Li, T. Maeno, S. Matsusaka, D. Murakami, A. Nakagawa, Y. Oguchi, M. Oikawa, T. Ota, K. Shiba, H. Shintaku, Y. Shirasaki, K. Suga, Y. Suzuki, N. Suzuki, Y. Tanaka, H. Tezuka, C. Toyokawa, Y. Yalikun, M. Yamada, M. Yamagishi, T. Yamano, A. Yasumoto, Y. Yatomi, M. Yazawa, D. Di Carlo, Y. Hosokawa, S. Uemura, Y. Ozeki and K. Goda, Cell, 2018, 175, 266–276.e13 CrossRef CAS.
- N. Nitta, T. Iino, A. Isozaki, M. Yamagishi, Y. Kitahama, S. Sakuma, Y. Suzuki, H. Tezuka, M. Oikawa, F. Arai, Y. Ozeki and K. Goda, Nat. Commun., 2020, 11, 3452 CrossRef CAS.
- N. Mehta, S. Shaik, R. Devireddy and M. R. Gartia, J. Biomech. Eng., 2018, 140, 020802 CrossRef.
- F. Merola, P. Memmolo, L. Miccio, R. Savoia, M. Mugnano, A. Fontana, G. D'Ippolito, A. Sardo, A. Iolascon, A. Gambale and P. Ferraro, Light: Sci. Appl., 2017, 6, e16241 CrossRef CAS PubMed.
- W. Chen, F. Shao and Y. Xianyu, Small, 2020, 16, 1903388 CrossRef CAS.
- J. Kittler, M. Hatef, R. P. W. Duin and J. Matas, IEEE Trans. Pattern Anal. Mach. Intell., 1998, 20, 226–239 CrossRef.
- J. Riordon, D. Sovilj, S. Sanner, D. Sinton and E. W. K. Young, Trends Biotechnol., 2019, 37, 310–324 CrossRef CAS PubMed.
- M.-H. Yang and J.-H. Tao, Virtual Reality & Intelligent Hardware, 2019, 1, 21–38 Search PubMed.
- R. V. Bruggner, B. Bodenmiller, D. L. Dill, R. J. Tibshirani and G. P. Nolan, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E2770–E2777 CrossRef CAS PubMed.
- P. Liu, S. Liu, Y. Fang, X. Xue, J. Zou, G. Tseng and L. Konnikova, Front. Cell Dev. Biol., 2020, 8, 234 CrossRef PubMed.
- S. P. Desai, A. Coston and A. Berlin, IEEE Trans. Nanobioscience, 2019, 18, 369–372 Search PubMed.
- D. Holmes, D. Pettigrew, C. H. Reccius, J. D. Gwyer, C. Van Berkel, J. Holloway, D. E. Davies and H. Morgan, Lab Chip, 2009, 9, 2881–2889 RSC.
- C. Van Berkel, J. D. Gwyer, S. Deane, N. Green, J. Holloway, V. Hollis and H. Morgan, Lab Chip, 2011, 11, 1249–1255 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00840k |
| This journal is © The Royal Society of Chemistry 2021 |