Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A correlative method to quantitatively image trace concentrations of elements by combined SIMS-EDX analysis†
Lluís
Yedra
a,
C. N.
Shyam Kumar
 *a,
Alisa
Pshenova
a,
Esther
Lentzen
b,
Patrick
Philipp
a,
Tom
Wirtz
a and
Santhana
Eswara
*a,
Alisa
Pshenova
a,
Esther
Lentzen
b,
Patrick
Philipp
a,
Tom
Wirtz
a and
Santhana
Eswara
 *a
*a
aAdvanced Instrumentation for Ion Nano-Analytics (AINA), MRT Department, Luxembourg Institute of Science and Technology (LIST), 41 rue du Brill, 4422 Belvaux, Luxembourg. E-mail: shyam.chethalaneelakandhan@list.lu; santhana.eswara@list.lu
bMaterials Characterization and Testing Platform (MCTP), MRT Department, Luxembourg Institute of Science and Technology (LIST), 41 rue du Brill, 4422 Belvaux, Luxembourg
First published on 26th November 2020
Abstract
The study demonstrates a new method to quantify Secondary Ion Mass Spectrometry (SIMS) data by using a synergetic combination of Energy Dispersive X-ray spectroscopy (EDX) and SIMS. The novelty of this approach lies in using a diffusion couple to produce a continuum of concentration variation to cover a large portion of the composition space (100 at% to sub-1000 ppm) in a single sample. Furthermore, this approach encompasses the concentration-dependent Relative Sensitivity Factor (RSF) which is essential when the concentrations span several orders of magnitude. By correlating EDX and SIMS profiles, the SIMS signal intensity can be converted to concentrations far below the detection limit of the EDX technique.
Introduction
Analytical characterization of trace elements is fundamental to scientific and technological research in both physical and life sciences. For instance, in semiconductor research, doping enables precise control of the electronic properties.1 In metallurgical research, trace elements are added to induce profound changes in the mechanical and chemical properties of materials.2 Likewise, in life science research, analysis of trace elements is essential in areas such as disease diagnosis and pathological investigations.3 For a comprehensive understanding of the underlying physical and chemical phenomena, it is imperative to determine the concentrations of trace elements quantitatively. Quantifications of trace elements determined globally on bulk samples using techniques such as Inductively Coupled Plasma Mass Spectrometry (ICP-MS) are often inadequate to establish a clear correlation between microstructural features and local concentration of trace elements.Secondary Ion Mass Spectrometry (SIMS) is a well-known characterization technique for high-sensitivity analysis and can be used to image the distribution of even trace elements down to ppm level (if the analysed volume is sufficiently high).4–7 Because of the high sensitivity, SIMS is widely accepted in different fields of research for the precise detection and quantification of different elements.6–8 Commercial state-of-the-art instruments can reach lateral resolutions ∼50 nm, which is primarily limited by the probe size of the primary beam. While higher concentrations are required to define the lateral resolution, the detection limit for small pixel sizes can be still quite low. For instance, a detection limit of 6 ppm (all fractional concentrations discussed in the manuscript are atoms/atom) with a pixel size of 39 nm has been reported for imaging boron dopants in silicon.9 Recently developed correlative approach with SIMS system coupled to the helium ion microscope showed an improved lateral resolution around 15 nm.8 It should be noted that there is a fundamental trade-off between lateral resolution and sensitivity because of the finite number of atoms per voxel. This makes high-resolution imaging of trace elements distribution particularly challenging.10 While SIMS is well known as a powerful high-sensitivity technique, a major limitation is that the quantification of the elemental composition is not straight forward and time consuming, mainly due to matrix effect, i.e. large variations in the ionization yields as a function of matrix composition. Typical strategies for quantification is the use of reference samples.9,11 Though the reference sample approach is a widely used method, only discrete data points in the composition space are covered and often the concentration range is narrow.11
Energy Dispersive X-ray spectroscopy (EDX) is an ubiquitous technique and can be used to quantify elemental concentrations, but the sensitivity of the technique is not adequate to detect concentrations <0.1 at%.12 Hence, the strengths and weakness of the EDX and SIMS techniques are complementary to each other. Indeed, the benefits of combining SIMS and EDX have been already recognized.13–15 As an example, Lorinčík et al.15 quantified dopant concentration profile across an optical fibre by linear extrapolation of EDX and SIMS correlation. In that method, first the concentration of an element is quantified on a location containing sufficiently high amounts by EDX analysis. Then SIMS is carried out on the same location. Subsequently, the SIMS signal ratio of the dopant element with respect to the matrix element is evaluated and correlated to the EDX quantification of that element. The linear conversion factor thus obtained is applied to quantify the SIMS signal. This method is relatively simple to apply, but there are a number of limitations: (i) the implicit assumption that the secondary ion signal varies linearly as a function of concentration is not valid in most cases due to matrix effect, especially when the concentration changes by orders of magnitude and (ii) the difference in the probed volumes between EDX (μm3 scale) and SIMS (nm3 scale) should be taken into account in extrapolating the concentration. Another approach was shown by Kudriavtsev et al.13 in which they demonstrated the use of EDX as a standard less internal calibration tool for SIMS quantification with the example of a mineral sample.14 Briefly, that method is based on experimentally measuring the Relative Sensitivity Factors (RSF) of the major elements by combining EDX and SIMS results and subsequently extrapolating the RSF for the minor and trace elements, detected as positive ions, as a function of their ionization potentials. The extrapolated RSF is then used to quantify SIMS results of the minor and trace elements and accuracies within a factor of 2 were reported for most of the elements analysed. The inherent limitations of this method is that the sample needs to contain elements in significant concentrations and distributed homogeneously. Moreover, that method assumes RSF is independent of concentration.
The present study demonstrates a new method to quantify SIMS data by using a synergetic combination of EDX and SIMS. The novelty of this approach lies in using a diffusion couple to produce a continuum of concentration variation to cover a large portion of the composition space, spanning 3–4 orders of magnitude (100 at% to sub-1000 ppm) in a single sample. Furthermore, this approach encompasses the concentration-dependent RSF which is essential when the concentrations span several orders of magnitude. By extrapolating the correlation between the EDX and SIMS profiles, the SIMS signal intensity can be converted to concentration far below the detection limit of the EDX technique. Here, we present the concept and demonstrate the method in Cu–Ni alloy system. The advantages and limitations of this combinatorial method are discussed in detail. Apart from this, the correlative approach enabled to understand the increased Ni SIMS intensity observed over a concentration range along the Cu–Ni interface. We believe that the present approach will contribute towards future realization of quantitative chemical imaging of trace elements in materials.
Experimental
High purity copper (99.95%) and nickel (99.98%) metal sheets were acquired from MaTecK GmbH (Germany). Due to the complete solubility of Cu and Ni in each other, the concentration decay is continuous and without the formation of any intermetallic phases. The method is however not limited to systems with complete solubility as intermetallic phases can also be used to form the original samples. For the study, smaller pieces measuring 5 × 10 mm were cut from the larges plates using a diamond wire saw. The bimetallic couples were formed placing the largest faces of the freshly cut Cu and Ni pieces together and they were held with a metallic clamp. Two sets of samples were heated to 900 °C for six hours, which allows for interdiffusion in the tens of micrometre range.16,17 The first set of samples was heated in a furnace at ambient pressure and was used to study the regions away from the interface region with low concentrations of nickel. The second set of samples used to study the interface region was heated in a high-vacuum furnace to ensure minimal oxidation. The samples were let to cool down at room temperature prior to mounting in conducting resin (Struers PolyFast). The samples were polished perpendicular to the interface so that the outer layer of oxide was removed, until a mirror-flat surface was achieved to avoid any topography effects in the results.Using an optical microscope the sample that showed the highest contact area between the two metals was selected for further analyses. Scanning Electron Microscopy (SEM) and Energy Dispersive X-ray spectroscopy (EDX) analyses were performed in a Hitachi SU-70 SEM attached with an Oxford Instruments X-Max EDX detector. Two EDX linescans were acquired with the SEM set to 20 kV acceleration voltage. The proportions of Ni and Cu in the interface region were calculated as a linear combination of the spectra of pure Ni and Cu using multiple linear least-squares (MLLS) fitting.
Elemental mapping by SIMS was performed on a Cameca NanoSIMS 50 instrument on exactly the same area as SEM-EDX linescans. NanoSIMS 50 has the ability to work with Cs+ and O− primary ions for detecting negative and positive secondary ions respectively. As Cu and Ni ionize more efficiently as positive ions, the O− primary ion source provides better sensitivity and was therefore chosen for our analyses. The SIMS mapping was carried out starting from the Cu–Ni interface and moving further away into bulk Cu until the local concentration of Ni was below the SIMS detection limit. The SIMS line profiles were obtained using the line scan beam control mode in the instrument (i.e. not extracted from images post-acquisition) in which the primary ion beam is rastered along a single line in a chosen direction. The secondary ions detected were 58Ni+ (57.94 amu) and 63Cu+ (62.93 amu) acquired simultaneously in multicollection mode. The natural isotopic abundances of 58Ni and 63Cu are 68.08%, and 69.2% respectively. The impact energy of the primary ions was 16 keV and the primary ion current on the sample was 35 pA. Images of (20 × 20) μm2 were recorded in a pixel format of 256 × 256 image points with a counting time of 30 ms per pixel. For the subsequent matrix effect studies, images of (60 × 60) μm2 were recorded in a pixel format of 256 × 256 image points with a counting time of 30 ms per pixel. The impact energy of the primary ions used was 16 keV and the primary ion current on the sample was 10 pA.
Copper signal was used for stitching the SIMS images from the serial acquisition because of the higher contrast observed. On areas where two images overlap, only the information from the first acquired image was kept, thus resulting in a stitched image with intensities avoiding bottom of craters of previous analyses. The spatial coincidence of SIMS and EDX is of vital importance for the outcome of the quantification. The features in the stitched Cu image are used for precise correlation with the SE image and EDX is acquired at the same region where SIMS was carried out.
Quantification combining EDX and SIMS
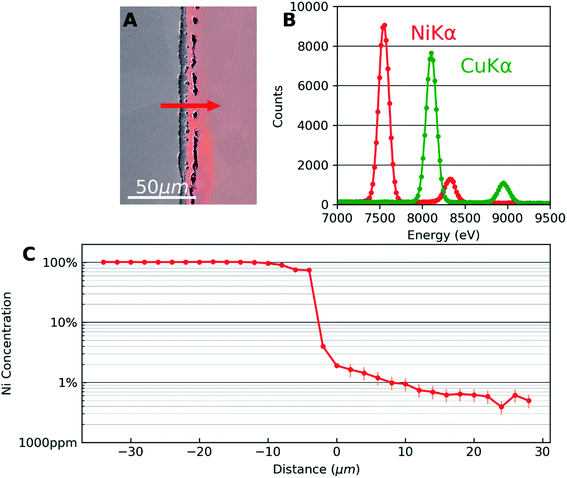
Fig. 1 shows the results of SEM-EDX analysis. Fig. 1(A) is an SEM secondary electron image superposed with an optical image of the same area to highlight the Cu side of the diffusion couple. The interface microstructure is visible with series of pores in the copper side. This is due to the faster diffusion of Cu in Ni than that of Ni in Cu which results in the well-known Kirkendall voids.18 The appearance of these voids is a good indicator that diffusion has taken place. Also, they were used as markers for locating the same areas of interest in different characterization techniques.Fig. 1(B) corresponds to the EDX spectra obtained away from the interface which are used as reference for Ni and Cu to deconvolute spectra from the interface region. The Kα and Kβ peaks of Cu and Ni are at the expected energies of the spectrum. A significant overlap of Cu Kα and Ni Kβ can be observed. Automatic standardless quantification failed for the low concentrations, even if the peaks were still visible. Therefore, multiple linear least squares (MLLS) fitting was performed on the data using the spectra of the two pure elements acquired far away from the interface as standards. In this approach, the measured intensities from pure elements are taken as the reference. This measured intensity is compared with the data to be quantified which is acquired under the same experimental condition as the reference thus taking into account detector efficiency, beam energy and dose.
Fig. 1(C) shows the concentration profile of Ni across the Cu–Ni interface taken along the line indicated by an arrow in Fig. 1(A). The quantification was done using the MLLS method. EDX analysis was carried out in the form of spectrum lines across the interface, avoiding pores in the interface material and copper. The spectrum lines spanned the two metals and showed that the third material formed between the metals was nickel oxide (Ni0.46O0.54, with Cu < 1%). The presence of the diffused elements in the matrix metals can be confirmed, decreasing rapidly in the first micrometres to the detection limit of the EDX technique. In the semi-log EDX profile of Ni in the Cu, a linear decay is seen from the first few micrometres from the interface until the concentration of 0.6 at% Ni is reached. A linear fit was calculated which can be expressed as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = −3.1 × 10−2x − 1.73, where log
C = −3.1 × 10−2x − 1.73, where log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C is the decimal logarithm of the concentration of Ni in Cu and x is the diffusion distance in micrometres from an arbitrary point in the sample. EDX error is set to 25%, according to previous quantitative study on the accuracy of EDX for trace element at very low concentrations.19
C is the decimal logarithm of the concentration of Ni in Cu and x is the diffusion distance in micrometres from an arbitrary point in the sample. EDX error is set to 25%, according to previous quantitative study on the accuracy of EDX for trace element at very low concentrations.19
The concentration profile seen in Fig. 1(C) is consistent with typical diffusion profiles seen in binary alloys with complete solid solubility. EDX thus gives quantitative information about the concentration. However, note that the EDX profile reaches the limit of detection around 0.6 at% in this case. Although the sensitivity could be slightly improved if larger solid angle of X-ray emission is covered by the EDX detector, the sensitivity of the technique is fundamentally limited by the Bremsstrahlung effect. Therefore, to quantify trace concentrations beyond the EDX detection limit, we combine results from SIMS analysis from exactly the same area.
The results of the SIMS analysis are shown in Fig. 2. The area investigated by SIMS is marked by a white box on Fig. 2(A). Signals for the most abundant isotopes of nickel (58Ni) and copper (63Cu) was acquired simultaneously. SIMS images were acquired starting from the interface area and progressively away from the interface until the Ni signal in Cu reached the noise level. Three partially overlapping square images (20 × 20 μm2) obtained were aligned side-by-side to obtain the rectangular images (48 × 20 μm2). These cover the full distance of diffusion length as shown in Fig. 2(B) and (C). The two edges of the overlapped images are noticeable as two vertical lines near the centre in Fig. 2(B). The subsequent analysis is performed using these composite images.
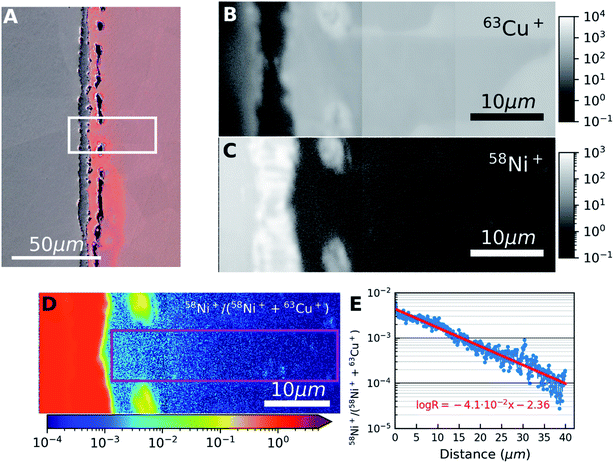 | ||
| Fig. 2 (A) Same as Fig. 1(A) but with the area used for SIMS acquisition outlined. (B and C) Montage SIMS images of 63Cu+ and 58Ni+ obtained by post-acquisition alignment of three overlapping images placed side-by-side with logarithmic intensity scales. (D) SIMS ratio image 58Ni+/(58Ni++63Cu+) obtained from (B and C). The colour bar indicates SIMS ratio values. (E) SIMS ratio plot (from D) obtained by vertically averaging the values in the pink rectangle in (D). The red line shows a linear fit of the data in the semi-log plot. | ||
The grain boundary contrast visible in the far-right side of Fig. 2(B) shows that the grain sizes are relatively large. This contrast arises due to crystal orientation dependent anisotropy in the sputtering rate. We can overcome this limitation by evaluating the relative signal intensities rather than the absolute signal intensities and hence, 58Ni+/(58Ni++63Cu+) ratio image was obtained as shown in Fig. 2(D).
An intensity profile taken along the diffusion direction of the ratio image is shown in Fig. 2(E). The intensity ratio profile was obtained by averaging 100 pixels (∼7.8 μm) in the direction perpendicular to the diffusive flux as shown by the rectangle in Fig. 2(D). The ratios were calculated from the three images separately and only the measurement obtained in the first acquisition was retained for the overlapped areas. In this semi-log plot, the linear fit (in red) shows how the concentration of Ni decays exponentially in Cu. The linear fit of the SIMS data was measured to be represented as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = −4.1 × 10−2x − 2.36, where log
R = −4.1 × 10−2x − 2.36, where log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R is the decimal logarithm of the ratio between 58Ni+ and 63Cu+. The goodness of fit is around 91%. Comparing Fig. 1(C) and 2(E), it can be seen that SIMS has captured Ni signal in Cu further away from the interface than the EDX technique. This is due to the higher sensitivity of the SIMS technique.
R is the decimal logarithm of the ratio between 58Ni+ and 63Cu+. The goodness of fit is around 91%. Comparing Fig. 1(C) and 2(E), it can be seen that SIMS has captured Ni signal in Cu further away from the interface than the EDX technique. This is due to the higher sensitivity of the SIMS technique.
One of the challenges involved in combining EDX and SIMS is the difference in information depths in both techniques, which can be clearly seen in the simulations given in the ESI.† The current method described here overcomes this because of the fact that the diffusive flux is not depth dependent in the diffusion couple. After the annealing treatment, the sample was embedded in a resin and polished to mirror finish thereby removing the material altered by fast surface diffusion. Hence, in our approach the concentration of Ni is essentially depth invariant. In this way we overcome the issues related to the difference in information depth between EDX and SIMS techniques.
Fig. 3 combines the concentration profile of Ni obtained from EDX (Fig. 1(C)) and the 58Ni+/(58Ni++63Cu+) SIMS ratio profile (Fig. 2(E)). The two Y axes (the EDX concentration profiles, indicated by red dots and the black axis and the 58Ni+/(58Ni++63Cu+) SIMS ratio profile, indicated by blue dots and blue axis) is plotted against the x axis representing the distance from the interface. The reference marks in the SEM and SIMS images are used to precisely overlay the two profiles. The figure consists of 3 regions indicated by the three colours. The top part (indicated by the rose colour) represents the region with high concentration of nickel and there is no correlation between the EDX data and the SIMS data in this region. The next region is represented in green colour. This region represents the area where both EDX data and SIMS data is acquired. As mentioned previously, the correlation is carried out by the reference marks in the SEM and SIMS images. SIMS data points correspond to the mean of 11 points around the EDX analysis point and their error bar (horizontal) to the standard deviation as shown in the inset in Fig. 3. Using the data from this region, the SIMS intensity is correlated to the nickel concentration. This correlation can be observed in the inset image, where the EDX data is plotted against the SIMS intensity represented by the same green colour. Nickel concentration and the SIMS ratio follows a linear relationship in this log–log plot and the SIMS intensity is calibrated for the concentration range represented by the green colour. Now this linear relationship between the EDX concentration and the SIMS intensity is extrapolated down to 1000 ppm as indicated by blue colour in the inset image. This region can be observed in the main image represented also by the blue colour. The linear fit between the EDX concentration and SIMS intensity is represented by the teal dashed line in the main image. As both profiles decrease linearly, the quantification from EDX can be extended via SIMS to concentrations below the limit of detection of EDX. As shown in Fig. 3, the limit of detection of the EDX profile seen around 0.6 at% indicated by a horizontal red line. However, the extrapolated SIMS results extend beyond that, down to about 1000 ppm indicated by a horizontal blue line. The experimentally calibrated region with the error bar in the inset shows a linear relationship. Considering the noise in the data for low concentration SIMS data points, a linear extrapolation will be a first order approximation. With the correlation of EDX and SIMS profiles shown in Fig. 3, the SIMS intensity ratio can be converted into concentration. Taking into account the uncertainties of both EDX and SIMS original data and linear fits, we can estimate the calibration uncertainty to be dominated by EDX. However, in the extrapolated region, the scatter in the data shows that the conversion to concentration is within 50% relative error.
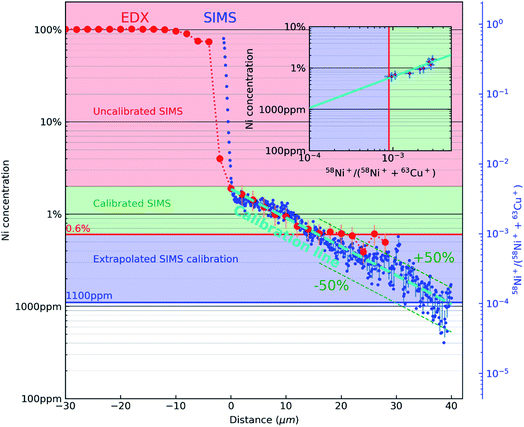 | ||
| Fig. 3 A semi-log plot correlating the concentration profile of Ni obtained from EDX (Fig. 1(C)) and the 58Ni+/(58Ni++63Cu+) SIMS ratio profile (Fig. 2(E)). EDX concentration profile is represented by red dots and black ordinate axis. 58Ni+/(58Ni++63Cu+) SIMS ratio profile is represented by blue dots and blue ordinate axis. The rose coloured region in the figure represent the region from 100% Ni until the interface where there is no experimental correlation between the EDX concentration and SIMS intensity. The green region shows the area where the SIMS intensity ratio is directly correlated with the EDX concentration. This experimentally determined relationship between Ni concentration and the 58Ni+/(58Ni++63Cu+) SIMS is shown in the inset (green colour region). The error bars in the inset are for SIMS (horizontal) and EDX (vertical) respectively. The blue region show the concentration range below the detection limit of EDX were the relationship between the EDX concentration and the SIMS intensity is extrapolated down to 1000 ppm (teal dashed line). The limits of detection of both datasets are displayed with a red horizontal line (EDX) and a blue horizontal line (SIMS, from the extrapolation). | ||
In this context, it is also interesting to note an additional outcome of the method. The SIMS intensities can be related to concentration through Relative Sensitivity Factor (RSF) as given by the following equation: 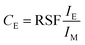 where CE is the concentration of element E while IE and IM are the SIMS intensities of element E and the matrix element M respectively. By comparing the above equation with the plot shown as an inset in Fig. 3, we see that the local slope of the line gives the RSF for a given concentration of Ni in Cu. Furthermore, as the SIMS ratio for concentrations lower than the investigated range is not expected to be affected by matrix effect, any smaller ratio can also be converted to concentration by the extrapolated RSF20–22 In this way, the approach of combining EDX and SIMS through diffusion profiles offers a simple and rapid way to investigate how RSF evolves with concentration over a few orders of magnitude.
where CE is the concentration of element E while IE and IM are the SIMS intensities of element E and the matrix element M respectively. By comparing the above equation with the plot shown as an inset in Fig. 3, we see that the local slope of the line gives the RSF for a given concentration of Ni in Cu. Furthermore, as the SIMS ratio for concentrations lower than the investigated range is not expected to be affected by matrix effect, any smaller ratio can also be converted to concentration by the extrapolated RSF20–22 In this way, the approach of combining EDX and SIMS through diffusion profiles offers a simple and rapid way to investigate how RSF evolves with concentration over a few orders of magnitude.
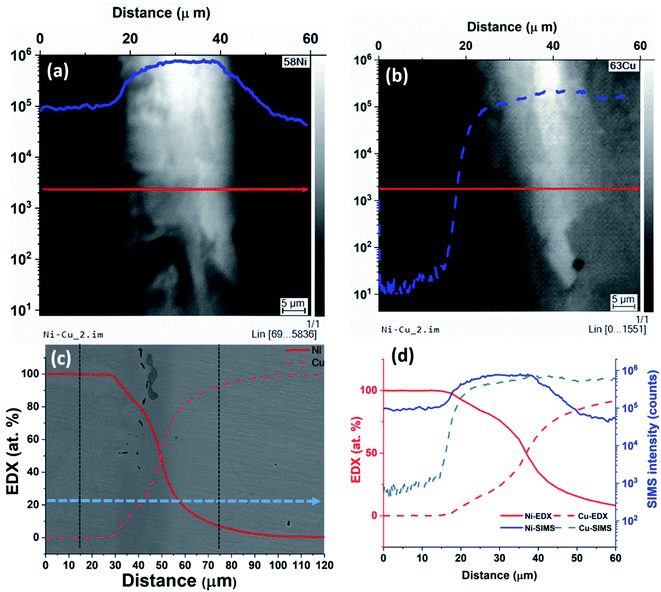
From the results, we can observe that at lower concentrations, SIMS intensity has a linear relation with the concentration and by combining EDX and SIMS we can precisely detect concentrations below the detection limit of the EDX. At higher concentrations, there is a deviation from the linear trend as shown in Fig. 3. To understand the behavior for higher concentrations, an analysis was carried out at the Cu–Ni interface on a sample with continuous interface. The sample for this study is from the second set of samples that were heat-treated in a high vacuum furnace to minimize oxidation effects. SIMS images of 58Ni+ and 63Cu+ are given in Fig. 4(a) and (b) respectively. The left hand side in the image is the nickel region and the right hand side is the copper region. From Fig. 4(a) and (b), we can see that the Ni signal intensity is increasing about an order of magnitude near the interface and decreasing away from the interface. Fig. 4(c) shows the EDX analysis (overlaid on SE image) carried out from the nickel region across the interface towards the copper region as indicated by an arrow in Fig. 4(c). In the case of EDX analysis, the concentration changes gradually for both nickel and copper across the interface as expected from Fick's law of diffusion. Fig. 4(d) gives the SIMS profiles aligned and correlated with the EDX profiles across the Cu–Ni interface. The first point of increase in the Cu signal is taken as a reference to align the EDX and SIMS data.
In the interface region, EDX data shows a continuous concentration profile for both nickel and copper. For SIMS intensity, when moving from nickel to copper, the nickel signal shows first an increase in intensity in the interface region, and starts decreasing only after about 20 μm when reaching the bulk copper. For copper, when moving from nickel towards copper and when getting closer to the interface region (i.e. at 20 μm), the SIMS intensity increases much faster than what could be expected from the EDX data. This clearly indicates the presence of a matrix effect, although the sample was prepared under high vacuum to avoid any oxidation. The EDX data shows also no oxygen, so that the sample handling between the EDX and SIMS measurements, and/or the experimental conditions for SIMS must have produced the matrix effect. The exact cause needs further investigation. Additionally, minor contributions can come from sputtering yield variation that can arise from non-uniform density. This artefact limits the applicability of the SIMS-EDX correlation method in the higher concentration range closer to the interface. This is nevertheless not a major restriction as there are other techniques including EDX by itself that can provide concentrations directly for the high concentration range. Thus, the present SIMS-EDX correlative method is demonstrated to work even in imaging mode, although only for lower concentrations where other methods fail.
In summary, it is demonstrated that the diffusion couple approach to combine EDX and SIMS results in a simple yet powerful method to quantify SIMS data for concentrations below the detection limit of EDX. The combined EDX-SIMS method offers the possibility to quantify trace concentrations down to the detection limit of SIMS. With the ability to convert SIMS intensity to concentration, alloy microstructures with inhomogeneous elemental distribution can be quantitatively mapped down to trace concentration. The method is demonstrated using Cu–Ni system as an example. The same approach can be applied to any other material systems even in cases where intermetallic compounds form.
Conclusions
A method to quantitatively map low concentrations of elements by combining EDX and SIMS is demonstrated. A concentration profile of Ni in Cu is obtained by EDX until the detection method of that technique is reached and SIMS images were obtained at the exact same location. By superposing EDX concentration profile and the SIMS ratio line profile, the two techniques can be correlated. As the concentration profile in diffusion couples (excluding surface effects) is depth invariant within a grain, the diffusion couple approach allows direct correlation of EDX and SIMS profiles. With this method Ni concentrations 10 times below the EDX detection limit were quantified. Furthermore, the relationship between Ni concentration and the 58Ni+/(58Ni++63Cu+) SIMS ratio was obtained from which the RSF can be determined. For elements showing strong matrix effects, the change in RSF as a function of concentration can be directly obtained using the simple and effective method described here. This novel method, here demonstrated for binary alloys, is promising for more complex matrices, where verification remains to be performed.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was funded by the Luxembourg National Research Fund (FNR) by the grants INTER/SNF/16/11536628 (NACHOS) and C13/MS/5951975 (LowZ-PIES).References
- S. C. Erwin, L. Zu, M. I. Haftel, A. L. Efros, T. A. Kennedy and D. J. Norris, Nature, 2005, 436, 91–94 CrossRef CAS.
- L. Jiang, J. K. Li, P. M. Cheng, G. Liu, R. H. Wang, B. A. Chen, J. Y. Zhang, J. Sun, M. X. Yang and G. Yang, Sci. Rep., 2015, 4, 3605 CrossRef.
- A. Biesemeier, O. Eibl, S. Eswara, J.-N. Audinot, T. Wirtz, G. Pezzoli, F. A. Zucca, L. Zecca and U. Schraermeyer, J. Neurochem., 2016, 138, 339–353 CrossRef CAS.
- P. Hoppe, S. Cohen and A. Meibom, Geostand. Geoanal. Res., 2013, 37, 111–154 CrossRef CAS.
- P. Kumar, M. Pfeffer, B. Willsch, O. Eibl, L. Yedra, S. Eswara, J.-N. Audinot and T. Wirtz, Sol. Energy Mater. Sol. Cells, 2017, 160, 398–409 CrossRef CAS.
- J. N. Audinot, S. Schneider, M. Yegles, P. Hallegot, R. Wennig and H. N. Migeon, Appl. Surf. Sci., 2004, 231–232, 490–496 CrossRef CAS.
- T. Long, S. W. J. Clement, H. Xie and D. Liu, Int. J. Mass Spectrom., 2020, 450, 116289 CrossRef CAS.
- T. Wirtz, O. De Castro, J.-N. Audinot and P. Philipp, Annu. Rev. Anal. Chem., 2019, 12, 523–543 CrossRef CAS.
- S. Eswara, A. Pshenova, E. Lentzen, G. Nogay, M. Lehmann, A. Ingenito, Q. Jeangros, F.-J. Haug, N. Valle, P. Philipp, A. Hessler-Wyser and T. Wirtz, MRS Commun., 2019, 9, 916–923 CrossRef CAS.
- T. Wirtz, P. Philipp, J. N. Audinot, D. Dowsett and S. Eswara, Nanotechnology, 2015, 26, 434001 CrossRef CAS.
- N. Valle, J. Drillet, O. Bouaziz and H.-N. Migeon, Appl. Surf. Sci., 2006, 252, 7051–7053 CrossRef CAS.
- D. B. Williams and C. B. Carter, The Transmission Electron Microscope, Springer, US, Boston, MA, 2009 Search PubMed.
- Y. Kudriavtsev and R. Asomoza, Surf. Interface Anal., 2013, 45, 506–509 CrossRef CAS.
- Y. Kudriavtsev, S. Gallardo, M. Avendaño, G. Ramírez, R. Asomoza, L. Manzanilla and L. Beramendi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 343, 153–157 CrossRef CAS.
- J. Lorinčík, I. Kašík, J. Vaniš, L. Sedláček and J. Dluhoš, Surf. Interface Anal., 2014, 46, 238–240 CrossRef.
- M. Reda Chellali, Z. Balogh and G. Schmitz, Ultramicroscopy, 2013, 132, 164–170 CrossRef CAS.
- Z. Wang, L. Fang, I. Cotton and R. Freer, Mater. Sci. Eng., B, 2015, 198, 86–94 CrossRef CAS.
- A. Paul, T. Laurila, V. Vuorinen and S. V. Divinski, Thermodynamics, Diffusion and the Kirkendall Effect in Solids, Springer International Publishing, Cham, 2014 Search PubMed.
- D. E. Newbury and N. W. M. Ritchie, J. Mater. Sci., 2015, 50, 493–518 CrossRef CAS.
- H. W. Benninghoven, A. Rudenauer and F. G. Werner, Secondary ion mass spectrometry: basic concepts, instrumental aspects, applications and trends, Wiley, New York, 1987 Search PubMed.
- N. Valle, J. Drillet, O. Bouaziz and H. N. Migeon, Appl. Surf. Sci., 2006, 252, 7051–7053 CrossRef CAS.
- C. Gu, Materials Science And Engineering, PhD thesis, North Carolina State University, 2009.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00289e |
| This journal is © The Royal Society of Chemistry 2021 |