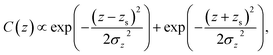Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Variability of physical meteorology in urban areas at different scales: implications for air quality
Denise
Hertwig
 a,
Sue
Grimmond
a,
Sue
Grimmond
 *a,
Simone
Kotthaus
*a,
Simone
Kotthaus
 b,
Christina
Vanderwel
b,
Christina
Vanderwel
 c,
Hannah
Gough
c,
Hannah
Gough
 a,
Martial
Haeffelin
a,
Martial
Haeffelin
 b and
Alan
Robins
d
b and
Alan
Robins
d
aDepartment of Meteorology, University of Reading, Reading, RG6 6ET, UK. E-mail: C.S.Grimmond@reading.ac.uk
bInstitut Pierre Simon Laplace (IPSL), CNRS, École Polytechnique, Institut Polytechnique de Paris, 91128 Palaiseau Cedex, France
cAerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton, SO17 1BJ, UK
dEnFlo, Department of Mechanical Engineering Sciences, University of Surrey, Guildford, GU2 7XH, UK
First published on 13th August 2020
Abstract
Air quality in cities is influenced not only by emissions and chemical transformations but also by the physical state of the atmosphere which varies both temporally and spatially. Increasingly, tall buildings (TB) are common features of the urban landscape, yet their impact on urban air flow and dispersion is not well understood, and their effects are not appropriately captured in parameterisation schemes. Here, hardware models of areas within two global mega-cities (London and Beijing) are used to analyse the impact of TB on flow and transport in isolated and cluster settings. Results show that TB generate strong updrafts and downdrafts that affect street-level flow fields. Velocity differences do not decay monotonically with distance from the TB, especially in the near-wake region where the flow is characterised by recirculating winds and jets. Lateral distance from an isolated TB centreline is crucial, and flow is still strongly impacted at longitudinal distances of several TB heights. Evaluation of a wake-flow scheme (ADMS–Build) in the isolated TB case indicates important characteristics are not captured. There is better agreement for a slender, shorter TB than a taller non-cuboidal TB. Better prediction of flow occurs horizontally further away and vertically further from the surface. TB clusters modify the shape of pollutant plumes. Strong updrafts generated by the overlapping wakes of TB clusters lift pollutants out of the canopy, causing a much deeper tracer plume in the lee of the cluster, and an elevated plume centreline with maximum concentrations around the TB mean height. Enhanced vertical spread of the pollutants in the near-wake of the cluster results in overall lower maximum concentrations, but higher concentrations above the mean TB height. These results have important implications for interpreting observations in areas with TB. Using real world ceilometer observations in two mega-cities (Beijing and Paris), we assess the diurnal seasonal variability of the urban boundary layer and evaluate a mixed layer height (MLH) empirical model with parameters derived from a third mega-city (London). The MLH model works well in central Beijing but less well in suburban Paris. The variability of the physical meteorology across different vertical scales discussed in this paper provides additional context for interpreting air quality observations.
1. Introduction
Air quality in cities is impacted not only by emissions and chemical transformations but also by the physical state of the atmosphere. In this paper we focus on the latter, particularly considering the impacts of tall buildings (TB). We consider both isolated tall buildings, which are common in Europe, and clusters of tall buildings, which occur more frequently in Asia and the Americas.Critical in our consideration is the vertical spatial structure of the urban atmosphere. We identify three scales with the following horizontal and vertical dimensions1–3 (Fig. 1):
 | ||
| Fig. 1 Schematic of key urban climate scales. These vary with height of the roughness elements (H) and their spacing (W), the order of magnitude of the vertical extent and two proxy methods to determine the inertial sub-layer (ISL). UCL – urban canopy layer, RSL – roughness sub-layer, SL – surface layer, UBL – urban boundary layer (note: not to scale). Inset (bottom) shows street-scale and tall-building flow regimes.37 | ||
(1) Micro-scale – buildings to streets impact the urban canopy layer (UCL) and the roughness sub-layer (RSL).
(2) Local-scale – neighbourhoods (areas with common repeated characteristics, e.g. low density residential, high density commercial) influence the inertial sub-layer (ISL) or constant flux layer above the RSL.
(3) Meso-scale – a city impacts the urban boundary layer (UBL), the depth of which changes with both time of day and season.
Flow, turbulence and dispersion vary rapidly in three dimensions based on the positioning of individual roughness elements (RE; e.g. buildings, trees) in the UCL–RSL.4 The UCL extends to the heights of the RE, but the vertical extent of the RSL varies with both the RE heights (mean, maximum, variability) and the spacing between them5–9 (Fig. 1, purple equations). The UCL, RSL and ISL combine to make the surface layer (SL), or lowest ∼10% of the UBL (Fig. 1).
Observations and modelling within cities need to consider this structure of the urban atmosphere. Basic micrometeorological theory is developed for the ISL. For example, the logarithmic wind profile and the Monin–Obukhov similarity theory both apply in the ISL but not within the UCL–RSL.2,10 Thus, our understanding and the ability to predict the transport close to the surface (UCL + RSL) is poor. As bluff body RE (e.g. buildings) are not porous, unlike trees, they can channel flow within the UCL and influence building ventilation.11,12 To enhance our theoretical understanding of processes and/or to undertake numerical predictions we typically simplify the urban form to capture what are thought to be the most relevant features.4,13,14 For example, buildings may be treated as having smooth walls,15 rather than accounting for variations caused by the presence of windows, doors, balconies (etc.) or even non-cuboid shapes.16 Similarly, buildings may be treated as having flat roofs that are all of the same height13,17 rather than being sloped at different angles and/or of variable heights.16
Given issues of access, observations in the real world are often undertaken in the UCL. These micro-scale measurements are challenging to interpret and generalise because small changes in sensor location can result in large changes in the observed flow and radiative characteristics because of the three-dimensional scaling well below the typical RE height.2,15,18,19
Undertaking measurements in the ISL, above the RSL (Fig. 1), becomes more representative (theoretically) because of the blended response from the surface so that individual micro-scale features no longer dominate, and the net transport is referred to as having one-dimensional scaling in extensive homogeneous areas. With sufficient homogeneous fetch, it is possible to use the eddy covariance technique to directly measure momentum, heat and mass fluxes.18 Urban land surface models are ideally evaluated using observations in the ISL.20,21 The patchwork of neighbourhoods across a city create the UBL. Despite its importance to pollutant concentrations and hence air quality, there are few continuous observations of the UBL.
In this paper we explore the impacts of tall buildings on the urban atmosphere across these three scales (UCL + RSL, ISL, UBL) using observations undertaken in a wind tunnel, a water flume and in the real world. The advection and diffusion of pollutants in urban environments is governed by complex, building-induced wind fields (Fig. 1). Combined effects of channelled or recirculating flow in street canyons, flow branching at intersections and the turbulent vertical exchange at roof-level between the urban canopy and the boundary layer, contribute to the strong spatio-temporal variability of street-level concentrations and local human exposure levels.22,23
Operational urban dispersion and air quality models need to parameterise building-induced dispersion features, as individual buildings are not resolved in the simulations. For example, the ADMS–Urban air quality model24 combines a Gaussian plume dispersion approach with the OSPM street canyon model25 to capture effects such as pollutant accumulation in recirculating flow or pollutant channelling through streets. The Lagrangian dispersion model QUIC–plume’s26 built-in flow-solver uses mass-conservation to give 3D building-resolved mean flow fields. SIRANE’s27 street-network approach parameterises dispersion through streets and intersections using bulk advection and vertical exchange velocities per street unit.
Typical operational settings rarely account for building effects down to the street-scale level. Urban applications of the widely used AERMOD28 air quality model or the NAME29 dispersion model, for example, use bulk parameterisations to reflect changes in surface roughness and heat-flux characteristics over cities, but do not model canopy-layer flow effects. Both ADMS–Urban and AERMOD have built-in modules to represent wake-flow effects for individual (isolated) buildings (ADMS–Build,30 AERMOD–PRIME31). However, these modules are not routinely used in the context of urban air quality modelling.
Street-canyon flow parameterisations often assume an equal-height canyon with the building height (H) to street width (W) ratio creating different flow regimes (0.35 ≤ H/W, 0.35 < H/W < 0.65, H/W ≥ 0.65; isolated < wake interference < skimming).2 However, the presence of tall buildings can strongly affect pollutant dispersion characteristics within and above street canyons.32–34 Tall-building wake effects, i.e. modifications of horizontal and vertical advection and diffusion characteristics on the leeward side of the buildings, can be important over large distances and hence can be crucial in urban air quality modelling on and across different spatial scales. However, little is known about the exact nature of flow and pollutant dispersion modifications, especially in the case of clusters of tall buildings. This currently limits the capability of air-quality and emergency-response dispersion models to represent such processes adequately.
In this study, at the micro to local-scale we explore morphologically complex areas in London and Beijing using laboratory observations to assess the effect of isolated tall buildings and tall-building clusters on flow and dispersion fields, respectively.
At the local to city scale we examine the mixed-layer height (MLH) evolution. A simple empirical model, with parameters informed by London observations,35,36 is evaluated using atmospheric profile measurements in Beijing and Paris.
2. Methods
2.1 Study areas
To explore the physical meteorological processes, we use real world observations and hardware models for parts of real cities. Naturally, the latter are simplifications as they do not have all the real-world details. For example, the roofs and walls are flat/smooth rather than sloped/crenulated, there are no anthropogenic heat emissions, nor radiative exchanges. The studies take place in three mega-cities: Beijing, London, and Paris.In Beijing, the observations are taken in a residential-commercial area of the Haidian District between the third and fourth north ring roads. This area, typical of central Beijing, is the urban site (39° 58′ 33′′ N, 116° 22′ 41′′ E) of the Atmospheric Pollution and Human Health in a Chinese Mega-city (APHH-Beijing)38 project. The Institute of Atmospheric Physics (IAP), Chinese Academy of Sciences 325 m meteorological tower is located here.38
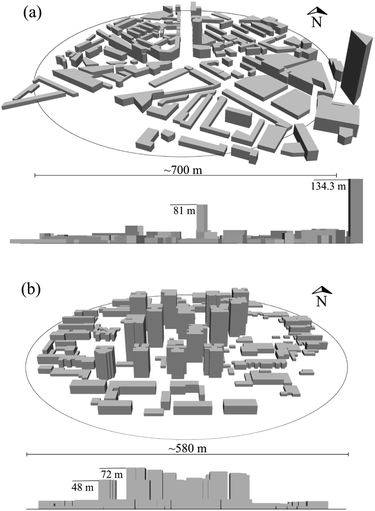
For the local-scale study, a hardware model is built of an area (∼580 m diameter) north of the IAP tower with a cluster of 14 tall buildings surrounded by a low-rise canopy (Fig. 2b). The MLH is determined from an instrument located near the base of the IAP tower.
Similarly, in London the micro-to-local scale processes are studied in a small area within the London Borough of Southwark (Fig. 2a). The hardware model of a ∼700 m diameter region around St George’s Circus (51.4987° N, 0.1048° W) has 148 buildings that are mostly (49%) low-rise residential (building height H ≤ 12 m) and mid-rise (12 to 24 m) office and commercial (39%). Only 17 of the buildings have H > 24 m (3, H > 32 m).
The MLH model coefficients used were derived36 from observations taken in central London, where surface roughness is high.10 The sensor was operated at King’s College London (KCL, 51° 30′ 42.408′′ N, 0° 7′ 0.3066′′ W, 1 January 2011–2 March 2011) and Marylebone Road (MR, 51° 31′ 21.108′′ N, 0° 9′ 16.4376′′ W, 9 March 2011–31 December 2017). The differences in heights above ground-level (agl) of 32.1 m (KCL) and 4 m (MR) are accounted for.
In Paris, only the larger scale MLH analyses are undertaken, using a sensor located at SIRTA (48.713° N and 2.208° E) in a suburban location 20 km south of central Paris.39
2.2 Wind-tunnel experiments of isolated tall buildings
An open-return boundary-layer wind-tunnel (test-section length: 20 m; cross-section: 3.5 m × 1.5 m) was used for flow experiments in a hardware scale model of buildings for the area in south London (Fig. 2a, Section 2.1). The ∼700 m extent of the study domain has two isolated TB with heights of HTB = H81 = 81 m (hereafter: T81) and H134 = 134.3 m (T134) surrounded by low-rise buildings (average H: ∼13.4 m) in a mixed residential-commercial neighbourhood (Fig. 2a). The hardware model is built at a scale of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200. T134 with a triangular footprint is located at the south-eastern edge of the domain (Fig. 2a) and the hexagonal T81 is located close to the model centre. Hence, the flow at T134 is also affected by the roughness transition between the approach-flow and model.40 The depth of the approach-flow internal boundary layer was ∼1 m, i.e. similar to the height of T134.
200. T134 with a triangular footprint is located at the south-eastern edge of the domain (Fig. 2a) and the hexagonal T81 is located close to the model centre. Hence, the flow at T134 is also affected by the roughness transition between the approach-flow and model.40 The depth of the approach-flow internal boundary layer was ∼1 m, i.e. similar to the height of T134.
Point-wise velocity measurements41,42 obtained using a two-component laser Doppler anemometry system,43 are analysed. In each experiment, neutral atmospheric stability conditions (i.e. thermal flow effects are negligible) are used. The wind-tunnel free-stream velocity Uref is steady at 2 m s−1 ±1% in all cases. Experimental design, measurement techniques and uncertainties are available.40 Here we analyse two configurations of the model: (i) Core and (ii) No Tall. In the Core case the hardware model includes both the tall buildings and the low-rise building canopy (Fig. 2a). Whereas in the No Tall case only the low-rise canopy buildings (H < 32 m) are present (i.e. there are no TB).
Analysis of the wind-tunnel observations for these two conditions allows the influence of the presence of the TB to be assessed. The buildings in this case have flat roofs and smooth walls, but are close to the ‘true’ general footprint shape (i.e. not rectangular in cross-section). The street orientations and building arrangements are realistic, but other roughness elements (e.g. trees, bus shelters, lamp posts) are missing. Thus, the model can be regarded as a realistic characterisation of the actual ‘chaotic’ building forms found in a small area of London. The combination of large building scale (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), the tallest building (T134) and wind tunnel dimensions allow profiles throughout the UCL, but it is not possible to undertake measurements well beyond the RSL of the full model.
200), the tallest building (T134) and wind tunnel dimensions allow profiles throughout the UCL, but it is not possible to undertake measurements well beyond the RSL of the full model.
2.3 Water-flume experiments with a cluster of tall buildings
A closed-loop water flume (test-section length: 6.25 m; width: 1.2 m; constant water depth: 0.6 m) with particle image velocimetry (PIV)44 and planar laser-induced florescence (PLIF)45 systems allowed simultaneous velocity and scalar concentration measurements in the Beijing–Haidian hardware model (Fig. 2b, Section 2.1). A two-dimensional measurement plane is illuminated by a 100 mJ Nd:YAG pulsed laser operating at 2 Hz. Two CMOS cameras (4 MP resolution) are used for the PIV flow measurements and one 16 bit sCMOS camera (5.4 MP) for PLIF, both with a shutter speed of 1200 μs. The free-stream velocity Uref is kept at 0.45 m s−1, assuring a constant water flow rate through the flume. No thermal effects are modelled.The dispersion of a passive scalar tracer is determined using an aqueous solution of fluorescent dye (Rhodamine 6G) released 5 mm upstream of the model domain from a 3 mm diameter ground source with a continuous source strength of 500 mm3 s−1. The tracer concentration at the source, Cs, was 0.3 mg l−1. The PLIF calibration procedure and general aspects of measurement uncertainty of the technique are discussed.46
In the ∼580 m extent model domain (Fig. 2b) there is a cluster of 14 tall buildings (maximum/minimum heights: H72 = 72 m/H48 = 48 m) surrounded by a low-rise canopy (typical building heights between 4.8 m and 14.4 m). The hardware model has a more detailed representation of the building cross-section than the London case (Fig. 2bcf.Fig. 2a), but still has flat roofs. Some simplification is required because of the small scale of the models. The two scales used (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2400 and 1
2400 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4800)47 allow analysis of both the RSL and ISL characteristics, but limited detail within the UCL (Fig. 1). The depth of the approach-flow boundary layer is ∼85 mm in the model scale (∼203 m at a scale of 1
4800)47 allow analysis of both the RSL and ISL characteristics, but limited detail within the UCL (Fig. 1). The depth of the approach-flow boundary layer is ∼85 mm in the model scale (∼203 m at a scale of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2400; i.e. ∼3H72).
2400; i.e. ∼3H72).
To investigate the influence of the Beijing TB cluster, multiple model configurations are used: (i) low-rise canopy without the tall-building cluster (Low), (ii) tall-building cluster with low-rise canopy (Tall + Low; Fig. 2b) and tall-building cluster in isolation without the low-rise buildings (Tall).
2.4 ADMS–Build wake model
The ADMS–Build wake model30,48 parameterises the velocity-deficit in the wake of an isolated, cuboidal-shaped building through a 3D extension of the 2D Counihan et al.49 constant eddy-viscosity wake theory. ADMS–Build provides an analytical expression for the flow field in the momentum deficit region of the main building wake (see Hertwig et al.40 eqn 3–5 and Fig. 12).The beginning of the main wake is determined by modelling the extent of the recirculation (cavity) zone that develops on the lee of the building (see inset Fig. 1) as a function of height, crosswind width and along-wind building length. In this case, the inflow to the model (i.e. flow upwind of the building) is based on wind tunnel flow conditions for the case without tall buildings (No Tall). Implementation of the model and further evaluation results are given elsewhere.40
2.5 A simple urban boundary layer height model
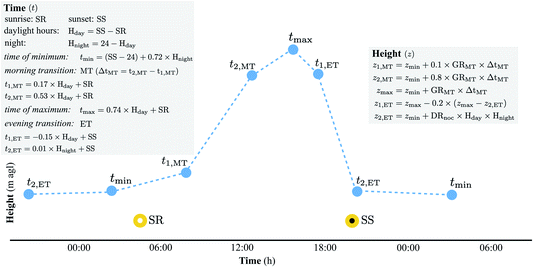
The average MLH is estimated in Beijing and Paris using a simple parameterisation with coefficients derived in London.36 The modelled MLH varies both diurnally and seasonally with differences in cloud cover. The cloud conditions considered are (Table 1): clear nights followed by cumulus clouds during the day (clearCu); same conditions in both the day and night – cloudless (clear), cumulus (Cu) or stratus (St); or when the MLH is below the cloud base height (CBH). Cloud conditions cause variations in minimum MLH (zmin), the morning transition (MT) growth rate (GRMT) and the nocturnal decay rate (DRnoc; Table 1). The MLH above ground level (agl) is approximated by calculations at six key times through the day (Table 1). These times vary with sunrise (SR) and sunset (SS) to identify the timing of minimum and maximum depth of the MLH, and the beginning and end of both the morning and the evening transition periods.Automatic lidar and ceilometer (ALC) measurements of attenuated backscatter allow the mixed layer height to be determined from observations. Here Vaisala CL31 observations are used. A background correction50 is undertaken prior to using the CABAM (characterising the atmospheric boundary layer based on ALC measurements) algorithm.35 The algorithm considers precipitation, cloud cover and cloud type, all obtained from the ALC measurements.
Instruments installed in Beijing,38 very close to the TB cluster (Fig. 2b), and in suburban Paris39 (Section 2.1; https://www.lmd.polytechnique.fr/sirta/mld/) are used to obtain the attenuated backscatter data. The APHH–Beijing38 data available for analysis are from November 2016 to June 2017. Although observations occur in all four seasons, both summer and autumn are incomplete. For Paris, data are analysed for a year (2018).51 During the analysis, the diurnal variability of the MLH is assessed using the median and the interquartile range (IQR). The four seasons are defined by month: winter (DJF, December, January, February), spring (MAM), summer (JJA), and autumn (SON).
3. Results and discussion
3.1 Tall-building wakes and model comparison in London
Prior analyses of tall-building wakes in the London domain40 (Fig. 2a) found wind fields above the low-rise canopy to be impacted for downwind distances of at least 5HTB of the towers. As numerical weather prediction (NWP) models are used to drive dispersion and air quality models, their horizontal resolution is important. With the resolution of next generation NWP models expected to be of the order of 100 m,52 tall-building wakes will span several grid cells.We use a Cartesian coordinate system to present the results. The longitudinal axis (x direction; u velocity component) is aligned with the mean forcing wind direction (i.e. along-wind). The y axis (v velocity) is the lateral (transverse) direction. The z axis (w velocity) indicates the vertical component. Time-averaged velocities (e.g. U) are written in uppercase and are scaled by the free-stream velocity (Uref).
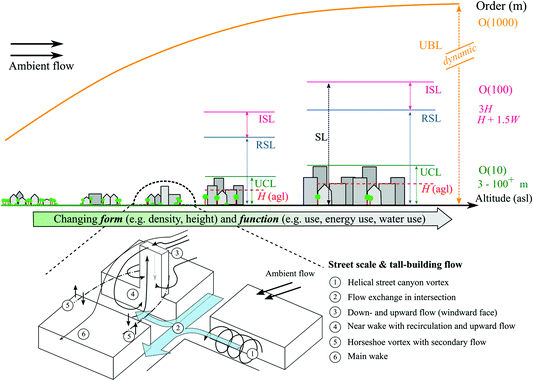
The logarithmic law allows the wind profile to be modelled in the ISL.53 Although not directly applicable within the RSL,10 it is often used above the UCL in air-quality models like ADMS–Urban, SIRANE or QUIC–plume. Analysis of measurements across the Core configuration (Fig. 2a) provides the ensemble mean vertical profiles (z) of the longitudinal (along-wind) velocity (U/Uref) at increasing radial distances (ri) from the TB (Fig. 3). These results show the spatial variability of the flow in the presence of the tall buildings and the extent of wake effects with increasing distance and number of measurement points included in the ensemble average. Ensemble-averaged wind profiles of the No Tall case (i.e. when T81 and T134 are removed) serve as a reference, as the profiles follow the logarithmic law from above the height of the roughness length plus displacement height (z0 + zd). However, for both T81 (Fig. 3a and c) and T134 (Fig. 3b and d) the Core profiles show very noticeable deviations from the logarithmic law for all radii.
 | ||
| Fig. 3 Profiles of mean longitudinal (along-wind) velocity (U/Uref) for the Core configuration of the London wind-tunnel model, which are ensemble averages for increasing distances from the tall building (radii r1 to r8 have increments of 0.5 HTB, colour-coded) plus the domain average across all sites for both Core and No Tall configurations for buildings (a) T81 (wind direction θ = 0°) and (b) T134 (θ = 101°). Logarithmic wind profile (log-law fit) using No Tall data with morphometrically8,40 derived roughness length (z0) and displacement height (zd) is shown. Measurement locations (dots) and radii (arcs) for (c) T81 and (d) T134, with the direct downwind transect in the building wakes (dashed lines) and wind direction of approaching flow (arrows) indicated. | ||
The flow profiles averaged over different radial distances only converge back to the reference state well above roof-level (z = H81) for the slender T81 tower near the model centre. The taller and wider T134 building has a much broader wake,40 with lateral fanning enhanced by the shape and orientation of the tower relative to the south-easterly forcing wind direction (Fig. 3d). The differences from the No Tall reference are enhanced (cf. T81) and remain large even when averaging over all available Core sites (note: no measurements are available above a height of H134).
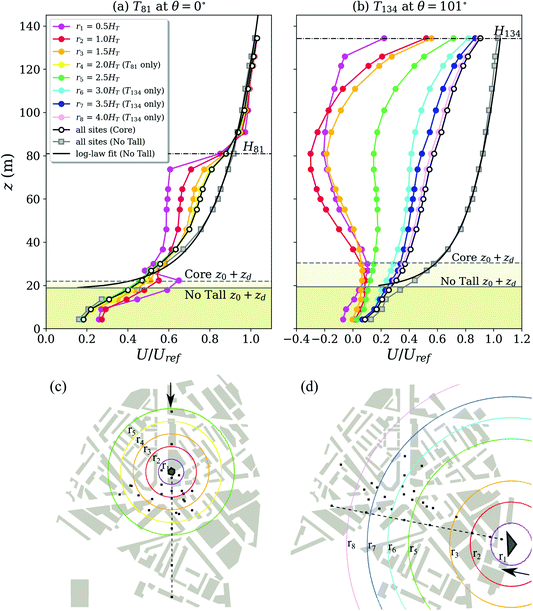
To explore further the impact of the T134 wake (Fig. 3d) velocity differences (Core – No Tall) are analysed for both the mean along-wind velocity (ΔU/Uref; Fig. 4a, c and e) and the mean vertical velocity (ΔW/Uref; Fig. 4b, d and f) without the spatial averaging. The velocity differences are shown as a function of their straight-line distance from the centre of T134 (d/H134), with the lateral displacement of the sites (|y − y134|/H134) from the building centreline (y134) indicated, at three heights: just above the low-rise canopy (z/H134 = 0.27; Fig. 4a and b), at close to half T134 (z/H134 = 0.48; Fig. 4c and d) and near roof-level of T134 (z/H134 = 0.91; Fig. 4e and f).
 | ||
| Fig. 4 Difference between Core and No Tall cases of the London model for the mean (a, c and e) longitudinal velocity (ΔU/Uref) and (b, d and f) vertical velocity (ΔW/Uref) as a function of straight-line distance (d/H134) from the centre of building T134 (south-east approach flow) at three heights z/H134 (a, b) 0.27, (c, d) 0.48 and (e, f) 0.91. Lateral displacement of the measurement points (|y − y134|/H134, colour) from the centreline of T134 (y134; dashed line, Fig. 2d) indicated: along the T134 centreline (◊), off the centreline (○) and affected by the wake of building T81 (△). | ||
The strongest impact on the flow is measured directly behind the building, with a velocity deficit ΔU of up to ∼1.2 times the reference velocity Uref (Fig. 4c) and residual updrafts (ΔW/Uref > 0) of up to ∼0.28 Uref (Fig. 4b) and downdrafts (ΔW/Uref < 0) of ∼0.22 Uref (Fig. 4f). The changes in the mean vertical flow over large distances are crucial, as in dispersion modelling it is typically assumed that on average W = 0 m s−1, i.e. the vertical pollutant exchange is taken to be governed by turbulent motions and not by the mean flow.27 This is clearly not the case in the presence of TB, which generate strong updrafts and downdrafts that affect street-level flow fields.34 The velocity differences (Fig. 4) do not decay monotonically with distance from the TB, especially in the near wake region where the flow is characterised by recirculating winds. Instead, the lateral distance of the measurement points from the building centreline is crucial. Despite being several building heights away (i.e. several 100 m), locations with small |y − y134|/H134 are strongly impacted by the TB.
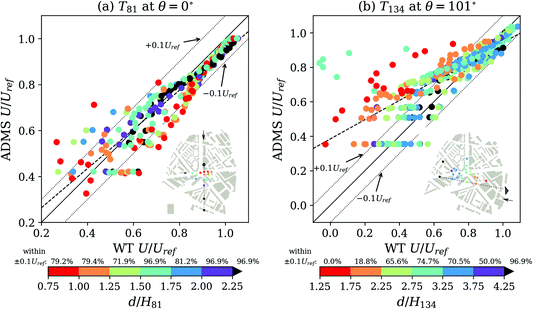
Some urban air-quality models (e.g. ADMS–Urban) have flow modules to account for the impact of isolated buildings on pollutant dispersion. Wake models (e.g. ADMS–Build3) represent flow around cuboidal buildings of modest height to length (or width) ratios, without accounting for the impact of neighbouring low-rise buildings. We evaluate ADMS–Build (Section 2.4) at the London site using our measurements in the main wake (i.e. behind the recirculation zone of the near wake, starting ∼51 m downwind of T81; ∼161 m downwind of T134;40 inset Fig. 1). Data are analysed for all available measurement heights, stratified by straight-line distance (d/HTB) between the tall building and the comparison sites (Fig. 5).
Overall, the agreement between ADMS–Build and wind tunnel is better for the slender, shorter T81 (Fig. 5a) than for the larger and wider T134 (Fig. 5b). The percentage of locations where the model and measurement agree within a tolerance threshold of ±0.1 U/Uref for either T81 or T134 clearly depends on the respective distance from the tower. The flow at sites closer to the towers is less well predicted (cf. sites at greater distances). Model performance improves with height above the urban canopy (i.e. larger U/Uref conditions). This is partially explained by the neglecting of aerodynamic effects from low-rise buildings surrounding the towers within ADMS–Build. For some sites this causes an over-prediction of velocities closer to the ground. The wake-flow close to T134 (located at the edge of the wind-tunnel model; Fig. 2a) is also affected by the roughness transition between the upwind boundary-layer and the building model, which is not accounted for in ADMS–Build.40 Such changes in roughness characteristics (e.g. induced by the local building morphology of a neighbourhood) occur frequently in mega-cities (e.g. central business districts, residential quarters, urban parks).
3.2 Beijing: plume characteristics in a cluster of tall buildings (TB)
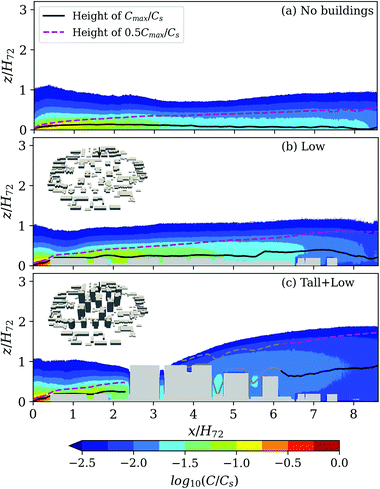
The effect of tall buildings on the dispersion of pollutants continuously emitted from an upwind ground source is analysed in the TB cluster in Beijing (Fig. 2b and 6). For reference, we compare the pollutant dispersion to an open area (i.e. without buildings, Fig. 6a) to identify changes in mean plume characteristics for dispersion through a low-rise building canopy (Low configuration; Fig. 6b) and through a high-rise building cluster surrounded by the low-rise buildings (Tall + Low, Fig. 2b, 6c). The time-averaged concentrations (C) are scaled by the concentration of the tracer solution at the release point (Cs). The elevation of the plume centreline is used to analyse the impact of the TB cluster. This is measured by the height of the maximum tracer concentration (Cmax/Cs) along the longitudinal direction. The vertical plume half-width is the distance over which Cmax/Cs has dropped to half its local maximum value vertically.Compared to the open-reference, the elevation of the plume centreline is noticeably enhanced in the presence of the low-rise canopy (Fig. 6a and b). An initial upward momentum of pollutants when released (i.e. at the source) is observed (Fig. 6a) causing Cmax to be initially away from the ground. However, in the presence of the building canopy, this is a secondary effect on the plume dispersion. The increased vertical transport and mixing of pollutants in the building canopy contribute to a faster decay of concentrations with increasing distance from the release point (cf. open reference). The along-wind decay is further enhanced by a stronger lateral plume spread from pollutant channelling and lateral plume branching in response to the local street topology (not measured in this experiment).
The vertical plume half-width is noticeably increased at the far end of the measurement domain (∼8.5 building heights H72 away from the source) in the Low configuration (cf. to the open case). Including the Tall-building cluster in the centre of the model domain leads to strong changes in the plume shape downwind of x/H72 = 2.5 (Fig. 6c). The strong updrafts generated in the overlapping wakes of the tall buildings lift pollutants out of the canopy, resulting in a much deeper tracer plume on the leeward side of the cluster (larger vertical plume half-width) and an elevated plume centreline (maximum concentrations just below z = H72). Note that the first building impacted by the plume is located at x/H72 = 3.25 (i.e. the TB at x/H72 = 2.75 is in front of the measurement plane, camera perspective).
The height of the plume envelope increases longitudinally (Fig. 6c; increasing from z/H72 = 1 to 2 over x/H72 = 3.25 to 8.5) and correlates with the region of maximum vertical wind shear (and maximum velocity variances; not shown). The enhanced mixing and vertical spread of the pollutants in the wake of the cluster results in overall lower maximum concentrations. Furthermore, on the windward face of the TB below the region of strong upward flow at roof-level, there is a region of enhanced downward motion (downwash; Fig. 1) and outflow near the building’s base resulting in a further lateral distribution of pollutants. A large portion of the pollutant plume behind the TB cluster is transported above the street canyons of the low-rise buildings. Hence, higher concentrations are observed above z/H72 = 1 compared to the open-terrain and Low cases at the same distances from the source.
To study the wake region behind the cluster over larger distances, measurements in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4800 scale model of the Tall configuration (no low-rise buildings) are analysed. Vertical profiles of mean concentrations normalised by the local maximum concentration at various up- and down-wind distances to the tall building cluster show the change in plume shape (Fig. 7). While the region upwind of the buildings has maximum concentrations close to the ground and a rapid decay of concentrations with height, in the wake region the pollutants are distributed over a much larger vertical depth, with Cmax elevation growing with distance from the buildings.
4800 scale model of the Tall configuration (no low-rise buildings) are analysed. Vertical profiles of mean concentrations normalised by the local maximum concentration at various up- and down-wind distances to the tall building cluster show the change in plume shape (Fig. 7). While the region upwind of the buildings has maximum concentrations close to the ground and a rapid decay of concentrations with height, in the wake region the pollutants are distributed over a much larger vertical depth, with Cmax elevation growing with distance from the buildings.
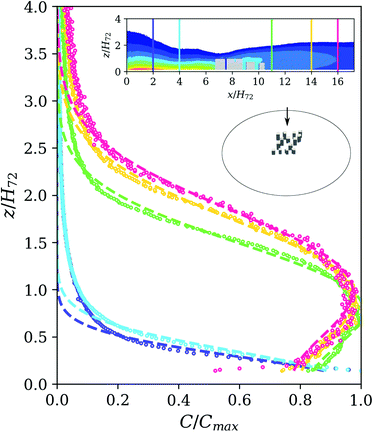 | ||
Fig. 7 Vertical profiles of normalised concentrations (C/Cmax) for the Tall case of the Beijing neighbourhood (θ = 0°; arrow in inset of building geometry; scale 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4800) showing measurements (circles) and Gaussian plume model fits (dashed lines) at two locations upwind of the building cluster (blue, cyan; modelled for a ground source release) and at three locations in the wake region (green, yellow, red; modelled for a release from an elevated source). The x/H72 locations of the profiles are indicated in the inset showing the concentration plume (log10(C/Cs); contours as in Fig. 6). For clarity, profiles show only every third measurement point and measurements closest to the ground (with larger uncertainties) are removed. 4800) showing measurements (circles) and Gaussian plume model fits (dashed lines) at two locations upwind of the building cluster (blue, cyan; modelled for a ground source release) and at three locations in the wake region (green, yellow, red; modelled for a release from an elevated source). The x/H72 locations of the profiles are indicated in the inset showing the concentration plume (log10(C/Cs); contours as in Fig. 6). For clarity, profiles show only every third measurement point and measurements closest to the ground (with larger uncertainties) are removed. | ||
We compare the measured concentration profiles with fits for a reflected Gaussian plume model:54
As the pollutants are released from a ground source (at x/H72 = 0), upwind of the buildings (i.e. over open terrain) the pollutant dispersion is modelled by setting zs = 0 m. While the measured upwind profiles decay less rapidly with height, overall their shape agrees with the Gaussian model (Fig. 7). After passing through the TB cluster, the plume shape in the wake is well approximated if a zs > 0 m is used, i.e. concentration profiles in the wake of the tall buildings resemble those obtained as if an elevated source release had occurred. Here, the “virtual” source height zs/H72 varies between 0.85 at x/H72 = 11 and 1.06 at x/H72 = 16 (Fig. 7).
Model development work supported by experimental evidence is needed for current (operational) air-quality and dispersion models to be able to capture such effects and make the models suitable for applications in cities with TB.
3.3 Mixed layer height (MLH) in Beijing and Paris
Here, the MLH is derived from observations of attenuated backscatter from aerosols and moisture. Hence, it is indicative of the depth of the atmospheric layer that the aerosols have mixed into, rather than the depth of the atmospheric layer that is undergoing active vertical motion (referred to as the mixing height).55 Layers of aerosols create gradients in the observed attenuated backscatter (here 10 m vertical and 15 s temporal resolution) and are used to identify the MLH.35The observed diurnal maxima of MLH during the study years (Section 2.5) in Beijing and Paris are, for both cities, larger in spring and summer than in the autumn and winter (Fig. 8, row 3). With the warmer season peak daytime medians (thick lines) are similar to the 75th percentile (thin upper lines) in autumn in both cities.
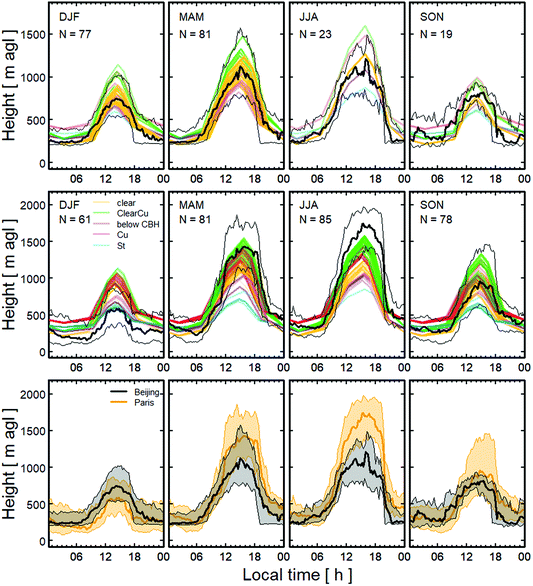 | ||
| Fig. 8 Diurnal variations of observed (obs) and modelled mixed layer height (MLH) by season in, (row 1) Beijing and (row 2) suburban Paris, and (row 3) the observed MLH in Beijing and Paris showing median (thick line) and interquartile range (thin lines). Modelled MLH (colour) are stratified by cloud conditions (colour, Table 1). The number of days (N) with data in each season varies. Observations (black, row 1 and 2, other colours in row 3) are Vaisala CL31 ceilometer attenuated backscatter data analysed with the CABAM algorithm (Section 2.5). Seasons are winter: DJF, spring: MAM, summer: JJA, autumn: SON. Note: y-axes are different for the two rows. | ||
The simple MLH model (Table 1) applied in the two mega-cities uses parameters derived from six years of observations undertaken in central London.36 Synoptic conditions generally differ between the three cities, with a clear oceanic influence in London, continental climate in Paris, and a mixture of orographic and maritime effects dominating Beijing.38 MLH growth is driven by the strength of the vertical motions and entrainment processes. The turbulent sensible heat (QH) as well as momentum exchange modify boundary layer dynamics within the synoptic context. The model accounts for differences in daylength (Section 2.5) as well as cloud cover and cloud type, but does not consider energy forcing differences associated with geographic location, surface cover, or human activities. As it effectively only has linear variations between the six key times within a day (Table 1, Fig. 8), the discussion of model performance should focus on these periods rather than other times.
On average the model (with London coefficients, Table 1) works surprisingly well in Beijing (Fig. 8, row 1) where parameterised diurnal patterns mostly fall within the inter-quartile range of the observations. For the London–Paris comparison (Fig. 8, row 2), the curves reveal an overprediction of MLH in winter and underprediction in summer. To evaluate the performance we compare the peak daytime values modelled with the corresponding observed MLH values (data point closest in time). Both the mean bias error (MBE) and the mean absolute error (MAE) are calculated. The overall MBE and MAE are greater for Paris (−230 m/431 m) than for Beijing (−136 m/306 m). The MBE by season indicates that peak values for suburban Paris are overestimated in winter by ∼100 m and underestimated in summer by ∼440 m. However, as the modelled MLH peak is dependent on the growth from the minimum it is important to assess this. The modelled zmin (Table 1) in Beijing and in Paris are generally reasonable with the MBE and MAE below ±40 m and 100 m for Beijing, and below ±80 m and 150 m for Paris, across all seasons. Only in winter, are the Paris modelled values too high (MBE = 142 m, Fig. 8). This suggests the growth rates derived from London characteristics are not large enough to capture MLH variability in Paris. Previous estimates of GRMT at SIRTA from ALC data were stratified by season (cf. cloud, Table 1). These varied from (mean ± standard deviation):56 DJF: 149 ± 119, SON: 196 ± 137, MAM: 225 ± 138, JJA: 247 ± 142 m h−1. These values are generally consistent with Table 1 but support the expectation of a larger peak MLH in Paris.
Given the lower latitudes (Section 2.1) of both cities (cf. London) the peak solar noon radiation on a clear day should be greater than in London. This could contribute to the MLH increment at the continental, suburban European site. The simple MLH parameterisation accounts for differences in cloud cover and cloud type, so that the greater probability of clear-sky days at the continental Paris site57 does not explain the contrast to the London conditions. It is likely that the continental synoptic setting of Paris (e.g. absence of sea breeze effects) explains some of the larger growths rates and resulting greater MLH at this site during spring and summer (Fig. 8, row 3). A strong relation between peak MLH and peak incoming solar radiation has been found in Paris.56 Given clear skies in London are less frequent in summer than in Paris (12% versus 27%),51 the London empirical data may not sample these synoptic conditions with the largest MLH as extensively as needed.
Potential increase in solar radiation might have less impact in the Asian mega-city, given increased aerosols will reduce the shortwave receipt at the surface.38,58,59 Further, energy partitioning may restrict the growth of the mixed layer. In central London, the surface energy balance is dominated by QH.60–62 In Beijing, QH is much greater in the summer at the IAP site than it is in suburban Meiyun.63 These two Beijing sites have very similar net all-wave radiation (Q*) but there are differences in outgoing longwave radiation characteristics, with the urban area having greater nocturnal emissions.63 The suburban site has larger latent heat fluxes (QE) making the Bowen ratio (β = QH/QE) smaller. However, given the land cover characteristics, the urban IAP site has smaller summertime β than expected.63 This is thought to be associated with extensive external water use for irrigation of vegetation and for wetting roads to reduce airborne particles and cleaning.63 Thus, the summertime β values are much greater in central London than in urban Beijing which could mean that even if more energy were available from radiation, the MLH growth is still restricted.
In both Beijing and London, the MLH observations were taken near the centre of the mega-cities, whereas in Paris the site is in a suburban area some distance from the centre (Section 2.1). Urban density greatly affects anthropogenic heat flux (QF) emissions. This additional source of energy (i.e. beyond Q*) is typically larger in dense central business districts than lower density residential areas.64–67 In colder climates the QF emissions are often greater in the winter than the summer65,68–70 because of building heating needs. Thus, winter QF emissions provide a proportionally larger additional source of energy relative to Q* than in summer, given the shortwave radiation differences.39 As QF is always a source of energy, unlike nocturnal Q*, it can have a large impact on the wintertime MLH. At night, this additional source of energy combined with storage heat flux (ΔQS) release and outgoing longwave radiation can contribute to QH, thereby maintaining the MLH at a greater depth. Obviously, this is important as both winter and nocturnal periods are times when the MLH is lower (Fig. 8), hence any increase in boundary-layer volume will have proportionally larger impact on potential dilution/concentration of air pollutants and hence on local air quality. From machine learning analyses of the meteorological drivers of PM1 variability at the Paris site, it is found that the impact of MLH up to about 900 m is particularly pronounced.71
During winter, empirical coefficients (Table 1) derived from the central London observations appear to capture the MLH evolution at the central Beijing site well, while suburban Paris (Fig. 8) conditions are overestimated. This is likely explained by the lower QF and ΔQS at the suburban location providing less energy to maintain QH and thereby a considerable MLH. MLH at SIRTA has been observed to be lower than in central Paris during winter and at night.72
Overall, these results suggest the form of the empirical model is reasonable and further analyses of both ALC MLH data and surface energy balance partitioning with consideration of synoptic conditions would allow a simple, extremely fast, first-order model to be developed with broader applicability.
4. Conclusions
Physical meteorology as well as chemical emissions and transformations need to be understood to interpret air quality changes and variations across mega-cities. Given that physical meteorological processes vary at micro, local and city scales (Fig. 1), awareness of these scales and their impact on atmospheric transport is important. Depending on the height of observations, physical and chemical characteristics of the atmosphere are influenced more/less by individual roughness elements. Given the complexity of the urban canopy layer (UCL, Fig. 1), observations taken within this layer are very dependent on the exact measurement site. This creates a significant challenge for those interested in air quality given that outdoor human exposure is most frequently at an order of 1–2 m agl. In mega-cities, there are increasing numbers of tall buildings (TB) in isolated and cluster settings. These expand the depth of both the UCL and the roughness sub-layer (RSL, Fig. 1), where atmospheric motions are more chaotic, and increase the inhomogeneity of the urban atmosphere, complicating the situation further.Models that yield results rapidly enough to provide air quality forecasts, parameterise the urban physical meteorology. To date, these parameterisations have not considered TB adequately. Using hardware scale models that characterize real areas in two global mega-cities (London, Beijing) we explore the impact of isolated TB and a cluster of TB on flow and dispersion. The studies consider the UCL, RSL and ISL. Using real world observations in two global mega-cities (Beijing, Paris) we assess the UBL height modelled with parameters derived from a third mega-city (London).
Isolated TB wakes impact the flow above the background low-rise buildings for at least 5HTB downwind, with stronger impacts in regions close to the centre-line of the wake. Wind profiles clearly still deviate from the logarithmic law at 4HTB radial distances from the TB. Flow profiles only converge back to the reference state well above roof-level over the horizontal distances analysed in this study. A taller and wider TB, or a group of such buildings, has a much broader wake, varying with building shape and wind direction.
The strongest impact on the mean flow is evident directly behind the TB, based on the magnitude of the velocity deficit and residual up- and down-drafts. As dispersion models typically assume W = 0 m s−1 with vertical pollutant exchange governed by turbulent motions and not by the mean flow, changes in mean vertical flow over distances of interest are crucial.
Velocity differences do not decay monotonically with distance from the TB, especially in the near-wake region where the flow is characterised by recirculation. Lateral distance from the TB centreline is crucial as strong effects persist close to the TB centreline even several HTB away (i.e. several 100 m).
Evaluation of ADMS–Build in the main TB wake considering straight-line distance (d/HTB) found better agreement for a slender, shorter TB (cf. larger TB). Prediction of flow horizontally is better further away (cf. nearer); whereas the prediction is better higher above the background low-rise buildings while overprediction occurs closer to them given that they are unaccounted for by the model.
A TB cluster causes strong changes in the plume dispersion shape downwind. Strong updrafts generated in the overlapping wakes of the TB lift pollutants out of the canopy. This results in a much deeper tracer plume in lee of the cluster (larger vertical plume half-width) and an elevated plume centreline (maximum concentrations just below HTB). Enhanced mixing and vertical spread of the pollutants in the wake of the cluster result in overall lower maximum concentrations for a surface source, but higher concentrations above HTB (cf. open terrain and low-rise) at the same distance from the source.
A low-rise canopy (cf. open terrain) increases the vertical transport and mixing of pollutants in the building canopy. This contributes to a faster decay of concentrations with increasing distance from the release point. The along-wind decay is further enhanced by a stronger lateral plume spread from pollutant channelling and lateral plume branching in response to the local street topology.
The building cluster causes both vertical displacement of the maximum concentration and wider spread of pollutants. This vertical distribution of pollutants in the wake of the TB can be approximated using a reflected Gaussian plume model for a release from an elevated source (“virtual” source height is ∼HTB but growing with distance from the buildings).
Observed diurnal maxima of mixed layer height (MLH) are greater in spring and summer (cf. autumn and winter), with median daytime peak in the warm seasons similar to the 75th percentiles of the cooler seasons (Fig. 8, row 3).
A simple empirical MLH model (Table 1) with central London coefficients works surprisingly well in central Beijing, but less well in suburban Paris where values are often over/under-predicted in winter/summer. Synoptic conditions, land cover characteristics, and human activities not accounted for by this simple parameterisation likely explain the discrepancies. Still, the results suggest the form of the model is reasonable, offering a simple, extremely fast, first-order MLH calculation method.
Our results indicate a need for more observations at each of the scales considered in this paper. Given both the wind tunnel and water flume results are for neutral stability conditions, the influence of TB (isolated and clusters) under non-neutral condition needs to be studied. At the microscale, large differences in surface temperatures occur.15,16 The variability of the urban form (e.g. TB height, number, low-rise building characteristics) and a wider range of upwind fetch conditions also need to be considered.
Using the hardware model results, development of models to improve current (operational) air-quality and dispersion models should aim to enable them to capture the effects found here, thus making the models more suitable for applications in cities with TB. Future work should combine thermal influences with TB observations (hardware, real world) for dispersion models so that there is improved capability to model vertical variability (wind, temperature, humidity) between buildings.73
The simple MLH model performance suggests further analyses of observations of both MLH data and surface energy balance partitioning across cities, with different synoptic and regional settings, would be beneficial. Beyond improving our understanding of the variability of the MLH within cities, it would increase the range of data for establishing empirical coefficients. Thus, it is useful to consider these results in light of surface energy balance characteristics. Comparison of observed Bowen ratio (β) between central London60,61 and suburban residential areas,74,75 and similarly in Beijing,63 indicates the latter is smaller. There is observational evidence that urban-rural contrasts in heat-flux partitioning explain spatial boundary layer depth variations56,76–78 when experiencing the same synoptic force. The timing of synoptic events, notably clear sky conditions, clearly needs to be considered to ensure the information within the empirical coefficients is appropriately disentangled.
Automatic lidar and ceilometer (ALC) observations provide much more information than MLH. For example, the high resolution attenuated backscatter gives vertical profiles of aerosol distribution79 which when modelled are improved with enhanced atmospheric chemistry details.80 Thus, there is clear benefit in conducting physical and chemical based urban meteorology research together to enhance our ability to predict the air quality exposure in mega-cities, which can also benefit the delivery of other integrated urban services (IUS).81–83
Conflicts of interest
There are no conflicts to declare.Acknowledgements
SG thanks the Royal Society of Chemistry and the conference organizers for the invitation to contribute this paper. The research reported here has been funded by NERC NE/N00700X/1, Newton Fund/Met Office CSSP-China (SG, DH, SK), EPSRC UK Fluids Network visiting scientist award, ERC Synergy urbisphere (855005), and ACTRIS-2 (SK). Facilities at the University of Southampton are supported by UKRI, and at the University of Surrey are supported by NERC. The EPSRC MAGIC project allowed use of the London hardware model. For the Beijing cluster model work we acknowledge the help of George Meachim (UR), Matthew Coburn (Southampton), Christoph Kent (UR) and Shiguang Miao (IUM, CMA). For the Paris MLH processing we thank Marc-Antoine Drouin for ongoing support. ALC measurements at SIRTA are performed by Météo-France. SIRTA is supported by CNES, Ecole Polytechnique, INSU-CNRS, and IPSL. London observations are funded with grants from NERC, EPSRC, the Met Office, EUf7, H2020 and ERC with support from KCL and the University of Reading. We thank the European Cooperation in Science and Technology (COST) actions “TOPROF” (ES1303) and “PROBE” (CA18235) which fostered collaborations that contributed to this work.References
- H. A. Cleugh and C. S. B. Grimmond, in The Future of the World’s Climate, ed. A. Henderson-Sellers and K. Mc Guffie, Elsevier, 2012 Search PubMed.
- T. R. Oke, G. Mills, A. Christen and J. A. Voogt, Urban Climates, Cambridge University Press, Cambridge, 2017 Search PubMed.
- M. Piringer, C. S. B. Grimmond, S. M. Joffre, P. Mestayer, D. R. Middleton, M. W. Rotach, A. Baklanov, K. De Ridder, J. Ferreira, E. Guilloteau, A. Karppinen, A. Martilli, V. Masson and M. Tombrou, Water, Air, Soil Pollut.: Focus, 2002, 2, 1–16 CrossRef.
- P. Kastner-Klein and M. W. Rotach, Boundary Layer Meteorol., 2004, 111, 55–84 CrossRef.
- C. S. B. Grimmond and T. R. Oke, J. Appl. Meteorol., 1999, 38, 1262–1292 CrossRef.
- M. R. Raupach, Boundary Layer Meteorol., 1992, 60, 375–395 CrossRef.
- M. Roth, Q. J. R. Metereol. Soc., 2000, 126, 941–990 CrossRef.
- M. Kanda, A. Inagaki, T. Miyamoto, M. Gryschka and S. Raasch, Boundary Layer Meteorol., 2013, 148, 357–377 CrossRef.
- J. T. Millward-Hopkins, A. S. Tomlin, L. Ma, D. Ingham and M. Pourkashanian, Boundary Layer Meteorol., 2011, 141, 443–465 CrossRef.
- C. W. Kent, S. Grimmond, J. Barlow, D. Gatey, S. Kotthaus, F. Lindberg and C. H. Halios, Boundary Layer Meteorol., 2017, 164, 183–213 CrossRef PubMed.
- H. Gough, T. Sato, C. Halios, C. S. B. Grimmond, Z. Luo, J. F. Barlow, A. Robertson, R. Hoxey and A. Quinn, J. Wind Eng. Ind. Aerod., 2018, 175, 408–418 CrossRef.
- H. L. Gough, Z. Luo, C. H. Halios, M.-F. King, C. J. Noakes, C. S. B. Grimmond, J. F. Barlow, R. Hoxey and A. D. Quinn, Build. Environ., 2018, 137, 246–256 CrossRef.
- V. Masson, Boundary Layer Meteorol., 2000, 94, 357–397 CrossRef.
- M. Kanda, Theor. Appl. Climatol., 2006, 84, 23–33 CrossRef.
- W. Morrison, S. Kotthaus, C. S. B. Grimmond, A. Inagaki, T. Yin, J.-P. Gastellu-Etchegorry, M. Kanda and C. J. Merchant, Remote Sens. Environ., 2018, 215, 268–283 CrossRef.
- W. Morrison, T. Yin, N. Lauret, J. Guilleux, S. Kotthaus, J.-P. Gastellu-Etchegorry, L. Norford and S. Grimmond, Remote Sens. Environ., 2020, 237, 111524 CrossRef.
- I. P. Castro, Z.-T. Xie, V. Fuka, A. G. Robins, M. Carpentieri, P. Hayden, D. Hertwig and O. Coceal, Boundary Layer Meteorol., 2017, 162, 207–230 CrossRef.
- C. S. B. Grimmond, Theor. Appl. Climatol., 2006, 84, 3–22 CrossRef.
- H. P. Schmid, Agr. Forest Meteorol., 1997, 87, 179–200 CrossRef.
- V. Masson, C. S. B. Grimmond and T. R. Oke, J. Appl. Meteorol., 2002, 41, 1011–1026 Search PubMed.
- C. S. B. Grimmond, M. Blackett, M. J. Best, J.-J. Baik, S. E. Belcher, J. Beringer, S. I. Bohnenstengel, I. Calmet, F. Chen, A. Coutts, A. Dandou, K. Fortuniak, M. L. Gouvea, R. Hamdi, M. Hendry, M. Kanda, T. Kawai, Y. Kawamoto, H. Kondo, E. S. Krayenhoff, S. H. Lee, T. Loridan, A. Martilli, V. Masson, S. Miao, K. Oleson, R. Ooka, G. Pigeon, A. Porson, Y.-H. Ryu, F. Salamanca, G. J. Steeneveld, M. Tombrou, J. A. Voogt, D. T. Young and N. Zhang, Int. J. Climatol., 2011, 31, 244–272 CrossRef.
- R. E. Britter and S. R. Hanna, Annu. Rev. Fluid Mech., 2003, 35, 469–496 CrossRef.
- S. E. Belcher, Philos. Trans. R. Soc., A, 2005, 363, 2947–2968 CrossRef PubMed.
- C. A. McHugh, D. J. Carruthers and H. A. Edmunds, Int. J. Environ. Pollut., 1997, 8, 666–674 CAS.
- R. Berkowicz, Environ. Monit. Assess., 2000, 65, 323–331 CrossRef CAS.
- M. D. Williams, M. J. Brown, B. Singh and D. Boswell, QUIC-PLUME Theory Guide, Los Alamos National Laboratory, 2004 Search PubMed.
- L. Soulhac, P. Salizzoni, F.-X. Cierco and R. Perkins, Atmos. Environ., 2011, 45, 7379–7395 CrossRef CAS.
- A. J. Cimorelli, S. G. Perry, A. Venkatram, J. C. Weil, R. J. Paine, R. B. Wilson, R. F. Lee, W. D. Peters and R. W. Brode, J. Appl. Meteorol., 2005, 44, 682–693 CrossRef.
- A. Jones, D. Thomson, M. Hort and B. Devenish, in Air Pollution Modeling and Its Application XVII, ed. C. Borrego and A.-L. Norman, Springer US, Boston, MA, 2007, pp. 580–589 Search PubMed.
- A. Robins and C. McHugh, Int. J. Environ. Pollut., 2001, 16, 161 CrossRef CAS.
- R. L. Petersen, S. Guerra and A. Bova, J. Air Waste Manage. Assoc., 2017, 67, 826–835 CrossRef PubMed.
- L. A. Brixey, D. K. Heist, J. Richmond-Bryant, G. E. Bowker, S. G. Perry and R. W. Wiener, J. Environ. Monit., 2009, 11, 2171 RSC.
- E. Aristodemou, L. M. Boganegra, L. Mottet, D. Pavlidis, A. Constantinou, C. Pain, A. Robins and H. ApSimon, Environ. Pollut., 2018, 233, 782–796 CrossRef CAS PubMed.
- V. Fuka, Z.-T. Xie, I. P. Castro, P. Hayden, M. Carpentieri and A. G. Robins, Boundary Layer Meteorol., 2018, 167, 53–76 CrossRef PubMed.
- S. Kotthaus and C. S. B. Grimmond, Q. J. R. Metereol. Soc., 2018, 144, 1511–1524 CrossRef.
- S. Kotthaus and C. S. B. Grimmond, Q. J. R. Metereol. Soc., 2018, 144, 1525–1538 CrossRef.
- A. G. Robins and R. W. Macdonald, Review of Flow and Dispersion in the Vicinity of Groups of Buildings, Atmospheric Dispersion Modelling Liaison Committee, ADMLC, UK, 2001 Search PubMed.
- Z. Shi, T. Vu, S. Kotthaus, R. M. Harrison, S. Grimmond, S. Yue, T. Zhu, J. Lee, Y. Han, M. Demuzere, R. E. Dunmore, L. Ren, D. Liu, Y. Wang, O. Wild, J. Allan, W. J. Acton, J. Barlow, B. Barratt, D. Beddows, W. J. Bloss, G. Calzolai, D. Carruthers, D. C. Carslaw, Q. Chan, L. Chatzidiakou, Y. Chen, L. Crilley, H. Coe, T. Dai, R. Doherty, F. Duan, P. Fu, B. Ge, M. Ge, D. Guan, J. F. Hamilton, K. He, M. Heal, D. Heard, C. N. Hewitt, M. Hollaway, M. Hu, D. Ji, X. Jiang, R. Jones, M. Kalberer, F. J. Kelly, L. Kramer, B. Langford, C. Lin, A. C. Lewis, J. Li, W. Li, H. Liu, J. Liu, M. Loh, K. Lu, F. Lucarelli, G. Mann, G. McFiggans, M. R. Miller, G. Mills, P. Monk, E. Nemitz, F. O’Connor, B. Ouyang, P. I. Palmer, C. Percival, O. Popoola, C. Reeves, A. R. Rickard, L. Shao, G. Shi, D. Spracklen, D. Stevenson, Y. Sun, Z. Sun, S. Tao, S. Tong, Q. Wang, W. Wang, X. Wang, X. Wang, Z. Wang, L. Wei, L. Whalley, X. Wu, Z. Wu, P. Xie, F. Yang, Q. Zhang, Y. Zhang, Y. Zhang and M. Zheng, Atmos. Chem. Phys., 2019, 19, 7519–7546 CrossRef CAS.
- M. Haeffelin, L. Barthès, O. Bock, C. Boitel, S. Bony, D. Bouniol, H. Chepfer, M. Chiriaco, J. Cuesta, J. Delanoë, P. Drobinski, J.-L. Dufresne, C. Flamant, M. Grall, A. Hodzic, F. Hourdin, F. Lapouge, Y. Lemaître, A. Mathieu, Y. Morille, C. Naud, V. Noël, W. O’Hirok, J. Pelon, C. Pietras, A. Protat, B. Romand, G. Scialom and R. Vautard, Ann. Geophys., 2005, 23, 253–275 CrossRef.
- D. Hertwig, H. L. Gough, S. Grimmond, J. F. Barlow, C. W. Kent, W. E. Lin, A. G. Robins and P. Hayden, Boundary Layer Meteorol., 2019, 172, 239–270 CrossRef.
- D. Hertwig, H. L. Gough, S. Grimmond, J. F. Barlow and A. G. Robins, 2019, https://zenodo.org/record/2563700.
- D. Hertwig, H. L. Gough, S. Grimmond, J. F. Barlow and A. G. Robins, 2020, https://zenodo.org/record/3974901.
- C. Tropea, Meas. Sci. Technol., 1995, 6, 605–619 CrossRef CAS.
- J. Westerweel, G. E. Elsinga and R. J. Adrian, Annu. Rev. Fluid Mech., 2013, 45, 409–436 CrossRef.
- J. P. Crimaldi, Exp. Fluids, 2008, 44, 851–863 CrossRef CAS.
- C. Vanderwel and S. Tavoularis, Exp. Fluids, 2014, 55, 1801 CrossRef.
- D. Hertwig, H. L. Gough, S. Grimmond and C. Vanderwel, 2020, https://zenodo.org/record/3768763.
- A. G. Robins, D. D. Apsely and CERC, Modelling building effects in ADMS, CERC, 2020 Search PubMed.
- J. Counihan, J. C. R. Hunt and P. S. Jackson, J. Fluid Mech., 1974, 64, 529–564 CrossRef.
- S. Kotthaus, E. O’Connor, C. Münkel, C. Charlton-Perez, M. Haeffelin, A. M. Gabey and C. S. B. Grimmond, Atmos. Meas. Tech., 2016, 9, 3769–3791 CrossRef.
- S. Kotthaus, M. Haeffelin, M.-A. Drouin, J.-C. Dupont, C. S. B. Grimmond, A. Haefele, M. Hervo, Y. Poltera and M. Wiegner, Remote Sens., 2020, 12, 3259 CrossRef.
- H. W. Lean, J. F. Barlow and C. H. Halios, Q. J. R. Metereol. Soc., 2019, 145, 1674–1689 CrossRef.
- C. W. Kent, C. S. B. Grimmond, D. Gatey and J. F. Barlow, J. Wind Eng. Ind. Aerod., 2018, 173, 100–111 CrossRef.
- S. R. Hanna, R. Britter and P. Franzese, Atmos. Environ., 2003, 37, 5069–5082 CrossRef CAS.
- S. Kotthaus, C. H. Halios, J. F. Barlow and C. S. B. Grimmond, Atmos. Environ., 2018, 190, 401–414 CrossRef CAS.
- S. Pal and M. Haeffelin, J. Geophys. Res.: Atmos., 2015, 120(11), 936–956 Search PubMed.
- S. Kotthaus, S. Grimmond, J.-A. Bravo-Aranda, M. Haeffelin and A. Haefele, EMS Annual Meeting Abstracts, 2017, vol. 14, EMS2017-560-1 Search PubMed.
- T. Petäjä, L. Järvi, V.-M. Kerminen, A. J. Ding, J. N. Sun, W. Nie, J. Kujansuu, A. Virkkula, X. Yang, C. B. Fu, S. Zilitinkevich and M. Kulmala, Sci. Rep., 2016, 6, 18998 CrossRef PubMed.
- T. V. Kokkonen, S. Grimmond, S. Murto, H. Liu, A.-M. Sundström and L. Järvi, Atmos. Chem. Phys., 2019, 19, 7001–7017 CrossRef CAS.
- S. Kotthaus and C. S. B. Grimmond, Urban Clim., 2014, 10, 261–280 CrossRef.
- S. Kotthaus and C. S. B. Grimmond, Urban Clim., 2014, 10, 281–307 CrossRef.
- B. Crawford, C. S. B. Grimmond, H. C. Ward, W. Morrison and S. Kotthaus, Q. J. R. Metereol. Soc., 2017, 143, 817–833 CrossRef.
- J. Dou, S. Grimmond, Z. Cheng, S. Miao, D. Feng and M. Liao, Int. J. Climatol., 2019, 39, 2793–2810 CrossRef.
- M. Iamarino, S. Beevers and C. S. B. Grimmond, Int. J. Climatol., 2012, 32, 1754–1767 CrossRef.
- D. J. Sailor, Int. J. Climatol., 2011, 31, 189–199 CrossRef.
- A. M. Gabey, C. S. B. Grimmond and I. Capel-Timms, Theor. Appl. Climatol., 2019, 135, 791–807 CrossRef.
- I. Capel-Timms, S. T. Smith, T. Sun and S. Grimmond, Geoscientific Model Development, 2020, 13, 4891–4924 CrossRef.
- I. G. Hamilton, M. Davies, P. Steadman, A. Stone, I. Ridley and S. Evans, Build. Environ., 2009, 44, 807–817 CrossRef.
- L. Allen, F. Lindberg and C. S. B. Grimmond, Int. J. Climatol., 2011, 31, 1990–2005 CrossRef.
- F. Lindberg, C. S. B. Grimmond, N. Yogeswaran, S. Kotthaus and L. Allen, Urban Clim., 2013, 4, 1–15 CrossRef.
- R. Stirnberg, J. Cermak, S. Kotthaus, M. Haeffelin, H. Andersen, J. Fuchs, M. Kim, J.-E. Petit and O. Favez, Atmos. Chem. Phys., 2020 DOI:10.5194/acp-2020-469.
- D. Cimini, M. Haeffelin, S. Kotthaus, U. Löhnert, P. Martinet, E. O’Connor, C. Walden, M. C. Coen and J. Preissler, Bulletin of Atmospheric Science and Technology, 2020, 1, 23–42 CrossRef.
- N. E. Theeuwes, R. J. Ronda, I. N. Harman, A. Christen and C. S. B. Grimmond, Boundary Layer Meteorol., 2019, 173, 321–348 CrossRef.
- H. C. Ward, J. G. Evans and C. S. B. Grimmond, Boundary Layer Meteorol., 2014, 152, 65–89 CrossRef.
- H. C. Ward, S. Kotthaus, C. S. B. Grimmond, A. Bjorkegren, M. Wilkinson, W. T. J. Morrison, J. G. Evans, J. I. L. Morison and M. Iamarino, Environ. Pollut., 2015, 198, 186–200 CrossRef CAS PubMed.
- J. F. Barlow, Urban Clim., 2014, 10, 216–240 CrossRef.
- N. E. Theeuwes, J. F. Barlow, A. J. Teuling, C. S. B. Grimmond and S. Kotthaus, npj Clim. Atmos. Sci., 2019, 2, 15 CrossRef.
- S. Pal, I. Xueref-Remy, L. Ammoura, P. Chazette, F. Gibert, P. Royer, E. Dieudonné, J.-C. Dupont, M. Haeffelin, C. Lac, M. Lopez, Y. Morille and F. Ravetta, Atmos. Environ., 2012, 63, 261–275 CrossRef CAS.
- E. Warren, C. Charlton-Perez, S. Kotthaus, H. Lean, S. Ballard, E. Hopkin and S. Grimmond, Atmos. Environ., 2018, 191, 532–547 CrossRef CAS.
- E. Warren, C. Charlton-Perez, S. Kotthaus, F. Marenco, C. Ryder, B. Johnson, D. Green, H. Lean, S. Ballard and S. Grimmond, Atmos. Environ., 2019, 117177 Search PubMed.
- A. Baklanov, C. S. B. Grimmond, D. Carlson, D. Terblanche, X. Tang, V. Bouchet, B. Lee, G. Langendijk, R. K. Kolli and A. Hovsepyan, Urban Clim., 2018, 23, 330–341 CrossRef.
- S. Grimmond, V. Bouchet, L. T. Molina, A. Baklanov, J. Tan, K. H. Schlünzen, G. Mills, B. Golding, V. Masson, C. Ren, J. Voogt, S. Miao, H. Lean, B. Heusinkveld, A. Hovespyan, G. Teruggi, P. Parrish and P. Joe, Urban Clim., 2020, 33, 100623 CrossRef.
- WMO, Guidance on Integrated Urban Hydrometeorological, Climate and Environmental Services - Volume I: Concept and Methodology, WMO-No: 1234, World Meteorological Organization, Geneva, 2019 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |