Open Access Article
Open Access ArticleAb initio molecular dynamics of hydrogen on tungsten surfaces
Alberto
Rodríguez-Fernández
 *ab,
Laurent
Bonnet
*ab,
Laurent
Bonnet
 ac,
Pascal
Larrégaray
ac and
Ricardo Díez
Muiño
ac,
Pascal
Larrégaray
ac and
Ricardo Díez
Muiño
 bd
bd
aUniversité de Bordeaux, ISM, UMR 5255, F-33400 Talence, France. E-mail: alberto.rodriguez-fernandez@u-bordeaux.fr
bCentro de Física de Materiales CFM/MPC(CSIC-UPV/EHU), Paseo Manuel de Lardizabal 5, 20018 Donostia-SanSebastián, Spain
cCNRS, ISM, UMR5255, F-33400 Talence, France
dDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-SanSebastián, Spain
First published on 21st December 2020
Abstract
The dissociation process of hydrogen molecules on W(110) was studied using density functional theory and classical molecular dynamics. We have calculated the dissociation probability for molecules with energies below 300 meV and analyzed the dynamics of the adsorption process. Our results show that the fate of each trajectory is determined at distances relatively far from the surface, at roughly 2–2.5 Å. This distance varies slightly with the initial kinetic energy of the molecule. Part of our simulations include van der Waals dispersion effects in the interaction between molecule and surface. We present a comparison between these results and other theoretical and experimental results previously published. The inclusion of the van der Waals term provokes an increase in the far-distance attraction that is compensated by a stronger repulsion at short distances. The combination of both effects appreciably decreases the value of the dissociation probability. The successful comparison of our results with experimental information confirms that the methodology employed can be considered as a rich and accurate instrument to study the dissociation of hydrogen on surfaces.
Introduction
In general, scientific and technological progress has very much improved life conditions for humankind. Scientific advance and the subsequent social and economical development have succeeded in making human life longer, healthier, and significantly dignified. The current challenge is to make this development sustainable and truly global. Among many other tasks, there is a continuous need of finding alternative energy sources that are efficient, sustainable, and environment friendly. Population growth and economic activity will very probably increase the energy demand worlwide in the decades to come.For a long time, fusion power has been a promising candidate to become a carbon-free, sustainable, long-term energy source. Fusion power is conceptually based on the generation of electricity from the heat released in nuclear fusion reactions. The most common reaction used for this purpose is the fusion of hydrogen isotopes to obtain helium and neutrons.
One of the most challenging engineering problems in fusion reactors is the design and maintenance of the vacuum vessel in which the plasma moves.1 The fusion process requires to confine the hydrogen isotopes, which act as fuel, under extreme temperature and pressure conditions in order to create a hot plasma where fusion reactions can occur. The enormous quantity of heat generated during the reaction makes of tungsten, a robust metal with the highest melting point, the standard material of choice to build many of the plasma-facing components.
Among plasma-facing components, the most vulnerable one is probably the divertor. The divertor is instrumental to extract heat, impurities, and ash from the plasma, as well as to protect parts of the plasma-facing walls. It receives a high flux (∼1020 cm−2 s−1) of relatively low-energy (∼100 eV) hydrogen and helium particles. The huge flux of hydrogen isotopes and helium towards the divertor can deteriorate the W properties. Surface blistering and exfoliation, among other problems, can appear due to the trapping and diffusion of these atoms within the material. Clustering of helium and hydrogen can lead to bubble formation, and migration of these bubbles to the surface induces the blistering. In this scenario, hydrogen recombination at the surface and molecular desorption is possible as well. The eventual fate of these desorbed molecules, i.e., whether they dissociate again at the surface or they return to the plasma, is relevant for the full process: the injection of atomic and molecular hydrogen from the walls again into the plasma can significantly perturb its ideal behavior. Therefore, for a correct operation of the global system, it is essential to understand and accurately model the interaction of hydrogen and its isotopes with W. The role of the W surface as an agent that either promotes or inhibits some of the elementary reactive processes leading to adsorption, recombination, diffusion, or desorption is crucial in this respect. Current theoretical and experimental activity on this topic is therefore extensive.
The traditional surface science approach, in which reactions take place under well-controlled conditions, shows however that the interaction between hydrogen and tungsten surfaces is a complex problem. Small differences in temperature, pressure, or crystalline face of the surface can dramatically change the output of a reaction. A remarkable feature in the adsorption of H2 on W is, for instance, the acute dependence on the crystalographic face of the surface, as proven in molecular beam experiments. For initial energies below 1 eV and normal incidence, adsorption of H2 can be as much as a factor of two higher in W(100) than in W(110).2 This effect is even more drastic when the incident molecule is N2 where the difference between the sticking coefficient in W(100) and W(110) is two orders of magnitude.3,4 The disparity can be understood from the differences in the long-distance interaction between the incident molecules and the surface, as well as from the associated phase space to access the precursor well where dynamic trapping takes place.5,6 A similar explanation in terms of long-distance interaction and dynamic trapping can be invoked to explain the differences in the chemisorption of H2 on W(100) and W(110), as proven by Busnengo et al.7
In the particular case of H2 on W(110), which is the one treated in this work, molecular beams experiments show that the initial sticking probability S0 at normal incidence increases monotonically from S0 ∼ 0.1 to S0 ∼ 0.3 for kinetic energies of the beam below 350 meV.2 Slightly lower values were found by Rettner et al. for incident HD molecules.8 Anyway, the measured values of S0 in W(110) are much smaller than those measured in the rough W(100) and W(111) surfaces.
From the theoretical point of view, Busnengo and Martínez performed classical dynamics for H2 on W(110) and W(100) using a six-dimensional potential energy surface (PES) built from density functional theory (DFT) calculations.7 Their results reproduce the higher reactivity of W(100) as compared with W(110), as well as the general trends of the sticking coefficient in both faces. They show that the difference in reactivity between W(100) and W(110) can be understood in terms of an indirect channel, in which dynamic trapping plays a role, that is significantly reduced in W(110). There is also a large theoretical activity on the study of hot atom and Eley–Rideal recombination processes of hydrogen and its isotopes on W surfaces.9–16 Absorption and diffusion of hydrogen on W surfaces have been analyzed as well.17
Our goal in this work is to provide additional insights on the adsorption mechanisms of H2 on W(110) and improve the accuracy of the currently existing theoretical results. For this purpose, we use ab initio molecular dynamics (AIMD), which is an effective and adaptable method to treat the dynamics of atoms and molecules at surfaces. In AIMD, the adiabatic forces between the atoms are calculated on the fly, at every step of the numerical integration. The value of the electronic energy is obtained in our case from DFT. In some of our calculations, we include van der Waals (vdW) contributions to the exchange correlation term. Comparison of our results with previous theoretical work on the same system allows us to evaluate the relevance of the vdW dispersion forces in the dynamics, as well as the effect of making a full AIMD description of the problem.
The improvement in the theoretical description of the H2/W adsorption is an objective per se, but it will also set the ground for further analysis of other systems of interest. One of the questions that is under study in the fusion community is the modification that the presence of oxygen at the W surface introduces in processes such as adsorption, absorption, diffusion, or recombination. The results obtained in this work will serve as a reference in a future comparison between adsorption features in clean and oxidized surfaces. The methodology employed, proven successful here, can be equally applied without much additional computational effort to the case of oxidized W surfaces.
The outline of the paper is as follows. The details of the theoretical procedure and the numerical implementation are described in Section 2. Our results and the comparison with available experimental data are shown in Section 3. Our main conclusions are summarized in Section 4.
Theory and methods
AIMD calculations within the Born–Oppenheimer approximation (BOA) have been performed using the Vienna Ab initio Simulation Package (VASP).18 These calculations are computationally expensive. Parameters have been chosen looking for an adequate balance between calculation times and accuracy. A statistically significant number of trajectories has been simulated using either the Perdew–Burke–Ernzerhof xc-functional (PBE) or the vdW xc-functional developed by Dion et al. (vdW-DF).19 We choose this specific form of the exchange–correlation term because it has proven to provide satisfactory results in previous calculations of the sticking coefficient for systems with, in principle, similar features in the energy landscape. It was shown to be among the best choices to describe the dissociation probabilities of H2 on Ru(0001).20 It also describes reasonably well the dissociation probabilities of N2 on W(110) at low energies and normal incidence.21 In all calculations, the electron–core interaction is treated within the plane augmented wave (PAW) approximation through the PBE pseudopotentials provided with VASP.22,23 AIMD calculations in VASP using the vdW-DF xc-functional are carried using the routine written and provided by Jiri Klimeš24 based on the Román-Pérez and Soler algorithm.25 The energy cutoff used in all of the calculations was 250 eV, the recommended maximum value for the pseudopotentials we are using. Tests using higher cutoff energies show that the difference in the interaction energy between the H2 molecule and the surface is below 2%. In Fig. 1 the coordinate system employed is depicted. Xcm, Ycm and Zcm represent the coordinates of the center of mass of the H2 molecule while r, θ and ϕ account for the internuclear distance, the polar angle, and the azimuthal angle, respectively. Different lattice constant a = 3.17 Å and a = 3.20 Å are used depending if the PBE xc-functional or the vdW-DF xc-functional are employed in the simulations.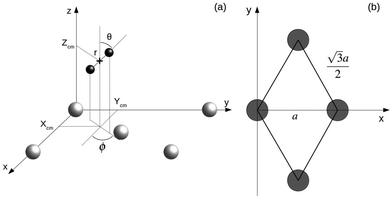 | ||
| Fig. 1 (a) Coordinate system employed to describe the system H2/W(110). Gray and black spheres represent W and H atoms respectively. (b) Surface unit cell of W(110). Gray circles represent W atoms. | ||
To represent the W(110) surface, a 5-layer periodic slab was used. The interlayer distances were relaxed keeping the third layer fixed. Differences in the interlayer distances are below 10−4 Å when comparing with a thicker slab of 7 layers thus allowing for similar precision with less computational effort. The total force acting on each atom is kept under 10 meV Å−1 when the slab reaches its equilibrium state. A (2 × 2) cell and a mesh of 5 × 5 × 1 k-points within the Monkhorst–Pack method26 was used in all cases. The fractional occupancies are determined through the broadening approach of Methfessel and Paxton27 with N = 1 and σ = 0.4. The W atoms are initially fixed to their equilibrium positions but they are allowed to move during the dynamics. The separation distance between the periodic slabs is approximately 18 Å after the surface relaxation. These dimensions ensure that the self interaction of hydrogen with its periodic image is maintained to a minimum and that the calculation times are kept under reasonable bounds. Tests doubling the dimensions of the supercell while removing the W surface and keeping only a H2 molecule show that the interaction energy between hydrogen atoms change in less than 0.3%. The center of mass of the H2 molecule is located initially at Zcm = 9 Å from the surface for every trajectory ensuring minimal interaction between the H and W atoms. The ZPE of the incident molecule is ignored thus all calculations are purely classical. On the plane parallel to the surface, the position of the H atoms and the polar and azimuthal angle are obtained for each trajectory using a conventional Monte-Carlo sampling over the whole 2 × 2 cell. The energies studied are in the range 30–300 meV, spaced approximately by 50 meV for the trajectories simulated using the PBE xc-functional and 25 meV in the case of the ones using the vdW-DF xc-functional. In this energy range theoretical and experimental results are available2,7 and a comparison with these works will be presented in the next section. The integration step for all trajectories is 2 fs and the energy convergence error for electronic relaxation is 10−6 eV. The dissociation probabilities are calculated from 400 trajectories per energy. The criteria for the dissociation of the H2 molecule is established as a separation in the internuclear distance between H atoms of r > 1.5 Å and dr/dt > 0. When the H2 molecule is moving away from the surface and the distance between molecule and surface is Zcm > 4.5 Å, a reflection event is considered.
Diverse theoretical data about the chemisorption of H2 on W(100) and W(110) surfaces have been obtained previously through molecular dynamics (MD) calculations.7 The six dimensional PES employed in this calculations by Busnengo et al.7 was built using the corrugation reducing procedure (CRP)28 to interpolate energy values previously calculated with DFT. The PW91 xc-functional29 was used in the scope of the generalized gradient approximation (GGA) to get these energies. Classical (C) and quasi-classical (QC) calculations were performed within the MD approach. The initial zero point energy (ZPE) of the former is not taken into account while the quantum ZPE of H2 in vacuum is used for the latter. In the following, MD-C and MD-QC will be employed to refer to the results of these calculations.
Results and discussion
Fig. 2 shows the sticking probabilities of H2 on W(110) as a function of the collision energy when using the PBE and vdW-DF xc-functionals. For comparison purposes, MD-C and MD-QC results from ref. 7 are displayed as well. MD-C results using the PW-91 xc-functional and AIMD results using the PBE xc-functional are very close quantitatively and qualitatively, despite the use of different functionals and methodology. On the other hand, once the vdW term is added, the sticking probability drops considerably (between 0.2–0.3) although the trend of the curve is still similar.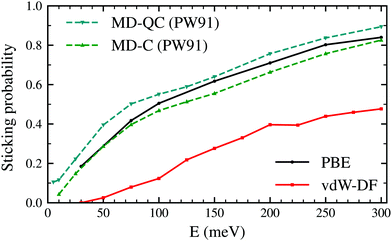 | ||
| Fig. 2 Sticking probabilities for H2 + W(110) as a function of the collision energy. Comparison between molecular dynamic classical and quasiclassical calculations (using a PES obtained with the PW91 xc-functional) from ref. 7 and our classical AIMD calculations using the PBE and vdW-DF xc-functionals. | ||
The latter results are closer quantitatively to what was obtained in molecular beam experiments2 as can be seen in Fig. 3. This suggests that the use of the vdW-DF xc-functional put us one step closer to accurately describe dissociative adsorption in this system. There are however some features absent in our calculation that may explain the still existing quantitative difference with the experimental results. First of all, we do include the motion of the W atoms in the dynamics but we do not fix any initial surface temperature, while the experimental data shown in Fig. 2 are obtained at 300 K. In addition to that, we do not include the zero point energy (ZPE) of H2 in the simulation, which we estimate can increase the value of the sticking coefficient by less than 0.1, as shown in ref. 7. Other possible improvements for our calculation include quantum effects in the dynamics30,31 and electronic non-adiabatic effects.32,33
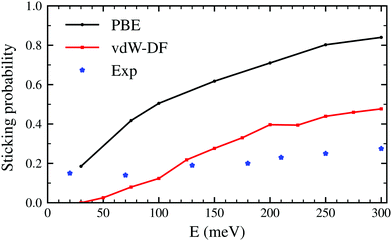 | ||
| Fig. 3 Sticking probabilities for H2 + W(110) as a function of the collision energy. Comparison between initial sticking probabilities obtained in molecular beam experiments as reported in ref. 2 and classical ab initio molecular dynamics using the PBE and vdW-DF xc-functionals. | ||
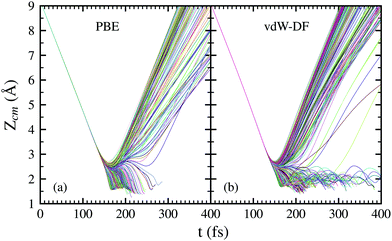
In Fig. 4, the time evolution of the distance between the H2 molecule's center of mass and the surface is displayed. Each line represents one trajectory starting with random initial values for Xcm, Ycm, θ and ϕ. The initial distance to the surface is fixed at Zcm = 9 Å and the separation of hydrogen atoms is set at the equilibrium distance r = 0.741 Å. Lines ending before 400 fs symbolize a dissociation event at that point. The initial collision energy is 200 meV in all cases. For other initial collision energies tested in our calculations, the general behavior is very similar. Differences arise, of course, in the number of reflected and dissociated molecules that varies according to Fig. 2.
Both panels of Fig. 4 exhibit a similar character for the whole process. After approaching the surface, either the molecule bounces back quickly or finds its way to get close to the W atoms. If the latter happens, the trajectories end up in a dissociation event in most of the cases. This effectively means that dissociative adsorption is determined far away from the surface, at roughly Zcm = 2–2.5 Å. Discussions about this behavior can be also found in ref. 7 and is similar to what happens with N2 on the same surface.5,6 For both xc-functionals this effect looks the same, although the dissociation process is more direct for the PBE functional. However, the distance at which adsorption is effectively determined depends on the initial collision energy, as can be seen in Fig. 5. The latter point can be explained if we consider that molecules with higher initial energy can get closer to the surface as it allows them to surpass to certain extent the potential energy of the surface on the repulsive zones of the PES. Below 150 meV all molecules that reach 2.5 Å will get dissociated while for higher energies that distance is reduced to approximately 2 Å.
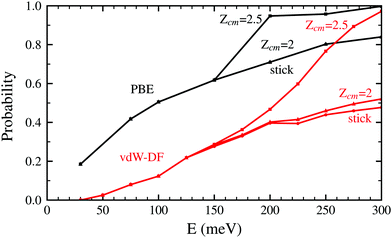 | ||
| Fig. 5 Probability to reach the distance Zcm = 2.5 Å and Zcm = 2 Å for H2 molecules approaching the W(110) surface as a function of the initial kinetic energy. Black lines correspond to the use of the PBE xc-functional while red lines are obtained using the vdW-DF functional. The sticking curves from Fig. 2 and 3 are shown here as well to facilitate the comparison. | ||
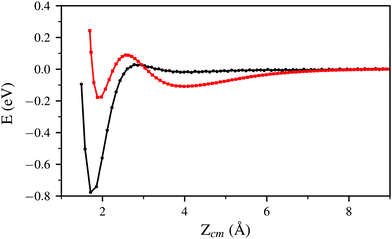
In Fig. 2 and 5 it is noticeable that the probability of sticking and the probability of H2 molecules reaching distances close to the surface is always higher when using the PBE xc-functional than when using the vdW-DF xc-functional. Fig. 6 helps to shed some light on this behavior by representing two trajectories leading to dissociative adsorption with equal initial coordinates and collision energy of 200 meV. The main difference between both trajectories is the use of the PBE xc-functional while simulating one of them and the vdW-DF xc-functional when simulating the other. From Fig. 6 we can appreciate the stronger attractive character of the vdW-DF xc-functional at distances far away from the surface (3–6 Å). On the other hand, at closer distances the use of this functional causes greater repulsion than when using the PBE xc-functional. This explains the decrease in probability seen in Fig. 2 and 5. Fig. 6 shows only two representative trajectories. Other trajectories at different energies have been analyzed and all of them share a similar behavior.
Even if the adsorption is determined far away from the surface, the subsequent dynamics of each trajectory may vary. In the case of the PBE functional, most of the dissociation takes place through a fast and direct process. In the case of the vdW functional, however, most of the molecules that are able to cross the bottleneck of Zcm = 2–2.5 Å spend some time hovering and bouncing on the surface before becoming eventually dissociated. This dynamical process includes the motion of the molecules looking for a more suitable position and/or angular configuration that allow them to approach the surface and finally dissociate. The time delay in the dissociation introduced by this dynamic trapping is longer for the vdW-DF xc-functional than for the PBE functional. In average, trajectories leading to sticking experience 0.9 rebounds before dissociation when using PBE while the number of rebounds raise to 1.8 when the vdW-DF xc-functional is employed.
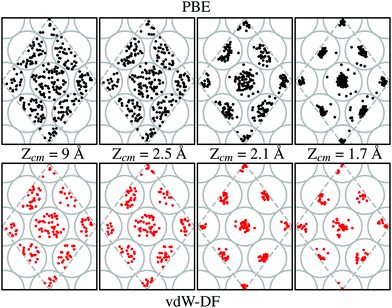
Our calculations show that the preferential path for the H2 molecules to approach the W(110) surface is above the top sites. This is shown in Fig. 7. Black and red dots (for calculations using PBE and vdW-DF respectively) represent the position of the center of mass of H2 on trajectories leading to dissociation over the 2 × 2 cell used in this work (gray dashed lines). Grey circles show the position of W atoms on the first layer to help with the interpretation at different distances from the surface. In each of the sub-panels the position of the black and red dots has been obtained from the step of the calculations whose Zcm coordinate is closer to the one displayed. Through cuts at different distances from the surface it can be observed a movement toward the top positions. This trend is independent of the xc-functional employed, although it seems that the higher concentration near these spots happens around 2.1 Å when vdW-DF is used and 1.7 Å when using PBE. This general behavior is consistent with previous theoretical works.7
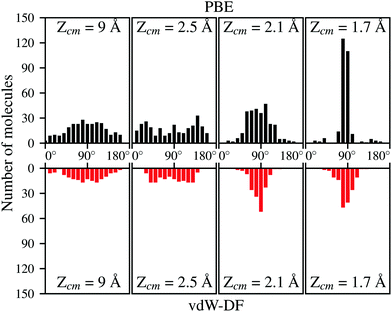
Apart from the positions in the XY plane, the angular configuration also plays an important role when deciding which molecules are undergoing adsorption on the surface. Fig. 8 show the distribution per molecule of the polar angle θ at the same distances from the surface than in Fig. 7. For both xc-functionals is easy to spot the predominance of angles close to 90°. The distribution of the azimuthal angle ϕ on the contrary does not present any remarkable features. It needs to be mentioned that for trajectories that spend a considerable time near the surface (most of them when using vdW-DF), the data from Fig. 7 and 8 are collected when molecules approach the surface for the first time. It seems then that molecules with axis parallel to the surface and above the top positions have the greatest chances to get closer to the surface and undergo a future dissociative adsorption. This behavior helps to explain why the dissociation is effectively decided far away from the surface. At roughly 2.1 Å for the initial kinetic energy of 200 meV, only the H2 molecules with suitable conditions (see Fig. 7 and 8) will not be reflected back to the vacuum, creating a bottleneck above top sites. In our simulations almost the totality of molecules passing this point will be dissociated hinting that, once the bottleneck is crossed, there is a very limited phase space for the molecules to be reflected back to the vacuum.
Conclusions
In summary, we have used AIMD to understand the dissociation dynamics of H2 on W(110). We have shown that the use of the vdW-DF xc-functional improves the comparison of the theoretical description with available experimental information. Our analysis of the process shows that the dissociation is decided at a distance relatively far from the surface, in a way similar to what happens in the dissociation of H2 on W(100) or in the dissociation of N2 on W surfaces. Almost all hydrogen molecules able to reach a given distance from the surface (≈2–2.5 Å, depending on the initial kinetic energy) are eventually dissociated. When using the vdW-DF xc-functional, we obtain a short dynamic trapping at the surface before the dissociation takes place. This is a mechanism that nevertheless has no influence in the final values of the dissociation probability.The use of AIMD is an alternative to other theoretical approaches based on the construction of interpolated PESs. A weakness of AIMD is that it can be computationally expensive and therefore the number of trajectories that are launched can be significantly smaller than those launched using interpolated PESs, with the subsequent damage in statistical accuracy for low probability processes. It has other advantages, however, and one of them is that it can address more complex systems, often without much additional computational effort. In the case of hydrogen interacting with tungsten surfaces, a problem of current interest is the effect that the oxidation of the surface may have in the hydrogen adsorption process. This is of particular interest for the fusion community, but not only. The methodology used in this work can be easily extended to the case of oxidized W surfaces and the results presented here can be used as a benchmark to quantify the effect that the presence of oxygen atoms adsorbed on the surface may have on the dissociation dynamics of H2 on these surfaces. Work along these lines is in progress.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. R. F. acknowledges financial support by the University of Bordeaux. This work was conducted in the scope of the transborder joint Laboratory “QuantumChemPhys: Theoretical Chemistry and Physics at the Quantum Scale” (ANR-10-IDEX-03-02). This work has been supported in part by the Basque Departamento de Educación, Universidades e Investigación, the University of the Basque Country UPV/EHU (Grant No. IT1246-19) and the Spanish Ministerio de Ciencia e Innovación (PID2019-107396GB-I00/AEI/10.13039/501100011033).References
- J. Knaster, A. Moeslang and T. Muroga, Nat. Phys., 2016, 12, 424–434 Search PubMed.
- H. F. Berger, C. Resch, E. Grösslinger, G. Eilmsteiner, A. Winkler and K. Rendulic, Surf. Sci., 1992, 275, L627–L630 CrossRef CAS.
- H. E. Pfnür, C. T. Rettner, J. Lee, R. J. Madix and D. J. Auerbach, J. Chem. Phys., 1986, 85, 7452–7466 CrossRef.
- C. T. Rettner, E. K. Schweizer and H. Stein, J. Chem. Phys., 1990, 93, 1442–1454 CrossRef CAS.
- M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2006, 97, 056102 CrossRef CAS.
- M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, J. Chem. Phys., 2006, 125, 144705 CrossRef CAS.
- H. F. Busnengo and A. E. Martínez, J. Phys. Chem. C, 2008, 112, 5579–5588 CrossRef CAS.
- C. Rettner, L. DeLouise, J. Cowin and D. Auerbach, Chem. Phys. Lett., 1985, 118, 355–358 CrossRef CAS.
- B. Jackson and M. Persson, J. Chem. Phys., 1992, 96, 2378–2386 CrossRef CAS.
- M. Rutigliano and M. Cacciatore, Phys. Chem. Chem. Phys., 2011, 13, 7475–7484 RSC.
- R. Pétuya, C. Crespos, E. Quintas-Sanchez and P. Larrégaray, J. Phys. Chem. C, 2014, 118, 11704–11710 CrossRef.
- R. Pétuya, M. A. Nosir, C. Crespos, R. D. Muiño and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15325–15332 CrossRef.
- O. Galparsoro, R. Pétuya, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15434–15442 CrossRef CAS.
- O. Galparsoro, R. Pétuya, H. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, Phys. Chem. Chem. Phys., 2016, 18, 31378–31383 RSC.
- O. Galparsoro, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2017, 121, 19849–19858 CrossRef CAS.
- C. I. Becerra, C. Crespos, O. Galparsoro and P. Larrégaray, Surf. Sci., 2020, 701, 121678 CrossRef CAS.
- D. F. Johnson and E. A. Carter, J. Mater. Res., 2010, 25, 315–327 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- M. Wijzenbroek and G. J. Kroes, J. Chem. Phys., 2014, 140, 084702 CrossRef CAS.
- L. Martin-Gondre, J. I. Juaristi, M. Blanco-Rey, R. D. Muiño and M. Alducin, J. Chem. Phys., 2015, 142, 074704 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. C. V. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- H. F. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- A. Rodríguez-Fernández, L. Bonnet, C. Crespos, P. Larrégaray and R. Díez Muiño, J. Phys. Chem. Lett., 2019, 10, 7629–7635 CrossRef.
- A. Rodríguez-Fernández, L. Bonnet, C. Crespos, P. Larrégaray and R. Díez Muiño, Phys. Chem. Chem. Phys., 2020, 22, 22805–22814 RSC.
- M. Alducin, R. D. Muiño and J. I. Juaristi, Prog. Surf. Sci., 2017, 92, 317–340 CrossRef CAS.
- P. Saalfrank, J. I. Juaristi, M. Alducin, M. Blanco-Rey and R. Díez Muiño, J. Chem. Phys., 2014, 141, 234702 CrossRef.
| This journal is © the Owner Societies 2021 |