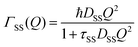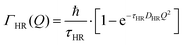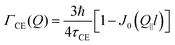Open Access Article
Open Access ArticleNeutron spectroscopy study of the diffusivity of hydrogen in MoS2
Vitalii
Kuznetsov
 ab,
Wiebke
Lohstroh
c,
Detlef
Rogalla
d,
Hans-Werner
Becker
d,
Thomas
Strunskus
e,
Alexei
Nefedov
ab,
Wiebke
Lohstroh
c,
Detlef
Rogalla
d,
Hans-Werner
Becker
d,
Thomas
Strunskus
e,
Alexei
Nefedov
 f,
Eva
Kovacevic
g,
Franziska
Traeger
b and
Peter
Fouquet
f,
Eva
Kovacevic
g,
Franziska
Traeger
b and
Peter
Fouquet
 *a
*a
aInstitut Laue-Langevin, CS 20156, 38042 Grenoble Cedex 9, France. E-mail: fouquet@ill.fr; Tel: +33 476 20 7204
bWestfälische Hochschule, Gelsenkirchen, Bocholt, Recklinghausen, August-Schmidt-Ring 10, 45665 Recklinghausen, Germany
cTechnische Universität München, Forschungsneutronenquelle Heinz Maier-Leibnitz (FRM II), Lichtenbergstr. 1, 85747 Garching, Germany
dRUBION, Ruhr-Universität Bochum, Universitätsstr. 150, 44801 Bochum, Germany
eTechnische Fakultät der Universität Kiel, Institut für Materialwissenschaft-Materialverbunde, Kaiserstr. 2, 24143 Kiel, Germany
fKarlsruher Institut für Technologie (KIT), Institut für Funktionelle Grenzflächen (IFG), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
gGREMI, UMR 7344 CNRS/Université d’Orléans, 45067 Orléans, Cedex 2, France
First published on 18th January 2021
Abstract
The diffusion of hydrogen adsorbed inside layered MoS2 crystals has been studied by means of quasi-elastic neutron scattering, neutron spin-echo spectroscopy, nuclear reaction analysis, and X-ray photoelectron spectroscopy. The neutron time-of-flight and neutron spin-echo measurements demonstrate fast diffusion of hydrogen molecules parallel to the basal planes of the two dimensional crystal planes. At room temperature and above, this intra-layer diffusion is of a similar speed to the surface diffusion that has been observed in earlier studies for hydrogen atoms on Pt surfaces. A significantly slower hydrogen diffusion was observed perpendicular to the basal planes using nuclear reaction analysis.
1 Introduction
Diffusion of molecules on surfaces is crucial for a range of chemical processes, such as catalysis or sensing, but it remains extremely difficult to observe experimentally on atomic length scales. This is particularly true for the case of light molecules that have few electrons, such as hydrogen. Substantial breakthroughs in this field have been achieved by quasi-elastic helium atom scattering (QHAS) and quasi-elastic neutron scattering (QENS) in recent years.1–3 In the following we present a study that exploits QENS in this tradition.With an increase in renewable energy production, the problem of energy storage becomes more and more significant. One of the most promising ideas is storage in form of hydrogen gas. It involves the production of hydrogen by electrolysis and later reconversion of hydrogen in fuel cells. It is of paramount importance for these processes to be carried out most efficiently with the most readily accessible materials. Therefore, there have been intense studies in the search for catalyst materials for the hydrogen and oxygen evolution reactions,4,5 in order to replace the expensive platinum, which is widely used today.
Molybdenum disulphide, MoS2, has shown promising behaviour as a catalyst in the hydrogen evolution reaction (HER),6–10 which is completely in line with its known activity for hydrogenation reactions. However, the structural properties are rather complex. MoS2 forms a crystal of hexagonal Mo and S layers, with an interlayer distance of 6.2 Å.11 On the basis of this structure, three stacking variants have been observed, each with slightly different conductivity and catalytic activity.6,12 In earlier studies catalytic activity had been attributed to amorphous particles,13 but recently it has been shown that although the active centres are probably sulphur edge atoms, the stoichiometry of the active surface is 1Mo:2S, the same as for the perfect crystal.6,7,10,14
However, the amount of active centres may not be the only reason for chemical activity. For palladium, for example, during hydrogen evolution also the movement of hydrogen atoms to sites below the surface has been observed (HIR, hydrogen injection reaction).15 For platinum surfaces, the recombinative desorption of hydrogen was shown to be the rate limiting step in HER.16 For MoS2 some theoretical studies suggest that intercalation of hydrogen is possible. Therefore, the diffusion of hydrogen can be expected to play a role in the overall reaction mechanism.17,18
Within the scope of the present study we investigated the adsorption and diffusion of hydrogen on MoS2 using quasi-elastic neutron scattering (QENS) and neutron spin-echo spectroscopy (NSE) together with nuclear reaction analysis (NRA) and X-ray photoelectron spectroscopy (XPS).
This paper is organised as follows: after this short introduction, we will give a short description of the theoretical model that we use to analyse the spectroscopic neutron scattering data. Then, we will describe the sample preparation and the experimental apparatus that we used. Finally we will describe our experimental findings and discuss them in the framework of earlier studies.
2 Theory
A general equation describing the incoherent neutron scattering off the adsorbed hydrogen consists of four parts:2 the Debye–Waller factor,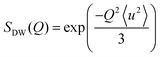 , the elastic scattering function, Sel(Q,ω), the quasi-elastic scattering function, Sqe(Q,ω), and a resolution function R(Q,ω):
, the elastic scattering function, Sel(Q,ω), the quasi-elastic scattering function, Sqe(Q,ω), and a resolution function R(Q,ω):| S(Q,ω) = SDW(Q)δ(ω) * [Sel(Q)δ(ω) + (1 − Sel(Q))Sqe(Q,ω)] × R(Q,ω). | (1) |
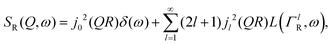 | (2) |
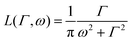 is a normalised Lorentzian function and
is a normalised Lorentzian function and 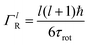 is the half-width at half-maximum (HWHM) of the corresponding rotational contribution with τrot being the characteristic time of rotation. We note that for describing the motion of hydrogen atoms, the rotational terms disappear (SR(Q,ω) ≡ δ(ω)).
is the half-width at half-maximum (HWHM) of the corresponding rotational contribution with τrot being the characteristic time of rotation. We note that for describing the motion of hydrogen atoms, the rotational terms disappear (SR(Q,ω) ≡ δ(ω)).
Depending on a system, translational motion can either have a free or a spatially constrained behaviour. In the former case it can be expressed as a simple normalised Lorentzian 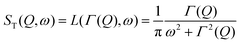 . In the latter case a part of the quasi-elastic scattering remains elastic and a delta-function term, A0(Q)δ(ω), is added:2
. In the latter case a part of the quasi-elastic scattering remains elastic and a delta-function term, A0(Q)δ(ω), is added:2
| ST(Q,ω) = A0(Q)δ(ω) + (1 − A0(Q))L(ΓT,ω), | (3) |
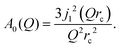 | (4) |
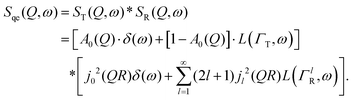 | (5) |
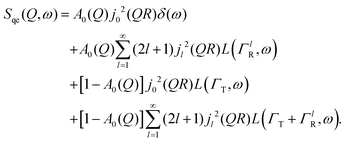 | (6) |
A quasi-elastic broadening caused by translational diffusion ΓT depends heavily on the type of motion, which can be continuous or jump-like. A number of different models have been considered that describe each kind of diffusion as usually several of them need to be tested on a system in order to get a reliable result. Three models will be discussed in detail later in the Results and discussion section.
Here, we will consider a commonly occurring case, ΓlR ≪ ΓT, which allows us to neglect ΓlR in the last series in (6). Thus, the fourth item becomes 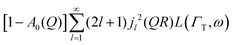 . The summation here starts from l = 1, however one can note that the third item [1 − A0(Q)]j02(QR)L(ΓT,ω) is actually a term of this sum with l = 0. Hence, withdrawing ΓT from the sum as it does not depend on l, one can get:
. The summation here starts from l = 1, however one can note that the third item [1 − A0(Q)]j02(QR)L(ΓT,ω) is actually a term of this sum with l = 0. Hence, withdrawing ΓT from the sum as it does not depend on l, one can get:
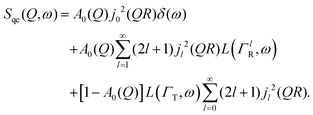 | (7) |
Within the scope of our experiment (R = 0.37 Å for the hydrogen molecule, Q < 2 Å−1) we generally have QR < 0.74 and in the first series we can neglect all terms higher than the 3rd order, as 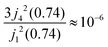 . The last sum equals unity as
. The last sum equals unity as 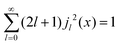 for any value of the variable x.28 Finally, we obtain:
for any value of the variable x.28 Finally, we obtain:
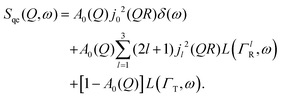 | (8) |
By substituting eqn (8) into eqn (1), adding a background term and regrouping elements we end up with the ultimate fitting expression for our quasi-elastic spectra:
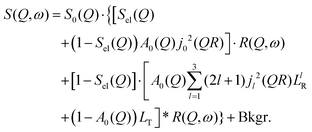 | (9) |
Here, S0(Q) = I0·SDW(Q) is an overall intensity factor, which accounts for signal loss/gain due to vibrations (Debye–Waller factor SDW(Q)) and due to hydrogen desorption/adsorption (scaling factor I0).
3 Experimental
3.1 Sample preparation
Molybdenum disulphide single crystals with a thickness of about 0.2 mm and edge lengths between 6 and 15 mm were obtained from PLANO (PLANO GmbH Wetzlar, Germany, distributor of SPI, USA). Hydrogen loading via electrolysis was performed several times, prior to every experiment. For nuclear reaction analysis (NRA) one MoS2 single crystal was loaded with hydrogen shortly before the experiments, and for the XPS study four days in advance. Neutron studies require a larger volume of material and therefore all 10 single crystals were used. They were hydrogen loaded 4–6 days prior to the experiments. The loading procedure was the same for every experiment with slight variations in the duration of the process. Those samples that had been used in experiments before were degassed at temperatures >750 K. Prior to each loading all MoS2 single crystals were cleaved by peeling off the surface layer using adhesive tape. Then the crystals were mounted onto a tantalum plate electrode and subsequently loaded by electrolysis in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of phosphoric acid (H3PO4 85%) and glycerol, using a Pt counter electrode. The electrolysis lasted 2 hours at 4 V on one side of the crystal for the nuclear reaction analysis, 4 hours at 4 V on one side for XPS and 4 hours at 3 V on each side for neutron experiments.
1 mixture of phosphoric acid (H3PO4 85%) and glycerol, using a Pt counter electrode. The electrolysis lasted 2 hours at 4 V on one side of the crystal for the nuclear reaction analysis, 4 hours at 4 V on one side for XPS and 4 hours at 3 V on each side for neutron experiments.
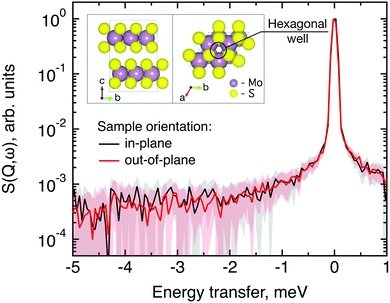
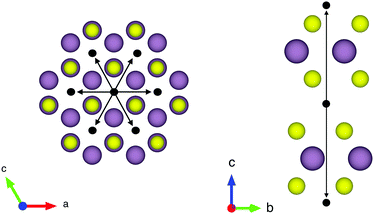
The structure of MoS2 shown in Fig. 5 and 12 was plotted using the VESTA 3 software.29
3.2 Nuclear reaction analysis
Hydrogen depth profiles were measured by irradiating the sample with a 15N ion beam and counting the emitted gamma-rays on the NRRA beamline at RUBION, Bochum, Germany. The underlying reaction is:| 15N + 1H → 12C + α + γ, |
3.3 X-ray photoelectron spectroscopy
XPS surface characterisation was carried out on the HE-SGM station34 at the BESSY II synchrotron, Helmholtz-Zentrum Berlin (HZB), Germany. The XPS signal was collected with a Scienta R3000 XPS analyser. The pass energy was set to 50 eV in order to decrease the background. Excitation energies used were 650 eV for the oxygen 1s line, and 385 eV for the other elements. The energy binning step was set to 50 meV. Data were collected posterior to the sample being heated to several temperatures: 300, 400, 450 and 500 K, respectively. During heating the pressure in the analysis chamber rose due to desorption from the sample. Therefore we had to wait several minutes until the pressure dropped to a value appropriate for the XPS experiment. The measurements thus show the state of the surface several minutes after the sample had been heated up to a certain temperature. For energy calibration the adventitious carbon peak at the corresponding temperature was used. The background was described by a Shirley step model.35 The intensities were corrected for the atomic subshell photoionisation cross sections obtained by Yeh and Lindau.36 Data treatment was performed using the XPST package within the Igor Pro software package (WaveMetrics, Portland, USA).3.4 Quasi-elastic neutron scattering experiments
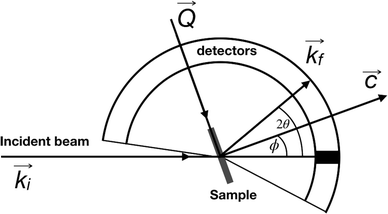
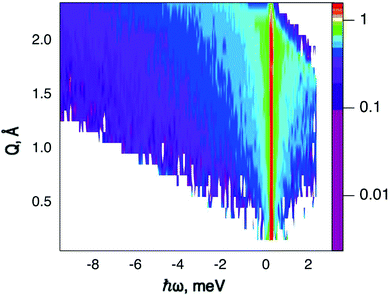
QENS data were collected at the neutron time-of-flight (TOF) spectrometer TOFTOF37 at the research neutron source Heinz Mayer-Leibniz (FRM II), Garching, Germany, at a wavelength λ = 5 Å. The samples were held in a flat aluminium sample cell. Two sample orientations, an in-plane and an out-of-plane set-up, were used in order to obtain information about dynamics parallel and perpendicular to the MoS2(0001) basal plane, respectively. For both set-ups the surface normal (crystallographic c-axis) was within the scattering plane. For the in-plane set-up, the c-axis was turned by ϕ = 20° away from the direct beam direction, i.e., Q was within the basal plane exactly for a scattering angle 2θ = 40° (Fig. 1). For the out-of-plane set-up we used ϕ = 110°, i.e., for 2θ = 40° the momentum transfer was perpendicular to the basal planes. The temperatures scanned in the out-of-plane set-up were 3, 100 and 300 K, whereas in the in-plane set-up data at 3, 50, 100, 200, 300, 400, and 500 K were measured. The spectra were measured consecutively with rising temperature up to 500 K and a further spectrum at 300 K in the in-plane set-up was measured after the last 500 K measurements to check for permanent changes of the sample upon heating to 500 K. Spectra at 3 K were used as a resolution function. Data reduction was performed using the Mantid software package.38 Every spectrum was normalised to the beam monitor signal and, after deduction of an empty container spectrum, corrected by a vanadium spectrum to calibrate for variations in detector efficiency. Both empty container and vanadium spectra were measured at room temperature. All data were binned in energy transfer space from −10 to 3 meV with a step of 0.05 meV and in momentum transfer space from 0.05 to 2.35 Å−1 with a step of 0.1 Å−1. A representative QENS scan of MoS2 at 400 K in the in-plane sample geometry is shown in Fig. 2. No Bragg reflections or significant data reduction artefacts are observed. Further in the text the geometry specification is dropped out, by default referring to the in-plane set-up. Every reference to the out-of-plane set-up is indicated explicitly.3.5 Neutron spin echo measurement
Neutron spin echo (NSE) measurements were performed on the NSE spectrometer IN11 at Institut Laue-Langevin (ILL), Grenoble, France,39 using the high signal set-up IN11C, which uses a 30° detector bank.40 Here, we used a wavelength of λ = 5.5 Å for maximum signal. Following the same procedure as in the QENS study, data were collected in two sample orientations with the surface parallel and perpendicular to the scattering vector Q. The spectra were normalised using a standard procedure: all data were divided by a spectrum that was obtained in situ at 2 and 5 K for the in-plane and out-of-plane geometry, respectively. At these temperatures the system can safely be assumed to be static in the dynamic window of the spectrometer. The experiment covered a range of momentum transfers of Q = [0.1 to 0.7] Å−1 and sample temperatures up to 600 K.4 Results and discussion
4.1 Nuclear reaction analysis
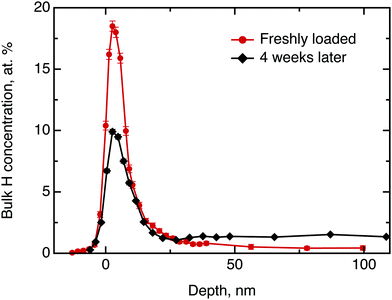
We commence the description of our experiments with the structural and chemical characterisation of the samples: Fig. 3 shows the hydrogen concentration in dependence of the depth measured by NRA quickly after electrolysis loading of MoS2 and after four weeks of ageing, respectively. For the freshly prepared sample the data clearly show a high concentration of hydrogen in the surface and sub-surface region and vanishing signal at higher depths (we note that the width of the surface peak is equal to the width dictated by the energy resolution of the incoming beam and, hence, the width of the surface peak gives only an upper limit for the width of the distribution function at the surface). After 4 weeks of ageing in ambient air environment, the surface peak decreased in intensity by half and a significant bulk signal was recorded that remained constant from a depth of 20 nm up to 100 nm, the maximum penetration depth recorded in our NRA measurements. Hence, the data show a diminution of hydrogen containing species in the surface layer and an increase of the concentration of hydrogen containing species in the bulk. After this first straightforward result, however, there remain two important further questions: (a) what hydrogen species do we have in this experiment and (b) can we say anything about the diffusivity?Considering the first question, one can imagine three hydrogen containing species that can be present in significant concentrations after the electrolytical loading: hydrogen atoms, hydrogen molecules and water. To distinguish between them, we have performed a test experiment with a sample as received and a sample that was exposed to pure water without electrolysis. In these cases, we also obtained a surface peak at the start of the experiment, but no diffusion into the bulk over time. Therefore, we can conclude that water may contribute significantly to the surface signal, but does not penetrate across the basal planes into the bulk in a significant amount. The hydrogen containing species that are found in the bulk of the sample after electrochemical loading are, hence, hydrogen atoms or hydrogen molecules. The concentration scale, in general, is not fully applicable to the surface peak due to several reasons, namely, hydrogen multilayer formation, surface contaminations and failure of the thick target approximation.33 The first is not expected in the current experiment, however, light organic contaminations and only partial validity of the thick target approximation renders the concentration scale, to some extent, overestimated. Nevertheless, it is still possible to extract some information from the decay of the surface peak over time: We have demonstrated above, that only hydrogen molecules or hydrogen atoms diffuse into the bulk. This migration must lead to a loss in intensity of the hydrogen surface peak. Simultaneously, a gain in intensity may be observed due to a possible water adsorption from the atmosphere at ambient air conditions. Since during the ageing process the surface peak area decreased approximately by half, we conclude that several hours after loading process at least half of surface and subsurface hydrogen is in form of atomic and molecular hydrogen.
Now, we will try to analyse the diffusion in some more detail. The above considerations about the limited usability of the concentration scale in application to the surface peak concern mostly the depth profile up to ≈15 nm. Therefore the data beyond 15 nm can be used to extract some quantitative results. Fitting the data for the freshly loaded sample to the solution of Fick's second law of diffusion in the form of a Gaussian yields an order of magnitude for the diffusion coefficient D⊥ of 10−21 m2 s−1. Thus, the observed diffusion is extremely slow. However, even such a slow diffusion would result in almost uniform hydrogen concentration across the bulk after a 4 weeks ageing period, which is clearly observed in the data.
4.2 X-ray photoelectron spectroscopy
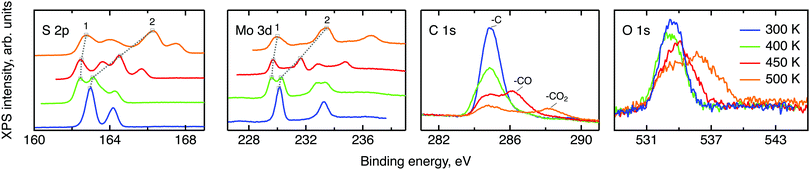
Prior to the neutron spectroscopy study of hydrogen diffusivity, see below, the chemical state of the MoS2 surface was monitored by X-ray photoelectron spectroscopy at temperatures up to 500 K (Fig. 4). The XPS spectra reveal dramatic changes in the electronic structure of the MoS2 surface upon heating. The splitting of the molybdenum and sulphur lines into two peaks each with almost identical areas was observed starting from 400 K up to the highest measured temperature 500 K, indicating the separation of the surface into oxidised and slightly reduced sections. These sections may be assigned to the surface and subsurface regions respectively. We note, that the analysis depths of the XPS experiment is limited to less than 10 nm.41 In view of the results of the NRA study, this covers the region, where we expect to find water and hydrogen. The analysis of the Mo and S binding energies suggests that at room temperature the surface consists mostly of clean MoS2, i.e. Mo4+ and S2−. Heating to 400 K partially reduces the surface, with Mo staying closer to the 4+ state than to 3+. Further increase in temperature prompts a new oxidation process, which results in a significant increase in the binding energy of the more oxidised state (labelled 2 in Fig. 4), causing Mo6+ to be formed at 500 K. The assignment of oxidation states remains tentative, however, since charging of the modified part of the surface may also have an impact on the observed binding energy. Keeping this reservation in mind we describe the occurring process as follows. During the loading procedure, apart from the production of –SH groups on the surface, a number of hydrogen atoms are incorporated into the bulk. At 400 K they become mobile and are subsequently bound also in the subsurface region, thus performing a reduction. At 450 K hydrogen atoms start to desorb from the surface, which leads to a surface oxidation. At the same time, as the H coverage on the surface decreases, subsurface hydrogen starts to migrate further to the surface, slowing down the surface oxidation and simultaneously oxidising the subsurface region. At 500 K the same process continues. It is also important to note that since MoS2 is considered relatively active for the hydrogen evolution reaction, another source of subsurface H atoms apart from the bulk H exists, namely, catalytically split H2 molecules. However in the XPS experiment little information can be drawn for hydrogen molecules, since they are not chemisorbed to the host material.The XPS data contain also carbon and oxygen lines. Both elements are likely to be adsorbed from the atmosphere in various forms. Prior measurements utilising deuterium induced gamma emission (DIGE) at RUBION, Bochum, Germany, showed a bulk oxygen content at a level of 0.5 at%. Hence, oxygen should mostly be located in the surface or subsurface region. The interpretation of the O 1s line requires a careful analysis: molybdenum oxides are expected to create an XPS signal around 530 eV42,43 and, thus, are not observed in this study. The other oxygen containing species that are expected in our samples are adsorbed water and organic molecules containing oxygen also in the form of –CO and –CO2. The binding energies of oxygen in these compounds are very similar and, therefore, cannot be resolved within the O 1s line. However, since the area under the peaks is proportional to the amount of corresponding C and O atoms in a sample, in first order approximation, some information can be drawn from the behaviour of the C and O lines under temperature treatment. If every oxygen atom was bound to carbon, then the desorption picture, i.e. the loss of area under a peak, would be the same for both the O 1s line and the peaks corresponding to –CO and –CO2. In our case no simple correlation can be established. Therefore it can be concluded that a significant amount of the observed oxygen is bound in water. As we have shown in the NRA study, however, this water has to be in the surface or subsurface regions. Additional XPS measurements of two MoS2 single crystals loaded with hydrogen under the same conditions and heated to 500 K ex situ showed a great difference between the areas of the corresponding O 1s lines. Given a very small measuring spot size, the most probable cause of this effect is water agglomeration within volume defects. In this case, the amount of oxygen seen in the XPS experiment would depend on whether the incoming X-ray beams hit the water agglomerate or not. The O 1s line splitting that appears at 500 K indicates that a large fraction of the water molecules transfer from a strongly adsorbed state to almost free H2O molecules at this temperature.44,45
To conclude, the XPS study shows that chemisorbed hydrogen shows a thermally activated mobility in MoS2 when the temperature of the sample is raised to 400 K or above. This leads to a chemical transformation of the sample as reduction and oxidation of MoS2 can be observed. Strongly adsorbed water is also present to some extent in the surface or subsurface region up to elevated temperatures and becomes free at 500 K.
4.3 Neutron time-of-flight spectroscopy – hydrogen dynamics
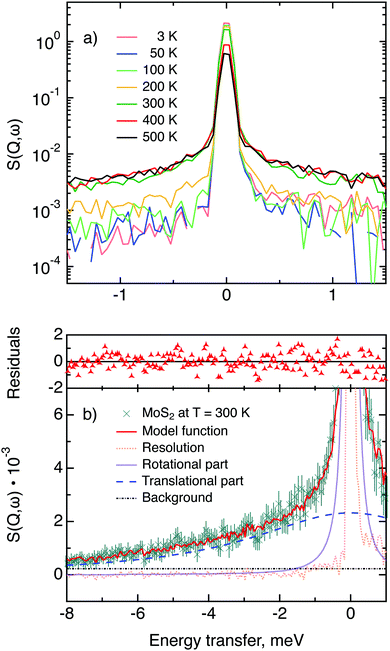
The first subject that we aimed to address in the neutron scattering study was the impact of the layered structure of MoS2 on the hydrogen dynamics. This should be observable through a difference between the quasi-elastic spectra obtained at different sample orientations, i.e., with the momentum transfer being parallel or perpendicular to the basal planes of the 2D samples (Fig. 5). In QENS measurements, the diffusive dynamics of sample atoms and molecules lead to a broadening of the elastic scattering line (around energy transfer ħω = 0).2 In our QENS spectra no systematic difference between the two sample orientations was found in the normalised data. This means that the properties of hydrogen diffusion parallel and perpendicular to the MoS2 basal planes are mostly indistinguishable within the spectroscopic window of the present TOF QENS measurements. However, since the lowest exploitable Q values were relatively high, this finding does not put strict constraints on the model of hydrogen diffusion. Based on the structure of molybdenum disulphide we assume two possible diffusion patterns. In the first case hydrogen moves identically between the layers of MoS2 and through the hexagonal wells (Fig. 5 inset), thus the length scale is of the order of the c unit cell parameter, i.e., 6.15 Å. The second possibility is a motion completely restricted by the sulphur planes, i.e., with no diffusion through the wells. In this case, the characteristic length of diffusion should be no larger than the gap between the sulphur planes of 3 Å. Fig. 5 displays the spectra at Q = 0.85 Å−1, the momentum transfer for which the corresponding scattering angle best satisfies the in-plane and out-of-plane condition.Now we turn to the in-plane data at various temperatures. Below 200 K any hydrogen motion appeared to be too slow to fit into the spectroscopic window of the instrument, thus yielding no detectable quasi-elastic broadening (Fig. 6a). At 200 K a clearly visible difference between the data and a resolution function occurs, however it is still too small to allow meaningful quantitative fits. A major gain in quasi-elastic signal takes place when heating the sample up to 300 K, and already at this temperature the QENS broadening exhibits clear signs of two different types of motion being present in the sample (Fig. 6b). Taking into account their dependence on the Q vector, which will be discussed later, we interpret these two modes preliminarily as translational and rotational diffusion of hydrogen. The assignment of these modes to specific hydrogen containing species, i.e., hydrogen atoms, hydrogen molecules or water, is difficult. The NRA experiments demonstrate that water does not penetrate into the sample volume and that at least half of the hydrogen is in the form of atoms and molecules. The XPS measurements also show that water changes its binding energy only just below 500 K. Since in the QENS data no radical alterations are observed when heating from 400 to 500 K and since the neutron signal comes from the whole sample simultaneously, we conclude that water may not play a major role in the QENS signal. Now we consider if we can distinguish between the mobility of H2 and H. Obviously, hydrogen molecules may exhibit both translational and rotational diffusion, whereas atoms are expected to show mostly translational motion with only some degree of frustrated rotational modes. In addition, the XPS experiment indicates that H atoms start moving at ≈400 K, whereas in the QENS data a quasi-elastic broadening can already be observed at room temperature. This signal does not change qualitatively at elevated temperatures, so we conclude that most of the signal in the QENS experiment is caused by H2 mobility.
In view of these considerations the whole set of data at temperatures higher than 200 K was treated by means of the rotational–translational model described in the Theory section above (eqn (9)). However, several spectra at low and high Q were not used in further analysis as the lack of data points in the QENS region (Fig. 2) made the corresponding analysis statistically unstable.
Based on a χ2 analysis and on the behaviour of the residuals function (difference between observed and calculated points weighted for statistical errors) we conclude that our model is sufficient for the description of the data and no extra fitting parameters are required. The χ2 values of the treated data set are distributed around 0.5 with a standard deviation of 0.1. The residuals functions for all spectra exhibit no systematic deviations from zero. The resulting fitting parameters are summarised in Table 1.
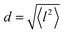 and residence time between jumps τ were estimated with the help of several models: Chudley–Elliot (CE), Singwi–Sjölander (SS) and Hall–Ross (HR) model. The subscripts denote, which model was applied for the corresponding numbers
and residence time between jumps τ were estimated with the help of several models: Chudley–Elliot (CE), Singwi–Sjölander (SS) and Hall–Ross (HR) model. The subscripts denote, which model was applied for the corresponding numbers
| T, K | 〈u2〉, Å2 | τ rot, ps | r c, Å | d CE, Å | d SS, Å | d HR, Å | τ CE, ps | τ SS, ps | τ HR, ps |
|---|---|---|---|---|---|---|---|---|---|
| 300 | 0.23 (1) | 2.1 (4) | 0.68 (2) | 2.8 (2) | 0.20 (1) | ||||
| 400 | 0.40 (1) | 2.1 (3) | 0.63 (1) | 2.1 (2) | 2.6 (6) | 2.2 (2) | 0.29 (3) | 0.19 (3) | 0.26 (2) |
| 500 | 0.51 (1) | 1.5 (3) | 0.74 (1) | 2.3 (2) | 2.9 (6) | 2.5 (2) | 0.32 (2) | 0.22 (3) | 0.29 (2) |
| 300* | 0.32 (1) | 1.7 (5) | 0.71 (3) | 1.9 (7) | 2.4 (16) | 2.1 (7) | 0.21 (8) | 0.15 (6) | 0.20 (5) |
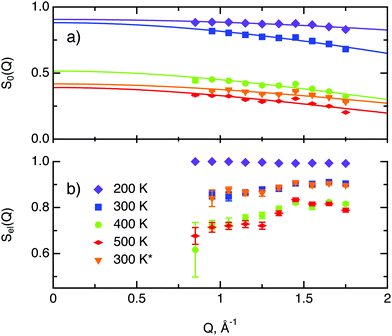
In the following we discuss the parameters of hydrogen diffusion in MoS2 obtained by fitting eqn (9) to the data. The change in the overall intensity S0(Q) at different temperatures that is shown in Fig. 7a reveals that a significant fraction of hydrogen was desorbed during the first heating from 300 to 400 K (of the order of 50%) and then from 400 to 500 K (an additional 10–20%). This desorption happened rather fast during the heating and temperature equilibration phases and did not impact the QENS profile. The hydrogen was not re-adsorbed upon cooling back to 300 K because the sample holder was not tightly closed and the environment around the sample holder was at low pressure during experiments. In the XPS data only minor changes are spotted during heating from room temperature to 400 K. Therefore, the desorbed species are interpreted as surface hydrogen molecules or water, which do not significantly impact on the chemistry and are, thus, not observable in the XPS study. The Q dependence of S0(Q) allows us to estimate the level of hydrogen vibrations 〈u2〉. The calculated values are moderate for the whole range of temperatures (Table 1).
The factor Sel, displayed in Fig. 7b, shows the ratio of the scattering intensity off the immobile hydrogen and the host material, to the total scattering intensity Sel = (IimH + IMoS2)/(ItotalH + IMoS2). The term “immobile” refers rather to atoms or molecules, whose movement is very slow and falls into the energy window of the resolution function, than to completely stationary particles. Although the incoherent scattering cross section of MoS2 is very small as compared to hydrogen, it still may contribute to the Sel factor due to a larger number of scatterers, and thus it is taken into account in the further considerations. Hence, the decrease of Sel with temperature indicates that a part of the immobile hydrogen either becomes mobile, i.e., becomes sufficiently fast to enter the spectroscopic window of the spectrometer, and thus contributes to 1 − Sel, or desorbs. Both room temperature runs, before and after heating to 500 K, give almost identical values of Sel. As no significant changes of Sel are observed between the two room temperature runs, it can be concluded that the balance between mobile H2 and H atoms that are immobile at room temperature is preserved, which is in line with the above observations of H and H2 desorption at elevated temperatures. During heating from 300 to 400 K the Sel factor drops and then remains similar upon heating to 500 K, indicating that heating from to 400 to 500 K does not induce any additional hydrogen to become mobile.
The decay of A0(Q) with Q (Fig. 8a) shows the presence of a certain confinement effect beyond the natural confinement of the rotational diffusion. The approximation of A0(Q) with a model of a diffusion confined in a sphere gives a good fit with a radius of confinement rc ≈ 0.7 Å. This length may indicate that hydrogen molecules are, to some extent, caged by four neighbouring sulphur atoms (the corresponding distance calculated on the basis of the MoS2 structure is around 0.6 Å). In order to better understand the confinement effect two further EISF models were tested, namely, jump reorientations between two and three equivalent sites, respectively, equally spaced on a circle.2 The fits of these models are of the same quality as for a spherical confinement model and yield a circle radius of around 0.6 Å, very close to what was obtained with the previous model. This result is not surprising as for such a small confining length all the sensitive information should be contained in a high Q region, which could not be assessed in the current experiment. We would like to stress that the presence of this additional confinement length, in addition to the radius of the hydrogen molecule, does not exclude the existence of long range diffusion, and can be interpreted by a motion in a confined space, occurring between long jumps. For all three models extrapolations of the fit functions to Q = 0 Å−1 yield values slightly higher than 1, despite the fact that the expected value is less or equal to unity. This is an indication of the existence of various hydrogen containing species inside the sample. Indeed, if slow motion of atomic hydrogen falls into the energy window of the rotational mode of H2, i.e. very close to the resolution function, it would increase the A0(Q) factor since the observed area of the rotational peak increases (see eqn (9)). As expected the effect is minor as it is caused by the presence of atomic hydrogen. The characteristic time of rotation τrot, as theoretically expected, does not depend on the momentum transfer Q (Fig. 8b).
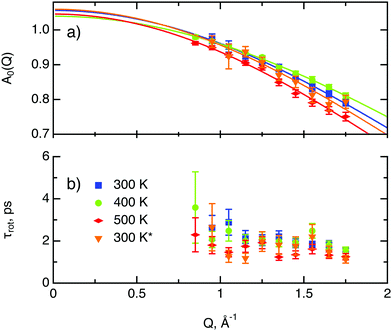 | ||
| Fig. 8 Diffusion parameters of hydrogen in MoS2 single crystals at various temperature. The asterisk represents second heating run. (a) A0(Q) factor and its approximation using a model of translational diffusion confined within an impermeable sphere (eqn (4)). (b) Characteristic time of rotational diffusion τrot. | ||
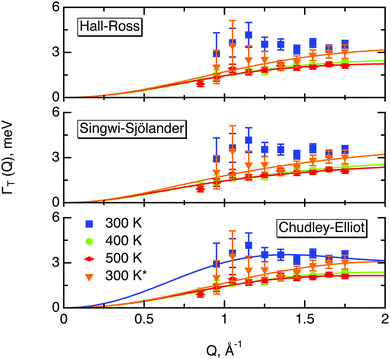
The part of the quasi-elastic broadening that is caused by translational diffusion of molecular hydrogen exhibits a typical behaviour for a jump-diffusion process (Fig. 9) following a DQ2 law at low values of momentum transfer and reaching a plateau at high Q.2 As was observed earlier,46 diffusion models with a continuous distribution of jump lengths, like the Singwi–Sjölander47 (SS) and the Hall–Ross48 (HR) model, are well suited for treating such cases. Both were tested in this work, together with a general discrete-jump-diffusion model by Chudley and Elliot49 (CE). The Singwi–Sjölander and Hall–Ross models consider different distributions of jump distances. The Singwi–Sjölander assumes an exponentially decaying distribution
| ρ(r) = r/r02·exp−r/r0, | (10) |
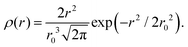 | (11) |
The Chudley–Elliot model, on the other hand, considers jump diffusion between periodic discrete jump sites. In the case of a Bravais lattice, the half-width-at-half-maximum (HWHM) of a translational Lorentzian can be derived from the following general expression:
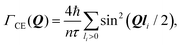 | (12) |
At this point we should recall the geometry of the experiment. The in-plane set-up implies that a momentum transfer vector Q is almost parallel to the basal planes of the MoS2 single crystals, i.e., Q‖ ≫ Q⊥. The SS and HR models assume isotropic diffusion, which implies that only the magnitude of the momentum transfer vector is relevant and the geometry of the experiment is insignificant. However, the CE model requires an averaging over all possible directions of Q, which in our case requires an averaging over Q‖. By substituting the pyramid jump array into (eqn (12)) and averaging over Q‖ one gets an expression for the width of the translational broadening as displayed in the table below (see Appendix A for details).
Here, D is the diffusion coefficient, τ is the residence time between jumps and J0(x) is a zeroth order Bessel function of the first kind. The mean squared jump length and the diffusion coefficient are related by the Einstein equation2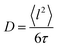 . The projection of Q in the current experiment can be evaluated as Q‖ = Q·sin(ϕ + arcsin(Qλ/4π)).
. The projection of Q in the current experiment can be evaluated as Q‖ = Q·sin(ϕ + arcsin(Qλ/4π)).
All three models describe most of the data equally well (in terms of a χ2 test). However, the Singwi–Sjölander and Hall–Ross models did not succeed in treating the data obtained during the first 300 K run. The calculated jump distances 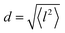 and residence times τ are listed in Table 1. The first room temperature scan indicates a faster diffusion than all the others. This is probably due to the weakly bound surface hydrogen and/or water, which can be expected to exhibit faster motion and which desorbs at higher temperatures. Therefore, it would be appropriate to exclude the 300 K results for the first temperature run from further consideration. That being so, one can note a slight, but consistent correlation of the jump distance with temperature, which holds for every model. An averaged value of the jump length for all temperatures and models is 2.3 Å. This value may be compared to certain characteristic distances in the MoS2 structure and to the confinement length rc, that was obtained from the A0(Q) factor. The most important distances in the MoS2 structure are the minimum distance between the surfaces of two neighbouring S atoms of 1.1 Å and a unit cell parameter of 3.15 Å. The obtained jump distance lies between those two values. The characteristic confinement length of about 1.4 Å appears to be smaller than the calculated average jump distance, therefore the observed jumps happen between neighbouring confinement regions and not within them. It is also important to note that this jump distance is much less than the 6.15 Å interval between two layers of MoS2. Therefore, what is observed in the QENS experiment is likely a movement completely restricted by the MoS2 layers, rather than a diffusion through the hexagonal wells.
and residence times τ are listed in Table 1. The first room temperature scan indicates a faster diffusion than all the others. This is probably due to the weakly bound surface hydrogen and/or water, which can be expected to exhibit faster motion and which desorbs at higher temperatures. Therefore, it would be appropriate to exclude the 300 K results for the first temperature run from further consideration. That being so, one can note a slight, but consistent correlation of the jump distance with temperature, which holds for every model. An averaged value of the jump length for all temperatures and models is 2.3 Å. This value may be compared to certain characteristic distances in the MoS2 structure and to the confinement length rc, that was obtained from the A0(Q) factor. The most important distances in the MoS2 structure are the minimum distance between the surfaces of two neighbouring S atoms of 1.1 Å and a unit cell parameter of 3.15 Å. The obtained jump distance lies between those two values. The characteristic confinement length of about 1.4 Å appears to be smaller than the calculated average jump distance, therefore the observed jumps happen between neighbouring confinement regions and not within them. It is also important to note that this jump distance is much less than the 6.15 Å interval between two layers of MoS2. Therefore, what is observed in the QENS experiment is likely a movement completely restricted by the MoS2 layers, rather than a diffusion through the hexagonal wells.
Since molybdenum sulphide is a promising catalyst for the hydrogen evolution reaction (HER), we would like to compare the parameters of hydrogen molecule diffusion in MoS2 to the currently most active catalyst, platinum. Unfortunately spectroscopic information about hydrogen diffusion on Pt is only available for hydrogen atoms. It was obtained by Graham et al.50 for a (111) surface of Pt by means of quasi-elastic helium atom scattering. We also add to the comparison the diffusion of hydrogen molecules on exfoliated graphite, studied by Bahn et al.46 with quasi-elastic neutron scattering. Exfoliated graphite has not shown any significant activity in the HER reaction4 but its layered structure is similar to MoS2, hence it can be used as a reference non catalytic material. An Arrhenius plot of the temperature dependence of the diffusion coefficients of these three materials is displayed in Fig. 10. The diffusion coefficient for platinum was extracted via the Chudley–Elliot model, whereas the data for MoS2 were averaged between the three models studied in this work (Table 2). The 300 K results from the first run were not used for this evaluation also because it was not possible to average over the models. The data for exfoliated graphite were extracted using the Singwi–Sjölander model. Interestingly, the diffusion coefficient of hydrogen atoms on Pt extrapolates quite well to the diffusion coefficient that was observed in the present study for hydrogen molecules at high temperatures. The diffusion coefficient of hydrogen on graphite, on the other hand, is substantially higher than the diffusion coefficient of hydrogen on MoS2 if extrapolated to a similar temperature. We also note that the activation barrier, EB, for the hydrogen molecule diffusion in MoS2 appears to be very small as indicated by the small inclination of the Arrhenius plot. In fact, EB appears to be similar to the activation barrier in graphite. However, we are unable to assert this finding with confidence and do not want to give a value here, since the number of temperatures that we were able to measure was limited and the error bars of the diffusion coefficients are quite significant.
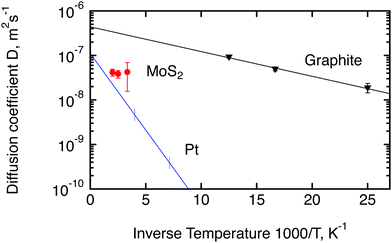 | ||
| Fig. 10 Comparison of diffusion coefficients calculated in the current work for hydrogen molecules on MoS2 (red circles) with the results obtained earlier for hydrogen atoms on platinum50 (blue line) and hydrogen molecules on exfoliated graphite46 (black triangles). Lines are calculated based on the activation energies and D0 factors stated in the corresponding papers. Vertical lines for Pt show the range of measured temperatures. The diffusion coefficient at room temperature shown here for MoS2 represents the second run. | ||
| T, K | D CE × 10−8, m2 s−1 | D SS × 10−8, m2 s−1 | D HR × 10−8, m2 s−1 | 〈D〉 × 10−8, m2 s−1 |
|---|---|---|---|---|
| 300 | 2.8 ± 1.5 | 6.4 ± 5.0 | 3.6 ± 1.6 | 4.3 ± 2.7 |
| 400 | 2.5 ± 0.3 | 5.8 ± 1.5 | 3.2 ± 0.4 | 3.8 ± 0.8 |
| 500 | 2.7 ± 0.2 | 6.3 ± 1.5 | 3.5 ± 0.4 | 4.2 ± 0.7 |
4.4 Neutron spin-echo study
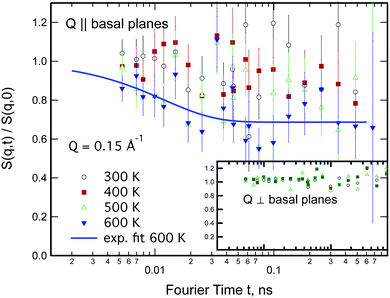
Neutron spin-echo (NSE) experiments provide a direct measurement of the time evolution of the space correlation function of the sample (also called the intermediate scattering function S(Q,t)).2,51 NSE data are complementary to TOF spectroscopy data, because they provide the Fourier transform with respect to energy and time of the TOF data. The spectroscopic window of the technique, in addition, allows the observation of dynamics with a characteristic time from ≈5 ps to several ns and therefore allows us to investigate the diffusion phenomena at lower Q values than the ones studied in the QENS experiment, i.e., testing substantially larger real space distances. NSE spectra are shown in Fig. 11. Starting from 400 K the intermediate scattering function S(Q,t) of the in-plane set-up shows a clearly visible decay that can be fit by an exponential law at Q = 0.15 Å−1, which is an indication of diffusive motion parallel to the surface. We note, that an exponential decay found with NSE is equivalent to a Lorentzian line shape in the TOF experiment, because S(Q,t) is the Fourier transform of S(Q,ω). Within the experimental error bar, we find the same diffusion coefficients through our NSE measurements as for the translational diffusion derived from the QENS data, i.e., (5 ± 3) × 10−8 m2 s−1 at 500 K. While we find a clear indication of diffusion parallel to the basal planes we observe that the signal in the out-of-plane orientation does not change substantially with temperature indicating that no significant diffusion is found perpendicular to the basal planes of MoS2 within the spectroscopic window of QENS spectroscopy. We would like to stress that this observation is not in contradiction to the TOF findings (where we did not observe a difference between spectra parallel or perpendicular to the basal planes) because the smallest Q values that were exploitable in the TOF spectra represent distances that are in the range of the interlayer distance in MoS2 of 6.2 Å. On the other hand, the distance corresponding to Q = 0.15 Å−1, probed in the NSE experiment, is about 40 Å. It was not possible to measure the dynamics at higher Q values using NSE, because the neutron beam polarisation was destroyed by the incoherent scattering of the hydrogen for higher Q values: coherent scatterers leave the neutron spin unaltered upon scattering, whereas incoherent scattering atoms cause spin-flips upon interaction with the scattering neutron leading to a final beam polarisation after scattering of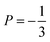 on average.51 We note, that rotational diffusion will not be visible at the low Q measured by our NSE measurement, since the intensity of the rotational diffusion vanishes at small Q.25
on average.51 We note, that rotational diffusion will not be visible at the low Q measured by our NSE measurement, since the intensity of the rotational diffusion vanishes at small Q.25
5 Conclusions
We have performed the analysis of hydrogen diffusion in the bulk of H-loaded MoS2 single crystals by means of quasi-elastic neutron scattering and neutron spin-echo spectroscopy. The results were compared to the currently most active HER catalyst platinum and a non-catalytic exfoliated graphite. A supplementary study of the surface chemistry of the MoS2 under temperature treatment and ageing was carried out with the help of X-ray photoelectron spectroscopy and nuclear reaction analysis.First of all, the nuclear reaction analysis has shown clear signs that hydrogen is able to penetrate the layered structure of MoS2 and migrate from the surface to the bulk across the basal planes of this layered material, though rather slowly with a diffusion coefficient of the order of 10−21 m2 s−1. The NRA and XPS data also showed that water does not penetrate into the bulk, but can be found adsorbed at the surface or subsurface layer. The QENS study showed a clear translational and rotational diffusion of hydrogen molecules and only a negligible contribution of hydrogen atom diffusion within the spectroscopic window of the present experiments. The low Q data from NSE spectroscopy demonstrated that the hydrogen diffusion between 300 and 600 K is limited to a motion constrained between the layers of MoS2. The QENS data could be fitted by models that consider a jump diffusion of rotating hydrogen molecules, that remain in a limited space of a dimension of about 1.4 Å between jumps. The calculated jump distance is of the order of 2.5 Å, supporting the idea that the diffusion observed here comes from hydrogen enclosed between the layers.
The calculated diffusion coefficients of hydrogen molecules in molybdenum disulphide were compared to the ones of hydrogen atoms in a catalytic platinum and of hydrogen molecules in non-catalytic exfoliated graphite. According to the Arrhenius plot (Fig. 10) the diffusion rate of H2 in MoS2 at room temperature or above is similar to the diffusion coefficient expected for hydrogen atoms on Pt at the same temperatures. This could have interesting technical implications even though the diffusion mechanisms are likely to be very different for hydrogen molecules and atoms. The Arrhenius plot indicates a significantly lower diffusivity for H2 in MoS2 than for hydrogen molecules in exfoliated graphite, however it also suggest a low activation barrier, which would be in accordance with the two-dimensional nature of the MoS2 samples.
Conflicts of interest
There are no conflicts to declare.Appendix
A Chudley–Elliot model for a pyramid array of jump sites
We start with a convenient representation of the Chudley–Elliot model for jump diffusion on a Bravais lattice: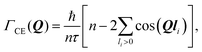 | (13) |
Substituting this jump array into eqn (13) one gets:
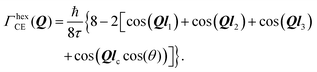 | (14) |
Setting a geometry of an experiment such that a momentum transfer vector Q is very close to the basal plane of the pyramid XY, i.e. θ ≈ π/2, allows to rewrite eqn (14) explicitly:
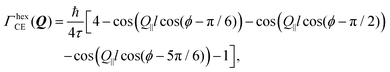 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ)) ≈ 1 depends not only on θ, but also on lc. It remains valid even for smaller θ if lc ≪ l and fails if lc ≫ l. In the latter case the lc containing cosine should be directly calculated.
cos(θ)) ≈ 1 depends not only on θ, but also on lc. It remains valid even for smaller θ if lc ≪ l and fails if lc ≫ l. In the latter case the lc containing cosine should be directly calculated.
In the case of an oriented polycrystalline sample, i.e. a set of single crystals whose basal planes are aligned, but may be rotated with respect to each other, the model requires further averaging over all the possible directions of Q‖, i.e. over ϕ:
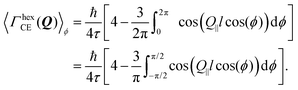 | (16) |
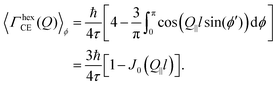 | (17) |
This is the final expression for an in-plane jump diffusion over a hexagonal array of jump sites with a unique jump distance l and residence time τ.
Acknowledgements
This work is based upon experiments performed at the TOFTOF instrument operated by Technische Universität München at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. This project has received support from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 730872 CALYPSO plus for the work at the HZB BESSY II synchrotron, Berlin, Germany, and under grant agreement no. 731096 FILL2030 for covering the open access fee. The authors want to thank HZB for the allocation of synchrotron radiation beam time at BESSY II via project 192-08548 CR. Neutron spin-echo experiments were carried out at Institut Laue-Langevin (ILL), Grenoble, France. The authors want to thank HZB, MLZ and ILL for the allocation of synchrotron and neutron beam time. The help provided by Dimitri Renzy and Simon Baudoin at ILL is gratefully acknowledged. The authors would like to thank Laurène Gallot for her contributions in the framework of an Erasmus internship. The work was financed within the scope of the joint PhD project ref. ILL-1709.1 between Institut Laue – Langevin and Westfälische Hochschule.Notes and references
- A. P. Graham and J. P. Toennies, Collective Diffusion on Surfaces: Correlation Effects and Adatom Interactions, Dordrecht, 2001, pp. 1–10 Search PubMed.
- M. Bée, Quasielastic neutron scattering: principles and applications in solid state chemistry, biology and materials science, Adam Hilger, Bristol and Philadelphia, 1988 Search PubMed.
- R. Hempelmann, Quasielastic neutron scattering and solid state diffusion, Oxford University Press, Oxford, 2000 Search PubMed.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS.
- Y. N. Regmi, G. R. Waetzig, K. D. Duffee, S. M. Schmuecker, J. M. Thode and B. M. Leonard, J. Mater. Chem. A, 2015, 3, 10085–10091 RSC.
- Y. Yan, B. Xia, Z. Xu and X. Wang, ACS Catal., 2014, 4, 1693–1705 CrossRef CAS.
- J. D. Benck, T. R. Hellstern, J. Kibsgaard, P. Chakthranont and T. F. Jaramillo, ACS Catal., 2014, 4, 3957–3971 CrossRef CAS.
- Z. Chen, D. Cummins, B. N. Reinecke, E. Clark, M. K. Sunkara and T. F. Jaramillo, Nano Lett., 2011, 11, 4168–4175 CrossRef CAS.
- X. Dai, K. Du, Z. Li, H. Sun, Y. Yang, W. Zhang and X. Zhang, Int. J. Hydrogen Energy, 2015, 40, 8877–8888 CrossRef CAS.
- X. Zou and Y. Zhang, Chem. Soc. Rev., 2015, 44, 5148–5180 RSC.
- P. A. Bertand, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 5745–5749 CrossRef.
- D. Voiry, M. Salehi, R. Silva, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nano Lett., 2013, 13, 6222–6227 CrossRef CAS.
- D. Merki, S. Fierro, H. Vrubel and X. Hu, Chem. Sci., 2011, 2, 1262–1267 RSC.
- J. D. Benck, Z. B. Chen, L. Y. Kuritzky, A. J. Forman and T. F. Jaramillo, ACS Catal., 2012, 2, 1916–1923 CrossRef CAS.
- C. Rozain and P. Millet, Electrochim. Acta, 2014, 131, 160–167 CrossRef CAS.
- J. O. Bockris, Modern electrochemistry 2B: electrodics in chemistry, engineering, biology and environmental science, Springer Science & Business Media, 1998, vol. 2 Search PubMed.
- I. N. Yakovkin and N. Petrova, Chem. Phys., 2014, 434, 20–24 CrossRef CAS.
- K. M. S. Takagi and T. Gotoh, Appl. Surf. Sci., 1999, 144, 278–282 CrossRef.
- V. F. Sears, Can. J. Phys., 1967, 45, 237–254 CrossRef CAS.
- V. F. Sears, Can. J. Phys., 1966, 44, 1299–1311 CrossRef CAS.
- T. R. Prisk, M. S. Bryan and P. E. Sokol, Phys. Chem. Chem. Phys., 2014, 16, 17960–17974 RSC.
- A. J. O'Malley and C. R. A. Catlow, in Neutron scattering – applications in biology, chemistry, and materials science, Experimental Methods in the Physical Sciences, ed. F. Fernandez-Alonso and D. Price, Elsevier, San Diego, 2017, vol. 49, pp. 349–401 Search PubMed.
- I. Calvo-Almazán, S. Miret-Artés and P. Fouquet, J. Phys.: Condens. Matter, 2012, 24, 104007 CrossRef.
- H. Jobic, Phys. Chem. Chem. Phys., 2016, 18, 17190–17195 RSC.
- S.-H. Chen, P. Gallo, F. Sciortino and P. Tartaglia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 56, 4231–4243 CrossRef CAS.
- M. Bée, Phys. B, 1992, 182, 323–336 CrossRef.
- F. Volino and A. Dianoux, Mol. Phys., 1980, 41, 271–279 CrossRef CAS.
- A. N. Vavreck and W. Thompson, Q. Appl. Math., 1984, 42, 321–324 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- J. F. Ziegler, Program SRIM (Stopping and Range of Ions in Matter), http://www.srim.org.
- F. Traeger, M. Kauer, C. Wöll, D. Rogalla and H.-W. Becker, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075462 CrossRef.
- H.-W. Becker and D. Rogalla, in Nuclear Reaction Analysis, ed. H. Fritzsche, J. Huot and D. Fruchart, Springer International Publishing, Cham, 2016, pp. 315–336 Search PubMed.
- A. Nefedov and C. Wöll, in Advanced Applications of NEXAFS Spectroscopy for Functionalized Surfaces, ed. G. Bracco and B. Holst, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 277–303 Search PubMed.
- D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709–4714 CrossRef.
- J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS.
- H. M.-L. Zentrum, J. Large-Scale Res. Facil., 2015, 1, A15 CrossRef.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- F. Traeger and P. Fouquet, Hydrogen diffusion in MoS 2 , Institut Laue-Langevin (ILL) , 2016 DOI:10.5291/ILL-DATA.7-05-460.
- B. Farago, Phys. B, 1998, 241–243, 113–116 Search PubMed.
- M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2 CrossRef CAS.
- J.-G. Choi and L. Thompson, Appl. Surf. Sci., 1996, 93, 143–149 CrossRef CAS.
- D. Ganta, S. Sinha and R. T. Haasch, Surf. Sci. Spectra, 2014, 21, 19–27 CrossRef CAS.
- L. Trotochaud, A. R. Head, S. Pletincx, O. Karsloğlu, Y. Yu, A. Waldner, L. Kyhl, T. Hauffman, H. Terryn, B. Eichhorn and H. Bluhm, J. Phys. Chem. B, 2018, 122, 1000–1008 CrossRef.
- D. I. Patel, D. Shah, S. Bahr, P. Dietrich, M. Meyer, A. Thißen and M. R. Linford, Surf. Sci. Spectra, 2019, 26, 014026 CrossRef.
- E. Bahn, L. A. H. Giraldo, V. Kuznetsov, I. Calvo-Almazán, M. Zbiri, M. M. Koza, T. C. Hansen, P. F. Henry, A. Lapp, S. Pouget, M. Mesa and P. Fouquet, Carbon, 2020, 166, 307–315 CrossRef CAS.
- K. S. Singwi and A. Sjölander, Phys. Rev., 1960, 119, 863–871 CrossRef CAS.
- P. L. Hall and D. Ross, Mol. Phys., 1981, 42, 673–682 CrossRef CAS.
- C. T. Chudley and R. J. Elliott, Proc. Phys. Soc., 1961, 77, 353–361 CrossRef.
- A. P. Graham, A. Menzel and J. P. Toennies, J. Chem. Phys., 1999, 111, 1676–1685 CrossRef CAS.
- Neutron Spin Echo, ed. F. Mezei, Springer, Berlin, 1980, vol. 128 Search PubMed.
| This journal is © the Owner Societies 2021 |