A new method of isotope enrichment and separation: preferential embedding of heavier isotopes of Xe into amorphous solid water
K. D.
Gibson
and
S. J.
Sibener
 *
*
The James Franck Institute and Department of Chemistry, The University of Chicago, 929 E. 57th Street, Chicago, Illinois 60637, USA. E-mail: s-sibener@uchicago.edu
First published on 10th December 2020
Abstract
In this paper, we examine a new method for isotope separation involving the embedding of atoms and molecules into ice. This method is based upon isotope dependent embedding, i.e. capture, in a cryogenic matrix which exhibits excellent single-pass enrichment as demonstrated successfully for selected isotopes of Xe. This is a totally new method that holds significant promise as a quite general method for enrichment and purification. It is based upon exploiting the energetic and momentum barriers that need to be overcome in order to embed a given isotope or isotopologue into the capture matrix, initially amorphous ice. From our previous experiments, we know that there is a strong dependence of the embedding probability with incident momentum. Using supersonic molecular beam techniques, we generated Xe atomic beams of controlled velocities, relatively narrow velocity distributions due to supersonic expansion, and with all of the entrained isotopes having identical velocities arising from the seeded molecular beam expansion. As we had postulated, the heavier isotope becomes preferentially absorbed, i.e., embedded, in the ice matrix. Herein we demonstrate the efficacy of this method by comparing the capture of 134Xe and 136Xe to the reference isotope, 129Xe. Enrichment of the heavier isotopes in the capture matrix was 1.2 for 134Xe and 1.3 for 136Xe greater than that expected for natural abundance. Note that enriched isotopic fractions can be collected from either the condensate or the reflected fraction depending on interest in either the heavier or lighter isotope, respectively. Cycling of these single-step enrichment events for all methods can lead to significantly higher levels of purification, and routes to scale-up can be realistically envisioned. This method holds significant promise to be quite general in applicability, including both atomic isotopes or molecular isotopologues across a wide range of particle masses spanning, essentially, the periodic table. This topic has profound implications and significant potential impact for a wide-variety of isotope-based technologies in the physical and biological sciences, medicine, advanced energy and energetic systems, including isotopically-purified materials that exhibit high-performance electronic and thermal characteristics, as well as isotopically purified spin-free materials for use in quantum information science platforms.
Introduction
Proposals for separating and enriching isotopes came about almost immediately after isotopes were discovered. In 1919, Lindemann and Aston examined a vast array of possible methods including fractional distillation, chemical separation, gaseous diffusion, gravitational and centrifugal separation, along with separation of positive ions with electric and magnetic fields.1 Their early analysis concluded that isotopes “must be separable in principle though possibly not in practice.” One of the first industrial processes was the electrolytic production of D2O,2 of interest as a moderator for a nuclear pile. At the same time, the Manhattan Project was developing methods for enriching 235U from a mainly 238U feedstock by a combination of electromagnetic methods3,4 and gaseous diffusion. Centrifugation of UF6 was also explored, but not employed at the time.5 In practice, fractional distillation, gaseous diffusion and magnetic sector mass spectrometers (Calutrons) were all used on an industrial scale to enrich 235U.3,4 Gaseous diffusion, distillation and gas centrifuges exhibit small isotopic separation effects that are overcome through large-scale installations where many separation stages are performed in sequence. Alternatively, a variety of laser-based techniques exist6 that are capable of separating isotopes to a much higher degree, but require ionization or excitation of the target isotope; illustrative examples include atomic vapor laser isotope separation (AVLIS)7 and techniques such as magnetically activated and guided isotope separation (MAGIS).8 Another recent method was demonstrated in the Sibener labs based upon the spatial and temporal separation of isotopes using gas-surface atomic diffraction.9 Today, isotope separation and enrichment underpins advanced technologies in a wide variety of fields, including isotopic labeling in the life science, the use of radioisotopes in medicine, and a variety of energy systems. Microelectronics may also begin to utilize isotopic enrichment as highly enriched 28Si wafers have markedly increased thermal conductivity10 and electron transport characteristics11 over natural abundance silicon wafers. Moreover, isotopically-purified materials such as 28Si and 12C are growing interest due to their potential applicability to quantum information science computing platforms.12,13In the current paper, a new method is presented, which is based upon our prior studies of embedding atoms and molecules into ice as a function of selected translational energies.14–18 Specifically, in these prior studies it was shown that there is a very strong correlation between the projectile's incident momentum and the embedding probability as illustrated in Fig. 5 of Langlois et al.18 The new method is based upon isotope dependent embedding, i.e. capture, in a cryogenic matrix which exhibits excellent single-pass enrichment as demonstrated in this paper for selected isotopes of Xe. It is based upon exploiting the energetic and momentum barriers that need to be overcome in order to embed a given isotope or isotopologue into the capture matrix, initially amorphous ice. Using supersonic molecular beam techniques,19,20 we generated Xe atomic beams of controlled velocities, relatively narrow velocity distributions due to supersonic expansion, and with all of the entrained isotopes having identical velocities arising from the seeded molecular beam expansion – and consequently that the heavier isotopes entrained in the high Mach number beam strike the surface with higher momenta. As we had postulated, we find that the heavier isotope becomes preferentially absorbed, i.e., embedded, in the ice matrix. Herein we demonstrate the efficacy of this method by comparing the capture of 134Xe and 136Xe to the reference isotope, 129Xe. Enrichment of the heavier isotope in the capture matrix is demonstrated in this paper to be 1.2 for 134Xe and 1.3 for 136Xe higher than expected as compared to natural abundance. Note that enriched isotopic fractions can be collected from either the condensate or the reflected fraction depending on interest in either the heavier or lighter isotope, respectively. Cycling of these single-step enrichment events for all methods can lead to significantly higher levels of purification, and routes to scale-up can be realistically envisioned. This method holds significant promise to be quite general in applicability, including both atomic isotopes or molecular isotopologues across a wide range of particle masses spanning, essentially, the periodic table.
Experimental
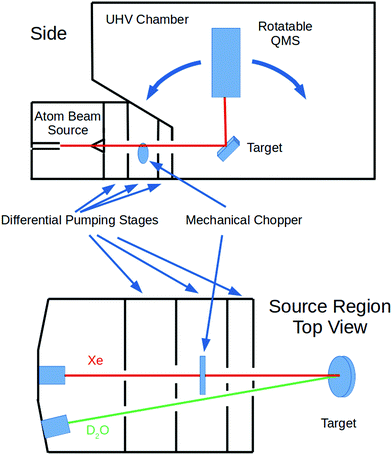
These experiments were done using our group's multiple-molecular-beam gas-surface scattering instrument; a schematic diagram is shown in Fig. 1. Independent beams of Xe and D2O were produced in the first region, passed through a skimmer, and then several regions of differential pumping before entering the ultra-high-vacuum (UHV) chamber. They converged on a manipulator holding an unpolished, polycrystalline Ta plate that was rotatable so that the incident angle (ΘI) was variable. (As is customary, all angles are measured from the surface normal.) The Ta plate was resistively heated and cooled with liquid nitrogen or liquid helium. The quadrupole mass spectrometer (QMS) resides in its own vacuum chamber. This is doubly-differentially-pumped and has entrance apertures that allows for a collection angle of ∼1° FWHM. It can be rotated with respect to the Ta surface so that the detection angle (ΘF) relative to the surface normal is variable. Ions for the QMS were created by an electron-bombardment ionizer.The Xe beam's incident intensity and velocity could be measured by lowering the sample plate and rotating the QMS so that its aperture was directly in line with the beam. The rotating mechanical chopper had small slots so that the beam velocity could be measured via time-of-flight techniques. For other experiments, the chopper had large slots so that when no longer spinning it could be positioned so that the beam was not blocked and a continuous exposure of the target surface was obtained.
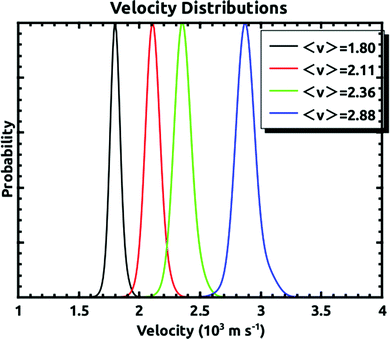
A D2O beam was produced by bubbling He at an absolute pressure of 300 torr through a room temperature reservoir containing the liquid and expanded through a 250 μm pinhole. D2O was used since the mass 20 background in the detector was much lower than that of mass 18. The Xe beam was produced using a mixture of ∼1% or less of Xe in H2 expanded through a 15 or 20 μm pinhole at 200 psig. The nozzle holding the pinhole could be held at a temperature between 300 K and 625 K. This allowed for the production of Xe atoms with average velocities between 1.8 × 103 and 2.9 × 103 m s−1. Some example velocity distributions which cover this velocity range are shown in Fig. 2. This shows that the velocity spreads of the beams were narrow enough as to allow us to make distinct embedding measurements. For the experiments described, we measured the quantity of three isotopes: 129, 134, and 136 with natural abundances of 26.4%, 10.44%, and 8.86% respectively.21 For any given supersonic beam conditions, the velocity distributions were the same for these three isotopes.
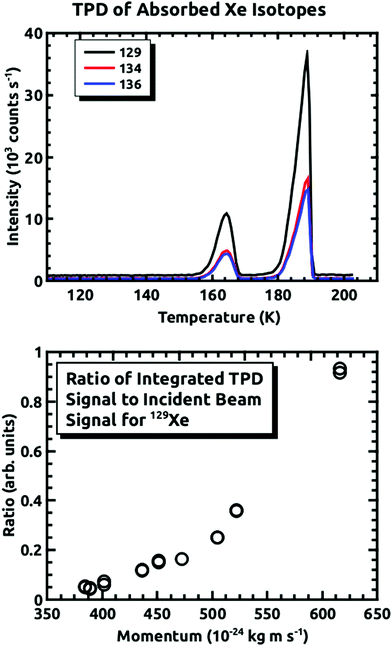
For all of the experiments, the temperature of the sample plate was held between 110 K and 125 K while being exposed to the D2O and Xe. At these temperatures, the condensed D2O forms non-porous amorphous solid water (ASW).22–24 Note, importantly, that during our previous experiments, we grew the ASW film, and then exposed it to the Xe beam. However, in these experiments we showed that the embedding rate is much higher initially, and subsequently falls off with continued exposure.15 In order to mitigate this issue for the experiments covered in this paper, we ran the D2O and Xe beams concurrently so that we were always exposing a fresh D2O surface to the incident seeded Xe beam. The procedure involved exposing the surface at ΘI = 10° for 45 minutes. Then, the amount of embedded Xe was measured using temperature programmed desorption (TPD). The sample plate was heated at a linear rate of 10 K min−1, while consecutively monitoring the desorbing D2O signal and that of the three Xe isotopes at 1 second intervals. The D2O signal was checked to ensure the ice growth rate was consistent between experiments. An example of the TPD spectra for the three Xe isotopes is shown in Fig. 3. The peak at ∼160 K occurs at the ASW–crystalline ice transition, which is where we saw most of the desorption in the previous experiments. The larger peak occurs where the D2O rate is greatest. The integrated intensity of each mass was used for determining the quantity of embedded Xe. Fig. 3 also shows the relative intensity of the 129Xe TPD spectra, normalized by the incident beam intensity, as a function of the incident momentum. We did not determine the absolute flux, but the general shape is consistent with what is shown in Fig. 5 of Langlois et al.18
We also wanted to perform null experiments to check the isotope ratios from the incident beam as determined by the detector. To measure the relative intensities of the Xe in the incident beam, the sample plate was heated to 250 K, and a mass spectrum of scattered Xe was taken with ΘI = ΘF = 45°. At this surface temperature, neither Xe or background water sticks to the surface. The angular intensity distribution of Xe from the relatively rough sample surface has a broad angular intensity distribution, and because of the low intensity could be taken at the same ionizer emission current as the TPD spectra, not possible with the straight through beam. As a check on this method, the surface was cooled with liquid helium, which allowed for the adsorption of Xe directly from the beam for a sufficient time to build up a many atom thick overlayer, based on the Xe TPD intensities from previous experiments.14 After a 45 minute exposure the ensuing Xe TPD gave the same ratios as that of the scattering measurements for the beam conditions used.
Results and discussion
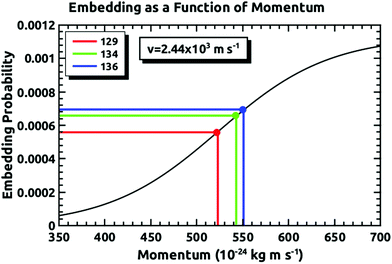
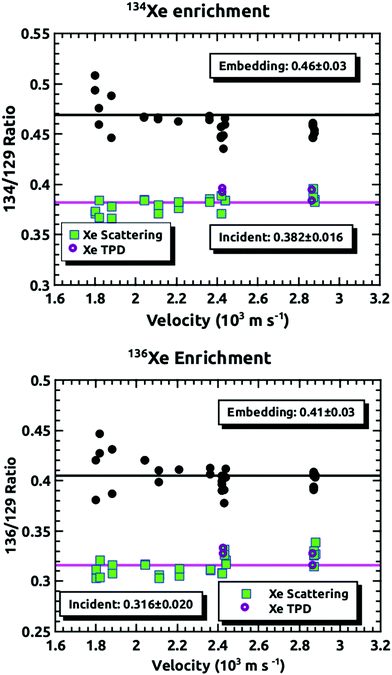
Fig. 4 demonstrates how we envisioned the isotope separation is accomplished. The solid black line is the embedding probability versus incident momentum from Langlois et al.18 For any given beam conditions, the velocities of the three isotopes are the same. The figure also shows the embedding probabilities for the three isotopes at an incident velocity of 2.44 × 103 m s−1, and the predicted increase in embedding probability for the heavier isotopes. Fig. 5 summarizes the principle results of the separation experiments. No attempt was made to measure the absolute flux of the incident Xe, so all of the data are given as a ratio of 134Xe and 136Xe signals to that of 129Xe. For the range of velocities explored, this ratio is higher than expected for equal embedding probabilities; 1.2 for 134Xe and 1.3 for 136Xe. This was calculated using the ratio of the average values of the signal from the heavier isotope to that of 129Xe determined from integrated TPD signals divided by the same ratio for the scattering measurements, which represent measured natural abundance. This range covers most of the momenta where our previous experiments18 have shown that the embedding probability is increasing.Fig. 6 shows the comparison between the data presented in this paper and what was calculated from our prior universal curve for embedding in ASW.18 The findings are in excellent agreement with predictions based upon our previous results for the momentum dependence of the embedding. This is a key outcome, confirming that the momentum can be used to preferentially separate the heavier isotopes by embedding them into amorphous solid water.
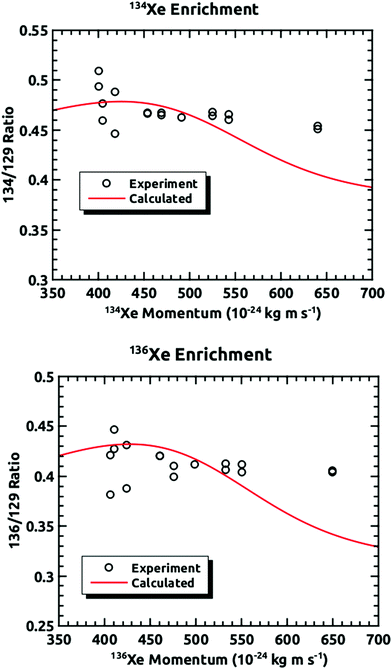 | ||
| Fig. 6 Comparisons of the experimentally measured mass ratios at different incident velocities plotted against the momentum of the heavier isotope and the mass ratios calculated from the results of our previous experiments.18 | ||
These results confirm that isotopes entrained in a supersonic seeded beam can be enriched using preferential embedding in an amorphous ice capture matrix. The efficacy of this method has been demonstrated, with these experiments being based upon previous experiments from the Sibener group that indicated that atoms and molecules can be embedded into ice, and the embedding probability is strongly momentum dependent. These findings are in excellent agreement with our predictions based upon our previous results for the momentum dependence of the embedding.
Conclusions
In this paper, we present a novel way of enriching and separating isotopes. In previous experiments, the Sibener group demonstrated that atoms and molecules can be embedded into ice, and the embedding probability is strongly momentum dependent. With this in mind, we exposed amorphous solid water to atomic beams of xenon with different translational kinetic energies. With supersonic molecular beam techniques, beams with a narrow Δv/v and velocities between 1.8 × 103 and 2.9 × 103 m s−1 were produced. In these experiments, the relative intensities of three xenon isotopes were monitored: 129, 134, and 136 amu. In any beam, the velocities for these three isotopes were the same, and so their incident momenta difference was directly related to their individual masses. Over the range of velocities investigated, the two higher masses were indeed preferentially embedded relative to mass 129. The ratios of 134Xe and 136Xe to 129Xe showed an increase of 1.2–1.3× compared to natural abundance. This was in good agreement with our previous results for the momentum dependence of the embedding. Besides possible technological uses, it might be a consideration for the relative abundances of isotopes in different parts of the universe.25Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Air Force Office of Scientific Research, Grant No. FA9550-19-1-0324.References
- F. A. Lindemann and F. W. Aston, London, Edinburgh Dublin Philos. Mag. J. Sci., 1919, 37, 523–534 CrossRef.
- M. Benedict and T. H. Pigford, Nuclear Chemical Engineering, McGraw-Hill, New York, 1957 Search PubMed.
- A. L. Yergey and A. K. Yergey, J. Am. Soc. Mass Spectrom., 1997, 8, 943–953 CrossRef.
- L. O. Love, Science, 1973, 182, 343–352 CrossRef CAS.
- B. C. Reed, Phys. Perspect., 2009, 11, 426–441 CrossRef.
- G. N. Makarov, Phys.-Usp., 2015, 58, 670–700 CrossRef.
- T. R. Mazur, B. Klappauf and M. G. Raizen, Nat. Phys., 2014, 10, 601–605 Search PubMed.
- P. A. Bokhan, V. V. Buchanov, N. V. Fateev, M. M. Kalugin, M. A. Kazaryan, A. M. Prokhorov and D. E. Zakrevskii, Laser Isotope Separation in Atomic Vapor, John Wiley & Sons, 2006 Search PubMed.
- K. J. Nihill, J. D. Graham and S. J. Sibener, Phys. Rev. Lett., 2017, 119, 176001 CrossRef PubMed.
- T. Ruf, R. W. Henn, M. Asen-Palmer, E. Gmelin, M. Cardona, H.-J. Pohl, G. G. Devyatych and P. G. Sennikov, Solid State Commun., 2000, 115, 243–247 CrossRef.
- J.-Y. Li, C.-T. Huang, L. P. Rokhinson and J. C. Sturm, Appl. Phys. Lett., 2013, 103, 162105 CrossRef.
- K. M. Itoh and H. Watanabe, MRS Commun., 2014, 4, 143–157 CrossRef CAS.
- B. E. Kane, Nature, 1998, 393, 133–137 CrossRef CAS.
- K. D. Gibson, D. R. Killelea, H. Yuan, J. S. Becker, S. Pratihar, P. Manikandan, S. C. Kohale, W. L. Hase and S. J. Sibener, J. Phys. Chem. C, 2012, 116, 14264–14273 CrossRef CAS.
- K. D. Gibson, G. G. Langlois, W. Li, D. R. Killelea and S. J. Sibener, J. Chem. Phys., 2014, 141, 18C514 CrossRef CAS.
- K. D. Gibson, D. R. Killelea, J. S. Becker, H. Yuan and S. J. Sibener, Chem. Phys. Lett., 2012, 531, 18–21 CrossRef CAS.
- S. Pratihar, S. C. Kohale, L. Yang, P. Manikandan, K. D. Gibson, D. R. Killelea, H. Yuan, S. J. Sibener and W. L. Hase, J. Phys. Chem. C, 2013, 117, 2183–2193 CrossRef CAS.
- G. G. Langlois, W. Li, K. D. Gibson and S. J. Sibener, J. Phys. Chem. A, 2015, 119, 12238–12244 CrossRef CAS.
- D. R. Miller, in Atomic and Molecular Beam Methods, ed. G. Scoles, Oxford University Press, New York – Oxford, 1988, vol. 1, pp. 14–53 Search PubMed.
- H. Pauly, in Atomic and Molecular beam Methods, ed. G. Scoles, Oxford University Press, New York – Oxford, 1988, vol. 1, pp. 124–152 Search PubMed.
- Atomic Weights and Isotopic Compositions for All Elements, https://physics.nist.gov/cgi-bin/Compositions/stand_alone.pl, accessed Jan 1, 2020.
- D. E. Brown, S. M. George, C. Huang, E. K. L. Wong, K. B. Rider, R. S. Smith and B. D. Kay, J. Phys. Chem., 1996, 100, 4988–4995 CrossRef CAS.
- K. P. Stevenson, G. A. Kimmel, Z. Dohnálek, R. S. Smith and B. D. Kay, Science, 1999, 283, 1505–1507 CrossRef CAS.
- G. A. Kimmel, Z. Dohnálek, K. P. Stevenson, R. S. Smith and B. D. Kay, J. Chem. Phys., 2001, 114, 5295–5303 CrossRef CAS.
- F. M. McCubbin and J. J. Barnes, Earth Planet. Sci. Lett., 2019, 526, 115771 CrossRef CAS.
| This journal is © the Owner Societies 2021 |