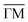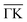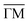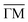Open Access Article
Open Access ArticleInelastic helium atom scattering from Sb2Te3(111): phonon dispersion, focusing effects and surfing
Adrian
Ruckhofer
 *a,
Simon
Halbritter
a,
Henriette E.
Lund
b,
Ann Julie U.
Holt
b,
Marco
Bianchi
*a,
Simon
Halbritter
a,
Henriette E.
Lund
b,
Ann Julie U.
Holt
b,
Marco
Bianchi
 b,
Martin
Bremholm
b,
Martin
Bremholm
 c,
Giorgio
Benedek
c,
Giorgio
Benedek
 de,
Philip
Hofmann
de,
Philip
Hofmann
 b,
Wolfgang E.
Ernst
b,
Wolfgang E.
Ernst
 a and
Anton
Tamtögl
a and
Anton
Tamtögl
 a
a
aInstitute of Experimental Physics, Graz University of Technology, 8010 Graz, Austria. E-mail: ruckhofer@tugraz.at
bDepartment of Physics and Astronomy, Interdisciplinary Nanoscience Center (iNANO), Aarhus University, 8000 Aarhus, Denmark
cCenter for Materials Crystallography, Department of Chemistry and iNANO, Aarhus University, 8000 Aarhus, Denmark
dDipartimento di Scienza dei Materiali, Universitá degli Studi di Milano-Bicocca, Milano, Italy
eDonostia International Physics Center (DIPC) and University of the Basque Country, 20018 Donostia/San Sebastian, Spain
First published on 21st October 2020
Abstract
We present an experimental study of inelastic scattering processes on the (111) surface of the topological insulator Sb2Te3 using helium atom scattering. In contrast to other binary topological insulators such as Bi2Se3 and Bi2Te3, Sb2Te3 is much less studied and the as-grown Sb2Te3 sample turns out to be p-doped, with the Fermi-level located below the Dirac-point as confirmed by angle-resolved photoemission spectroscopy. We report the surface phonon dispersion along both high symmetry directions in the energy region below 11 meV, where the Rayleigh mode exhibits the strongest intensity. The experimental data is compared with a study based on density functional perturbation theory calculations, providing good agreement except for a set of additional peculiar inelastic events below the Rayleigh mode. In addition, an analysis of angular scans with respect to a number of additional inelastic events is presented, including resonance enhancement, kinematical focusing, focused inelastic resonance and surfing. In the latter case, phonon-assisted adsorption of the incident helium atom gives rise to a bound state where the helium atom rides the created Rayleigh wave.
1 Introduction
Antimony telluride (Sb2Te3) is a prominent p-type semiconductor and multifunctional material, well known for its outstanding thermoelectric properties at room temperature1 and is used in power generation, heat pumping, cooling applications and data storage.2 Approaches to further improve thermoelectric efficiency in low dimensional systems3–5 and the contribution of topological surface states to thermoelectric properties have been investigated by Hinsche et al.6 and show a possible involvement to enhanced phonon scattering. Sb2Te3 also plays a major role in phase change memory alloys7 and recently sparked great interest in the field of topological insulators (TIs).8–10TIs are described as a new type of quantum material, where the band gap present in the bulk, is closed by topologically protected surface states, forming a single Dirac-cone at the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) -point. These states arise from the combination of spin–orbit interaction and time-reversal symmetry.11–13 Besides the well investigated binary compounds Bi2Se3 and Bi2Te3, Sb2Te3 has been confirmed to be a three-dimensional TI with a single Dirac cone on the surface.8,14–16
-point. These states arise from the combination of spin–orbit interaction and time-reversal symmetry.11–13 Besides the well investigated binary compounds Bi2Se3 and Bi2Te3, Sb2Te3 has been confirmed to be a three-dimensional TI with a single Dirac cone on the surface.8,14–16
The Fermi-level of as-grown p-doped Sb2Te3 is located below the Dirac-point and Sb2Te3 can exhibit hole pockets in the 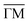 direction, depending on the position of the Fermi-level.16 However, it has been shown that the surface Fermi level can be shifted above the Dirac point, without changing the band structure, by n-doping with Cs.17 While the surface electronic states of Sb2Te3(111) have been investigated, by angle-resolved photoemission spectroscopy (ARPES)16,18–21 and theoretical band structure calculations,22,23 no experimental study exists for the surface phonon dispersion curves. On the one hand, for van der Waals layered structures, often the dynamics of surface layers does not differ that much from the bulk and preliminary information can be extracted from experimental24–26 and theoretical27 bulk data. On the other hand, the presence of topological surface electronic states at the Fermi level promises peculiar effects on the surface.28–30 So far information about the surface phonon dispersion curves of Sb2Te3(111) was limited to ab initio calculations using density functional perturbation theory (DFPT).30 In this work we determine the surface phonon dispersion and discuss several additional inelastic events in atom-surface scattering such as kinematical focusing, resonance enhancement and surfing. Using the time-of-flight (TOF) technique31 we determine the surface phonon dispersion in the energy region below 11 meV based on helium atom scattering (HAS) and compare the results with existing ab initio calculations. HAS with incident energies in the low meV range has been widely used to probe low-energy surface excitations with the best available resolution, while being an inert completely non destructive technique.31,32
direction, depending on the position of the Fermi-level.16 However, it has been shown that the surface Fermi level can be shifted above the Dirac point, without changing the band structure, by n-doping with Cs.17 While the surface electronic states of Sb2Te3(111) have been investigated, by angle-resolved photoemission spectroscopy (ARPES)16,18–21 and theoretical band structure calculations,22,23 no experimental study exists for the surface phonon dispersion curves. On the one hand, for van der Waals layered structures, often the dynamics of surface layers does not differ that much from the bulk and preliminary information can be extracted from experimental24–26 and theoretical27 bulk data. On the other hand, the presence of topological surface electronic states at the Fermi level promises peculiar effects on the surface.28–30 So far information about the surface phonon dispersion curves of Sb2Te3(111) was limited to ab initio calculations using density functional perturbation theory (DFPT).30 In this work we determine the surface phonon dispersion and discuss several additional inelastic events in atom-surface scattering such as kinematical focusing, resonance enhancement and surfing. Using the time-of-flight (TOF) technique31 we determine the surface phonon dispersion in the energy region below 11 meV based on helium atom scattering (HAS) and compare the results with existing ab initio calculations. HAS with incident energies in the low meV range has been widely used to probe low-energy surface excitations with the best available resolution, while being an inert completely non destructive technique.31,32
2 Experimental details and sample characterisation
The reported measurements were performed on a HAS apparatus which generates a nearly monochromatic beam (ΔE/E ≈ 2%) of 4He that is scattered off the sample surface in a fixed 91.5° source-sample-detector geometry. The beam is produced in a supersonic expansion of He through a 10 μm nozzle followed by extracting the core of the supersonic expansion via a 310 μm skimmer. For a detailed description of the apparatus refer to ref. 33.The analysis of the inelastically scattered He atoms allows to determine the surface phonon branches in the acoustic and optical regions. The impinging He atoms with energies in the low meV range are exclusively scattered by the surface charge density.34,35 Inelastic scattering from surface phonons occurs via the phonon-induced charge density oscillations, which can be used for the determination of the electron–phonon (e–ph) interaction constant.36,37 Antimony telluride has a rhombohedral crystal structure consisting of five atomic layers, arranged along the z-direction (perpendicular to the surface), known as quintuple layers (QLs) as seen in Fig. 1c.38 Each QL consists of two equivalent tellurium atoms, two equivalent antimony atoms and a third tellurium atom. The bonding is strong between the atomic layers within a QL but much weaker, predominantly of the van der Waals type, between two QLs. When cleaved along the (111) plane the upper-most atomic layer consists of tellurium, followed by an antimony layer below and so forth.
The investigated crystal was formed by slowly cooling the melt in a quartz tube similar to the procedure described in ref. 39 and 40 and the phase purity of the synthesised sample was measured by X-ray diffraction. The unit cell parameters were extracted based on a Rietveld refinement. Afterwards the crystal rod was cleaved along the (111) plane and for the measurements a small sample was attached onto a sample plate with electrically and thermally conductive epoxy. The surface electronic structure of the samples was characterised by ARPES at the SGM-3 beamline of ASTRID2.41 The total energy and angular resolution were ≈30 meV and 0.1°, respectively. The sample temperature was ≈30 K and the photon energy was chosen to be 22 eV.
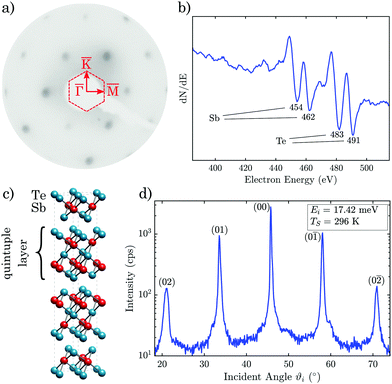
Previously to the HAS measurements, in order to obtain a clean surface, the sample was cleaved in situ under high vacuum conditions in a separate load lock chamber,42 before storing the sample in the sample mount of the main chamber, to ensure minimal surface contamination. The sample can be heated using a button heater on the backside of the sample mount or cooled down to 115 K via a thermal connection to a liquid nitrogen reservoir. Low energy electron diffraction was used for a first alignment of the sample along the high symmetry orientation (Fig. 1a). Additionally, before running scattering experiments, the composition of the sample was analysed by Auger electron spectroscopy. The obtained spectrum can be seen in Fig. 1b, which shows significant intensities at the expected energies for single-elemental antimony and tellurium, when compared to spectra from literature.43
The angular HAS distribution along the 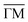 azimuth in Fig. 1d shows diffraction peaks up to second order. The scattered intensity is plotted on a logarithmic scale with an incident energy of Ei = 17.4 meV and the sample held at room temperature. The high signal-to-noise ratio and the small full width at half maximum of the specular peak are an indication of the good crystal quality after cleaving. The high intensity of the diffraction peaks suggests a large surface electronic corrugation (Sb2Te3(111) exhibits a surface electronic corrugation of 6.6% of the lattice constant44) which is a necessary ingredient for various phenomena, e.g. involving bound state resonances.
azimuth in Fig. 1d shows diffraction peaks up to second order. The scattered intensity is plotted on a logarithmic scale with an incident energy of Ei = 17.4 meV and the sample held at room temperature. The high signal-to-noise ratio and the small full width at half maximum of the specular peak are an indication of the good crystal quality after cleaving. The high intensity of the diffraction peaks suggests a large surface electronic corrugation (Sb2Te3(111) exhibits a surface electronic corrugation of 6.6% of the lattice constant44) which is a necessary ingredient for various phenomena, e.g. involving bound state resonances.
Energy dispersive spectra for inelastic scattering were performed using TOF measurements with a pseudo-random chopper disc. After deconvolution with the pseudo-random chopper sequence, the TOF signal is further transformed to an energy transfer scale which allows to determine inelastic (phonon) scattering events.33 The scattering spectra were mainly taken with the crystal at room temperature, while a few spectra were taken with the sample cooled down to 115 K and the incident He beam energy was varied between 10 and 18 meV.
3 Results and discussion
Details of the phonon dispersion are closely linked to the electronic structure and screening of a system and this is particularly relevant for the surface phonon dispersion of topological insulators where the surface electronic properties are drastically different from those of the bulk. It is therefore important to characterise the crystals in terms of their bulk doping in order to identify the Fermi surface elements that can contribute to screening. For Sb2Te3 the as-grown crystals are typically strongly p-doped, up to a degree where the valence band maximum at![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) and a hole pocket along the
and a hole pocket along the 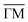 direction can contribute to the surface Fermi surface.19,20,30 The latter is confirmed in ARPES measurements of the current sample as described in the following.
direction can contribute to the surface Fermi surface.19,20,30 The latter is confirmed in ARPES measurements of the current sample as described in the following.
3.1 Surface electronic structure
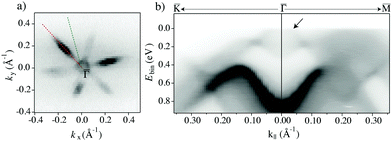
The photoemission intensity at the Fermi energy is given in Fig. 2a, showing a flower-like pattern. The closed contour around![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) and the petals of the flower have both the character of hole pockets, as can be seen from the detailed dispersion in Fig. 2b.
and the petals of the flower have both the character of hole pockets, as can be seen from the detailed dispersion in Fig. 2b.
Indeed, it is seen that the state near ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) results from both the valence band maximum, leading to the blurred intensity near the Fermi level at k‖ ≈ 0, and the lower part of the topological surface state dispersion that gives rise to a somewhat sharper linear feature, marked by an arrow in the figure. The band forming the hole pocket (flower petal) along
results from both the valence band maximum, leading to the blurred intensity near the Fermi level at k‖ ≈ 0, and the lower part of the topological surface state dispersion that gives rise to a somewhat sharper linear feature, marked by an arrow in the figure. The band forming the hole pocket (flower petal) along 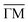 is seen as a diffuse intensity in an energy interval between ≈0.3 eV and the Fermi energy. Note that the observation of broad bands from bulk states is common in ARPES and related to the k⊥ smearing that results from the short inelastic mean free path of the photoelectrons. The conclusion from the ARPES characterisation is that the sample is indeed strongly p-doped, giving rise to two different types of (bulk) hole pockets.
is seen as a diffuse intensity in an energy interval between ≈0.3 eV and the Fermi energy. Note that the observation of broad bands from bulk states is common in ARPES and related to the k⊥ smearing that results from the short inelastic mean free path of the photoelectrons. The conclusion from the ARPES characterisation is that the sample is indeed strongly p-doped, giving rise to two different types of (bulk) hole pockets.
3.2 Surface phonon dispersion
The surface phonon events were determined from a multitude of TOF spectra at various incident energies Ei and incident angles ϑi to fully cover the Brillouin zone along both high symmetry directions (see Appendix A for various TOF spectra). The peaks in the energy domain of the TOF spectra were transformed to the wavevector domain using the so called scancurve (SC). The SC links all accessible energy transfers to the corresponding parallel momentum transfer during an inelastic event and is given by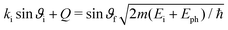 | (1) |
As shown by D. Campi et al.,30 the inclusion of spin–orbit coupling (SOC) in ab initio calculations of the surface phonon dispersion has negligible effects. Hence, the reported surface phonon dispersion curves based on DFPT calculations (without SOC) for a slab consisting of three QLs are reproduced in Fig. 3 as solid grey lines. The experimentally obtained surface phonon energies are plotted as symbols on top of the theoretical calculations in Fig. 3.
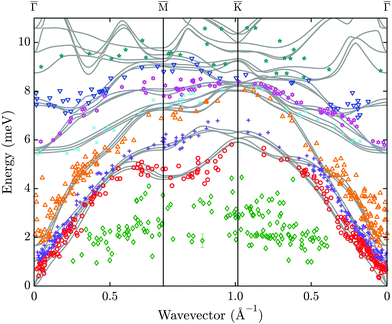 | ||
| Fig. 3 Experimental surface phonon dispersion of Sb2Te3(111) from helium atom scattering (symbols) in comparison with DFPT calculations for three quintuple layers in the lower part of the phonon spectrum (solid grey lines).30 The assignment of the data points (colour and tag) to different modes is based on the proximity to the theoretical modes. One exemplary error bar is shown at an energy of ≈2 meV. | ||
We are able to resolve surface phonon events with energies up to 11 meV along both high symmetry directions. Each phonon event has been marked with a mode related colour and tag, according to its vicinity to the calculated modes. Due to many avoided crossings an accurate assignment of the optical modes becomes more difficult. In general the experimental surface phonon dispersion is in good agreement with the DFPT calculations except for the low energy modes (1–4 meV) marked as green diamonds which will be discussed below (Section 3.4).
According to the DFPT calculations, there are altogether 45 phonon branches (of which only the lower 24 are displayed as solid grey lines in Fig. 3), organised into 15 bands associated with the 15 degrees of freedom of Sb2Te3. Besides the 3 acoustic modes, there are two low-energy bands (<2 meV at ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) ) where in each QL the central Te layer is at rest and the two external bilayers move rigidly and symmetrically normal (Ag(1)) or parallel (Eg(1)) to the slab.27
) where in each QL the central Te layer is at rest and the two external bilayers move rigidly and symmetrically normal (Ag(1)) or parallel (Eg(1)) to the slab.27
The corresponding experimentally obtained acoustic branches are shown as red circles, purple crosses and orange triangles in Fig. 3, with the red circles being the Rayleigh wave (RW), starting with zero energy at the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) point. In general, a high concentration of experimental data points is found in the acoustic region, including the Rayleigh mode. Inelastic events from the RW give the highest intensity in the respective TOF spectra, confirming the high intensity of the RW as also found for other binary TIs such as Bi2Se3 and Bi2Te3, respectively.28,29 Note that in contrast to the recent report of two RWs in Bi2Te346 there exists only one RW, either as a surface-localised wave or as an in-band resonance (pseudo-surface wave), as a result of continuum theory.28,29,32
point. In general, a high concentration of experimental data points is found in the acoustic region, including the Rayleigh mode. Inelastic events from the RW give the highest intensity in the respective TOF spectra, confirming the high intensity of the RW as also found for other binary TIs such as Bi2Se3 and Bi2Te3, respectively.28,29 Note that in contrast to the recent report of two RWs in Bi2Te346 there exists only one RW, either as a surface-localised wave or as an in-band resonance (pseudo-surface wave), as a result of continuum theory.28,29,32
3.3 Phonon group velocity
As mentioned above, the energetically lowest mode in the surface phonon dispersion is the RW. Its band starts at zero energy at the![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) -point of the surface Brillouin zone with a linear dispersion in the long wavelength (Q → 0) limit.
-point of the surface Brillouin zone with a linear dispersion in the long wavelength (Q → 0) limit.
The group velocity of the RW can be determined from the slope of its dispersion curve at small wavevectors. Therefore, the measured data points are fitted with a linear relation in the low energy range assuming an intercept with the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) -point at Q = 0. Due to the fact, that for Sb2Te3 the RW and the second acoustic mode proceed parallel and rather close to each other, the assignment of measured points is not always unambiguous, which leads to a rather high uncertainty for the determined slopes along
-point at Q = 0. Due to the fact, that for Sb2Te3 the RW and the second acoustic mode proceed parallel and rather close to each other, the assignment of measured points is not always unambiguous, which leads to a rather high uncertainty for the determined slopes along  and
and  in Table 1.
in Table 1.
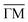 and
and 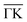 direction based on a linear fit and the corresponding group velocities vRW of the RW
direction based on a linear fit and the corresponding group velocities vRW of the RW
By means of the elastic constants of Sb2Te3 calculated ab initio by Lu et al.,47 and a crystal density of 6.488 g cm−3,48 the bulk transverse speed of sound along 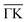 can be calculated49 and is found to be 1620 m s−1. As seen in Table 1, the group velocity of the RW along this direction is only slightly less than the bulk transverse acoustic speed of sound with a difference that is, however, much smaller than the experimental uncertainty.
can be calculated49 and is found to be 1620 m s−1. As seen in Table 1, the group velocity of the RW along this direction is only slightly less than the bulk transverse acoustic speed of sound with a difference that is, however, much smaller than the experimental uncertainty.
3.4 Low energy modes
When looking at Fig. 3 it becomes evident that several peaks at energies between 1–4 meV are not reproduced in the DFPT calculations. These events cannot be assigned to any surface phonon mode and need further discussion. One could possibly ascribe two separate branches with a dispersion to the plotted data points, though with some difficulty given the number of data points and their spread.Similar low-energy excitations observed with HAS in the gap below the RW branch have been reported previously in two other topological materials, Sb(111)50 and Bi2Se3(111).29 In both cases they could be assigned to low-energy surface electron collective excitations, namely phasons and amplitons, associated with a charge density wave (CDW) induced by e–ph interaction. In Sb(111) a quasi-commensurate CDW originates from the Kelly–Falicov multivalley e–ph coupling connecting ![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) -point electron pockets,50 while in Bi2Se3(111) a long-period CDW has been associated with e–ph coupling connecting surface quantum-well states.29 In both cases distinct CDW features are observed at low temperature in the HAS diffraction spectra, though under bound-state resonance enhancement conditions in Bi2Se3(111).
-point electron pockets,50 while in Bi2Se3(111) a long-period CDW has been associated with e–ph coupling connecting surface quantum-well states.29 In both cases distinct CDW features are observed at low temperature in the HAS diffraction spectra, though under bound-state resonance enhancement conditions in Bi2Se3(111).
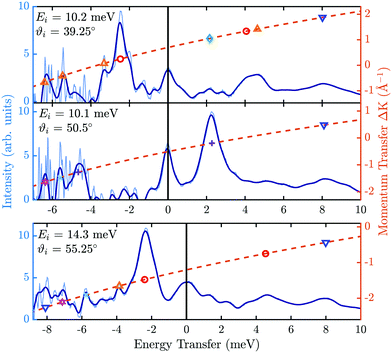
Although the similarities of present low-energy data with those observed in Sb(111) and Bi2Se3(111) are quite evident, low-lying frustrated translational modes of adsorbates can be another possible source of these data points.51 This possibility is however rather remote in view of the good quality of the surface during experiments, as witnessed by the comparatively low intensity of the diffuse elastic peak in the TOF spectra (see, e.g.Fig. 4a)
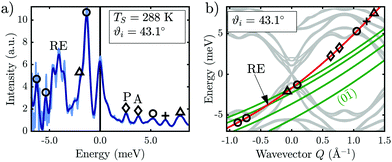 | ||
Fig. 4 (a) shows a TOF-spectrum at ϑi = 43.1° with the sample at room temperature, exhibiting phonon processes and low energy excitations as well as a resonance-enhanced phonon process. The light blue line depicts the raw data after conversion to an energy transfer scale while the dark blue line shows the signal after binning based on constant energy bins (see Appendix). In (b) the resonance conditions (eqn (2)) for the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) G-vector together with the scancurve are drawn on top of the DFPT calculations (grey lines). The symbols correspond to the phonon events of the TOF spectrum to the left. ) G-vector together with the scancurve are drawn on top of the DFPT calculations (grey lines). The symbols correspond to the phonon events of the TOF spectrum to the left. | ||
Hence we conclude that the two branches are likely to be caused by phasons/amplitons in analogy to the observations made on Sb(111) and Bi2Se3(111), although a more thorough investigation is needed in order to unambiguously assign and understand these excitations.
3.5 Resonance enhancement
The intensity of a specific phonon event might be increased if a bound state resonance is involved – therefore termed resonance enhancement. A He atom might go into a final state which is a bound state of energy −|εn| + ħ2Kf2/2m*, with Kf being the final parallel vector and m* the effective mass of the atom in the bound state.51 Based on the conservation of energy and parallel momentum, the corresponding equation for inelastic selective adsorption is51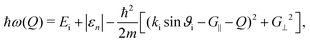 | (2) |
If the resonance condition (2) intersects with the SC (1) at a specific phonon branch, the intensity of this particular phonon will be enhanced in the TOF spectrum. Based on the bound states εn for Sb2Te3 (ε0 = 4.27 meV, ε1 = 2.37 meV, ε2 = 0.9 meV, ε3 = 0.4 meV),44 the condition is fulfilled in Fig. 4b, where the bound state ε2 of the resonance curve with an interacting G-vector (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) intersects the SC at an energy of −4 meV. The intensity of this created phonon is greatly enhanced in the TOF spectrum (Fig. 4a), when compared to measurements which do not satisfy the condition. Recent work showed that these resonance enhancing effects can in turn be used to observe low-energy surface electron collective excitations.29
) intersects the SC at an energy of −4 meV. The intensity of this created phonon is greatly enhanced in the TOF spectrum (Fig. 4a), when compared to measurements which do not satisfy the condition. Recent work showed that these resonance enhancing effects can in turn be used to observe low-energy surface electron collective excitations.29
3.6 Kinematical focusing, focussed inelastic resonance and surfing
In addition to phonon resonance enhancement a variety of other resonance and focusing phenomena can arise upon scattering from a corrugated surface,51 as listed below. These processes can be described by looking at the equations for the SC and the resonance conditions as well as the lowest modes of the surface phonon dispersion. The upper left graph of Fig. 5 shows an angular scan where the incident angle ϑi is varied along the azimuth with the sample at a temperature of 113 K. Upon enlarging the y-scale compared to Fig. 1d, additional peaks and dips appear in the diffuse inelastic background. Below the measured curve the bound state resonances for the four known bound states44 are depicted. The different colours correspond to the different interacting reciprocal lattice vectors.
azimuth with the sample at a temperature of 113 K. Upon enlarging the y-scale compared to Fig. 1d, additional peaks and dips appear in the diffuse inelastic background. Below the measured curve the bound state resonances for the four known bound states44 are depicted. The different colours correspond to the different interacting reciprocal lattice vectors.
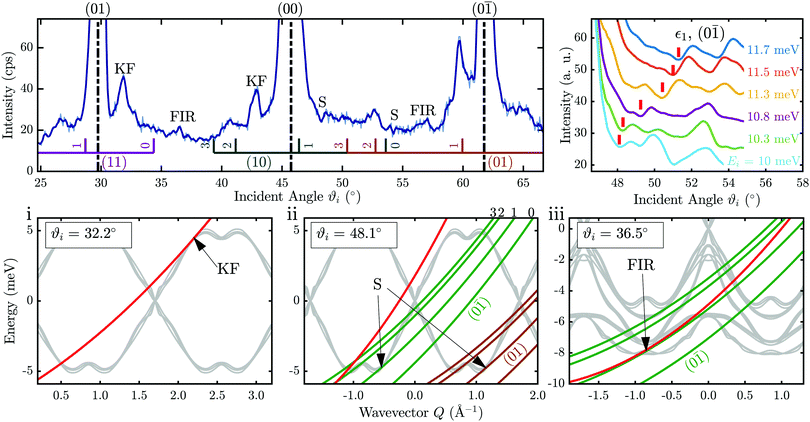 | ||
Fig. 5 Diagrams illustrating various HAS focusing effects as a function of parallel momentum (wavevector) Q, for an incident energy Ei = 10.3 meV. Top left panel: Angular scan along the  azimuth at a surface temperature Ts = 113 K (light blue line: raw data, dark blue line: smoothed data). The lines below the measured curve indicate selective adsorption resonance processes with the colours corresponding to different interacting G-vectors. Top right: Tracking of the surfing feature (highlighted by the red bar) with increasing incident beam energy Ei. The lower panels show (from left to right) the effects kinematical focusing (KF), surfing (S) and focused inelastic resonance (FIR). The red curves depict the scancurve while the green curves show the resonance conditions (eqn (2)) with the corresponding G-vector. azimuth at a surface temperature Ts = 113 K (light blue line: raw data, dark blue line: smoothed data). The lines below the measured curve indicate selective adsorption resonance processes with the colours corresponding to different interacting G-vectors. Top right: Tracking of the surfing feature (highlighted by the red bar) with increasing incident beam energy Ei. The lower panels show (from left to right) the effects kinematical focusing (KF), surfing (S) and focused inelastic resonance (FIR). The red curves depict the scancurve while the green curves show the resonance conditions (eqn (2)) with the corresponding G-vector. | ||
The three scattering phenomena kinematical focusing (i), surfing (ii) and resonance enhancement (iii) are plotted in the lower panels of Fig. 5 as energy ħω(Q) versus wavevector Q. Here we use the convention that the forward creation process is displayed in the third quadrant (Q < 0, ħω(Q) < 0) as frequently used in HAS analysis.29,52 Therefore positive energies in Fig. 5 correspond to annihilation and backward propagation. The purely inelastic process occurs when the SC intersects with a branch in the phonon dispersion and can be measured with the TOF technique described above.
(i) An effect known as kinematical focusing53 (KF) might show up at a specific incident angle ϑi and incident energy Ei when the SC lies tangent to a phonon branch. KF gives rise to a saw-tooth peak in the angular scattering distribution due to the increased inelastic background in the elastic signal. The characteristic peak shape can clearly be identified in the angular scan (upper left panel of Fig. 5) at ϑi = 32° and ϑi = 43°. For the first angle the corresponding SC is plotted in red in Fig. 5i together with the two lowest modes of the calculated phonon dispersion. The point of tangency is marked with KF and can be observed in the angular distribution as well as in the corresponding TOF spectrum.
(ii) We now turn to the effect of surfing, which occurs when a resonance curve lies tangent to a surface phonon branch. In this case, the impinging He atom is selectively adsorbed into a bound state εn with the aid of a surface phonon. In comparison to the “ordinary” elastic selective adsorption this process can occur even without the exchange of a reciprocal lattice vector. The tangency condition yields a concentration of beams inelastically scattered into the given bound state and therefore a dip in the final beam around a special incident angle. Using the bound state energy values for Sb2Te344 a set of resonance curves are plotted as green lines in Fig. 5ii. The tangency of one of these curves with a phonon branch gives rise to a dip in the angular distribution. If this special condition is fulfilled the atom and the phonon wave exhibit the same velocity on the surface and travel together, hence the effect is called surfing. According to ref. 51 the atom stays on the surface for a longer time during surfing compared to the lifetime of the He atom in a bound state.44 However, based on the signal-to-noise ratio of our data it is difficult to extract an actual linewidth and thus the corresponding lifetime. Hence we cannot conclude on any values for the lifetime.
In Fig. 5ii the surfing effect is shown for an incident angle of ϑi = 57.1°, where the resonance curves of the bound state ε1 for the G-vectors (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and (01) are tangent to the acoustic phonon branch. In the angular spectrum the surfing conditions at various angles are indicated with an S, yielding a dip in the scattered intensity. To further support the finding of the surfing feature the dip can be monitored in dependence of the incident energy Ei. In the top right panel of Fig. 5 the surfing dip is shown for incident energies between Ei = 10.7 and 11.7 meV. The angular spectra were smoothed using a Savitzky–Golay filter and the red bars mark sequences of features assigned to the (0
) and (01) are tangent to the acoustic phonon branch. In the angular spectrum the surfing conditions at various angles are indicated with an S, yielding a dip in the scattered intensity. To further support the finding of the surfing feature the dip can be monitored in dependence of the incident energy Ei. In the top right panel of Fig. 5 the surfing dip is shown for incident energies between Ei = 10.7 and 11.7 meV. The angular spectra were smoothed using a Savitzky–Golay filter and the red bars mark sequences of features assigned to the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) surfing condition including the ε1 bound state.
) surfing condition including the ε1 bound state.
(iii) Finally we discuss the effect of focussed inelastic resonance (FIR), which occurs when the SC (1) is tangent to a resonance curve (2) within an energy region where surface phonons are expected.32,54 When combining these two equations the expected FIR position is given by
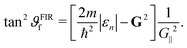 | (3) |
In the angular scan of Fig. 5 two FIR features are present at ϑi = 36.5° and ϑi = 56.4° yielding an increased scattered intensity. A comparison with angular scans at similar incident energies shows that the FIR peaks are still present at the same incident angle as expected, according to (3). In the lower right most plot of Fig. 5 (ϑi = 36.5) the resonance curve becomes tangent to the SC for an optical phonon branch at around 8 meV.
Following this systematic approach we are able to interpret all significant peaks of the angular scan in Fig. 5 using the effects described above. All peaks which are not labelled are attributed to selective adsorption resonances indicated by the vertical coloured lines below the measured data.
4 Conclusions
In summary, we have investigated various inelastic interactions of helium with Sb2Te3 which are experimentally detected in TOF spectra as well as in angular scans. A multitude of TOF spectra was used to determine the surface phonon dispersion for the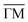 and
and 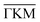 directions. A comparison with theoretical calculations based on density functional perturbation theory shows good agreement with the experimental data. Similar to earlier works, the strongest phonon intensities originate from the Rayleigh mode. From the slope of the Rayleigh mode the phonon group velocity is determined to be vR ≈ 1600 m s−1. In addition to phonon creation and annihilation processes, we observe further peculiar inelastic events below the Rayleigh mode. In view of similar observations made on the topological materials Sb(111) and Bi2Se3(111), they are tentatively assigned to the dispersion curves of phasons and amplitons associated with a charge density wave.
directions. A comparison with theoretical calculations based on density functional perturbation theory shows good agreement with the experimental data. Similar to earlier works, the strongest phonon intensities originate from the Rayleigh mode. From the slope of the Rayleigh mode the phonon group velocity is determined to be vR ≈ 1600 m s−1. In addition to phonon creation and annihilation processes, we observe further peculiar inelastic events below the Rayleigh mode. In view of similar observations made on the topological materials Sb(111) and Bi2Se3(111), they are tentatively assigned to the dispersion curves of phasons and amplitons associated with a charge density wave.
Furthermore, a systematic analysis of angular diffraction scans shows that several additional inelastic scattering events are observable for He atom scattering from Sb2Te3. These include resonance enhancement, kinematical focusing, focused inelastic resonances and surfing.
Conflicts of interest
There are no conflicts to declare.A Additional TOF spectra
For the determination of the surface phonon dispersion (Fig. 3) a multitude of TOF spectra were measured with different incident energies Ei and incident angles ϑi. In Fig. 6 three exemplary TOF spectra are shown in the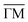 direction, after conversion to an energy transfer scale. Negative energy transfer corresponds to phonon creation, while positive energy transfer corresponds to phonon annihilation.
direction, after conversion to an energy transfer scale. Negative energy transfer corresponds to phonon creation, while positive energy transfer corresponds to phonon annihilation.
Because of the non-linearity introduced by the conversion from the flight time to the energy transfer scale, the data has to be multiplied with the corresponding Jacobian in order to preserve the intensity. Due to the process, experimental noise increases on the creation side (ΔE = Ef − Ei < 0) as seen in the light blue line in Fig. 6. The latter makes it difficult to distinguish peaks in the (far) creation side and therefore, the (non-linear) energy scale is usually divided in equally spaced energy bins over which the signal is averaged.55 The dark blue line shows the signal after binning, resulting in a smoother line.
The peaks in Fig. 6 identified as phonon events are indicated with different symbols, which attribute the peaks to the specific phonon branches (same symbols as in Fig. 3). The symbols are drawn on the SC (1) plotted as a dashed orange line, relating the energy transfer of a phonon event to the momentum transfer ΔK (right ordinate in Fig. 6).
Acknowledgements
We would like to thank D. Campi for many helpful discussions and the ab initio surface phonon dispersion curves from ref. 30. The authors are grateful for financial support by the FWF (Austrian Science Fund) within the project P29641-N36, as well as by NAWI Graz. We would like to thank the Aarhus University Research Foundation, VILLUM FOUNDATION via the Centre of Excellence for Dirac Materials (Grant No. 11744) and the SPP1666 of the DFG (Grant No. HO 5150/1-2) for financial support. M. Bremholm acknowledges financial support from the Center of Materials Crystallography (CMC) and the Danish National Research Foundation (DNRF93).References
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS.
- M. Wuttig and N. Yamada, Nat. Mater., 2007, 6, 824–832 CrossRef CAS.
- L. D. Hicks and M. S. Dresselhaus, MRS Proc., 1993, 326, 413 CrossRef.
- S. Zastrow, J. Gooth, T. Boehnert, S. Heiderich, W. Toellner, S. Heimann, S. Schulz and K. Nielsch, Semicond. Sci. Technol., 2013, 28, 035010 CrossRef.
- Z. Zhang, H. Zhang, Y. Wu, Z. Zeng and Z. Hu, Appl. Phys. A: Mater. Sci. Process., 2015, 118, 1043–1051 CrossRef CAS.
- N. F. Hinsche, S. Zastrow, J. Gooth, L. Pudewill, R. Zierold, F. Rittweger, T. Rauch, J. Henk, K. Nielsch and I. Mertig, ACS Nano, 2015, 9, 4406–4411 CrossRef CAS.
- S. Fujimori, S. Yagi, H. Yamazaki and N. Funakoshi, J. Appl. Phys., 1988, 64, 1000–1004 CrossRef CAS.
- H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Nat. Phys., 2009, 5, 438 Search PubMed.
- J. Zhang, C.-Z. Chang, Z. Zhang, J. Wen, X. Feng, K. Li, M. Liu, K. He, L. Wang, X. Chen, Q.-K. Xue, X. Ma and Y. Wang, Nat. Commun., 2011, 2, 574 Search PubMed.
- P. Sessi, O. Storz, T. Bathon, S. Wilfert, K. A. Kokh, O. E. Tereshchenko, G. Bihlmayer and M. Bode, Phys. Rev. B, 2016, 93, 035110 CrossRef.
- O. A. Pankratov, S. V. Pakhomov and B. A. Volkov, Solid State Commun., 1987, 61, 93–96 CrossRef CAS.
- C. Wu, B. A. Bernevig and S.-C. Zhang, Phys. Rev. Lett., 2006, 96, 106401 CrossRef.
- L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2007, 98, 106803 CrossRef.
- X.-L. Qi and S.-C. Zhang, Phys. Today, 2010, 63, 33–38 CrossRef CAS.
- C. Pauly, G. Bihlmayer, M. Liebmann, M. Grob, A. Georgi, D. Subramaniam, M. R. Scholz, J. Sánchez-Barriga, A. Varykhalov, S. Blügel, O. Rader and M. Morgenstern, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235106 CrossRef.
- L. Plucinski, A. Herdt, S. Fahrendorf, G. Bihlmayer, G. Mussler, S. Döring, J. Kampmeier, F. Matthes, D. E. Bürgler, D. Grützmacher, S. Blügel and C. M. Schneider, J. Appl. Phys., 2013, 113, 053706 CrossRef.
- G. Wang, X. Zhu, J. Wen, X. Chen, K. He, L. Wang, X. Ma, Y. Liu, X. Dai, Z. Fang, J. Jia and Q. Xue, Nano Res., 2010, 3, 874–880 CrossRef CAS.
- C. Seibel, H. Maaß, M. Ohtaka, S. Fiedler, C. Jünger, C.-H. Min, H. Bentmann, K. Sakamoto and F. Reinert, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 161105 CrossRef.
- J. Reimann, J. Güdde, K. Kuroda, E. V. Chulkov and U. Höfer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 081106 CrossRef.
- S. Zhu, Y. Ishida, K. Kuroda, K. Sumida, M. Ye, J. Wang, H. Pan, M. Taniguchi, S. Qiao, S. Shin and A. Kimura, Sci. Rep., 2015, 5, 13213 CrossRef CAS.
- Y. C. Arango, L. Huang, C. Chen, J. Avila, M. C. Asensio, D. Grützmacher, H. Lüth, J. G. Lu and T. Schäpers, Sci. Rep., 2016, 6, 29493 CrossRef CAS.
- B. Y. Yavorsky, N. F. Hinsche, I. Mertig and P. Zahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165208 CrossRef.
- I. A. Nechaev, I. Aguilera, V. De Renzi, A. di Bona, A. Lodi Rizzini, A. M. Mio, G. Nicotra, A. Politano, S. Scalese, Z. S. Aliev, M. B. Babanly, C. Friedrich, S. Blügel and E. V. Chulkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245123 CrossRef.
- W. Richter and C. R. Becker, Phys. Status Solidi B, 1977, 84, 619–628 CrossRef CAS.
- Y. Kim, X. Chen, Z. Wang, J. Shi, I. Miotkowski, Y. P. Chen, P. A. Sharma, A. L. Lima Sharma, M. A. Hekmaty, Z. Jiang and D. Smirnov, Appl. Phys. Lett., 2012, 100, 071907 CrossRef.
- V. Bragaglia, M. Ramsteiner, D. Schick, J. E. Boschker, R. Mitzner, R. Calarco and K. Holldack, Sci. Rep., 2020, 10, 12962 CrossRef CAS.
- G. C. Sosso, S. Caravati and M. Bernasconi, J. Phys.: Condens. Matter, 2009, 21, 095410 CrossRef CAS.
- A. Tamtögl, D. Campi, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, N. Marzari, G. Benedek, J. Ellis and W. Allison, Nanoscale, 2018, 10, 14627–14636 RSC.
- A. Ruckhofer, D. Campi, M. Bremholm, P. Hofmann, G. Benedek, M. Bernasconi, W. E. Ernst and A. Tamtögl, Phys. Rev. Res., 2020, 2, 023186 CrossRef CAS.
- D. Campi, M. Bernasconi and G. Benedek, Surf. Sci., 2018, 678, 46–51 CrossRef CAS.
- D. Farias and K.-H. Rieder, Rep. Prog. Phys., 1998, 61, 1575–1664 CrossRef CAS.
- G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer Berlin Heidelberg, 2018 Search PubMed.
- A. Tamtögl, M. Mayrhofer-Reinhartshuber, N. Balak, W. E. Ernst and K. H. Rieder, J. Phys.: Condens. Matter, 2010, 22, 304019 CrossRef.
- A. Tamtögl, M. Mayrhofer-Reinhartshuber, P. Kraus and W. E. Ernst, Surf. Sci., 2013, 617, 225–228 CrossRef.
- A. Tamtögl, P. Kraus, M. Mayrhofer-Reinhartshuber, D. Campi, M. Bernasconi, G. Benedek and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035410 CrossRef.
- G. Benedek, S. Miret-Artés, J. R. Manson, A. Ruckhofer, W. E. Ernst and A. Tamtögl, J. Phys. Chem. Lett., 2020, 1927–1933 CrossRef CAS.
- G. Benedek, J. R. Manson and S. Miret-Artés, Adv. Mater., 2020, 32, 2002072 CrossRef CAS.
- X. Chen, H. D. Zhou, A. Kiswandhi, I. Miotkowski, Y. P. Chen, P. A. Sharma, A. L. Lima Sharma, M. A. Hekmaty, D. Smirnov and Z. Jiang, Appl. Phys. Lett., 2011, 99, 261912 CrossRef.
- J.-L. Mi, M. Bremholm, M. Bianchi, K. Borup, S. Johnsen, M. Søndergaard, D. Guan, R. C. Hatch, P. Hofmann and B. B. Iversen, Adv. Mater., 2013, 25, 889–893 CrossRef CAS.
- M. Michiardi, I. Aguilera, M. Bianchi, V. E. de Carvalho, L. O. Ladeira, N. G. Teixeira, E. A. Soares, C. Friedrich, S. Blügel and P. Hofmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075105 CrossRef.
- S. V. Hoffmann, C. Søndergaard, C. Schultz, Z. Li and P. Hofmann, Nucl. Instrum. Methods Phys. Res., Sect. A, 2004, 523, 441 CrossRef CAS.
- A. Tamtögl, E. A. Carter, D. J. Ward, N. Avidor, P. R. Kole, A. P. Jardine, J. Ellis and W. Allison, Rev. Sci. Instrum., 2016, 87, 066108 CrossRef.
- L. E. Davis, Handbook of Auger Electron Spectroscopy: A Reference Book of Standard Data for Identification and Interpretation of Auger Electron Spectroscopy Data, Physical Electronics, 1996 Search PubMed.
- A. Tamtögl, A. Ruckhofer, D. Campi, W. Allison and W. E. Ernst, Phys. Chem. Chem. Phys., tbd Search PubMed , to be published.
- J. P. Toennies, in Surface Phonons, ed. W. Kress and F. W. de Wette, Springer Berlin Heidelberg, Berlin, Heidelberg, 1991, pp. 111–166 Search PubMed.
- A. Trzaskowska and B. Mroz, Sci. Rep., 2020, 10, 11812 CrossRef CAS.
- Q. Lu, H.-Y. Zhang, Y. Cheng, X.-R. Chen and G.-F. Ji, Chin. Phys. B, 2016, 25, 026401 CrossRef.
- D. Bessas, I. Sergueev, H.-C. Wille, J. Perßon, D. Ebling and R. P. Hermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 224301 CrossRef.
- Y. C. Akgöz, G. A. Saunders and Z. Sümengen, J. Mater. Sci., 1972, 7, 279–288 CrossRef.
- A. Tamtögl, P. Kraus, M. Mayrhofer-Reinhartshuber, G. Benedek, M. Bernasconi, D. Dragoni, D. Campi and W. E. Ernst, npj Quantum Mater., 2019, 4, 28 CrossRef.
- G. Benedek, P. M. Echenique, J. P. Toennies and F. Traeger, J. Phys.: Condens. Matter, 2010, 22, 304016 CrossRef CAS.
- G. Brusdeylins, R. B. Doak and J. P. Toennies, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 3662–3685 CrossRef CAS.
- G. Benedek, G. Brusdeylins, J. P. Toennies and R. B. Doak, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2488–2493 CrossRef CAS.
- G. Benedek, R. Gerlach, A. Glebov, G. Lange, S. Miret-Artes, J. G. Skofronick and J. P. Toennies, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 11211–11217 CrossRef.
- P. Kraus, A. Tamtögl, M. Mayrhofer-Reinhartshuber, G. Benedek and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245433 CrossRef.
| This journal is © the Owner Societies 2021 |