 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal clusters synthesized in helium droplets: structure and dynamics from experiment and theory
Wolfgang E.
Ernst
 * and
Andreas W.
Hauser
* and
Andreas W.
Hauser
 *
*
Institute of Experimental Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: wolfgang.ernst@tugraz.at; andreas.w.hauser@gmail.com; Fax: +43-316-873-108140; Tel: +43-316-873-8157 Tel: +43-316-873-8140
First published on 29th September 2020
Abstract
Metal clusters have drawn continuous interest because of their high potential for the assembly of matter with special properties that may significantly differ from the corresponding bulk. Controlled combination of particular elements in one nanoparticle can increase the options for the creation of new materials for photonic, catalytic, or electronic applications. Superfluid helium droplets provide confinement and ultralow temperature, i.e. an ideal environment for the atom-by-atom aggregation of a new nanoparticle. This perspective presents a review of the current research progress on the synthesis of tailored metal and metal oxide clusters including core–shell designs, their characterization within the helium droplet beam, deposition on various solid substrates, and analysis via surface diagnostics. Special attention is given to the thermal properties of mixed metal clusters and questions about alloy formation on the nanoscale. Experimental results are accompanied by theoretical approaches employing computational chemistry, molecular dynamics simulations and He density functional theory.
1 Introduction
Initial interest in nanoclusters or nanoparticles originated in a purely curiosity driven exploration of an intermediate state of matter between free molecules and solid phase. Co-condensing a stream of atoms or molecules with large amounts of noble gas on a cold finger allowed an aggregation process for the production of clusters in a cold matrix.1 Early research on metal clusters was mainly based on the spectroscopy of dimers and trimers or the size-dependent measurement of ionization thresholds.2 The two volumes on ‘Clusters of Atoms and Molecules’ edited by Haberland3 give an excellent overview of the field about 25 years ago. Concentrating on the electronic properties evolving with metal cluster size, de Heer summarized ionization potentials, polarizabilities, and optical properties in connection with an electronic shell model.4 Optical properties of metal clusters were the topic of a monograph by Kreibig and Vollmer around the same time.5 Applying beam deflection methods,6 de Heer and coworkers were able to assign magnetic moments via inhomogeneous magnetic fields7 or electric dipole moments via inhomogeneous electric fields8 to individual cluster sizes.Beyond the fundamental interest, clusters as building blocks for new materials gained importance, when it was realized that ‘size matters: why nanomaterials are different’.9 As a result, cluster materials became the hot topic. In order to generate a material of use, clusters have to be deposited in large quantities. On surfaces, other diagnostic methods are applicable like magnetic circular dichroism (MCD) measurements10,11 or X-ray photoelectron spectroscopy (XPS). Larger amounts of clusters can be synthesized from precursor molecules in solution by chemical methods yielding so-called ligand stabilized clusters12 with the advantage of being prevented from further coagulating and the disadvantage of changing their properties to some extent due to the presence of the ligands.
Another approach to create clusters of atoms or molecules in a cold environment is based on the development of efficient sources for generating superfluid helium droplets in beam expansions. The droplets can serve as cold traps for the accumulation of other species to form clusters that may be deposited on solid substrates. As we will show, this method has the advantage of producing nanoparticles of virtually any combination of elements in the inert environment of superfluid helium, free of any chemicals or additives. With all processes including the deposition taking place in ultrahigh vacuum, contaminations of the produced samples are excluded.
This article is structured in the following way: the next section will provide some general background on the generation of helium droplets, their function as cold matrix, and the doping with metals. Experimental techniques for the investigation of metals in droplets and after deposition will be described in a separate chapter followed by a section explaining the applied theoretical methods for modelling the aggregation process, the soft landing on a substrate, and the observed structure and dynamics of deposited metal clusters with regard to temperature dependent nanoscale phase transitions. Selected results will exemplify the advantages of this seemingly exotic method to generate metal clusters. The article will conclude with a summary and an outlook toward future developments.
2 Helium droplets as cold matrix
About three decades ago, helium clusters were recognized to present an excellent opportunity for the experimental study of collective phenomena in a finite size quantum system. The helium–helium interaction is so weak that it took rather sophisticated experiments to even prove the existence of helium dimers.13 Aggregation of helium atoms to clusters requires a supersonic expansion from a cold nozzle which was realized as early as 1961.14 Later, doping rare gas clusters with foreign atoms gained interest and allowed to probe the van der Waals forces between the dopant and the surrounding rare gas, i.e. the solvation in a finite size weakly interacting medium.15,16 In connection with the topic of finite size superfluidity, the community more frequently has used the name helium nanodroplets or just helium droplets, abbreviated as HeN. Spectroscopy of dopant atoms and molecules in helium droplets provided an indirect measure of the internal properties of the helium aggregate itself such as the temperature inside and at the surface, vorticity, and an idea about collective oscillations. The temperature inside helium droplets was determined as 0.37 K from the relative intensities of lines in rotationally resolved spectra of the SF6 molecule in helium droplets.17 Alkali atoms were observed to reside on the surface of HeN and the measurement of populations of Zeeman sublevels in the a 3Σ+u lowest triplet state of Rb2 and K2 molecules yielded the same temperature,18 at the same time showing the fast relaxation of these levels to the internal helium temperature. The narrow linewidth of the OCS spectra in 4HeN in contrast to corresponding recordings in 3HeN, were taken as clear evidence of the finite size superfluidity of 4HeN droplets.19 Additional evidence was provided by the observation of special features in the phonon wings of spectra of molecules in 4HeN that correspond to the roton and maxon peaks in the dispersion curve of bulk superfluid helium obtained by neutron scattering, i.e. elementary excitations in He II.20 By femtosecond X-ray coherent diffractive imaging Vilesov, Gessner, and colleagues succeeded to observe vorticity in 4HeN droplets, the signs of quantized collective rotations as evidence of superfluidity.21 For a long time, the spectroscopy of doped helium droplets mainly served the purpose to explore the influence of the helium surrounding on line widths and shifts, but slowly the new opportunities for the creation of new weakly bound molecular complexes were realized and applied. The probability for the survival of doped droplets was found to be larger if the coagulating species in or on droplets set less energy free. The formation of triplet ground state alkali dimers22 or quartet state trimers23 ‘boils off’ fewer helium atoms from the droplet than that of singlets or doublets, respectively. Nauta and Miller identified new aggregates such as ‘Long Chains of Polar Molecules in Superfluid Helium’24 and ‘Cyclic Water Hexamer in Liquid Helium: The Smallest Piece of Ice’.25 The dynamics of quartet state alkali trimers after laser excitation was followed26 and more homo- and heterogeneous trimers were investigated in frequency27,28 and time domain.29 Larger alkali clusters from a certain size on, seem to merge into helium droplets,30 with questions about high-spin state stability remaining.31,32 Metal ions tend to take center positions in helium droplets with a polarized helium shell, resulting in a so-called snowball.33 Among numerous reviews during the first 10 years of spectroscopy of doped helium droplets, the article by Toennies and Vilesov34 gives an excellent overview, while a chapter in the ‘Handbook of High-resolution Spectroscopy’35 provides a detailed review of spectroscopic methods covering the range from vacuum ultraviolet to microwave frequencies. The synthesis of metal clusters other than alkali or alkaline earth that were extensively studied (for alkali metals see the references above, for alkaline earth elements see e.g.ref. 36–38) requires the construction of high temperature efficient metal doping cells inside the helium droplet machines. High temperature metals can be pulse-laser ablated with the helium cluster beam passing through the metal vapour cloud. With a kilohertz repetition rate laser, this metal pick-up has been combined with continuous helium cluster beams39 or even more efficiently with pulsed helium cluster beams.40 A better control of the atomic vapour pressure in the pick-up region can be achieved by thermodynamic heating or controlled continuous electron bombardment of a crucible. In our lab, a home-built electron bombardment oven for up to 1700 °C was applied to study chromium in helium droplets41 and could be extended to max. 2000 °C, while for Cu,42 Ag,43 Au,44 Pd, and Co, Ni, Fe45 or In46 sufficient vapour pressure is generated around 1000 to 1300 °C or lower and ohmically heated ovens are used. In the following, the experimental methods for the creation of metal clusters of different sizes in helium droplets, their diagnostic in the beam apparatus, deposition on different solid surfaces, and the investigation of deposited metal clusters are described.3 Experimental methods for cluster synthesis
3.1 Synthesis of metal clusters and diagnostics in the droplet beam
Helium droplets are generated in a supersonic expansion of high pressure helium gas through a cold nozzle. Conditions for clustering of helium atoms range typically from 10 to 20 K nozzle temperature and 20 to 80 bar pressure before expansion. At nozzle temperatures between 6 and 10 K, liquid helium exits the nozzle with fragmentation into large droplets. Below 4 K, a liquid helium jet was observed.47 The Vilesov group explored the size dependence of helium droplets on the expansion parameters in detail.48 For a rough estimate, eqn (1) lists approximate droplet sizes for operation with a nozzle of 5 μm diameter and 20 to 40 bar backing pressure, and the corresponding droplet sizes (N in atoms per droplet):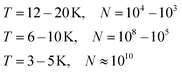 | (1) |
| Ediss ≈ 7 K ≈ 5 cm−1 ≈ 0.6 meV ≈ 60 J mol−1 ≈ 14 cal mol−1 | (2) |
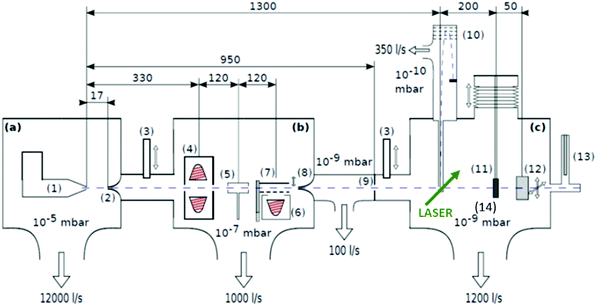 | ||
| Fig. 1 Schematics of the three chamber setup ((a) SC, (b) PC, (c) DC) of the HeN beam machine used for the experiments described in this paper, see also ref. 55. The droplet beam produced by the cooled nozzle (1) is shaped by the skimmers (2, 8) and an aperture (9). The droplets can be sequentially doped using different sources (4, 5, 6); (7) beam flag to engage pickup (6) (the solid line symbolises the opened state). As diagnostic tools a TOFMS (10), substrates for ex situ TEM investigations (11) and a quartz crystal microbalance (12) are available on axis, as well as an off-axis QMS (13). The TOFMS is equipped with an electron gun for electron impact ionization (not shown) but also allows photoionization using an external laser. A UHV-transfer system (14) enables the transport of surface deposited samples to external diagnostics without breaking the vacuum. Reproduced from ref. 55 [P. Thaler, A. Volk, D. Knez, F. Lackner, G. Haberfehlner, J. Steurer, M. Schnedlitz and W. E. Ernst, J. Chem. Phys., 2015, 143, 134201], with the permission of AIP Publishing. | ||
In the source chamber, helium gas (99.9999% purity) at a stagnation pressure of 20–60 bar is expanded through a 5 μm diameter nozzle which is cooled by a closed cycle refrigeration unit (Sumitomo RDK-408D2, cooling power 1 W at 4 K) down to only a few Kelvin. The expansion into high vacuum (≈10−5 mbar) results in a beam of superfluid HeN with an internal temperature of 0.37 K.34,35 The droplet sizes can be controlled by the temperature and the stagnation pressure of the helium gas. Typically, a setup with a pressure of 20 bar at 8 K is used for the synthesis of spherical nanoparticles, resulting in a He droplet diameter of about 70 nm with a mean number of about 5 × 106 He atoms.48 For extended wire-like particles that aggregate along vortices in larger droplets, the parameters are changed to 20 bar and 5 K, leading to HeN with diameters of around 1 μm, and consisting of about 2 × 1010 He atoms.48 Subsequently, the collimated HeN beam passes through another chamber (≈10−7 mbar) where resistively heated tungsten baskets coated with aluminium oxide (no. 4 and 6 in Fig. 1) are used as pickup cells for the evaporation of high purity metals. Only chromium required a different oven (see above). While passing through the respective metal vapor, the HeN are doped with the evaporated atoms. A gas pickup cell (no. 5) is optional and can serve for adding reactive species like oxygen. The superfluidity of the HeN matrix enables an unobstructed and frictionless roaming of dopant atoms. Upon statistical collisions within the HeN, the dopants accumulate and start to form clusters.56 Initially, these clusters are grown as multicenters inside a droplet before they further agglomerate to larger structures. The final size of the nanoparticles depends on the doping rate and on the initial HeN size, since both affect the average time between collisions and, thereby, the growth rate.49 The synthesis of wire-like nanoparticles is enabled by the presence of vortices in larger He droplets with diameters of several 100 nm. These vortices form due to the angular momentum acquired by the superfluid droplets during the expansion of the helium through the nozzle into vacuum.21,57 The dopant metal atoms and grown clusters inside the droplets can agglomerate along such vortices due to a pressure gradient directed towards the vortex core.58 By adjusting the size of the droplets accordingly and by doping enough material into them, elongated wire-like structures can be formed along the vortices.59–62 As stated above for the two employed parameter settings in our experiments, a change in the helium source conditions directly influences the size of the HeN and allows for a facile switching between the different nanoparticle types. It should be noted that by decreasing the source temperature not only the droplet size is increased, also the total HeN flux and the deposition rate are enhanced. During agglomeration of atoms and clusters, the released binding energy is dissipated by the evaporation of He atoms from the droplet. The attenuation of the HeN beam due to the decrease in droplet size caused by this process is measured in order to monitor the particle growth process.49 The synthesis of core@shell particles is enabled by the subsequent doping of two different metals in consecutive pickup cells.43,60 Before entering the second pickup cell holding the shell material, the particle cores have already formed with the metal provided in the first cell. The metal doped to the droplets in the second pickup cell forms a shell layer around the core. The dopant vapor pressure in each cell and, thereby, the metal atom doping rate and the nanoparticle growth are directly controlled by the temperature of the resistively heated pickup cells. Since the pickup cells are separately controlled, the amount of doped core and shell material can be adjusted independently. This allows for a tailoring of the core diameter and the shell thickness of the synthesized nanoparticles within a certain range, as has been shown for Ag@Au63 and Fe@Au.64 After leaving the pickup region, the HeN beam reaches a third chamber at UHV conditions (≈5 × 10−10 mbar), where a time-of-flight mass spectrometer (TOFMS) with reflectron (Stefan Kaesdorf RFT50) is mounted, which is specifically designed for the detection of large compounds. It is used for the in situ analysis of the clusters formed in the HeN and enables both electron impact ionization and laser ionization. The built-in electron gun can be tuned in energy (0–89 eV), repetition rate (0–10 kHz), and duty cycle (0–20 μs). In most experiments presented in this work, the highest available ionization energy (89 eV) with approximately 10 μA average electron emission current at 5 kHz repetition frequency and 20 μs duty cycle was chosen in order to get the maximum ionization cross section for He. Fig. 2 shows an example of gold clusters aggregated in HeN. The higher the oven temperature, the wider the mean cluster size is shifted to the right, i.e. toward bigger clusters. The intensity drop for TTC = 1250 °C indicates that too many helium droplets have been extinguished by too high a load of gold atoms. A part of the mass spectrum of silver clusters created in helium droplets, is depicted in Fig. 3. The odd even oscillations are caused by the fact that an odd numbered cluster can be ionised more easily, i.e. has a lower ionisation potential as an even numbered cluster because of the unpaired electron. Magic numbers are indicated that refer to higher stability of those cluster sizes (black numbers) ascribed to closed electronic shells in the spherical jellium model.65 The high abundance of the cluster of 55 Ag atoms may be due to the predicted structural stability of an icosahedral silver cluster.66
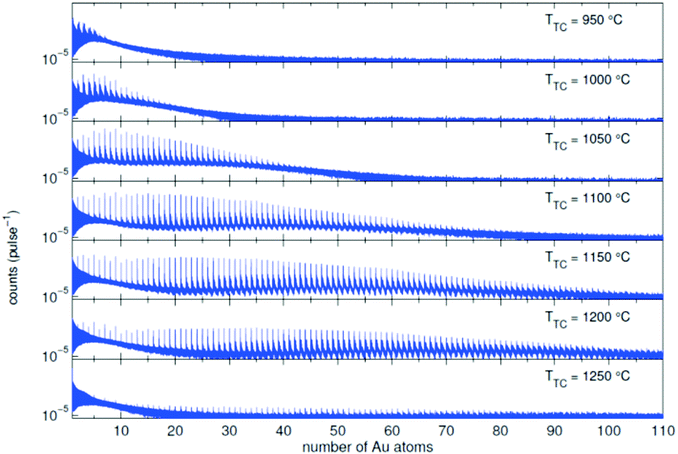 | ||
| Fig. 2 Mass spectra of an Au doped He droplet beam (T0 = 9 K and p0 = 20 bar, NHe ≈ 1.8 × 106) for different oven temperatures TTC. Additional peaks appear due to the adsorption of water molecules in the pickup chamber.70 | ||
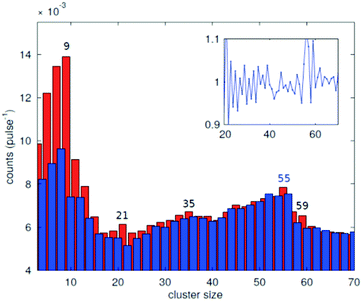 | ||
| Fig. 3 Abundance of the different cluster sizes for an Ag doped He droplet beam. The red and blue bars mark the odd and even numbered cluster sizes, respectively. The inset shows the ratio of adjacent peaks. The magic numbers are indicated.70 | ||
As had been observed by the Scheier group,67,68 ionization seems to be less destructive to aggregates if they are immersed in He nanodroplets compared to direct electron ionization of the free aggregates. Probably the more indirect ionization through a charge hopping process inside the droplets and the high cooling rate of the surrounding helium are reasons for this softer process, which allowed us recently to measure a distribution of unfragmented V2O5 clusters.69
As latest improvement of the apparatus, another laser interaction region was added with an optical detection channel to measure integrated or wavelength selected laser induced fluorescence in a scheme previously employed in our other helium droplet experiments, see e.g.ref. 71.
Laser-optical spectroscopy of metal clusters has usually been restricted to small sizes, e.g. via setups monitoring the laser-induced fluorescence as in the mentioned case of alkali trimers, or by resonant multiphoton ionization as for Au oligomers.44 Tiggesbäumker, Meiwes-Broer and coworkers used two-photon laser excitation to measure the shift of the optical absorption of Ag8 in a helium droplet when exposed to additional rare gas impurities,72 which triggered a recent theoretical study on the medium-induced change of the optical response of metal clusters in rare-gas matrices.73
A quadrupole mass spectrometer (QMS) at the end of the beam path (see Fig. 1) monitors the particle flux. Set at mass number 8 that occurs upon fragmentation of helium aggregates, the intensity of the helium droplet beam can be checked. Upon each pickup of a dopant, the energy dissipation requires helium atoms to leave the droplet which diminishes the intensity of the QMS mass 8 signal. A reasonable estimate of the mean number of dopant atoms nx per droplet is then given by51
| nx = Nevap × EHe/EX, | (3) |
The QMS at the end of the beam path can also be employed for beam depletion spectroscopy of larger metal clusters if the wavelength of a counterpropagating laser beam is scanned and the number of arriving metal-loaded droplets is monitored. Resonant excitation of a metal surface plasmon will lead to a blow up of the droplet and deplete the signal.74
3.2 Deposition of nanoparticles and diagnostic tools
Before the actual production of cluster samples, the deposition rate can be tested via the quartz crystal microbalance (INFICON QCM “IPN 074-156”). With temperature stabilization, we have reached a long term stability of ±0.002 μg cm−2 s−1 in the idle state. Using the QCM, not only the nanoparticle mass deposition rate, but also mass gain or loss due to chemical reactions can be measured. For this purpose, by controlled dosing of a reactant gas through a precision leak valve, the chemical reaction changes the mass of the deposited particles, which is detected time resolved. This way, chemical reaction rates can be determined. After such tests, newly created samples should be investigated with typical surface diagnostics not implemented in the helium droplet machine. Different substrates are necessary depending on the diagnostic tools such as electron microscopy or optical absorption spectroscopy. For deposition of the nanoparticles the substrates are inserted into the beam path with a wobblestick transfer system coupled to a vacuum suitcase (Ferrovac GmbH, NexGeneration UHV Suitcase). The suitcase allows for the storage and transport of the samples at UHV conditions (10−10 mbar). Due to the different employed analysis methods, support grids for scanning transmission electron microscopy (STEM) (Ted Pella Inc., Ultra-thin Carbon Film on Lacey Carbon Support Film, 300 mesh, Au) as well as silicon nitride, self-prepared hexagonal boron nitride,75 or glass coverslips coated with indium tin oxide (ITO) (spi Supplies, 30–60 Ω, 18 × 18 mm, No. 1) were used as substrates. As the HeN beam is terminated at the substrate, the particles are cushioned by the surrounding helium and, therefore, keep their shape upon deposition under soft landing conditions76,77 as observed by atomic resolution electron tomography.78 The primary analysis tool so far has been electron microscopy at the neighbouring Institute of Electron Microscopy and Nanoanalysis where various instruments are available such as several transmission electron microscopes (TEM) and an atomic resolution scanning transmission electron microscope FEI Titan3 60-300 STEM with an X-FEG field emission source operated at a beam energy of 300 keV. The STEM system is equipped with an FEI Super-X four-quadrant detector for energy dispersive x-ray spectroscopy (EDXS). Elemental mapping is provided by EDXS and electron energy loss spectroscopy (EELS). The STEM instrument is prepared to take images under a large range of tilting angles for a tomographic reconstruction of the three-dimensional shape of the investigated nano object.78 In practice, a measurement time slot at the STEM has to be efficiently used which means that metal clusters of different size may be synthesized applying different beam conditions but deposited on the same substrate. Fig. 4 depicts two Ni clusters of different size that have been exposed to air. With EELS, the oxygen coverage (blue) on the nickel (red) is obvious. | ||
| Fig. 4 A comparison between the high-angular annular dark-field technique (HAADF) and the electron energy loss spectroscopy method (EELS). All three images are taken from the same region on a heatable carbon TEM substrate, where two nickel nanoclusters are deposited. In the left image the HAADF signal is illustrated, where a material contrast and also a Z-contrast is clearly visible. This is caused by the different number of layers stacked above each other. When using EELS, it is possible to separate nickel and its covering oxide layer, as the energy lost by the low angle scattered electrons is highly sensitive to changes in the atomic number for small Z. As there are material specific energy bands for EELS a separation of the elements can easily be done. Taken from ref. 79. | ||
For temperature dependent studies, substrates had to be prepared that allow heating or cooling. Two TEM grids used for such studies are shown in Fig. 5. As the scale is very large, the elongated Ag nanoparticles appear just as little bright spots.
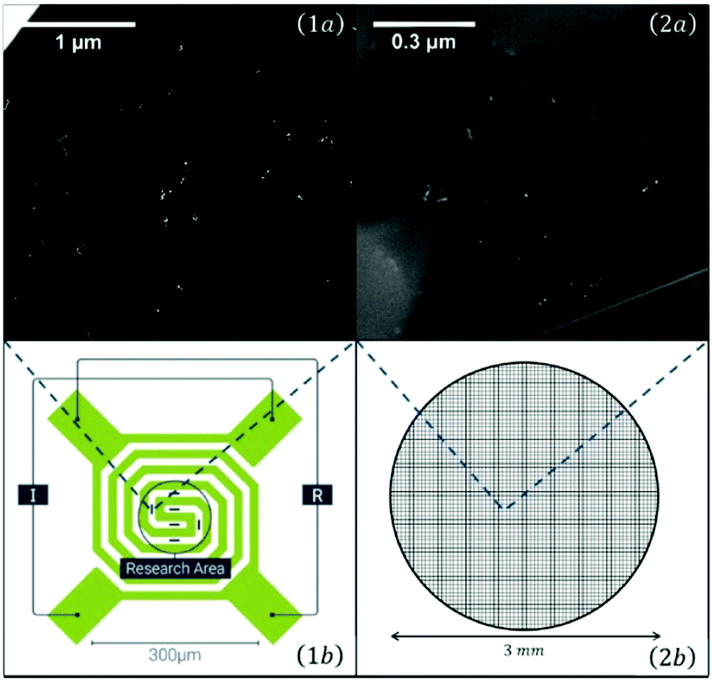 | ||
| Fig. 5 Overview of the two different transmission electron microscopy (TEM) grids used for temperature dependent measurements: On the left a heatable carbon TEM grid (1) (DENSsolutions Nano-Chip XT carbon) which is able to provide a temperature range between room temperature and 1300 °C. The carbon windows are embedded inside a heatable filament. The second grid (2) is an amorphous carbon grid used for cryogenic experiments, ranging from −150 °C up to room temperature. A close up view of the two different carbon windows can be seen in the upper two panels (1a and 2a). It is easy to identify the difference between the larger, but less numerous windows of the heatable grid and the amorphous carbon grid, which consists out of several smaller windows. Taken from ref. 79. | ||
A comparison of the results of computer modeling the cluster landing,76 the atomic resolution electron tomography,78 and an intensity based evaluation of HAADF images let us conclude that the originally formed cluster shape inside the droplet is only weakly altered upon deposition. Further comparison of the cluster size distribution measured by TOF-MS in the beam with that on the TEM grids indicates that the clusters do not break up.55
For optical absorption measurements of cluster samples, fused silica microscope slides for deposition and a Shimadzu UV-1800 spectrophotometer have been employed.63 Plasmon resonances of metal clusters obtained this way, represent an average over a certain size distribution, but significant differences for single metal as opposed to core shell particles were found. Furthermore, such ensemble averaged measurements were conducted for surface enhanced Raman studies.63 Plasmon resonances for individual nanoparticles on a thin h-BN substrate, which provides very low background absorption, could be studied with EELS.75
Atomic Force Microscopy (AFM) required exposure to air and was only applied to Ag@Au core@shell particles on fused silica (see Fig. 6). Comparison of the AFM scans was made with an image obtained with an Environmental Scanning Electron Microscope (ESEM) such as to test the compatibility of the prepared sample with a real world environment. For a high surface coverage, the core–shell nanoparticles were synthesized in a strong helium droplet flux generated by cooling the nozzle to 5 K. Under these conditions, the particles are nanowire-like with elongated shapes due to the presence of vortices in the droplets. A surface coverage of about 20% is reached in about 15 min, while the production using a nozzle temperature of about 9 K yields more uniform spherical metal particles but only about 9% coverage per hour. A comparison of low resolution electron microscopy and AFM images gives the impression that the AFM leads to an overestimation. In the depicted case, the AFM was operated in the tapping mode and no effort was made to optimize the tip size. We believe that the resolution is even worse than in the ESEM recording and that the particle shapes are not reproduced correctly but may have been influenced by the tip.
 | ||
| Fig. 6 Ag@Au core@shell nanoparticles of elongated shape, similar to ref. 60, imaged with an ESEM at only 10 nm resolution (left panel) compared to an AFM image in the tapping mode with an undetermined tip size (right panel). The scale is the same with the total area being 2 μm × 2 μm. The coverage is estimated as 26% based on the ESEM image while the AFM gives the impression of a higher coverage.80 | ||
For STM studies, gold clusters were deposited on HOPG to provide enough conductivity, but the cluster mobility on this substrate turned out too high leading to unwanted new cluster patterns.81
With the recently acquired NanoESCA (Scienta Omicron), energy resolved photoemission electron microscopy has become possible. By illumination with a helium lamp (21.2 eV), a first workfunction mapping of a 8.6 μm × 8.6 μm field of view of the pristine p-type silicon substrate compared to the same substrate covered with ZnO nanoparticles was obtained (see Fig. 7).
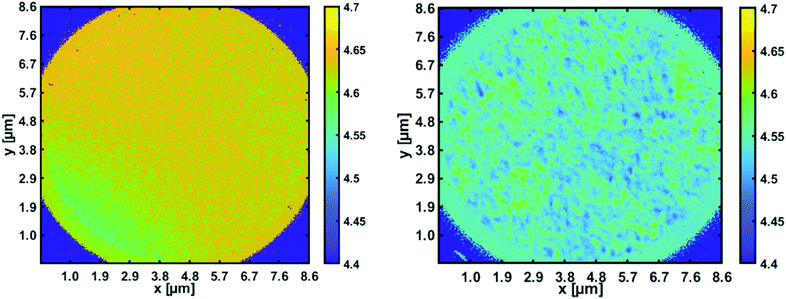 | ||
| Fig. 7 Workfunction mapping with the energy resolved photoemission microscope. Left panel: Space resolved work function for a pristine p-type silicon wafer [4.7 eV]; right panel: reduction to about 4.5 eV in areas covered with ZnO nanoparticles.82 | ||
4 Theoretical methods for modelling cluster aggregation and thermally induced dynamics
4.1 Metal cluster formation
Theoretical descriptions of metallic cluster aggregation processes inside He droplets must either employ reasonable estimates of atomic collision probabilities or try to model the actual dynamics of the immersed impurities at a molecular level. Attempts have been made in both directions, but with different intentions and scopes due to the inherent complexity of the matter.Accurate descriptions of He droplets with sizes in the range of several thousand He atoms and a few impurity molecules or atoms are currently achieved via Helium Density Functional Theory (He-DFT),83,84 most effectively through the Barcelona–Toulouse program package.85 This powerful open source software tool allows the simulation of metallic impurities together with quantum vortices,21,86,87 an interesting phenomenon which affects cluster formation in larger He droplets. While interactions with the desired impurities are introduced by summations over effective two-body potentials, the actual quantum behavior of the surrounding He is nicely captured with this technique. In more recent time-dependent studies, even the coupling between helium density fluctuations, i.e. the ‘nuclear part’ of the total wavefunction, and the electronic excitation of single impurity atom inside the helium droplet has been simulated successfully in order to interpret femtosecond pump–probe spectroscopy measurements.46 Of further interest is the interaction between impurities and vortices, which are known to exert an attractive ‘pinning’ force on the letter.58,83,88 Although this circumstance is crucial (as will be detailed below) for certain metal cluster formation processes, the still ongoing and fruitful fundamental research on superfluid helium dynamics still resides almost fully disjoint from the actual experimental research in the field of helium-mediated metal cluster synthesis. The reason for the discrepancy lies in a certain limit of the He DFT approach with regards to the emulation of pronounced collective excitations and very large deformations produced by strongly interacting or very fast impurities.88,89 Also, the rather crude ansatz of pair-sum potentials does only hold for certain cases. Yet, the fascinating insights gained by He-DFT can currently not be delivered by any competing method such as e.g. full ab initio calculations, path integral molecular dynamics90 or quantum Monte Carlo treatments91,92 (such as Green's function Monte Carlo or diffusion Monte Carlo methods) of the systems at hand due to the high computational cost of these alternatives which forbid their application in size regimes relevant for metal cluster growth. However, these techniques have been successfully applied to smallest, helium-immersed metallic clusters of Na and Mg,93,94 partially aiming to answer the long-ongoing debate concerning the existence of metastable, foam-like metallic structures formed by weakly interacting metal atoms.95
A less refined but effective strategy to bridge this gap between simulation capabilities and current experimental research was based on the combination of classical Newtonian molecular dynamics for a given impurity with He DFT calculations to obtain estimates for the retaining force which acts on it and keeps it inside the He droplet.56 This technique was easily extended to droplet sizes which were realistic for metal cluster formation, and could be used to derive approximate collision times for two metal atoms immersed into a helium droplet. By comparing the latter to averaged pickup rates, tentative estimates of the actual ‘growth’ mechanism inside the droplets could be made, as the process switches from single- to multi-center growth if the pickup rate exceeds the average collision time. Via time evolution studies, where the number and mass of all metal particles was tracked over time (but not their actual position), a time-dependent distribution of metal particle sizes could be obtained for time intervals in the range of milliseconds.49 These simulations also took the evaporation of He due to collision energy dissipation into account, which leads to a shrinking of the actual droplet size over time, and even allowed the implementation of vortex pinning effects via an effective correction based on averaged times for impurity trapping in a single, simplified (i.e. straight) vortex line. Inclusion of the latter effects turned out to be crucial for the explanation of metallic nanowire formation as it had been observed in numerous experiments,59–62 since the impurity-collecting nature of vortex lines enforces a preferred one-dimensional growth of metallic structures in the form of irregularly shaped nanowires. An interesting finding of these simulations was that these wires are formed by a coagulation of larger metal clusters, baked together through the pinning effect, but without a complete melting upon contact.49,96 Therefore, the morphologies of the initial building blocks, i.e. the interfaces of spherical clusters, are preserved in the final structures, as was seen in TEM images with atomic resolution. Examples will be shown in Section 5.
4.2 Deposition and restructuring effects
Between the growth of a metallic structure inside a He droplet and its final imaging on a suitable substrate lies the crucial process of its preferably non-invasive deposition. As it turns out, the deposition of loaded He droplets can truly be considered a non-damaging type of soft-landing, no matter the size of the actual impurity, but for different reasons.In the case of single metal atoms, the helium embedding plays a crucial role as it facilitates a sticking probability of almost one and a negligible delocalization of the impurity atom upon impact, as was shown for the case of He-immersed Au atoms on a TiO2 surface.77 This original study used (electronic) density functional theory to evaluate the interaction potential of a single He atom with bulk titanium oxide and used this information in follow-up simulations of the impact dynamics via time-dependent He density functional theory, allowing for a realistic treatment of the helium environment as a quantum fluid. In contrast to classical simulations, a time evolution of the bosonic, macroscopically extended helium droplet wavefunction showed a continuous, well behaved spreading of the helium over the bulk surface instead of any chaotic splashing behavior.
In a second article of the same research group the deposition of larger silver clusters (consisting of up to 5000 atoms) on amorphous carbon and on graphene was investigated,97 this time via molecular dynamics simulations only, but with more complex interaction potentials carefully derived from preliminary ab initio studies. Interestingly, these simulations reveal that even bare Ag clusters can be deposited without damaging (if impact velocities and cluster temperatures of He-immersed species are assumed) due to their ability to temporarily deform and to dissipate the impact energy without considerable structural changes. In the larger size regime, the soft-landing is therefore more ‘assisted’ than enabled by the He droplets. A more pronounced effect of the helium immersion was discovered regarding the actual distribution of clusters on the support after deposition, suggesting that secondary impacts play a larger role than surface migration of clusters residing already on the surface.
A third and final look at this fascinating step in metal cluster production is concerned with cluster sizes in between these two extremes mentioned above. Ref. 76 was dedicated to the study of deposition effects on silver clusters of different morphology (icosahedral, dodecahedral and face centered cubic) in the range between 100 and 2000 atoms as a function of the landing conditions, using the Sutton–Chen potential for metallic interactions and a Morse potential for the surface, with its parameters chosen to emulate an unstructured, rigid carbon model surface. While this study confirms the stability of larger clusters which remain mostly unaffected by the impact, its also predicts structural transitions in smaller clusters for certain landing conditions. A clear tendency to restructure into a single domain close-packed morphology is noted and in good agreement with structure statistics derived from experimental findings. The occurrence of a structural transition seems to depend on the initial structure, suggesting that decahedral clusters tend to conserve their morphology better than icosahedral ones.
4.3 Metal structure stability
The ability to grow and deposit metallic nanowires triggered a series of detailed studies on their structural features after deposition. Particularly disturbing was the experimental finding for silver, which did not form wires but ‘pearl chains’ of small droplets, which caused vivid discussions in the community regarding potentially different growth scenarios for different metals inside the He droplets or a possibly destructive deposition. The actual reason for this exceptional behavior could be revealed in ref. 98, after the successful deposition of intact silver structures onto a sample holder which had been cooled down to 77 K. At this temperature, and almost up to room temperature, silver also shows the expected formation of wires with diameters in the range of about 5 nm, but starts to decompose at higher temperatures due to Rayleigh breakup. This phenomenon, a well-known effect in fluid dynamics, where the growth of initial diameter perturbations leads to the disintegration of the respective jet, is driven by diffusion of metal atoms on the wire surface, attempting to minimize their energy by a relocalization away from thinner areas with larger curvatures toward less strained cluster regions. As a consequence, ‘dents’ in the irregularly shaped wires tend to become more and more constricted until a full breakup into separate parts is established. Computationally, this behavior was reproduced at first through a two-dimensional model, employing a relation99 between the local atomic diffusion tendency and the actual curvature of a piece of wire at this particular point.98 TEM images of intact nanowires, effectively two-dimensional projections of the actual structures, were translated into closed contour loops which served as initial structures for the numerical integration of a resulting partial differential equation. This way, time evolutions of the contour shape were obtained, which also included breakups, emerging in this treatment as the formation of two new closed loops produced from the original one by constriction. While this method could correctly predict structural changes over time, it suffered from a lack of computational practicality, in particular when applied to complicated, more realistic and better resolved initial contour lines or in time evolutions of several wires simultaneously. For this reason an alternative computational concept based on cellular automata had been developed.100 In this ansatz, the actual distribution of material is approximately reconstructed from TEM images and translated into a three-dimensional grid model. Each cubic cell of this model, called a voxel, represents approximately 55 to 85 metal atoms if filled with material. The determining feature of a cellular automaton is that the current state of a voxel, i.e. filled or empty, is updated in a periodic fashion, but only dependent on the states of its neighboring voxels. In a series of time steps, each one corresponding to a state update of all cells or voxels in the model, the migration of metal atoms is enabled through update rules, here realized by a Monte Carlo method deciding whether a flow of material from one voxel to a neighbor voxel is taking place or not. This approach turned out to be much more robust and less costly compared to the contour-based method and could be successfully applied to real Ni, Cu, Ag and Au nanowire structures.101 It allowed the prediction of wire breakup positions as well as their correct order of appearance in time upon heating.4.4 Structural behavior of mixed-metallic clusters
A last topic to be addressed in the theoretical part of this review is the description and simulation of structural behavior of mixed-metallic structures after deposition onto a given substrate. Numerous, well-established methods are applicable to this objective in principle, but the final choice is mostly determined by the system size and the accuracy required to test a certain hypothesis via a computational experiment. With this being a very general problem of cluster physics, and fully independent of any specific route chosen for the synthesis of the desired metal structures, even an attempt to briefly summarize current developments in this field would be misplaced in the scope of this much more specific review. Instead, after referring to a few more recent, excellent overviews on the theoretical treatment of (mixed-)metallic clusters,102–106 we present and discuss some concrete attempts addressing the peculiarities of He-grown, mixed-metallic structures.Obviously, all of these peculiarities are a consequence of the still not fully understood growth mechanisms inside a He droplet. The cold and fully inert environment suggests an undisturbed, preferably spherical growth of a metallic cluster in its structural configuration of lowest energy, presuming that the rate of metal atom pickup and particle agglomeration are set up accordingly through appropriate choices of He droplet size and vapour pressure in the pickup chamber. For mono-metallic clusters, this specific way of synthesis is not expected to produce structures which differ significantly from those created by any other method, as long as the inevitable external influences (templates, seeds, precursors and solvents) which compromise the latter are kept at a minimum. However, for metallic cluster compositions consisting of two or more elements, the nature of the experimental setup enforces a highly specific growth in the form of spherical layers. The resulting onion-type structures, in their simplest form core–shell clusters, have been studied in great detail recently.45,63,64,105,107–111
For cluster sizes in the range of several thousand atoms a computational treatment with advanced methods of electronic structure theory is not feasible, at least not the metallic structure as a whole. On the other side, meso-scaled approaches such as the coarse-grained Monte Carlo approach discussed above are incapable of describing diffusion and alloying processes which take place on the atomic scale. This leaves the application of suitable force fields as the only choice, which are typically based on the embedded atom model.112 The latter ansatz includes the pair energy between two atoms as well as contributions stemming from the embedding of each metal atom into its local environment. In our recents works,111 we employed potentials of the Zhou group for Au113 and for the iron triade elements Fe, Co and Ni,114 which are of the quantum Sutton–Chen type.115,116 Attempts have also been made to build improved force fields via machine learning methods such as Gaussian regression or artificial neural networks.117,118
When used in large-scale molecular dynamics simulations, preferably run in parallel on supercomputers, molecular dynamics simulations can be performed to study the structural behavior of finite, mixed-metallic structures at various temperatures. With methods similar to those described in ref. 111 and 119, even the process of cluster formation inside the droplet can be (at least very rudimentarily) emulated by a certain choice of metal atom spawning followed by heating and cooling to allow for a continuous structural minimization during particle growth. The same methods also allow for investigations of metal alloying, at least in the onset, but are limited by the unfeasible time lengths needed to simulate the experimentally observed diffusion processes in the range of several nanometers. This problem can be overcome by less realistic but more efficient sampling techniques, preferably on a discrete grid, where single atom motion is fully replaced by artificial, temperature-dependent hopping moves or ‘atomic swaps’ within a Monte Carlo approach.111 After each artificial move a structural minimization is performed. This way, a much larger portion of the accessible state space can be sampled, however at the cost of no longer simulating real transitions from one geometry to the other. In this simplified picture, even free energies can be estimated as a function of temperature, since the configuration entropy, i.e. the portion of the total entropy stemming from the multitude of possible arrangements (e.g. n atoms of type A and m atoms of type B, given n + m possible lattice positions), is the leading contribution to the total entropy.105 For largest metallic clusters, where even the crude, yet still atomistic lattice models reach their computational limit, empirical corrections of the well-known bulk phase diagrams can be employed, e.g. the CALPHAD method120 in combination with a 1/r correction to account for the increasing surface to volume ratio with decreasing cluster radius r.121
In the case of surface reactions such as e.g. the simple oxidation of one metal component, the application of electronic structure methods becomes inevitable, although tentative ‘reactive’ force fields have been suggested and tested for selected reactions.122 Typically, these calculations are based on density functional theory, employing plane wave basis sets in a periodic setup. Small slabs, i.e. representative areas of the material, comprising several unit cells of the actual bulk metals, are used to simulate either inner regions of a given mixed-metallic cluster, e.g. to study the interface of a certain core–shell structure, or regions of the cluster surface, e.g. to investigate reactions with gas molecules. On the downside, although local features such as surface reactions on active centers can be nicely simulated, alloying or diffusion behavior on a larger scale can barely be captured by these accurate but computationally very expensive methods.
5 Results
In this section, we present a selection of results on metal clusters synthesized in helium droplets that show the high potential of this method for the investigation of fundamental properties of nanoparticles undisturbed by residuals from chemical preparation.5.1 Metallic nanowires and their thermal stability
In the late 1940's, Onsager put forward the idea of quantized circulation in superfluid helium which was followed up by other low temperature physicists like Feynman who predicted details about the related vortex cores.86 Visualizing quantum vortices in an experiment took a long time since their discovery until Bewley, Lathrop, and Sreenivasan could photographically image the hydrogen particles that had accumulated along vortex cores in their liquid helium cell.123 Shortly after this, Gordon and coworkers injected a hydrogen gas jet into a cryogenically cooled helium II bath and observed the formation of narrow filaments of hydrogen as traces of vortex lines.124 Gordon and coworkers together with Weiss and Moroshkin followed this path and created metallic filaments inside bulk superfluid helium taking advantage of the attracting forces of the vortex cores,125,126 deposited nanowire networks on substrates by evaporation of the liquid helium, and even measured the electric conductivity of such nanowire bundles.127Vilesov and coworkers doped large helium droplets produced at low nozzle temperatures, with silver atoms. After deposition on a solid substrate they recognized arrays of silver clusters that lined up like an interrupted nanowire.59 Those traces were interpreted as first evidence of vortices in helium droplets. Similar broken chains of Ag clusters were observed by Spence et al.61 but there was no explanation why the Ag clusters would not have grown together.
Suspecting the breakup being an effect of the room temperature substrate and as such happening after the deposition, we terminated the Ag-doped helium droplet beam on a liquid nitrogen cooled amorphous carbon substrate.98 Furthermore, we conducted similar experiments under the same HeN source conditions with Au, Cu, and Ni dopant atoms.101 For room temperature deposition, Fig. 8 shows the metal cluster traces for Ag (left panel), Au (center panel) as well as Cu and Ni. Obviously, other metals than silver yielded uninterrupted cluster chains or nanowire like structures.
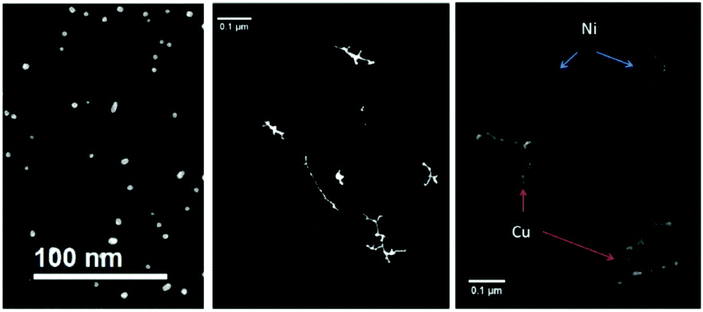 | ||
| Fig. 8 Four different nanowire materials studied at room temperature. All of them are synthesized at Tnozzle = 5.4 K and with α = 0.75. In the left panel the thermally very unstable silver nanowires are already fully patternized, as a result of a very low energy barrier towards starting the surface diffusion process. In the central panel the noble metal gold is illustrated. Gold is not only stable at room temperature, but it also shows no or nearly no oxidation at its surface. As a result, gold is an ideal candidate to study the unperturbed phenomenon of surface diffusion. The non-noble metals nickel and copper are presented in the right panel. Both of them are covered with an oxide layer due to the vacuum conditions in the electron microscope, which effectively stabilizes the synthesized nanowires. From ref. 79. | ||
Deposition on a liquid nitrogen cooled substrate revealed the survival of a vortex induced Ag nanowire formation even after deposition. As depicted in Fig. 9, the uninterrupted chain is stable up to 253 K and then starts to disintegrate at higher temperature. Au nanowires can be heated much higher before they fall apart at about 573 K. This different behaviour can be seen in the electron microscope images in Fig. 10, which are shown in panels a and b. Panels c and d are model pictures derived from the cellular automaton approach explained in the previous section.
 | ||
| Fig. 9 Structure evolution of a Ag nanowire at increasing temperatures of 253 K (a), 268 K (b), 293 K (c), 363 K (d). Structure as deposited (no change to situation at 77 K) is shown in (a). (b) Marks the begin of wire breakup after surface smoothing, while (c) shows the fully segmented wire at ambient conditions. At higher temperatures the relaxation into spheres is suppressed by a carbonaceous capping layer (d). Scale is the same for all images. Ref. 98 – reprinted with permission of the PCCP Owner Societies. | ||
 | ||
| Fig. 10 Comparison between measured surface diffusion processes and cellular automaton prediction of Au and Ag nanowires. In (a and c) one can see the initial structure and the converted structure used in the cellular automaton approach, respectively. Those structures evolve to the ones shown in (d), when heating is applied, in very good agreement with the final structures observed experimentally (b). Ref. 101 – reprinted with permission of the PCCP Owner Societies. | ||
Because of the large size of the nanowire system, the model calculation of the observed Rayleigh breakup uses cell sizes of a volume that corresponds to the resolution of the transmission electron microscope images. As shown in ref. 100 and 101, the simulations are in good agreement with the experimental observations for Ni, Cu, Ag, and Au nanowires of about 2 to 5 nm diameter. The differences in the behaviour of the different metals are expressed by an equation connecting the nanowire breakup temperature with the corresponding bulk metal melting temperature, the nanowire diameter and a metal specific constant being parameters. The breakup itself, however, is purely due to surface diffusion and does not require melting. In Fig. 11, the simulated temporal evolution of the diffusion process leading to breakup is compared with a sequence of electron microscope images for a gold nanowire structure kept at 423 K.
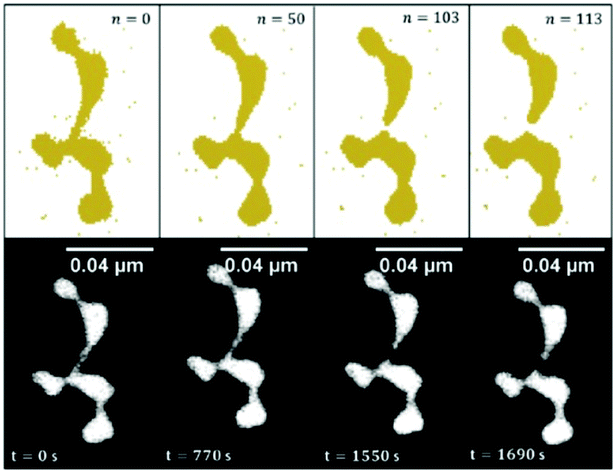 | ||
| Fig. 11 Time evolved surface diffusion process of a gold nanowire at 150 °C. The observed in situ breakup event is studied over a time period of nearly half an hour (lower images) and are compared to the results obtained with the CA (upper images) in order to draw a fit between iteration steps and experimental observation time. Ref. 101 – reprinted with permission of the PCCP Owner Societies. | ||
Depending on the doping rate of the helium droplet beam, the nanowire growth along a vortex line leads to longer or shorter structures. In ref. 49 the doping rate is expressed by a parameter α between 0 and 1 that gives the attenuation of the HeN beam arriving at the QMS at the end of the beam apparatus. For example, α = 0.75 (‘heavy doping’) means that the attenuation amounts to 75%, and the large amount of metal atoms loaded on to a helium droplet caused strong evaporation of helium. Our simulation of the initial multicenter growth of spherical metal clusters via the collisional model of ref. 55 and subsequent attraction into the vortex core yields the trapping times listed in Table 1 (see also the correction of ref. 49 in Phys. Chem. Chem. Phys., 2016, 18, 3359). For comparison, individual metal clusters of 1000 atoms are formed already after ≈1 μs while the vortex trapping times are more than 10 times longer.
| Element | α | d D/nm | t trap/μs |
|---|---|---|---|
| Ag | 0.75 | 720 | 24 |
| 0.20 | 1060 | 52 | |
| Au | 0.75 | 720 | 33 |
| 0.20 | 1060 | 71 | |
| 0.04 | 1130 | 80 |
A close-up of the structure of a gold nanowire near the seam between the clusters lining up along a vortex line is depicted in Fig. 12 and reveals the changes of the lattice geometry like in a statistically grown connection.
 | ||
| Fig. 12 Image of a Au nanowire portion in which the lattice structures are shown. Three different regions were evaluated: (red) a lattice distance of 0.24 nm was measured indicating the (111) surface (0.234 nm), (blue) lattice distance of 0.12 nm was measured which may correspond to a (222) (0.117 nm) lattice and (green) a lattice distance of 0.20 nm was measured indicating the (200) (0.2035 nm) lattice. Note that for the blue region also different lattice assignments would be possible. The error of this measurement is ≈0.01 nm. From ref. 96. | ||
While the results of detailed investigations of core@shell clusters are presented in the next section, it is worth mentioning that long core@shell nanowires, formed by weakly connected clusters, clearly exhibit the character of a chain of individual core@shell clusters rather than having a long well connected core with a uniform coating over the full length.60 This can be understood when considering the sequential growth process explained above.
5.2 Core@shell particles and alloying
With our setup as depicted in Fig. 1, almost any core@shell nanoparticle of an atomic or molecular composition can be synthesized if the constituents can be provided in a pickup cell at a vapour pressure of 10−5 to 10−4 mbar. Due to the helium mediated soft ionization,67–69 the TOF-MS shows the element specific loading of the droplet. The ultrahigh vacuum (UHV) in the deposition chamber guarantees almost contamination-free samples. UHV-transport is facilitated by the Ferrovac Vacuum Suitcase (see Section 3). Oxidation of highly reactive metals can occur when the vacuum conditions cannot be maintained. For example, our own experiments with deposited chromium clusters on the quartz microbalance with 10−6 mbar rest gas in the chamber have shown an enormous mass increase over a time interval of 2 hours. It can be estimated that under these ‘high vacuum’ conditions a sample with chromium clusters will be fully oxidized in a day. This experience motivated us to start coating reactive metal clusters with an inert metal like gold. Such core@shell metal clusters exhibit additional advantages if they provide interesting combinations of material properties like plasmonic resonances, magnetism, or semiconductor features paired with a metallic core.First experimental studies concentrated on Ag–Au combinations because they provided clean nanoscale structures without any impurities. Fig. 13 shows a detailed structural and elemental analysis via electron microscopy methods.78 The clusters stay intact and subsequent work concentrated on the questions of thermal stability and phase changes towards nanosized alloy formation. Transmission electron microscopy images of Ag@Au and Au@Ag core@shell particles were recorded for sample temperatures from room temperature up to 300 °C at which the clusters appeared fully alloyed while a crystalline structure was resolved over the full temperature range.43 The mixing process was therefore interpreted as solid state diffusion. Density profiles for the core and shell materials were determined from the images and a diffusion model with a temperature dependent effective diffusion constant for the Ag–Au nanomixture presented. The results were compared with an existing phase diagram for the AgAu system as a function of the particle radius. It turned out that in the size range of our clusters, mixing occurs already at about 200 to 300 K lower temperature than previous scaling laws would predict. We conclude that the diffusion on this length scale (below 5 nm) is initiated at lower temperatures than in the corresponding bulk material, which is a consequence of dominant surface size effects in this regime. For both systems (Ag@Au and Au@Ag), alloying takes place between 500 and 550 K.43
 | ||
| Fig. 13 EELS and EDXS elemental maps of an Ag@Au core@shell nanocluster acquired at a tilt angle of 65°. The boxed region in the HAADF STEM image indicates the area of the mapped region and the size of the cluster. The maps have been generated from the EDXS signal of the Ag and Au L-lines, and for the EELS signal the Ag M-edge intensity was extracted. The color overlay was formed from the Ag EELS and the Au EDXS signal. Reprinted from ref. 78 under the Creative Common License. | ||
The elements Fe, Co, Ni (also known as iron triade) provide a magnetic moment which makes them interesting candidates for nanosensor applications. Because of their reactivity, a gold coating appeared attractive as passivation layer.111 Experiments with different Au-shell thickness had revealed that 3 atomic gold layers provide a minimum protection of a 2 nm diameter Fe-core.64 A similar protection layer is necessary for a Ni-core under normal environmental condition. Heating experiments, however, showed that a cycle of heating up to 400 °C with subsequent cooling to room temperature in the presence of small traces of oxygen resulted in a core–shell inversion with nickel oxide outside a gold core.109 The influence of oxygen on the observed intermetallic diffusion was theoretically studied employing density functional theory. It could be shown that the presence of oxygen lowers the diffusion barrier for the migration of Ni core atoms through the Au shell to the surface.109
A recent study of iron triade nanoparticles passivated by gold layers was conducted to probe for the temperature dependent alloying in an oxygen-free vacuum.111 Starting from the synthesis of spherical Fe@Au, Co@Au, and Ni@Au core@shell clusters with centralized cores, the same heating procedures were applied to all combinations inside the electron microscope. The three different combinations exhibit rather different responses to thermal treatment: at 400 °C, the Fe core breaks up into several smaller decentralized cores still surrounded by Au atoms and a complete alloying is only observed at 1100 °C after entering the liquid phase. For Co@Au, a structural transition to a decentralized Co core is observed at 400 °C (see Fig. 14) which is stable up to the melting temperature of 1100 °C when complete alloying takes place. In contrast, the Ni@Au clusters undergo a complete mixing already at 400 °C, i.e. alloying takes place by diffusion through lattice before any liquid phase would set in (Fig. 15).
 | ||
| Fig. 14 EELS Co observations and EDX Au observations as well as complementary HAADF scans of temperature-induced structural transition from centralized (left) to decentralized (right) Co–Au clusters. The temperatures correspond to 25 °C (left) and 400 °C (right). Reprinted from ref. 111 with the permission of the American Chemical Society. | ||
 | ||
| Fig. 15 HAADF observation of temperature-induced rearrangements within a Ni–Au cluster. The cluster is embedded centrally inside an Au shell. At 300–400 °C the Ni and Au atoms start to form an alloy, still exhibiting a lattice structure. Reprinted from ref. 111 with the permission of the American Chemical Society. | ||
Initially, the three bimetallic cluster combinations were not expected to exhibit such different behaviour. Searching for an explanation, theoretical calculations were performed employing two different approaches, one based on the embedded atom method (EAM) and the other using a density functional theory (DFT) ansatz.111 A comparison of vacancy energies at the EAM and the DFT level, calculated for the four metals, and studies of Helmholtz free energies of the three bimetallic systems at various degrees of intermixing, provides a satisfactory explanation.
The size and shape dependent plasmonic properties of metal clusters promise interesting applications in the areas of photonics, optical sensing, or surface enhanced Raman spectroscopy (SERS). As shown in ref. 63, the optical absorption of a deposited cluster sample of Ag@Au core@shell clusters can be shifted between the silver cluster resonance around 450 nm and the gold cluster absorption near 550 nm depending on the number ratio of Ag atoms in the core and Au atoms in the shell. The study also demonstrated the use of such core@shell cluster samples for SERS by measuring Raman spectra of 4-methylbenzenethiol (4-MBT) enhanced by clusters of different core and shell contents in combination with different laser excitation wavelengths.63 As expected, blue laser light excitation yielded the best Raman intensities in combination with pure silver clusters. For red light, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ration of Ag and Au contents yielded the best Raman enhancement.
1 ration of Ag and Au contents yielded the best Raman enhancement.
While the absorption spectroscopy in ref. 63 required a sample of deposited nanoparticles that consisted of some cluster size distribution always present in our synthesis, the plasmon resonance of a single particle can be probed by electron energy loss spectroscopy (EELS). Fig. 16 shows the example of an elongated Ag@Au core@shell particle or nanorod that was created by doping a helium droplet beam at nozzle temperature of 6.7 K and 20 bar pressure.75 As mentioned before, by choosing the helium source conditions and the amount of doping, the synthesized particle shape and distribution can be controlled to some extent. As seen in panels (a) to (d), the nanorod has a regular shape with a connected silver core and an absorption peaked near 1.95 eV, i.e. about 640 nm. The plasmon resonance map shows the spatial distribution with the maximum of the absorption lying near the ends of the particle.75
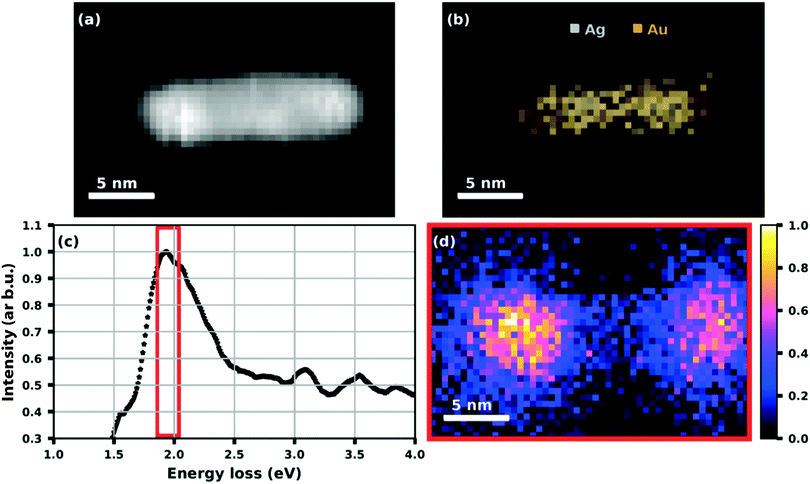 | ||
| Fig. 16 HAADF image (a) of a Ag@Au core@shell nanorod with (b) an elemental map extracted from the EDS data showing the Ag core and Au shell structure. (c) A plot of the processed EELS data integrated over the whole image area where the red framed section is used for (d) a plasmon resonance map at (1.95 + 0.09) eV. Reproduced from ref. 75 [A. Schiffmann, D. Knez, F. Lackner, M. Lasserus, R. Messner, M. Schnedlitz, G. Kothleitner, F. Hofer and W. E. Ernst, J. Appl. Phys., 2019, 125, 023104], with the permission of AIP Publishing. | ||
5.3 Metal oxide nanoparticles
Like their respective bulk versions, metal oxide nanoparticles are expected to become efficient nano catalysts for reactions like heterogeneous oxidation in depollution, photocatalysis, or hydrogen production with the advantage of their large surface to volume ratio. Only recently, we began to explore the potential of helium droplet assisted synthesis of metal oxide nanoparticles for the fundamental investigation of the morphology, stability, and electronic properties of these particles.In order to produce V2O5 nanoparticles and deposit them on solid substrates, we heated V2O5 powder with a purity of 99.9%, kept in a small quartz crucible (Kurt Lesker EVC2Q), to temperatures between 1000 and 1200 K, which yielded a vapour pressure of about 10−3 mbar.69 Helium droplets were generated at 20 bar stagnation pressure and various nozzle temperatures for different droplet size distributions. The TOF-MS served as diagnostic tool for the observation of aggregation products formed in the droplets. To our surprise, no measurable number of V2O5 molecules showed up in the mass spectra, but significant abundances of even multiples of V2O5 such as (V2O5)2 and (V2O5)4. The experimental measurements were accompanied by a computational study on a single layer of bulk vanadium(V) oxide, which suggests a preferred sublimation of the dimers (V2O5)2.69
For the deposition of V2O5 nanoparticles,128 the nozzle temperature was lowered to 5.4, 6.7 and 8 K, which corresponds to average sizes of 1.68 × 1010, 6 × 107 and 5.31 × 106 helium atoms per droplet, respectively. Larger V2O5 nanoparticles of 10 nm side length were deposited this way as depicted in Fig. 17. Lattice constants were extracted from a large number of electron microscope images with the drawback that only projections of the deposited particles on the substrate are obtained. However, the large number of analyzed particles and comparison with tabulated lattice structures for vanadium oxides in the literature, supported by the observed UV-visible absorption spectra of our samples (Fig. 18), let us conclude that the V2O5 nanoparticles synthesized in helium droplets stayed intact during the deposition.
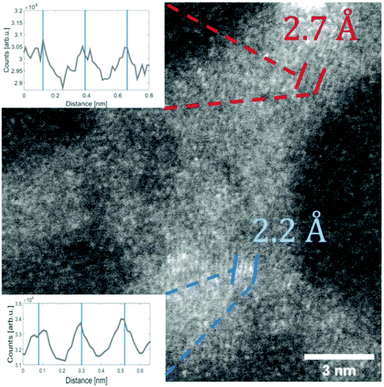 | ||
| Fig. 17 STEM HAADF image of a V2O5 particle (synthesised at 5.4 K cold head temperature). Two regions are marked where lattice constants could be extracted from the image. The respective intensity profile between the lines is shown in the inset. The black lines indicate a group of planes with a spacing of 2.7 Å the blue lines mark a group of planes with a spacing of 2.2 Å. Ref. 128 – reprinted with permission of the PCCP Owner Societies. | ||
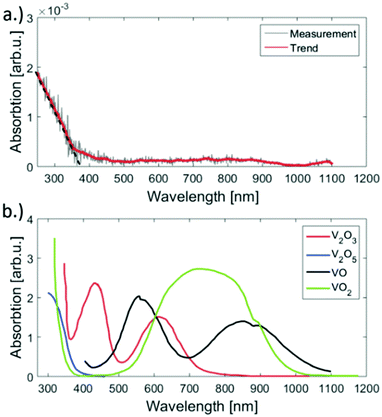 | ||
| Fig. 18 UV-vis absorption spectra of the synthesised V2O5 clusters on fused silica (a) and reference spectra taken from ref. 141 (b). Apparently our sample has significant absorption only below 450 nm but no bands above. The spectrum was acquired by subtracting the signal of an uncovered plane spot on the substrate from the spot of cluster deposition. When comparing the reference spectra of various vanadium oxides to the measurement, only V2O5 has no absorption in the range from 450 to 1100 nm. Ref. 128 – reprinted with permission of the PCCP Owner Societies. | ||
 | ||
| Fig. 19 (a) STEM HAADF image of the synthesized Ag@ZnO nanosized particles. Spherically shaped as well as wire-like structures can be identified. The core@shell structure is obvious as silver cores appear brighter than zinc oxide shells. The smaller spherical particles and the elongated larger particles were created at different helium droplet beam conditions and were deposited on the same substrate subsequently. (b) Detailed HAADF image showing ZnO along the [001] axis with the hexagonal structure highlighted in red for a selected unit cell. Inset plot (c) shows the fast Fourier transform (FFT) of the STEM image, yielding periodicities of (0.30 + 0.02) nm and (0.18 + 0.01) nm marked by the dashed orange circles. The sixfold symmetry of the FFT pattern is identified and all visible features are assigned. The schematic in inset plot (d) explains the origin of the two observed lengths within the 2D projection of the hexagonal unit cell of wurtzite ZnO in [001] direction. Reprinted from ref. 130 under the Creative Common License. | ||
6 Summary and outlook
With this perspective, we have shown that helium droplets provide an excellent cryogenic environment for building clusters in a controlled composition atom by atom without any additional chemicals or additives. By varying the helium droplet source conditions and the vapour pressure of the dopants, size, shape, and elemental mixture can be influenced within certain distributions. While the method will not be suitable for mass production of cluster material, it is an excellent means for fundamental studies on clean nanoparticles without any contamination answering questions about nanoscale elemental mixing and alloying or phase transitions in general. As shown in our work depending on the particle size, surface coverages in the range between 10% and a monolayer can be achieved in realistic operating times.As diagnostics of the generated particles inside the helium droplets, basically any technique known from molecular beam spectroscopy can be applied, such as laser spectroscopy, ionization with mass analysis, or double resonance.35,71 The analytics can be continued within the beam apparatus even after the soft landing deposition by employing a quartz crystal microbalance that will measure the effect of either adding reactants or of depleting the coverage by resonant laser heating. Once deposited on exchangeable solid substrates that may be mounted on a rotatable holder, the created samples are transported under UHV to various surface diagnostic instruments.
Single particle diagnostics are provided by a large range of electron microscopy tools such as transmission electron microscopes or scanning electron microscopes equipped with high-angular annular dark-field technique (HAADF), energy-dispersive X-ray spectroscopy (EDXS), and the electron energy loss spectroscopy (EELS). At the loss of individual particle resolution, we have investigated samples with UV-optical absorption spectroscopy and photoelectron spectroscopy. A recently set up femtosecond laser lab46 in combination with high harmonic generation131 and the new NanoESCA lab will open up new opportunities like time-resolved photoemission electron microscopy,132 ultrafast charge carrier dynamics measurements,133 or time-resolved magnetic circular dichroism detection.134 For polar particles in helium droplets, Merthe and Kresin demonstrated electrostatic deflection as direct measure in the doped helium droplet beam,135 and built, with the group of Schäfer in Darmstadt, a setup for a magnetic deflection experiment.136 In this way, the magnetic properties of synthesized nanoparticles could directly be probed.
On the theoretical side, He density functional theory has been mentioned as the currently most suitable simulation method, allowing for a quantum treatment of He droplets containing vortices as well as impurities, but also having its limits with respect to droplet size and the ability to describe large collective excitations. Collision time estimates for impurities, derived from a simplified model, have been linked to growth scenarios of metallic structures inside He droplets. The deposition process could be identified as minimally perturbative to the grown structures. Suitable theoretical treatments for He-grown metallic clusters depend on their actual size, ranging from first principle treatments for smallest systems to force field descriptions based on the embedded atom model for particles in the nanometer range. A theoretical treatment of diffusion processes for even larger metallic structures via cellular automata on a coarse-grained lattice has been demonstrated. Challenges for future developments, in particular with respect to surface reactions on catalytically active sites of the synthesized mixed-metallic structures, will be the suitable coupling of various levels of computational treatment,137 and the implementation of novel machine learning techniques.117,118
Especially core@shell cluster configurations for catalysis or photocatalysis seem to be very promising in this context,138 as has been proven by recent experiments.139,140 We think that a combination of a theoretical screening via systematic first principle studies with the subsequent, He-assisted creation of the most promising core@shell candidates, followed by their deposition on suitable substrates, could accelerate the ongoing search for optimum configurations. A test apparatus for small scale catalysis experiments is in preparation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been supported by the Austrian Science Fund (FWF) under Grant No. P 29893-N36 and by the FWF in cooperation with the Christian Doppler Research Association (CDG) under Grant No. PIR8-N34. Further support by NAWI Graz is gratefully acknowledged. The described cluster lab was built in 2011–2014, supported by the European Commission and the Styrian Government within the ERDF program (7th framework). An infrastructure grant from the HRSM program of the Austrian Government enabled the aquisition of the NanoESCA instrument. The authors are grateful to F. Lackner, A. Schiffmann, T. Jauk, M. Schnedlitz, M. Lasserus, D. Knez, H. Fitzek, G. Kothleitner, F. Hofer and M. P. de Lara-Castells for the highly productive years of joint collaboration.References
- M. Moskovits and J. E. Hulse, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 471–484 RSC.
- M. D. Morse, Chem. Rev., 1986, 86, 1049–1109 CrossRef CAS.
- H. Haberland, Springer Series in Chemical Physics, Clusters of Atoms and Molecules: Theory, Experiment, and Clusters of Atoms, Springer, Berlin, 1994 Search PubMed.
- W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676 CrossRef CAS.
- U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters, Springer, Berlin, 1995, p. 535 Search PubMed.
- W. A. de Heer and P. Milani, Rev. Sci. Instrum., 1991, 62, 670–677 CrossRef CAS.
- I. M. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1682–1684 CrossRef CAS.
- R. Moro, X. Xu, S. Yin and W. A. de Heer, Science, 2003, 300, 1265–1269 CrossRef CAS.
- E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592 RSC.
- J. Bansmann, S. Baker, C. Binns, J. Blackman, J.-P. Bucher, J. Dorantes-Dávila, V. Dupuis, L. Favre, D. Kechrakos, A. Kleibert, K.-H. Meiwes-Broer, G. Pastor, A. Perez, O. Toulemonde, K. Trohidou, J. Tuaillon and Y. Xie, Surf. Sci. Rep., 2005, 56, 189–275 CrossRef CAS.
- M. Martins and W. Wurth, J. Phys.: Condens. Matter, 2016, 28, 503002 CrossRef.
- G. Schmid and L. F. Chi, Adv. Mater., 1998, 10, 515–526 CrossRef CAS.
- W. Schöllkopf and J. P. Toennies, Science, 1994, 266, 1345–1348 CrossRef.
- E. W. Becker, R. Klingelhöfer and P. Lohse, Zeitschrift für Naturforschung A, 1962, 17, 432–438 Search PubMed.
- A. Scheidemann, J. P. Toennies and J. A. Northby, Phys. Rev. Lett., 1990, 64, 1899–1902 CrossRef CAS.
- S. Goyal, D. L. Schutt and G. Scoles, J. Phys. Chem., 1993, 97, 2236–2245 CrossRef CAS.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569 CrossRef CAS.
- G. Auböck, J. Nagl, C. Callegari and W. E. Ernst, J. Phys. Chem. A, 2007, 111, 7404–7410 CrossRef.
- S. Grebenev, J. P. Toennies and A. F. Vilesov, Science, 1998, 279, 2083–2086 CrossRef CAS.
- M. Hartmann, F. Mielke, J. P. Toennies, A. F. Vilesov and G. Benedek, Phys. Rev. Lett., 1996, 76, 4560–4563 CrossRef CAS.
- L. F. Gomez, K. R. Ferguson, J. P. Cryan, C. Bacellar, R. M. P. Tanyag, C. Jones, S. Schorb, D. Anielski, A. Belkacem, C. Bernando, R. Boll, J. Bozek, S. Carron, G. Chen, T. Delmas, L. Englert, S. W. Epp, B. Erk, L. Foucar, R. Hartmann, A. Hexemer, M. Huth, J. Kwok, S. R. Leone, J. H. S. Ma, F. R. N. C. Maia, E. Malmerberg, S. Marchesini, D. M. Neumark, B. Poon, J. Prell, D. Rolles, B. Rudek, A. Rudenko, M. Seifrid, K. R. Siefermann, F. P. Sturm, M. Swiggers, J. Ullrich, F. Weise, P. Zwart, C. Bostedt, O. Gessner and A. F. Vilesov, Science, 2014, 345, 906–909 CrossRef CAS.
- J. Higgins, C. Callegari, J. Reho, F. Stienkemeier, W. E. Ernst, M. Gutowski and G. Scoles, J. Phys. Chem. A, 1998, 102, 4952–4965 CrossRef CAS.
- J. Higgins, W. E. Ernst, C. Callegari, J. Reho, K. K. Lehmann, G. Scoles and M. Gutowski, Phys. Rev. Lett., 1996, 77, 4532–4535 CrossRef CAS.
- K. Nauta and R. E. Miller, Science, 1999, 283, 1895–1897 CrossRef CAS.
- K. Nauta and R. E. Miller, Science, 2000, 287, 293–295 CrossRef CAS.
- J. Higgins, C. Callegari, J. Reho, F. Stienkemeier, W. E. Ernst, K. K. Lehmann, M. Gutowski and G. Scoles, Science, 1996, 273, 629–631 CrossRef CAS.
- J. Nagl, G. Auböck, A. W. Hauser, O. Allard, C. Callegari and W. E. Ernst, Phys. Rev. Lett., 2008, 100, 063001 CrossRef.
- A. W. Hauser and W. E. Ernst, Phys. Chem. Chem. Phys., 2011, 13, 18762–18768 RSC.
- C. Giese, F. Stienkemeier, M. Mudrich, A. W. Hauser and W. E. Ernst, Phys. Chem. Chem. Phys., 2011, 13, 18769–18780 RSC.
- C. Stark and V. V. Kresin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085401 CrossRef.
- M. Theisen, F. Lackner and W. E. Ernst, J. Phys. Chem. A, 2011, 115, 7005–7009 CrossRef CAS.
- O. Bünermann and F. Stienkemeier, Eur. Phys. J. D, 2011, 61, 645–655 CrossRef.
- M. Theisen, F. Lackner and W. E. Ernst, Phys. Chem. Chem. Phys., 2010, 12, 14861–14863 RSC.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS.
- C. Callegari and W. E. Ernst, Helium Droplets as Nanocryostats for Molecular Spectroscopy—from the Vacuum Ultraviolet to the Microwave Regime, American Cancer Society, 2011.
- F. Stienkemeier, F. Meier and H. O. Lutz, J. Chem. Phys., 1997, 107, 10816–10818 CrossRef CAS.
- E. Loginov and M. Drabbels, J. Chem. Phys., 2012, 136, 154302 CrossRef.
- L. Kazak, S. Göde, K.-H. Meiwes-Broer and J. Tiggesbäumker, J. Phys. Chem. A, 2019, 123, 5951–5956 CrossRef CAS.
- M. Mudrich, B. Forkl, S. Müller, M. Dvorak, O. Bünermann and F. Stienkemeier, Rev. Sci. Instrum., 2007, 78, 103106 CrossRef CAS.
- R. Katzy, M. Singer, S. Izadnia, A. C. LaForge and F. Stienkemeier, Rev. Sci. Instrum., 2016, 87, 013105 CrossRef CAS.
- M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2012, 136, 104201 CrossRef.
- F. Lindebner, A. Kautsch, M. Koch and W. E. Ernst, Int. J. Mass Spectrom., 2014, 365–366, 255–259 CrossRef CAS.
- M. Lasserus, M. Schnedlitz, D. Knez, R. Messner, A. Schiffmann, F. Lackner, A. W. Hauser, F. Hofer and W. E. Ernst, Nanoscale, 2018, 10, 2017–2024 RSC.
- R. Messner, A. Schiffmann, J. V. Pototschnig, M. Lasserus, M. Schnedlitz, F. Lackner and W. E. Ernst, J. Chem. Phys., 2018, 149, 024305 CrossRef.
- M. Schnedlitz, D. Knez, M. Lasserus, F. Hofer, R. Fernández-Perea, A. W. Hauser, M. Pilar de Lara-Castells and W. E. Ernst, J. Phys. Chem. C, 2020, 124, 16680–16688 CrossRef CAS.
- B. Thaler, S. Ranftl, P. Heim, S. Cesnik, L. Treiber, R. Meyer, A. W. Hauser, W. E. Ernst and M. Koch, Nat. Commun., 2018, 9, 4006 CrossRef.
- R. E. Grisenti and J. P. Toennies, Phys. Rev. Lett., 2003, 90, 234501 CrossRef.
- L. F. Gomez, E. Loginov, R. Sliter and A. F. Vilesov, J. Chem. Phys., 2011, 135, 154201 CrossRef.
- A. Volk, P. Thaler, D. Knez, A. W. Hauser, J. Steurer, W. Grogger, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2016, 18, 1451–1459 RSC.
- V. Mozhayskiy, M. N. Slipchenko, V. K. Adamchuk and A. F. Vilesov, J. Chem. Phys., 2007, 127, 094701 CrossRef.
- E. Loginov, L. F. Gomez and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 7199–7204 CrossRef CAS.
- S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binns, Nanoscale, 2013, 5, 11545–11553 RSC.
- S. B. Emery, K. B. Rider, B. K. Little and C. M. Lindsay, J. Phys. Chem. C, 2013, 117, 2358–2368 CrossRef CAS.
- A. Volk, P. Thaler, M. Koch, E. Fisslthaler, W. Grogger and W. E. Ernst, J. Chem. Phys., 2013, 138, 214312 CrossRef.
- P. Thaler, A. Volk, D. Knez, F. Lackner, G. Haberfehlner, J. Steurer, M. Schnedlitz and W. E. Ernst, J. Chem. Phys., 2015, 143, 134201 CrossRef.
- A. W. Hauser, A. Volk, P. Thaler and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 10805–10812 RSC.
- O. Gessner and A. F. Vilesov, Annu. Rev. Phys. Chem., 2019, 70, 173–198 CrossRef CAS.
- Y. A. Sergeev and C. F. Barenghi, J. Low Temp. Phys., 2009, 157, 429 CrossRef CAS.
- L. F. Gomez, E. Loginov and A. F. Vilesov, Phys. Rev. Lett., 2012, 108, 155302 CrossRef.
- P. Thaler, A. Volk, F. Lackner, J. Steurer, D. Knez, W. Grogger, F. Hofer and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155442 CrossRef.
- D. Spence, E. Latimer, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Phys. Chem. Chem. Phys., 2014, 16, 6903–6906 RSC.
- E. Gordon, A. Karabulin, V. Matyushenko, V. Sizov and I. Khodos, Phys. Chem. Chem. Phys., 2014, 16, 25229–25233 RSC.
- F. Lackner, A. Schiffmann, M. Lasserus, R. Messner, M. Schnedlitz, H. Fitzek, P. Pölt, D. Knez, G. Kothleitner and W. E. Ernst, Eur. Phys. J. D, 2019, 73, 104 CrossRef.
- M. Lasserus, D. Knez, M. Schnedlitz, A. Hauser, F. Hofer and W. E. Ernst, Nanoscale Adv., 2019, 1, 2276–2283 RSC.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143 CrossRef CAS.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155408 CrossRef.
- P. Bartl, K. Tanzer, C. Mitterdorfer, S. Karolczak, E. Illenberger, S. Denifl and P. Scheier, Rapid Commun. Mass Spectrom., 2013, 27, 298–304 CrossRef CAS.
- S. Denifl, Eur. Phys. J.: Spec. Top., 2013, 222, 2017–2033 Search PubMed.
- M. Lasserus, M. Schnedlitz, R. Messner, F. Lackner, W. E. Ernst and A. W. Hauser, Chem. Sci., 2019, 10, 3473–3480 RSC.
- J. Steurer, MSc thesis, Graz University of Technology, Graz, 2014.
- M. Koch, J. Lanzersdorfer, C. Callegari, J. S. Muenter and W. E. Ernst, J. Phys. Chem. A, 2009, 113, 13347–13356 CrossRef CAS.
- T. Diederich, J. Tiggesbäumker and K.-H. Meiwes-Broer, J. Chem. Phys., 2002, 116, 3263–3269 CrossRef CAS.
- F. Xuan and C. Guet, Phys. Rev. A, 2017, 96, 043404 CrossRef.
- E. Loginov, L. F. Gomez, N. Chiang, A. Halder, N. Guggemos, V. V. Kresin and A. F. Vilesov, Phys. Rev. Lett., 2011, 106, 233401 CrossRef.
- A. Schiffmann, D. Knez, F. Lackner, M. Lasserus, R. Messner, M. Schnedlitz, G. Kothleitner, F. Hofer and W. E. Ernst, J. Appl. Phys., 2019, 125, 023104 CrossRef.
- P. Thaler, A. Volk, M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2014, 140, 044326 CrossRef.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 CrossRef.
- G. Haberfehlner, P. Thaler, D. Knez, A. Volk, F. Hofer, W. E. Ernst and G. Kothleitner, Nat. Commun., 2015, 6, 8779 CrossRef CAS.
- M. Schnedlitz, MSc thesis, Graz University of Technology, Graz, 2017.
- A. Schiffmann and H. Fitzek, unpublished.
- C. Nacci and L. Grill, unpublished.
- T. Jauk, MSc thesis, Graz University of Technology, Graz, 2019.
- M. Barranco, R. Guardiola, S. Hernández, R. Mayol, J. Navarro and M. Pi, J. Low Temp. Phys., 2006, 142, 1 CrossRef CAS.
- F. Ancilotto, M. Barranco, F. Coppens, J. Eloranta, N. Halberstadt, A. Hernando, D. Mateo and M. Pi, Int. Rev. Phys. Chem., 2017, 36, 621–707 Search PubMed.
- M. Pi et al. 4He-DFT BCN-TLS: A Computer Package for Simulating Structural Properties and Dynamics of Doped Liquid Helium-4 Systems, 2016, https://github.com/bcntls2016/.
- R. J. Donnelly, Quantized Vortices in Helium II, Cambridge University Press, Cambridge, 1991 Search PubMed.
- F. Ancilotto, M. Pi and M. Barranco, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 100503 CrossRef.
- F. Coppens, F. Ancilotto, M. Barranco, N. Halberstadt and M. Pi, Phys. Chem. Chem. Phys., 2019, 21, 17423–17432 RSC.
- F. Coppens, A. Leal, M. Barranco, N. Halberstadt and M. Pi, J. Low Temp. Phys., 2017, 187, 439–445 CrossRef CAS.
- F. Calvo, Phys. Rev. B, 2017, 95, 035429 CrossRef.
- J. Höller, E. Krotscheck and R. E. Zillich, Eur. Phys. J. D, 2014, 68, 372 CrossRef.
- J. Höller, E. Krotscheck and R. E. Zillich, Eur. Phys. J. D, 2015, 69, 198 CrossRef.
- J. Höller, E. Krotscheck and R. E. Zillich, Eur. Phys. J. D, 2015, 69, 198 CrossRef.
- E. Krotscheck and R. E. Zillich, J. Chem. Phys., 2016, 145, 244317 CrossRef.
- A. Hernando, M. Barranco, R. Mayol, M. Pi and F. Ancilotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 184515 CrossRef.
- M. Lasserus, PhD thesis, Graz University of Technology, 2020.
- R. Fernández-Perea, L. F. Gómez, C. Cabrillo, M. Pi, A. O. Mitrushchenkov, A. F. Vilesov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 22248–22257 CrossRef.
- A. Volk, D. Knez, P. Thaler, A. W. Hauser, W. Grogger, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 24570–24575 RSC.
- R. Thouy, N. Olivi-Tran and R. Jullien, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5321–5327 CrossRef CAS.
- A. W. Hauser, M. Schnedlitz and W. E. Ernst, Eur. Phys. J. D, 2017, 71, 150 CrossRef.
- M. Schnedlitz, M. Lasserus, D. Knez, A. W. Hauser, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2017, 19, 9402–9408 RSC.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS.
- Nanoalloys – From Fundamentals to Emergent Applications, ed. F. Calvo, Elsevier, 2013 Search PubMed.
- Structure and Properties of Nanoalloys, ed. R. Ferrando, Elsevier, 2016 Search PubMed.
- J.-P. Palomares-Baez, E. Panizon and R. Ferrando, Nano Lett., 2017, 17, 5394–5401 CrossRef CAS.
- M. Jäger, R. Schäfer and R. L. Johnston, Adv. Phys.: X, 2018, 3, 1516514 Search PubMed.
- S. Liu, Z. Sun, Q. Liu, L. Wu, Y. Huang, T. Yao, J. Zhang, T. Hu, M. Ge, F. Hu, Z. Xie, G. Pan and S. Wei, ACS Nano, 2014, 8, 1886–1892 CrossRef CAS.
- V. Dupuis, A. Hillion, A. Robert, O. Loiselet, G. Khadra, P. Capiod, C. Albin, O. Boisron, D. Le Roy, L. Bardotti, F. Tournus and A. Tamion, J. Nanopart. Res., 2018, 20, 128 CrossRef.
- M. Schnedlitz, M. Lasserus, R. Meyer, D. Knez, F. Hofer, W. E. Ernst and A. W. Hauser, Chem. Mater., 2018, 30, 1113–1120 CrossRef CAS.
- D. Nelli and R. Ferrando, Nanoscale, 2019, 11, 13040–13050 RSC.
- M. Schnedlitz, D. Knez, M. Lasserus, F. Hofer, R. Fernández-Perea, A. W. Hauser, M. Pilar de Lara-Castells and W. E. Ernst, J. Phys. Chem. C, 2020, 124, 16680–16688 CrossRef CAS.
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7983–7991 CrossRef CAS.
- Z. Qiao, H. Feng and J. Zhou, Phase Transitions, 2014, 87, 59–70 CrossRef CAS.
- X. W. Zhou, R. A. Johnson and H. N. G. Wadley, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 10 Search PubMed.
- A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146 CrossRef.
- Y. Qi, T. Ç. Çağın, Y. Kimura and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3527–3533 CrossRef CAS.
- Z. Claudio, R. Kevin, G. Aldo, F. Ádám, G. Nicola, B. Francesca and D. V. Alessandro, J. Chem. Phys., 2018, 148, 241739 CrossRef.
- C. Zeni, K. Rossi, A. Glielmo and F. Baletto, Adv. Phys.: X, 2019, 4, 1654919 CAS.
- M. Schnedlitz, R. Fernández-Perea, D. Knez, M. Lasserus, A. Schiffmann, F. Hofer, A. W. Hauser, M. P. de Lara-Castells and W. E. Ernst, J. Phys. Chem. C, 2019, 123, 20037–20043 CrossRef CAS.
- J. Ågren, Curr. Opin. Solid State Mater. Sci., 1996, 1, 355–360 CrossRef.
- M. Cui, H. Lu, H. Jiang, Z. Cao and X. Meng, Sci. Rep., 2017, 7, 41990 CrossRef CAS.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- G. P. Bewley, D. P. Lathrop and K. R. Sreenivasan, Nature, 2006, 441, 588 CrossRef CAS.
- E. B. Gordon, R. Nishida, R. Nomura and Y. Okuda, JETP Lett., 2007, 85, 581–584 CrossRef CAS.
- P. Moroshkin, V. Lebedev, B. Grobety, C. Neururer, E. B. Gordon and A. Weis, EPL, 2010, 90, 34002 CrossRef.
- E. B. Gordon, A. V. Karabulin, A. A. Morozov, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, J. Phys. Chem. Lett., 2014, 5, 1072–1076 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, Appl. Phys. Lett., 2012, 101, 052605 CrossRef.
- M. Lasserus, D. Knez, F. Lackner, M. Schnedlitz, R. Messner, D. Schennach, G. Kothleitner, F. Hofer, A. W. Hauser and W. E. Ernst, Phys. Chem. Chem. Phys., 2019, 21, 21104–21108 RSC.
- Y. Zhang, ZnO Nanostructures: Fabrication and Applications, Nanoscience & Nanotechnology Series, The Royal Society of Chemistry, 2017, pp. 1–291 Search PubMed.
- A. Schiffmann, T. Jauk, D. Knez, H. Fitzek, F. Hofer, F. Lackner and W. E. Ernst, Nano Res., 2020, 13(11), 2979–2986 CrossRef CAS.
- A. Schiffmann, B. W. Toulson, D. Knez, R. Messner, M. Schnedlitz, M. Lasserus, F. Hofer, W. E. Ernst, O. Gessner and F. Lackner, J. Appl. Phys., 2020, 127, 184303 CrossRef CAS.
- K. Yu, D. Bayer, C. Wiemann, O. Gaier, M. Bauer and M. Aeschlimann, J. Nanomater., 2008, 2008, 249514 Search PubMed.
- M. E. Vaida, B. M. Marsh and S. R. Leone, Nano Lett., 2018, 18, 4107–4114 CrossRef CAS.
- F. Siegrist, J. A. Gessner, M. Ossiander, C. Denker, Y.-P. Chang, M. C. Schröder, A. Guggenmos, Y. Cui, J. Walowski, U. Martens, J. K. Dewhurst, U. Kleineberg, M. Münzenberg, S. Sharma and M. Schultze, Nature, 2019, 571, 240–244 CrossRef CAS.
- D. J. Merthe and V. V. Kresin, J. Phys. Chem. Lett., 2016, 7, 4879–4883 CrossRef CAS.
- J. Liang, T. M. Fuchs, R. Schäfer and V. V. Kresin, Rev. Sci. Instrum., 2020, 91, 053202 CrossRef CAS.
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- Y. Hu, J. Huo, X. Wang and R. Wang, J. Phys.: Condens. Matter, 2017, 29, 435701 CrossRef.
- V. A. Bharathan, R. Jain, C. S. Gopinath and C. P. Vinod, Catal. Sci. Technol., 2017, 7, 4489–4498 RSC.
- P. B. O'Mara, P. Wilde, T. M. Benedetti, C. Andronescu, S. Cheong, J. J. Gooding, R. D. Tilley and W. Schuhmann, J. Am. Chem. Soc., 2019, 141, 14093–14097 CrossRef.
- N. H. Choi, S.-k. Kwon and H. Kim, J. Electrochem. Soc., 2013, 60, A973–A979 CrossRef.
| This journal is © the Owner Societies 2021 |


