Full-dimensional potential energy surface for acetylacetone and tunneling splittings†
Chen
Qu
 a,
Riccardo
Conte
a,
Riccardo
Conte
 *b,
Paul L.
Houston
*b,
Paul L.
Houston
 *cd and
Joel M.
Bowman
*cd and
Joel M.
Bowman
 *e
*e
aDepartment of Chemistry & Biochemistry, University of Maryland, College Park, Maryland 20742, USA
bDipartimento di Chimica, Università Degli Studi di Milano, via Golgi 19, 20133 Milano, Italy. E-mail: riccardo.conte1@unimi.it
cDepartment of Chemistry and Chemical Biology, Cornell University, Ithaca, New York 14853, USA. E-mail: plh2@cornell.edu
dDepartment of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332, USA
eCherry L. Emerson Center for Scientific Computations and Department of Chemistry, Atlanta, Georgia 30322, USA. E-mail: jmbowma@emory.edu
First published on 18th September 2020
Abstract
We present a full-dimensional potential energy surface for acetylacetone (AcAc) using full and fragmented permutationally invariant polynomial approaches. Previously reported MP2/aVTZ energies and gradients are augmented by additional calculations at this level of theory for the fits. Numerous stationary points are reported as are the usual metrics to assess the precision of the fit. The electronic barrier height for the H-atom transfer is roughly 2.2 kcal mol−1. Diffusion Monte Carlo (DMC) calculations are used to calculate the ground state wavefunction and zero-point energy of acetylacetone. These together with fixed-node DMC calculations for the first excited-state provide the predicted tunneling splitting due to the barrier to H-transfer separating two equivalent wells. Simpler 1d calculations of this splitting are also reported for varying barrier heights including the CCSD(T) barrier height of 3.2 kcal mol−1. Based on those results the DMC splitting of 160 cm−1 with a statistical uncertainty of roughly 21 cm−1, calculated using the MP2-based PES, is estimated to decrease to 100 cm−1 for a barrier of 3.2 kcal mol−1. The fragmented surface is shown to be fast to evaluate.
1 Introduction
It is a truism that potential energy surfaces (PESs) play a central role in all of computational chemistry. There has been breathtaking progress in the past 15 years in developing so-called non-parametric, machine learning approaches to fit large data sets of electronic energies. These include permutationally invariant polynomials (PIPs), Gaussian process regression (GPR), neural networks (NN), combinations of all three as well as variants of the GPR and NN approaches. Numerous reviews have appeared that cover much of this field and we refer the reader to a handful that provide a good overview.2–9 These methods have steep scaling with respect to the number of atoms in the molecule or cluster and the size of the data set. (By far the steepest scaling is with respect to the electronic energy calculation.) Several comparative studies of these methods have recently appeared.10–13These methods all have in common that they do not rely on a model for representing potentials, e.g., Lennard-Jones, LEPS, exp/6, force-fields, etc. In this sense they are all non-parametric in the language of machine-learning (ML). Also, they use a universal set of inputs, also known as descriptors, for the fitting. In the PIP approach the input is all Morse variables, which are transformed internuclear distances. In the PIP-NN6,14 and PIP–GPR11 the input is a limited number of PIPs. This is distinct from earlier approaches using models, where the variables are molecule-specific. So, based on these aspects, all the methods mentioned above (not a comprehensive list) are machine-learning methods. However, there is a fundamental difference in the way the data are used in these methods. In PIP and NN the parameters contained in those approaches are optimized, generally using a least squares minimization criterion. In PIP, where parameters are linear, the optimization is performed by means of linear least-squares. In NN the fitting parameters are non-linear and so the least squares optimization is non-linear. The number of parameters in both approaches can be thousands or even tens of thousands, depending on the dimensionality of the space. As an aside, it is worth noting that if Morse variables are used as the inputs for PIP or PIP-NN, then the range parameter(s) of the variables could be treated as additional non-linear parameters. The number of such parameters is very small, however, compared to the thousands of parameters just mentioned. In any case, in these methods the data are used in the optimizations but not for prediction. By contrast, other machine-learning methods use the data explicitly for prediction. GPR is a prominent example of this method. All these methods have the same goals, which are a precise representation of the known data (GPR can reproduce the data exactly but, since this generally leads to a singular matrix for prediction, “noise” is added to the data) and smooth and accurate predictions. It is of course of interest to compare the performance of these different ML approaches.
Based now on numerous applications using these methods, some fairly general comments can be made about them. A strength of the GPR approach is that it does produce a quality PES from a relatively small amount of data.3,15 On the other hand this approach becomes computationally very demanding for datasets with more than 104 energies. By contrast, PIP/FI-NN PESs with 4–7 atoms typically use more than 104 energies.6,8 For example, the recent PIP-NN and atom-based HD-NN PESs for H + CH3OH were fit to 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electronic energies.13 The PIP approach developed in our group spans both these limits, i.e., it can easily fit ca. 105 energies (and/or gradients) and it also provides a faithful fit with very few configurations. This was explicitly the focus of a recent paper assessing the performance, i.e., speed and accuracy, of the GPR and PIP approach to PES fitting for four case studies, H3O+, OCHCO+, H2CO (including cis- and trans-HCOH isomers) and 10 atom formic acid dimer.11 That paper, which also extended the GPR method to use PIP inputs, examined the fidelity of GPR and PIP fits for these four molecules with respect to size of the training set of energies as well as the time for fitting and evaluation. One example is the PES for 5-atom OCHCO+. The original PIP PES was constructed with just 8613 CCSD(T)-F12/aVTZ energies.16 GPR, PIP–GPR and PIP fits were done using between 520 and 2600 scattered energies. All methods fit the training data with about equal precision; however, the GPR precision was significantly better for the remaining test data. The PIP fits were roughly 60 times faster to evaluate than the GPR ones. Both fits, using 1560 training data, gave harmonic frequencies at the minimum and proton transfer saddle point with maximum differences from direct ab initio results of no more than 4 cm−1.
000 electronic energies.13 The PIP approach developed in our group spans both these limits, i.e., it can easily fit ca. 105 energies (and/or gradients) and it also provides a faithful fit with very few configurations. This was explicitly the focus of a recent paper assessing the performance, i.e., speed and accuracy, of the GPR and PIP approach to PES fitting for four case studies, H3O+, OCHCO+, H2CO (including cis- and trans-HCOH isomers) and 10 atom formic acid dimer.11 That paper, which also extended the GPR method to use PIP inputs, examined the fidelity of GPR and PIP fits for these four molecules with respect to size of the training set of energies as well as the time for fitting and evaluation. One example is the PES for 5-atom OCHCO+. The original PIP PES was constructed with just 8613 CCSD(T)-F12/aVTZ energies.16 GPR, PIP–GPR and PIP fits were done using between 520 and 2600 scattered energies. All methods fit the training data with about equal precision; however, the GPR precision was significantly better for the remaining test data. The PIP fits were roughly 60 times faster to evaluate than the GPR ones. Both fits, using 1560 training data, gave harmonic frequencies at the minimum and proton transfer saddle point with maximum differences from direct ab initio results of no more than 4 cm−1.
Finally, on the matter of data size and PES fitting, we note that our PIP software was recently extended to fit gradients as well as energies.17 With this approach a PIP PES for CH4 was obtained at the DFT level of theory with just 100 configurations. In a more recent application, a PIP PES for 12-atom N-methyl acetamide was reported using a dataset of 244![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459 energies and gradients.18 An even larger applicaton was to 15-atom tropolone19 with a data size of 311
459 energies and gradients.18 An even larger applicaton was to 15-atom tropolone19 with a data size of 311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328.
328.
To summarize this short review of these ML methods, all can achieve high precision, depending on the application. In our opinion it is not particularly meaningful to focus on a root-mean-square (RMS) error difference of even tens of cm−1 between methods, except in cases where the electronic energies being fit are themselves within or less that level of accuracy. Perhaps speed of evaluation of the PES and for many applications the gradient of the energy are more relevant.
As for applications, PESs for reaction dynamics are perhaps the most demanding. By definition, reactions involve large amplitude motions and so local methods, e.g., harmonic or perturbative extensions of harmonic theory, are totally inadequate. Second, bond breaking is demanding on electronic structure methods. Third, many reactions of interest involve H-atom motion and this can require a quantum or semi-classical treatment of the dynamics. Thus, PESs for reactive systems are a major challenge as they must describe large, indeed very large amplitude motion. The above ML methods have been employed over the past 10 or so years to develop high-dimensional PESs for reactive systems.8,9,12,13,20–23 Some time ago Fu et al. reported a PIP PES for the 7-atom O(3P) + C2H4 reaction (which included spin–orbit coupling to the singlet PES). This PES was used in quasiclassical trajectory calculations which yielded excellent agreement with experiment for the branching ratio of numerous products.23 Recently, Li et al. reported PIP-NN and HD-NN PESs for several chemical reactions.12,13 The most recent example is the 7-atom H + CH3OH reaction. Although these are both neural network methods, they are different in the way the potential is represented. In the HD-NN one the energy is represented as a sum of atomic energies and there is a neural network for each atom (identical atoms share the same set of NN parameters). So in this example there are 7 NNs. For the PIP-NN6 approaches there is one NN and the input consists of a limited number of PIPs.6 (Also, see the related fundamental invariant-NN (FI-NN) approach.8,14) The authors noted that the PIP-NN PES is faster to evaluate than the HD-NN one. This is as expected since the number of parameters in the NN in each approach is about the same. However, the strength of the atom-based HD-NN approach is that it scales linearly with the number of atoms and so it is feasible to apply to large systems, ideally of the same atom type. The strength of the PIP and the PIP-NN approaches lies in the speed and high precision for molecular systems of around 10 atoms. The speed of the PIP-NN approach decreases significantly with the number of atoms because the number of PIP inputs grows non-linearly with the number of atoms.24,25 Recently, Zhang and co-workers have extended the techniques in the FI-NN approach to ten atoms,26 however, without yet reporting a 10-atom PES.
Among reactive systems, perhaps the simplest ones are isomerization reactions and, among these, symmetric double well isomerizations are the most studied. Of these malonaldehyde is perhaps the most studied both experimentally and theoretically. In 2008 we reported a PIP PES for the 9-atom malonaldehyde27 This was a precise fit to highly-accurate “focal point” electronic energies. This PES was subsequently used in various full-dimensional calculations of the tunneling splittings for H and D-transfer and finally agreement (to within less than 10%) with experiment was obtained for both. A much more recent isomerization example is 15-atom tropolone, for which we reported a PIP PES.19 For this PES, owing to the very high computational cost of CCSD(T) calculations, DFT ones were done for energies and gradients. Thus, this PES, without further modification, will not yield quantitative tunneling splittings.
Clearly, there is major motivation to extend all ML methods to large molecules of interest in chemistry and specifically reaction dynamics. We recently described a strategy to do this for the PIP approach.18,28 The key points derive from the fact the fitting basis is made of permutationally invariant polynomials of Morse variables. For an n-atom molecule there are n(n − 1)/2 variables and so this quadratic dependence on n is not favorable for large molecules. A second issue is the non-linear growth in the number of terms in the basis, for a fixed total polynomial order. For example, for 12-atom N-methyl acetamide there are 66 Morse variables and with a highly reduced permutational symmetry 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111, which accounts for the symmetry of the three H atom of the two distant methyl groups, the basis contains 8040 terms (and unknown linear coefficients) at maximum polynomial order of 3, but grows to 95
111, which accounts for the symmetry of the three H atom of the two distant methyl groups, the basis contains 8040 terms (and unknown linear coefficients) at maximum polynomial order of 3, but grows to 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 at polynomial order of 4. (Increasing the permutational symmetry reduces the number of terms dramatically;2 however, with a much increased cost to obtain them and often also to evaluate each basis function.) The strategy mentioned above is briefly reviewed next.
965 at polynomial order of 4. (Increasing the permutational symmetry reduces the number of terms dramatically;2 however, with a much increased cost to obtain them and often also to evaluate each basis function.) The strategy mentioned above is briefly reviewed next.
2 Short review of fragmented PIP theory
To begin, recall that in the PIP approach the potential is given by the compact expression: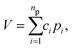 | (1) |
In the usual approach, a serious computational issue arises when the basis set is too large to be practically useful, either because the number of coefficients is so large that the least squares optimization becomes problematic or because calculating the PIPs becomes expensive. The size of the basis depends in a complicated and non-linear way on the maximum polynomial order, the number of Morse variables, and the order of the symmetric group.25 This growth in the size of the PIP basis was the origin of for the estimate of a 10-atom limit for the method.25
However, as noted above, the fragmented basis approach is an effective way to deal with this apparent 10-atom limit. By fragmenting a molecule into groups of smaller moieties the basis for each moiety can be calculated rapidly and then combined with those of other fragments to provide a compact and hopefully still precise representation of the PES.28 Consider a simple example of a 5-atom molecule with atoms labeled as 1–5 and a scheme in which the molecule is fragmented into three fragments, say {1,2,3}, {2,3,4}, {3,4,5}. In this 3-fragment scheme the potential is given compactly by
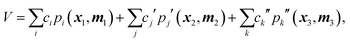 | (2) |
In this example, and in general, there are some Morse variables in common among the fragments, and thus there are some redundant basis functions in this expression in terms of common Morse variables. These issues were pointed out previously;18,28 however, they were not serious numerically, because the linear least squares method used is able to deal with a modest number of identical basis functions. Nevertheless, there is motivation to eliminate these redundant basis functions and thereby reduce the size of the basis. We do note the redundant-term issue is similar to one that two of us identified earlier for developing PIP representations of interaction potentials that should rigorously vanish in asymptotic regions where there is no inter-fragment interaction. In that case the issue was basis functions involving Morse variables of fragments that do not go to zero at large internuclear distances where there is no inter-fragment interaction. An effective pruning procedure was then employed to eliminate such basis functions and applied to several systems.29–31
It is worth recalling the key point that motivated the fragment approach. The PIP basis can be generated by starting with “seed” monomials24 given by eqn (3)
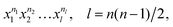 | (3) |
As noted already this approach was applied successfully to cis and tran-NMA (including the saddle point(s)) between them. Very recently it was applied to 15-atom tropolone,19 where a full PIP basis was also used.
Here we apply the fragmented PIP approach to obtain a PES 15-atom acetylacetone (AcAc). (We use the PES to obtain the H and D-tunneling splitting.) It is worth going over the history of AcAc PEs for the usual reasons and also since the molecule is an excellent example of the rapid pace of progress mentioned above. In 1997 Hinsen and Roux reported an empirical valence bond (EVB) potential (using input from a well-known force field and limited HF calculations).32,33 The barrier for the H-atom transfer of roughly 9 kcal mol−1 is about a factor of three larger than the current best value from CCSD(T) calculations of 3.2 kcal mol−1.34 (This large overshoot of an HF-based barrier is certainly in-line with many other calculations of barriers using HF theory.) This was followed in 2001 with a systematic study of the barrier height using DFT/B3LYP and MP2 theory and a variety of basis sets by Mavri and Grdadolnik.22 To quote from that paper “For description of the intramolecular degrees of freedom… one would need 39-dimensional hypersurface, which is impossible to construct….” Considering accuracy based on MP2 calculations and speed the authors went on to develop a 4d EVB potential based on B3LYP/6-311+G(2d,2p) calculations with a classical barrier of around 2 kcal mol−1. In 2015 Meuwly and co-workers developed and employed a full-dimensional semi-empirical molecular-mechanics-proton transfer PES (with input from MP2 calculations) to calculate a classical IR spectrum and to compare with a new experimental spectrum. In 2020, Meuwly and co-workers using a novel Neural Network approach in the PhysNet software35 developed a full-dimensional PES for AcAc based on MP2/aVTZ energies and gradients.1 This PES was used in molecular dynamics calculations of the infrared spectrum. Thus, in 19 years a full dimensional PES for 15-atom AcAc has gone from “impossible” to a reality.
In this paper we apply the fragmented PIP approach to obtain a new PES for AcAc. Although a NN-based PES for AcAc has recently been reported,1 as noted above, we decided to augment the data set for that fit with additional MP2/aVTZ energies and gradients to obtain and investigate a new PES. The two approaches are very different and so it is worthwhile to report on this new PES, providing additional insight on accuracy and computational timing. We use the new fit in diffusion Monte Carlo calculations of the ground vibrational state wavefunction and zero-point energy and fixed-node DMC calculations of the first excited state in the H and D-atom transfer motion to obtain the tunneling splitting. Also, a simple 1d approach to obtain the tunneling splitting is also used, mainly to determine the effect of increasing the barrier height on the tunneling splitting.
Of course, AcAc is just one example of the rapid progress in the field. Already in 2005 permutationally invariant PESs for CH5+ and H5O2+ based on fitting tens of thousands “gold standard” CCSD(T)/aVTZ energies were reported.36,37 The six and seven atom molecules were already “large” by the standards in 2005 and in both cases the PESs dissociated smoothly to fragments, CH3+ + H2 and H3O+ + H2O, respectively.
3 Computational details
3.1 PIP bases
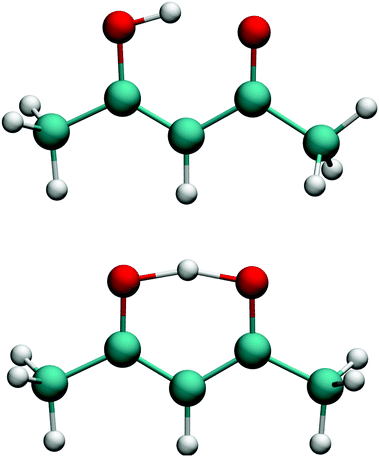
PIP software that incorporates gradients into fitting was introduced recently and first applied in a demonstration to CH417 and in the first application of the fragmentation approach to N-methyl acetamide.28,38 This software was refined for the fragmented approach to eliminate redundant basis functions39 and very recently applied to obtain a full-dimensional PES for tropolone.19We investigated two bases for the fits to the present data set. The first, which we assumed would be the benchmark, was a full PIP basis of maximum polynomial order three. The atom numbering scheme employed is shown in the top panel of Fig. 1, which also gives the minimum energy structure of AcAc. The symmetry designation for this fit is {1,2,2,2,6,1,1}, meaning that the two oxygens (atoms 2 and 3) are treated as equivalent, as are the two carbons (atoms 4 and 5), the two end carbons (atoms 6 and 7), and the six hydrogens (atoms 8–13) on the terminal carbons. The remaining H atoms and the central carbon are treated as unique.
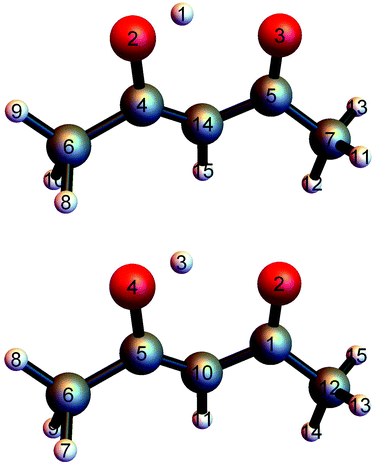 | ||
| Fig. 1 (top) Numbering scheme used for the full-symmetry basis set. (bottom) Numbering scheme used for the 4-(9,11,11,8) basis set. | ||
The second fit we examined was based on fragmentation of AcAc into four fragments and again using a maximum polynomial order of three. The details of this approach have been described previously.18,28,39 The permutational symmetries and atom numbers (using the scheme in the bottom panel of Fig. 1) are as follows: symmetry {1, 1, 1, 1, 1, 1, 1, 1, 1} with atoms {1, 2, 3, 4, 5, 6, 10, 11, 12}; symmetry {3, 1, 1, 1, 1, 1, 1, 1, 1} with atoms {13, 14, 15, 1, 2, 3, 4, 5, 10, 11, 12}; symmetry {3, 1, 1, 1, 1, 1, 1, 1, 1} with atoms {7, 8, 9, 1, 2, 3, 4, 5, 6, 10, 11}; and symmetry {3, 3, 1, 1} with atoms {7, 8, 9, 13, 14, 15, 6, 12}. We will refer to this fragmentation as 4-(9,11,11,8), where the numbers in parentheses represent the number of atoms in each fragment.
Properties of these basis sets are shown in Table 1 along with their performance. At this point we just note that while the fragmented basis has more terms it is faster to evaluate for both the potential and gradient. This may seem counter intuitive; however, it must be recalled that the higher symmetry of the full basis results in more complex polynomials, which in this case ends up in significantly increased computational effort. We go back to this table after we discuss the database of energies and gradients.
| Full symmetry | 4-(9,11,11,8) | |
|---|---|---|
| Monomials | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 616 |
3609 |
| Polynomials | 6207 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
| N(fitted points) | 5454 | 5454 |
| wRMSE (pot) | 49 | 22 |
| wRMSE (grad) | 29 | 16 |
| Time (pot/grad) | 0.95/80.91 | 0.43/26.61 |
3.2 Potential energy surfaces
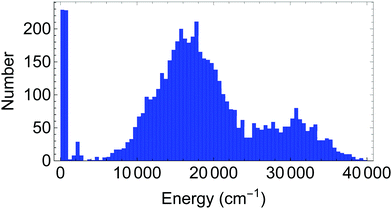
The database for the potential energy surface consists of ab initio energies and gradients at 5454 different molecular configurations, using MP2/VTZ level of theory. Of these configurations, 5000 were provided by the authors of ref. 1, while an additional 454 configurations were generated through grids of points near the transition state to H transfer and near the global minimum, as well as by running ab initio molecular dynamics trajectories at an energy of 4000 cm−1. A histogram of the distribution of energies is provided in Fig. 2. At these configurations, energies and full gradients were obtained and used in the database. Subsequently, an additional 4 points were added as a result of locating some holes using diffusion Monte Carlo studies (see below). For the 4-(9,11,11,8) basis, in order to guarantee that the H-transfer potential is symmetric, the database is expanded by including geometries after the permutation shown in Fig. 3.Fits using these PIP bases were inverse energy weighted and also gradients were weighted by a factor of 1/3 relative to energies. The precision of these PESs are given in Table 1. As seen the fragmented PES fit is more precise. In particular, the barrier to H atom transfer, TS(H) in Table 2 is given more precisely in the fragmented PES than in the full basis PES. This is important for the predictions of splittings.
| Full symmetry | 4-(9,11,11,8) | MP2/aVTZ | |
|---|---|---|---|
| GM | 0 | 0 | 0 |
| TS(T)-I | 176 | 159 | 77 |
| TS(T)-II | 270 | 399 | 468 |
| TS(T)-III | 418 | 541 | 519 |
| TS(H) | 714 | 745 | 763 |
| TS(HT)-I | 703 | 820 | 970 |
| TS(HT)-II | 678 | 864 | 1171 |
3.3 Diffusion Monte Carlo calculations
Diffusion Monte Carlo (DMC) simulation is an approach to compute quantum zero-point energy (ZPE) of a molecule, and if the fixed-node approximation is applied, it can also be used to calculate the energies of certain excited states.40,41 In this work, we calculate the ground-state splitting of the H-transfer motion by calculating the energies of the ground state and the relevant excited state. This is done for H, a single D (the transferring atom) and fully deuterated AcAc.The simple unbiased algorithm,40–42 briefly described next, was applied. An ensemble of random walkers is used to represent the nuclear wavefunction of the molecule. At each step, a random displacement in each degree of freedom is assigned to each walker, and this walker may remain alive (and may give birth to a new walker) or be killed by comparing its potential energy, Ei, with a reference energy, Er. For the ground state, the probability of birth or death is given as:
| Pbirth = exp[−(Ei − Er)Δτ] − 1(Ei < Er) | (4) |
| Pdeath = 1 − exp[−(Ei − Er)Δτ](Ei > Er), | (5) |
After removing all dead walkers, the reference energy is updated using the equation
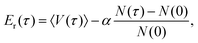 | (6) |
For AcAc, DMC calculations were performed in two coordinate systems: the Cartesian and normal coordinates. Calculations done in normal coordinates are not rigorous because the Hamiltonian is given as
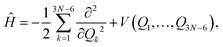 | (7) |
Ten DMC simulations were performed for each state and each coordinate system, and for three deuterated isotopologues (all H, all D, and one D). so the total number of simulations is 10 × 2 × 2 × 3 = 120. In each simulation, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 walkers were equilibrated for 5000 steps, and then were propagated for 50
000 walkers were equilibrated for 5000 steps, and then were propagated for 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps to compute the energy, with a step size of 5.0 a.u. In these simulations, ∼1011 potential energy evaluations are required; clearly these cannot be done without an efficient PES.
000 steps to compute the energy, with a step size of 5.0 a.u. In these simulations, ∼1011 potential energy evaluations are required; clearly these cannot be done without an efficient PES.
4 Results and discussion
4.1 Potential energy surface
Seven low-energy stationary points can be located on the PES: the global minimum (GM), 3 transition states with respect to the torsion of the two methyl rotors (denoted as TS(T)-I, TS(T)-II, and TS(T)-III), the transition state of the H transfer (denoted as TS(H)), and 2 higher-order saddle points with imaginary frequencies in both H-transfer motion and the methyl torsion (denoted as TS(HT)-I and TS(HT)-II). The geometries of GM and TS(H) are shown in Fig. 4, and the coordinates and harmonic frequencies of all the 7 stationary points can be found in the ESI.† The GM has Cs symmetry, while the H-transfer transition state is a C2v structure.The energies of the 7 stationary points from two PESs are shown in Table 2, and compared with MP2/aVTZ values. It can be seen that the 4-(9,11,11,8) PES has better agreement with MP2 than the PES using full symmetry basis, as expected, due to the smaller fitting errors shown in Table 1. The 4-(9,11,11,8) PES also shows better agreement with MP2 harmonic frequencies; the mean absolute errors (MAE) in frequencies are listed in Table 3.
| Full symmetry | 4-(9,11,11,8) | |
|---|---|---|
| GM | 22.2 | 14.4 |
| TS(T)-I | 19.0 | 13.2 |
| TS(T)-II | 28.2 | 18.1 |
| TS(T)-III | 24.0 | 15.7 |
| TS(H) | 31.8 | 20.4 |
| TS(HT)-I | 31.0 | 21.5 |
| TS(HT)-II | 38.2 | 23.5 |
There are two methyl rotors in AcAc; by allowing the permutations of the three H atoms in each rotor, the fragmented 4-(9,11,11,8) can still ensure the 3-fold symmetry of the methyl rotors, as is shown in Fig. 5.
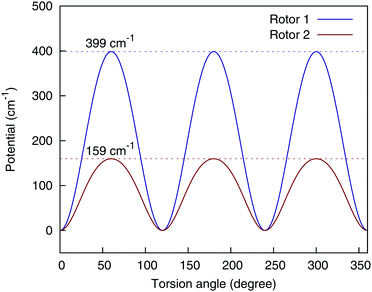 | ||
| Fig. 5 Torsional potential of the two methyl rotors, using the 4-(9,11,11,8) basis. Rotor 1 consists of atom {6,7,8,9}, and rotor 2 consists of atom {12,13,14,15}, using the numbering scheme in the bottom panel of Fig. 1. | ||
From data reported in Table 1 it is possible to estimate the computational cost of a single AcAc energy evaluation performed on a 2.7 GHz Intel Core i7 processor. We found the 4-fragment surface to be faster than the full symmetry one. The result for the 4-fragment surface is about 0.08 ms per energy, while one gradient call is about 55 times more expensive at about 5 ms. This is to be compared with values reported in ref. 1 for an NN PES of the smaller malonaldehyde molecule. In that paper one potential and one gradient evaluation on a faster (3.4 GHz) processor were timed at 4 and 9 ms respectively. This fact hints at substantially increased efficiency of our fragmented PIP PES. However, we cannot rule out that part of the PIP speedup might be due to the way the surface was coded (Fortran 90 for the PIP PES; Python for the NN malonaldehyde PES) rather than the way it was built. Overall, then, our PES is full-dimensional and does describe satisfactorily the region of the stationary points shown.
4.2 Splitting dynamics
All DMC and 1d calculations are done with the fragmented PES, which is both faster and more precise than the full basis PES. Before discussing the tunneling splitting dynamics, we present the ZPEs of three isotopologues of AcAc and the ground-state wavefunction, which are also important properties and closely related to tunneling. The ZPEs of un-deuterated, singly deuterated, and fully deuterated AcAc from DMC calculations in Cartesian coordinates are 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 ± 16 cm−1, 26
637 ± 16 cm−1, 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 ± 7 cm−1, and 21
048 ± 7 cm−1, and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 223 ± 12 cm−1, respectively. The numbers from DMC in normal coordinates are 26
223 ± 12 cm−1, respectively. The numbers from DMC in normal coordinates are 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587 ± 6 cm−1, 26
587 ± 6 cm−1, 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 ± 8 cm−1, and 21
005 ± 8 cm−1, and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177 ± 16 cm−1; the difference between Cartesian and normal coordinates, roughly 45 cm−1, is due to the neglect of vibrational angular momentum terms when using normal coordinates.
177 ± 16 cm−1; the difference between Cartesian and normal coordinates, roughly 45 cm−1, is due to the neglect of vibrational angular momentum terms when using normal coordinates.
Fig. 6 shows the isosurface depiction of the ground vibrational state wavefunction. As seen the “structure” is close to the H-transfer saddle point with an effective symmetry of C2v.
The tunneling splittings of H-atom and two deuterated isotopologues obtained from DMC calculations and a 1d approach (described below) are summarized in Table 4. As seen, the DMC results using Cartesian coordinates and normal coordinates are in good agreement and this indicates a small systematic uncertainty in using these different approaches. It should be noted that statistical uncertainties for each set of DMC calculations are larger than these differences. Also, we stress that these DMC splittings are not expected to be absolutely accurate owing to the MP2/aVTZ underestimation of the H-atom transfer barrier height by roughly 1 kcal mol−1. At the suggestion of a Reviewer we investigated using a CBS extrapolation based on MP2/aVDZ and MP2/aVTZ energies.43 We found a 0.1 kcal mol−1 lowering of the H-transfer barrier height doing this. This is a small change and actually in the direction away from the higher CCSD(T) barrier, so we did not pursue this further.
| All H | One D | All D | |
|---|---|---|---|
| DMC (Cartesian) | 160 | 43 | 37 |
| DMC (normal) | 156 | 40 | 36 |
| 1d-DVR (586 cm−1) | 141 | 57 | 57 |
| 1d-DVR (763 cm−1) | 113 | 41 | 40 |
| 1d-DVR (1119 cm−1) | 74 | 22 | 21 |
In view of this, we investigated the dependency of the splitting as a function of the barrier height, using a simple 1d approach. In brief, a 1d potential, denoted V(Qim), which is the minimum energy path as a function of the imaginary-frequency mode (Qim) of the H-transfer saddle point, was obtained by optimizing all the other coordinates at fixed Qim values except the methyl rotors, which cannot be described using rectilinear normal coordinates. These are held fixed at the saddle point values all the way along the path. Then 1d-DVR calculations were done using the 1d potential to compute the energies of the ground and first excited states, and thus the splitting.
Owing to fixing the methyl rotors the 1d Qim potential has a barrier to H or D transfer of 586 cm−1 relative to the minima at Qmin = ±27.9 a.u. for H transfer and Qmin = ±36.8 a.u. for D transfer. Thus, The 1d Qim barrier is about 160 cm−1 less than the barriers of 745 cm−1 for the fitted surface or 763 cm−1 for the MP2 result. The 1d-DVR splittings for H and D transfer were found to be 141 cm−1 and 57 cm−1, respectively for this barrier height of 586 cm−1.
In order to investigate the dependence of the splitting on the barrier height a simple potential morphing approach was used.44–46 Specifically, the morphed 1d potential is Ṽ(Qim) = f(Qim)V(Qim), where V(Qim) is the potential from the original PES, and f(Qim) is the scaling factor, which is 1.0 at the minima (Qim = Qmin) and equal to a value greater than 1.0 that can bring the barrier to the desired height at Qim = 0.0. The scaling factor we employed is
| f(Qim) = (Rbh − 1)[1 − s(Qim)] + 1, | (8) |
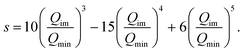 | (9) |
The simple morphing of the 1d Qim potentials would not be expected to work for the PES in full dimensionality. (Indeed the attempt to do so was not satisfactory.) A multi-dimensional approach is probably needed and we present some preliminary thoughts on this in the next section.
To summarize this section, we finally use the 1d-DVR splitting results in Table 4 to estimate the DMC splittings corresponding to the barrier of 1119 cm−1. This is done just using the ratio of the 1d splitting for 763 and 1119 cm−1. From these we estimate 104 cm−1 for H-atom transfer and 23 and 19 cm−1 for the single-D and all-D isotopologues, respectively.
5 Morphing with Gaussian process regression
Morphing is a term that refers to a procedure to change an existing PES with various goals in mind. In the simplest version, a coordinate is scaled by a dimensionless factor to bring “exact” numerical vibrational transition energies into agreement with experiment.44 A more elaborate procedure was applied to an approximate semi-empirical PES describing HCN/HNC isomerization to change the isomerization saddle point location as well as to increase the energy substantially.45 Meuwly and Hutson used the general approach of scaling a coordinate and the PES energy to obtain a highly accurate intermolecular PES for Ne–HF.46In these approaches the scaling was done using analytical expressions. This could be done without difficulty for these triatomics since there are only three internal degrees of freedom. For larger molecules with tens of degrees of freedom a more general, non-parametric approach is probably called for. This is essentially the suggestion made in this short section, motivated by the present PES for AcAc.
As noted both here and previously1 the CCSD(T) barrier height for H-atom transfer is roughly 50% higher than the MP2 one. Thus, even a perfect fit to MP2 energies would produce an inaccurate barrier. Morphing such a PES to produce the correct CCSD(T) barrier obviously would be the goal. However, in principle a scaling factor to do this would be function of all the variables of the PES. In addition, moving the configuration of the saddle point to the “correct” one would require scaling of all the variables, which in the present case are all the Morse variables. We note that an approach based on energy switching to build single and multi-sheeted PESs to account for improved barrier descriptions has been developed by Varandas and co-workers.47
To improve the MP2-based AcAc PES Meuwly and co-workers proposed a transfer learning approach based on approximate local CCSD(T) energies (no gradients) at 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries for the series malonaldehyde, acetoacetaldehyde, and acetylacetone. This appeared to be successful, however 49
000 geometries for the series malonaldehyde, acetoacetaldehyde, and acetylacetone. This appeared to be successful, however 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 full CCSD(T) energies just for AcAc would be prohibitive. Our proposal is to make use of on the order of a thousand CCSD(T) energies strategically done, at least at and in the vicinity of stationary points. Then an efficient ML approach could be applied to develop high dimensional morphing functions. Gaussian process regression appears to be an excellent choice as it is known to perform well on relative small data sets.11,48 We plan to do this in the near future.
000 full CCSD(T) energies just for AcAc would be prohibitive. Our proposal is to make use of on the order of a thousand CCSD(T) energies strategically done, at least at and in the vicinity of stationary points. Then an efficient ML approach could be applied to develop high dimensional morphing functions. Gaussian process regression appears to be an excellent choice as it is known to perform well on relative small data sets.11,48 We plan to do this in the near future.
6 Summary and conclusions
We reported permutationally invariant polynomial (PIP) fits to energies and gradient components for 15-atom acetylacetone. These include standard and fragmented PIP bases. Approximately 500 energies and associated gradient components are obtained from direct-dynamics calculations using MP2/avTZ supplemented by grid calculations spanning an energy range up to roughly 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, and are combined with an existing database1 to form the database for this study. A fragmentation scheme was investigated with respect to efficiency and fit precision. Properties such as stationary points, harmonic frequencies and the barrier to H-atom transfer are reported and compared to direct calculations. Diffusion Monte Carlo (DMC) calculations are used to calculate the ground state wavefunction and zero-point energy of acetylacetone. These together with fixed-node DMC calculations for the first excited-state of H-transfer provide the predicted tunneling splitting due to the barrier separating two equivalent wells. Simpler 1d calculations of this splitting are also reported for varying barrier heights including the CCSD(T) barrier height of 3.2 kcal mol−1. Based on those results the DMC splitting of roughly 160 cm−1 with a statistical uncertainty of about 30 cm−1, calculated using the MP2-based PES, is estimated to diminish to about 100 cm−1 for a barrier of 3.2 kcal mol−1.
000 cm−1, and are combined with an existing database1 to form the database for this study. A fragmentation scheme was investigated with respect to efficiency and fit precision. Properties such as stationary points, harmonic frequencies and the barrier to H-atom transfer are reported and compared to direct calculations. Diffusion Monte Carlo (DMC) calculations are used to calculate the ground state wavefunction and zero-point energy of acetylacetone. These together with fixed-node DMC calculations for the first excited-state of H-transfer provide the predicted tunneling splitting due to the barrier separating two equivalent wells. Simpler 1d calculations of this splitting are also reported for varying barrier heights including the CCSD(T) barrier height of 3.2 kcal mol−1. Based on those results the DMC splitting of roughly 160 cm−1 with a statistical uncertainty of about 30 cm−1, calculated using the MP2-based PES, is estimated to diminish to about 100 cm−1 for a barrier of 3.2 kcal mol−1.
In the abstract and along the text we have adopted the expressions “full basis” or “full symmetry” to refer to the non-fragmented fit. This is to mean that a unique fitting basis extended to the full molecule has been employed with the theoretical possibility for all atoms to permute with same-kind ones. In practice we generated a basis set characterized by partial permutational symmetry to be able to deal with the large dimensionality of the molecule (15 atoms), as detailed in Section 3.1. This is expected since fully permutationally invariant bases have generally been limited to 10-atom systems.
We conclude spending a few words about the possibility to employ fragmentation to reactive or dissociative systems, as already done in one of our previous papers.19 It should be possible to reduce the basis set of a dissociating molecule by choosing fragments that either (a) remain in one of the products or (b) are the simplest fragments that represent the dissociation. In the end, of course, the choice of basis polynomials and the ab initio data set are closely linked. If the data set is chosen, it is easy to examine it to see which Morse variables are most and least important. But if the data set is subsequently extended, say to examine a particular conformer or product, the choice of the most or least important Morse variables must be re-evaluated. Preliminary and encouraging work in this direction is being undertaken.
Finally, the fragmented PES is available upon request to the authors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Silvan Käser and Markus Meuwly for sending their MP2 dataset and for help using it. JMB thanks the Army Research Office, DURIP grant (W911NF-14-1-0471), for funding a computer cluster where most of the calculations were performed.Notes and references
- S. Käser, O. Unke and M. Meuwly, New J. Phys., 2020, 22, 055002 CrossRef.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- J. Cui and R. V. Krems, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 224001 CrossRef.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 6.1–6.25 CrossRef PubMed.
- B. Fu and D. H. Zhang, J. Chem. Theory Comput., 2018, 14, 2289–2303 CrossRef CAS.
- B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS.
- T. T. Nguyen, E. Székely, G. Imbalzano, J. Behler, G. Csányi, M. Ceriotti, A. W. Götz and F. Paesani, J. Chem. Phys., 2018, 148, 241725 CrossRef.
- C. Qu, Q. Yu, B. L. Van Hoozen, J. M. Bowman and R. A. Vargas-Hernández, J. Chem. Theory Comput., 2018, 14, 3381–3396 CrossRef CAS.
- J. Li, K. Song and J. Behler, Phys. Chem. Chem. Phys., 2019, 21, 9672–9682 RSC.
- D. Lu, J. Behler and J. Li, J. Phys. Chem. A, 2020, 124, 5737–5745 CrossRef CAS PubMed.
- K. Shao, J. Chen, Z. Zhao and D. H. Zhang, J. Chem. Phys., 2016, 145, 071101 CrossRef.
- J. Dai and R. V. Krems, J. Chem. Theory Comput., 2020, 16, 1386–1395 CrossRef CAS.
- R. C. Fortenberry, Q. Yu, J. S. Mancini, J. M. Bowman, T. J. Lee, T. D. Crawford, W. F. Klemperer and J. S. Francisco, J. Chem. Phys., 2015, 143, 071102 CrossRef PubMed.
- A. Nandi, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2019, 15, 2826–2835 CrossRef CAS.
- A. Nandi, C. Qu and J. M. Bowman, J. Chem. Phys., 2019, 151, 084306 CrossRef.
- P. L. Houston, R. Conte, C. Qu and J. M. Bowman, J. Chem. Phys., 2020, 153, 024107 CrossRef CAS.
- J. M. Bowman, B. J. Braams, S. Carter, C. Chen, G. Czako, B. Fu, X. Huang, E. Kamarchik, A. R. Sharma, B. C. Shepler, Y. Wang and Z. Xie, J. Phys. Chem. Lett., 2010, 1, 1866–1874 CrossRef CAS.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- J. Mavri and J. Grdadolnik, J. Phys. Chem. A, 2001, 105, 2039–2044 CrossRef CAS.
- B. Fu, Y.-C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9733–9738 CrossRef CAS.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- R. Chen, K. Shao, B. Fu and D. H. Zhang, J. Chem. Phys., 2020, 152, 204307 CrossRef CAS.
- Y. Wang, B. Braams, J. M. Bowman, S. Carter and D. P. Tew, J. Chem. Phys., 2008, 128, 224314 CrossRef PubMed.
- C. Qu and J. M. Bowman, J. Chem. Phys., 2019, 150, 141101 CrossRef.
- R. Conte, P. L. Houston and J. M. Bowman, J. Chem. Phys., 2014, 140, 151101 CrossRef.
- R. Conte, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2015, 11, 1631–1638 CrossRef CAS PubMed.
- C. Qu, R. Conte, P. L. Houston and J. M. Bowman, Phys. Chem. Chem. Phys., 2015, 17, 8172–8181 RSC.
- K. Hinsen and B. Roux, J. Chem. Phys., 1997, 106, 3567–3577 CrossRef CAS.
- K. Hinsen and B. Roux, J. Comput. Chem., 1997, 18, 368–380 CrossRef CAS.
- D. L. Howard, H. G. Kjaergaard, J. Huang and M. Meuwly, J. Phys. Chem. A, 2015, 119, 7980–7990 CrossRef PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef PubMed.
- Z. Jin, B. J. Braams and J. M. Bowman, J. Phys. Chem. A, 2006, 110, 1569–1574 CrossRef CAS PubMed.
- X. Huang, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2005, 122, 044308 CrossRef.
- A. Nandi, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2019, 15, 2826–2835 CrossRef PubMed.
- R. Conte, C. Qu, P. L. Houston and J. M. Bowman, J. Chem. Theory Comput., 2020, 16, 3264–3272 CrossRef PubMed.
- J. B. Anderson, J. Chem. Phys., 1975, 63, 1499–1503 CrossRef.
- J. B. Anderson, J. Chem. Phys., 1976, 65, 4121–4127 CrossRef CAS.
- I. Kosztin, B. Faber and K. Schulten, Am. J. Phys., 1996, 64, 633–644 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, MOLPRO, version 2015.1, a package of ab initio programs, 2015, see http://www.molpro.net Search PubMed.
- J. M. Bowman and B. Gazdy, J. Chem. Phys., 1991, 94, 816–817 CrossRef.
- B. Gazdy and J. M. Bowman, J. Chem. Phys., 1991, 95, 6309–6316 CrossRef CAS.
- M. Meuwly and J. M. Hutson, J. Chem. Phys., 1999, 110, 8338–8347 CrossRef CAS.
- B. R. L. Galvao, S. P. J. Rodrigues and A. J. C. Varandas, J. Chem. Phys., 2008, 129, 044302 CrossRef PubMed.
- A. Kamath, R. A. Vargas-Hernández, R. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04221h |
| This journal is © the Owner Societies 2021 |