Three states global fittings with improved long range: singlet and triplet states of H+3†
Alfredo
Aguado
 a,
Octavio
Roncero
a,
Octavio
Roncero
 b and
Cristina
Sanz-Sanz
b and
Cristina
Sanz-Sanz
 *c
*c
aUnidad Asociada UAM-CSIC, Departamento de Química Física Aplicada, Módulo 14, Universidad Autónoma de Madrid, 28049 Madrid, Spain
bInstituto de Física Fundamental, CSIC, C/Serrano, 123, 28006 Madrid, Spain
cDepartamento de Química Física Aplicada, Módulo 14, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: cristina.sanz@uam.es; Tel: +34 91 497 3922
First published on 9th September 2020
Abstract
Full dimensional analytical fits of the coupled potential energy surfaces for the three lower singlet and triplet adiabatic states of H+3 are developed, providing analytic derivatives and non-adiabatic coupling matrix elements. The fits are highly accurate and include an improved description of the long range interactions, including new terms for the description of the long range in the diatomic fits and the atom–diatom dissociation channels. The fits are based on the DIM formalism including three body terms in Hamiltonian matrix elements, each of them obeying S2 permutational symmetry, where the positive charge is placed in either of the three hydrogen atoms, but the full system obeys S3 permutational symmetry, invariant under all permutations of the nuclei. The ab initio points used in the fitting are obtained from a complete basis set extrapolation, made for all electronic states. Total root mean square errors of the fits are 27 and 12 cm−1, for the singlet and triplet states, respectively. The errors in the channels are lower than 2 cm−1 and 6 cm−1 for the H + H+2 and H+ + H2 channels respectively. The new fits have been used to calculate the rovibrational bound states of the lowest singlet and lowest triplet states showing very good agreement with previous calculations in the literature.
1 Introduction
H+3 plays a central role in astrochemistry, being the most abundant ionic molecule in the Universe and the main protonator, leading to the formation of many hydrides, which constitutes the first step of chemistry in the interstellar medium.1–3In the past two decades much effort has been made experimentally trying to determine the rovibrational bands in the lab including higher and higher energies and vibrational hot bands4 of the ground singlet electronic state. The same amount of effort has been made by theoreticians in improving the description of the ground electronic state,5–8 aiming to reproduce the experimental rovibrational energy levels and bands using local9 and global potential energy surfaces. In addition, many works have been devoted to the description of the ground and excited electronic states of H+3 molecule in the attempt of obtaining a global surface that could be used for spectroscopic calculations as well as reactivity simulations. The description of ground and excited states of H+3 is crucial for reactivity simulations. The ground state dissociates into H2 + H+ while the first excited state dissociates into H+2 + H. Both states cross when H2 intermolecular distance increases, so for vibrational states of H2 with v ≥ 3 the collision simulations would require the excited state dissociating into H+2 + H. In addition, the description of the H+2 + H channel is of particular interest since the formation of H2 by collisions between H+2 and H are very important in the Early Universe, where cosmic grains are not present. Another key point is the description of the long range interactions. Most of the works including the long range interactions have only considered the ground electronic states.8,10
The description of the lowest11–13 and first excited triplet14,15 states have been the main goal of several studies with special attention to the degeneracy at the conical intersection between the two first triplet states.16,17 An extension to the standard single-valued double many-body expansion was developed by the group of Prof. Varandas12,14,16 for the representation of the double-valued potential energy surface ensuring the degeneracy at the intersection line. This same method15,17 has been used recently to analyse the effect of the geometrical phase, at the conical intersection, on the vibrational state calculations of the lowest triplet states showing a change of sign after a full circle in the hyperspherical angle ϕ.
In this work we use a formalism very similar to that developed by Viegas and coworkers,6,7,18 based on the diatomic-in-molecules (DIM) approach to represent the electronic matrix. The 3 × 3 DIM based matrix of singlet and triplet states can be used in the triatomic-in-molecules (TRIM) formalism used for the fitting of larger hydrogen-like molecules as H+4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and H+5.20 The better the fitting of the H+3 electronic states are, the better the description of the channels of H+3 + H and H+3 + H2 would be, crucial for the simulation of astrophysical processes.
19 and H+5.20 The better the fitting of the H+3 electronic states are, the better the description of the channels of H+3 + H and H+3 + H2 would be, crucial for the simulation of astrophysical processes.
In this paper we provide with a multisheeted potential fit of very high accuracy up to energies above the complete dissociation including the long range interactions, for the three lowest singlet and triplet states. Extra terms are added in the description of the long range of the diatomic molecules (H2, H+2) and for the long range of the two triatomic channels (H2 + H+ and H+2 + H). These terms not only add accuracy in the long and medium range regions of the potential surface, but they also help to restrict the area of the surface in which the many body fitting applies, thus allowing higher global accuracy.
In Section II, devoted to the description of the theoretical methodology, are described the ab initio calculations and the fitting procedure. Section III presents an analysis of the potential energy surfaces separated in individual subsections for singlet and triplet states. The definite test that proves the accuracy of the fit near the minimum is the calculation of vibrational states, those are presented and compared with previous calculations in Section IV.
2 Theoretical methodology
2.1 Ab initio calculations
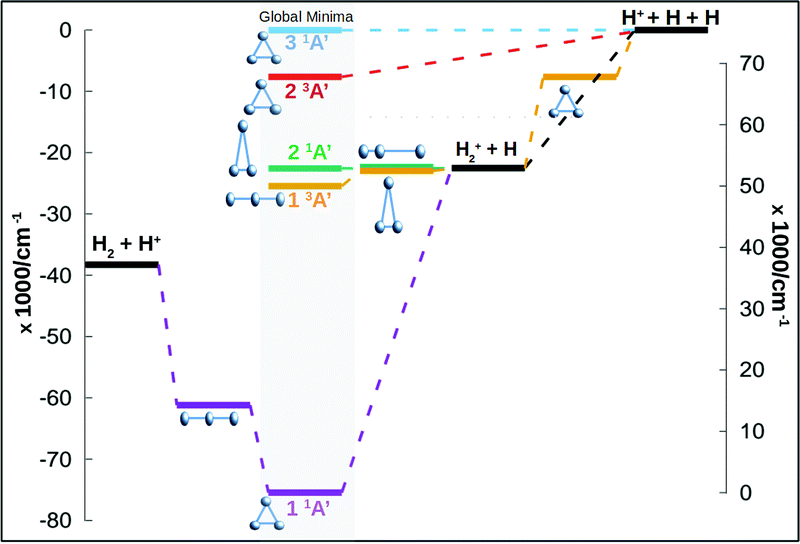
In this work we calculate new energy points for the three first singlet states of Cs symmetry (1A′) and for the three first triplet states (for a global idea of the energetics of the system see Fig. 1). The ab initio calculations use the Dunning augmented correlation-consistent polarised basis sets, aug-cc-pVXZ, where X runs from 2 to 6, to estimate the complete basis set (CBS) energies. The total energies are fitted using an extrapolation scheme based in the results of Dunning and coworkers21–23 and probed and used already in the ground state of this system.24 For the ground state of H+3 a single two point extrapolation scheme, using aug-cc-pV5Z and aug-cc-pV6Z basis set, appeared to give accurate and reliable CBS energies according to the eqn (3) of Velilla and coworkers.24 In this work the extrapolation procedure has been used in singlet excited states as well as the triplet states. A total of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy ab initio points are calculated for the six states using Molpro25 package of programs. The points are calculated using the complete active space self-consistent field/multireferece configuration interaction (CASSCF/MRCI) scheme using Cs symmetry. The active space consists of 2 electrons in 5 orbitals, 4 orbitals of A′ symmetry and 1 orbital of A′′ symmetry. This active space for this system produces results very close to the full CI. In Table 1 are listed some asymptotic and stationary points using the aug-cc-pV6Z basis set and the extrapolation to CBS procedure, both are compared with the most accurate values from literature. The fits presented below are made using the extrapolated values.
000 energy ab initio points are calculated for the six states using Molpro25 package of programs. The points are calculated using the complete active space self-consistent field/multireferece configuration interaction (CASSCF/MRCI) scheme using Cs symmetry. The active space consists of 2 electrons in 5 orbitals, 4 orbitals of A′ symmetry and 1 orbital of A′′ symmetry. This active space for this system produces results very close to the full CI. In Table 1 are listed some asymptotic and stationary points using the aug-cc-pV6Z basis set and the extrapolation to CBS procedure, both are compared with the most accurate values from literature. The fits presented below are made using the extrapolated values.
| System | r e | aV6Z | CBS | Literature |
|---|---|---|---|---|
| H (2S) | — | −0.499999 | −0.500003 | −0.500000 |
| H2 (X1Σ+g) | 1.4 | −1.174360 | −1.744473 | −1.744476 |
| H+2 (X2Σ+g) | 2.0 | −0.602632 | −0.602643 | −0.602635 |
| H+3 (11A′) | 1.65 | −1.343718 | −1.343837 | −1.343836 |
2.2 Three states global fitting procedure
The DIM approximation has been used as an starting point for several hydrogen-like systems, as H+3,18,26 H+4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and H+5.20 In particular for the H+3 system it has been used to fit very accurately the ground state26 and the first three singlet states.10,18,27 The three states fit used in this work is very similar to the one proposed by Viegas and coworkers18 in which extra terms are added inside the DIM matrix at the diabatic level, to improve the accuracy in certain regions of the surfaces, and the adiabatic states are obtained after diagonalisation. Although both works are similar, there are several differences between them. We list here the main differences:
19 and H+5.20 In particular for the H+3 system it has been used to fit very accurately the ground state26 and the first three singlet states.10,18,27 The three states fit used in this work is very similar to the one proposed by Viegas and coworkers18 in which extra terms are added inside the DIM matrix at the diabatic level, to improve the accuracy in certain regions of the surfaces, and the adiabatic states are obtained after diagonalisation. Although both works are similar, there are several differences between them. We list here the main differences:
1. The full system must obey the S3 permutational symmetry. However, each element must obey S2 permutational symmetry since each term of the matrix corresponds to an electron hole in one hydrogen atom. In Viegas and coworkers work they claim that the same three body term must be added into the diagonal elements of the matrix to fulfill this condition, but we show here that the S3 permutation symmetry for the full system is obeyed even when different three body terms are added into the diagonal elements of the matrix.
2. We add several terms into the off-diagonal elements that fulfill the S2 permutational symmetry. The three body terms added into the off-diagonal elements ensure a very accurate adiabatic description of the non adiabatic coupling matrix elements (NACME).
3. The two-body long range term is not enough to ensure an accurate description of the intermediate and long distances regions. A new three-body long range term has been added into the fitting for the improvement of the long range of the singlet states.
The full 3 × 3 electronic matrix describing the diabatic states of H+3 is written as
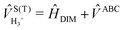 | (1) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DIM is the DIM matrix and
DIM is the DIM matrix and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (3B)ABC is the three-body matrix. The DIM matrix elements for singlet and triple states are very similar, and are written only once in a compact form, denoting in parenthesis the difference corresponding to triplet states, as11,26
(3B)ABC is the three-body matrix. The DIM matrix elements for singlet and triple states are very similar, and are written only once in a compact form, denoting in parenthesis the difference corresponding to triplet states, as11,26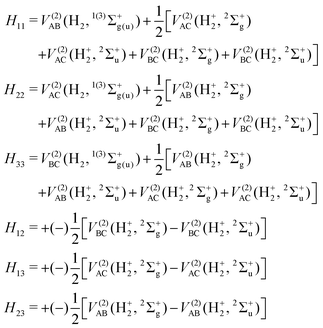 | (2) |
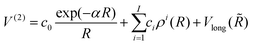 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βR) are Rydberg functions, and the term Vlong is the long range interaction where
exp(−βR) are Rydberg functions, and the term Vlong is the long range interaction where ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) is been modified to eliminate the divergence for R = 0, avoiding the use of switching functions, by
is been modified to eliminate the divergence for R = 0, avoiding the use of switching functions, byR = R + R0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(R − Re)) exp(−(R − Re)) | (4) |
The long range interaction, for the ground and first excited states of H2, is expanded in an asymptotically converging series29
Vlong(R) = −6.499027R−6 − 124.4R−8 − (1135 + 2150)R−10 − 3986R−11 − (+)0.818 R5/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2R) + ⋯ exp(−2R) + ⋯ | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10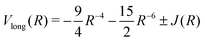 | (6) |
The second term of eqn (1) is the sum of the three body terms and the long range contributions. Each element of the ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ABC matrix is expressed as
ABC matrix is expressed as
| VABCij = V(3)kij + Vlong(R,r,θ) × δij. | (7) |
The long range term in eqn (7), only added to the diagonal terms, depends of the channel considered, H2 + H+ or H+2 + H. This long range term is a function of Jacobi coordinates since these coordinates are better adapted to the interaction between an atom and a diatomic molecule.10 Considering the channel H2(1(3)Σ+g(u)) + H+, the long range interaction includes two contributions
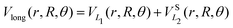 | (8) |
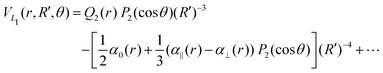 | (9) |
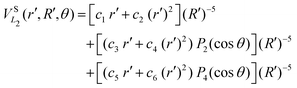 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−r), R′ = R + RLIM exp(−α(R − Re)) (RLIM = 20, α = 1 and Re = 1.4 for the singlets and RLIM = 10, α = 0.5 and Re = 4.0 for the Triplets). R is the distance between the centre-of-mass of the diatomic molecule (H2 or H+2 depending of the channel) and the nucleus (H+ or H depending of the channel), r is the interatomic distance, and θ is the angle between R and r. In the first long range term of eqn (9) the term in R−3 is the anisotropic charge-quadrupole dispersion energy and the term in R−4, which has spherical and anisotropic components, is the charge-induced dipole dispersion energy, α0(r), α‖(r) and α⊥(r) are the average, parallel and perpendicular polarizabilities of H2, respectively, and Q2(r) is the quadrupole moment of H2. The variation of H2 polarizabilities and the quadrupole moment with the r internuclear distance is calculated numerically as the energy derivative using the extrapolated CBS energies. This magnitudes are as well calculated for the terms required in the DIM matrix elements of the triple states.
exp(−r), R′ = R + RLIM exp(−α(R − Re)) (RLIM = 20, α = 1 and Re = 1.4 for the singlets and RLIM = 10, α = 0.5 and Re = 4.0 for the Triplets). R is the distance between the centre-of-mass of the diatomic molecule (H2 or H+2 depending of the channel) and the nucleus (H+ or H depending of the channel), r is the interatomic distance, and θ is the angle between R and r. In the first long range term of eqn (9) the term in R−3 is the anisotropic charge-quadrupole dispersion energy and the term in R−4, which has spherical and anisotropic components, is the charge-induced dipole dispersion energy, α0(r), α‖(r) and α⊥(r) are the average, parallel and perpendicular polarizabilities of H2, respectively, and Q2(r) is the quadrupole moment of H2. The variation of H2 polarizabilities and the quadrupole moment with the r internuclear distance is calculated numerically as the energy derivative using the extrapolated CBS energies. This magnitudes are as well calculated for the terms required in the DIM matrix elements of the triple states.
The Legendre polynomial of fourth order, P4, is added to correct the angle dependency that is introduced by the DIM approximation at intermediate distances. The values of the coefficients are optimised fitting the points of only the ground state of H+3. These optimised coefficients are maintained constant during the three states fitting.
The long range interaction for the channel H+2 + H is the same for the fitting of singlet and triplet states. The term includes two contributions, one describing the interaction between a proton and an H-atom (the two terms of eqn (6)) and a multiple expansion as the one in eqn (9).
In the DIM matrix, each diagonal element i corresponds to a charge in atom i, that imposes a permutation symmetry on the VABCij elements added to the matrix. Thus the relevant three body elements are
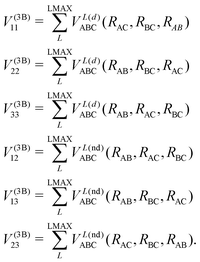 | (11) |
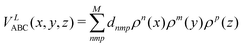 where n + m + p ≤ M, and dnmp = dmnp to ensure the S2 permutational symmetry of the three-body terms, meaning that VLABC(x,y,z) = VLABC(y,x,z).
where n + m + p ≤ M, and dnmp = dmnp to ensure the S2 permutational symmetry of the three-body terms, meaning that VLABC(x,y,z) = VLABC(y,x,z).
All the elements of eqn (11) fulfill the S2 symmetry explained above, one of the main differences between the fitting in this work and the fitting of Viegas and coworkers.18
In this work we generate the analytic full 3 × 3 diabatic electronic matrix, in eqn (1), and the first derivatives as a function of the internuclear distances. The derivatives of the adiabatic potentials and the non-adiabatic couplings among all the states can then be obtained using the Hellmann–Feynman theorem, given in eqn (8) and (9) of our previous work.28 All of them are analytical, depending on the analytical terms of the diabatic matrix and the eigenvectors obtained in the diagonalisation. All these derivatives with respect to the internuclear distances can be transformed to any other set of coordinates applying the chain rule.
3 Results
3.1 Analytical fit of singlet states
The three lowest singlet states of the H+3 molecule present several features that makes the fitting very challenging. The system presents an avoided crossing in the entrance channel due to the swapping of the positive charge between the initial fragments. There are saddle points appearing at symmetric linear geometries and the first and second states are degenerate for D3h geometries. The multisheeted fitting presented in this work can reproduce well the avoided crossings, degeneracies and symmetry of the system, intrinsically included into the DIM matrix.The channels considering the approaching of an atom to a diatomic molecule (H + H+2(X3Σ+g) or H+ + H2(X1Σ+g)) in the three singlet states lie below the complete dissociation (H + H + H+) of the system. In this fit are included energies up to −0.9EH, energy above the global dissociation. Adding points at higher energies ensure that main features of the three states are well described at very short distances. Considering energies only below −0.9EH, the number of points used for the fitting are 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 331, 11
331, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 and 2555 for the first, second and third singlet states respectively. The order of the expansion in products of modified Rydberg functions is M = 10. The points up to 14
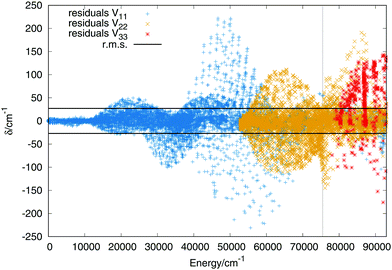
564 and 2555 for the first, second and third singlet states respectively. The order of the expansion in products of modified Rydberg functions is M = 10. The points up to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the global minimum of the ground state have been weighted with a value of 25 to make sure that the vibrational states of the global minimum present errors not higher than 1 cm−1. In Fig. 2 are plotted the residuals as a function of the energy where the zero is placed at the global minimum of the ground state.
000 cm−1 above the global minimum of the ground state have been weighted with a value of 25 to make sure that the vibrational states of the global minimum present errors not higher than 1 cm−1. In Fig. 2 are plotted the residuals as a function of the energy where the zero is placed at the global minimum of the ground state.
The errors are shown in Table 2 in intervals of energy and Jacobi distance R for the present fit and the DIM matrix with the long range terms. For the upper states we only include the total error. The errors in intervals of the Jacobi R coordinate include points in which the Jacobi r coordinate varies within values 1.2 a0 ≤ r ≤ 1.6 a0, giving an idea of the error in the entrance channel H2 + H+. The error in intervals of energy shows a small rms for energies up to the energy of the linear saddle points, about 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, the error increases along with the energy increasing. More detailed characterization of the three sheets would show that the higher errors do not necessary means a poor fit, since it reproduces all the stationary and crossing points correctly. Including in the fit simultaneously the three states add problems such as: larger convergence times and higher number of parameters. Higher degrees means larger number of parameters which would slow down the calculation of the potential energy in the dynamical calculations. The first excited state has an rms error around 24 cm−1, similar to that of the ground state, while the error of the third state is slightly higher, of 48−1. For extra details on the rms in the long range region (H2 + H+) see section A in the ESI.†
000 cm−1, the error increases along with the energy increasing. More detailed characterization of the three sheets would show that the higher errors do not necessary means a poor fit, since it reproduces all the stationary and crossing points correctly. Including in the fit simultaneously the three states add problems such as: larger convergence times and higher number of parameters. Higher degrees means larger number of parameters which would slow down the calculation of the potential energy in the dynamical calculations. The first excited state has an rms error around 24 cm−1, similar to that of the ground state, while the error of the third state is slightly higher, of 48−1. For extra details on the rms in the long range region (H2 + H+) see section A in the ESI.†
| DIM + LR | 3-State fit | |
|---|---|---|
| rms/cm−1 | rms/cm−1 | |
| Distances/a0 | ||
| 3.0 ≤ R ≤ 7.0 | 1955.5 | 13.3 |
| 7.0 ≤ R ≤ 15.0 | 8.9 | 3.9 |
| 15.0 ≤ R ≤ ∞ | 0.07 | 0.07 |
| Energies (11A′) | ||
| Minimum to linearity | 3255.4 | 3.1 |
| Minimum to H2 + H+ | 2446.8 | 17.0 |
| H2 + H+ to H+2 + H | 837.2 | 19.0 |
| H+2 + H to H + H + H+ | 1664.8 | 29.8 |
| Energies (21A′) | ||
| All points | 2856.2 | 23.6 |
| Energies (31A′) | ||
| All points | 646.1 | 47.9 |
The stationary points for the three singlet electronic states are given in Table 3 for ab initio energies, the multi-sheet fitted values and some previous results from the literature.18,36,37 The results published by Röhse and coworkers used an optimised basis set, (16s10p8d)/[10s8p3d], in configuration interaction calculation with explicit linear r12-term (CISD-R12), equivalent to a full CI for a two-electron system. The absolute and relative errors claimed by the authors is of a few micro-hartrees in the relevant regions. The other set of results published by Viegas et al.18 applied the same CASSCF/MRCI procedure followed in this work using MOLPRO package.25 However, they used the correlation consistent cc-pV5Z basis set of Dunning. In their work they added 187 points of very high accuracy, calculated by other groups.38,39 The results published by Wolniewicz37 are one of the most precise calculations for the molecule of H2 which include relativistic and adiabatic corrections.
| r 12 | r 13 | r 23 | CBS | Fit | Literature |
|---|---|---|---|---|---|
| a Röhse et al.36 b Viegas et al.18 c Wolniewicz.37 | |||||
| Ground state (X1A′) | |||||
| Global minimum (D3h) | |||||
| 1.65 | 1.65 | 1.65 | −1.343837 | −1.343839 | −1.343834a |
| Linear saddle points (D∞h) | |||||
| 1.54 | 1.54 | 3.08 | −1.278687 | −1.278756 | −1.278682a |
| H2 + H+ channel | |||||
| 1.40 | ∞ | ∞ | −1.174473 | −1.174473 | −1.174476c |
| Avoided crossing between 1st and 2nd states | |||||
| 2.5 | 10.0 | 10.0 | −1.095046 | −1.095094 | −1.093938c |
| First excited state (21A′) | |||||
| Global minimum | |||||
| 1.992 | 7.5 | 9.492 | −1.103053 | −1.103015 | −1.102894b |
| Saddle points (C2v) | |||||
| 2.0 | 8.16 | 8.16 | −1.103041 | −1.103042 | −1.102882b |
| Saddle points (D∞h) | |||||
| 5.423 | 5.423 | 10.846 | −1.001782 | −1.001743 | −1.001319b |
| H+2 + H channel | |||||
| 2.0 | ∞ | ∞ | −1.102647 | −1.102647 | −1.102625b |
| Second excited state (31A′) | |||||
| Global minimum | |||||
| 11.04 | 11.04 | 11.04 | −1.000197 | −1.000198 | −1.000097b |
| Global dissociation (H + H + H+) | |||||
| ∞ | ∞ | ∞ | −1.000008 | −1.000008 | −1.000003c |
The ground singlet state has a global minimum in a D3h geometry, the extrapolated ab initio value used in this work is 0.66 cm−1 lower that the one from Röhse et al.36 This state presents three equivalent saddle points for linear configurations 14298.77 cm−1 above the minimum, underestimating the best from literature36 by 0.44 cm−1. The dissociation energy into the H2(X2Σ+g) + H+, coinciding with the minimum of the H2 molecules, is 37170.99 cm−1 above the global minimum, overestimating the exact dissociation energy37 in less than 1 cm−1. As it has been already mentioned, the two lowest singlet states present an avoided crossing when the inter-atomic distance of H2 (X2Σ+g) and H+2 (X 3Σ+g) is equal to 2.5 a0, explained by the swapping of charge between both diatomic systems (H2 and H+2). This crossing appears 17432.21 cm−1 above the H2(X2Σ+g) + H+ dissociation channel.
The first excited state presents the global minimum in a linear configuration with two of the atoms in a shorter distance than the equilibrium of H+2 and the third atom far away. This state dissociates into the H+2 (X2Σ+g) + H(2S) channel, 22615.76 cm−1 below the complete dissociation. There is a shallow well, for a linear geometry, just 89.11 cm−1 below the dissociation limit corresponding to H+2 + H. The depth of this well is 32.04 cm−1 deeper than that reported by Viegas et al.18 The three equivalent minima are separated by two types of saddle points, three of C2v symmetry only few wavenumbers above the minimum and three of D∞h 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the minimum.
000 cm−1 above the minimum.
The first and second excited states cross for all D3h configurations of H+3. The minimum of the third single state lies along the intersection line with a depth of 41.48 cm−1 with respect to global dissociation (H + H + H+).
In Fig. 3 are plotted two-dimensional cuts of the potential energy surfaces using stereographic projections of hyperspherical coordinates.40 The zero of energy is placed in the complete dissociation (H + H + H+). The left/middle/right panels correspond to ρ = 2.18, 6.6 and 10.2 a0, respectively. The minimum of the well of the ground electronic state is at ρ = 2.18 a0, and the avoided crossing between the first two singlet states, appearing for Jacobi R distances larger than 7–8 a0 (see Fig. 4) is clearly apparent at ρ = 10.2 a0. The ground state and the first excited state present an avoided crossing (Fig. 4) at configurations where two H atoms have an internuclear distance of 2.5 a0 and the third H atom is far away. To better understand the stereographic projections of Fig. 3, the D3h, C2v and D∞h geometries are included in the figure using balls and sticks representation. In the first column (ρ = 2.18 a0) the global minimum of the ground electronic state, with a D3h geometry appears in the centre of the plot. For this configuration the upper states are much higher in energy and present an avoided crossing. The avoided crossing between the two excited states appears for all the D3h configurations, as it has been mentioned before (see Fig. 3). For longer values of hyperradius (second and third columns) the two excited surfaces approach to the ground state, and within each other. In Fig. 4 are represented several one-dimensional cuts of the ground and first excited singlet states showing the approaching of the surfaces using Jacobi coordinates. In this figure are plotted several values of R Jacobi coordinate showing that the avoided crossing appears for R > 7 a0.
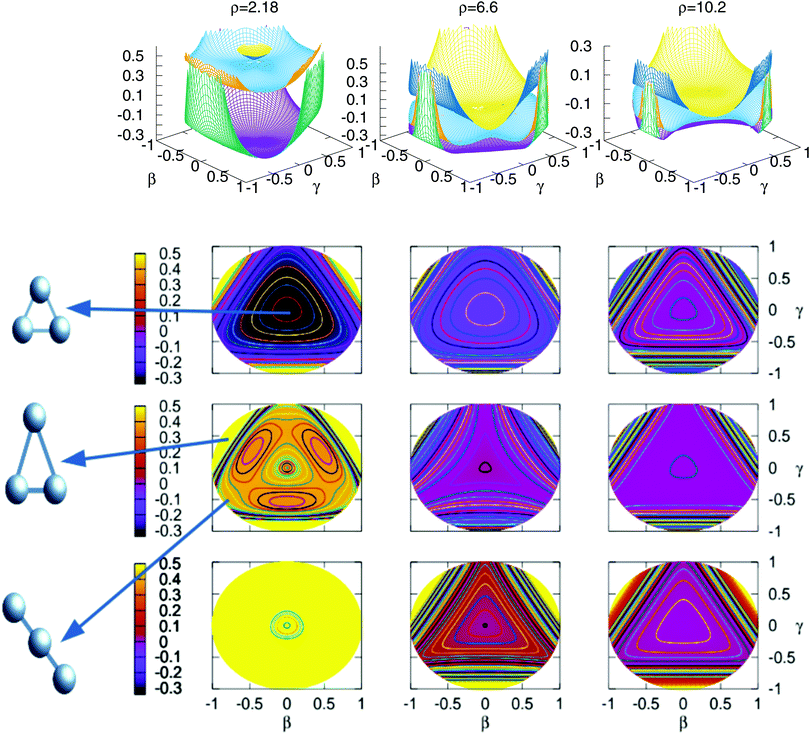 | ||
Fig. 3 Stereographic projections (β = sin(θ)cos(φ − 30) and γ = sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(φ − 30)) of hyperspherical coordinates40 of the potential energy of the three singlet states for three constant values of ρ. The top/middle/bottom contourplots correspond to the 11A′/21A′/31A′ states, respectively. sin(φ − 30)) of hyperspherical coordinates40 of the potential energy of the three singlet states for three constant values of ρ. The top/middle/bottom contourplots correspond to the 11A′/21A′/31A′ states, respectively. | ||
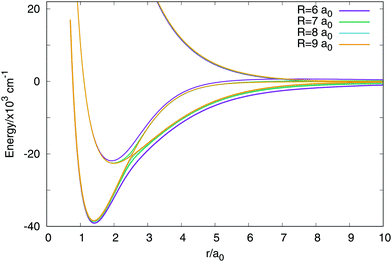 | ||
| Fig. 4 Avoided crossing between the ground and first excited electronic singlet states. The representation uses the two distances Jacobi coordinates with a fixed value of the angle in 90 degrees. | ||
The full dimensional NACMEs, obtained analytically using the Hellmann–Feynman theorem,28 are specially important at conical intersections (where they diverge) and at avoided crossings. The potential energy curves and NACMEs are plotted in Fig. 5 together with the ab initio points as a function of the hyperspherical angle φ at a fixed hyperradius ρ = 10 Bohr for three different values of hyperspherical angle θ, specified in every plot. The transformation between bond coordinates and hyperspherical coordinates assumed in this work is the one given by Billing and coworkers,40 and the derivatives and NACMEs in any of the hyperspherical coordinates can be obtained using the chain rule.
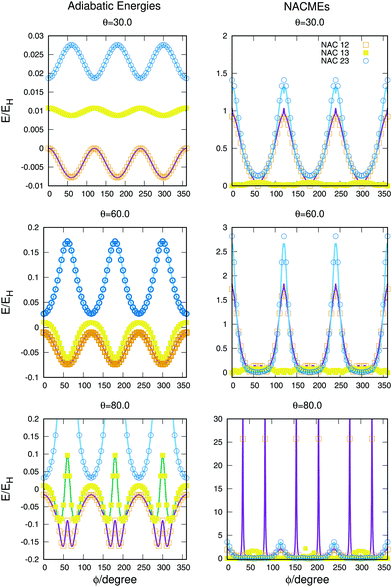 | ||
| Fig. 5 Potential energy curves (left column) and NACMEs (right column) of the three singlet states as a function of the hyperspherical40 angle coordinate ϕ for a fixed value of ρ = 10 a.u. The value of θ angle is specified in each plot. Points correspond to ab initio points and the line is the analytical fit and/or NACME. The zero of energy corresponds to H + H + H+. | ||
The zero of energies is displaced so that the ground state is zero for θ = 30o and φ = 0o. The agreement between the ab initio points atnd the fitting is very good, even when energies above −0.9EH (0.1EH in the figure) are not included in the fitting. The right column representing the NACMEs shows as well a good agreement. The position and magnitude agree well and the main disagreements, in the NACMEs between the two upper states, represented by blue empty circles and blue lines, occur at the cusps of the NACMEs where the analytical functions slightly underestimate the value. These disagreements could be due to several things, the NACMEs calculated with MOLPRO package are obtained by means of finite differences method, and it has problems at the divergence occurring at conical intersections. On the other side the fitting procedure, although is expected to be correct at these points thanks to the DIM approximations, is as well very sensitive because the surfaces present changes that can be challenging for the optimisation of the three body terms.
3.2 Analytical fit of triplet states
The fit of the triplet states includes ab initio points up to values above the dissociation energy, −0.98EH. Higher energies are not included, as in the case of the singlet states, because all stationary points lie below the energy chosen, in addition the upper sheet is repulsive what increases the error of the lower sheets when higher energies are considered. The order of the expansion of the three body terms (eqn (11)) is M = 6. In Fig. 6 are plotted the residuals as a function of the energy, where the zero of energies is kept at the minimum of the ground (singlet) electronic state. The total rms deviation (12 cm−1) is showed using the horizontal black lines and the global dissociation with the vertical line. The errors obtained for the lowest triplet state remain lower than 50 cm−1 and the errors for the first triplet state increase up to maximum errors of 200 cm−1 for energies above the complete dissociation. For a detailed description of the long range interaction in the lowest Triplet state see section B in the ESI.†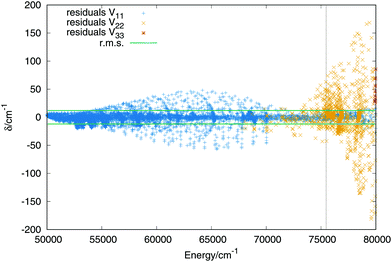 | ||
| Fig. 6 Residuals (algebraic deviations) of the three triplet PESs vs. the energy (in cm−1). The black dashed vertical line specifies the energy of the complete dissociation (H + H + H+). | ||
In Table 4 we present the rms as a function of the Jacobi coordinate R for the lowest sheet, to show the error in the entrance channel (H+2 + H). The rms for the lowest triplet state remains lower than 8 cm−1 for all intervals considered and lower than 0.5 cm−1 for the long-range region. Only the two lowest sheets are included in the table since all the points of the third state lie out of the maximum energy considered in the fit. Since the two upper singlet state dissociate directly into the complete dissociation, no rms for intervals is included for the second triplet state, the rms of the all points included in the fit is 25 cm−1.
| DIM + LR | 3-State fit | |
|---|---|---|
| rms/cm−1 | rms/cm−1 | |
| Distances/a0 | ||
| 3.0 ≤ R ≤ 7.0 | 2893.2 | 3.5 |
| 8.0 ≤ R ≤ 15.0 | 4.4 | 6.7 |
| 15.0 ≤ R ≤ ∞ | 0.02 | 0.4 |
| Energies (13A′) | ||
| Minimum to H+2 + H | 3563.0 | 4.7 |
| H+2 + H to H + H + H+ | 3201.9 | 7.4 |
| All points | 3445.5 | 7.1 |
| Energies (23A′) | ||
| All points | 459.5 | 25.1 |
A list of the stationary points of the two lowest triplet states is given in Table 5. The third triplet states presents no minima or stationary points for energies below the global dissociation. In the table are included the CBS extrapolated values, the multi-sheet fit values of this work and the ones obtained from literature.16 The results published by Varandas and coworkers for the two lowest triplet states are based on the single-valued double many-body expansion (DMBE) theory, applied to a grid of points calculated with MOLPRO package using the cc-pV5Z basis set. The lowest triplet state presents three equivalent minima at D∞h configurations 52528.18 cm−1 above the minimum of the ground singlet state (2957.2 cm−1 below the dissociation channel H+2 + H), 10 cm−1 lower than the one from literature. The saddle points between these minima, of C2v symmetry, appear 2550.3 cm−1 above the linear minimum, 64 cm−1 lower than the one provided by Varandas et al. The dissociation into the H+2 + H is placed 2957 cm−1 above the minimum, only 2 cm−1 lower than the one from literature.
| r 12 | r 13 | r 23 | CBS | Fit | Literaturea |
|---|---|---|---|---|---|
| a Varandas et al.16 | |||||
| First triplet state (13A′) | |||||
| Global minimum (D∞h) | |||||
| 2.456 | 2.456 | 4.912 | −1.116121 | −1.116103 | −1.116061 |
| Saddle points (C2v) | |||||
| 1.99 | 5.286 | 5.286 | −1.104501 | −1.104570 | −1.104234 |
| H+2 + H channel | |||||
| 2.000 | ∞ | ∞ | −1.102647 | −1.102647 | −1.102598 |
| Avoided crossing between 1st and 2nd states | |||||
| 3.654 | 3.654 | 3.654 | −1.034843 | −1.034842 | −1.034590 |
| First triplet excited State (23A′) | |||||
| Global minimum (D3h) | |||||
| 3.654 | 3.654 | 3.654 | −1.034843 | −1.034842 | −1.034590 |
| Global dissociation (H + H + H+) | |||||
| ∞ | ∞ | ∞ | −1.000008 | −1.000008 | — |
The minimum of the upper sheet, of D3h symmetry, is produced by the conical intersection between the first and second triplet states. Both states approach to each other creating a conical intersection for all equilateral triangle configurations. The global minimum of the second triplet state appears in this type of configuration, 14881 cm−1 above the H+2 + H channel. This state dissociates directly into the global dissociation channel (H + H + H+), the channel is 7645.40 cm−1 above the minimum. A global idea of the energetic of the full system, including singlet and triplet states, can be seen in Fig. 1.
The stationary points of Table 5 are shown graphically in Fig. 9 using stereographic projections of hyperspherical coordinates. The zero of energies is placed in the global dissociation (H + H + H+). The top row presents a three dimensional representation of the three states, which are plotted below using the two-dimensional stereographic representations. The three columns represent three cuts of the hyperradius ρ of the potential energy surface. The first column, ρ = 4.53 a.u. corresponds to the minimum of the lowest triplet state, appearing in this plots in the vertices of the imaginary triangle (see Section 3.1). The saddle points joining the minima appear in the sides of the triangle. The value of ρ in the minimum of the second triplet state is 4.80 a.u., no apparent differences show with respect to the value of ρ for the minimum of the lowest triplet state, this is the reason why not a separate plot is added. The minimum of the second sheet can be easily seen in the three dimensional plots, where the two opposite cones form the conical intersection producing the global minimum of the second triplet state. In the two dimensional representations this minimum appears in the middle of the plot in the second row. The other values of ρ included in the figure show global features of the three states as the approaching of the surfaces with the increasing of the ρ value. However, there are no points in the third triplet state for any value of ρ that lie below the global dissociation. The first and second triplets form the double cone creating the conical intersection that can be seen for all values of ρ.
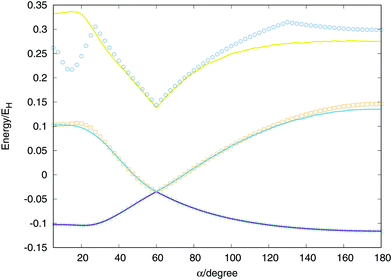
Considering two equivalent H–H distances, we have performed an optimisation of these distances for angles between (α) two vectors running from 0 to 180 degrees at CI level using the aug-cc-pVTZ basis set of Dunning.41 With the optimised values we calculate the extrapolated values and called the global fit, the results are plotted in Fig. 7. The global minimum of the lowest triplet state appears for a value of α = 180° (D∞h), the conical intersection and minimum of the second triplet state at α = 60° (D3h) and the saddle point of the lowest singlet state at α = 21.5° (C2v). All features are well described by the global fit and the discrepancies obtained for the second and triplet states are due to the maximum energy value considered for the points included in the fit, −0.98EH (0.02EH in the figure, since the zero of energy is placed in the global dissociation). Nevertheless, the fit provides very good agreement for much higher energies, including the third triplet state which no ab initio points have been included in the fit.
The potential curves and NACMEs as a function of the hyperspherical angle ϕ, for a fixed value of the hyperradius ρ = 10 Bohr and three values of the hyperspherical angle θ are shown in Fig. 8. The value of ρ was chosen so that closeness of the surfaces would show larger values of NACMEs. For values of ρ near the conical intersection only the NACMEs in the intersection was appreciable, due to degeneracy lifting stated by Jahn–Teller theorem.42 The agreement of the fit in the potential energy curves and the NACMEs is very good and only some disagreements are obtained for the NACMEs between the second and third states for θ = 70° for the values ϕ = 60,180 and 240°. The disagreements are a consequence of the error in the fit due to the non included points for higher energies. The three peaks appearing in the ab initio NACME points, not reproduced by the analytical fit, are between values of both states higher than 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the global dissociation.
000 cm−1 above the global dissociation.
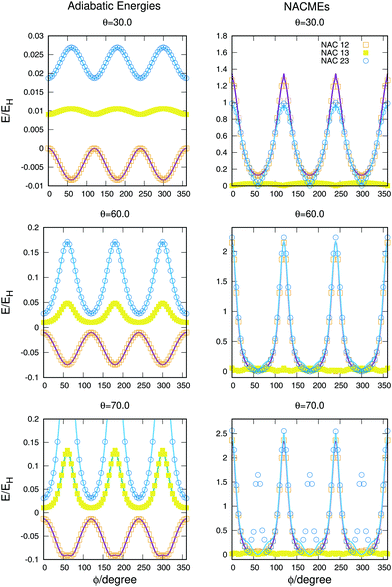 | ||
| Fig. 8 Potential energy curves (left column) and NACMEs (right column) of the three triplet states as a function of the hyperspherical40 angle coordinate ϕ for a fixed value of ρ = 10 a.u. The value of θ angle is specified in each plot. Points correspond to ab initio points and the line is the analytical fit and/or NACME. | ||
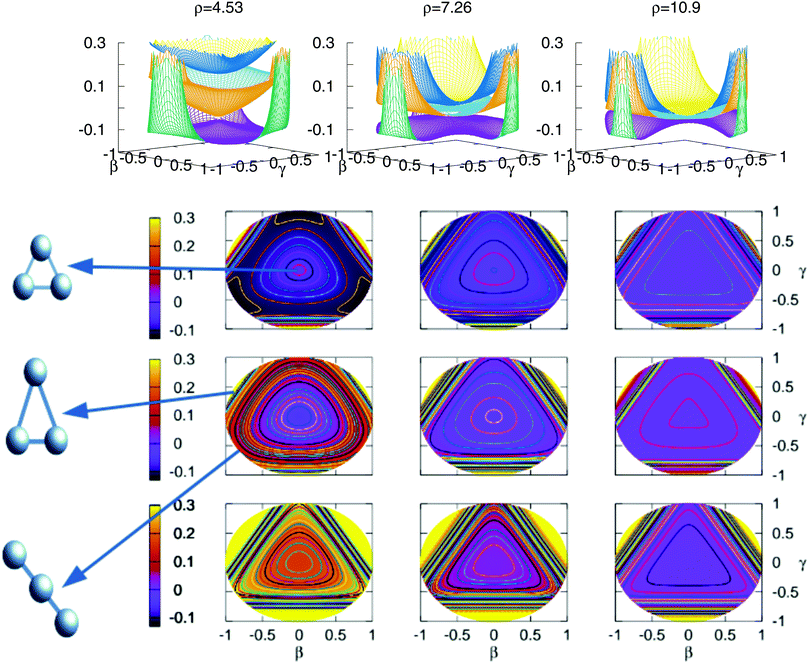 | ||
Fig. 9 Stereographic projections (β = sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos (φ − 30) and γ = sin(θ) cos (φ − 30) and γ = sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(φ − 30)) of hyperspherical coordinates40 of the potential energy of the three triple states for three constant values of ρ. In the top row there are the three-dimensional curves of the three states. The top/middle/bottom contourplots correspond to the 13A′/23A′/3 3A′ states, respectively. sin(φ − 30)) of hyperspherical coordinates40 of the potential energy of the three triple states for three constant values of ρ. In the top row there are the three-dimensional curves of the three states. The top/middle/bottom contourplots correspond to the 13A′/23A′/3 3A′ states, respectively. | ||
3.3 Rovibrational analysis
Rovibrational bound states on the adiabatic PES are calculated using hyperspherical coordinates with the same methods previously described and used for the singlet24,26 and triplet states.11 For the details with respect to the hyperspherical coordinates, symmetry and Hamiltonian/wavefunction representations we refer the reader to these publications.| (v1,vl2) | Γ | This work | Exp.43 | MSGPES18 | GPES7 |
|---|---|---|---|---|---|
| (1,00) | A 1′ | 3180.96 | 3179.32 | 3178.29 | |
| (0,20) | 4777.10 | 4777.87 | 4778.15 | ||
| (2,00) | 6265.03 | 6265.09 | 6262.13 | ||
| (0,33) | 7283.32 | 7286.25 | 7285.56 | ||
| (1,20) | 7770.10 | 7770.79 | 7769.23 | ||
| (0,40) | 8999.52 | 9002.03 | 9001.57 | ||
| (3,00) | 9252.86 | 9256.88 | 9251.91 | ||
| (1,33) | 9967.41 | 9970.31 | 9968.94 | ||
| (2,20) | 10593.04 | 10596.63 | 10593.19 | ||
| (0,53) | 10920.72 | 10922.82 | 10923.36 | ||
| (1,40) | 11813.80 | 11816.95 | 11814.52 | ||
| (4,00) | 12144.28 | 12146.46 | |||
| (0,60) | 12377.37 | 12382.15 | |||
| (2,33) | 12587.53 | 12590.53 | |||
| (3,20) | 13286.84 | 13288.91 | |||
| (1,53) | 13401.70 | 13405.25 | |||
| (0,73) | 13719.95 | 13725.43 | |||
| (2,40) | 14195.50 | 14198.51 | |||
| (1,60) | 14663.36 | 14666.18 | |||
| (0,80) | 14904.23 | 14909.87 | |||
| (4,00) | 14934.84 | 14940.15 | |||
| (0,66) | 15075.84 | 15080.18 | |||
| (3,33) | 15163.65 | 15168.30 | |||
| (0,33) | A 2′ | 7491.26 | 7492.91 | 7493.86 | 7492.78 |
| (1,33) | 10209.79 | 10212.20 | 10210.33 | ||
| (0,53) | 11527.20 | 11530.21 | 11529.24 | ||
| (2,33) | 12831.24 | 12832.17 | |||
| (1,53) | 13755.51 | 13756.61 | |||
| (0,73) | 14564.54 | 14566.28 | |||
| (0,66) | 15188.77 | 15190.71 | |||
| (0,11) | E′ | 2520.88 | 2521.41 | 2520.84 | 2521.30 |
| (0,22) | 4996.77 | 4998.05 | 4997.43 | 4997.89 | |
| (1,11) | 5555.78 | 5554.06 | 5555.45 | 5554.20 | |
| (0,31) | 7004.33 | 7006.18 | 7005.97 | ||
| (1,22) | 7870.39 | 7871.61 | 7870.23 | ||
| (2,11) | 8489.09 | 8491.08 | 8488.01 | ||
| (0,42) | 9110.73 | 9113.54 | 9113.04 | ||
| (1,31) | 9651.87 | 9654.96 | 9653.70 | ||
| (0,44) | 9996.90 | 9999.10 | 9997.18 | ||
| (2,22) | 10644.76 | 10645.38 | 10648.17 | 10645.31 | |
| (0,51) | 10859.73 | 10862.90 | 10862.46 | 10862.75 | |
| (3,11) | 11322.17 | 11323.10 | 11327.69 | 11323.12 | |
| (0,55) | 11656.08 | 11658.40 | 11659.89 | 11658.31 | |
| (1,42) | 12077.64 | 12081.86 | 12079.40 | ||
| (2,31) | 12300.93 | 12303.36 | 12303.33 | ||
| (0,62) | 12473.80 | 12477.38 | 12477.39 | ||
| (1,44) | 12696.24 | 12697.40 | |||
| (3,22) | 13315.70 | 13318.19 | |||
| (1,51) | 13392.26 | 13395.2 | |||
| (0,64) | 13589.82 | 13592.25 | |||
| (0,71) | 13696.81 | 13702.37 | 13702.58 | ||
| (4,11) | 14051.62 | 14055.01 | |||
| (1,55) | 14215.51 | 14218.02 | |||
| (2,42) | 14475.26 | 14478.22 | |||
| (1,62) | 14888.78 | 14890.47 | |||
| (3,31) | 14896.84 | 14901.82 | |||
| (0,82) | 15117.62 | 15122.80 | 15122.64 | ||
In Table 7 are presented the rovibrational states of the first triplet state (a 3A′) for the present fit and the latest found in literature.17 The potential representation used by Alijah et al. is made using the diabatization procedure proposed by Longuet–Higgins44 to transform two adiabatic potential energy surfaces to a 2 × 2 diabatic matrix. In their paper they present the eigenstates considering either 1- or 2-states for the calculations. Because in our calculations we use the diagonalised electronic states we compare our results with the one-state calculation given in their work.17 The quantum numbers used for the assignment of the vibrational levels use the same procedure that the one proposed by Watson.45 In hyperspherical coordinates, v1 and v3 corresponds to symmetric and antisymmetric stretching vibrations, and vl2 corresponds to the bending vibration, where l is the associated vibrational angular momentum. Considering all the above the agreement between both calculations is very good with errors lower than 4 cm−1 for the states below the dissociation channel (H+2 + H, 2957.20 cm−1 above the minimum), discrepancy increases for higher vibrational states. These disagreements are attributed to the description of the long-range region of the potential energy surface. In Table 4 where the rms of the fit was presented for for several ranges of distances (i.e. long-range) and energies, the rms remains lower than 8 cm−1 for all points in the lowest sheet. The effect of the 2-state calculation, studied by Alijah and coworkers, never lead to differences with the 1-state calculation larger than 2–3 cm−1. The comparison between some previous calculations of the same authors16 using the same potential energy surface for the lowest sheet, shows that the geometrical phase does not produce changes in the eigenvalues larger than 3–4 cm−1, except in some of the higher vibrational states, very near the conical intersection. For all this, we conclude that the difference between the present work and the results of Alijah et al. might arise from the analytical fit and particularly from the long-range description, of very high accuracy in the present work.
| (v1,vl2,v3) | i | A 1′ | i | A 2′ | i | E′ |
A
1′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
i |
A
2′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
i |
E′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Bound states computed with a two-surface potential calculated by Alijah et al.17 | |||||||||||
| (0,00,0) | 0 | 0.0 | 0 | 0.0 | 0.0 | 0 | 0.0 | ||||
| (0,00,1) | 0 | 738.93 | 1 | 736.93 | 0 | 738.49 | 1 | 738.49 | |||
| (1,00,0) | 1 | 974.21 | 2 | 974.21 | 975.05 | 2 | 975.06 | ||||
| (0,20,0) | 2 | 1269.41 | 3 | 1269.48 | 1273.73 | 3 | 1273.79 | ||||
| (1,00,1) | 1 | 1467.06 | 4 | 1466.96 | 1 | 1474.57 | 4 | 1474.4 | |||
| (0,00,2) | 3 | 1566.29 | 5 | 1566.42 | 1573.70 | 5 | 1573.8 | ||||
| (0,20,1) | 2 | 1720.43 | 6 | 1718.21 | 2 | 1730.39 | 6 | 1728.4 | |||
| (2,00,0) | 4 | 1912.83 | 7 | 1913.33 | 1922.55 | 7 | 1923.1 | ||||
| (1,20,0) | 5 | 1922.22 | 8 | 1934.50 | 1940.34 | 3 | 8 | 1951.0 | |||
| … | 3 | 1956.74 | 9 | 1954.26 | 4 | 1972.87 | 9 | 1970.7 | |||
| … | 6 | 2145.24 | 10 | 2111.48 | 2158.72 | 10 | 2136.9 | ||||
| … | 7 | 2165.66 | 11 | 2152.99 | 2188.49 | 11 | 2166.4 | ||||
| … | 4 | 2183.87 | 12 | 2238.51 | 5 | 2205.01 | 12 | 2251.0 | |||
| … | 5 | 2259.96 | 13 | 2246.28 | 6 | 2271.13 | 13 | 2259.3 | |||
| … | 8 | 2313.36 | 14 | 2337.17 | 2308.61 | 14 | 2334.9 | ||||
| … | 9 | 2330.54 | 15 | 2344.14 | 2340.09 | 15 | 2357.0 | ||||
4 Conclusions
In the present work we have obtained an analytical representation of the potential energy surfaces, derivatives and non-adiabatic coupling matrix elements of the three lowest singlet and triplet states of the system of H+3. New terms have been included to improve the long range interaction in the diatomic systems, and both dissociation channels, H+ + H2 and H + H+2. Those terms are particularly important to properly describe the collision dynamics at low and ultracold temperatures. In addition, we have shown that the present fits also describe very accurately the bound rovibrational states of H+3, in singlet and triplet states. The NACME obtained in the present work are also very accurate and reliable. For all these reasons we consider these fits as the most accurate nowadays available in the literature to describe the non-adiabatic and low temperature collision dynamics for this system, of particular relevance in astrochemistry.Conflicts of interest
There are no conflicts to declare.References
- T. Oka, Philos. Trans. R. Soc., A, 2012, 113, 8738–8761 Search PubMed.
- T. Oka, Chem. Rev., 2013, 370, 4991–5000 Search PubMed.
- J. Pelley, ACS Cent. Sci., 2019, 5, 741–744 CAS.
- B. J. McCall, Philos. Trans. R. Soc. London, Ser. A, 2000, 358, 2385–2401 CrossRef CAS.
- M. Pavanello, W.-C. Tung, F. Leonarski and L. Adamowicz, J. Chem. Phys., 2009, 130, 074105 CrossRef.
- O. L. Polyansky, A. Alijah, N. F. Zobov, I. I. Mizus, R. I. Ovsyannikov, J. Tennyson, L. Lodi, T. Szidarovszky and A. G. Császár, Philos. Trans. R. Soc., A, 2012, 370, 5014–5027 CrossRef CAS.
- M. Pavanello, L. Adamowicz, A. Alijah, N. F. Zobov, I. I. Mizus, O. L. Polyansky, J. Tennyson, T. Szidarovszky and A. G. Császár, J. Chem. Phys., 2012, 136, 184303 CrossRef.
- I. I. Mizus, O. L. Polyansky, L. K. McKemmish, J. Tennyson, A. Alijah and N. F. Zobov, Mol. Phys., 2019, 117, 1663–1672 CrossRef CAS.
- S. M. Bijit Mukherjee and S. Adhikari, J. Phys.: Conf. Ser., 2016, 7, 012050 CrossRef.
- L. Velilla, B. Lepetit, A. Aguado, J. A. Beswick and M. Paniagua, J. Chem. Phys., 2008, 129, 084307 CrossRef.
- C. Sanz-Sanz, O. Roncero, C. Tablero, A. Aguado and M. Paniagua, J. Chem. Phys., 2001, 114, 2182 CrossRef.
- M. Cernei, A. Alijah and A. J. C. Varandas, J. Chem. Phys., 2003, 118, 2637 CrossRef CAS.
- T. M. Ferreira, A. Alijah and A. J. C. Varandas, J. Chem. Phys., 2008, 128, 054301 CrossRef.
- L. P. Viegas, M. Cernei, A. Alijah and A. J. C. Varandas, J. Chem. Phys., 2004, 120, 253–259 CrossRef CAS.
- L. P. Viegas, A. Alijah and A. J. C. Varandas, J. Phys. Chem. A, 2005, 109, 3307–3310 CrossRef CAS.
- A. J. Varandas, A. Alijah and M. Cernei, Chem. Phys., 2005, 308, 285–295 CrossRef CAS.
- A. Alijah and V. Kokoouline, Chem. Phys., 2015, 460, 43 CrossRef CAS.
- L. P. Viegas, A. Alijah and A. J. C. Varandas, J. Chem. Phys., 2007, 126, 074309 CrossRef.
- C. Sanz-Sanz, O. Roncero, M. Paniagua and A. Aguado, J. Chem. Phys., 2013, 139, 184302 CrossRef.
- A. Aguado, P. Barragán, R. Prosmiti, G. Delgado-Barrio, P. Villarreal and O. Roncero, J. Chem. Phys., 2010, 133, 024306 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 99, 1914 CrossRef CAS.
- K. A. Peterson, R. A. Kendall and T. H. Dunning, J. Chem. Phys., 1993, 99, 1930–1944 CrossRef CAS.
- K. A. Peterson, R. A. Kendall and T. H. Dunning, Jr., J. Chem. Phys., 1993, 99, 9790 CrossRef CAS.
- L. Velilla, M. Paniagua and A. Aguado, Int. J. Quantum Chem., 2010, 111, 387–399 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schützet al., MOLPRO, version 2015.1, a package of ab initio programs, 2015, see http://www.molpro.net Search PubMed.
- A. Aguado, O. Roncero, C. Tablero, C. Sanz-Sanz and M. Paniagua, J. Chem. Phys., 2000, 112, 1240 CrossRef CAS.
- S. Ghosh, S. Mukherjee, B. Mukherjee, S. Mandal, R. Sharma, P. Chaudhury and S. Adhikari, J. Chem. Phys., 2017, 147, 074105 CrossRef.
- C. Sanz-Sanz, A. Aguado, O. Roncero and F. Naumkin, J. Chem. Phys., 2015, 139, 184302 CrossRef.
- J. O. Hirschfelder and W. J. Meath, The Nature of Intermolecular Forces, Wiley, Chichester, 1967, vol. 12 Search PubMed.
- C. A. Coulson, Proc. - R. Soc. Edinburgh, Sect. A: Math. Phys. Sci., 1941, 161, 20 Search PubMed.
- P. Gniewek and B. Jeziorski, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 022506 CrossRef.
- P. Gniewek and B. Jeziorski, Mol. Phys., 2016, 14, 1176 CrossRef.
- T. Holstein, J. Phys. Chem., 1952, 56, 832 CrossRef CAS.
- C. Herring, Rev. Mod. Phys., 1962, 34, 631 CrossRef CAS.
- A. Aguado, C. Tablero and M. Paniagua, Comput. Phys. Commun., 1998, 108, 259 CrossRef CAS.
- R. Röhse, W. Kutzelnigg, R. Jaquet and W. Klopper, J. Chem. Phys., 1994, 101, 2231–2243 CrossRef.
- L. Wolniewicz, J. Chem. Phys., 1993, 99, 1851–1868 CrossRef CAS.
- W. Cencek, J. Rychlewski, R. Jaquet and W. Kutzelnigg, J. Chem. Phys., 1998, 108, 2831 CrossRef CAS.
- O. L. Polyansky, R. Prosmiti, W. Klopper and J. Tennyson, Mol. Phys., 2000, 98, 261–273 CrossRef CAS.
- G. D. Billing and J. T. Muckerman, J. Chem. Phys., 1989, 91, 6830–6838 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- H. A. Jahn, E. Teller and F. G. Donnan, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CAS.
- T. Furtenbacher, T. Szidarovsky, E. Matyus, C. Fabri and A. G. Csaszar, J. Chem. Theory Comput., 2013, 9, 5471–5478 CrossRef CAS.
- H. C. Longuet-Higgins, Adv. Spectrosc., 1961, 2, 429–472 Search PubMed.
- J. K. Watson, Mol. Phys., 1970, 19, 465–487 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04100a |
| This journal is © the Owner Societies 2021 |