Open Access Article
Open Access ArticleInsights into the behavior of nonanoic acid and its conjugate base at the air/water interface through a combined experimental and theoretical approach†
Man
Luo
a,
Nicholas A.
Wauer
 a,
Kyle J.
Angle
a,
Kyle J.
Angle
 a,
Abigail C.
Dommer
a,
Abigail C.
Dommer
 a,
Meishi
Song
a,
Christopher M.
Nowak
a,
Rommie E.
Amaro
a,
Meishi
Song
a,
Christopher M.
Nowak
a,
Rommie E.
Amaro
 *a and
Vicki H.
Grassian
*a and
Vicki H.
Grassian
 *ab
*ab
aDepartment of Chemistry and Biochemistry, University of California, La Jolla, San Diego, CA 92093, USA. E-mail: ramaro@ucsd.edu; vhgrassian@ucsd.edu
bDepartment of Nanoengineering, Scripps Institution of Oceanography, University of California, La Jolla, San Diego, CA 92093, USA
First published on 15th June 2020
Abstract
The partitioning of medium-chain fatty acid surfactants such as nonanoic acid (NA) between the bulk phase and the air/water interface is of interest to a number of fields including marine and atmospheric chemistry. However, questions remain about the behavior of these molecules, the contributions of various relevant chemical equilibria, and the impact of pH, salt and bulk surfactant concentrations. In this study, the surface adsorption of nonanoic acid and its conjugate base is quantitatively investigated at various pH values, surfactant concentrations and the presence of salts. Surface concentrations of protonated and deprotonated species are dictated by surface-bulk equilibria which can be calculated from thermodynamic considerations. Notably we conclude that the surface dissociation constant of soluble surfactants cannot be directly obtained from these experimental measurements, however, we show that molecular dynamics (MD) simulation methods, such as free energy perturbation (FEP), can be used to calculate the surface acid dissociation constant relative to that in the bulk. These simulations show that nonanoic acid is less acidic at the surface compared to in the bulk solution with a pKa shift of 1.1 ± 0.6, yielding a predicted surface pKa of 5.9 ± 0.6. A thermodynamic cycle for nonanoic acid and its conjugate base between the air/water interface and the bulk phase can therefore be established. Furthermore, the effect of salts, namely NaCl, on the surface activity of protonated and deprotonated forms of nonanoic acid is also examined. Interestingly, salts cause both a decrease in the bulk pKa of nonanoic acid and a stabilization of both the protonated and deprotonated forms at the surface. Overall, these results suggest that the deprotonated medium-chain fatty acids under ocean conditions can also be present within the sea surface microlayer (SSML) present at the ocean/atmosphere interface due to the stabilization effect of the salts in the ocean. This allows the transfer of these species into sea spray aerosols (SSAs). More generally, we present a framework with which the behavior of partially soluble species at the air/water interface can be predicted from surface adsorption models and the surface pKa can be predicted from MD simulations.
Introduction
Atmospheric aerosol particles are ubiquitous in the atmosphere. Sea spray aerosols (SSAs) are a major component of primary aerosols as the ocean covers more than 70% of the earth's surface.1 SSAs can impact climate by scattering or absorbing solar radiation,2,3 reacting with gases in the Earth's atmosphere,4–6 and affecting the formation of clouds.7 As SSAs are generated from wave breaking and bubble bursting from the sea surface microlayer (SSML), the aerosol particles enrich a variety of organic species to the aerosol phase, especially surface-active molecules.8–10 Fatty acids contribute to a large fraction of surface-active organic species found in SSML and SSA.8,11,12 The fatty acid organic coating on SSA surfaces can affect the climate–relevant properties of these particles, such as their reactivity,3,13,14 hygroscopicity,15 optical properties,3 cloud condensation nucleation3,15,16 and ice nucleation activity.3,17 Although the most abundant fatty acids found in the SSML and SSA are palmitic acid (C16) and stearic acid (C18),9,11,18 medium-chain fatty acids (C8–C10) have also been identified in previous studies.8,9,11 It has been found that medium-chain fatty acids make up about 7.4%, 0.9%, and 1.7% of the total saturated fatty acids in the SSML, coarse SSAs (2.5–10 μm wet diameter), and fine SSAs (<2.5 μm), respectively.11Medium-chain fatty acids are both less surface-active and more soluble compared to longer-chain fatty acids such as palmitic and stearic acids.8,19 For example, the solubility for palmitic acid is 0.72 mg L−1 at 20 °C, which is about 400 times lower than the solubility of nonanoic acid (300 mg L−1). The protonated form of fatty acids is more surface-active while the deprotonated form is relatively surface inactive.20,21 This is of particular interest since studies have shown that the pH of aerosol particles can vary dramatically within a large range (0–8).22–26 Therefore, it is crucial to understand the behavior of protonated and deprotonated medium-chain fatty acids at the surface and in the bulk and how changes in pH alter their behavior in order to understand how this pH range affects the properties of the aerosol surface.
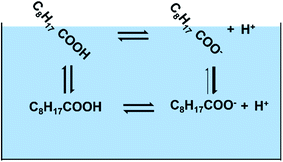
In this study, we have combined experiments with theory to better understand the behavior of nonanoic acid and its conjugate base at the air/water interface. The behavior of nonanoic acid can be expressed as due to the presence of different species in the bulk and at the surface as shown in Scheme 1.
The acid dissociation constant (pKa) of nonanoic acid in the bulk in Scheme 1, has been reported in other studies.20,27 However, most of the studies have used weak acid titration, which requires the bulk concentration of nonanoic acid to be at least 1 mM. As we aim to study nonanoic acid at more environmentally relevant bulk concentrations, a method based on NMR spectroscopy is used to measure the bulk pKa of nonanoic acid at 4 lower concentrations.28 The detailed calculations for the bulk pKa of nonanoic acid and NMR data can be found in ESI (see Fig. S1 and S2†).
The partitioning of both forms, HA and A− , of nonanoic acid and nonanoate, respectively, between the air/water interface and the bulk is examined by obtaining surface pressure versus nonanoic acid concentration curves at either pH 2.1 ± 0.1 or pH 11.5 ± 0.5. Surface pressure is defined as the difference between surface tension when the surfactant is present compared to the surface tension of the pure aqueous solution. At these pH values, the HA and A− are present in the bulk at concentrations of 0.01 mM to 1 mM and 0.05 mM to 15 mM, respectively. Two adsorption models were fitted with the experimental data to obtain the partitioning of both HA and A− .19,21 To close the cycle shown in Scheme 1, we include the surface acid dissociation constant. This constant is usually called the “surface pKa”20,29 and it is a value of great interest.14,30 However, this constant is difficult to determine from experiments alone. There have been studies which stated that the acid dissociation of surfactants at the interface cannot be directly quantified by the surface concentrations of the protonated and deprotonated forms as they are coupled with the adsorption processes.31–33 Therefore, molecular dynamics (MD) simulations and free energy perturbation (FEP) calculations were performed to directly investigate the surface stability and free energy differences of protonation for the surface versus bulk acids. Since MD can resolve chemical systems at a molecular level and on a nanosecond timescale, it remains an essential tool for understanding chemical properties not readily obtained by experimental methods. Here, the combination of experimental and computational methods has provided advanced insight into the behavior and properties of nonanoic acid at the surface and in the bulk. Furthermore, a thermodynamic cycle between the four species plus the hydronium ions shown in Scheme 1 can be established based on the combination of the experimental and computational results.
Additionally, given the large ionic strength in the ocean environment and the fact that salts can affect the surface adsorption and stability of surfactants at the air/water interface,34–36 it is also crucial to study the impact of salts on the surface activity of HA and A− . Here a salt concentration of 0.5 M NaCl was chosen for this study based on its concentration in the ocean. By using surface pressure titration curves, surface adsorption model calculations and Infrared Reflection Absorption Spectroscopy (IRRAS), we are able to elucidate the perturbation of salts on the behavior of nonanoic acid at the air/(salt)water interface and in the bulk.
Experimental methods and materials
Nonanoic acid (analytical standard) was purchased from Sigma Aldrich and used without further purification. NaCl salt was purchased from Fisher Scientific and was baked at 200 °C overnight to remove organic contaminants. Aqueous solutions were prepared using Milli-Q water with an electric resistance of 18.2 MΩ. Hydrochloric acid (1 N stock solution) and sodium hydroxide (1 N stock solution) were purchased from Fisher Chemical.1H NMR experiments for bulk pKa studies were performed using a 500 Jeol ECA NMR spectrometer with wet suppression of H2O. Solutions of nonanoic acid were prepared at concentrations of 1 mM in both water and 0.5 M NaCl salt solutions. The nonanoic acid solution in water was then diluted to different concentrations. NMR samples were prepared volumetrically with 90% (v/v) nonanoic acid solutions and 10% D2O (99.9%, Cambridge Isotope Laboratories, Inc.) for NMR field frequency lock. Solution pH was determined from an Oakton 700 pH meter and was adjusted by either 1 N HCl or 1 N NaOH. The detailed calculations for bulk pKa of nonanoic acid from NMR data are included in Fig. S1 and S2.†
Surface tension measurements were done with a Kibron AquaPi tensiometer. Acidic solutions of nonanoic acid were prepared by dissolving 1 mM in water or 0.5 M NaCl solution at around pH 11 to fully dissolve the nonanoic acid, and then the pH was adjusted to 2.1 ± 0.1. These solutions were subsequently diluted with water (or 0.5 M NaCl solution) at pH 2.1 ± 0.1 to different concentrations. Basic solutions of nonanoic acid were prepared at concentrations of 15 mM in water or 0.5 M NaCl solution with 20 mM of NaOH. These solutions were then diluted into samples with different nonanoic acid concentrations while maintaining the same Na+ concentration as the starting solution. The pH of these solutions ranged from 11 to 12.
Surface pressure titration experiments were performed by a computer-controlled film balance (KSV NIMA LB, S/N AAA100505) with a slightly modified side hole Petri dish, designed by Allen and co-workers.37 Nonanoic acid solutions at different concentrations were made in water or 0.5 M NaCl with an initial pH around 11.5. A 40 mL solution was used for each experiment and was titrated with 1 N HCl via a syringe through the side hole of the Petri dish. The solution was stirred to ensure efficient mixing of the titrant. The surface pressure and pH were monitored throughout the titration experiments. The balance was zeroed before each experiment (pH 11.5) and therefore the surface pressure results were corrected by adding the surface pressure measurement of each system at pH 11.5 from the tensiometer to all the data points. After the pH of the solution was titrated to around 2, it was titrated back with 1 N NaOH to basic pH. There is no obvious difference found in this work between the different methods, i.e. from low to high pH or high to low pH.
The Infrared Reflection Absorption Spectroscopy (IRRAS) setup has been described previously.38,39 The IR beam from an infrared spectrometer (Bruker Tensor 37) is directed onto the aqueous solution surface in the Petri dish at an angle of 30° from the surface. We chose 30° because that is the optimal angle for the incident beam at an air–water interface for the unpolarized beam used in our setup.40,41 The reflected beam is sent to an MCT detector (Infrared Associates Inc., midband with ZnSe window). The reflectance absorbance (RA) for the IRRAS spectra was plotted as a function of wavenumber, where
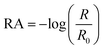 | (1) |
All-atom MD simulations were performed on nonanoic acid monolayer systems. Nonanoic acid monolayers were constructed using PACKMOL42 by placing nonanoic acid molecules into two symmetrical leaflets, which were then placed above and below a block of TIP3P43 water molecules, with the carboxylic acid headgroups pointing towards the water and the hydrophobic tails pointing towards vacuum. To directly compare to experimental conditions, the fatty acids were packed at an area per lipid of 30 Å2. The systems were parameterized using the CHARMM36 (ref. 44) force field and simulated with NAMD 2.13 at 298.15 K in an NVT ensemble.45 These simulations were completed on NVIDIA GTX 1080Ti GPU (GeForce GTX Titan, NVIDIA, Santa Clara, CA). For a detailed figure and description of the simulation box, see Fig. S3.†
To evaluate the relative stability of monolayers of protonated versus deprotonated forms of nonanoic acid, 50 Å × 50 Å systems were constructed with 0.5 M NaCl to balance the charges and mimic experimental conditions. These simulations were first energy-minimized for 42 picoseconds and then equilibrated by gradually releasing constraints placed on all atoms in 5 consecutive steps, each run for 100 ps. For each of the protonated and de-protonated systems, triplicate simulations of 25 nanoseconds were run and subsequently analyzed using MDTraj46 and PyTraj47 MD analysis packages. Markers of fatty acid monolayer stability such as energies, tilt angles, and headgroup position distributions were evaluated (Fig. S4†).
Alchemical FEP calculations were performed using the free energy methods implemented in NAMD which utilize a dual-topology paradigm.48,49 Two nonanoic acid FEP systems were set up as described above, one at 30 Å2 for 100 Å × 100 Å leaflets with a single nonanoic acid in bulk water and another with a single nonanoic acid at the surface as well as a single acid in bulk water, and were simulated for 20 ns using all-atom MD. Afterwards, 8 replicates of FEP/MD simulations were carried out for both monolayer and bulk environments. The FEP/MD simulations were divided into 32 equidistant λ-states between 0 and 1 for forward and backward alchemical transformations with a total of 2.5 ns of FEP/MD sampling for each replicate. These systems were equilibrated locally using a NVIDIA Quadro P4000 GPU. All production runs and calculations utilized the Extreme Science and Engineering Discovery Environment (XSEDE).50 Specifically, simulations were performed on the Comet supercomputer. The FEP calculations were analyzed using the ParseFEP51 plugin for VMD52 using the Bennett acceptance ratio estimator of the free energy. The pKa shift for a nonanoic acid molecule in a monolayer environment was calculated using eqn (2) and (3)53–55 where ΔGmonodeprot and ΔGbulkdeprot refer to the free energy gap between the protonated and deprotonated forms of nonanoic acid in a monolayer at the air/water interface and in the bulk, respectively.
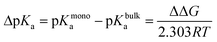 | (2) |
| ΔΔG = ΔGmonodeprot − ΔGbulkdeprot | (3) |
Results and discussion
The bulk pKa of nonanoic acid at different concentrations was determined by NMR spectroscopy. The bulk pKa of nonanoic acid was found to be 4.8 ± 0.1 over the range of concentrations used from 0.1 to 0.9 mM, which is in agreement within experimental error to the literature value of 4.97 ± 0.05.20,27 Details of the NMR spectra are found in the ESI (Fig. S1 and S2†). In this study the activities for nonanoic acid at different bulk concentrations were represented simply by its concentrations as Fig. S2† suggests that the activity coefficients must be close to one in order to obtain the same pKa value at different nonanoic acid concentrations. As nonanoic acid is both slightly surface active and slightly soluble, it will be present both at the surface and in the bulk. In addition, the HA is much more surface active than A− in pure water (vide infra) in the concentration range studied. To show this we reduced the number of species by fixing the pH at very acidic (pH 2.1 ± 0.1) and very basic (pH 11.5 ± 0.5) values. The surface pressure versus nonanoic acid concentration curves were obtained at both acidic and basic pH, which is shown in Fig. 1a. This result is in agreement with previous studies.20,21 It is obvious that HA is much more likely to partition to the surface than the A− and at low concentrations the deprotonated form (A− ) is negligible on the surface.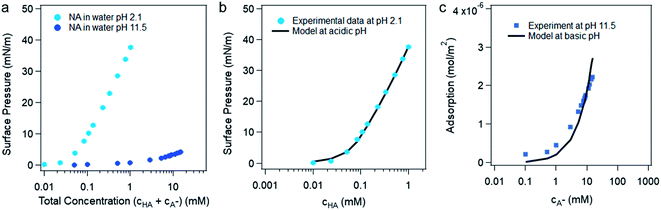 | ||
| Fig. 1 (a) Surface pressure versus the total concentration of nonanoic acid in water at pH 2.1 ± 0.1 and pH 11.5 ± 0.5. (b) The experimental and model fitting of the surface pressure versus protonated nonanoic acid concentration at pH 2.1 ± 0.1. The blue dots are experimental data and the black line represents the fit by the van der Waals model from Danov et al.19 (c) Model fitting for deprotonated nonanoic acid surface adsorption at pH 11.5 ± 0.5 with a constant concentration of NaOH (20 mM). The blue dots represent the left-hand side of eqn (6) from the experimental data and the black line represent the right-hand side of eqn (6) with best fit of the parameters. | ||
Danov and co-workers have developed a van der Waals model for the surface adsorption of protonated fatty acids, including nonanoic acid, where they link the bulk concentration of protonated fatty acid with the surface pressure measurement.19 The equations are expressed in eqn (4) and (5):
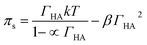 | (4) |
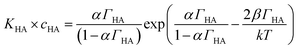 | (5) |
For the surface adsorption of A− , a slightly modified version of another ion-binding model reported from Badban et al. was used to fit the experimental data.21 The final equation that links the derivative of surface tension with the concentration of A−eqn (6) below:
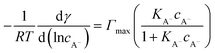 | (6) |
At intermediate pH, the four species shown in Scheme 1 will co-exist in the system. Then the surface pressure versus pH plot will show a reverse “S” shaped curve as can be seen in Fig. 2. The blue open circles represent the data due to the soap effect that is caused by the interaction between the HA and A− forming an acid–soap complex (HA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A− ) at the surface, which has been discussed in previous studies.20,56–59 The reverse s-shaped curve looks similar to a weighted average surface pressure from surface protonated and surface deprotonated nonanoic acid, which would be a measure of “surface pKa” as suggested from an earlier study.20 However, when the pH of the solution varies, the speciation of protonated and deprotonated forms of nonanoic acid change in the bulk solution as well. Therefore, due to the different surface adsorption properties between A− and HA, the surface concentration of both species will vary with different pH. Thus, the reversed s-shaped curves will have contributions from surface adsorption process (i.e. partitioning from the bulk to the surface) which need to be accounted for.
A− ) at the surface, which has been discussed in previous studies.20,56–59 The reverse s-shaped curve looks similar to a weighted average surface pressure from surface protonated and surface deprotonated nonanoic acid, which would be a measure of “surface pKa” as suggested from an earlier study.20 However, when the pH of the solution varies, the speciation of protonated and deprotonated forms of nonanoic acid change in the bulk solution as well. Therefore, due to the different surface adsorption properties between A− and HA, the surface concentration of both species will vary with different pH. Thus, the reversed s-shaped curves will have contributions from surface adsorption process (i.e. partitioning from the bulk to the surface) which need to be accounted for.
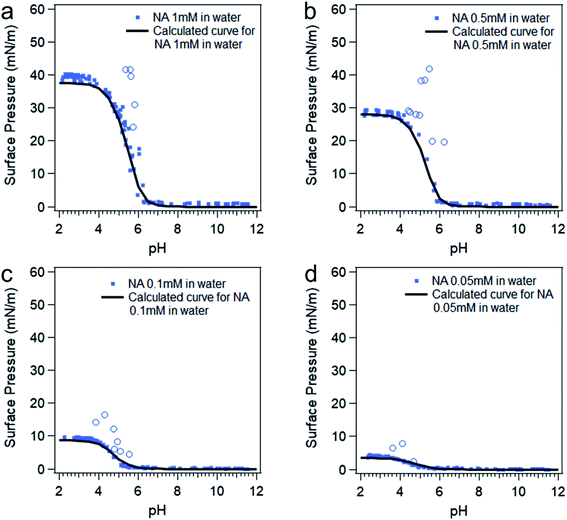 | ||
| Fig. 2 Surface pressure versus pH curves at different nonanoic acid concentrations: experimental data (blue dots) and model calculated curves (black curves) using eqn (4), (5) and (7). The blue open circles represent the data due to the “soap effect” as discussed in detail in previous studies.20,56–59 | ||
Since surface adsorption processes play a key role in these surface pressure curves, we investigated whether these data could be fitted by a surface adsorption model. As already shown, the surface adsorption of A− is negligible at the concentration used here (see Fig. 1). Therefore, the surface adsorption model of HA was applied to calculate surface pressure versus pH curves that are only due to the surface adsorption process of HA, which is shown as black lines in Fig. 2. The calculated curves (the black lines) were obtained from the eqn (4) and (5). The cHA in eqn (4) was calculated from eqn (7) below:
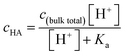 | (7) |
The surface dissociation process has always been of great interest to atmospheric chemists as the chemical reactivities of the atmospheric aerosol particles with the trace gases are significantly affected by their surface acidity or basicity.14,30 Many studies have been conducted to determine the “surface pKa” or the “surface acid dissociation”;20,32,60–66 however, the results have been controversial amongst different studies that utilize different methods. A spectroscopic study on acid/base pairs at the surface stated that the surface favors the non-charged form of the acid/base pair relative to the bulk.67 Some studies have stated that the carboxylic acid group is less acidic (higher surface pKa, less likely to deprotonate) on the surface than in the bulk, which agrees with the “surface favors non-charged species” statement.20,32 However, other studies have posited that the carboxylic acid group is more acidic (lower surface pKa, more likely to deprotonate) on the surface than in the bulk.60–62 Aside from the study with insoluble long chain fatty acids like stearic acid,64 the surface pressure and spectroscopic studies with soluble compounds have the possibility of containing interference from surface adsorption process of the protonated and deprotonated species. To circumvent this issue, some studies use insoluble molecules with long alkyl chains to obtain the surface pKa and compare with the bulk pKa obtained from the same functional group with a short, soluble alkyl chain.65,66 However, the pKa of the functional group may be affected by the alkyl chain length or the environment it faces at the surface.20,68 Some other studies used mass spectrometry to test carboxylic acids dosed on the surface of microdroplets generated from electrospray, which seem more reliable as there are no bulk species.60,61 However, the carboxylic acid they tested is dosed on a charged surface which may affect its surface acid dissociation process. Therefore, in summary, it has proven very difficult to get reliable experimental measurements of the surface acid dissociation process for soluble species.
To demonstrate an alternative method for investigating this process, MD simulations on the system containing nonanoic acid at both the air/water interface and in the bulk were performed in order to compare the “surface pKa” relative to the bulk pKa. MD simulations show that protonated nonanoic acid forms a more stable monolayer than the deprotonated nonanoate, despite any additional stability conferred by sodium-ion coordination. The decreased stability of the anionic form could be attributed to the inhibited access of cations to coordinate the carboxylate headgroups due to the geometric constraint of the planar interface. The dissolution of the monolayer structure, resulting in the partial solvation of the acid(s), allows for more ion–ion binding with the consequence of reduced surface-activity. A detailed description of these simulations and some standard equilibrium measurements are provided in Fig. S4.†
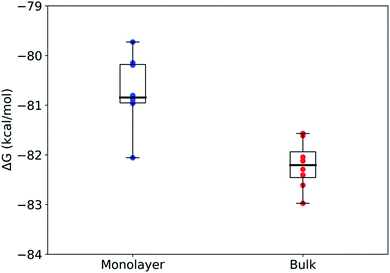
Using rigorous alchemical methods, the pKa shift between monolayer and bulk was calculated for nonanoic acid from the difference in ΔG of deprotonation (Fig. 3). The predicted surface pKa can be calculated from the experimentally determined pKa of nonanoic acid in bulk, thereby integrating theoretical and experimental results.
The alchemical transformations show a clear free energy difference dependent on the surrounding microenvironment with the deprotonation process being more favorable in bulk solution as compared to in a monolayer. Using eqn (2) and (3) described above, we calculated ΔpKa to be 1.1 ± 0.6, leading to a surface pKa of 5.9 ± 0.6 for nonanoic acid in a packed monolayer. This finding suggests that nonanoic acid is slightly less acidic when located at the interface than it is in bulk solution (bulk pKa 4.8 ± 0.1), which is in agreement with the results of this paper as well as previous work on longer-chain fatty acids.29,35,69,70
The highly negative ΔG values in Fig. 3 for both the bulk and surface systems are caused by the exclusion of certain terms that were assumed to be constant between the two systems, such as intramolecular interactions, in the alchemical method used here. Therefore, the ΔG values are, by themselves, not complete free energy differences for the real-world deprotonation process. The difference between ΔG values reflects the effect the environment has on the electrostatic and van der Waals forces on the molecule and therefore is an accurate representation of the difference in pKa. Other studies that have investigated similar deprotonation processes have shown that reasonable pKa values can be successfully calculated from these types of ΔG differences.50
We also investigated the role of the packing density of the monolayer on the surface pKa of nonanoic acid by repeating the free energy calculations on a single nonanoic acid at the air–water interface (Fig. S5†). These calculations gave similar results to the monolayer system packed at 30 Å2, with ΔpKa = 0.9 ± 0.5, suggesting that the shift in pKa is mostly due to the acid's location at the interface, and not necessarily the surrounding acids.
So far, we have calculated the four constants associated with the four equilibria in the Scheme 1. Although the adsorption constants KHA and KA− are not strictly equilibrium constants, they can be treated as equilibrium constants at infinite dilution condition. Therefore, we have pKa (surf) = 5.9 ± 0.6, pKa (bulk) = 4.8 ± 0.1, pKHA = −3.4 ± 0.1, pKA− = −1.0 ± 0.3, which are proportional to the free energies. However, these four equilibria are not a full thermodynamic cycle, as the two acid dissociation processes include hydronium ions whose surface adsorption constant is necessary but unknown form this study. If hydronium ion adsorption is ignored, then the cycle is not a true loop since the final state has different numbers of hydronium ions at the surface and bulk than the initial state. Therefore, in order to close the loop, we used the value from a recent report by Das et al.71 that ΔG(H+) = −1.3 ± 0.2 kcal mol−1, which is the free energy for the hydronium ion surface adsorption. From this, the pKH+ = −0.95 ± 0.15. As the pK values are proportional to the free energy, they should sum to zero for the full thermodynamic cycle. From our results, the numbers sum to be: pKHA + pKa (surf) − pKA− − pKH+ − pKa (bulk) = −3.4 + 5.9 + 1.0 + 0.95–4.8 = −0.35 ± 0.7, which is close to zero within error.
Given the large ionic strength present in marine-relevant systems, it is crucial to also investigate the impact of salt on the surface adsorption model of medium-chain fatty acids. The bulk pKa of nonanoic acid in the presence of 0.5 M NaCl solution is tested first. The chemical shift versus pH plot for nonanoic acid in water compared to in 0.5 M NaCl solution is shown in Fig. S6.† The bulk pKa for nonanoic acid in the presence of salt is calculated to be 4.6 ± 0.1, which demonstrates that the presence of salt slightly lowers the apparent bulk pKa value of nonanoic acid, compared to a pKa value of 4.8 ± 0.1 for nonanoic acid in pure water. Although the pKa value of nonanoic acid with the presence of NaCl has not been reported in the literature, it is known that the presence of Na+ has the ability to enhance deprotonation of carboxylic acids.72
The surface pressure versus nonanoic acid concentration curves in pure water and in 0.5 M NaCl solution at acidic and basic pH can be found in Fig. 4. It is obvious that the presence of salt increases the surface adsorption of both HA and A−, and this effect is more pronounced at basic pH. At acidic pH, HA is already surface active and the surface adsorption of nonanoic acid is already high. In addition, the interaction between HA and Na+ ion is relatively weak as it is not an ion–ion binding. Therefore, the stabilization effect of salt is less prominent at acidic pH compared to that at basic pH. When nonanoic acid is deprotonated at basic pH, the Na+ ion can stabilize it at the air/water interface by forming the ion-binding pair.34,35
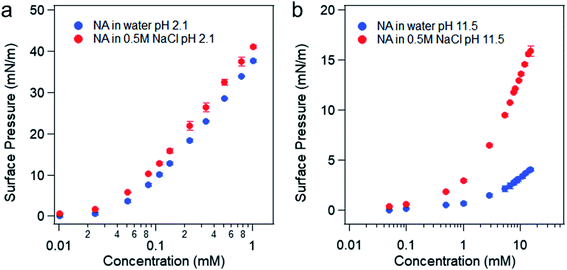 | ||
| Fig. 4 Surface pressure versus concentration of nonanoic acid in water and in 0.5 M NaCl solution at pH 2 (a) and pH 11–12 (b). | ||
The slightly modified model from Badban et al. that was applied to surface pressure versus nonanoic acid concentration at basic pH in pure water is also applied to that in the 0.5 M NaCl solution to obtain the adsorption constant for A– in the presence of salt (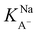 ).21 The fitted curve is shown in Fig. S7† and the fitted parameter
).21 The fitted curve is shown in Fig. S7† and the fitted parameter 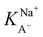 was found to be 55 M−1. It should be noted that this model is a simplified model as it eliminates some parameters and does not take into account the difference in surface adsorption equilibrium between organic species and the cations such as Na+.21,34 Therefore, it cannot predict the shape of the curve with the presence of Na+ very well. However, we want to obtain a semi-quantitative comparison between the adsorption constant of nonanoic acid with and without the presence of salt. Based on what we obtained from the model fitting,
was found to be 55 M−1. It should be noted that this model is a simplified model as it eliminates some parameters and does not take into account the difference in surface adsorption equilibrium between organic species and the cations such as Na+.21,34 Therefore, it cannot predict the shape of the curve with the presence of Na+ very well. However, we want to obtain a semi-quantitative comparison between the adsorption constant of nonanoic acid with and without the presence of salt. Based on what we obtained from the model fitting, 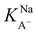 is about 5 times greater than KA− in water. This demonstrates that in the presence of salt, the surface adsorption of A− is significantly increased.
is about 5 times greater than KA− in water. This demonstrates that in the presence of salt, the surface adsorption of A− is significantly increased.
The pH titration curves for nonanoic acid at different concentrations in the presence of 0.5 M NaCl compared with that in water is shown in Fig. 5. Data points due to the soap effect on surface pressure versus pH curves are removed to more clearly show the differences. Although we have concluded that the presence of salt will affect the surface adsorption of A− more than the HA, the differences in surface pressure between the one in water (blue dots) and that in salt solution (red dots) at basic pH (pH 8–12) in the titration curves in Fig. 5a, c, e and g are small due to the low concentration used. However, we can see clearly the difference in surface pressure at acidic pH. The IRRAS spectra for the C–H stretching region at pH 2 are also shown in Fig. 5. It is obvious that the peak intensity with the presence of salt is greater than that in water, which demonstrates that the presence of salt enhances the surface adsorption of HA. The IRRAS spectra also shows that at a lower nonanoic acid concentration at pH 2, the intensity difference with and without salt is more obvious. This could be due to the fact that at a nonanoic acid concentration of 1 mM, the surface adsorption of the HA is reaching its maximum19 and therefore the interaction with salt cannot provide a significant increase in surface adsorption. The percent increase values of the integration of these peaks due to the presence of salt at different nonanoic acid bulk concentrations agree qualitatively and change in the same direction with the percent increase values of surface pressure at pH 2 due to the presence of salt, as can be seen from Table 1. We did not see IRRAS signal for nonanoic acid in both water and salt solution at pH 12 with the concentrations used in the titration curves (data not shown). The IRRAS signal for 14 mM nonanoic acid at basic pH in water compared with in 0.5 M NaCl solution can be found in Fig. S8,† which demonstrates that the salt increases the surface adsorption of A− as well.
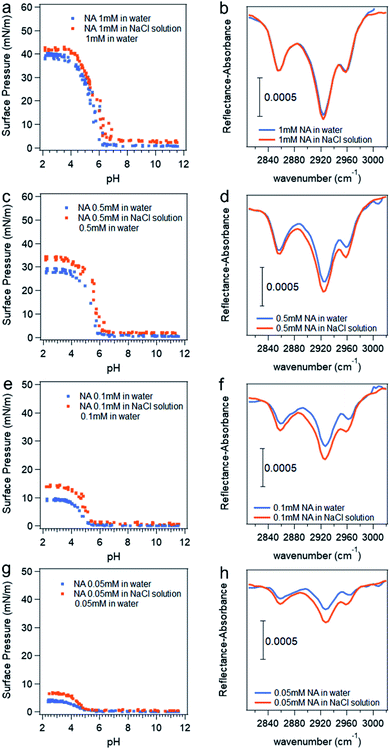 | ||
| Fig. 5 Surface pressure versus pH curves (a, c, e and g) and IRRAS spectra at pH 2 (b, d, f and h) with different nonanoic acid concentration in water compare to in 0.5 M NaCl solution. *Data points attributed to the “soap effect” in the middle range of the curves shown in Fig. 2 are removed to more clearly show the differences. | ||
| Nonanoic acid bulk concentration (mM) | The percent increase of surface pressure at pH 2 due to the presence of 0.5 M NaCl (%) | The percent increase of the integration of the peaks in the IRRAS spectra due to the presence of 0.5 M NaCl (%) |
|---|---|---|
| 1 | 6.7 ± 0.2 | 2.6 ± 0.3 |
| 0.5 | 18 ± 1 | 22 ± 2 |
| 0.1 | 50 ± 2 | 47 ± 6 |
| 0.05 | 66 ± 4 | 76 ± 21 |
Conclusions
In this work, the surface adsorption of nonanoic acid and its conjugate base has been established and the impact of salt on these equilibria is investigated using experimental and theoretical approaches for the first time to better understand the driving force of surface species. It has been found that the surface adsorption of nonanoic acid is controlled by the pH of the bulk phase and the very different surface activity of the two different components, protonated versus deprotonated. The surface acid dissociation constants for soluble surfactants are therefore difficult to define and/or directly measure since the ratio of protonated and deprotonated species on the surface does not directly connect with the surface acid dissociation process and could be due to the difference in the surface adsorption properties of both forms. However, MD simulations with alchemical free energy methods were used to calculate the pKa shift of nonanoic acid at the air/water interface versus in the bulk. These calculations suggest that nonanoic acid in a monolayer at the air/water interface is less acidic than acids in the bulk by roughly 1 pKa unit. We show here that simple free energy calculations can provide a valuable supplement to experimental methods when investigating surface properties of partially soluble lipids. We also have established a thermodynamic cycle for nonanoic acid and its conjugate base between the air/water interface and the bulk phase.In addition, the presence of salt, namely NaCl, is found to slightly decrease the bulk pKa of nonanoic acid and increase the surface adsorption of both HA and A− . This explains why medium-chain fatty acids are found in the SSML and SSA despite the fact that one might assume they should be negligible at the surface because they exist in their deprotonated forms at ocean pH and should not be too surface active at low concentrations (<1 mM).8,11 Overall, these results can be applied to other partially soluble surface-active species that contain multiple solution phases with varying surface activities. Understanding air/water and air/salt water interfaces is critically important in aerosol chemistry as the nature of the aerosol surface composition can impact a number of important properties including aerosol reactivity, hygroscopicity and aerosol lifetimes.3,13,14
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Center for Aerosol Impacts on Chemistry of the Environment (CAICE), a National Science Foundation funded Center of Chemical Innovation through Grant CHE-1801971. The Extreme Science and Engineering Discovery Environment (XSEDE), which is used for all production runs and calculations for the simulations, is supported by National Science Foundation grant number ACI-1548562.50 Specifically, the Comet supercomputer, which the simulations were performed on, is supported by NSF award number 1341698 at the San Diego Supercomputer Center. The authors would like to thank Professors Heather Allen and Gil Nathanson for helpful discussions.The data utilized to generate the figures in this paper are hosted by the UCSD Library Digital Collections (https://doi.org/10.6075/J0JQ0ZJD).
References
- P. K. Quinn, D. B. Collins, V. H. Grassian, K. A. Prather and T. S. Bates, Chem. Rev., 2015, 115, 4383–4399 CrossRef CAS PubMed.
- B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the Upper and Lower Atmosphere, Academic Press, San Diego, 2000 Search PubMed.
- R. E. Cochran, O. S. Ryder, V. H. Grassian and K. A. Prather, Acc. Chem. Res., 2017, 50, 599–604 CrossRef CAS PubMed.
- J. Haywood and O. Boucher, Rev. Geophys., 2000, 38, 513–543 CrossRef CAS.
- M. A. Shaloski, T. B. Sobyra and G. M. Nathanson, J. Phys. Chem. A, 2015, 119, 12357–12366 CrossRef CAS PubMed.
- O. S. Ryder, N. R. Campbell, H. Morris, S. Forestieri, M. J. Ruppel, C. Cappa, A. Tivanski, K. Prather and T. H. Bertram, J. Phys. Chem. A, 2015, 119, 11683–11692 CrossRef CAS PubMed.
- D. K. Farmer, C. D. Cappa and S. M. Kreidenweis, Chem. Rev., 2015, 115, 4199–4217 CrossRef CAS PubMed.
- R. E. Cochran, T. Jayarathne, E. A. Stone and V. H. Grassian, J. Phys. Chem. Lett., 2016, 7, 1692–1696 CrossRef CAS PubMed.
- R. E. Cochran, O. Laskina, J. V. Trueblood, A. D. Estillore, H. S. Morris, T. Jayarathne, C. M. Sultana, C. Lee, P. Lin, J. Laskin, A. Laskin, J. A. Dowling, Z. Qin, C. D. Cappa, T. H. Bertram, A. V. Tivanski, E. A. Stone, K. A. Prather and V. H. Grassian, Chem, 2017, 2, 655–667 CAS.
- H. Tervahattu, J. Geophys. Res., 2002, 107, 4319 CrossRef.
- R. E. Cochran, O. Laskina, T. Jayarathne, A. Laskin, J. Laskin, P. Lin, C. Sultana, C. Lee, K. A. Moore, C. D. Cappa, T. H. Bertram, K. A. Prather, V. H. Grassian and E. A. Stone, Environ. Sci. Technol., 2016, 50, 2477–2486 CrossRef CAS PubMed.
- M. Mochida, N. Umemoto, K. Kawamura, H. J. Lim and B. J. Turpin, J. Geophys. Res.: Atmos., 2007, 112, D15209 CrossRef.
- O. S. Ryder, N. R. Campbell, M. Shaloski, H. Al-Mashat, G. M. Nathanson and T. H. Bertram, J. Phys. Chem. A, 2015, 119, 8519–8526 CrossRef CAS PubMed.
- J. V Trueblood, A. D. Estillore, C. Lee, J. A. Dowling, K. A. Prather and V. H. Grassian, J. Phys. Chem. A, 2016, 120, 6444–6450 CrossRef PubMed.
- E. Fuentes, H. Coe, D. Green and G. McFiggans, Atmos. Chem. Phys., 2011, 11, 2585–2602 CrossRef CAS.
- S. D. Forestieri, S. M. Staudt, T. M. Kuborn, K. Faber, C. R. Ruehl, T. H. Bertram and C. D. Cappa, Atmos. Chem. Phys., 2018, 18, 10985–11005 CrossRef CAS.
- P. J. DeMott, R. H. Mason, C. S. McCluskey, T. C. J. Hill, R. J. Perkins, Y. Desyaterik, A. K. Bertram, J. V. Trueblood, V. H. Grassian, Y. Qiu, V. Molinero, Y. Tobo, C. M. Sultana, C. Lee and K. A. Prather, Environ. Sci.: Processes Impacts, 2018, 20, 1559–1569 RSC.
- M. Mochida, Y. Kitamori, K. Kawamura, Y. Nojiri and K. Suzuki, J. Geophys. Res.: Atmos., 2002, 107, AAC 1-1–AAC 1-10 CrossRef.
- K. D. Danov, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, J. Colloid Interface Sci., 2006, 300, 809–813 CrossRef CAS.
- B. A. Wellen, E. A. Lach and H. C. Allen, Phys. Chem. Chem. Phys., 2017, 19, 26551–26558 RSC.
- S. Badban, A. E. Hyde and C. M. Phan, ACS Omega, 2017, 2, 5565–5573 CrossRef CAS PubMed.
- R. L. Craig, L. Nandy, J. L. Axson, C. S. Dutcher and A. P. Ault, J. Phys. Chem. A, 2017, 121, 5690–5699 CrossRef CAS PubMed.
- A. Bougiatioti, P. Nikolaou, I. Stavroulas, G. Kouvarakis, R. Weber, A. Nenes, M. Kanakidou and N. Mihalopoulos, Atmos. Chem. Phys., 2016, 16, 4579–4591 CrossRef CAS.
- A. H. Young, W. C. Keene, A. A. P. Pszenny, R. Sander, J. A. Thornton, T. P. Riedel and J. R. Maben, J. Geophys. Res.: Atmos., 2013, 118, 9414–9427 Search PubMed.
- J. G. Murphy, P. K. Gregoire, A. G. Tevlin, G. R. Wentworth, R. A. Ellis, M. Z. Markovic and T. C. VandenBoer, Faraday Discuss., 2017, 200, 379–395 RSC.
- H. Guo, L. Xu, A. Bougiatioti, K. M. Cerully, S. L. Capps, J. R. Hite, A. G. Carlton, S. H. Lee, M. H. Bergin, N. L. Ng, A. Nenes and R. J. Weber, Atmos. Chem. Phys., 2015, 15, 5211–5228 CrossRef CAS.
- W. M. Haynes and D. R. Lide, CRC Handbook of Chemistry and Physics: A Ready-reference Book of Chemical and Physical Data, CRC Press, Boca Raton, 2011 Search PubMed.
- A. Lopalco, J. Douglas, N. Denora and V. J. Stella, J. Pharm. Sci., 2016, 105, 664–672 CrossRef CAS PubMed.
- T. Zhang, S. L. Brantley, D. Verreault, R. Dhankani, S. A. Corcelli and H. C. Allen, Langmuir, 2018, 34, 530–539 CrossRef CAS.
- A. P. Ault, T. L. Guasco, O. S. Ryder, J. Baltrusaitis, L. A. Cuadra-Rodriguez, D. B. Collins, M. J. Ruppel, T. H. Bertram, K. A. Prather and V. H. Grassian, J. Am. Chem. Soc., 2013, 135, 14528–14531 CrossRef CAS PubMed.
- C. M. Phan, Ionization of Surfactants at the Air-Water Interface, Elsevier Inc., 2018 Search PubMed.
- S. Strazdaite, K. Meister and H. J. Bakker, J. Am. Chem. Soc., 2017, 139, 3716–3720 CrossRef CAS PubMed.
- J. Werner, I. Persson, O. Björneholm, D. Kawecki, C. M. Saak, M. M. Walz, V. Ekholm, I. Unger, C. Valtl, C. Caleman, G. Öhrwall and N. L. Prisle, Phys. Chem. Chem. Phys., 2018, 20, 23281–23293 RSC.
- V. V. Kalinin and C. J. Radke, in Colloids and Surfaces A: Physicochemical and Engineering Aspects, Elsevier Science B.V., 1996, vol. 114, pp. 337–350 Search PubMed.
- E. M. Adams, B. A. Wellen, R. Thiraux, S. K. Reddy, A. S. Vidalis, F. Paesani and H. C. Allen, Phys. Chem. Chem. Phys., 2017, 19, 10481–10490 RSC.
- A. M. Brzozowska, M. H. G. Duits and F. Mugele, Colloids Surf., A, 2012, 407, 38–48 CrossRef CAS.
- T. Zhang, M. Fiamingo and H. C. Allen, J. Geophys. Res.: Oceans, 2018, 123, 5286–5297 Search PubMed.
- M. Shrestha, M. Luo, Y. Li, B. Xiang, W. Xiong and V. H. Grassian, Chem. Sci., 2018, 9, 5716–5723 RSC.
- M. Luo, A. C. Dommer, J. M. Schiffer, D. J. Rez, A. R. Mitchell, R. E. Amaro and V. H. Grassian, Langmuir, 2019, 35, 9050–9060 CrossRef CAS PubMed.
- R. A. Dluhy, J. Phys. Chem., 1986, 90, 1373–1379 CrossRef CAS.
- M. R. Sierra-Hernández and H. C. Allen, Langmuir, 2010, 26, 18806–18816 CrossRef PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. Huang and A. D. Mackerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L. P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- D. A. Pearlman, J. Phys. Chem., 1994, 98, 1487–1493 CrossRef CAS.
- J. Henin, J. Gumbart and C. Chipot, In silico alchemy: A tutorial for alchemical free-energy perturbation calculations with NAMD, Centre National de la Recherche Scientifique, University of Illinois, Urbana–Champaign, 2017 Search PubMed.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkens-Diehr, Comput. Sci. Eng., 2014, 16, 62–74 Search PubMed.
- P. Liu, F. Dehez, W. Cai and C. Chipot, J. Chem. Theory Comput., 2012, 8, 2606–2616 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Xiao and H. Yu, Phys. Chem. Chem. Phys., 2016, 18, 30305–30312 RSC.
- G. Li and Q. Cui, J. Phys. Chem. B, 2003, 107, 14521–14528 CrossRef CAS.
- D. Riccardi, P. Schaefer and Q. Cui, J. Phys. Chem. B, 2005, 109, 17715–17733 CrossRef CAS PubMed.
- J. R. Kanicky and D. O. Shah, Langmuir, 2003, 19, 2034–2038 CrossRef CAS.
- R. Pugh and P. Stenius, Int. J. Miner. Process., 1985, 15, 193–218 CrossRef CAS.
- J. Rudin and D. T. Wasan, Colloids Surf., 1992, 68, 81–94 CrossRef CAS.
- R. S. Andino, J. Liu, C. M. Miller, X. Chen, S. W. Devlin, M. K. Hong, R. Rajagopal, S. Erramilli and L. D. Ziegler, J. Phys. Chem. A, 2020, 12, 2020 Search PubMed.
- H. Mishra, S. Enami, R. J. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18679–18683 CrossRef CAS PubMed.
- A. J. Eugene, E. A. Pillar, A. J. Colussi and M. I. Guzman, Langmuir, 2018, 34, 9307–9313 CrossRef CAS PubMed.
- E. C. Griffith and V. Vaida, J. Am. Chem. Soc., 2013, 135, 710–716 CrossRef CAS PubMed.
- B. N. Dickhaus and R. Priefer, Colloids Surf., A, 2016, 488, 15–19 CrossRef CAS.
- P. D. Cratin, J. Dispersion Sci. Technol., 1993, 14, 559–602 CrossRef CAS.
- X. Zhao, S. Ong, H. Wang and K. B. Eisenthal, Chem. Phys. Lett., 1993, 214, 203–207 CrossRef CAS.
- X. Zhao, S. Subrahmanyan and K. B. Eisenthal, Chem. Phys. Lett., 1990, 171, 558–562 CrossRef CAS.
- K. B. Eisenthal, Chem. Rev., 1996, 96, 1343–1360 CrossRef CAS.
- J. R. Kanicky, A. F. Poniatowski, N. R. Mehta and D. O. Shah, Langmuir, 2000, 16, 172–177 CrossRef CAS.
- E. M. Adams, C. B. Casper and H. C. Allen, J. Colloid Interface Sci., 2016, 478, 353–364 CrossRef CAS PubMed.
- A. Habartová, M. Roeselová and L. Cwiklik, Langmuir, 2015, 31, 11508–11515 CrossRef PubMed.
- S. Das, S. Imoto, S. Sun, Y. Nagata, E. H. G. Backus and M. Bonn, J. Am. Chem. Soc., 2020, 142, 945–952 CrossRef CAS PubMed.
- M. Luo, D. Shemesh, M. N. Sullivan, M. R. Alves, M. Song, R. B. Gerber and V. H. Grassian, J. Phys. Chem. A, 2020, 124, 5071–5080 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02354j |
| This journal is © The Royal Society of Chemistry 2020 |