The effect of bisimidazolium-based ionic liquids on a bimolecular substitution process. Are two head(group)s better than one?

Abstract

A homologous series of biscationic ionic liquids based on two imidazolium centres, separated by alkyl chains of varying length, were examined as solvents for a bimolecular substitution reaction across a range of proportions of ionic liquid in the reaction mixture. Their effects on the rate constant of the process were compared to monocationic ionic liquids, with generally a greater rate constant increase observed. Importantly, it was observed that the magnitude of the effect was shown to vary with the length of the linking chain. To investigate the origins of these solvent effects, temperature dependent kinetic studies were performed to obtain activation parameters at high and low mole fractions of ionic liquid. The observed activation parameters showed the rate constant enhancement was due to interaction of the ionic liquid with the starting materials, consistent with previous results. Significantly, however, these data also showed that the balance of enthalpic and entropic effects varied dramatically with the length of the alkyl chain between the cationic centres.

---

Introduction

Ionic liquids, arbitrarily defined as salts with melting points below 100 °C,¹ have garnered great attention in chemical, engineering, industrial and pharmaceutical applications, such as catalysis,² extractions,³ as electrolytes,⁴ and for facilitating inorganic and organic reactions as solvents.^5–7 Much of the interest in their use is centred around their attractive properties, such as their negligible volatility,⁸ non-flammability,⁹ thermal stability,⁹ and ability to solvate a wide range of substances.^10–12

An additional benefit to using ionic liquids is that, in principle, they can be ‘tuned’.¹³ This tunability is best demonstrated via their physical properties, where changing the nature of the ions that make up the salt can give an ionic liquid with, say, desired density, viscosity, and miscibility with other solvents.¹⁴ In principle, this tailoring of an ionic liquid could be extended to their use as solvents, such that the components are chosen to achieve a desired outcome for a given reaction. The potential for such use of ionic liquids has been shown with previous studies illustrating that ionic liquids can be used to manipulate rate constants and control reaction selectivity.^15,16 Such applications require an understanding of the microscopic origins of the observed solvent effects in terms of the interactions of the components of the ionic liquid with species along the reaction co-ordinate which can then be exploited to control reaction outcome, however this understanding is currently limited.¹⁷ In order to develop this predictive framework, systematic studies of well-understood reactions in solvents containing ionic liquids are needed to develop a broad knowledge of the solvent effects of ionic liquids on organic processes.^18–20

An example of such a well-understood reaction is the bimolecular reaction between benzyl bromide 1 and pyridine 2 (a Menschutkin reaction, Scheme 1) to form 1-benzylpyridinium bromide 3, which has been thoroughly studied in mixtures of acetonitrile and an ionic liquid.^21–28 As an example of the solvent effects, the extremely well-studied ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([bmim][N(SO₂CF₃)₂],‡4), when present in the reaction mixture, caused an increase in the rate constant for the reaction at all proportions (relative to the acetonitrile case), with greater proportions of the ionic liquid 4 resulting in larger rate constants.²⁶ Investigation into the microscopic origins of these increases in rate constant showed that the presence of the ionic liquid caused an increase in the enthalpy of activation, ΔH^‡, but an accompanying increase in the entropy of activation, ΔS^‡; the latter entropic benefit was dominant, resulting in a net decrease in the Gibbs energy of the activation at the temperature considered.²¹ Molecular dynamics²² and deconvolution studies²³ have revealed that the principal microscopic interactions responsible for the changes in rate constant involve the cationic component of the ionic liquid interacting with the nucleophilic heteroatom of the pyridine 2.

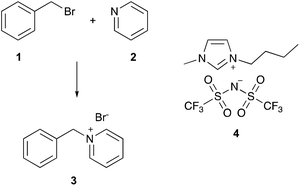Scheme 1 The Menschutkin reaction between benzyl bromide 1 and pyridine 2 to give benzylpyridinium bromide 3, which has been studied in mixtures containing ionic liquids, including [bmim][N(SO₂CF₃)₂] 4.^21–28

With this knowledge, rational selection of ionic liquids was demonstrated to exploit and maximise these interactions, through maximising accessibility to the charged centre and inclusion of electron withdrawing substituents in the cationic component of the ionic liquid.²⁷ Of particular relevance in this work was the investigation of the bisimidazolium ionic liquid, 1,5-bis(3-methylimidazolium-1-yl)pentane bis(trifluoromethanesulfonyl)imide ([p_e(mim)₂][N(SO₂CF₃)₂]₂,‡5d), which, when compared to when the monocationic imidazolium salt 4 was used, showed greater rate constants at all corresponding mole fractions of ionic liquid for the reaction shown in Scheme 1.

Whilst biscationic imidazolium salts have been considered previously as high temperature lubricants,²⁹ as surfactants,³⁰ for catalysis,³¹ and for the formation of antibacterial gels,³² as well as their use as solvents for high temperature reactions,³³ this observed increase in rate constant relative to the corresponding monocationic salt suggested that having two charged centres on the cation was beneficial in terms of reaction outcome but the origin of the effect is not clear. Is the effect general or is it dependent on how far apart the two charged groups are? If there is a dependency, how does it vary with the length of the alkyl chain between them? Given these queries, the work described herein aims to consider the effects on the rate constant of the reaction shown in Scheme 1 of a homologous series of bisimidazolium-based ionic liquids 5, including determining the microscopic origins of any changes observed.

Results and discussion

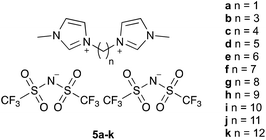
The ionic liquids 5 used in this study (Fig. 1§), were synthesised using methods analogous to those reported in the literature from N-methylimidazole and the corresponding α,ω-dihalide, followed by anion metathesis.²⁷ Of particular note are salts 5a–c, f, which were isolated as solids at room temperature. The series includes the previous example 5e, which has been considered before,²⁷ and specifically seeks to answer the question posed in the title. Whilst other alkyl systems larger than methyl could be considered as the other substituent, any effects of the ionic liquid would be expected to be smaller based on reducing the accessibility of the charged centre.^23,27

Fig. 1 The bisimidazolium-based ionic liquids 5a–k that were used in this study.

The bis(trifluoromethanesulfonyl)imide anion was specifically chosen because the effects of such salts have been extensively considered in this^21–28 and other systems²⁰ previously, particularly because it is relatively non-coordinating (as measured by, for example, the Kamlet–Taft β parameter³⁴) and hence ‘frees’ the cation to maximise the key interaction responsible for rate constant enhancement. Whilst other anions might be used, introducing greater anion–cation interactions would be anticipated to reduce the observed solvent effect. Previous work has also shown effects beyond ion-pairing in such cases,²⁴ complicating analysis.

Based on the initial studies with the pentyl linked system 5d, it was anticipated that the series of ionic liquids 5 would result in a rate constant enhancement of the reaction shown in Scheme 1 when present in the reaction mixture and that this rate constant enhancement would be greater than for the simple imidazolium-based ionic liquid 4 at corresponding mole fractions of ionic liquid. As such, the reaction outlined between benzyl bromide 1 and pyridine 2 was performed with each of the ionic liquids 5 as the solvent (at χ_IL > 0.7, with the ionic liquid only diluted by reagents), monitored using ¹H NMR spectroscopy and the rate constants determined at 295 K. However, as the salts 5a–c, f were solids, reaching such high proportions in the reaction mixture was not possible. As such, the reaction was also performed in mixtures of acetonitrile and ionic liquid at χ_ILca. 0.2 in order to compare all the ionic liquids 5. This proportion of ionic liquid has been used in similar systems, where similar changes in rate constant with proportion of ionic liquid, based on similar microscopic interactions, have been observed.^35–37 These data are shown in Table 1 and in Fig. S2 in the ESI.†

Table 1 The rate constants at 295.35 K for the reaction of benzyl bromide 1 with pyridine 2, shown in Scheme 1, in mixtures of an ionic liquid and acetonitrile at χ_IL = 0, ca. 0.2, and >0.7

Solvent	k 2/10^−4 L mol^−1 s^−1
Acetonitrile	6.64 ± 0.05
Solvent component^‡	k 2, χILca. 0.2^a/10^−4 L mol^−1 s^−1	k 2, χIL > 0.7^a^,^b/10^−4 L mol^−1 s^−1
a Uncertainties quoted are the standard deviation of triplicate results. b Ionic liquid diluted only by reagents, exact value reported in ESI.† c Data was interpolated from Yau et al. through an Eyring analysis. Uncertainties are compounded from uncertainties in activation parameters.^21 d Compound was isolated as a solid, and as such, k2 where χIL > 0.7 was not able to be acquired. e Data reproduced from Hawker et al.^27
[bmim][N(SO2CF3)2] 4	12.3 ± 0.3	14.5 ± 0.1^c
[m(mim)2][N(SO2CF3)2]25a^d	34.9 ± 1.2	—
[pr(mim)2][N(SO2CF3)2]25b^d	27.3 ± 0.4	—
[b(mim)2][N(SO2CF3)2]25c^d	10.3 ± 0.2	—
[pe(mim)2][N(SO2CF3)2]25d^e	17.9 ± 2.4	19.9 ± 1.2
[hx(mim)2][N(SO2CF3)2]25e	13.6 ± 1.5	19.6 ± 1.9
[hp(mim)2][N(SO2CF3)2]25f^d	16.5 ± 0.3	—
[o(mim)2][N(SO2CF3)2]25g	16.9 ± 0.2	15.3 ± 1.1
[n(mim)2][N(SO2CF3)2]25h	16.9 ± 0.2	20.8 ± 2.2
[d(mim)2][N(SO2CF3)2]25i	14.9 ± 0.4	19.6 ± 1.9
[ud(mim)2][N(SO2CF3)2]25j	14.5 ± 0.2	16.3 ± 1.9
[dd(mim)2][N(SO2CF3)2]25k	13.6 ± 0.3	16.2 ± 0.9

---

Immediately apparent from the data presented above is that there is a rate constant enhancement for the reaction shown in Scheme 1 on moving from acetonitrile to mixtures containing one of the ionic liquids 5 at χ_ILca. 0.2; ionic liquid 5a gave the greatest rate constant seen for this reaction in ionic liquids. For those ionic liquids 5 for which mixtures could be made containing a high proportion of the ionic liquid, the rate constants observed were either the same as, or slightly larger than, the rate constants for a lower mole fraction of ionic liquid. This comparison is consistent with what has been observed previously for this reaction.^26,27

It is now worth returning to the questions raised earlier. Significantly, carrying out the reaction between species 1 and 2 in each of the ionic liquids 5 did not result in the same rate constant in each case. That is, the length of the alkyl chain bridging the two centres is important. Further, the variation of rate constant with alkyl chain length is not straightforward (see Fig. S2 in the ESI†) though it might be argued to approach a constant value as the alkyl chain length increases. Irrespective, the chain length is important in determining the observed solvent effects and these results suggest that a combination of conformation and length restrictions in the alkyl linker affect the interactions between the cation of the ionic liquid and the reagent 2.

It is worth making a comparison between the reaction outcome in the bisimidazolium systems 5 and a representative monocationic ionic liquid 4. Generally, with the notable exception of ionic liquid 5c (again, reinforcing the potential of constraint in that case), all of the ionic liquids 5 resulted in an equal, if not greater, enhancement of the rate constant compared to [bmim][N(SO₂CF₃)₂] 4 for the reaction in Scheme 1 at corresponding mole fractions.¶ To a certain extent, this answers the question posed in the title; having two charged headgroups generally is at least as good as, if not better than, one in increasing the rate constant of the reaction shown in Scheme 1.

A final comparison of interest is between the rate constants for the ionic liquid 4 and the salt 5g containing an octyl linker between two imidazolium centres; this comparison is reasonable as the cation in salt 5g might be considered as two of the cations in salt 4 linked together. Importantly, molecular dynamics simulations have suggested that organisation (as measured by radial distribution functions) of the ions in solution is very similar between the two systems in neat ionic liquids.³⁸ The data presented for the higher mole fraction of salt (which best corresponds to those molecular dynamics simulations) show the same rate constant, consistent with similar organisation and interactions between the cation of the ionic liquid and pyridine 2 in each case. However, comparison of the data presented for the lower mole fraction of salt indicates that the bisimidazolium salt 5g reaches its “plateau” sooner than salt 4, importantly showing that the organisation of the cation of the ionic liquid about the pyridine 2 differs between the cases in these dilute solutions.

The data in Table 1 highlights two key points related to the impact of the proportion of ionic liquids 5 in the reaction mixture on the reaction outcome. The first is that the most significant change in rate constant occurs at low proportions of salt in the reaction mixture. The second point is that the effect of changing the proportion of salt in the reaction mixture is not clear for those systems with limited solubility. With these points in mind, Fig. 2 shows data from Table 1 augmented with rate constants over a broader range of concentrations for the solid cases 5a–c and the ionic liquids 5f, i (the latter as representative examples of longer chain alkyl linkers). The rate constants for the reaction in Scheme 1 were monitored as previously in these mixtures and Fig. 2 also includes data for the reference salt 4²⁶ and the pentyl linked system 5d²⁷ considered previously.

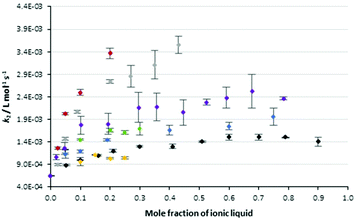Fig. 2 The bimolecular rate constants for the reaction between benzyl bromide 1 and pyridine 2 in different mole fractions of the salts 4 (◆), 5a (), 5b (), 5c (), 5d (), 5f () and 5i () in acetonitrile at 295.35 K. Uncertainties are reported as the standard deviation of three replicates; some uncertainties fall within the size of the markers used. Data for the salt 4 is reproduced from Schaffarczyk McHale et al.²⁶ Data for the salt 5d is reproduced from Hawker et al.²⁷

Before continuing, it is worth noting that the ordinate axis is the mole fraction of ionic liquid in the reaction mixture. An alternate analysis would use the mole fraction of the cation in the reaction mixture; while this does result in a slight offset of the data (as can be seen in Fig. S3 in the ESI†) it does not change the shape of the plots significantly and the interpretation below holds. This argument is consistent with that presented previously,²⁷ where no significant differences in the shape of the mole fraction dependence curves was seen between the two different analysis methods.

In general, the rate constant for the reaction of species 1 and 2 in mixtures containing the bisimidazolium-based ionic liquids showed similar dependence on the proportion of salt in the reaction mixture to that seen previously for other ionic liquids, including [bmim][N(SO₂CF₃)₂] 4. Specifically, a sharp increase in rate constant is observed on transitioning from acetonitrile to a mixture containing a low mole fraction of ionic liquid. The slope of this increase in rate constant reduces as the mole fraction of ionic liquid increases until a “plateau” is observed above χ_ILca. 0.6. For those salts 5 identified earlier as not being able to reach high proportions in the reaction mixture, this consistency was over a smaller range of mole fractions. Importantly, these data show that the effects of the bisimidazolium-based ionic liquids vary with the proportion of salt in the reaction mixture in the same way as been seen for other ionic liquids, allowing a degree of predictability in their effects.

Given that the principal interaction responsible for these changes in rate constant for this reaction is known to be the interaction of the cationic component of the ionic liquid with the nitrogen heteroatom of pyridine 2,^22,23 it is important to consider how this interaction might change with the presence of multiple charged centres on the cation of the ionic liquid. In order to evaluate these differences and to understand the origins of the observed rate constant changes shown in Fig. 2, temperature dependent kinetic studies, analogous to previous studies,^21–28 were performed to construct Eyring plots (Fig. S4–S6, ESI†) and thus quantify the activation parameters of the reaction shown in Scheme 1 in various solvent mixtures; the activation parameters at representative ionic liquid concentrations are shown in Table 2. Previous studies of the reaction described in Scheme 1 quantified the activation parameters when the ionic liquid of interest was the only solvent in the reaction mixture; the only other components of the mixture are the reagents. However, given that some of the salts of interest in this study were solid at room temperature (5a–c, f) and therefore required acetonitrile to give an homogeneous reaction medium, the activation parameters for the system were also quantified at χ_ILca. 0.2 (consistent with earlier in the work, but also previous literature on other, related systems^35–37).

Table 2 The activation parameters for the Menschutkin reaction of benzyl bromide 1 and pyridine 2, shown in Scheme 1, in varying mixtures of an ionic liquid and acetonitrile

Solvent component^‡	χ IL	ΔH^‡^a/kJ mol^−1	ΔS^‡^a/J K^−1 mol^−1
a Uncertainties quoted are derived from the fit of the linear regression. b Data reproduced from Yau et al.^21 c Data reproduced from Hawker et al.^27
Acetonitrile^b	0	43.3 ± 0.8	−241 ± 3
[bmim] [N(SO2CF3)2] 4	0.20	49.6 ± 0.6	−197 ± 2
	0.79^c	50.0 ± 0.8	−195 ± 3
[m(mim)2][N(SO2CF3)2]25a	0.19	60.7 ± 1.1	−151 ± 4
[pr(mim)2][N(SO2CF3)2]25b	0.20	50.3 ± 1.0	−189 ± 3
[b(mim)2][N(SO2CF3)2]25c	0.20	57.1 ± 1.1	−173 ± 4
[pe(mim)2][N(SO2CF3)2]25d	0.19	50.5 ± 1.8	−191 ± 6
	0.78^c	50.2 ± 1.9	−191 ± 7
[d(mim)2][N(SO2CF3)2]25i	0.21	51.1 ± 0.7	−191 ± 2
	0.76	48.8 ± 1.4	−197 ± 5

---

Before considering the effects of the ionic liquids 5, it is worth briefly considering the activation parameters in acetonitrile and mixtures containing the salt 4. Importantly, in acetonitrile, a large negative activation entropy (consistent with an associative process³⁹) is observed. On moving to mixtures containing the ionic liquid 4 an increase in both activation parameters is observed;|| the increase in the entropy of activation is more significant, and this balance results in an increase in the rate constant of the reaction at the temperatures considered. No significant difference is seen between activation parameters at the two proportions of ionic liquid considered, as is consistent with the limited difference between the rate constants at those two solvent compositions. These changes have been previously ascribed to organisation of the ionic liquid around the starting material, including the key interaction between the cation and pyridine 2.

For the ionic liquids 5d and 5i, for which activation parameters were quantified at both low and high χ_IL, the same effects were seen as was the case for salt 4, with an increase in both activation parameters and no significant difference between the cases with different proportions of ionic liquid in the reaction mixture.** Immediately, these data suggest that the interactions present in solution involving the bisimidazolium-containing systems 5d and 5i and the imidazolium-based salt 4 are not significantly different and that these are consistent across the different proportions of salt in the reaction mixture studied. These results are consistent with the data presented in Fig. 2 and with previous studies of other related systems.^35–37 Importantly, as the extents of interaction at the microscopic level do not significantly change as the proportion of ionic liquid increases past χ_IL = 0.2, this suggests that comparing the data at the lower mole fraction is valid in terms of identifying interactions in solution responsible for the observed solvent effects in ionic liquids, and allows comparison between these ionic liquids and those that were solids at room temperature.

Considering the mixtures containing one of the salts 5a–c, d, i at χ_IL = 0.2 together, it is clear that all of the salts have the same effects on the activation parameters; an increase in both parameters relative to the acetonitrile case, with the contribution of the entropy of activation being greater at the temperatures considered, accounting for the observed increases in rate constant relative to acetonitrile. Crucially, however, the magnitudes of these changes are not all the same.

Consider first the mixtures containing the salts 5b, d, i; these all have the same enthalpy of activation, and that enthalpy is the same as (or trivially higher than) for the reaction in mixtures containing the salt 4. Similarly, the entropy of activation values are the same for mixtures containing the salts 5b, d, i, and these are equal to (or slightly higher) than in the salt 4 case. Importantly, these similarities are indicative of similar extents of microscopic interactions in solution and suggest that the effects of having two cationic centres linked by an alkyl chain of 3, 5 or 10 carbon atoms has perhaps surprisingly does not change these interactions compared to the parent salt 4.

It is worth noting that the while the activation parameter data is the same for these systems 5b, d, i, they do have different rate constants (Table 1) for the reaction shown in Scheme 1. This outcome is consistent with the uncertainties in the activation parameter data, whilst reasonable, being large relative to the differences between the rate constants measured. Importantly, it does not alter the argument as to the origin of the rate constant change, that being the key interaction between the cation of the ionic liquid and the pyridine 2.

The similarities in activation parameters for the cases involving the salts 5b, d, i are even more surprising given the significant differences to those examples containing the salts 5a and 5c. In both of these latter cases, significant increases in the activation parameters are seen relative to both acetonitrile and the cases containing salts 5b, d, i; the effect is greater in the case of the ionic liquid 5a with the shorter methyl linker than it is in the case with propyl linker. Irrespective, greater interactions (which are broken on reaction occurring) are seen in these cases than others and there is a significant increase in the degrees of freedom of the system on moving to the transition state.

These different activation parameters implicate different mode of interactions and imply a measurable degree of cooperativity between the imidazolium centres in terms of interacting with the pyridine 2 in the case of the salts 5a and 5c. A bidentate interaction is implied, with the length of the alkyl chain being particularly important. While limited (and likely unmeasurable) cooperativity is reasonable for the systems with a long linker (salt 5i), the significant (and alternating) differences seen between the salts 5a–d suggest that the conformation of the linker chain is also significant and that predicting the magnitude of the solvent effect of these bisimidazolium-based ionic liquids is non-trivial.

Importantly, it is worth revisiting the rate constant data for the reaction in the presence of salts 5a and 5c; in the presence of the former, the rate constant is much greater than the latter (which is also slower than in the reference ionic liquid 4). Importantly, this comparison also indicates that the balance of enthalpic and entropic effects is markedly different between the two cases. This feature is represented pictorially in Fig. 3,†† which shows the contributions of enthalpy and entropy of activation to the change in the activation energy on moving to mixtures containing ionic liquids. Whilst this balance does vary between the systems considered, the potential for using biscationic systems is clear.

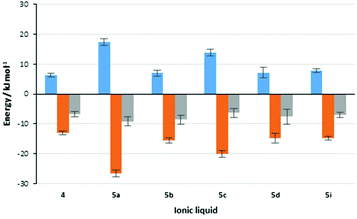Fig. 3 Contributions to the changes in rate constant for the reaction shown in Scheme 1 on moving from acetonitrile to a reaction mixture containing one of the ionic liquids 4 and 5a–d, I at χ_ILca. 0.2. Shown (left to right) are the change in activation enthalpy (Δ(ΔH^‡), ), the change in activation entropy multiplied by the negative temperature (−Δ(TΔS^‡), ) and the change in activation energy, which is the sum of the two previous terms (Δ(ΔG^‡), ). Uncertainties are derived from the uncertainties of the activation parameters described in Table 2.

Whilst the above arguments identify the microscopic interactions responsible for the rate constant increases seen, questions are often posed as to whether other properties, either measured or macroscopic, correlate (or not) with the observed rate constant date. Polarity is often invoked, but is a fraught concept in ionic liquids (as well-articulated by Kobrak; “the dipole moment of an ion is known to be dependent on the coordinate scheme chosen, making it an ill-defined physical quantity [for ionic liquids]”⁴⁰) and even ‘apparent’ polarity, based on a probe molecule, cannot explain the changes that are readily argued based on the microscopic interactions outlined above.²⁶ Viscosity measurements might be argued to potentially mirror the interactions responsible for the rate constant increase, but data at both χ_ILca. 0.2 and χ_IL > 0.7 (for the systems that are liquid at room temperature) do not parallel the changes in rate constant across the series 5a–k (see Fig. S8 and S9†).

Experimental

Benzyl bromide 1 was purified through distillation and stored over 3 Å molecular sieves at −6 °C and away from light until use. Pyridine 2 was purified through distillation and stored over 3 Å molecular sieves and sodium hydroxide at −20 °C until use. Acetonitrile was purified through distillation from phosphorus pentoxide and stored in an inert nitrogen atmosphere until use.⁴¹ The ionic liquids 4 and 5a–k were synthesised from freshly distilled N-methylimidazole and the corresponding freshly distilled 1-bromobutaine or an appropriate α,ω-dihaloalkane, then subsequent anion metathesis with lithium bis(trifluoromethanesulfonyl)imide; for full details of the preparation for each ionic liquid, see the ESI.† Before use, each ionic liquid was dried in vacuo for at least 5 hours resulting in <200 ppm water as determined by Karl Fischer titrimetry.

¹H NMR kinetic analyses were performed on a Bruker Avance III 400 with either a BBFO probe, a Bruker Avance III 500 with a TBI probe, or a Bruker Avance III 600 with a BBFO probe, using ca. 0.5 mL of reaction mixture in a 5 mm NMR tube. Results were shown to be reproducible between spectrometers.

For the studies involving varying the proportion of each of the ionic liquids 5 present in the reaction mixtures to determine their effect on reaction outcome, the reaction was carried out in solutions containing benzyl bromide 1 (ca. 3 mg), pyridine 2 (ca. 0.5 mol L⁻¹) and acetonitrile at 295.35 K. For the temperature dependent kinetic studies, the reactions were performed using mixtures of the above compositions in a temperature range of 295–318 K. In all cases, the reaction was monitored in situ with the spectrometer set to the desired temperature, measured using an external thermocouple, for the duration of the reaction.

All reactions were monitored until at least 95% of the benzyl bromide 1 was depleted, and all kinetic analyses were performed in at least triplicate. NMR spectra were processed using MestReNova software. The pseudo-first order rate constants (k_obs) for each reaction‡‡ were calculated from the linear fit of the extent of reaction based on the integrals of the benzylic proton of benzyl bromide 1 at δ ca. 4.0 using Microsoft Excel's LINEST function. The second order rate constants (k₂) were subsequently determined by dividing the calculated k_obs by the initial concentration of pyridine 2 in the mixtures; representative nucleophile 2 dependence studies (see Fig. S10–S12†) demonstrate that there is no first order contribution, consistent with previous analyses.^21–28 Activation parameters for the mixtures were determined by fitting all obtained data to the bimolecular Eyring equation using Microsoft Excel's LINEST function.^21,42

Viscosity data was determined using a Lovis 2000 ME microviscometer through the Rolling Ball Principle.

Conclusions

The effects of a series of bisimidazolium-based ionic liquids on a bimolecular substitution reaction were investigated, and the microscopic origins of these effects were determined. Significantly, the dependence of the rate constant on the proportion of ionic liquid in the reaction mixture followed a similar trend to those observed in previous studies; that is, in general, greater proportions of ionic liquid in the reaction mixture resulted in greater rate constants. This similarity is important as it allows the predictive framework developed for ionic liquids on this and similar reactions to be applied to broadly to these systems.

When compared to a monocationic imidazolium-based ionic liquid, the bisimidazolium-based ionic liquids generally resulted in greater rate constants at corresponding proportions of salt present in the reaction mixtures. In simple terms, this answers the question posed in the title – two headgroups are better than one if a greater rate constant for this reaction is required. However, this simplistic answer belies more subtle differences within the homologous series. The “best” bisimidiazolium salts (those that give the greatest rate constants) are not liquids at room temperature, and are limited in the amount that can be added to the reaction mixture. Further, the length of the linking alkyl chain influences the extent of rate constant enhancement and there is no immediately clear trend in the effect of the bisimidazolium salts on the reaction as the linking alkyl chain length increases. This latter point is significant as it demonstrates that understanding the effect of changing the length of the alkyl linker in the biscationic systems is important in choosing an appropriate ionic liquid.

Such understanding was obtained through considering the microscopic interactions of the bisimidazolium salts with components of the reaction mixture that effect reaction outcome. Whilst generally effects on activation parameters were the same as reported previously for this reaction and suggest that the key interaction involved the cation and the starting material, the balance of enthalpic and entropic effects differed markedly as the cation of the bisimidazolium systems changed. Importantly, these differences suggest that there are changes in the mode of interaction of the cation with the pyridine 2 starting material, particularly some degree of cooperativity between the two imidazolium centres of the ionic liquids used.

Overall, bisimidazolium-based ionic liquids can be used to enhance the rate constants of a bimolecular substitution reactions to greater extents than their monocationic counterparts. Although some bisimidazolium ionic liquids were isolated as solids and therefore had limited miscibility in the reaction mixtures, their effects were still significant and there is potential to exploit this property for easier recovery of the salts during the workup of the reactions. Further study will be required to fully understand the significance of linking alkyl chain length, and the importance of the conformation of the cations on their interactions with solutes, in order to fully optimise the interactions of bisimidazolium-based, and in general, biscationic, ionic liquids for use in organic reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. T. C. L. acknowledges the Australian Government for the award of a Research Training Program Scholarship. J. B. H. acknowledges financial support from the Australian Research Council Discovery Project Funding Scheme (Project DP180103682). The support of the Mark Wainwright Analytical Centre and the UNSW NMR facility are gratefully acknowledged.

Notes and references

1. J. S. Wilkes, J. Mol. Catal. A: Chem., 2004, 214, 11–17.
2. W. Ma, C. Chen, K. Kong, Q. Dong, K. Li, M. Yuan, D. Li and Z. Hou, Chem. – Eur. J., 2017, 23, 7287–7296.
3. B. Tang, W. Bi, M. Tian and K. H. Row, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2012, 904, 1–21.
4. L. Yu and G. Z. Chen, Front. Chem., 2019, 7, 272.
5. C. Verma, E. E. Ebenso and M. A. Quraishi, J. Mol. Liq., 2019, 276, 826–849.
6. S. Santner, S. Yogendra, J. J. Weigand and S. Dehnen, Chem. – Eur. J., 2017, 23, 1999–2004.
7. J. P. Hallett, C. L. Liotta, G. Ranieri and T. Welton, J. Org. Chem., 2009, 74, 1864–1868.
8. F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Green Chem., 2011, 13, 1453–1466.
9. S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517.
10. P. Painter, N. Pulati, R. Cetiner, M. Sobkowiak, G. Mitchell and J. Mathews, Energy Fuels, 2010, 24, 1848–1853.
11. Y. Pu, N. Jiang and A. J. Ragauskas, J. Wood Chem. Technol., 2007, 27, 23–33.
12. A. F. Cláudio, M. C. Neves, K. Shimizu, J. N. Canongia Lopes, M. G. Freire and J. A. P. Coutinho, Green Chem., 2015, 17, 3948–3963.
13. M. Freemantle, Chem. Eng. News, 1998, 76, 32–37.
14. R. R. Hawker, R. S. Haines and J. B. Harper, in Targets in Heterocyclic Systems, ed. R. Noto, Società Chimica Italiana, 2014, vol. 18, pp. 141–213.
15. C. Dai, J. Zhang, C. Huang and Z. Lei, Chem. Rev., 2017, 117, 6929–6983.
16. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
17. M. J. Earle, S. P. Katdare and K. R. Seddon, Org. Lett., 2004, 6, 707–710.
18. S. T. Keaveney, R. S. Haines and J. B. Harper, in Encyclopedia of Physcial Organic Chemistry, ed. U. Wille, Wiley, 2017, ch. 27, vol. 2.
19. A. Gilbert, R. S. Haines and J. B. Harper, in Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, ed. J. Reedjik, Elsevier, Waltham, MA, 2018,  DOI:10.1016/B978-0-12-409547-2.14212-X,  DOI:10.1016/B1978-1010-1012-409547-409542.414212-X.
20. R. R. Hawker and J. B. Harper, Adv. Phys. Org. Chem., 2018, 52, 49–85.
21. H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575.
22. H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371.
23. E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175.
24. S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35.
25. R. R. Hawker, J. Panchompoo, L. Aldous and J. B. Harper, ChemPlusChem, 2016, 81, 574–583.
26. K. S. Schaffarczyk McHale, R. R. Hawker and J. B. Harper, New J. Chem., 2016, 40, 7437–7444.
27. R. R. Hawker, R. S. Haines and J. B. Harper, Chem. Commun., 2018, 54, 2296–2299.
28. K. S. Schaffarczyk McHale, M. J. Wong, A. K. Evans, A. Gilbert, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 9243–9250.
29. C.-M. Jin, C. Ye, B. S. Phillips, J. S. Zabinski, X. Liu, W. Liu and J. N. M. Shreeve, J. Mater. Chem., 2006, 16, 1529–1535.
30. F. M. Menger and C. A. Littau, J. Am. Chem. Soc., 1991, 113, 1451–1452.
31. C. Rizzo, F. D'Anna and R. Noto, RSC Adv., 2016, 6, 58477–58484.
32. C. Rizzo, R. Arrigo, N. T. Dintcheva, G. Gallo, F. Giannici, R. Noto, A. Sutera, P. Vitale and F. D'Anna, Chem. – Eur. J., 2017, 23, 16297–16311.
33. X. Han and D. W. Armstrong, Org. Lett., 2005, 7, 4205–4208.
34. S. Spange, R. Lungwitz and A. Schade, J. Mol. Liq., 2012, 192, 137–143.
35. S. T. Keaveney, K. S. Schaffarczyk McHale, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2014, 12, 7092–7099.
36. S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 13, 3771–3780.
37. S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 13, 8925–8936.
38. R. M. Lynden-Bell, Mol. Phys., 2020, 118, e1580782.
39. J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, McGraw-Hill, New Yorks, 1995.
40. M. N. Kobrak and H. Lin, Phys. Chem. Chem. Phys., 2010, 12, 1922–1932.
41. W. L. F. Armarego and C. L. L. Chai, in Purification of Laboratory Chemicals, ed. W. L. F. Armarego and C. L. L. Chai, Butterworth-Heinemann, Oxford, 7th edn, 2009, pp. 88–444,  DOI:10.1016/B978-1-85617-567-8.50012-3.
42. H. Eyring, J. Chem. Phys., 1935, 3, 107–115.

---

Footnotes

† Electronic supplementary information (ESI) available: General experimental; details of the syntheses of the ionic liquids 5a–k; experimental details of the kinetic analyses; representative stacked plots; exact compositions of standard solutions and rate constants for the mole fraction dependence studies; plot of variation of rate constant with chain length in mixtures containing the ionic liquids 5; normalised mole fraction dependence plots for ionic liquids 5a–c,f,i; exact compositions of standard solutions and rate constants for the temperature dependent kinetic analyses; Eyring plots from which the activation parameters in Table 2 were calculated; pictorial representation of competing enthalpic and entropic effects χ_ILca. 0.7; ionic liquid 5 viscosity data at χ_ILca. 0.2 and χ_IL > 0.7; representative nucleophile dependence rate constant data; NMR spectra for ionic liquids used. See DOI: 10.1039/d0ob01500h

‡ Nomenclature used throughout is based upon common nomenclature for the 1-alkyl-3-methylimidazolium series; members of this series are frequently abbreviated [xmim]⁺, where x is the first letter of the name of the alkyl chain. A subscript second letter is used to distinguish between groups with the same first letter, say, propyl and pentyl substituents, and second (normal type) letter is used for carbon chains above 10 carbons in length (for example, dd for dodecyl).

§ Note that the ethyl-linked cation was not prepared, due to the difficulty in obtaining the carcinogenic 1,2-dibromoethane precursor.

¶ It should be noted that the comparison is done on the mole fraction of ionic liquid rather than the mole fraction of charged centres. This feature will be discussed explicitly below, but does not change the argument significantly here (in fact, it reinforces it).

|| Note that there is a decrease in the magnitude of the entropy of activation, but the value increases (becomes more positive).

** Note that for salt 5i, the activation enthalpies at the different mole fractions are beyond the uncertainty limits; however, this difference remains small compared to the other differences considered here.

†† The equivalent representation for the larger proportion of salt in the reaction mixture is presented in Fig. S7 in the ESI.†

‡‡ No deviation from first order behaviour was seen as the reaction proceeded, consistent with no observable effect of the ionic species 3 produced. This outcome is perhaps unsurprising, given the extremely small amount being formed in the reaction mixture, and is consistent with previous studies.^21–28

---