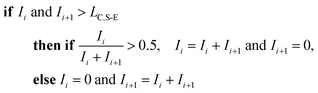Open Access Article
Open Access ArticleMonodisperse microdroplets: a tool that advances single-particle ICP-MS measurements
Alexander
Gundlach-Graham
 *a and
Kamyar
Mehrabi
*a and
Kamyar
Mehrabi
 b
b
aDepartment of Chemistry, Iowa State University, Ames, Iowa 50011, USA. E-mail: alexgg@iastate.edu
bDepartment of Chemistry and Applied Biosciences, ETH Zurich, 8093 Zurich, Switzerland
First published on 12th August 2020
Abstract
In single-particle inductively coupled plasma mass spectrometry (sp-ICP-MS), individual nanoparticles are detected by measuring ICP-MS signals with high temporal resolution. At high time resolution, particle-based signals—which are around 200–500 μs in duration—make up a larger fraction of the signal measured. If the dissolved background is low enough and the mass of element(s) of interest in the particles is high enough, then nanoparticle (NP) signals are recognized as signal spikes on the time trace. With modern instrumentation, sp-ICP-MS can be used to quantify NPs with element mass down to single-digit attogram levels. Monodisperse microdroplets composed of elemental solutions are vehicles for the transport of discrete amounts of elemental species into the ICP, and signals produced from microdroplets closely match those produced by NPs. Temporal durations and element sensitivities obtained from microdroplets and NPs are so similar that microdroplets may be used as NP proxies. Unlike NPs, microdroplets offer a flexible platform for user-designed sp-ICP-MS measurements because—with microdroplets—we can precisely control the absolute mass of elements injected into the plasma in each droplet. Controlled introduction of analyte mass into the ICP enables us to use microdroplets to generate sensitivity calibration factors and also to use microdroplets as NP proxies to study sp-ICP-MS measurement accuracy. Here, were report several instances of how measuring microdroplet-based element signals with ICP-TOFMS has allowed us to expand the versatility, as well as the general understanding, of sp-ICP-TOFMS measurements. First, we summarize how microdroplets can be used for online calibration of analyte NP element mass and particle-number concentration. Second, we describe how the measurement of microdroplets with tailored analyte masses helps us to refine, test, and validate sp-ICP-TOFMS data analysis strategies. Specifically, we use microdroplets to study the accuracy and robustness of split-event correction and signal-thresholding approaches for NP detection. Together, these experiments describe how the use of monodisperse microdroplets allows us to design better sp-ICP-MS experiments.
Introduction
Monodisperse microdroplets are not a new addition to the atomic spectroscopist's toolbox. In the past sixty years, many researchers have employed monodisperse microdroplets to study the interaction of aerosolized analyte with various atomization, excitation, and ionization sources for both optical and mass spectrometry. In principle, the use of uniform microdroplets is advantageous for fundamental studies because microdroplets replicate typical sample introduction approaches, i.e. nebulized aerosol, but are a well-controlled system which allows for the isolation of flame/plasma interactions from phenomena arising from the size heterogeneity of an ensemble of droplets.The use of monodisperse microdroplets in atomic spectrometry was pioneered in the late 1960's by Hieftje and Malmstadt for the study of droplet behavior in air–acetylene laminar flames.1,2 From the onset, microdroplet sample introduction was identified as an approach well-suited to probe sample–source interactions, with Hieftje's 1968 paper in Analytical Chemistry entitled, “A unique system for studying flame spectrometric processes.”1 Following this initial work, the Hieftje research group employed microdroplet measurements to study various fundamental aspects of sample–laminar flame interaction including processes of liquid-aerosol desolvation,3 particle evaporation,4 and atomic diffusion,5 and determinations of aerosol velocity.6,7 Several research groups have used monodisperse microdroplets to study fundamental properties of the inductively coupled plasma combined with either optical emission or mass spectrometric detection.8 Of specific note, most contemporary microdroplet introduction systems trace their roots back the monodisperse dried microparticulate injector (MDMI) system first reported by French et al.9 Over the years, variations of this microdroplet injection system have been used to study many processes in the ICP, including droplet desolvation,10,11 particle evaporation,12,13 local heating or cooling of the plasma,14,15 plasma-mass spectrometer interface characteristics,16 space-charge effects,17 and other matrix effects.18–21
Researchers have also employed monodisperse microdroplets as a sample carrier. Dissolved analyte can be introduced into the ICP as monodisperse microdroplets (or dried microdroplet particles) in order to have better control of sample-introduction related phenomena and thus better control of matrix effects and optimization for best absolute sensitivities.9,22–25 Discrete samples, such as single nanoparticles26–29 or cells30–32 can also be introduced within microdroplets for a more controlled sample introduction strategy compared to conventional pneumatic nebulization. For both single-nanoparticle and single-cell ICP-MS measurements, introduction of a sample with monodisperse microdroplets presents an attractive approach for quantitative transfer of analyte particles/cells into the plasma with the possibility of direct counting experiments for number concentration determinations. Quantitative transfer of individual microdroplets into the ICP allows for direct determination of absolute detection efficiencies (counts per g) of analyte elements in the microdroplet solution,26 which can be used to quantify the mass of elements in discrete entities injected into the plasma, such as single nanoparticles,28,29,33–38 or cells.
In 1994, Olesik and Hobbs wrote an article in Analytical Chemistry entitled “Monodisperse Dried Microparticulate Injector: A New Tool for Studying Fundamental Processes in Inductively Coupled Plasmas.”39 In that article, they discussed how time-resolved measurements of monodisperse microdroplets allow researchers to study previously inaccessible characteristics of ICP-OES and -MS. Likewise, here we explore how monodisperse microdroplets are a “tool” that we can use to help us understand and develop new measurement approaches for time-resolved ICP-MS measurements, such as with single-particle and single-cell ICP-MS. For this purpose, we use microdroplets in two general ways: as a calibration standard for absolute mass quantification and as a nanoparticle proxy to study acquisition and data processing strategies for accurate sp-ICP-MS quantification. Microdroplets are an excellent option for studying fundamentals of sp-ICP-MS because they overcome limitations of studies based solely on nanoparticle materials as a reference: namely, microdroplets can be delivered at known frequency, have a narrow analyte-mass distribution, and their elemental composition is easily adjusted.
Experimental
All experiments and experiment concepts presented here make use of a dual sample introduction setup, as depicted in Fig. 1. This setup has been described elsewhere.33,35–38,40,41 In this setup, microdroplets are produced by a microdroplet generator (50 μm diameter Autodrop Pipette, AD-KH-501-L6, MD-E-3000 dispensing system, Microdrop Technologies, GmbH, Germany) and introduced via a falling tube that is filled with a He/Ar gas mixture to accelerate solvent evaporation so that microdroplets are reduced to dried droplet residues by the end of the falling tube.26,42 Continuously nebulized samples are introduced via a pneumatic nebulizer and spray chamber, and then mixed with microdroplet-aerosols via a t-piece just in front of the injector base of the ICP torch. A video camera and triggered LED are used to stroboscopically image droplets to measure diameter—and, by calculation, volume—of spherical monodisperse microdroplets.43 RSDs for dropet volume are ∼1%. For ICP-MS measurements presented here, we used an ICP-TOFMS instrument (icpTOF 2R, TOFWERK AG, Switzerland), as already described elsewhere.34,44 Because the TOF mass analyzer provides simultaneous full mass spectrum detection at a high speed (21.739 kSpectra per s) and continuous readout of averaged spectra at ∼1000 Hz, the full analyte composition of each microdroplet can be quantitatively measured. Solutions for microdroplets were prepared by dilution of commercially available single-element standard solutions into either 1% sub-boiled HNO3 or a mixture of 1% HNO3 and 1% HCl. All dilutions were performed gravimetrically. TOFMS data are stored in the HDF5 file format, and all post-acquisition data processing was performed in LabVIEW (ver. 18.0, National Instruments, TX, USA). Data were plotted in OriginPro (ver. 2019b, OriginLab Corp., MA, USA) and final figures were assembled in Adobe Illustrator (ver. 24.1, Adobe Systems Inc., USA).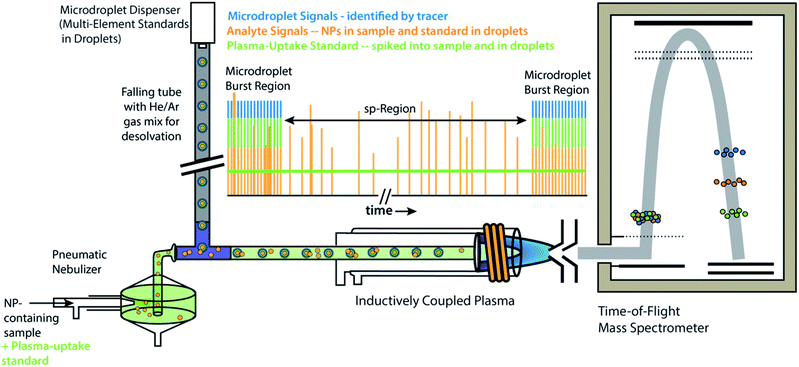 | ||
| Fig. 1 Schematic diagram online microdroplet calibration. In this setup, signals from analyte standards in microdroplets from the “Burst Regions” are used to determine absolute detection efficiencies (counts per g) for each analyte, which are then used to quantify the mass of elements in NPs from the “sp-Region.” The ratio of sensitivities from a plasma uptake standard in both microdroplets and spiked into NP-containing samples is used to determine volumetric flux of sample into the plasma (qplasma), which is necessary for particle-number concentration (PNC) determinations. This figure is adapted from Mehrabi et al.37 and is used under the creative common license. | ||
Results and discussion
sp-ICP-MS is often recognized as a premier analytical approach for the high-throughput determination of nanoparticle size (via element-mass quantification) and particle-number concentration (PNC). One reason sp-ICP-MS has been adapted broadly is because it makes use of widely available ICP-MS instrumentation. In addition, sp-ICP-MS remains the most viable approach for quantitative detection of inorganic nanomaterials at environmentally relevant concentrations.45,46 Since the first description of sp-ICP-MS for colloid measurements,47 hundreds of papers have been published about sp-ICP-MS, as well as several review papers.48–50 In those years, researchers have developed novel instrumentation26,51 and measurement strategies in order to improve the approach.52–55 Further, ICP-MS instrumentation companies have released updated instruments and software that enable more-or-less “plug-and-play” sp-ICP-MS measurements. Today, sp-ICP-MS is used as a routine approach.When nanoparticles (or micron-sized particles) are introduced into the ICP at low enough number concentrations, the ion clouds formed by the vaporization, atomization, and ionization of these particles are measurably discrete in both time and space. In sp-ICP-MS, these discrete ion clouds are registered as individual events by discrimination of their signals across time. The temporal duration of an individual particle in the ICP is usually 200–500 μs, and so by recording MS signals with millisecond (or sub-millisecond) time resolution, responses from individual particles can be measured as signal spikes. If analyte particles are quantitatively vaporized and ionized in the plasma, then sp-ICP-MS can—in principle—be used determine particle number concentrations (PNCs) and the amount of element(s) in individual particles. Very simply, quantification in sp-ICP-MS involves three steps, all of which affect the measurement's accuracy: first, NP signals must be accurately found, i.e. distinguished from background signals; second, found particle signals must be calibrated to reflect the amount of analyte elements in the particles; third, sample flux into the plasma must be determined to relate the number of found particles to number concentration.
It is an easy task itemize the fundamental requirements of a quantitative sp-ICP-MS experiment; however, validation of these measurements for a range of NP types and in various samples matrices is difficult. Basic understanding of the accuracy of sp-ICP-MS measurement and data analysis approaches is hampered by a lack of NP reference materials certified for both element mass and number concentration. This lack of standards has led to inconsistent measurement practices among researchers, which may cause confusion for new practitioners of sp-ICP-MS. For example, there is little consensus on significant measurement conditions such as optimal dwell time, most accurate method to determine transport efficiency and absolute elemental sensitivities,55–58 or robust signal-thresholding criteria for NP identification.59 There are, indeed, many researchers working to harmonize and standardize sp-ICP-MS measurements,60–63 but, without a suite of well-characterized reference NPs, this process remains a challenge.
In this paper, we present some recent efforts we've made to develop accurate methods for NP quantification for sp-ICP-TOFMS. Unlike ICP-MS with a quadrupole or sector-field mass spectrometer, with TOFMS, we have the ability to measure full elemental mass spectra at a time resolution suitable for single-particle analysis. Full-mass-spectrum detection with TOFMS allows us to perform multiplexed sp-ICP-MS experiments in which we can simultaneously measure signals from single-element NPs, multi-element NPs, microdroplets, and dissolved elemental species. Recently, sp-ICP-TOFMS has gained heightened interest for high-throughput screening of NPs and for measurement of multi-element signatures in NPs as a means to source single particles, i.e. as natural or engineered.37,64–68 In our sp-ICP-TOFMS measurements, we use microdroplet sample introduction in two distinct ways: (1) for online calibration of NP mass in individual NPs, and (2) as a tool to study data analysis approaches for the quantitative detection of fast transient signals, which is critical for reliable PNC determination in sp-ICP-TOFMS. In both of these applications, microdroplets are a flexible platform for controlled introduction of discrete masses of analytes which allow us to better probe sp-ICP-TOFMS measurements.
Calibration with microdroplets
We have described online microdroplet calibration in several recent publications.35–37 Here, we provide a brief overview of how microdroplet-generated signals provide a route for calibration of element mass in individual analyte nanomaterials. Unlike all other approaches for sp-ICP-MS quantification, online microdroplet calibration does not rely on the use of external reference nanoparticles or the stability of analyte sensitivities and sample transmission efficiencies into the plasma between measurements. Instead, analyte sensitivities and plasma uptake rate are calibrated in every measurement for each sample. A schematic diagram of our sample introduction setup is provided as Fig. 1, and a flow chart of the overall online microdroplet calibration procedure is provided in Fig. 2.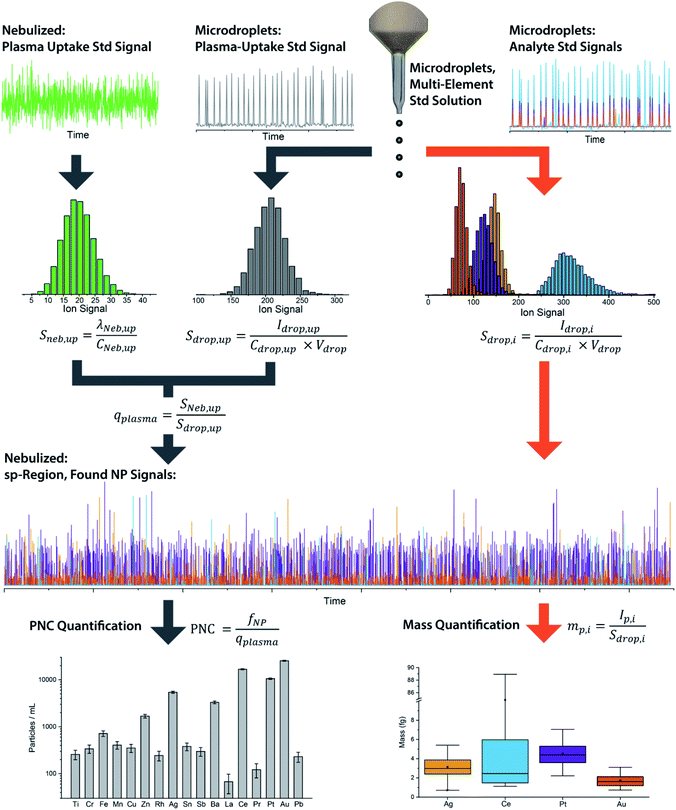 | ||
| Fig. 2 Flow chart of the basic steps and equations in online microdroplet calibration. In this calibration approach, no external NP reference materials are required. For each measurement, sample-dependent absolute sensitivities (Sdrop,i) of each element, i, and volumetric flux into the plasma (qplasma) are determined in order to correct for any potential matrix-effects. Mass calibration of analytes in NPs is done based on the average absolute sensitivities of analytes in microdroplets (Sdrop,i). The absolute sensitivities of the uptake standard in microdroplets (Sdrop,up, counts per g) divided by the concentration-based sensitivity for the plasma uptake standard spiked into the nebulized sample (Sneb,up, count per s per g per mL) is used to determine qplasma. Data used here is for explanatory purposes only and is taken from our study of the quantification of Ag, Pt, and Au NPs spiked into waste-water treatment plant effluent.37 | ||
In online microdroplet calibration, we use a dual sample introduction approach in which microdroplets composed of solutions with known multielement concentrations are introduced into the ICP along with sample nebulized via conventional pneumatic nebulizer and spray chamber. Because the volume of each microdroplet can be measured, we know the mass of analyte injected with each microdroplet. Based on the average intensities recorded from microdroplets, we obtain absolute detection efficiencies for each analyte, i, (Sdrop,i, counts per g), which are then used to calibrate the mass(es) of element(s) in NPs. In addition to analyte standards, we add a known amount of a plasma-uptake standard into both microdroplets and nebulized samples in order to determine the sample-specific flow rate (mL s−1) into the plasma (qplasma). This plasma uptake rate is equal to the ratio of the relative sensitivity of the plasma-uptake standard in the nebulized sample (Sneb,up, cps g mL−1) to the absolute sensitivity from microdroplet signal (Sdrop,up, counts per g).
With online microdroplet calibration, microdroplet standards, analyte particles, and sample matrix all are introduced concurrently, and so experience the same plasma conditions, which leads to inherit matrix-matched calibration.36 Because sensitivities from the plasma-uptake standard in the sample and in microdroplets are matrix-matched, online determination of qplasma corrects for sample-introduction related matrix effects.37 To date, we have tested our system for direct quantification of NPs in beverages,35 solutions with variable acid concentrations,36 heavy-element-rich matrices,36 surfactant-containing matrices,37 waste-water,37 and biologically-relevant matrices.36,37 In all of these cases, online microdroplet calibration has provided accurate element mass quantification, and—in those studies where we studied PNC—accurate PNCs. While we have demonstrated online microdroplet calibration with ICP-TOFMS analysis, the approach is also applicable for analysis with quadrupole or sector-field MS instruments; however, signals from multiple element standards will likely need to be obtained in separate runs.38
Microdroplets as NP proxies
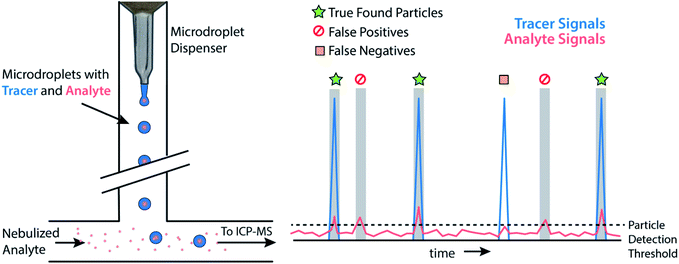
Monodisperse microdroplets are an excellent tool to study the effects of instrument parameters and data analysis procedures on the results produced by sp-ICP-MS. Here, microdroplets can be thought of as a nanoparticle proxy: microdroplet-derived ICP-MS signals have comparable temporal durations and sensitivities as their NP counterparts. However, unlike NPs or other particle reference materials, such as element-doped polymer beads,69 researchers can easily adjust the composition of microdroplets by controlling analyte concentration and the size of produced microdroplets. This allows researchers to quickly probe an instrument's analytical figures of merit such as absolute mass detection limits or linear dynamic range for single-particle analysis.23,34 It also allows for the design of unique experiments to quantitatively investigate critical parameters of sp-ICP-MS, such as the ability to accurately count NP signals.In Fig. 3, we provide a general outline of microdroplet tracer-analyte experiments that can be used to assess the accuracy of NP counting by sp-ICP-MS. In these experiments, microdroplets are composed of a solution with at least two elements: one of which serves as the “tracer” and is at high concentration so that it is easily detectable, and the other of which is the “analyte” at a lower concentration to simulate a challenging sp-ICP-MS measurement. Analyte element(s) may also be introduced via pneumatic nebulizer/spray chamber in order to simulate dissolved background. With this setup, we can probe the ability to quantify signals from analyte microdroplets at controlled particle-to-background signal ratios.
Accurate single-particle finding
A limiting factor in the determination of PNCs is the accurate counting of particles. To detect particle signals against a dissolved-ionic background, one must be able to statistically determine the likelihood that a given signal comes from a steady-state background. If that signal is considered “unlikely” to come from the background, i.e. it is an “outlier,” then it is counted as a particle. The threshold above which signals can be considered to reside outside the signal distribution from dissolved background is called the “critical value,”70 and is calculated based on the shape of the background distribution and the acceptable false-positive rate as defined by the experimenter. In typical sp-ICP-MS analyses, the background distribution is considered normally distributed and the critical value for particle detection is usually defined as μ + nσ, where μ is the average background signal, σ is the background standard deviation, and n is a user-defined factor that controls the number of standard deviations away from the mean to set the single-particle threshold.53,71 In most cases, n is selected as an integer, and for a Normal Distribution, critical values of 3σ or 5σ have defined false-positive rates of 0.135% or 0.0032%, respectively. For low-count-rate backgrounds, several researchers have proposed defining critical values based on the Poisson distribution, such that the critical value is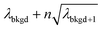 , where λbkgd is the average background count rate and n is an integer.59,72
, where λbkgd is the average background count rate and n is an integer.59,72
For ICP-TOFMS, we have shown that ion signals are neither Gaussian nor Poisson distributed; instead, signals follow a compound-Poisson distribution that is the result of Poisson-distributed ion arrival and the response function of the electron-multiplier detection system.40,41 Because distributions of ICP-TOFMS signals have a unique compound-Poisson shape, accurate separation of background signals from particle signals requires a distinct critical value, LC(ADC), that is calculated via Monte Carlo methods.40LC(ADC) is the net-signal critical value, i.e. critical value for background-subtracted-signal, and can be calculated for any false-positive rate, which is defined as the alpha (α) value. For particle identification, we typically set α = 0.01%, and term this the single-particle critical value, LC,sp. Every element has a unique LC,sp based on their average background count rates (λbkgd) in each measurement. Detailed explanation of how element-specific background rates and critical values are determined is beyond the scope of this paper. What is essential for discussion here is that the measurement of monodisperse microdroplets offers a unique possibility to experimentally examine and validate sp-ICP-TOFMS data analysis strategies.
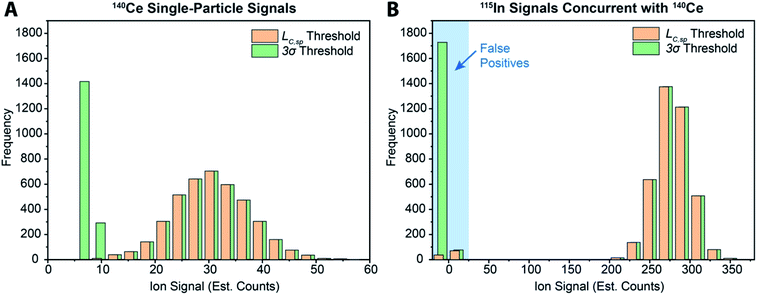
While various signal-thresholding approaches have been proposed to discriminate particle signals from background in sp-ICP-MS, there is no direct way to study the accuracy of single-particle finding using NPs. Even with well-defined NP reference materials, the possibilities of particle dissolution, aggregation, or adsorption to sample-introduction surfaces always cause uncertainty in the true PNC of sample reaching the ICP-MS. Here, the detection of multi-elemental microdroplets in a tracer-analyte experiment offers an absolute method for assessing the accuracy of single-particle detection thresholds. For example, in Fig. 4, we present results in which microdroplets were composed of a solution with 100 ng mL−1 In (tracer) and 10 ng mL−1 Ce (analyte). The microdroplets were 66.7 μm in diameter, so each droplet contained 15 fg 115In and 1.4 fg 140Ce, and microdroplets were introduced in a background created by nebulization of a solution containing 1 ng mL−1 Ce. Microdroplets were introduced at 20 Hz for 202.4 s, which resulted in 4048 true microdroplet events. Analyte Ce particle events are then “detected” based on either 3σ or LC,sp. In both cases, data were background-subtracted and split-event corrected prior to particle-event thresholding. After Ce single particles are identified, the amount of tracer signal concurrent with each detected particle event is determined. If 115In signal is present concurrent with a found Ce-particle signal, then that particle is a true detection event. However, if no 115In signal is present with the found Ce particle event, then the Ce signal actually originates from the dissolved background and is classified as a false positive.
As can be seen in Fig. 4a, with a 3σ single-particle detection threshold, many false positive events are measured: of the 5782 Ce particles “found,” 1805 of them are false positives, which corresponds to a false-positive rate of ∼0.9%—well above the 0.135% false-positive rate predicted for a 3σ critical value. Because the number of measured particle-events is always low compared to background events, small discrepancies in false-positive rates can lead to large errors in particle-number determination. The 3σ particle-event detection threshold is unsatisfactory for sp-ICP-TOFMS because background distributions are not normally distributed, and so the standard deviation does not accurately describe the spread of the background signals. On the other hand, thresholding data with LC,sp results in just 108 false positives, i.e. a 0.05% false-positive rate. However, even with LC,sp, we overshoot the number of predicted false positives: at an α value of 0.01%, we expect to measure just 20 false-positive events. As will be shown in the next section, about 70% of the false-positive Ce signals are caused by mis-registration of data following split-event correction; the remaining false-positive Ce signals are in-line with that predicted by thresholding with LC,sp.
In Table 1, we provide NP-detection thresholds and false-positive rates found for thresholding our Ce-microdroplet data with normal statistics using standard-deviation-based critical values (3σ and 5σ) and Poisson statistics using lambda-based critical values (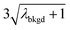 and
and 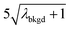 ),59 as well as compound-Poisson based critical values (LC(ADC)) for false-positive rates of 0.1% and 0.01%. We find that neither the sigma-based method or the solely Poisson method for critical value assignment is able to accurately predict the number of false positives measured. Reasonable discrimination of single-particle signals does seem to be possible with both 5σ and
),59 as well as compound-Poisson based critical values (LC(ADC)) for false-positive rates of 0.1% and 0.01%. We find that neither the sigma-based method or the solely Poisson method for critical value assignment is able to accurately predict the number of false positives measured. Reasonable discrimination of single-particle signals does seem to be possible with both 5σ and 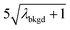 ; however, we still measure a much higher false positive rate than we would expect for signals that were truly Gaussian or Poisson distributed. In the case of unknown particles analysis, it is crucial to be able to predict the number of false positive detection events in order to evaluate their contribution to measured PNCs and particle-mass distributions. Because we know the TOFMS background signal follows a compound-Poisson distribution, it is best to assign NP-detection thresholds according to this distribution. As shown in Table 1, the thresholding particle signals based on LC(ADC) is more robust: the false-positive rates found nearly match the numbers predicted.
; however, we still measure a much higher false positive rate than we would expect for signals that were truly Gaussian or Poisson distributed. In the case of unknown particles analysis, it is crucial to be able to predict the number of false positive detection events in order to evaluate their contribution to measured PNCs and particle-mass distributions. Because we know the TOFMS background signal follows a compound-Poisson distribution, it is best to assign NP-detection thresholds according to this distribution. As shown in Table 1, the thresholding particle signals based on LC(ADC) is more robust: the false-positive rates found nearly match the numbers predicted.
| Threshold ion signal | Number particles found | Number false positivesa | False-positive rate (%) | Predicted false-positive rate (%) | Error in particle counting (%) | |
|---|---|---|---|---|---|---|
| a Number of false positives is corrected for mis-registered Ce–In multi-element particle events. b L C(ADC) expressions are determined empirically from Monte-Carlo simulations of the Poisson-distributed arrival of ions compounded with the detector response function of the TOF detector. | ||||||
| Sigma-based thresholding | ||||||
| σ bkgd | 2.03 | |||||
| 3σbkgd | 6.08 | 5782 | 1734 | 0.867 | 0.135 | 42.8 |
| 5σbkgd | 10.13 | 4079 | 34 | 0.017 | 0.003 | 0.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Poisson-distribution based thresholding | ||||||
| λ bkgd | 3.76 | |||||
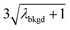
|
6.55 | 5203 | 1155 | 0.578 | ∼0.135 | 28.5 |
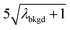
|
10.91 | 4074 | 30 | 0.015 | ∼0.003 | 0.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Compound-Poisson based thresholding | ||||||
L
C(ADC) (α = 0.1%), 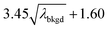 |
8.30 | 4272 | 225 | 0.113 | 0.100 | 5.5 |
L
C(ADC) (α = 0.01%), 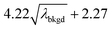 |
10.45 | 4082 | 37 | 0.019 | 0.010 | 0.8 |
Split-event correction
In sp-ICP-MS measurements in which dwell times are larger than the temporal duration of particle events, particle-signals that span across data measurement bins are called “split events.”73 If not corrected, these split-event signals will lead to the truncation of signal intensities, and can lead to errors in particle counting because single NP events may be registered as multiple particles. A distinction should be made for between split events with millisecond sp-ICP-MS and sp-ICP-MS in which microsecond dwell times are used.51,74–76 In the latter, all NP signal durations are longer than measurement bins and so signals from every NP are “split.” Microsecond data acquisition can be used to improve S/N ratio to some extent because less noise is integrated in each measurement bin.77 We will not discuss microsecond sp-ICP-MS here; instead, we study the necessity of finding and correcting split events for millisecond sp-ICP-MS.In the beginning of sp-ICP-MS development, the quadrupole-based ICP-MS instruments employed had a settling time between each measurement bin so that data from split events was not recoverable and dwell times were chosen to be long (ca. 10 ms) to reduce the chance of split events.78,79 However, most ICP-MS instruments now offer continuous data acquisition, so that single-particle data spread across two or more measurement bins can be put back together.80 This is the case for our ICP-TOFMS measurements: with our setup, mass spectra are measured continuously at a rate of ∼1000 Hz, which is comparable to a “dwell time” of 1 ms, though all isotopes are measured in this “dwell.” With a measurement time resolution of 1 ms or higher, signals from single particles are most often contained within a single spectral acquisition, but are sometimes split across two acquisitions.
To correct for split events with sp-ICP-TOFMS, we again must consider the shape of the background-signal distribution. In the case of ICP-TOFMS, the background distribution has a compound-Poisson shape that we can model by Monte Carlo methods.40 For split-event correction, we'd like to be able to find as many true split events as possible, but also avoid adding noise to the particle distribution through false identification of split events. To find split events, we use an outlier approach similar to that used for identifying single NPs, but use a lower split-event (S-E) threshold in order to find split events for low-intensity NPs that might not have a signal above the single-particle threshold (i.e. LC,sp). In particular, we set the S-E threshold to LC(ADC) with α = 1%: split events are found if two adjacent signals are both above the S-E threshold (LC,S-E). With the LC,S-E set at a false positive rate of 1%, the chances of having two adjacent events above this critical value is (0.01)2 or 0.01%. Following identification of a split event, the signals are summed and this summed signal is registered into the measurement bin that has the largest ion signal of the pair; a zero is placed in the other measurement bin. For adjacent signals, Ii and Ii+1, located at times ti and ti+1, the split event correction algorithm can be written:
For sp-ICP-TOFMS, the signals from all m/z-channels of interest are processed individually for split-event correction because multi-elemental composition of NPs cannot be assumed.
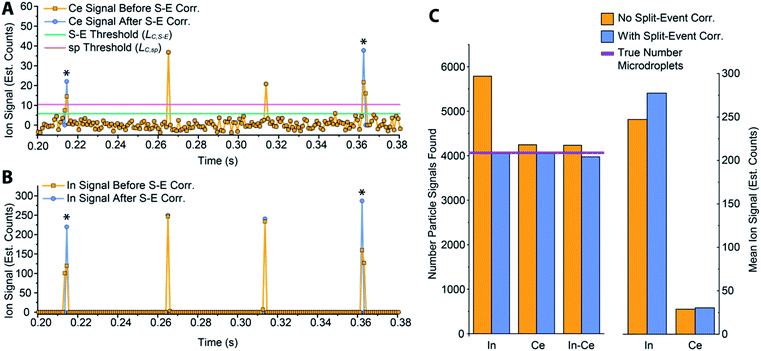
In Fig. 5, we provide a subsection of the background-subtracted time traces before and after split-event correction for the same tracer-analyte microdroplet experiment described in the previous section. In these time traces, split-event signals are marked with an asterisk, and it can be seen that split events found for analyte (140Ce) match those from the tracer (115In). In Fig. 5c, we plot the number of split-event signals found for the tracer and analyte. Many more split events are found for 115In because the signal:background ratio (SBR) is over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, whereas the SBR for Ce is ∼10. For 115In signals, tails of the split-particle events are well above the background and so are easily found based on LC,S-E. Because 115In signals have such high SBR, it is extremely important to find all split events; without S-E correction, In signals would be counted 43% higher than the true number, and the average signal intensity would be 11% too low. For the Ce signals, which have lower SBR, S-E correction is less important; however, no S-E correction would still result in a 5% overshoot in particle number and 5% undershoot in terms of average signal intensity.
000, whereas the SBR for Ce is ∼10. For 115In signals, tails of the split-particle events are well above the background and so are easily found based on LC,S-E. Because 115In signals have such high SBR, it is extremely important to find all split events; without S-E correction, In signals would be counted 43% higher than the true number, and the average signal intensity would be 11% too low. For the Ce signals, which have lower SBR, S-E correction is less important; however, no S-E correction would still result in a 5% overshoot in particle number and 5% undershoot in terms of average signal intensity.
After split-event correction, the particle number for both the tracer (115In) matches the number of microdroplets introduced into the ICP: 4048 droplets. The number of found Ce-particle events is slightly more: 4082 events. However, as seen in Fig. 5c, the number of concurrent In–Ce is not quantitatively determined. This occurs because 115In and 140Ce signals from split events are summed and then registered into the first or second bin of the split event. For low Ce-signals, ion statistics are a dominate factor in whether the first or second bin of the split event is more intense, and so the ratio of signal from the first to the second bin of a S-E for 140Ce does not necessarily match the ratio of these signals for 115In. Additionally, in the icpTOF instrument, m/z-dependent travel time through ion optics upstream of the TOF mass analyzer can cause slight m/z-dependent time shifts in measured droplet or NP signals.44 Overall, 74 of the 4048 microdroplet signals, or 1.8%, had mis-registered 115In–140Ce signals. This multi-element mis-registration rate is a limitation of current ICP-TOFMS instrumentation and split-event correction strategies. However, it only through the development of analyte-tracer microdroplet experiments that we are able to quantify and begin to understand the possibility of such sources of error in multi-elemental sp-ICP-TOFMS analysis.
In Fig. 6, we report uncorrected and split-event-corrected histograms for 115In and 140Ce. As shown, without split-event correction, a broad tail of signal intensities due to partial microdroplet detection events stretches across the ion signal range. Through using LC,S-E—which is controlled by the average dissolved background signal—as a decision threshold for the presence of split-events, there is no defined ratio of high-to-low signals that must be present to flag a split event.80 In turn, this means that our split-event correction method functions equally well for high-intensity and low-intensity particle signals and will capture as many split-event signals as possible. Independence of split-event correction on particle signal intensity is essential for characterization of unknown particles in real samples, where the particle intensity distributions will likely be broad and varied for different elements present in particle form. For our split-event correction method to function appropriately, the complete signal duration from a single-particle event needs to be less than the duration of one spectral acquisition, e.g. 1 ms for the given experiment, so that a given particle can have signal split across a maximum of two measurement bins. In addition, PNC needs to be low enough to have a low likelihood of single particles in adjacent measurement bins.80 Here, we demonstrate capabilities of split-event correction for a two-element microdroplet system; however, in the future this could be extended to explore split-event correction and particle-signal registration for many-element systems.
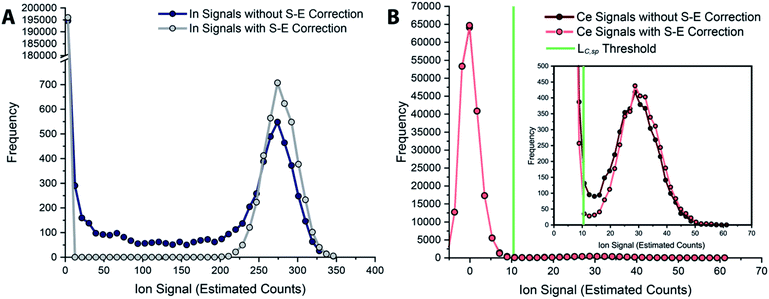 | ||
| Fig. 6 Histograms of tracer (A) and analyte (B) signals without and with split-event correction. Signals from both datasets are background subtracted. | ||
Conclusions
For highly time-resolved ICP-MS measurements, microdroplets composed of multi-elemental acidic solutions behave very similarly to nanoparticles with similar total analyte masses (attograms to 100s of femtograms). This similar response allows us to substitute microdroplets for NP reference materials for the quantification of NP analytes, as well as for the characterization of sp-ICP-MS data collection and analysis strategies. Microdroplets are an attractive tool for use with sp-ICP-TOFMS due to a number of special characteristics:(1) Tunable droplet size with highly repeatable volume.
(2) Controllable generation frequency.
(3) Flexible elemental composition.
(4) Quantitative analyte transfer; known injection of discrete element masses into plasma with no sample carryover.
(5) Well-defined temporal response; comparable to that of NPs.
(6) Similar detection efficiencies (counts per g) as NPs with ICP-MS.
(7) Possibility of concurrent microdroplet and nebulized sample introduction.
Here, we have explored how microdroplets can be used to calibrate sp-ICP-MS, both in terms of NP mass and particle number concentration. When combined with sp-ICP-TOFMS, online microdroplet calibration is a powerful method for untargeted quantitative single-particle analysis. This methodology enables detection of NPs in situ in varied matrices and at relevant PNCs. We anticipate expanded application and validation of online microdroplet calibration as an alternative to NP-based calibration approaches for sp-ICP-MS.
In addition to the benefits of microdroplets for particle calibration, microdroplets are an ideal medium through which to test performance of sp-ICP-MS measurements. Through the development of tracer-analyte microdroplet experiments, we can—for the first time—provide a truly quantitative assessment of the accuracy of sp-ICP-MS data acquisition and processing procedures. Here, we demonstrate microdroplets as a tool to study approaches for split-event correction and single-particle detection with ICP-TOFMS. In the future, microdroplets as proxies for multi-elemental NPs may serve as tools to improve robustness of multi-elemental fingerprinting approaches.
Finally, while we focused on use of microdroplets for calibration and as NP proxies, microdroplets can also be carriers of analyte particles. With even the most sophisticated pneumatic nebulization/spray chamber designs, sample transport is non-quantitative and particle-size fractionation in polydisperse aerosols from the nebulizer can lead to sampling biases, which could affect the particles measured by ICP-MS. With microdroplet-based sample introduction, total consumption and quantitative transport of analyte in each microdroplet could reduce sampling bias and thus improve quantification of element-mass distributions in analyte particles or cells. Low volumetric throughput for microdroplet sample introduction remains a challenge for detection of anthropogenic NPs at environmentally relevant PNCs (102 to 106). Nonetheless, we anticipate continued development of high-frequency microdroplet sample introduction systems for improved low-volume sample introduction and also for single-NP and single-cell analyses.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors dedicate this manuscript to Prof. Gary M. Hieftje. A. G.-G. obtained his PhD under the guidance of Prof. Hieftje; much of work presented here is built upon the transformative work of Prof. Hieftje's group, who pioneered both use of monodisperse microdroplets in atomic spectrometry and the development of ICP-TOFMS. The authors also acknowledge the support of Prof. Detlef Günther and the entire Trace Element and Microanalysis research group at ETH Zurich for the use of instrumentation and lab space, and fruitful discussions. A. G.-G. and K. M. K. would like to thank the Swiss National Science Foundation for funding through an Ambizione grant, project no. PZ00P2_174061. A. G.-G. also acknowledges funding through a faculty start-up grant at Iowa State University.References
- G. M. Hieftje and H. V. Malmstadt, Unique system for studying flame spectrometric processes, Anal. Chem., 1968, 40, 1860–1867 CrossRef CAS.
- G. M. Hieftje and H. V. Malmstadt, New approach to flame spectrometric analysis utilizing isolated droplets of sample solution, Anal. Chem., 1969, 41, 1735–1744 CrossRef CAS.
- N. C. Clampitt and G. M. Hieftje, Mechanism of desolvation of sample droplets in flame spectrometry, Anal. Chem., 1972, 44, 1211–1218 CrossRef CAS.
- G. J. Bastiaans and G. M. Hieftje, Vaporization of individual solute particles in flame spectrometry, Anal. Chem., 1974, 46, 901–910 CrossRef CAS.
- C. B. Boss and G. M. Hieftje, Theoretical study of the spatial distribution of atoms surrounding an individual solute particle vaporizing in an analytical flame, Anal. Chem., 1979, 51, 895–901 CrossRef CAS.
- C. B. Boss and G. M. Hieftje, Calculation of the velocity of a desolvating aerosol droplet in an analytical flame, Anal. Chem., 1977, 49, 2112–2114 CrossRef CAS.
- R. E. Russo and G. M. Hieftje, An accurate model for sample droplet acceleration in an air—acetylene flame, Anal. Chim. Acta, 1980, 118, 293–299 CrossRef CAS.
- J. W. Olesik, Elemental Analysis Using ICP-OES and ICP/MS, Anal. Chem., 1991, 63, 12A–21A CrossRef CAS.
- J. B. French, B. Etkin and R. Jong, Monodisperse Dried Microparticulate Injector for Analytical Instrumentation, Anal. Chem., 1994, 66, 685–691 CrossRef CAS.
- J. A. Horner, S. A. Lehn and G. M. Hieftje, Computerized simulation of aerosol-droplet desolvation in an inductively coupled plasma, Spectrochim. Acta, Part B, 2002, 57, 1025–1042 CrossRef.
- C. C. Garcia, A. Murtazin, S. Groh, M. Becker and K. Niemax, Characterization of particles made by desolvation of monodisperse microdroplets of analyte solutions and particle suspensions for nanoparticle calibration in inductively coupled plasma spectrometry, Spectrochim. Acta, Part B, 2010, 65, 80–85 CrossRef.
- J. A. Horner, G. C. Y. Chan, S. A. Lehn and G. M. Hieftje, Computerized simulation of solute–particle vaporization in an inductively coupled plasma, Spectrochim. Acta, Part B, 2008, 63, 217–233 CrossRef.
- O. Borovinskaya, M. Aghaei, L. Flamigni, B. Hattendorf, M. Tanner, A. Bogaerts and D. Gunther, Diffusion- and velocity-driven spatial separation of analytes from single droplets entering an ICP off-axis, J. Anal. At. Spectrom., 2014, 29, 262–271 RSC.
- G. C. Y. Chan and G. M. Hieftje, Local cooling, plasma reheating and thermal pinching induced by single aerosol droplets injected into an inductively coupled plasma, Spectrochim. Acta, Part B, 2016, 121, 55–66 CrossRef CAS.
- S. Groh, C. C. Garcia, A. Murtazin, V. Horvatic and K. Niemax, Local effects of atomizing analyte droplets on the plasma parameters of the inductively coupled plasma, Spectrochim. Acta, Part B, 2009, 64, 247–254 CrossRef.
- I. I. Stewart, C. E. Hensman and J. W. Olesik, Influence of Gas Sampling on Analyte Transport within the ICP and Ion Sampling for ICP-MS Studied Using Individual, Isolated Sample Droplets, Appl. Spectrosc., 2000, 54, 164–174 CrossRef CAS.
- J. W. Olesik and M. P. Dziewatkoski, Time-resolved measurements of individual ion cloud signals to investigate space-charge effects in plasma mass spectrometry, J. Am. Soc. Mass Spectrom., 1996, 7, 362–367 CrossRef CAS PubMed.
- J. W. Olesik, Investigating the Fate of Individual Sample Droplets in Inductively Coupled Plasmas, Appl. Spectrosc., 1997, 51, 158A–175A CrossRef CAS.
- A. C. Lazar and P. B. Farnsworth, Matrix Effect Studies in the Inductively Coupled Plasma with Monodisperse Droplets. Part II: The Influence of Matrix on Spatially Integrated Ion Density, Appl. Spectrosc., 1999, 53, 465–470 CrossRef CAS.
- A. C. Lazar and P. B. Farnsworth, Matrix Effect Studies in the Inductively Coupled Plasma with Monodisperse Droplets. Part I: The Influence of Matrix on the Vertical Analyte Emission Profile, Appl. Spectrosc., 1999, 53, 457–464 CrossRef CAS.
- A. Murtazin, S. Groh and K. Niemax, Investigation of sample introduction- and plasma-related matrix effects in inductively coupled plasma spectrometry applying single analyte droplet and particle injection, Spectrochim. Acta, Part B, 2012, 67, 3–16 CrossRef CAS.
- K. Shigeta, H. Traub, U. Panne, A. Okino, L. Rottmann and N. Jakubowski, Application of a micro-droplet generator for an ICP-sector field mass spectrometer – optimization and analytical characterization, J. Anal. At. Spectrom., 2013, 28, 646–656 CAS.
- O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Gunther, A prototype of a new inductively coupled plasma time-of-flight mass spectrometer providing temporally resolved, multi-element detection of short signals generated by single particles and droplets, J. Anal. At. Spectrom., 2013, 28, 226–233 RSC.
- J. O. Orlandini v. Niessen, J. N. Schaper, J. H. Petersen and N. H. Bings, Development and characterization of a thermal inkjet-based aerosol generator for micro-volume sample introduction in analytical atomic spectrometry, J. Anal. At. Spectrom., 2011, 26, 1781–1789 RSC.
- Y. Kaburaki, A. Nomura, Y. Ishihara, T. Iwai, H. Miyahara and A. Okino, Development of Injection Gas Heating System for Introducing Large Droplets to Inductively Coupled Plasma, Anal. Sci., 2013, 29, 1147–1151 CrossRef CAS PubMed.
- S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Gunther, Capabilities of inductively coupled plasma mass spectrometry for the detection of nanoparticles carried by monodisperse microdroplets, J. Anal. At. Spectrom., 2011, 26, 1166–1174 RSC.
- B. Franze, I. Strenge and C. Engelhard, Single particle inductively coupled plasma mass spectrometry: evaluation of three different pneumatic and piezo-based sample introduction systems for the characterization of silver nanoparticles, J. Anal. At. Spectrom., 2012, 27, 1074–1083 RSC.
- S. Gschwind, H. Hagendorfer, D. A. Frick and D. Günther, Mass Quantification of Nanoparticles by Single Droplet Calibration Using Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2013, 85, 5875–5883 CrossRef CAS PubMed.
- O. Borovinskaya, S. Gschwind, B. Hattendorf, M. Tanner and D. Günther, Simultaneous Mass Quantification of Nanoparticles of Different Composition in a Mixture by Microdroplet Generator-ICPTOFMS, Anal. Chem., 2014, 86, 8142–8148 CrossRef CAS PubMed.
- K. Shigeta, G. Koellensperger, E. Rampler, H. Traub, L. Rottmann, U. Panne, A. Okino and N. Jakubowski, Sample introduction of single selenized yeast cells (Saccharomyces cerevisiae) by micro droplet generation into an ICP-sector field mass spectrometer for label-free detection of trace elements, J. Anal. At. Spectrom., 2013, 28, 637–645 RSC.
- P. E. Verboket, O. Borovinskaya, N. Meyer, D. Günther and P. S. Dittrich, A new microfluidics-based droplet dispenser for ICPMS, Anal. Chem., 2014, 86, 6012–6018 CrossRef CAS PubMed.
- K. Shigeta, Y. Kaburaki, T. Iwai, H. Miyahara and A. Okino, Evaluation of the analytical performances of a valve-based droplet direct injection system by inductively coupled plasma-atomic emission spectrometry, J. Anal. At. Spectrom., 2015, 30, 1609–1616 RSC.
- B. Ramkorun-Schmidt, S. A. Pergantis, D. Esteban-Fernández, N. Jakubowski and D. Günther, Investigation of a Combined Microdroplet Generator and Pneumatic Nebulization System for Quantitative Determination of Metal-Containing Nanoparticles Using ICPMS, Anal. Chem., 2015, 87, 8687–8694 CrossRef CAS PubMed.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of a new ICP-TOFMS instrument with continuous and discrete introduction of solutions, J. Anal. At. Spectrom., 2017, 32, 548–561 RSC.
- L. Hendriks, A. Gundlach-Graham and D. Günther, Analysis of Inorganic Nanoparticles by Single-Particle Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, Chimia, 2018, 72, 221–226 CrossRef CAS PubMed.
- L. Hendriks, B. Ramkorun-Schmidt, A. Gundlach-Graham, J. Koch, R. N. Grass, N. Jakubowski and D. Günther, Single-particle ICP-MS with online microdroplet calibration: toward matrix independent nanoparticle sizing, J. Anal. At. Spectrom., 2019, 34, 716–728 RSC.
- K. Mehrabi, D. Günther and A. Gundlach-Graham, Single-particle ICP-TOFMS with online microdroplet calibration for the simultaneous quantification of diverse nanoparticles in complex matrices, Environ. Sci.: Nano, 2019, 6, 3349–3358 RSC.
- D. Rosenkranz, F. L. Kriegel, E. Mavrakis, S. A. Pergantis, P. Reichardt, J. Tentschert, N. Jakubowski, P. Laux, U. Panne and A. Luch, Improved validation for single particle ICP-MS analysis using a pneumatic nebulizer/microdroplet generator sample introduction system for multi-mode nanoparticle determination, Anal. Chim. Acta, 2020, 1099, 16–25 CrossRef CAS PubMed.
- J. W. Olesik and S. E. Hobbs, Monodisperse Dried Microparticulate Injector: A New Tool for Studying Fundamental Processes in Inductively Coupled Plasmas, Anal. Chem., 1994, 66, 3371–3378 CrossRef CAS.
- A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Monte Carlo Simulation of Low-Count Signals in Time-of-Flight Mass Spectrometry and its Application to Single-Particle Detection, Anal. Chem., 2018, 90, 11847–11855 CrossRef CAS PubMed.
- L. Hendriks, A. Gundlach-Graham and D. Günther, Performance of sp-ICP-TOFMS with signal distributions fitted to a compound Poisson model, J. Anal. At. Spectrom., 2019, 34, 1900–1909 RSC.
- J. Koch, L. Flamigni, S. Gschwind, S. Allner, H. Longerich and D. Gunther, Accelerated evaporation of microdroplets at ambient conditions for the on-line analysis of nanoparticles by inductively-coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2013, 28, 1707–1717 RSC.
- L. Flamigni, Doctoral thesis, ETH Zürich, 2014.
- M. Burger, L. Hendriks, J. Kaeslin, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of inductively coupled plasma time-of-flight mass spectrometry in combination with collision/reaction cell technology – insights from highly time-resolved measurements, J. Anal. At. Spectrom., 2019, 34, 135–146 RSC.
- F. Laborda, E. Bolea, G. Cepriá, M. T. Gómez, M. S. Jiménez, J. Pérez-Arantegui and J. R. Castillo, Detection, characterization and quantification of inorganic engineered nanomaterials: a review of techniques and methodological approaches for the analysis of complex samples, Anal. Chim. Acta, 2016, 904, 10–32 CrossRef CAS PubMed.
- M. F. Hochella, D. W. Mogk, J. Ranville, I. C. Allen, G. W. Luther, L. C. Marr, B. P. McGrail, M. Murayama, N. P. Qafoku, K. M. Rosso, N. Sahai, P. A. Schroeder, P. Vikesland, P. Westerhoff and Y. Yang, Natural, incidental, and engineered nanomaterials and their impacts on the Earth system, Science, 2019, 363 Search PubMed.
- C. Degueldre and P. Y. Favarger, Colloid analysis by single particle inductively coupled plasma-mass spectroscopy: a feasibility study, Colloids Surf., A, 2003, 217, 137–142 CrossRef CAS.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Single particle ICP-MS: advances toward routine analysis of nanomaterials, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef PubMed.
- D. Mozhayeva and C. Engelhard, A critical review of single particle inductively coupled plasma mass spectrometry – a step towards an ideal method for nanomaterial characterization, J. Anal. At. Spectrom., 2020 10.1039/c9ja00206e.
- B. Meermann and V. Nischwitz, ICP-MS for the analysis at the nanoscale – a tutorial review, J. Anal. At. Spectrom., 2018, 33, 1432–1468 RSC.
- I. Strenge and C. Engelhard, Capabilities of fast data acquisition with microsecond time resolution in inductively coupled plasma mass spectrometry and identification of signal artifacts from millisecond dwell times during detection of single gold nanoparticles, J. Anal. At. Spectrom., 2016, 31, 135–144 RSC.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Determining Transport Efficiency for the Purpose of Counting and Sizing Nanoparticles via Single Particle Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, Size Discrimination and Detection Capabilities of Single-Particle ICPMS for Environmental Analysis of Silver Nanoparticles, Anal. Chem., 2012, 84, 3965–3972 CrossRef CAS.
- G. Cornelis and M. Hassellov, A signal deconvolution method to discriminate smaller nanoparticles in single particle ICP-MS, J. Anal. At. Spectrom., 2014, 29, 134–144 RSC.
- H. El Hadri, E. J. Petersen and M. R. Winchester, Impact of and correction for instrument sensitivity drift on nanoparticle size measurements by single-particle ICP-MS, Anal. Bioanal. Chem., 2016, 408, 5099–5108 CrossRef CAS PubMed.
- J. Tuoriniemi, G. Cornelis and M. Hassellov, Improving the accuracy of single particle ICPMS for measurement of size distributions and number concentrations of nanoparticles by determining analyte partitioning during nebulisation, J. Anal. At. Spectrom., 2014, 29, 743–752 RSC.
- S. Gschwind, M. Aja Montes and D. Günther, Comparison of sp-ICP-MS and MDG-ICP-MS for the determination of particle number concentration, Anal. Bioanal. Chem., 2015, 407, 4035–4044 CrossRef CAS PubMed.
- S. Cuello-Nuñez, I. Abad-Álvaro, D. Bartczak, M. E. del Castillo Busto, D. A. Ramsay, F. Pellegrino and H. Goenaga-Infante, The accurate determination of number concentration of inorganic nanoparticles using spICP-MS with the dynamic mass flow approach, J. Anal. At. Spectrom., 2020 10.1039/C9JA00415G.
- F. Laborda, J. Jimenez-Lamana, E. Bolea and J. R. Castillo, Critical considerations for the determination of nanoparticle number concentrations, size and number size distributions by single particle ICP-MS, J. Anal. At. Spectrom., 2013, 28, 1220–1232 RSC.
- A. R. Montoro Bustos, E. J. Petersen, A. Possolo and M. R. Winchester, Post hoc Interlaboratory Comparison of Single Particle ICP-MS Size Measurements of NIST Gold Nanoparticle Reference Materials, Anal. Chem., 2015, 87, 8809–8817 CrossRef CAS PubMed.
- A. R. Montoro Bustos, K. P. Purushotham, A. Possolo, N. Farkas, A. E. Vladár, K. E. Murphy and M. R. Winchester, Validation of Single Particle ICP-MS for Routine Measurements of Nanoparticle Size and Number Size Distribution, Anal. Chem., 2018, 90, 14376–14386 CrossRef CAS PubMed.
- C. Minelli, M. Wywijas, D. Bartczak, S. Nunez and H. Goenaga-Infante, VAMAS TWA34, Project 10: Inter-Laboratory Study of the Measurement of Number Concentration of Colloidal Nanoparticles: Protocol for Sample Handling, Preparation and Measurements, 2018 Search PubMed.
- E. J. Petersen, A. R. Montoro Bustos, B. Toman, M. E. Johnson, M. Ellefson, G. C. Caceres, A. L. Neuer, Q. Chan, J. W. Kemling, B. Mader, K. Murphy and M. Roesslein, Determining what really counts: modeling and measuring nanoparticle number concentrations, Environ. Sci.: Nano, 2019, 6, 2876–2896 RSC.
- A. Gondikas, F. von der Kammer, R. Kaegi, O. Borovinskaya, E. Neubauer, J. Navratilova, A. Praetorius, G. Cornelis and T. Hofmann, Where is the nano? Analytical approaches for the detection and quantification of TiO2 engineered nanoparticles in surface waters, Environ. Sci.: Nano, 2018, 5, 313–326 RSC.
- F. Loosli, J. Wang, S. Rothenberg, M. Bizimis, C. Winkler, O. Borovinskaya, L. Flamigni and M. Baalousha, Sewage spills are a major source of titanium dioxide engineered (nano)-particle release into the environment, Environ. Sci.: Nano, 2019, 6, 763–777 RSC.
- A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Günther, T. Hofmann and F. von der Kammer, Single-particle multi-element fingerprinting (spMEF) using inductively-coupled plasma time-of-flight mass spectrometry (ICP-TOFMS) to identify engineered nanoparticles against the elevated natural background in soils, Environ. Sci.: Nano, 2017, 4, 307–314 RSC.
- A. Azimzada, J. M. Farner, I. Jreije, M. Hadioui, C. Liu-Kang, N. Tufenkji, P. Shaw and K. J. Wilkinson, Single- and Multi-Element Quantification and Characterization of TiO2 Nanoparticles Released From Outdoor Stains and Paints, Front. Environ. Sci., 2020, 8, 91 CrossRef.
- S. Bevers, M. D. Montaño, L. Rybicki, T. Hofmann, F. von der Kammer and J. F. Ranville, Quantification and Characterization of Nanoparticulate Zinc in an Urban Watershed, Front. Environ. Sci., 2020, 8, 84 CrossRef.
- A. I. Abdelrahman, O. Ornatsky, D. Bandura, V. Baranov, R. Kinach, S. Dai, S. C. Thickett, S. Tanner and M. A. Winnik, Metal-containing polystyrene beads as standards for mass cytometry, J. Anal. At. Spectrom., 2010, 25, 260–268 RSC.
- L. A. Currie, Limits for qualitative detection and quantitative determination. Application to radiochemistry, Anal. Chem., 1968, 40, 586–593 CrossRef CAS.
- C. Degueldre, P. Y. Favarger and S. Wold, Gold colloid analysis by inductively coupled plasma-mass spectrometry in a single particle mode, Anal. Chim. Acta, 2006, 555, 263–268 CrossRef CAS.
- F. Laborda, A. C. Gimenez-Ingalaturre, E. Bolea and J. R. Castillo, Single particle inductively coupled plasma mass spectrometry as screening tool for detection of particles, Spectrochim. Acta, Part B, 2019, 159, 105654 CrossRef CAS.
- A. Hineman and C. Stephan, Effect of dwell time on single particle inductively coupled plasma mass spectrometry data acquisition quality, J. Anal. At. Spectrom., 2014, 29, 1252–1257 RSC.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Improvements in the detection and characterization of engineered nanoparticles using spICP-MS with microsecond dwell times, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- I. Abad-Álvaro, E. Peña-Vázquez, E. Bolea, P. Bermejo-Barrera, J. R. Castillo and F. Laborda, Evaluation of number concentration quantification by single-particle inductively coupled plasma mass spectrometry: microsecond vs. millisecond dwell times, Anal. Bioanal. Chem., 2016, 408, 5089–5097 CrossRef PubMed.
- D. Mozhayeva and C. Engelhard, A quantitative nanoparticle extraction method for microsecond time resolved single-particle ICP-MS data in the presence of a high background, J. Anal. At. Spectrom., 2019, 34, 1571–1580 RSC.
- O. Mestek, M. Loula, A. Kaňa and M. Vosmanská, Can ultrafast single-particle analysis using ICP-MS affect the detection limit? Case study: silver nanoparticles, Talanta, 2020, 210, 120665 CrossRef CAS PubMed.
- F. Laborda, J. Jimenez-Lamana, E. Bolea and J. R. Castillo, Selective identification, characterization and determination of dissolved silver(i) and silver nanoparticles based on single particle detection by inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2011, 26, 1362–1371 RSC.
- J. W. Olesik and P. J. Gray, Considerations for measurement of individual nanoparticles or microparticles by ICP-MS: determination of the number of particles and the analyte mass in each particle, J. Anal. At. Spectrom., 2012, 27, 1143–1155 RSC.
- J. Liu, K. E. Murphy, R. I. MacCuspie and M. R. Winchester, Capabilities of Single Particle Inductively Coupled Plasma Mass Spectrometry for the Size Measurement of Nanoparticles: A Case Study on Gold Nanoparticles, Anal. Chem., 2014, 86, 3405–3414 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |