Open Access Article
Open Access ArticleA novel confocal XRF-Raman spectrometer and FPM model for analysis of solid objects and liquid substances
I.
Szalóki
 *a,
T.
Pintér
*a,
T.
Pintér
 b,
I.
Szalóki
jnr.
c,
G.
Radócz
b,
I.
Szalóki
jnr.
c,
G.
Radócz
 a and
A.
Gerényi
a and
A.
Gerényi
 a
a
aInstitute of Nuclear Techniques, Budapest University of Technology and Economics, Műegyetem rkp. 9, H-1111 Budapest, Hungary. E-mail: szaloki@reak.bme.hu
bPaks II. Ltd., H-7030 Paks, POB 116, Hungary
cIndependent researcher, H-1103 Budapest, Hungary
First published on 17th June 2019
Abstract
A new table-top combined spectrometer was designed and constructed consisting of X-ray fluorescence and Raman spectrometers for spot-analysis of elementary and chemical composition of solid and liquid substances for industrial analytical applications. For XRF analysis a silicon drift detector and an air-cooled low-power transmission type X-ray tube were built in the combined XRF-Raman spectrometer. Both spectrometer units were connected hermetically to a sealed radiation chamber that can be optionally evacuated or it can be filled with helium under atmospheric pressure in order to improve the analytical sensitivity in the region of low-atomic numbers. The XRF and the Raman devices operate in a confocal geometrical arrangement, where the three axes of the Raman laser beam, the exciter X-ray beam, and the X-ray detection channel focus on the same spot of the examined object. The confocal spot of the combined spectrometer can be positioned along the vertical axis with an optional selected step-size of over 0.2 mm. For the precise geometrical adjustment of the focal spot on the sample surface an optical positioning system was designed and built into the irradiation chamber consisting of a mini camera and two mini laser modules. A new FPM model, its algorithm of numerical solution and software were developed for quantitative XRF analysis. The FPM model is based on application of a series of virtual monochromatic X-ray sources used for excitation of the sample elements substituting the experimentally determined spectra of the X-ray tube. The numerical FPM calculations were performed in a matrix-oriented MATLAB programming environment by using self-made software. The model uses both K- and L-lines for the improvement of the accuracy of the calculations and to extend the range of the atomic number of the analysed chemical elements. This FPM model is suitable for the calculation of the concentrations of chemical elements in 4–5 orders of magnitude for liquid and solid materials. In order to maximise the analytical information simultaneous analyses of the Cu content were performed by Raman and XRF spectrometry in an aqueous solution of CuSO4 and citric acid. This experiment proved the synergy of the combined use of these two analytical methods, since both molecular and atomic composition could be analysed quantitatively in the same liquid sample.
Introduction
In the last 20 years several new low-power X-ray tubes and compact X-ray spectrometers based on thermoelectric cooled silicon drift detectors (SDD) were designed and constructed. These technical developments offered a new analytical opportunity for in-field or in situ X-ray fluorescence (XRF) analysis of objects of cultural heritages, industrial materials, and harmful or radioactive materials.1 The best analytical parameters such as the detection limit (DL), analysed volume of the sample, and total analytical time can be achieved by application of polycapillary lenses used for focusing the excitation and secondary X-rays. This type of measuring set-up requires rather a complex moving system for sample positioning that facilitates high spatial resolution in 2D or 3D for spot analysis on the sample surface or in deep layers. However, in many cases, it is necessary to carry out a non-destructive surface analysis which does not necessarily have a high spatial resolution. Typical applications are the tasks of industrial control for the determination of quantitative chemical composition of substances, safeguards or forensic investigations of dangerous materials. In the nuclear industry there often arises the need for a rapid analysis of average composition of such types of solid/liquid substances or objects, which sometimes contain radioactive components as well. The XRF analysis is ideally a powerful solution for these kinds of special analytical conditions because it partly replaces rather complex destructive analytical procedures such as ICP-MS. Moreover, XRF devices can be produced in a mobile form offering the possibility of in situ and in-field quantitative spot analysis.2 A very simple solution for XRF analysis was developed by the authors of ref. 3 using a compact AMPTEK SD detector equipped with a complete electronic unit. The device was applied for spot-type XRF analysis of historical objects using a portable-type geometrical arrangement. A portable microXRF spectrometer was designed and built for the extension of the XRF analysis for low-atomic-number elements,4 carrying out in-field analysis on different art and archaeological objects.5 The device is equipped with polycapillary lenses and it can be applied in outdoor locations for in-field analysis. Another similar mobile application was designed by Hocquet et al.6 for in-door XRF analysis of unique archaeological and historical objects. The main difficulty was the flexible positioning in a large geometrical region along the surface of the object that has to approach very close to the surface of the object. Two versions of a more sophisticated and specialized mobile XRF system were designed in the laboratory of the IAEA in Seibersdorf for XRF analysis of archaeological items.7–9 Since historical glass objects often contain sodium the mechanical design of the analytical equipment also ensures the optional possibility of XRF measurement under vacuum conditions. In this operation mode the greater part of the beam paths of the excitation and the secondary X-ray radiation propagates under vacuum or a He atmosphere. The analysed sample surface is located outside the chamber and the paths of the two beams propagate through a thin Kapton™ window. The proper positioning of the sample surface was ensured by two laser modules which cross each other on the focal spot determined by the excitation beam and the axis of the SDD. A unique mechanical solution is demonstrated by the authors of ref. 10 where an XRF device is mounted on an articulating arm boom stand that allows approaching the surface of the analysed object with appropriate precision for XRF analysis with an X-ray beam having a diameter of about 1.5 mm. In our R + D project overviewed in this paper some technical ideas were utilized which were published in the above cited papers: laser positioning system, vacuum closed chamber for the SDD/X-ray tube and partially reduced absorption for the X-ray beam path by using a He atmosphere.Design and construction of the table-top XRF spectrometer
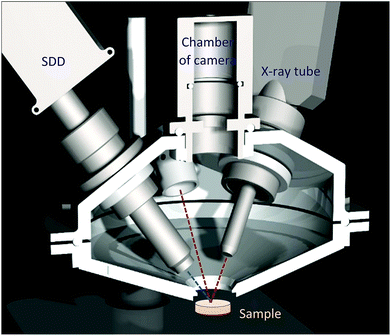
The ultimate goal of this R + D project was to design and build a mobile XRF spectrometer and an optionally added portable Raman spectrometer for providing local analytical information on atomic and chemical compositions in the surface layer of unknown solid samples with industrial/safeguard origins in a non-destructive manner. Primarily the interest of this type of analysis is the investigation of nuclear, radioactive, forensic, waste and dangerous type materials and solid objects. In accordance with the purpose of this project, the main criterion of design was that for this analytical apparatus a special structure has to be built up that protects the elements of the spectrometer from contamination during the investigation of the sample material. For this reason, the X-ray detector and the probe of the Raman spectrometers together with the X-ray tube were inserted into a round-shaped irradiation chamber made from high purity aluminium. The inside volume of the chamber can be evacuated or fill with normal He gas. A Kapton™ window (6 μm) was built at the bottom of the upper part of the chamber which allows the excitation of the sample that is located outside under the chamber (Fig. 1 and 2). The X-ray tube, SD detector and optionally the Raman probe were mounted hermetically to the upper part of the chamber. The mini web-camera was installed in a cylindrical-shaped additional chamber that was connected hermetically to the top of the upper part of the chamber as well. The whole irradiation chamber was fixed on a manually screw-driven system, which provided an opportunity for vertical moving within a 250 mm distance with about 200 μm minimum step-size. All the electronic devices are controlled by independent software products such as 123-SDD and Mini-X-Ag X-ray tube which are produced by Amptek Inc. The total mass of the chamber with all the spectrometric equipment was less than 4 kg. The sample has to be placed in a fixed position under the XRF chamber and the whole spectrometer has to be moved vertically to the appropriate vertical position to perform the analysis. For setting the whole chamber close to the sample surface an optical positioning system was constructed (Fig. 2 and 3) and that part of the device consists of two mini laser modules and a high resolution web-camera. The two laser beams are collimated and their directions are orientated to the centre of the cross point of the 3 axes: primary X-ray beam, axis of the SDD and optical beams of the Raman device. The main structure and positioning mode of the spectrometric elements of the analytical device are introduced by CAD design showing the cross section of the chamber in Fig. 2. The excitation spot is located outside the chamber, nearby the Kapton™ window as close as possible, approximately 2–5 mm. | ||
| Fig. 3 Inside the upper part of the irradiation chamber (a), mechanical structure of the eccentric interface module with the X-ray tube (b), and two laser spots on the sample surface (c). | ||
X-ray spectrometer
All the X-ray spectrometric equipment (X-ray tube, SDD and Raman probe) is hermetically connected to the chamber with mechanical interfaces which isolate the inner volume from the atmospheric outer environment and stabilize the geometrical position of the spectrometric devices. In order to set the triple-confocal measuring geometry, namely, Raman laser beams, detector axis and excitation X-ray beam, changing independently the directions of two of the three axes is needed. On the basis of the mechanical feasibility of the set-up structure, the SD detector was fastened motionless to the chamber, but both the Raman probe and the X-ray tube were connected to the chamber wall in variable directions. The Mini-X-Ag X-ray tube has a large beam divergence (≈120°) and the spot-size of the electron beam on the Ag anode is about 2 mm which enables us to set the collimator of the X-ray tube within a wide angle range without changing drastically the X-ray flux. Taking advantage of this feature both the Raman probe and the collimator of the X-ray tube were locked with an eccentric mechanical unit, which allows us to set the direction of these devices in an optional direction (by rotation of these units) within approximately 15′ degrees. The XRF spectrometer is equipped with a Mini-X-Ag X-ray tube and 123-SDD compact X-ray spectrometer (AMPTEK Inc.) having a Be window of 12.5 μm. Due to the high divergence of the primary beam a low-cost collimator for both the SD detector and the X-ray tube was designed and constructed. The tube's collimator was made from copper with its inner surface covered by a pure (99.99 m/m%) aluminium layer with 1 mm thickness and 80 mm length. The collimator for the SDD had two apertures between which the distance was set to 10 mm. In conventional X-ray spectrometers both the excitation and detection channels have relatively large solid angles in order to maximise the X-ray fluxes. In contrast to this technique, in confocal measuring geometry X-ray optics are applied in front of both the X-ray tube and the detector, and they are set in such a way that the two X-ray beams cross each other. This geometry allows detecting characteristic and scattered X-ray photons emitted from the focal volume of the sample while most of the photons originating from the other part of the sample volume do not get into the detector. Moreover, collimators reduce the flux of scattered radiation originated from scattering of the primary beam on surrounding objects. Since those photons emitted from outside of the focal volume and of the two beam channels can only reach the detector with very low probability, this limitation effect improves the signal-to-noise ratio and the detection limits (DL).The other reason of the necessity of this quasi-confocal geometry is the FPM based evaluation of the XRF data in order to determine the element concentrations of the analysed samples. The intense heat production of the X-ray tube reduces the duration of continuous operation (less than 1 hour) due to the upper limit determined by the manufacturer with 60 °C as the achievable temperature of the anode block. The maximum duration of continuous operation with maximum power (4 W) is less than 1 hour at 22 °C room temperature. Since adding an electric fan for intensification of the forced air-cooling is not possible, due to the limited space in the irradiation chamber, the only solution was to increase the heat conduction of the connected interface parts of the chamber. A built-in aluminium interface unit (Fig. 3a and b) keeps the X-ray tube in a fixed position to the upper part of the chamber and besides that it acts as a heat sink providing enough heat conduction that extends the possible operation time up to 3 hours while the temperature of the anode block does not rise above 42 °C.
Optical positioning system and He flooding of the irradiation chamber
For the surface analysis in the confocal spot determined by the collimated primary X-ray beam on the sample surface, the cone-shaped solid angle of the SDD must be oriented to the direction of this spot on the sample where the local analysis is going to be carried out. For this, there are two possible alternative technical solutions: (i) an appropriate microscope is used which is focused on the confocal spot, where the primary X-ray beam and the detector axis cross each other and (ii) using two laser beams crossing in the centre of the confocal spot. The first design demands a high resolution optical microscope with large magnification capability, which requires a rather large volume inside or on the top of the irradiation chamber. Therefore, the second solution was selected as can be seen in Fig. 3. The mini laser modules were built in aluminium cylindrical containers mounted in lubrication-free pillow block bearing units which allow setting the directions of the collimated laser beams crossing each other in the centre of the confocal spot. The description of the working principle of the geometrical alignment based on the application of laser beams can be found in ref. 5, 8 and 11. Due to the well collimated laser beams a simple web-camera was enough for precise optical positioning. For the collimation of the laser beams doubled apertures were constructed, which produced well-defined thin laser spots allowing the high resolution mechanical setting of the XRF spectrometer. As an example of the working principle of the optical positioning system, in Fig. 3c the sample is in a non-ideal vertical position relative to the chamber.In order to extend the analytical capability of the XRF spectrometer by decreasing the atomic number of the analysed elements down to 12, the design of the chamber allows measurements in a vacuum or in a normal He atmosphere. A typical example for the spectroscopic capability of the XRF spectrometer is shown in Fig. 4, where three XRF spectra were plotted: Al alloy and MgO samples in He- and air-atmospheres using a high-anode voltage of 50 kV and 50 μA anode current. Comparing these spectra measured with or without He gas filled into the chamber significant differences can be found in the intensity of Mg, Al and Si. Moreover, the amplitude of the Ar and Ag (anode) peaks is reduced significantly. The increases of the characteristic radiations are 1–2 orders of magnitude under He than in air atmosphere.
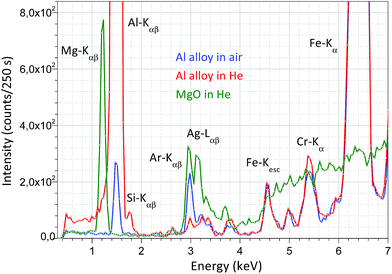 | ||
| Fig. 4 XRF spectrum of MgO in a He atmosphere and Al alloy XRF in air and a normal He atmosphere measured with 50 kV anode voltage and 50 μA anode current. | ||
Measurement of XRF spectra in helium requires a simple technical criterion, since only the chamber should be filled with helium and this condition should be maintained during the measuring time. For this, a He in/outlet unit was built in the upper part of the chamber (Fig. 3a). During the measurement period the continuous flow rate must be kept at about 1–5 cm3 s−1 which ensures the fully filled chamber by He at the 99% level. Under these conditions the total air content in the whole chamber can be exchanged in about 2 minutes with He. Since the absorption effect of He gas with 1 bar pressure is approximately equivalent to attenuation of normal air with a pressure of 10−3 bar,11 the He effectively substitutes the vacuum for extending the range of the atomic number of the measurable elements down to 12.
Focal spot of the excitation X-ray beam
In order to analyse a relatively small irradiated spot the primary X-ray beam has to be collimated. The diameter of the collimated and cylindrically shaped beam determines the analysed spot area of the sample. Therefore, for getting this information the intensity distribution of the beam was measured in a perpendicular geometry (in a temporarily assembled measuring set-up), where the degree between the axes of the primary and secondary beams was about 75°. Thin Cu foil (thickness ≈ 10 μm) was applied for the experiment and that sample was constructed on the surface of circuit board with diameters between 100 and 450 μm. The result of the XRF measurements i.e. the intensity distribution of the Cu-Kα line is plotted in Fig. 5. In the experiment the diameter of the collimators was set as 2 mm for both the X-ray tube and the SDD. In Fig. 5, the beam does not show a Gaussian-type shape, since it is saturated in the centre. On the basis of the beam intensity distribution the diameter of the irradiated spot on the sample surface should be determined by the FWHM value which in this case was about 3.0 mm. This diameter of the irradiated spot can be reduce down to 1 mm applying aluminium collimators11 with different diameters used for both the excitation X-ray beam and the secondary radiation at the front of the SDD in confocal measuring geometry.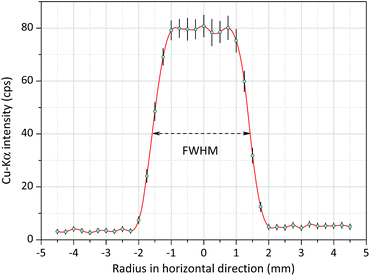 | ||
| Fig. 5 Radial intensity distribution of the white spectra of the Mini-X-Ag X-ray tube obtained on Cu spots (200 μm) constructed on a printed circuit board, FWHM ≈ 3.0 mm. | ||
Raman spectrometer
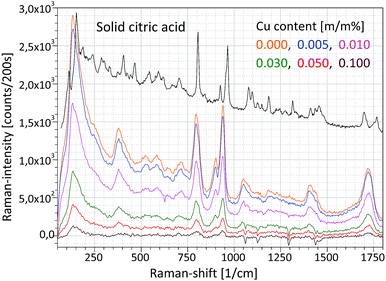
The Raman unit consists of an AvaSpec2048-USB2 spectrometer, PRB-785 glass fiber optic Raman probe and laser source (500 mW) operating at a wavelength of 785 nm. The reflection type PRB is connected to a double optic fiber, which transfers the excitation laser beam to the sample and the sample's optical radiation to the CCD sensor of the Raman spectrometer. An optical lens installed in the PRB focuses the excitation laser beam on the focal spot (focal distance is 10 mm) and another lens collects the secondary light emitted by the sample material, namely the PRB operates in confocal mode. The PRB is connected hermetically to the aluminium chamber as is visible in Fig. 4a. The excitation laser beam crosses the focal spot of the XRF unit and that spot is located on the surface of the irradiated sample and therefore this experimental arrangement allows investigation by both spectrometric methods simultaneously the same sample spot. One of the typical applications of this combined spectrometer in the nuclear industry should be the quality control of the composition of waste material originated from decontamination procedures. Applying the XRF-Raman spectrometer two main components of the investigated substances can be quickly identified: (i) type of molecule of the matrix involving low-Z (Z < 12) elements and (ii) elementary composition in the range of higher atomic numbers (11 < Z). In Fig. 6 the same type of Raman spectrum is plotted which was measured on pure citric acid in (i) solid and (ii) liquid forms and (iii) CuSO4 dissolved in citric acid. The concentrations of copper in the citric acid solutions were set between 0 and 0.1 m/m%.Energy dispersive X-ray spectra of these solutions were recorded and the result is plotted in Fig. 7, where the different concentrations of CuSO4 can easily be distinguish on the basis of Cu-Kα or S-Kα peaks. Coherently and incoherently scattered bremsstrahlung radiation and the characteristic peaks of the anode material (Ag) are independent of the specific solution.
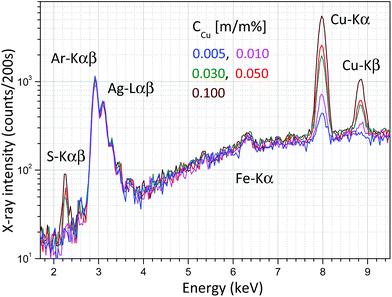 | ||
| Fig. 7 X-ray spectra measured in an aqueous solution of CuSO4 and citric acid at an anode voltage of 40 kV and anode current of 5 μA. | ||
Finally, Fig. 8 shows a double calibration of the combined application of Raman and XRF spectrometry. The Raman spectra were evaluated numerically (AVA-Soft) in a similar way to the XRF spectra (WinQXAS). In a low-concentration range (0.0–0.015 m/m%) Raman spectrometry provides a very sensitive calibration, while in a higher concentration range XRF spectrometry is more sensitive. This example demonstrates the synergy of application of these two analytical techniques simultaneously. On the basis of Raman and XRF spectra measured on the same object both the molecular composition of liquid samples and the atomic number of the dissolved chemical elements can be identified. This example shows that the excellent analytical capability of the combined application of these two methods seems to be very useful for the control of the efficiency of decontamination procedures when surface contaminant is removed from the surface of solid objects.
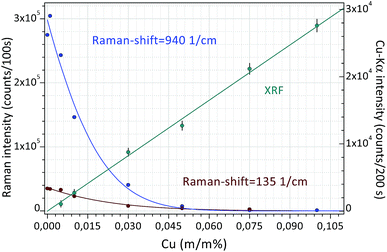 | ||
| Fig. 8 Calibration curves for Raman and XRF spectrometry measured in an aqueous solution of citric acid and CuSO4 solutions. | ||
FPM model
The FPM model can be applied in etalon-free mode due to the existence of an appropriate physical model offering a mathematical relationship between the measured characteristic intensities of the samples' elements and their unknown concentrations. The general FPM model can be given by the system of eqn (1),12,13 where the number of FPM equations is equal to the number of measured chemical elements (n).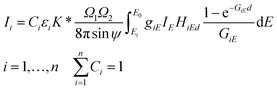 | (1) |
The parameter K* is a multiplicative (instrumental) constant factor of the actual set-up that can be determined by the solution of the FPM equations or by empirical calibration. The calculation of the K multiplicative factor, term of matrix effect (GiE), mass absorption of the sample (μSE) and excitation functions (giE) are given by eqn (2).
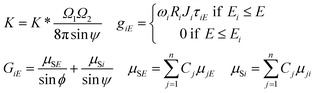 | (2) |
The second order excitation (enhancement) effects that occur in the sample mass can be described mathematically by eqn (3) for calculation of all the excitation events caused by characteristic radiation of the sample elements.14 Functions giE and gij are given in eqn (2) and (3) referring to the energy dependent excitation level of the ith element.12 Below, brief definitions and explanations of variables, parameters and functions used in FPM eqn (1)–(3) are outlined.
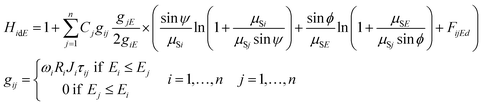 | (3) |
K is the multiplicative factor, Ω1 and Ω2 the solid angles of the X-ray source and the detector, φ the entering angle of the primary X-ray beam to the surface of the sample (≈45°), ψ the take-off angle of the secondary X-ray beam to the surface of the sample (≈45°), E the energy of the excitation beam 0 ≤ E ≤ E0, E0 the maximum energy of the radiation (primary) emitted by the X-ray tube, IE the intensity distribution function of the primary X-ray radiation depending on energy E, εi the efficiency function15 of the energy dispersive detector at energy for the ith element, d the thickness of the sample (g cm−2), n the number of measured chemical elements in the sample, Ci the concentration of the ith element in the sample, Ii the counts of the characteristic peak of the ith element, Ei, K or L the edge energy of the absorption function of the ith element, giE and gij the excitation functions of the ith element at energy E or jth element's characteristic radiation, μSE and μSi the attenuation of the sample at energy E and ith characteristic radiation, μjE and μji the attenuation of the jth element at energy E and ith characteristic radiation, HiEd the rate of the enhancement effect14 for the ith element at excitation energy E, FijEd the rate of the enhancement effect for the ith element depending on sample thickness,16ωi the fluorescence yield,17Ri the radiative rate,18Ji the absorption jump ratio,19 and τiE the photoelectric cross section.20
This FP model is capable of considering the excitation of sub-shells L1, L2 and L3 especially for high atomic number elements that require the energy dependent calculation of the excitation level of the L shells.21 For this reason, the dataset of H. Ebel et al.22 was applied. The parameter K defined in (2) includes all the multiplicative parameters that are independent of the energy and the atomic number: geometrical parameters and amplitude of the function IE. In the system of eqn (1) the excitation energy of the primary X-ray beam is in the range of Ei < E ≤ E0 and these are the boundaries of the integration. Due to the non-linear properties of the basic FPM equations, they must be solved by a suitably selected numerical procedure. In order to construct the simplest and quickest calculation algorithm to solve the equations, a series of discrete and monochromatic virtual X-ray sources were defined instead of automatic numerical integration.
The set of energy channels were determined by the relationship Ei ≤ Ek ≤ Em = E0. Applying the above defined virtual X-ray sources for the excitation of sample elements, system (4) can be derived from eqn (1)–(3). In these equations the energy-integrated terms were substituted in (1) with simple summation.
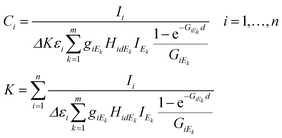 | (4) |
In eqn (4)k = 1,…,m is the index of the energy channels, and Δ is the energy width of each channel in X-ray tube spectra. The variable Ek is defined as the average energy of the kth channel and IEk is the intensity of the primary beam in the kth energy channel. The unknown variables in the system of eqn (4) are the concentrations Ci and the multiplicative factor K. The number of unknown variables (n + 1) is equal to the number of equations. One of the suitable and convergent procedures for obtaining the numerical solution of these FPM equations is fixed point iteration.23 In eqn (5) the two last expressions show how to approximate the initial values of the unknown variables for the numerical iteration procedure. Those values can be approximated by simplification of formula (1) neglecting the expression of enhancement and matrix effects. The Si is the elementary sensitivity of the ith element under experimental conditions described above.
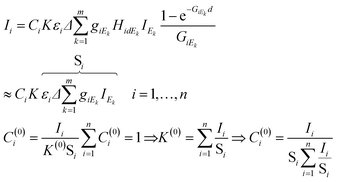 | (5) |
An appropriate recursive algorithm for the calculation of elementary concentrations can be defined by formula (6), where the (r + 1)th approximation of concentrations and proportional factor are estimated from the results of the rth approximation.
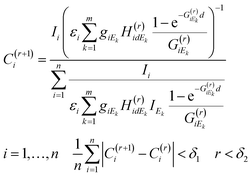 | (6) |
The numerical procedure should be continued until the average difference between the two consecutive results of the approximation procedure is less than a predetermined limit (δ1) or the number of iteration steps exceeds a maximum (δ2). For obtaining a solution to the FPM problem new software was developed in a MATLAB operation and programming environment.
One of the basic presuppositions in the FPM model described in eqn (1)–(6) is the detectability of characteristic X-ray radiation of each sample element. If the matrix contains low-atomic-number elements in the range of atomic numbers of 1 ≤ Z ≤ 11 the characteristic X-ray lines of these elements can be detected with only thin-window or windowless detectors.15 These elements are undetectable with conventional ED detectors equipped with a Be window, and therefore this part of the sample is called in related literature a dark24–27 or residual28 matrix. For the FPM calculation the energy dependent absorption function of the dark matrix has to be known. For elements having a higher atomic number (12 ≤ Z) both measured K and L-lines can be used for FPM calculation. One of the possible solutions to the dark matrix problem is feasible by definition of an effective atomic number as proposed by Wegrzynek et al.24 and Sitko.29 Replacing the real chemical composition of the dark matrix with a single virtual chemical element the energy dependent absorption function of this not-detectable sub-sample can be approximated. In order to define the effective atomic numbers ZS and ZD for the entire sample matrix and the dark matrix it is supposed that the sample elements can be divided into two groups as detectable (Z1,…, Zn) and not-detectable (Zn+1,…, Zq) elements. In order to calculate the absorption of the dark matrix versus the atomic number, an energy simple empirical power function (7) can be applied30 between energies 1 keV and 40 keV. In this function aZE and bZE depend on both energy and atomic number. A new version of authenticated data sets has been proposed in recent publications,31,32 and they are valid in a wider range of energy than earlier versions. The absorption of the dark matrix can be calculated by using the second function in (7), where CD is the concentration of the dark matrix in the sample and μDE and μDi are the mass absorption of the dark matrix at energy E and the characteristic radiation of the ith element.33
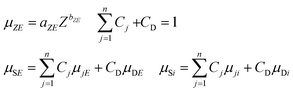 | (7) |
If the sample contains a dark matrix, the number of unknown variables is n + 2 (C1,…,Cn, CD, K). Since the number of independent equations is less than the number of unknown variables additionally measured characteristic intensities of pure chemical elements or standard reference materials (SRMs) are necessary for the calculation of K. These additional measurements must be performed in exactly the same measuring set-up and excitation conditions as those applied for the experiment carried out on the sample. The best selection of pure elements are metals whose atomic numbers cover the range of the atomic numbers of the measured sample elements. Each identical sample element can be assigned to the closest pure element involved in the set of pure elements. The K factors can be calculated by using formula (9) derived from the second expression of eqn (4), where p = 1,…,t is the index and t is the number of pure elements.
Assignment between sample elements and pure elements can be determined by minimization of the double summation as it given in the last expression of eqn (8).
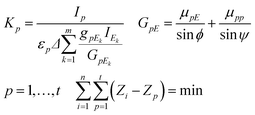 | (8) |
One of the estimation methods of the effective atomic number is based on the measurement of scattered radiations of the sample matrix. After the calibration of the intensity ratio of the elastic and inelastic scattering radiations emitted from SRM or pure element specimens the unknown effective atomic number can be estimated. An alternative solution to the dark matrix problem is knowing the effective atomic number in advance or estimating it from other properties of the sample material. For example, in the case of an oxide-type matrix the effective atomic number of the dark matrix is about 8.0. The uncertainty of the measured intensity distribution (IEk) of the X-ray tube should increase the relative error of the numerically calculated concentrations. This effect is caused by transportation of this error through the FPM equations to the numerically calculated concentrations. When the enhancement or matrix phenomena are stronger the increment of the errors becomes more significant. Smoothed intensity distribution of the primary X-ray beam can be obtained by substitution of the measured spectra of the primary beam by an appropriate mathematical function fitted to the empirical data (Fig. 10). The other source of the uncertainty of the calculated concentrations should originate from the numerical evaluation of the X-ray emission spectra since the characteristic intensity of minor and trace elements can be determined with relatively higher uncertainty than the major elements. Finally, the system of eqn (9) offers a recursive formula if the sample contains a dark matrix.
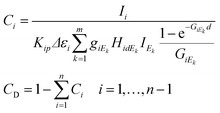 | (9) |
For performing the numerical calculation of the concentrations for the sample's element in-house software (QXRF) was designed and developed in a MATLAB programming environment. The QXRF system involves a database containing all the necessary atomic parameters (density, atomic mass, etc.) and set of fitted parameters used for mathematical descriptions of the function of atomic properties (fundamental parameters): fluorescence yield, ionization probability, absorption jump ratio, and energy dependent mass absorption functions. The solution algorithm of QXRF offers an optional selection of the type of the sample to be analysed such as (i) all the elements are detected by a SDD equipped with a Be window or (ii) the sample contains a dark matrix. If the concentrations of some elements or the whole dark matrix are known preliminarily the code allows keeping optionally these concentrations as constant values during the numerical iteration process. The excitation and detection parameters can be loaded in a separate menu and setting this additional data as a model file can be saved for further calculations. The calculated XRF data of the sample and pure chemical elements are read from the *.asr files which contain all the output data calculated by WinQXAS37 software applied for the mathematical evaluation procedure of the spectra: identification of the analysed chemical elements, X-ray fluorescence peak areas and their standard deviations. The input model file contains all the measuring conditions such as detector parameters needed for the calculation of the efficiency, the length of beam paths in air or a He absorber and the numerical description of the spectral distribution of the excitation beam.
Determination of the white spectra of the X-ray tube
The FPM model introduced in the previous chapter is a non-empirical calibration method which makes it possible to solve some of the XRF analytical problems in standard-free mode. However, for the FPM calculations the preliminary knowledge of the intensity distribution of the white spectrum of the X-ray tube is required. There are three possible ways to know this energy dependent function: (i) application of an appropriate theoretical model, (ii) direct measurement of the energy distribution of the primary X-ray beam34 and (iii) measurement of X-ray radiation scattered by a thin sheet of a pure chemical element with a low-atomic-number (Al).35 One of the great benefits of the experimental-based method published by Ebel et al.34 is that the energy distributions of the primary beam can be measured with different collimator layouts and spectral filters and this setting is also used in the measuring set-up of unknown samples. Fig. 9 shows the measuring set-up applied for the determination of the white X-ray beam. The distance between the X-ray source and the SD detector was set to be about 1 m which was enough for reducing the primary intensity down to such a low value that the dead time was less than 5%. The high voltages were set in the range of 15–50 kV with a 5 kV step and the anode current was kept as 5 μA. The X-ray beam entered into an evacuated Plexiglas tube equipped with two Kapton windows on both ends of the Plexiglas tube with a thickness of 6 μm. The X-ray beam was collimated by an aluminium aperture (99.99 m/m%) that was fixed in the evacuated tube just in front of the X-ray tube. Due to the divergence of the X-ray beam it may scatter on the pipe-wall, and therefore another collimator had to be used before the X-ray beam would have left the tube.11 A typical white spectrum is plotted in Fig. 10 applying 50 kV anode voltage. The low-intensity Fe-Kαβ and Ni-Kαβ peaks perhaps originated from the steel made housing of the X-ray tube or the SD detector. The electronic unit of the SD detector also contributes to the broadening (FWHM) of the Ag-Kα and Ag-Kβ peaks emitted by the anode atoms. Therefore, in reality the energy resolutions of the characteristic radiations after emission from the X-ray tube are probably less than the FWHM calculated after the evaluation of the detected electronic signal. This broadening effect on the shape of anode peaks should cause distortion of the FP results, especially if the binding energy belonging to an excited characteristic X-ray line is close to the energy of the Ag-Kα and Ag-Kβ lines. One of the solutions to the problem is to replace the measured version of the anode peaks with peaks having a natural width.36 For performing this modification of the empirically determined spectra they were fitted using WinQXAS software37 that is based on the AXIL software package.38 Comparative test-calculations were carried out with the measured white spectra and the fitting function (polynomial and Gauss-type functions in Fig. 9) after the modification of the FWHM of the Ag-K peaks to a natural FWHM. Using these two types of white spectra a significant deviation of the FPM calculated concentrations of chemical elements in various samples in the atomic range of 13 ≤ Z ≤ 40 was not found. Hereinafter the empirical FWHM was applied for numerical FPM calculations.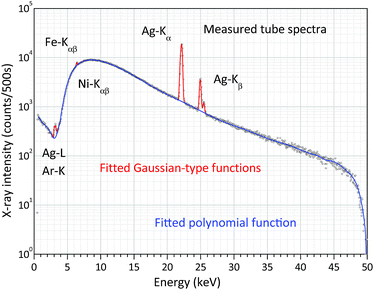 | ||
| Fig. 10 Measured and fitted (WinQXAS) white X-ray spectrum of the X-ray tube with 50 kV anode voltage and 5 μA anode current. | ||
Applications of XRF analysis
For testing the hardware elements of the XRF spectrometer and validating the FPM reference-free calibration technique a set of standard alloys39 and NIST glass SRM40 were analysed. In order to detect XRF spectra in a low-energy region with high enough efficiency namely low-atomic-number elements (Mg, Al and Si) helium gas was used for substituting the air content in the chamber. The results of the FPM calculated and the nominal concentrations are given in Tables 1–3, where the measuring mode is indicated in the bracket as (air) or (He). Where symbol “<” is used instead of concentration values, the subsequent number is the MDL value of the given element in the matrix.| Sample elements | RA 18/78 | RC 14/24 | RH 34/1 | |||
|---|---|---|---|---|---|---|
| C nom | C FPM (He) | C nom | C FPM (air) | C nom | C FPM (air) | |
| Mg | 0.189 | <0.177 | <0.01 | |||
| Al | 71.20 | 70.735 | <0.01 | <0.01 | ||
| Si | 15.30 | 17.004 | 0.034 | 0.034 | 0.220 | 0.334 |
| Ca | 0.0177 | 0.010 | ||||
| Ti | <0.005 | 0.058 | <0.02 | |||
| V | <0.005 | 0.273 | <0.55 | |||
| Cr | 0.0086 | <0.028 | 0.931 | 0.895 | 16.300 | 18.426 |
| Mn | 0.352 | 0.349 | <0.01 | 7.950 | 7.207 | |
| Fe | 0.507 | 0.504 | 0.0177 | <0.01 | 51.50 | 50.599 |
| Co | <0.005 | <0.01 | 0.322 | <0.45 | ||
| Ni | 3.200 | 2.804 | 0.0116 | <0.06 | 20.800 | 19.910 |
| Cu | 8.050 | 7.164 | 98.8 | 98.176 | 1.93 | 1.835 |
| Zn | 0.304 | 0.327 | 0.136 | <0.05 | ||
| Nb | 0.443 | 0.410 | ||||
| Sr | 0.0573 | 0.053 | ||||
| Sn | 0.344 | 0.486 | <0.04 | <0.04 | ||
| W | 0.063 | 0.064 | ||||
| Pb | 0.310 | 0.259 | <0.015 | <0.1 | <0.19 | |
| Sample elements | RN 19/28 | RA 19/49 | |||
|---|---|---|---|---|---|
| C nom | C FPM (He) | C FPM (air) | C nom | C FPM (air) | |
| C | 0.987 | 0.987 | 0.987 | ||
| Mg | 8.44 | 8.44 | |||
| Al | 0.505 | 0.643 | 0.500 | 78.5 | 78.388 |
| Si | 1.390 | 1.007 | 1.376 | 1.02 | 1.499 |
| Ti | 0.128 | 0.254 | 0.247 | 0.032 | 0.036 |
| V | 0.507 | 0.661 | 0.658 | 0.01 | <0.02 |
| Cr | 3.03 | 3.587 | 3.657 | 0.165 | 0.327 |
| Mn | 1.42 | 1.789 | 1.815 | 1.13 | 1.440 |
| Fe | 85.6 | 84.435 | 84.158 | 1.23 | 1.400 |
| Co | 0.751 | 1.209 | 1.141 | 0.233 | 0.315 |
| Ni | 2.89 | 2.817 | 2.893 | 0.706 | 0.686 |
| Cu | 0.565 | 0.670 | 0.826 | 0.509 | 0.562 |
| Zn | 7.34 | 6.467 | |||
| Zr | 0.041 | 0.038 | |||
| Nb | 0.658 | 0.497 | 0.494 | ||
| Mo | 0.94 | 0.890 | 0.788 | ||
| Ag | 0.233 | 0.233 | |||
| W | 0.593 | 0.557 | 0.560 | ||
| Pb | <0.1 | 0.005 | |||
| Sample elements | RC 32/32 | NIST SRM 1873/458 | ||||
|---|---|---|---|---|---|---|
| C nom | C FPM (He) | C FPM (air) | Elements | C nom | C FPM (He) | |
| C | O | 31.86 | 31.86 | |||
| Mg | <0.01 | 0.010 | Si | 23.05 | 22.040 | |
| Al | 1.39 | 2.103 | 1.380 | K | 0.302 | |
| Si | 0.336 | 0.385 | 0.379 | Ca | 0.474 | |
| Ti | V | 0.115 | ||||
| V | Cr | 0.888 | ||||
| Cr | 0.0107 | 0.039 | 0.028 | Fe | 0.261 | |
| Mn | 1.590 | 1.665 | 1.627 | Ni | 0.269 | |
| Fe | 0.0651 | 0.099 | 0.097 | Cu | 0.026 | |
| Co | <0.01 | Zn | 3.01 | 1.976 | ||
| Ni | 0.0235 | 0.269 | 0.264 | Ge | 0.269 | |
| Cu | 59.3 | 58.611 | 57.589 | Br | 0.006 | |
| Zn | 36.7 | 36.784 | 36.521 | Sr | 0.109 | |
| Zr | Zr | 0.460 | ||||
| Nb | Ba | 41.79 | 39.868 | |||
| Mo | Eu | 0.522 | ||||
| Ag | Pb | 0.018 | ||||
| Sn | <0.04 | Bi | 0.006 | |||
| W | Th | 0.089 | ||||
| Pb | 0.348 | 0.344 | 0.353 | U | 0.144 | |
Tables 1–3 show the comparison of the results of quantitative analysis performed on standard alloys (CFPM) to the nominal values (Cnom). Table 3 contains similar results of analysis carried out on reference material NIST SRM 1873/458. Due to the large statistical error of the characteristic intensities of the trace elements, most of the trace elements with concentrations less than 50 ppm were disregarded in the quantitative evaluations. The non-detectable low-atomic-number elements (B, Be, and C) were neglected due to their small concentrations (CLAN < 0.001 m/m%). The concentrations of the high-atomic-number elements (Pb and W) were determined by using their L-lines.
Using He gas to decrease the attenuation of the medium in the secondary beam-path the accuracy of determination of the relative amount of Mg, Al and Si elements can be increased. This measuring option is indicated in Tables 1–3, where the certified concentrations are marked as well. In some cases, under normal atmospheric conditions the intensities of the K-type characteristic peaks of low-atomic-number elements (11 < Z < 15) are less than the MDL (method detection limit) of the quantitative determination. However, by applying He gas during the detection of these elements the concentrations of these elements can be determined quantitatively.
In Table 2 some concentrations are bold, and those elements' nominal content was considered in the numerical calculations as known values. Another type of analysis, when the sample contained a dark matrix as well, was performed: NIST SRM 1873/458 (glass SRM). The reference paper for this sample published only the concentrations of the main component; however we found more additional minor and trace elements as well.
Detection limit (MDL) of the XRF spectrometer
For the characterization of the analytical capability of the XRF device, its detection limits (MDL)41 or lower level of detection (LLD)42 for chemical elements were determined experimentally for NISTR SRM 1577c. This biological SRM was used in a pressed pellet form having a density of 1.85 g cm−3. The mathematical definition of the MDL can be given by comparison of the characteristic intensity and the spectral background under the analytic line according to formula (8). The MDLi is a relative detection limit for the ith element in the reference sample, and SLPi is the elementary sensitivity (counts per s per ppm) which is equal to the slope of the calibration curve for the ith element in a low concentration region (Ci → 0). The IiB is the background count under the characteristic X-ray peak and t is the measuring time.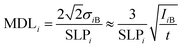 | (10) |
Formula (10) refers to an optionally selected unit of the measuring time. Fig. 11 shows the dependence of the MDLs at 15 kV and 50 kV high voltage while the anode current was set as 50 μA and the reference measuring time was 500 s. According to the result of the measurements carried out on NIST SRM 1577c under a He atmosphere the MDLs for elements with a low-atomic number (Mg) were more than two-times smaller than those under normal air conditions. At higher atomic numbers (20 < Z) this advantageous property is less significant. Increasing the anode voltage does not improve the analytical performance for the determination of low-atomic-number elements, since the background in the secondary XRF spectra is much higher than that at low voltage, due to intense bremsstrahlung. However, the He-atmosphere improves the MDLs significantly up to an atomic number of approximately 20. These MDL experimental data in Fig. 11 have large uncertainty, due to the low characteristic intensities belonging to the low concentrations of the trace elements. The relative MDLs were determined for biological matrix NIST SRM 1577c and were compared to the results of another laboratory micro-XRF spectrometer.41 The relative MDLs were found approximately equal for both devices; however the absolute MDL in mass units in the case of XRF Raman is about 106 times less. The reason for this large difference is the smaller focal volume, higher power of the X-ray tube and gain factor of the polycapillary optics. But, for industrial analytical applications MDLs plotted in Fig. 11 and the 15–20 mm3 analysed volume of the sample are more than enough.
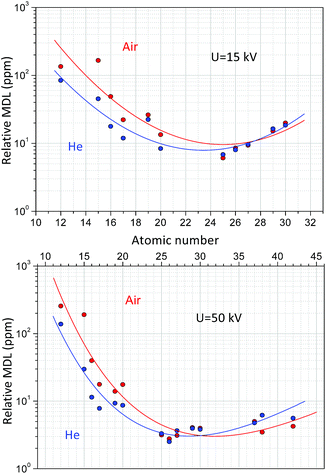 | ||
| Fig. 11 Detection limit (DL) for NIST SRM 1577c at U = 50, 15 kV anode voltage, 50 μA anode current and 500 s measuring time. | ||
Conclusions
Our research group designed and built a new table-top mobile XRF spectrometer that is equipped with a Raman spectrometer. The XRF spectrometer is capable of elemental analysis of solid/liquid substances primarily for daily use of safeguards and nuclear industrial applications for the analysis of harmful or radioactive materials. The construction of the XRF-Raman spectrometer has a sufficiently enough mechanical stability and consists of a very simple mechanical construction for the vertical moving of the XRF chamber with a minimum interval of 0.2 mm. In order to position the X-ray device an optical system was built into the hermetically closed irradiation chamber. The optical system consists of two mini laser modules and a high resolution web-camera. The chamber has been designed that it can fully dissipates the heat generated by the X-ray tube and SDD to the environment. During 3 hours continuous operation on medium power (2–3 watt) the temperature of the X-ray tube does not increase significantly. This period can be extended by approximately half an hour additionally filling the chamber with normal He gas. The XRF device operates in confocal mode that improves the signal-to-noise ratio in XRF spectra and creates an opportunity to analyse a relatively small surface spot (≈5–8 mm2). A new FPM model was developed for the quantitative analysis of several types of solid/liquid materials which was tested by the analysis of standard alloys and glass samples. For the numerical calculations of the concentrations of the chemical elements in the sample new software (QXRF) was developed in a MATLAB programming environment.The main element of the XRF-Raman combined spectrometer is a closed irradiation chamber allowing the measurement in a helium atmosphere or vacuum to reduce the attenuation effect of the secondary X-ray beam. The Kapton™ window at the bottom of the chamber and the aluminium chamber itself protect the main elements of the spectrometers against contamination that may originate from the harmful or radioactive materials investigated by the XRF-Raman device. Most of the table-top XRF spectrometers are designed in a way that the spectrometer is in a fixed position and the sample has to be moved linearly in order to measure its surface; however bigger or heavier samples cannot be moved without technical difficulty with high enough geometrical precision. In this new construction, this technical problem is partly terminated due to the vertical moving possibility of the XRF spectrometer. A simple specialized mechanical solution for collimation of the primary X-ray beam was applying an eccentric collimator in order to adjust the appropriate direction of the excitation X-ray beam. This unique technical element allows setting together appropriately the geometrical axes of the three spectroscopic devices (SDD, X-ray tube and PRB) to analyse the same sample spot.
The confocal measuring set-up allows the spot-type-analysis with an excitation beam of about 3 mm diameter. This measuring arrangement improves the signal-to-noise ratio compared to conventional measuring set-ups, when no confocal mode is applied. The narrow exciter and detection channels largely exclude the scattered radiation emitted by the volume of the sample which is outside the analysed confocal volume. The FPM model was improved in such a way that the experimentally determined X-ray tube spectra were substituted with a series of virtual monochromatic X-ray sources. The advantage of this construction is that the numerical solution of the FPM model can be obtained in matrix-oriented mode which results in a much faster procedure than conventional integration calculus. For the calculation of the concentration of chemical elements with a high atomic number the FPM model was extended to the L-lines. The algorithm of the numerical solution automatically uses the L-line intensities if no experimental intensities of K-lines are available. If the sample contains undetectable elements (dark matrix) the FPM model requires SRM or pure chemical elements as reference samples. The joint analysis of Raman and XRF spectrometers used individually for the same object is capable of identifying quantitatively both the molecular and atomic composition of liquid/solid samples. In comparison of our Raman-XRF (RXRF) combined spectrometer with handheld XRF (HXRF) spectrometers some advantageous analytical properties are found: (i) the diameter of the focal spot of the RXRF is 3 mm, but most of the HXRF has a larger diameter of the spot, about 4–10 mm,43 (ii) using the optical system built in the RXRF device the measurements can be reconstructed with high enough precision, (iii) combined use of Raman and XRF spectrometers provides an opportunity to maximize the analytical information, and (iv) filling the irradiation chamber of the RXRF spectrometer with normal He offers an easy solution to improve the analytical sensitivity in the low-atomic-number region.
These analytical properties make this new combined spectrometer very beneficial for nuclear industrial applications especially for the control of the efficiency of decontamination procedures and this combined technique offers an excellent analytical synergy.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been partly carried out in the frame of projects supported by MVM Paks Nuclear Power Plant Ltd., Hungarian Atomic Energy Authority (OAH-ABA-29/17-M) and the National Research, Development and Innovation Found (VKSZ-14-1-2015-0021).References
- T. Pantazis, J. Pantazis, A. Huber and R. Redus, X-Ray Spectrom., 2010, 39, 90–97 CrossRef CAS.
- M. Alfeld, J. Vaz Pedroso, M. v. E. Hommes, G. Van der Snickt, G. Tauber, J. Blaas, M. Haschke, K. Erler, J. Dik and K. Janssens, J. Anal. At. Spectrom., 2013, 28, 760 RSC.
- R. Cesareo, C. Calza, M. Dos Anjos, R. T. Lopes, A. Bustamante, J. Fabian, W. Alvad and L. Chero, Appl. Radiat. Isot., 2010, 68, 525–528 CrossRef CAS.
- F. He and P. Van Espen, Nucl. Instrum. Methods Phys. Res., Sect. A, 1990, 299, 580–583 CrossRef.
- G. Buzanich, P. Wobrauschek, C. Streli, A. Markowicz, D. Wegrzynek, E. Chinea-Cano and S. Bamford, Spectrochim. Acta, Part B, 2007, 62, 1252–1256 CrossRef.
- F.-P. Hocquet, H.-P. Garnir, A. Marchal, M. Clar, C. Oger and D. Strivay, X-Ray Spectrom., 2008, 37, 304–308 CrossRef CAS.
- K. Uhlir, M. Griesser, G. Buzanich, P. Wobrauschek, C. Streli, D. Wegrzynek, A. Markowicz and E. Chinea-Cano, X-Ray Spectrom., 2008, 37, 450–457 CrossRef CAS.
- G. Buzanich, P. Wobrauschek, C. Streli, A. Markowicz, D. Wegrzynek, E. Chinea-Cano, M. Griesser and K. Uhlir, X-Ray Spectrom., 2010, 39, 98–102 CrossRef CAS.
- K. Uhlir, B. Frühmann, G. Buzanich, M. Griesser, C. Streli, P. Wobrauschek, B. Grossmayer and S. Smolek, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 37, 012008 Search PubMed.
- J. L. Ruvalcaba Sil, D. Ramírez Miranda, V. Aguilar Melo and F. Picazo, X-Ray Spectrom., 2010, 39, 338–345 CrossRef CAS.
- I. Szalóki, A. Gerényi and G. Radócz, X-Ray Spectrom., 2017, 46, 497–506 CrossRef.
- I. Szalóki, A. Somogyi, M. Braun and A. Tóth, X-Ray Spectrom., 1999, 28, 399–405 CrossRef.
- R. Sitko and B. Zawisza, Quantification in X-Ray Fluorescence Spectrometry, in X-Ray Spectroscopy, ed. Dr Shatendra and K. Sharma, InTech, 2012, ISBN: 978-953-307-967-7 Search PubMed.
- Handbook of Practical X-Ray Fluorescence Analysis, ed. B. Beckhoff, B. Kanngießer, N. Langhoff, R. Wedell and H. Wolff, Springer-Verlag, Berlin Heidelberg, 2006 Search PubMed.
- F. Scholze and M. Procop, X-Ray Spectrom., 2005, 34, 473–476 CrossRef CAS.
- P. M. Van Dyck, S. B. Török and R. E. Van Grieken, Anal. Chem., 1986, 58(8), 1761–1766 CrossRef CAS.
- T. Schoonjans, A. Brunetti, B. Golosio, M. S. del Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66, 776–784 CrossRef CAS.
- C. Poehn, J. Wernisch and W. Hanke, X-Ray Spectrom., 1985, 14, 120–124 CrossRef CAS.
- H. Ebel, R. Svagera, M. F. Ebel, A. Shaltout and J. H. Hubbell, X-Ray Spectrom., 2003, 32, 442–451 CrossRef CAS.
- T. P. Thinh and J. Leroux, X-Ray Spectrom., 1979, 8, 85–91 CrossRef.
- P. Hönicke, M. Kolbe and B. Beckhoff, X-Ray Spectrom., 2016, 45, 207–211 CrossRef.
- H. Ebel, R. Svagera, M. F. Ebel, A. Shaltout and J. H. Hubbell, X-Ray Spectrom., 2003, 32, 442–451 CrossRef CAS.
- J. F. Epperson, An Introduction to Numerical Methods and Analysis, John Wiley & Sons, Inc., Hoboken, New Jersey, 2013, ISBN 978-1-118-36759-9 Search PubMed.
- D. Wegrzynek, A. Markowich and W. Chinea-Cano, X-Ray Spectrom., 2003, 32, 119–128 CrossRef CAS.
- I. Mantouvalou, K. Lange, T. Wolff, D. Grötzsch, L. Lühl, M. Haschke, O. Hahn and B. Kanngießer, J. Anal. At. Spectrom., 2010, 25, 554–561 RSC.
- I. Mantouvalou, T. Lachmann, S. P. Singh, K. Vogel-Mikuš and B. Kanngießer, Anal. Chem., 2017, 89, 5453–5460 CrossRef CAS PubMed.
- M. Szczerbowska-Boruchowska, X-Ray Spectrom., 2012, 41, 328–337 CrossRef CAS.
- L. Vincze, A. Somogyi, J. Osán, B. Vekemans, S. Török, K. Janssens and F. Adams, Anal. Chem., 2002, 74, 1128–1135 CrossRef CAS PubMed.
- R. Sitko, Spectrochim. Acta, Part B, 2009, 64, 1161–1172 CrossRef.
- T. P. Thinh and J. Leroux, X-Ray Spectrom., 1979, 8(2), 85–91 CrossRef.
- T. Schoonjans, A. Brunetti, B. Golosio, M. S. Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66(11), 776–784 CrossRef CAS.
- A. Thomson, et al., X-Ray Data Booklet, Centre for X-Ray Optics and Advances Light Source, Lawrence Berkeley National Laboratory, LBNL/PUB-490 Rev.3, http://henke.lbl.gov, 2011 Search PubMed.
- I. Szalóki, A. Gerényi, G. Radócz, A. Lovas, B. De Samber and L. Vincze, J. Anal. At. Spectrom., 2017, 32, 334–344 RSC.
- H. Ebel, X-ray tube spectra, X-Ray Spectrom., 1999, 28(4), 255–266 CrossRef CAS.
- I. Szalóki, D. G. Lewis, C. A. Bennet and A. Kilic, Phys. Med. Biol., 1999, 44, 1245–1255 CrossRef.
- E. G. Kessler Jr, R. D. Deslattes, D. Girard, W. Schwitz, I. Jacobs and O. Renner, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26(5), 2696–2706 CrossRef.
- Win QXAS, IAEA Laboratories, Seibersforf (Austria), 2008, Version 1.3 Search PubMed.
- B. Vekamans, K. Janssens, L. Vincze, F. Adams and P. Van Espen, X-Ray Spectrom., 1994, 23, 278–285 CrossRef.
- WAS Worldwide Analytical System AG, Wellesweg 31, D-47589, Uedem, Germany.
- R. B. Marinenko, D. H. Blackburn, and J. B. Bodkin, Standard Reference Materials: Glasses for Microanalysis: SRM's 1871-1875, NIST Spec. Publ., 1990, 260–112, p. 60 Search PubMed.
- B. Laforce, B. Vermeulen, J. Garrevoet, B. Vekemans, L. Van Hoorebeke, C. Janssen and L. Vincze, Anal. Chem., 2016, 88, 3386–3391 CrossRef CAS PubMed.
- A. N. Kadachi and M. A. Al-Eshaikh, X-Ray Spectrom., 2012, 42(5), 350–354 CrossRef.
- C. Vanhoof, K. A. Holschbach-Bussian, B. M. Bussian, R. Clevend and K. Furtmanne, X-Ray Spectrom., 2013, 42, 224–231 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |