Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Turning the challenge of quantum biology on its head: biological control of quantum optical systems
Anna
Lishchuk
 a,
Cvetelin
Vasilev
b,
Matthew P.
Johnson
b,
C. Neil
Hunter
a,
Cvetelin
Vasilev
b,
Matthew P.
Johnson
b,
C. Neil
Hunter
 b,
Päivi
Törmä
b,
Päivi
Törmä
 c and
Graham J.
Leggett
c and
Graham J.
Leggett
 *a
*a
aDepartment of Chemistry, University of Sheffield, Brook Hill, Sheffield S3 7HF, UK. E-mail: Graham.Leggett@sheffield.ac.uk
bDepartment of Molecular Biology and Biotechnology, University of Sheffield, Western Bank, Sheffield S10 2TN, UK
cDepartment of Applied Physics, Aalto University, School of Science, P.O. Box 15100, 00076 Aalto, Finland
First published on 25th March 2019
Abstract
When light-harvesting complex II (LHCII), isolated from spinach, is adsorbed onto arrays of gold nanostructures formed by interferometric lithography, a pronounced splitting of the plasmon band is observed that is attributable to strong coupling of the localised surface plasmon resonance to excitons in the pigment–protein complex. The system is modelled as coupled harmonic oscillators, yielding an exciton energy of 2.24 ± 0.02 eV. Analysis of dispersion curves yields a Rabi energy of 0.25 eV. Extinction spectra of the strongly coupled system yield a resonance at 1.43 eV that varies as a function of the density of nanostructures in the array. The enhanced intensity of this feature is attributed to strong plasmon–exciton coupling. Comparison of data for a large number of light-harvesting complexes indicates that by control of the protein structure and/or pigment compliment it is possible to manipulate the strength of plasmon–exciton coupling. In strongly coupled systems, ultra-fast exchange of energy occurs between pigment molecules: coherent coupling between non-local excitons can be manipulated via selection of the protein structure enabling the observation of transitions that are not seen in the weak coupling regime. Synthetic biology thus provides a means to control quantum-optical interactions in the strong coupling regime.
Introduction
Organic semiconductors, produced from earth-abundant elements via low-energy pathways, are attractive for the sustainable production of devices and materials for many new and emerging technologies, including consumer electronics, solar energy capture, quantum computing, quantum communications and photocatalysis. However, molecular systems are intrinsically disordered; dephasing rates are thus high,1,2 and excitons are transported via incoherent hopping processes and have small diffusion lengths, typically ∼10 nm but rising to ∼50 nm in exceptional cases.2 Design rules for the efficient transport of excitons across long distances are lacking, placing significant constraints on device architecture and impeding the development of these technologies.2The importance of coherence as a design concept for molecular photonic materials has thus been recognised.3–5 Theory6–9 and measurements by ultra-fast spectroscopy10–14 have suggested that quantum coherent excitations of multiple pigment molecules in photosynthetic light-harvesting complexes (LHCs) facilitate efficient energy transfer, leading to the delocalisation of excitation around individual complexes and also to more efficient transfer of energy between complexes via Förster resonance energy transfer (FRET).15 There has thus been a resurgence of interest in quantum biology, and it has been suggested that photosynthetic mechanisms provide a model for the design of molecular photonic structures to achieve efficient transport of excitons.5,16
However, the idea remains controversial.17,18 For example, Miller and co-workers recently argued that decoherence rates in light harvesting proteins are so fast under physiological conditions that electronic coherence could not contribute to photosynthesis.19 Moreover, while it is thought that intra-membrane FRET transfers are efficient and enable excitonic transport across distances of at least several 10s of nm, a direct experimental determination of the exciton diffusion length is still lacking.
Here we describe a different approach based on the strong coupling of plasmon modes to excitons in light harvesting proteins. In contrast to the electronic coherence posited to occur in LHCs, strong plasmon–exciton coupling does not rely upon achieving a superposition of excitonic wavefunctions; instead, pigment molecules exchange energy coherently via a confined electromagnetic mode.
Plasmons are collective oscillations of surface electrons.20,21 Their characteristic frequencies are typically in the visible region of the electromagnetic spectrum, and resonant coupling of a plasmon to incident electromagnetic radiation yields a surface plasmon polariton. When the plasmon is formed at the surface of a nanostructure the polariton mode is confined – it is a localised surface plasmon resonance (LSPR). In strong plasmon–exciton coupling,22–27 light and matter states exchange energy faster than their respective decay channels, giving rise to new quasiparticles called plasmon–exciton polaritons (“plexcitons”) in which the electronic states of the plasmon and exciton are mixed to form hybrid light-matter states.27 The coupling is a collective phenomenon: the plasmon is hybridised to an array of emitters.28 The properties of the plexcitons are thus determined by the arrangement of the emitters as well as the properties of the plasmon and exciton. An important consequence of this is that all of the emitters coupled to a particular nanostructure – which may be 200–300 nm in size – are coherent.27
Recently we reported the first example of strong coupling of a plasmon mode to a biological molecule.28 Gold nanostructure arrays were found to exhibit surface plasmon resonances that split after attachment of light harvesting complexes 1 and 2 (LH1 and LH2) from purple bacteria. The splitting was attributed to strong coupling between the localized surface plasmon resonances and excitons in the light-harvesting complexes, and the coupling was modelled as coupled harmonic oscillators.
Here we show that plasmon modes are strongly coupled to excitons in plant light-harvesting complexes. Furthermore we show that there is enhanced evanescent coupling between nanostructures in arrays of gold nanostructures as a result of this strong coupling. Data from a wide range of natural and synthetic light-harvesting complexes demonstrate that the energies of plexcitonic states can be controlled via selection of the protein structure and the spatial arrangement of emitters, and that coherent ultra-fast exchange of energy between non-local pigments occurs via the plasmon mode.
Experimental
Materials and chemicals
Microscope coverslip slides (22 mm × 50 mm, no. 1.5 thickness) were obtained from Menzel-Gläser, Germany. Gold wire (99.997% trace metals basis) and chromium chips (99.5% trace metals basis) used for the thermal evaporation were purchased from Sigma-Aldrich. The 30% hydrogen peroxide solution and 95% concentrated sulfuric acid used for preparation of the piranha solution were supplied by VWR Chemicals, UK. For preparation of the gold etchant solution, 32% ammonia solution, HPLC purity ethanol, and cysteamine, obtained from Sigma-Aldrich, were used. 1-Octadecanethiol (98%) and HEPES were also obtained from Sigma-Aldrich. Chemicals used for the gold nanostructures functionalization, i.e. 11-amino-1-undecanethiol hydrochloride, glutaraldehyde (25%), Nα,Nα-bis(carboxymethyl)-L-lysine trifluoroacetate salt (AB-NTA), and nickel sulfate were supplied by Sigma-Aldrich. All chemicals were used as received.Fabrication of gold nanostructures
All glassware, i.e. the microscope coverslip slides and vials used, were cleaned initially by submersion in piranha solution, a mixture of hydrogen peroxide and concentrated sulfuric acid in the ratio 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, for 40–60 min, until the solution has stopped bubbling and cooled down to room temperature. The glassware was rinsed thoroughly with deionized water and sonicated for 10 min before being placed in the oven (ca. 90 °C) to dry.
7, for 40–60 min, until the solution has stopped bubbling and cooled down to room temperature. The glassware was rinsed thoroughly with deionized water and sonicated for 10 min before being placed in the oven (ca. 90 °C) to dry.
Gold substrates were prepared by evaporating a 3–5 nm thick chromium film followed by a 20–22 nm (unless otherwise is stated) thick gold layer. Chromium and gold were both deposited by thermal evaporation using an Edwards Auto 306 bell jar vacuum coating system under pressure of 8 × 10−7 mbar. Evaporation rates of 0.1 nm s−1 for Cr and 0.1–0.2 nm s−1 for Au were used. It should be noted that the above-stated thickness values were taken from the evaporator QCM thickness monitor. They may differ (by up to 8%) from the actual thickness values, which were determined later on by spectroscopic ellipsometry.
Chromium/gold coated glass slides were immersed in a 1 mM solution of 1-octadecanethiol (ODT) in ethanol for at least 24 h to form closely packed self-assembled monolayers (SAMs). SAMs of ODT on gold were photopatterned by interferometric lithography (IL) using a Lloyd’s mirror two-beam interferometer in conjunction with the frequency-doubled argon ion laser emitting at 244 nm (Innova FreD 300C, Coherent, UK). The angle between the mirror and the sample in the interferometer was 30 ± 2.5°. Samples were patterned using IL with a dose of 34 J cm−2. Subsequently, samples were rotated by different angles on the sample stage and exposed again, to a dose of 20 J cm−2.29
Photopatterned ODT monolayers on gold were etched by immersion in 2 mM cysteamine with an added 8% v/v of ammonia in HPLC ethanol. After etching, the samples were then rinsed with ethanol, dried under a steam of nitrogen and annealed in a chamber furnace (Carbolite, UK) at 500–550 °C for 60–90 min. The heating rate was ca. 7 °C min−1 and the annealed samples were left to cool in air to room temperature. Highly crystalline structures and strong plasmon bands were observed in extinction spectra after annealing.
Samples were cleaned for re-use by immersion in piranha solution (which was allowed to cool down to room temperature) for 5–7 min, washed thoroughly with deionized water and blown dry with nitrogen.
Surface functionalization and protein adsorption
Arrays of gold nanostructures were functionalized with 11-amino-1-undecanethiol (AUT) by immersion in a 2 mM solution of the adsorbate in ethanol for 18 h, washed with ethanol and dried with nitrogen. The samples were then immersed in LHCII in 20 mM HEPES buffer, 0.03% BDDM, pH 7.5. The surfaces were immersed in the protein/buffer solution overnight in a humid chamber in a fridge. Finally, the samples were then gently washed with HEPES buffer and deionized water and dried under a steam of nitrogen.Characterization
Morphology of the as-fabricated and annealed gold nanostructures was determined with atomic force microscopy (AFM). AFM images were acquired in air using a Nanoscope Multimode 8 atomic force microscope (Bruker, Germany) operated in a tapping mode. Tapping mode probes used were OTESPA-R3 model (Bruker), with a resonance frequency of ca. 300 kHz and a nominal tip radius of 7 nm. Image analysis was performed with the Bruker NanoScope Analysis (v.1.5) software.UV-visible absorption spectra at normal incidence were recorded in air using a Cary50 spectrophotometer (Agilent Technologies, USA). The wavelength scan range was 350–850 nm (unless otherwise stated). The samples were placed in a special holder enabling absorption measurements of the same spot on the sample during all experimental stages.
Results and discussion
Extinction spectra
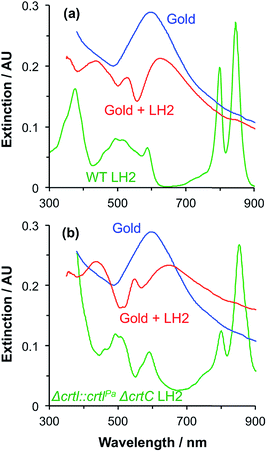
LHCII is the most abundant antenna protein in the photosynthetic apparatus of higher plants, and its primary function is to funnel energy into the photosystem II reaction centre. It is a trimeric protein,30 containing 7–8 chlorophyll (Chl) a, 5–6 Chl b and 3–4 carotenoids (Crt),31 the latter being a mixture of lutein, neoxanthin and violaxanthin. Fig. 1 shows the extinction spectrum for LHCII isolated from spinach and dissolved in buffer (green trace). The Chl a and Chl b Qy transitions are observed at 1.83 and 1.90 eV, respectively. The Chl b Soret band is observed at 2.84 eV, and a broad feature peaking at 2.63 eV results from overlapping bands due to the Chl Soret transitions and the S0 → S2 transitions in the Crt.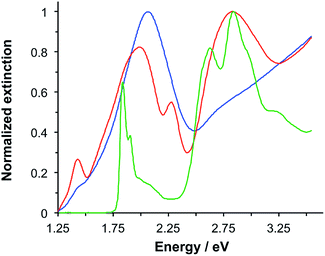 | ||
| Fig. 1 Normalized extinction spectra of LHCII in buffer solution (green), clean gold nanostructures (blue) and gold nanostructures after adsorption of LHCII (red). | ||
Macroscopically extended (∼1 cm2) arrays of gold nanostructures were fabricated using interferometric lithography in a double-exposure process, as described previously.32 An advantage of fabricating nanostructures over large areas is that spectroscopic measurements can be made with a simple bench-top spectrophotometer with illumination at low light intensities. The blue trace in Fig. 1 is the extinction spectrum of an array of clean gold nanostructures. The nanostructures were approximately disc-shaped with a height of 60 ± 10 nm and diameter 140.5 ± 17.5 nm at a pitch of 296 ± 16 nm. A strong feature is observed at 2.06 eV corresponding to the localised surface plasmon resonance (LSPR) of the gold nanostructures. The LSPR energy, ELSPR, can be controlled by varying the angle 2θ between the sample and mirror in the spectrophotometer, the angle of rotation between exposures and the etch conditions.
Fig. 1 also shows an extinction spectrum of the same array after adsorption of a monolayer of light-harvesting complex II (LHCII) (red trace). It can be seen that after adsorption of LHCII onto the gold nanostructures there is a dramatic change in the spectrum. The plasmon mode is split to yield a broad feature at 1.98 eV and a narrow feature at 2.27 eV. This type of splitting is characteristic of a type of asymmetric Fano resonance in which a broad mode (the plasmon mode) is coupled to a narrow one (the exciton).
Modelling
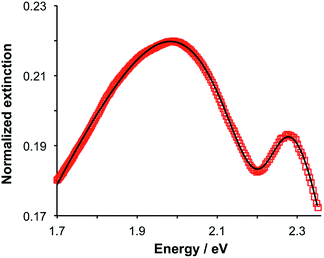
Gallinet and Martin provided a first-principles analysis of strong plasmon–exciton coupling.33 They demonstrated that in the case of a broad resonance coupled to a narrow one, the coupling may be modelled as coupled harmonic oscillators. In our previous work we described the application of such a model to the strong coupling of LSPRs to excitons in bacterial light-harvesting complexes. The same approach was used here to model the extinction spectra obtained after adsorption of LHCII onto arrays of metal nanoparticles. Fig. 2 shows the region of the extinction spectrum from 1.7 to 2.35 eV, containing the plasmon band (red symbols) together with a spectrum fitted using our coupled oscillator model. It can be seen that the fit is very good. The model yields an exciton energy of 2.22 ± 0.01 eV and a coupling strength of 0.27 ± 0.015 eV. These data are consistent with strong plasmon–exciton coupling.To test this hypothesis further, measurements were made for a series of arrays of nanostructures with different LSPR energies after adsorption of LHCII. The spectra were modelled and the energies of the upper and lower polariton branches of the coupled system were determined. The data are shown in Fig. 3. The data were fitted to yield dispersion curves using the relationship:34
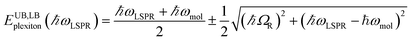 | (1) |
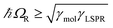 ,27 where γLSPR and γmol are the linewidths of the uncoupled LSPR and exciton states. In the present case, γLSPR is ∼ 0.6 eV and γmol is ∼ 0.1 eV, hence the Rabi splitting should be greater than 0.24 eV, a condition that is satisfied here.
,27 where γLSPR and γmol are the linewidths of the uncoupled LSPR and exciton states. In the present case, γLSPR is ∼ 0.6 eV and γmol is ∼ 0.1 eV, hence the Rabi splitting should be greater than 0.24 eV, a condition that is satisfied here.
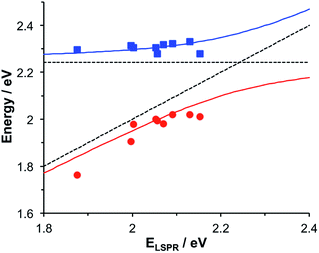 | ||
| Fig. 3 Dispersion curves for the plexcitonic states determined from experimental data (circles and squares) together with curves fitted using eqn (1). The dotted lines represent the energies of the uncoupled exciton and LSPR states. | ||
Modelling of the spectra yields the exciton energy Emol. Fig. 4 shows the variation in Emol with the plasmon energy. As expected, the value of Emol remains invariant within experimental error at a mean value of 2.24 eV. However, this value does not match the energy of any of the main transitions in the LHCII pigment molecules. In our previous work on bacterial photosynthetic proteins, the calculated value of Emol was found to be equal to that of the Crt S0 → S2 transition for Crt-containing LHCs, and that of the bacteriochlorophyll (BChl) Qx transition for a Crt-free mutant of LH1. In the present study the value of Emol lies close to the energy of the Crt S0 → S2 transitions between 2.5 and 2.6 eV, but is smaller in magnitude. We hypothesise that this reflects the fact that the plasmon mode couples strongly to an ensemble of emitters.
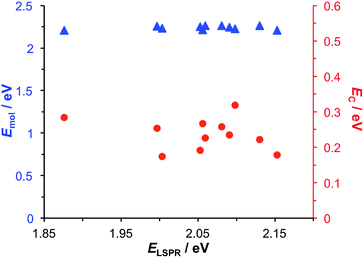 | ||
| Fig. 4 Variation in the exciton energy (triangles) and scaled coupling energy (circles) as a function of the LSPR energy for a monolayer of LHCII attached to gold nanostructures. | ||
The coupling energy depends on the square root of the density of excitons, but is proportional to the transition dipole moment:27
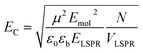 | (2) |
In LH2, there are 3 BChl for each Crt and the Crt S0 → S2 transition dipole moment is ∼10 × that of the BChl Qx transition dipole moment. Given that the coupling energy is  but that EC ∝ μ, it seems reasonable that plasmon–exciton coupling for LH2 is dominated by coupling to the Crt S0 → S2 transition. However, in LHCII there are ∼4 Chl for each Crt and, moreover, the transition dipole moment for the S0 → S2 transition in lutein is ∼3× the magnitude of that for the Qy transition dipole moments of the Chl.35 Thus the situation is more complicated and one might not expect the coupling to simply be dominated by coupling to the Crt S0 → S2 transition. Our current model is unable to separate the couplings to different excitons, but instead models the ensemble behaviour. In the future it is expected that more sophisticated models may be capable of analysing the separate contributions to the plasmon–exciton coupling.
but that EC ∝ μ, it seems reasonable that plasmon–exciton coupling for LH2 is dominated by coupling to the Crt S0 → S2 transition. However, in LHCII there are ∼4 Chl for each Crt and, moreover, the transition dipole moment for the S0 → S2 transition in lutein is ∼3× the magnitude of that for the Qy transition dipole moments of the Chl.35 Thus the situation is more complicated and one might not expect the coupling to simply be dominated by coupling to the Crt S0 → S2 transition. Our current model is unable to separate the couplings to different excitons, but instead models the ensemble behaviour. In the future it is expected that more sophisticated models may be capable of analysing the separate contributions to the plasmon–exciton coupling.
In the coupled harmonic oscillator model, the coupling constant g has the dimensions of frequency squared. When scaled to be expressed in units of energy, the coupling constant is G and the coupling energy (equal to the splitting between the normal modes) is EC = G/ELSPR, where ELSPR is the energy of the LSPR. The variation in EC with ELSPR is shown in Fig. 4 (red circles). It can be seen that as the LSPR energy is decreased below 2.24 eV, the coupling gradually increases to reach values close to 0.3 eV. This behaviour is consistent with that predicted using eqn (2).
Plasmonic coupling in arrays
After adsorption of LHCII onto gold nanostructure arrays, features are observed at 2.83 eV and 1.43 eV in addition to the features at 1.98 eV and 2.27 eV. The feature at 2.83 eV is of unknown origin. Although the energy of this feature is close to that of the Soret transition in the protein, a similar feature was observed at the same energy in extinction spectra of bacterial LHCs and synthetic light-harvesting maquette proteins, which have Soret transitions at significantly different energies. Thus, because it appears to be independent of the exciton energies in the LHCs, it seems unlikely that this feature is due to strong plasmon–exciton coupling. Its origin is currently unclear.The feature at 1.43 eV is smaller, although distinct. A very small shoulder is just visible at this energy in the spectrum of the clean gold arrays, suggesting that this feature results from a process that is present in the clean gold nanostructure arrays but which is enhanced by strong plasmon–exciton coupling. Coupling between nanostructures is known to yield resonances at low energies. To examine whether the feature at 1.43 eV was associated with coupling between nanostructures, its area was measured and plotted as a function of the nanostructure density (Fig. 5). It was found that the intensity of the feature at 1.43 eV increased with increasing array density but that the relationship was non-linear, increasing slowly at high densities (8–18 × 1012 m−2) but changing more rapidly at lower densities. As the density of nanostructures increases, the amount of analyte increases, and it is expected that extinction will increase, but in a linear fashion. Moreover, the feature at 1.43 eV increases relative to the intensity of the plasmon mode as a function of array density.
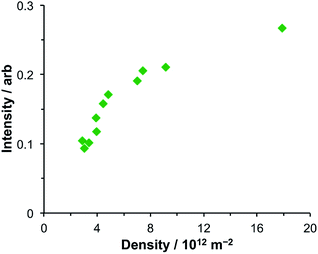 | ||
| Fig. 5 Variation in the intensity of the feature at 1.43 eV in the extinction spectra of nanostructure arrays coupled to LHCII as a function of the density of nanostructures in the array. | ||
The non-linearity in Fig. 5 suggests that the feature at 1.43 eV is associated with distance-dependent coupling between nanostructures. Determination of the mechanism of this coupling will be a subject for further research.
Discussion
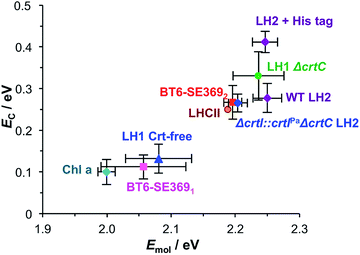
These data may now be combined with results from previous studies of strong coupling of plasmon modes to bacterial light-harvesting complexes28 and synthetic maquette proteins36 to begin to assemble a detailed picture of the way that protein structure may be used to control strong plasmon–exciton coupling.The pigment complement of light harvesting complexes determines the coupling strength
In strong plasmon–exciton coupling, the energies of the resulting plexcitonic states are determined by the energy of the LSPR (which is controllable, via modification of the lithographic process),32 the energy and transition dipole moment of the exciton, and the organisation of the excitons. Because of their exquisitely controlled architectures, light-harvesting complexes provide powerful model systems within which to explore strong plasmon–exciton coupling.Fig. 6 combines data from all three studies completed to date. It shows the mean coupling energy EC determined from fitting the extinction spectra for a number of strongly coupled systems as a function of the exciton energy Emol. The data are clustered into two broad groups. Three points lie just outside the threshold for the strong coupling regime: a monolayer derivatised with Chl a, BT6 maquettes containing a single binding site for a chlorin (BT6-SE3691), and “blue” LH1, a carotenoid-free mutant of LH1 from R. sphaeroides all yield coupling energies that are significant but not sufficiently large to be said to have entered the strong coupling regime. In all cases the pigment is a chlorin (or bacteriochlorin) with a comparatively small transition dipole moment, and in all cases the exciton density is low (∼1017 m−2).
A second group of points exhibits larger coupling energies. For each of these proteins, the coupling energy is large enough to yield strong splitting of the plasmon mode. This group includes wild-type (WT) LH2, in which the Crt is spheroidenone, and the Δcrtl::crtlPaΔcrtC LH2 mutant, which has the same structure as WT-LH2 save that spheroidenone has been replaced by lycopene. In the case of these proteins, the Crt transition dipole moment is aligned perpendicular to the surface of the gold nanostructure to which they are attached, meaning that it lies in the direction of the electric field associated with the LSPR. The Qx transition dipole moment lies in this direction, but its transition dipole moment is much smaller and the extinction spectra appear to be dominated by strong coupling of plasmon modes to the Crt S0 → S2 transition, yielding clear differences in the splitting for different mutants (Fig. 7). The Qy transition dipole moment lies orthogonal to the LSPR field direction and it does not couple to the plasmon mode. In blue LH2 it is the Qx transition dipole moment that couples to the LSPR.
The coupling energy is still larger for the ΔcrtC mutant of LH1, in which the Crt is neurosporene which has a larger transition energy than those of spheroidenone and lycopene.28 The Crt in LHCII have energies closer to that of the S0 → S2 transition in neurosporene than the other mutants of LH2, so that the coupling energy measured here for LHCII appears slightly small. This is probably a consequence of the different structure of the protein: LH2 has a pronounced circular symmetry and the transition dipole moments of the Crt will consequently lie close to the direction of the LSPR field, but the structure of LHCII is more complex and the transition dipole moments of neither the Crt nor the Chl lie in a single direction. This will inevitably reduce the coupling strength.
His-tagged LH2 yields the largest coupling energy measured in our studies of light harvesting systems, at 0.41 eV, significantly larger than the value obtained for WT LH2. This is attributed to the strong binding of His-tagged proteins to nanostructures that are functionalised with nitrilotriacetic acid (NTA), which is expected to lead to a higher surface coverage of immobilised LH2 and thus a higher density of excitons within the plasmon mode volume.
Synthetic biology enables the control of ultra-fast non-local exchange of energy in strongly coupled systems
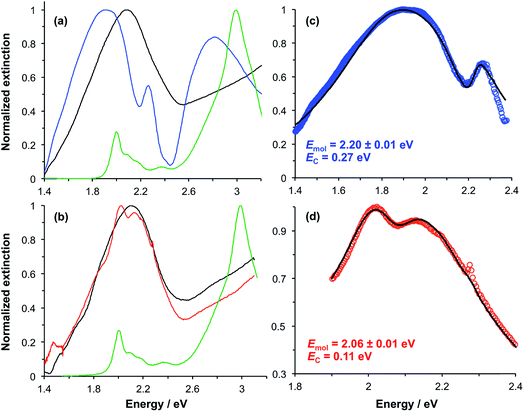
In our previous studies we demonstrated that for bacterial light harvesting complexes and synthetic maquette proteins the coupling strength varied with the square root of the density of proteins at the gold surface. These observations reflect the fact that in strong plasmon–exciton coupling, an LSPR couples to an ensemble of emitters. Although we have successfully used a simple classical model to analyse our strongly coupled systems, this dependence of the coupling strength on the organisation of the excitons within the plasmon mode volume is a reflection of the quantum optical character of strong plasmon–exciton coupling. The strongly coupled system effectively consists of macroscopically extended states in which the LSPR is coupled coherently to all excitons within the mode volume of each nanostructure. This allows ultra-fast exchange of energy between non-local excitons.Evidence for this comes from the unexpectedly large coupling energy of the synthetic light-harvesting maquette protein BT6-SE3692 (0.27 eV) when attached to gold nanostructures (Fig. 6). This protein contains two binding sites for synthetic SE369 chlorins. The neighbouring data points in Fig. 6 are all for proteins that contain Crt, which have larger transition dipole moments. However, BT6-SE3692 contains no carotenoids. Moreover, its two chlorin binding sites are separated by >2 nm; at such separations dipole coupling is weak. Consistent with this, the absorption spectrum of BT6-SE3692 when collected in solution is indistinguishable from that of the protein BT6-SE3691 that contains only a single chlorin binding site (Fig. 8a and b, green traces). However, when attached to gold nanostructures, BT6-SE3691 yields a coupling energy of only 0.11 eV, less than half that of BT6-SE3692 and similar in magnitude to the coupling energies calculated for the ΔcrtC mutant of LH1 and Chl a functionalised surfaces.
Modelling of the extinction spectra yields an exciton energy for BT6-SE3691 of 2.06 ± 0.07 eV, close to that of the Qy transition in the protein. For BT6-SE3692, however, an exciton energy of 2.20 ± 0.01 eV is obtained, intermediate between the energies of the Qx and Qy transitions of the chlorin. A transition with this energy is not observed in the absorption spectrum of either protein.
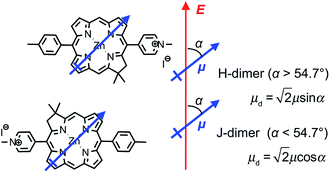
We hypothesise that these surprising observations are explained by strong coupling of the LSPR to a dimer state not observed under weak coupling. Transition dipole moments in aggregates of pigment molecules may couple to form J-dimers (or aggregates) leading to a red shift in the exciton energy,37 or H-dimers (or aggregates) leading to a blue shift38 (as shown in Fig. 9). However, as noted above, the chlorins in BT6-SE3692 are too far apart for effective dipole coupling. We hypothesise that in the strongly coupled system, the dimer state results from ultra-fast exchange of energy between non-local pigment molecules via the plasmon mode. The observation of this dipole coupling is thus a consequence of the coherence that is intrinsic to strongly coupled systems.
The blue shift in the exciton energy that results from strong coupling of the plasmon mode to excitons in BT6-SE3692 suggests the formation of H-dimers. Such coupling of the chlorins would also yield an increase in the transition dipole moment, which, combined with the larger exciton energy, would account for the much larger coupling energy determined for the two-chlorin maquette. However, the use of an H-dimer model here may represent an over-simplification of what may be a more complex coupling mechanism: given that in strong plasmon–exciton coupling the plasmon mode couples to an array of emitters, it is indeed plausible that the observed couplings involve chlorins in different proteins. These data, combined with the close similarity of the absorption spectra acquired for the two proteins under weak coupling conditions, provide evidence that by changing the structure of the maquette it was possible to manipulate the coherent non-local transfer of energy in the strongly coupled system.
Conclusions
Plasmon modes are strongly coupled to excitons in light-harvesting complexes from plants and bacteria. The strong coupling regime is reached when the plasmon mode and the excitons in pigment molecules exchange energy faster than their respective decay channels. By manipulating the structures of these pigment–protein complexes, the organisation of excitons within the plasmon mode volume can be controlled precisely, enabling the properties of the coupled states to be manipulated through the ultra-fast exchange of energy via the plasmon mode. Non-local coupling between excitons can be manipulated via the design of synthetic proteins and through the control of protein organisation at the surfaces of plasmonic nanostructures. Strong plasmon–exciton coupling achieves coherent transport of energy across distances of at least 100s of nm, but this can be extended by manipulation of plasmonic coupling mechanisms in extended arrays of plasmonic nanostructures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the EPSRC (Programme Grant EP/I012060/1 and equipment grant EP/M028437/1) for Financial Support. C. V., M. P. J. and C. N. H. were supported by research grant BB/M000265/1 from the Biotechnology and Biological Sciences Research Council (UK) and Advanced Award 338895 from the European Research Council.Notes and references
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Rev., 2017, 117, 796–837 CrossRef CAS PubMed.
- A. Chenu and G. D. Scholes, Annu. Rev. Phys. Chem., 2015, 66, 69–96 CrossRef CAS PubMed.
- J.-L. Bredas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2017, 16, 35–44 CrossRef CAS PubMed.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647 CrossRef CAS PubMed.
- M. G. Cory, M. C. Zerner, X. Hu and K. Schulten, J. Phys. Chem. B, 1998, 102, 7640–7650 CrossRef CAS.
- A. Damjanović, T. Ritz and K. Schulten, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 3293–3311 CrossRef.
- M. L. Cartron, J. D. Olsen, M. Sener, P. J. Jackson, A. A. Brindley, P. Qian, M. J. Dickman, G. J. Leggett, K. Schulten and C. Neil Hunter, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1769–1780 CrossRef CAS PubMed.
- M. Sener, J. Strumpfer, A. Singharoy, C. N. Hunter and K. Schulten, eLife, 2016, 5, e09541 CrossRef PubMed.
- H. Lee, Y.-C. Cheng and G. R. Fleming, Science, 2007, 316, 1462–1465 CrossRef CAS PubMed.
- G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786 CrossRef CAS PubMed.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647 CrossRef CAS PubMed.
- P. D. Dahlberg, G. J. Norris, C. Wang, S. Viswanathan, V. P. Singh and G. S. Engel, J. Chem. Phys., 2015, 143, 101101 CrossRef PubMed.
- P. D. Dahlberg, P.-C. Ting, S. C. Massey, M. A. Allodi, E. C. Martin, C. N. Hunter and G. S. Engel, Nat. Commun., 2017, 8, 988 CrossRef PubMed.
- J. Strümpfer, M. Şener and K. Schulten, J. Phys. Chem. Lett., 2012, 3, 536–542 CrossRef PubMed.
- F. Fassioli, R. Dinshaw, P. C. Arpin and G. D. Scholes, J. R. Soc., Interface, 2014, 11, 20130901 CrossRef PubMed.
- A. Halpin, P. J. M. Johnson, R. Tempelaar, R. S. Murphy, J. Knoester, T. L. C. Jansen and R. J. D. Miller, Nat. Chem., 2014, 6, 196–201 CrossRef CAS PubMed.
- D. M. Wilkins and N. S. Dattani, J. Chem. Theory Comput., 2015, 11, 3411–3419 CrossRef CAS PubMed.
- H.-G. Duan, V. I. Prokhorenko, R. J. Cogdell, K. Ashraf, A. L. Stevens, M. Thorwart and R. J. D. Miller, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8493–8498 CrossRef CAS PubMed.
- T. W. Ebbesen, H. J. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff, Nature, 1998, 391, 667–669 CrossRef CAS.
- W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830 CrossRef CAS PubMed.
- J. Dintinger, S. Klein, F. Bustos, W. L. Barnes and T. W. Ebbesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035424 CrossRef.
- Y. Sugawara, T. A. Kelf, J. J. Baumberg, M. E. Abdelsalam and P. N. Bartlett, Phys. Rev. Lett., 2006, 97, 266808 CrossRef CAS PubMed.
- S. Aberra Guebrou, C. Symonds, E. Homeyer, J. C. Plenet, Y. N. Gartstein, V. M. Agranovich and J. Bellessa, Phys. Rev. Lett., 2012, 108, 066401 CrossRef PubMed.
- L. Shi, T. K. Hakala, H. T. Rekola, J. P. Martikainen, R. J. Moerland and P. Törmä, Phys. Rev. Lett., 2014, 112, 153002 CrossRef CAS PubMed.
- A. I. Väkeväinen, R. J. Moerland, H. T. Rekola, A. P. Eskelinen, J. P. Martikainen, D. H. Kim and P. Törmä, Nano Lett., 2014, 14, 1721–1727 CrossRef PubMed.
- P. Törmä and W. L. Barnes, Rep. Prog. Phys., 2015, 78, 013901 CrossRef PubMed.
- A. Tsargorodska, M. L. Cartron, C. Vasilev, G. Kodali, O. A. Mass, J. J. Baumberg, P. L. Dutton, C. N. Hunter, P. Törmä and G. J. Leggett, Nano Lett., 2016, 16, 6850–6856 CrossRef CAS PubMed.
- S. R. J. Brueck, Proc. IEEE, 2005, 93, 1704–1721 CAS.
- X. Wei, X. Su, P. Cao, X. Liu, W. Chang, M. Li, X. Zhang and Z. Liu, Nature, 2016, 534, 69–74 CrossRef CAS PubMed.
- C. C. Gradinaru, I. H. M. van Stokkum, A. A. Pascal, R. van Grondelle and H. van Amerongen, J. Phys. Chem. B, 2000, 104, 9330–9342 CrossRef CAS.
- A. Tsargorodska, O. El Zubir, B. Darroch, M. l. L. Cartron, T. Basova, C. N. Hunter, A. V. Nabok and G. J. Leggett, ACS Nano, 2014, 8, 7858–7869 CrossRef CAS PubMed.
- B. Gallinet and O. J. F. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235427 CrossRef.
- A. E. Schlather, N. Large, A. S. Urban, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 3281–3286 CrossRef CAS PubMed.
- P. López-Tarifa, N. Liguori, N. van den Heuvel, R. Croce and L. Visscher, Phys. Chem. Chem. Phys., 2017, 19, 18311–18320 RSC.
- A. Lishchuk, G. Kodali, J. A. Mancini, M. Broadbent, B. Darroch, O. A. Mass, A. Nabok, P. L. Dutton, C. N. Hunter, P. Törmä and G. J. Leggett, Nanoscale, 2018, 10, 13064–13073 RSC.
- S. Shoji, T. Ogawa, T. Hashishin, S. Ogasawara, H. Watanabe, H. Usami and H. Tamiaki, Nanotubes of Biomimetic Supramolecules Constructed by Synthetic Metal Chlorophyll Derivatives, Nano Lett., 2016, 16, 3650–3654 CrossRef CAS PubMed.
- B. Z. Packard, D. T. Toptygin, A. Komoriya and L. Brand, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 11640–11645 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |