Open Access Article
Open Access ArticleMesoporous ZnO thin films obtained from molecular layer deposited “zincones”†
Alberto
Perrotta
 *,
Richard
Berger
,
Fabian
Muralter
*,
Richard
Berger
,
Fabian
Muralter
 and
Anna Maria
Coclite
and
Anna Maria
Coclite

Institute of Solid State Physics, NAWI Graz, Graz University of Technology, Petersgasse 16, 8010 Graz, Austria. E-mail: a.perrotta@tugraz.at; perrotta.alberto@gmail.com
First published on 28th August 2019
Abstract
The delivery of porous ZnO thin films represents a challenge due to the low porosity achievable by conventional thin film deposition methods. In this contribution, the synthesis of mesoporous ZnO thin films is demonstrated through calcination in air of hybrid Zn-based polymers (zincone) obtained by molecular layer deposition (MLD). The calcination process was followed as a function of temperature using X-ray reflectivity and diffraction, together with spectroscopic ellipsometry. Temperature ranges were identified for the removal of the organic ligands (120 °C) and ZnO crystallization (340 °C). The total porosity and open porosity were also determined by ellipsometric porosimetry (EP) and grazing incidence small-angle X-ray scattering (GISAXS). The calcination temperature was identified as a control parameter for obtaining different (open) porosity contents and pore size distributions (PSDs). Open porosity values of 12.6% and 19.6% were obtained by calcining the zincones up to 600 °C and 400 °C, respectively. Open PSDs with a mean value of 3.2 nm (400 °C) and 4.6 nm (600 °C) were obtained. The formation of larger slit-shaped pores was demonstrated at higher temperatures, due to the growth and coalescence of ZnO crystallites.
1. Introduction
Porous ZnO thin films are often employed in sensing (bio- and gas-) and as a host material for biomedical applications, such as drug delivery and tissue engineering.1–3 However, classical thin film technologies often suffer from some major limitations, such as an intrinsic low surface area and lack of framework porosity.1 For this reason, new synthetic methods for the production of porous ZnO thin films are sought.Molecular layer deposition (MLD) is a sequential self-limiting vapor-phase deposition method for the delivery of (ultra-)thin organic and hybrid films.4,5 The layer-by-layer nature of such a method allows the deposition of highly conformal thin films with sub-nm thickness control that can be applied to complex high aspect ratio nanostructured substrates and devices.
While in the delivery of pure polymeric structures the combination of two or more organic ligands is adopted,6 hybrid organic–inorganic materials can be synthesized with the combination of metalorganic precursors with the ligands used in organic MLD.4,7,8 These materials possess unique properties, often differing from their pure organic and inorganic counterparts.9,10 In the literature, several functional hybrid films have been reported, adopting different metallic precursors (e.g., Al,11–15 Ti,16,17 Zr,16 Hf,18 Zn,19–22 V,23,24 Li,25 Fe,26,27 Mo,28 Sn,29 and Er30). Generally, the composition of the thin films includes the metallic element, oxygen and/or nitrogen, and an organic backbone, and they are referred to as ‘metalcones’, e.g., alucones, zincones, and titanicones.4,8
From the metal-alkoxide produced by MLD, porous metal oxide thin films can be achieved through water etching or thermal treatments in the presence of oxygen.19 In the literature, (ultra-)thin porous alumina11,15,31–34 and titania17,35–39 are the most studied MLD-derived oxides, and recently, vanadium-23,40 and tin-29 based materials have also been investigated. The oxide layers were applied as functional thin films in photocatalysis35,38 and as electrodes for lithium-ion batteries,17,23 or for protective and passivating layers.34,37,41
In this contribution, starting from the results obtained from Zn-alkoxides deposited by sub-saturated plasma enhanced atomic layer deposition (PE-ALD) and reported in a previous study,42 porous ZnO was obtained by the calcination of MLD zincone layers. The calcination process was followed by spectroscopic ellipsometry (SE), X-ray diffraction (XRD), and reflectivity (XRR). The pore content and pore size distribution were investigated by ellipsometric porosimetry (EP), already successful in determining the open porosity in hybrid and polymer-derived oxides.15,17,23,42–45 Grazing incidence small-angle X-ray scattering (GISAXS) was used for gaining more insight into the total porosity.
In the literature, the transformation of zincones into porous ZnO has not received the same attention as the Ti- and Al-based counterparts, due to their low surface area achieved so far. Liang et al.20 reported on the calcination in air of zincone layers coating titania nanoparticles. Low surface area ZnO as well as a wide distribution of micro- and meso-pores was obtained. By changing the post-deposition annealing temperature, the surface area and mesopore content decreased, and clogging of the pores was hypothesized to be due to the crystallization of ZnO. Temperatures up to 400 °C were investigated by means of thermogravimetric analyses, and loss of the material was witnessed starting from 70 °C. However, the pore content was not reported, and the crystallinity and crystal development were not investigated. Furthermore, the study was limited to ultra-thin zincone films (40 cycles, 0.25 Å per cycle). Consequently, the aim of this work was an investigation of the crystallinity of zincone layers to show the evolution of the ZnO crystals and, in turn, the consequent possible clogging of the forming pores. Moreover, specific calcination temperatures were identified in order to balance the crystalline formation with the pore content.
2. Experimental
(a) MLD system
A custom-built MLD reactor was used to deposit the zincone thin films on single side polished c-Si (100) substrates (Siegert Wafer). Diethyl zinc (DEZ, Sigma-Aldrich) was used as the metalorganic precursor. Ethylene glycol (EG, Sigma-Aldrich) was used as the organic co-precursor. A constant flow of Ar (16 sccm) was adopted during the whole process as purging and carrier gas. An automation platform (MKS PAC 1000) and a mass flow controller (MKS MF1-C) were used to control the Ar flow rates. ALD-valves (Swagelok ALD3) were used to pulse DEZ and EG into the reactor. Due to the high vapor pressure of DEZ, no further heating or bubbling system was adopted. EG was instead heated to 80 °C. All depositions were carried out at a substrate temperature of 110 ± 5 °C.(b) Chemical and structural characterization
Spectroscopic ellipsometry (J.A. Woollam M-2000V) was used to determine the thickness and optical properties of the layers after deposition. The measurements were carried out at three different angles (65°, 70°, and 75°) in the wavelength range from 370–1000 nm. The analysis of the spectra was performed with the software CompleteEASE®. The thickness was determined by applying a three-layer model consisting of a silicon substrate, a native silicon oxide layer with a fixed thickness of 1.5–2 nm, and a Cauchy layer, as follows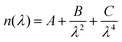 | (1) |
X-ray diffraction (XRD) and reflectivity (XRR) were performed on the MLD zincone layers. The diffractometer (Panalytical Empyrean), working in a θ/2θ-configuration, was equipped with a copper tube (λ = 1.5418 Å). XRD was used to analyze the crystalline properties of the films in specular direction, that is, with the crystallographic planes parallel to the substrate. The beam was further parallelized with a layered X-ray mirror and a PIXcel3D-detector was operated in the 1D-mode. A 1/8° divergence, a 10 mm mask, and a P7.5 anti-scatter slit were used in the setup. The integration time per measurement was set to 600 s with a step size of 0.0263°. In order to quantify the crystal growth, an estimation of the average crystallite size D was performed. D can be obtained from a Bragg peak in the XRD spectrum using Scherrer's formula,46
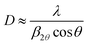 | (2) |
XRR was used to determine the density and thickness of the layers. A 1/32° divergence was used in the setup. The measurement was performed between 0° and 5° with a step size of 0.007° and a total integration time of 720 s. The fitting was performed using X'Pert Reflectivity software by PANalytical.
For the chemical analysis of the obtained thin films, prior and after calcination, Fourier-transform infrared (FTIR) was performed. A BOMEM MB-102 was adopted. For each spectrum, 1000 scans were recorded in transmission mode with a resolution of 4 cm−1 between 300 cm−1 and 3700 cm−1. All spectra were baseline corrected and normalized to the film thickness. In order to exclude or reduce the contribution of atmospheric gases and vapors, a stream of N2 was used.
Grazing incidence small angle X-ray scattering (GISAXS) experiments were performed at the SAXS beamline at the synchrotron Elettra in Trieste, Italy. A wavelength of 0.154 nm was used, whereas the incidence angle for all the scattering experiments was set to 0.21°. The SAXS signal was recorded with a Pilatus3 1M detector at a sample detector distance of 2 meters. The recorded intensity maps were transferred into the reciprocal space and plotted via the software package GIDVis.47 The value of the scattering vector (q) can then be used to calculate real space distances (d) via the Debye-Scherrer equation d = 2π/q.48
Atomic force microscopy (AFM) was performed in non-contact mode on a Nanosurf Easyscan 2, equipped with a PPP-NCLR-10 cantilever (NanoWorld AG, Switzerland). Correction of artifacts, plotting and data evaluation were performed with the freely available software package Gwyddion.49
(c) Calcination: method and porous ZnO characterization
In order to remove the organic ligands to obtain porous ZnO, the zincone layers were calcined in air up to a temperature of 600 °C. To follow the calcination, in situ temperature-dependent studies were performed by both SE and X-ray based techniques. The SE system was equipped with a THMS600 temperature stage (Linkam, UK), with a sealing capping chamber. The temperature was varied from room temperature to either 400 °C or 600 °C at 200 °C per hour. Subsequently, the system was cooled down at the same rate. For these experiments, the acquisition angle was fixed at 70°.For the determination of the porosity in the porous ZnO layers, the THMS600 temperature stage was equipped with a custom-made humidity pump, and the principles of ellipsometric porosimetry (EP) were used.50 The relative humidity was monitored via a sensor in the measurement chamber (Sparkfun SHT-15) and tuned in the range of 0–95%.51 In this way, pores with a diameter ≥0.33 nm (the kinetic diameter of the water molecules) were probed. A dry atmosphere (i.e., 0% relative humidity) was reached using a flow of N2, ensuring the removal of water from the measurement chamber. In order to tune the relative humidity, the flow of humid air is mixed with N2 and adjusted in equilibrium steps. The temperature of the stage was kept at room temperature, ensuring that the measured relative humidity in the chamber was the same as on top of the samples.
In EP with water vapor, the variation of both the refractive index (n) and water multilayer thickness/swollen thin films is reported as a function of the relative humidity, resulting in classical adsorption/desorption isotherms, generally categorized according to the IUPAC classification.52–55 A type I isotherm is associated with porous materials with a narrow distribution of pore size with a diameter below 2 nm (nano-porous or microporous materials), and a type II isotherm is associated with non-porous materials. Mesoporous materials are instead characterized by a type IV isotherm, in which a hysteresis arises in the desorption step, due to the condensation of water in the pores. The adsorptive uptake was expressed as the adsorptive volume obtained from the Lorentz–Lorenz relationship and calculated as:
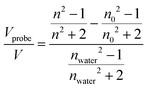 | (3) |
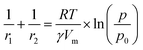 | (4) |
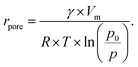 | (5) |
In situ temperature-dependent XRD and XRR studies were performed with a DHS900 heating stage attachment (Anton-Paar, Austria), as previously reported,42,60 using a heating rate of 200 °C per hour up to either 400 °C or 600 °C.61
3. Results and discussion
(a) MLD zincone: growth and chemistry
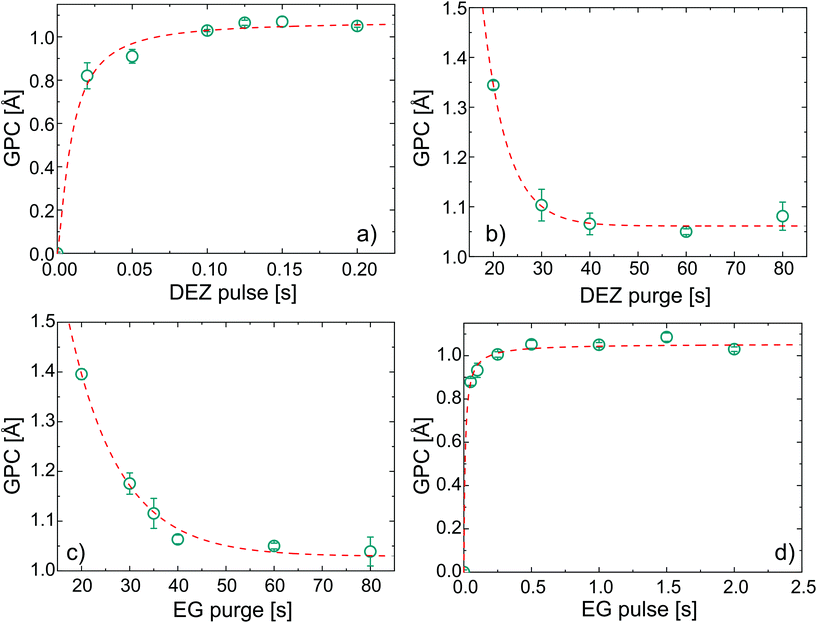
In order to verify the self-limited MLD growth and exclude any chemical vapor deposition (CVD)-like growth contribution, the exposure and subsequent purging timings for DEZ and EG were optimized to saturation. The growth per cycle as a function of the four MLD-cycle parameters is shown in Fig. 1 for a substrate temperature of 110 °C.Under saturated conditions, the DEZ/purge/EG/purge sequence was 0.15/60/1/60 s and the GPC had an average value of 1.05 ± 0.01 Å for 100 cycles of deposition.‡ With increasing the number of cycles up to 500 (see ESI, Fig. S1†), the GPC was found to be constant at 1.05 Å, with an increase of the error up to ±0.08 Å. In the literature, a wide range of growth rates were reported for EG-DEZ zincone layers. Yoon et al.62 reported a variation in the GPC between 4 Å at 90 °C and 0.25 Å at 170 °C when measured in the first 10 cycles of deposition on ZrO2 nanoparticles. On the other hand, the GPC measured on Si by means of X-ray reflectivity showed a constant value of 0.7 Å at 130 °C. Peng et al.21 reported a GPC on oxidized Si of 0.57 Å at 120 °C and of 0.39 Å at 165 °C. These values were calculated from the linear increase of thickness with the number of cycles, although the measurements were carried out on aged samples showing thickness loss after exposure to air. Due to the linearity of the thickness increase, the GPC values were considered reliable. Finally, Liang et al.20 reported a GPC on TiO2 nanoparticles of 0.25 Å measured at 120 °C and the low GPC was attributed to decomposition of DEZ during the deposition. All the different values reported in the literature reflect the variability often reported for MLD processes even under saturation conditions,44 likely depending on different experimental factors such as the reactor geometry, substrate, working pressure, and cycle pulse/purging times. The values we reported of 1.05 ± 0.01 Å are therefore in the same range of the previous literature. The linearity of the GPC was tested up to 500 cycles, confirming the stability and reproducibility of the process (see ESI, Fig. S1†). In order to confirm the successful MLD process, FT-IR was performed on the zincone layers after few minutes of exposure to air (Fig. 2a). The FT-IR spectrum of the calcined zincone is also reported in Fig. 2b and is commented in the next section.
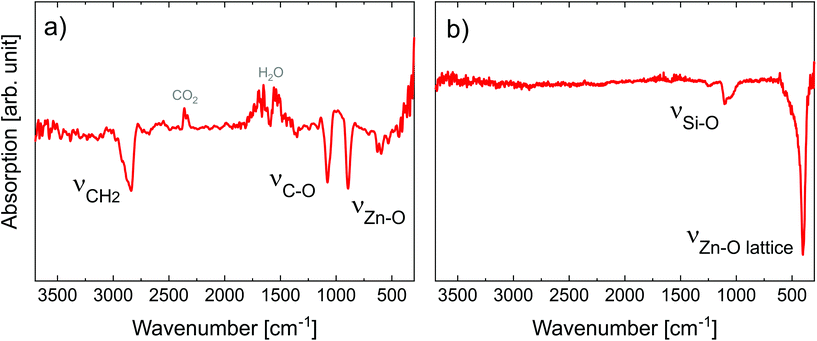 | ||
| Fig. 2 FT-IR spectra of (a) 50 nm-thick MLD zincone layer right after deposition and (b) 27 nm-thick calcined MLD-derived ZnO treated up to 600 °C. ν symbols refer to the stretching modes. | ||
The spectrum showed the typical absorption modes generally assigned to EG-DEZ zincones.21,62 The absorption modes between 2950 and 2690 cm−1 are attributed to the symmetric/antisymmetric/combination C–H vibration mode in –CH2–. The strong absorption at 1100 cm−1 and 888 cm−1 was assigned to C–O stretching in C–C–O and Zn–O–C moieties62 and to Zn–O stretching,21 respectively. O–H stretching absorption bands (3500–3000 cm−1) were not present in the spectrum, indicating that the MLD reactions were complete and no hydrolyzation due to air exposure occurred, yet. The FT-IR spectrum confirmed the successful MLD deposition, starting point for the transformation of the zincone into porous ZnO.
(b) Calcination of zincone into porous ZnO
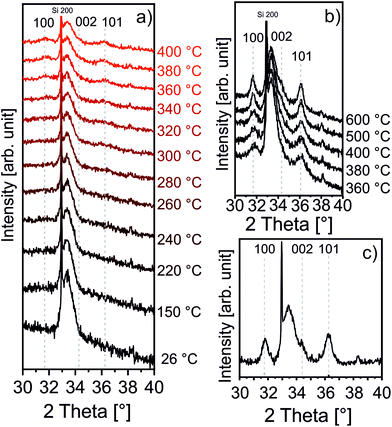
As afore-mentioned in the Experimental section, the zincone layers were heated in air to 400 °C and 600 °C, with a heating rate of 200 °C h−1. The calcination process was meant to remove the organic ligands, in turn forming (porous) ZnO. It was followed in situ by means of XRD, XRR, and SE, as previously reported in ref. 42 and 60. The XRD measurements are reported in Fig. 3.The zincone layers were amorphous before calcination, as no diffraction peaks were present in the diffractogram, except for the Si 200 peak (see the spectrum at 26 °C in Fig. 3a and Fig. S3 in the ESI†). In order to find the temperature at which the zincone starts to form crystalline ZnO, measurements with quick integration times were taken every 20 °C between 220 °C and 400 °C (Fig. 3a). Below 220 °C, the layer was found still amorphous. At 340 °C, the first characteristic Bragg peaks of crystalline ZnO appear at 2-theta of 31.7° and 36.1°, corresponding to the (100) and (101) net plane of ZnO, respectively, as in the reference ZnO powder (26170-ICSD63). Already between 340 °C and 400 °C, the Bragg peaks, referring to ZnO, increase in height, pointing out the growth of the ZnO crystallites. In order to provide high-resolution scans in the temperature range where the crystallization takes place, XRD measurements with long acquisition times were performed in the temperature range between 360 °C and 600 °C (Fig. 3b). Between 360 °C and 500 °C, the ZnO 100 and 101 diffraction peaks were found to increase in intensity while simultaneously decreasing in width, pointing out an increase in the crystallite size. For temperatures above 500 °C, a small peak at 34.3° was found corresponding to the diffraction at the ZnO (002) net plane. It is worth noting that the 002 peak is shadowed by the Si 200 diffraction peak and it is hypothesized to be present already starting from 340 °C. The presence of the three different Bragg peaks points out the polycrystalline nature of the ZnO formed by calcination of the zincone layer. This is in agreement with the study performed on the amorphous zincone-like layers deposited by plasma enhanced ALD.42 From the shape of the corresponding Bragg peaks, the crystallite size was estimated according to eqn (2), with the aim of representing the crystallite length perpendicular to the sample surface as a function of temperature (see ESI, Fig. S4†). At 600 °C, the crystallite size was between 21 ± 2 nm (for the (100) planes) and 17 ± 2 nm (for the (002) planes). The final diffractogram of the calcined MLD-derived ZnO is reported in Fig. 3c, as measured at room temperature, showing a clearly polycrystalline ZnO. The presence of residual carbon was excluded from the FT-IR measurement on the calcined MLD-derived ZnO (Fig. 2b). In the spectrum, the C–H and C–O stretching bands are absent, and the Zn–O stretching shifted to 404 cm−1, due to the formation of the crystalline lattice.64 It is worth reporting that the SiO stretching band appearing at 1104 cm−1 is due to the further oxidation of the c-Si substrate (see ESI, Fig. S2†). When comparing the MLD zincone crystal formation upon annealing in air to the one of the zincone-like42 and pure ZnO60 previously reported, the temperature at which the Bragg peaks are formed/grow was found the same and is therefore independent of the amount of carbon present in the layer but only dependent on the ZnO matrix. This result is different from what was previously reported for other MLD-derived oxides, i.e., TiO2,16 where the carbon matrix was found to inhibit the crystal formation.
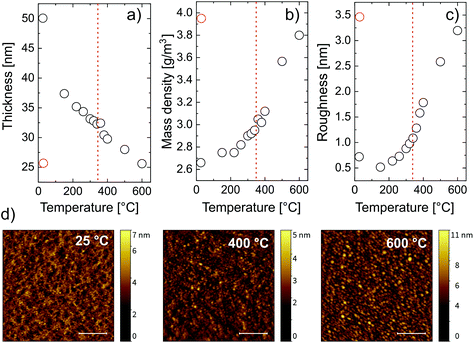
XRR measurements were carried out to investigate the evolution of the mass density and thickness of the zincone layers upon calcination (Fig. 4).
For every measured XRR spectrum, the critical angle was defined as the incidence angle where the intensity of the reflected X-ray beam is half of its initial value. From the critical angle, the electron density of the film was calculated. Assuming an appropriate model for the chemical composition of the thin film and the substrate material, the measured XRR spectra could be fitted. While the electron density of the film has a one-to-one correspondence to the critical angle in each XRR spectrum, the mass density depends on the choice of the chemical composition of the layer. The chemical composition of the film changes during the temperature increase since carbon and hydrogen are removed from the system, as witnessed from FT-IR. There are two temperature regimes for which the chemical composition can be predicted, namely before and after calcination. The chemical composition of the metalcone before calcination was chosen as ZnO2C2H4. After calcination, based on the FTIR data, a pristine ZnO model was chosen to properly describe the film. The first fit was done at room temperature with a zincone film model of the composition ZnO2C2H4. Since this first fit provided important initial parameters for the further fits at higher temperatures, the same zincone film model was used for the fits at higher temperatures.
From the fitting, three parameters were calculated, namely the layer thickness (Fig. 4a), the mass density (Fig. 4b) and the layer roughness (Fig. 4c). The mass density increases with increasing temperature. Two regimes can be identified, namely below 340 °C and above 340 °C. Below 340 °C, the removal of the organic content accounted for an increasing mass density of the film. This is confirmed by the drastic decrease in thickness, going from 50 nm to 32 nm at 340 °C (Fig. 4a). Above 340 °C, the crystallization of ZnO occurs, causing a further and accelerated increase in mass density and a further decrease in thickness, down to 52% of its initial value. This agrees with the XRD measurements that show the beginning of the crystallization at the same temperature. A higher content of crystalline ZnO over non-crystalline ZnO clearly increases the density of the film. Besides, the XRD measurement showed the growth of the crystallite size mainly between 340 °C and 500 °C. Growing crystallites cause a decrease in cavities between crystal grains also resulting in an increased mass- and electron density of the film. These results suggest that, in order to have C-free crystalline ZnO, the calcination temperature should be right above the crystallization temperature of ZnO. The chemical composition of MLD-derived ZnO calcined up to 400 °C confirmed this hypothesis. FT-IR spectra of these layers (see the ESI†) showed no absorption of carbon functionalities, and, in turn, only partially crystallized ZnO is present after calcination at 400 °C, with the Zn–O lattice stretching absorption at 400 cm−1. Finally, when the film is cooled to room temperature, the mass density increases, with a final value of 4.5 g cm−3. This is related to thermal expansion since the XRD data suggest no change in the crystal structure and composition of the film within the cooling process. Comparing the final value of mass density with the one of bulk ZnO of 5.1 g cm−3, a total film porosity of 20% can be assumed. The roughness of the film (Fig. 4c) increases with temperature mainly between 300 °C and 600 °C. This can be ascribed to the formation of cavities at the film surface as well as to the crystallization process. This is confirmed by the AFM pictures recorded before and after calcination at different temperatures (Fig. 4d). The formation of crystallites roughening the surface starts to be visible at 400 °C and it is more evident at 600 °C, where the whole surface showed regular structures attributed to the ZnO crystallites. The root mean square deviation of the heights (σrms) and the autocorrelation length in lateral dimension (T) were gained from fitting the height–height correlation function (HHCF) calculated directly from the AFM images with a Gaussian HHCF. For the investigated samples (pristine, after calcination at 400 °C and at 600 °C), σrms was determined to be 0.5, 0.6 and 1.3 nm, respectively; correspondingly, T was evaluated to be 24, 26 and 40 nm, respectively. Hence, the described roughening appears to be accompanied by a lateral growth of structures on the surface with increasing the temperature during calcination.
The transformation of the zincone to ZnO was also followed by SE (Fig. 5).
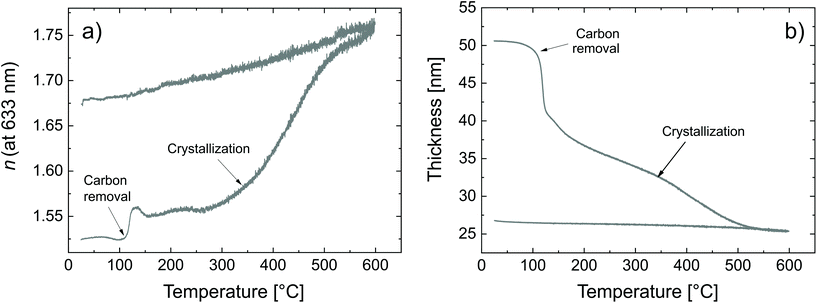 | ||
| Fig. 5 Calcination of the zincone as measured by SE (a) refractive index and (b) thickness as a function of the calcination temperature. | ||
Two critical regions can be identified. The film thickness (Fig. 5b) and refractive index (Fig. 5a) are constant below 120 °C. At 120 °C, a dramatic drop in the film thickness and a rapid increase in the refractive index were observed. The thickness drop indicates a collapse of the hybrid structure inside the film explained by the removal of the organic content of the film. The sudden removal of carbon and hydrogen from the film together with the collapse of the film structure is in line with an increased electron density which explains the quick increase in the refractive index at 120 °C. The thickness drop occurred in the same temperature range as the one observed with XRR, confirming the robustness of both models adopted. Between 120 °C and 340 °C, the film thickness is slowly decreasing which is mainly related to reorientation processes of the remaining amorphous ZnO and further carbon and hydrogen removal. The refractive index only slightly increases, confirming that only minor rearrangements and residual carbon removal occurred in this temperature range. At 340 °C the crystallization of the remaining ZnO started, in agreement with the XRR and XRD measurements. Both the thickness and refractive index abruptly changed due to the phase transition. The film thickness continuously decreases with increasing temperature up to 500 °C, where the crystallization ends. The refractive index was found to increase, in agreement with the increase in electron density also measured by XRR. When the film was brought back to room temperature, no significant changes in the film thickness could be measured by ellipsometry. The refractive index, however, was found to decrease. For non-porous crystalline ZnO, the temperature dependency of the below-band-gap refractive index at a wavelength of 630 nm is reported to be in the range of 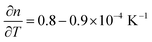 .65,66 In Fig. 5b, a temperature dependency of
.65,66 In Fig. 5b, a temperature dependency of 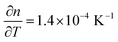 was measured during the cooling process. Comparing the refractive index to the electron density measured by XRR, the electron density cannot be the determinant property for the decrease of the refractive index while decreasing the temperature. Instead, a decreased electronic polarizability is responsible for the behaviour of the refractive index while cooling. The difference between the measured and literature values could arise from the porous nature of the film, together with its polycrystalline texture and possible residual impurities. The final refractive index of 1.67 suggests the presence of porosity in the layer, confirming the hypothesis put forth from the XRR measurements. In the literature, Liang et al.20 followed the weight loss of TiO2 nanoparticles coated with 1 nm-thick MLD zincone with thermal gravimetric analysis, reporting similar temperature ranges and supporting the in situ study so far.
was measured during the cooling process. Comparing the refractive index to the electron density measured by XRR, the electron density cannot be the determinant property for the decrease of the refractive index while decreasing the temperature. Instead, a decreased electronic polarizability is responsible for the behaviour of the refractive index while cooling. The difference between the measured and literature values could arise from the porous nature of the film, together with its polycrystalline texture and possible residual impurities. The final refractive index of 1.67 suggests the presence of porosity in the layer, confirming the hypothesis put forth from the XRR measurements. In the literature, Liang et al.20 followed the weight loss of TiO2 nanoparticles coated with 1 nm-thick MLD zincone with thermal gravimetric analysis, reporting similar temperature ranges and supporting the in situ study so far.
Comparing the in situ study here reported with the previous ones on zincone-like and pure ZnO layers, some differences can be observed in the temperature ranges where the impurities are removed from the layers. When the layer shows crystallinity or oxidized carbon (included up to 7% in the layers), removal of adsorbed gas or residual carbon starts between 170 °C and 230 °C. The inclusion of the oxidized C functionalities in a partially crystalline or amorphous ZnO increases the energy necessary for its removal. ZnO crystallization starts at 340 °C, despite the amount of carbon present, as aforementioned. The polycrystallinity of ZnO starting from an amorphous layer is in agreement with the amorphous zincone-like transformation, highlighting that in the absence of a seed layer/crystallite with a specific orientation, the self-texturing of ZnO will not deliver a specific orientation of the crystallites.
(c) Porosity in MLD-derived ZnO
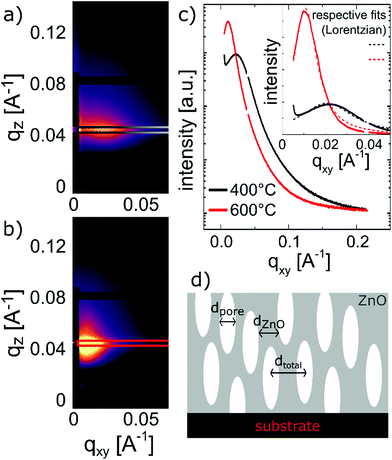
In order to calculate the total and open porosity§ of the layers, GISAXS and EP measurements were performed, respectively.From GISAXS experiments performed on the samples calcined at 400 °C and 600 °C, firstly, the (meso-)porous nature of the thin films could be confirmed by the scattering maps exhibiting distinct peaks along the in-plane direction (Fig. 6c). Secondly, by analysing the interference peaks close to the specular direction (distance of the Kiessig fringes above the beam stop in qz), a film thickness of ∼30 nm could be determined for the sample calcined at 400 °C, in line with SE and XRR measurements. The roughening of the surface (as also confirmed by AFM) leads to the more distinct decrease of the scattering intensity in the mentioned direction for the sample calcined at 600 °C; no distinct Kiessig fringes were present and the evaluation of the film thickness was not possible for the respective sample. In the maps of the recorded scattering intensities of the samples calcined at 400 °C and 600 °C, respectively, the distinct interference peaks along the in-plane direction are present due to the samples exhibiting a certain kind of order in the lateral dimension; from them, the dimensionalities of the porous structure could be assessed (Leroy et al.67). The peak positions correspond to average distances (dtotal) of (28.8 ± 1.5) and (59.3 ± 1.7) nm for the samples calcined at 400 °C and at 600 °C, respectively. These can be attributed to overall domain sizes in the lateral dimension, comprising both ZnO and pores (i.e., dtotal = dZnO + dpore, see Fig. 6d). From fitting the peaks with Lorentzian functions and extracting the peak width δ (inset of Fig. 6c), one obtains the domain size of the ordered domain, again, via the Debye-Scherrer equation d = 2π/δ.48 Hence, the ZnO domain size (dZnO) was estimated to be (20.6 ± 0.8) nm for the sample calcined at 400 °C and (48 ± 3) nm for the sample calcined at 600 °C. The difference between the distances calculated from the lateral peak position and the peak width can, thus, be interpreted as a measure for the pore diameter (dpore), (7.8 ± 1.7) and (11.3 ± 3.4) nm, respectively.
A sketch of the extracted distances in the porous structure is given in Fig. 6d. Furthermore, from evaluating the Porod invariant Qinv and the fit of the Porod plot at large q, the surface-to-volume ratio for the two samples was evaluated to be 0.5 nm−1 (400 °C) and 0.3 nm−1 (600 °C).48 Although estimating the measured area of the samples is not trivial, and in turn a significant measure of the surface area is not possible, this shows that the overall porosity of the zincone calcined at 400 °C is larger than the one of the sample calcined at 600 °C, despite exhibiting smaller pores. Please note that GISAXS probes the total porosity of the thin films and could only be applied on an in-plane peak, thus, repeating porous structures parallel to the substrate.
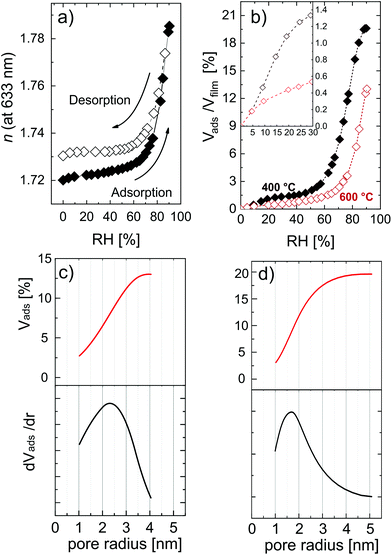
Complementing the total porosity evaluation, the determination of the open porosity can be measured with EP. This kind of porosity is directly related to applications where the material interacts with species present on the surface, e.g., filtration membranes, bio- and gas-sensors, and photocatalysis. In this study with EP, water was used as a probing molecule, with a kinetic diameter of 0.27–0.33 nm.54,58 In Fig. 7, the adsorption isotherms and the relative pore size distributions are reported.
Fig. 7a shows the refractive index variation upon exposure to different relative humidity values. The shape of the isotherms suggests that ZnO is mesoporous, that is, with a pore size distribution (PSD) within 2 nm and 50 nm in pore diameter. The adsorption at very low humidity is solely attributed to nanopores (elsewhere also called micropores),54,68 and does not represent the major water uptake in the isotherm, indicating a low amount of narrow pores. The condensation of water, typical of mesoporous materials and resulting in a sudden uptake of the probe molecule, in the porosity of ZnO started at a relative humidity of 70%. The high partial pressure at which the condensation takes place indicates pores with a slit-shape, while in the case of cylindrical pores the condensation would usually occur at lower partial pressure (40–50%). Water uptake was found to slow down when approaching condensation, but a plateau was not found in the partial pressure range explored. Moreover, the hysteresis between the adsorption and desorption branch is relatively small, and the desorption almost completely follows the adsorption branch. This kind of hysteresis loop is typical of clay-like materials or sintered nano-particles.53 In the MLD-derived ZnO formed by calcination, several crystallites oriented in different directions are growing simultaneously and coalescing in time, possibly resulting in a clay-like structure. The AFM picture of the MLD-derived ZnO at 600 °C (Fig. 5d) supports this hypothesis, clearly showing periodical structures standing out of the surface. Eqn (3) was applied to the adsorption branch of the MLD-derived ZnO calcined at 400 °C and 600 °C and showed in Fig. 7b. The layer calcined up to 600 °C showed a porosity value of 12.6 ± 0.5%, while the one calcined at 400 °C showed a value of porosity up to 19.6 ± 0.5%, in line with the surface-to-volume ratios calculated from the GISAXS maps. The temperature can therefore be used as a parameter to tune the pore content, because it directly affects the packing and dimension of the crystallites and, in turn, the free volume in the ZnO films. Moreover, the nanoporosity is affected by the calcination temperature, as shown in the inset in Fig. 7b. However, the low values achieved (0.5% and 1.3% as measured at 30% relative humidity for the layers calcined at 600 °C and 400 °C, respectively) point out that this method cannot deliver significant amounts of nanoporosity. It is worth reporting that this is a slight underestimation of the total open porosity, especially in the mesoporous region at very high partial pressure. The high polarity of water and the high affinity with the material cause a strong multilayer adsorption, interfering with the ellipsometry measurements. In the literature, porosity in hydrolyzed zincone was reported by Peng et al.21 and MLD-derived ZnO obtained by calcination was reported by Liang et al.20 Transmission electron microscopy and AFM carried out on the hydrolyzed zincone layers suggested the presence of nano-scale porosity due to the degradation of the zincone layers upon exposure to the atmosphere, although no further chemical characterization and a specific analysis of the porosity were performed. Instead, the calcined MLD-derived ZnO was characterized by nitrogen sorption. In the study, the surface area obtained by calcined zincone was suggested to be limited by the crystallization of ZnO. In our work, we demonstrate that the crystallization indeed lowers the available open porosity but can additionally be tuned by acting on the temperature, knowing that the crystallization occurs at 340 °C. In the literature, crystalline oxides with very limited porosity have been achieved by calcination in air, so far. Van de Kerckhove reported on MLD-derived titania17 and vanadia23 annealed under different atmospheres. Annealing in air delivered very limited porous titania (2%) and nonporous vanadia as measured by EP. While not achieving the high porosity of MLD-derived alumina,15,32 MLD-derived ZnO can be produced with sufficient porosity to be adopted in photocatalysis and sensing applications.
Applying the Kelvin equation (eqn (5)), the PSD can be calculated. In Fig. 7c and d the PSD of the MLD-derived ZnO is reported for layers calcined at 600 °C and 400 °C, respectively. At 600 °C, the PSD is wide and with a maximum at a pore width of 4.6 nm. Instead, at 400 °C the PSD is sharper and shifted at a lower pore size, namely 3.2 nm. This result confirms the relative difference in the pore dimension as measured from GISAXS. The crystallization of ZnO, with crystallite coalescence and growth, creates lower open porosity but wider pores, showing the possibility to control, to a certain extent, the pore size.
4. Conclusions
The development of porosity and crystallinity upon the calcination of MLD zincones into ZnO is investigated. Zincone layers were deposited by means of MLD adopting EG and DEZ as precursors and the process and the material characteristics were studied in detail. The zincone layers were subsequently calcined in air up to 400 °C and 600 °C at a rate of 200 °C h−1. In situ techniques, namely XRD, XRR, and SE, were adopted to gather insights into the transformation of the zincone layers into ZnO. The removal of the carbon functionalities related to the EG was found to occur starting from 120 °C, causing a reduction of the thickness and an increase of the mass density and refractive index. At 340 °C, the crystallization of the ZnO was found to start and a polycrystalline texture developed, showing (100), (002), and (101) planes as measured by XRD. At this temperature, a drastic change of the physical–chemical properties was measured, and no carbon content was detected by means of FT-IR. The final mass density (4.5 g cm−3) and refractive index (1.67 at 633 nm) are below the ones of bulk ZnO, suggesting the presence of porosity.In order to define the amount of closed and open porosity in the layer, GISAXS and EP measurements were performed, respectively. The calcination temperature can be used to control the open pore content and pore size distribution in the layers. With GISAXS, layers deposited at 400 °C showed a higher surface-to-volume ratio (0.5 nm−1) and a lower pore size of (7.8 ± 1.7) nm compared with a calcination temperature of 600 °C, which showed a lower surface-to-volume ratio (0.3 nm−1) and a larger pore size of (11.3 ± 3.4) nm. With EP, a porosity up to 19.5% was found. Layers deposited at 400 °C show a higher pore content (19.5%) and a lower mean pore size (3.2 nm), while adopting temperatures up to 600 °C a lower pore content (12.6%) and a higher mean pore size (4.6 nm) can be achieved. These results may open new applications for the MLD-derived ZnO in the fields of photocatalysis and bio- and gas-sensing.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
A. P. acknowledges the 8. Ausschreibung der Anschubfinanzierung funding scheme of TU Graz Research and Technology House (Grant No. F-AF8-513-01). This project was partly funded by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 715403). The authors thank Elettra Sincrotrone Trieste for the allocation of synchrotron radiation beamtime and H. W. Amenitsch for helping with the GISAXS measurements.References
- M. Laurenti and V. Cauda, Coatings, 2018, 8 Search PubMed.
- M. Laurenti and V. Cauda, Nanomaterials, 2017, 7 Search PubMed.
- J. K. Park, Y. J. Kim, J. Yeom, J. H. Jeon, G. C. Yi, J. H. Je and S. K. Hahn, Adv. Mater., 2010, 22, 4857–4861 CrossRef CAS.
- P. Sundberg and M. Karppinen, Beilstein J. Nanotechnol., 2014, 5, 1104–1136 CrossRef.
- Y. Zhao and X. Sun, ACS Energy Lett., 2018, 3, 899–914 CrossRef CAS.
- H. Zhou and S. F. Bent, J. Vac. Sci. Technol., A, 2013, 31, 040801 CrossRef.
- K.-H. H. Yoon, K.-S. S. Han and M.-M. M. Sung, Nanoscale Res. Lett., 2012, 7, 1–6 CrossRef.
- X. Meng, J. Mater. Chem. A, 2017, 5, 18326–18378 RSC.
- B. H. Lee, B. Yoon, V. R. Anderson and S. M. George, J. Phys. Chem. C, 2012, 116, 3250–3257 CrossRef CAS.
- B. Yoon, B. H. Lee and S. M. George, J. Phys. Chem. C, 2012, 116, 24784–24791 CrossRef CAS.
- X. Liang, M. Yu, J. Li, Y.-B. Jiang and A. W. Weimer, Chem. Commun., 2009, 7140 RSC.
- J. W. DuMont and S. M. George, J. Phys. Chem. C, 2015, 119, 14603–14612 CrossRef CAS.
- Y. Lee, B. Yoon, A. S. Cavanagh and S. M. George, Langmuir, 2011, 27, 15155–15164 CrossRef CAS.
- S. Jen, S. M. George, R. S. McLean and P. F. Carcia, ACS Appl. Mater. Interfaces, 2013, 5, 1165–1173 CrossRef CAS.
- K. Van de Kerckhove, M. K. S. Barr, L. Santinacci, P. M. Vereecken, J. Dendooven and C. Detavernier, Dalton Trans., 2018, 47, 5860–5870 RSC.
- A. I. Abdulagatov, K. E. Terauds, J. J. Travis, A. S. Cavanagh, R. Raj and S. M. George, J. Phys. Chem. C, 2013, 117, 17442–17450 CrossRef CAS.
- K. Van de Kerckhove, F. Mattelaer, D. Deduytsche, P. M. Vereecken, J. Dendooven, C. Detavernier, W. L. Vasconcelos, C. Detavernier, B.-Z. Li and X.-P. Qu, Dalton Trans., 2015, 45, 1176–1184 RSC.
- B. H. Lee, V. R. Anderson and S. M. George, ACS Appl. Mater. Interfaces, 2014, 6, 16880–16887 CrossRef CAS.
- X. Liang and A. W. Weimer, Curr. Opin. Solid State Mater. Sci., 2015, 19, 115–125 CrossRef CAS.
- X. Liang, Y.-B. Jiang and A. W. Weimer, J. Vac. Sci. Technol., A, 2012, 30, 01A108 CrossRef.
- Q. Peng, B. Gong, R. M. VanGundy and G. N. Parsons, Chem. Mater., 2009, 21, 820–830 CrossRef CAS.
- D. Choudhury, G. Rajaraman and S. K. Sarkar, RSC Adv., 2015, 5, 29947–29952 RSC.
- K. Van de Kerckhove, F. Mattelaer, J. Dendooven and C. Detavernier, Dalton Trans., 2017, 46, 4542–4553 RSC.
- B. H. Lee, B. Yoon, A. I. Abdulagatov, R. A. Hall and S. M. George, Adv. Funct. Mater., 2013, 23, 532–546 CrossRef CAS.
- M. Nisula and M. Karppinen, Nano Lett., 2016, 16, 1276–1281 CrossRef CAS.
- A. Tanskanen, M. Karppinen, J. Lahtinen, Z. I. Simpson, G. McMahon, S. Zhou, D. Wang, K. Nielsch, M. Mathieu and E. F. Vansant, Dalton Trans., 2015, 44, 19194–19199 RSC.
- A. Tanskanen and M. Karppinen, Sci. Rep., 2018, 8, 8976 CrossRef CAS.
- C. MacIsaac, J. R. Schneider, R. G. Closser, T. R. Hellstern, D. S. Bergsman, J. Park, Y. Liu, R. Sinclair and S. F. Bent, Adv. Funct. Mater., 2018, 28, 1800852 CrossRef.
- K. Van de Kerckhove, J. Dendooven and C. Detavernier, J. Vac. Sci. Technol., A, 2018, 36, 051506 CrossRef.
- L. Mai, Z. Giedraityte, M. Schmidt, D. Rogalla, S. Scholz, A. D. Wieck, A. Devi and M. Karppinen, J. Mater. Sci., 2017, 52, 6216–6224 CrossRef CAS.
- X. Liang and A. W. Weimer, J. Nanopart. Res., 2010, 12, 135–142 CrossRef CAS.
- X. Liang, B. W. Evanko, A. Izar, D. M. King, Y.-B. B. Jiang and A. W. Weimer, Microporous Mesoporous Mater., 2013, 168, 178–182 CrossRef CAS.
- Y. Qin, Y. Yang, R. Scholz, E. Pippel, X. Lu and M. Knez, Nano Lett., 2011, 11, 2503–2509 CrossRef CAS.
- T. D. Gould, A. Izar, A. W. Weimer, J. L. Falconer and J. W. Medlin, ACS Catal., 2014, 4, 2714–2717 CrossRef CAS.
- D. Sarkar, S. Ishchuk, D. H. Taffa, N. Kaynan, B. A. Berke, T. Bendikov and R. Yerushalmi, J. Phys. Chem. C, 2016, 120, 3853–3862 CrossRef CAS.
- Z. Song, M. Fathizadeh, Y. Huang, K. H. Chu, Y. Yoon, L. Wang, W. L. Xu and M. Yu, J. Membr. Sci., 2016, 510, 72–78 CrossRef CAS.
- R. L. Patel, Y. B. Jiang and X. Liang, Ceram. Int., 2015, 41, 2240–2246 CrossRef CAS.
- S. Ishchuk, D. H. Taffa, O. Hazut, N. Kaynan and R. Yerushalmi, ACS Nano, 2012, 6, 7263–7269 CrossRef CAS.
- S. Wu, Z. Wang, S. Xiong and Y. Wang, J. Membr. Sci., 2019, 578, 149–155 CrossRef CAS.
- A. I. Abdulagatov, K. N. Ashurbekova, K. N. Ashurbekova, R. R. Amashaev, M. K. Rabadanov and I. M. Abdulagatov, Russ. J. Appl. Chem., 2018, 91, 347–359 CrossRef CAS.
- X. Liang, J. Li, M. Yu, C. N. McMurray, J. L. Falconer and A. W. Weimer, ACS Catal., 2011, 1, 1162–1165 CrossRef CAS.
- A. Perrotta, J. Pilz, S. Pachmajer, A. Milella and A. M. Coclite, Beilstein J. Nanotechnol., 2019, 10, 746–759 CrossRef CAS.
- N. D. Boscher, M. Wang, A. Perrotta, K. Heinze, M. Creatore and K. K. Gleason, Adv. Mater., 2016, 28, 7479–7485 CrossRef CAS.
- A. Perrotta, P. Poodt, F. J. (Fieke) van den Bruele, W. M. M. (Erwin) Kessels and M. Creatore, Dalton Trans., 2018, 47, 7649–7655 RSC.
- M. Aghaee, J. P. Niemelä, W. M. M. Kessels and M. Creatore, Dalton Trans., 2019, 48, 3496–3505 RSC.
- M. Birkholz, P. F. Fewster and C. Genzel, Thin film analysis by X-ray scattering, John Wiley & Sons, Wiley-VCH, 2006 Search PubMed.
- B. Schrode, S. Pachmajer, M. Dohr, C. Röthel, J. Domke, T. Fritz, R. Resel and O. Werzer, IUCr, J. Appl. Crystallogr., 2019, 52, 683–689 CrossRef CAS PubMed.
- S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S. S. Funari, P. Mulvaney and R. Knott, J. Phys. Chem. B, 2005, 109, 1347–1360 CrossRef PubMed.
- D. Nečas and P. Klapetek, Cent. Eur. J. Phys., 2012, 10, 181–188 Search PubMed.
- J. Dendooven, B. Goris, K. Devloo-Casier, E. Levrau, E. Biermans, M. R. Baklanov, K. F. Ludwig, P. Van Der Voort, S. Bals and C. Detavernier, Chem. Mater., 2012, 24, 1992–1994 CrossRef CAS.
- P. Salzmann, A. Perrotta and A. M. Coclite, ACS Appl. Mater. Interfaces, 2018, 10, 6636–6645 CrossRef CAS.
- S. J. Gregg and K. S. W. Sing, Adsorption, surface area, and porosity, Academic Press Inc. Ltd, London, England, 1991 Search PubMed.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. S. W. Sing, Adsorption by Powders and Porous Solids: Principles, Methodology and Applications, Academic Press, 2013 Search PubMed.
- A. Perrotta, E. R. J. van Beekum, G. Aresta, A. Jagia, W. Keuning, M. C. M. van de Sanden, W. M. M. Kessels and M. Creatore, Microporous Mesoporous Mater., 2014, 188, 163–171 CrossRef CAS.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619 CAS.
- A. Perrotta, S. J. García, J. J. Michels, A.-M. Andringa and M. Creatore, ACS Appl. Mater. Interfaces, 2015, 7, 15968–15977 CrossRef CAS.
- A.-M. Andringa, A. Perrotta, K. de Peuter, H. C. M. Knoops, W. M. M. Kessels and M. Creatore, ACS Appl. Mater. Interfaces, 2015, 7, 22525–22532 CrossRef CAS.
- M. R. Baklanov, K. P. Mogilnikov, V. G. Polovinkin and F. N. Dultsev, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2000, 18, 1385 CrossRef CAS.
- J. Dendooven, K. Devloo-Casier, E. Levrau, R. Van Hove, S. P. Sree, M. R. Baklanov, J. A. Martens and C. Detavernier, Langmuir, 2012, 28, 3852–3859 CrossRef CAS.
- A. Perrotta, J. Pilz, A. Milella and A. M. Coclite, Appl. Surf. Sci., 2019, 483, 10–18 CrossRef CAS.
- P. Christian and A. M. Coclite, Beilstein J. Nanotechnol., 2017, 8, 933–942 CrossRef CAS.
- B. Yoon, J. L. O'Patchen, D. Seghete, A. S. Cavanagh and S. M. George, Chem. Vap. Deposition, 2009, 15, 112–121 CrossRef CAS.
- S. C. Abrahams and J. L. Bernstein, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1233–1236 CrossRef CAS.
- S. Peulon and D. Lincot, Adv. Mater., 1996, 8, 166–170 CrossRef CAS.
- C. Bundesmann, R. Schmidt-Grund and M. Schubert, Optical Properties of ZnO and Related Compounds, Springer, Berlin, Heidelberg, 2008, pp. 79–124 Search PubMed.
- R. Schmidt-Grund, N. Ashkenov, M. M. Schubert, W. Czakai, D. Faltermeier, G. Benndorf, H. Hochmuth, M. Lorenz and M. Grundmann, in AIP Conference Proceedings, AIP, 2007, vol. 893, pp. 271–272 Search PubMed.
- F. Leroy, J. Eymery, D. Buttard, G. Renaud and R. Lazzari, J. Cryst. Growth, 2005, 275, e2195–e2200 CrossRef CAS.
- A. Perrotta, S. J. García and M. Creatore, Plasma Processes Polym., 2015, 12, 968–979 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9dt02824b |
| ‡ It is worth reporting that the standard deviation of the GPC was calculated considering the asymptotic value of the four saturation curves obtained through a fitting procedure. By averaging the data points at and after saturation, the error bar increases to ±0.03 Å. |
| § The total porosity comprises both open and closed porosity. Open porosity is defined as all of the pores which are connected to the surface. Closed porosity is defined as all of the pores which are included in the material matrix and do not have access to the surface.52,53 |
| This journal is © The Royal Society of Chemistry 2019 |