Mechanisms of fluorescence quenching in prototypical aggregation-induced emission systems: excited state dynamics with TD-DFTB†
Thierry
Tran
 ,
Antonio
Prlj
*,
Kun-Han
Lin
,
Antonio
Prlj
*,
Kun-Han
Lin
 ,
Daniel
Hollas
,
Daniel
Hollas
 and
Clémence
Corminboeuf
and
Clémence
Corminboeuf
 *
*
Laboratory for Computational Molecular Design, Institute of Chemical Sciences and Engineering, Ecole Polytechnique Federale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch
First published on 6th March 2019
Abstract
A recent implementation of time-dependent tight-binding density functional theory is employed in excited state molecular dynamics for the investigation of the fluorescence quenching mechanism in 3 prototypical aggregation-induced emission systems. An assessment of the accuracy of the electronic structure method is done by comparison with previous theoretical work while dynamics simulations were extended to the condensed phase to obtain excited state lifetimes comparable to experiment. A thorough investigation is done on tetraphenylethylene in order to resolve the on-going debate on the role of specific deactivation mechanisms. Both gas phase and solvent dynamics were computed for fulvene and silole derivatives.
1 Introduction
Small organic fluorescent molecules are a class of compounds with a wide range of applications in fields such as imaging and sensing,1–3 optoelectronics,4,5 and photodynamic therapy.6 Among these small organic molecules, some chromophores have the unusual property of being non-fluorescent in solution and emissive in the solid state/aggregate. This important photophysical phenomenon is called aggregation-induced emission (AIE), first reported in 2001 by Luo et al.7 for silole derivatives. Since this discovery, the design of AIE-active molecules and their applications have become a topic of high interest.8–15To design efficient AIE systems, a fundamental understanding of their excited state deactivation pathways is essential. Many experimental and theoretical studies have tried to provide a photophysical rationale for the AIE phenomenon. Two major mechanisms have been proposed: the restriction of intramolecular motion (RIM)8,16–18 and restricted access to a conical intersection (RACI).19–21 Both models try to rationalize the twofold process: (i) fluorescence quenching in solution and (ii) induced fluorescence in the aggregate. Several other explanations of the induced emission can be found in the literature, such as the formation of excimers22 and J-aggregates,23,24 and intramolecular planarization.25 In the general RIM model, motions such as vibrations and rotations which are responsible for the nonradiative decay of the excited state in solution (by dissipating energy to the environment) are blocked upon aggregation. The hindered motion induces radiative decay through fluorescence. This model is currently accepted as the state-of-the-art by the experimental community.8,9,15,26 In the RACI model, which has gained more importance recently, the molecule in solution can decay to the ground state due to the presence of an energetically accessible conical intersection (i.e. crossing seam) between the potential energy surface of the excited state and the ground state. Upon aggregation, the conical intersection is no longer energetically accessible and the molecule relaxes to the ground state radiatively through fluorescence. Both models agree that the restriction of intramolecular motion is responsible for the induced fluorescence in the aggregate. However, the main challenge that remains is to unravel the detailed (i.e. atomistic) mechanisms behind the fluorescence quenching in solution.
In earlier work, the main explanation for the fluorescence quenching of the most representative AIE molecules, such as tetraphenylethylene (TPE),27–29 diphenyldibenzofulvene (DPDBF),30,31 and silole derivatives,32 was in terms of energy dissipation through the intramolecular motion upon photoexcitation. However, this explanation (in the spirit of the RIM hypothesis) appears somewhat vague and too general. Recent investigations have shown the importance of a conical intersection for the deactivation of the excited state in these molecules.19,20,33,34 Moreover, it was reported that the excited state decay of TPE35–37 and DPDBF31 in solution occurs on the picosecond timescale. Nonradiative decay on ultrafast timescales is consistent with dynamics involving conical intersections, rather than vibration-mediated decay (typically described within the Fermi's golden rule approximation), which occurs on the nanosecond to microsecond timescales.38 The assessment of the accessibility of conical intersections and their localization on a potential energy surface is a computational challenge for large systems.
The present work has a twofold objective. Our primary goal is to employ a computational protocol to investigate the fluorescence quenching mechanisms of relatively large molecular systems in solution. Nonadiabatic dynamics will give insight into the main deactivation pathways as well as the possible side-channels for the nonradiative decay. The computation in the presence of solvent will grant us the possibility to qualitatively determine solvation effects on the timescales and decay mechanisms and to make direct comparisons with available experiments. However, reaching such timescales is challenging for standard quantum chemical methods (such as TD-DFT, wavefunction-based). Thus the second goal is to validate the accuracy of recently proposed linear-response time-dependent tight-binding density functional theory (TD-DFTB) with long-range correction (LC-TD-DFTB).39–41 LC-TD-DFTB is a promising method to describe complex and big system due to its low computational cost. We employ nonadiabatic molecular dynamics in the framework of LC-TD-DFTB, which was recently implemented by Mitrić et al.41–43 The three prototypical AIE systems (TPE, DPDBF and dimethyltetraphenylsilole, DMTPS; see Fig. 1) investigated in this work are ideal model systems to confirm the reliability of LC-TD-DFTB due to available computational results obtained at higher levels of theory (TD-DFT, CASPT2).19,20,33,34 To find the most appropriate TD-DFTB approximation, we particularly focus on TPE, for which dynamics investigations already exist (gas phase).33,34 Thus, the “benchmarking” part (Section 3.1.1) refers to the system in the gas phase. Overall, a validation of the reliability of TD-DFTB will offer the possibility to use this new promising method for rational design and screening of new AIEgens with superior properties.
 | ||
| Fig. 1 Investigated molecules: (a) tetraphenylethylene, (b) diphenyldibenzofulvene and (c) dimethyltetraphenylsilole. | ||
2 Computational details
2.1 Electronic structure methods
The electronic structure was described using LC-TD-DFTB within the monopole approximation, as implemented by Mitrić et al. in the DFTBaby 0.1.0 code.41–43 We use the default DFTB parameters in DFTBaby, which are based on the mio parametrization; all TD-DFTB computations are done with these parameters unless stated otherwise. The two available implementations of long-range correction41,44,45 were used for the three investigated molecules. The main difference between the two long-range corrections is the underlying DFT functional used to obtain the reference density. In the original implementation (LC1) by Mitrić et al., the DFTB Hamiltonian is based on a local exchange correlation functional with a GGA reference density (i.e. PBE) and the long-range contribution is included using the full density. The latter implementation (LC2) by Niehaus et al. is based on the Hamiltonian evaluated with the BNL functional and the long-range correction is added using a density difference. It was argued that the use of a density difference for the long-range contribution is a more sensible choice rather than the full density matrix (i.e. LC1-TD-DFTB).42The TD-DFTB, TD-DFT and ADC(2) gas phase vertical excitation energies were computed at the ground state geometry optimized at ωB97XD46/def2-SVP.47 The geometry optimization and TD-DFT vertical excitation energies were computed with Gaussian 09.48 The TD-DFTB (with mio parameters) and ADC(2) vertical excitation energies were computed with DFTBaby and Turbomole 7.1,49 respectively. The TD-DFTB vertical excitation energies with 3ob parameters were computed with DFTB+ 18.1.50
2.2 QM/MM approach
The computation in solvent was performed using a QM/MM (quantum mechanics/molecular mechanics) approach. We extended the already existing framework for QM/MM in DFTBaby and implemented an interface to Gromacs 5.1.4.51,52 The interactions of the atoms in the MM part are described with the General Amber Force Field (GAFF).53 The QM region of the system consists of the AIE molecule and the solvent is made of 100 molecules of hexane. Mechanical embedding is used for the QM/MM computation, which is sufficient to describe the interaction of the nonpolar AIE molecule with an apolar solvent such as hexane. Thus, the small polarization of the QM part by the partial charges of the MM part may be ignored.2.3 Spectra, dynamics and initial conditions
The photoabsorption spectra of both TPE and the cyclized form of TPE (c-TPE) are computed from the vertical excitation energies (the 2 lowest singlet states) with LC2-TD-DFTB. 500 structures (both TPE and c-TPE) were taken from a semi-classical Wigner distribution based on the ground state harmonic vibrational frequencies. The spectral transitions were broadened by a Lorentzian with a phenomenological broadening of 0.1 eV.Two types of dynamics simulations (nonadiabatic and adiabatic) were performed based on the interstate gap between S1 and S2 (see Tables S1 and S3 in the ESI† for details) for all 3 molecules. The nonadiabatic dynamics within the framework of Tully's fewest switches surface hopping54 was computed using a time step of 0.1 fs and the nonadiabatic couplings were computed between the three lowest singlet excited states. The adiabatic dynamics (i.e. dynamics restricted to the S1 state) was computed using a time step of 0.5 fs and considering only the ground and S1 state, in order to speed-up the computation. Simulations were run for all 3 molecules in both the gas phase and solution using the two implementations of long-range correction, LC1 (see the ESI†) and LC2 (see Section 3). A comparison is made with standard TD-DFTB (without long-range correction) for TPE with both mio and 3ob parameters for the electronic structure. The adiabatic dynamics is computed using the ABIN code55 with a time step of 0.48 fs (i.e. 20 a.u.) while the electronic structure is computed with DFTB+ 18.1 (DFTB3).50 An overview of all the performed dynamics simulations is given in the ESI† (Table S3).
The initial conditions (atomic positions and velocities) for the gas phase molecular dynamics were generated using a Wigner distribution (with harmonic frequencies from ωB97XD/def2-SVP). The initial conditions for the molecular dynamics in solvent were prepared following a variation of a protocol suggested by Ruckenbauer et al.56 where the initial conditions of the QM part were generated from a Wigner distribution in the gas phase. The unit cell for the system was generated by putting the frozen solute molecule in the center and filling the remaining space with 100 hexane molecules randomly with a density of 0.655 g cm−3 using Packmol.57 The generated unit cell undergoes a structure relaxation. The system was then equilibrated at 300 K (with the canonical velocity rescaling thermostat),58 with a time coupling constant of 1 ps for 1 ns of dynamics and a time step of 1 fs. In all the steps, the solute was kept frozen. Bonds involving hydrogen atoms were constrained using a linear constraint solver algorithm. The dynamics was computed with Gromacs 5.1.4.
A swarm of 100 trajectories was initiated in the brightest low-lying singlet excited states for all systems except for nonadiabatic dynamics in solution where for some systems a swarm of only 30 trajectories was propagated due to the higher computational cost (i.e. longer timescales and slower dynamics, see Table S3 in the ESI† for details). Each system (isolated and solvated molecules) was propagated within the NVE ensemble. All simulations were performed with the DFTBaby code, which was interfaced to Gromacs for dynamics in solution. Trajectories were propagated until the S1/S0 crossing was reached (i.e. up to a certain gap threshold value; see Table S3 in the ESI† for details), which is a common practice when single reference methods are employed.59,60 We assume that for trajectories reaching the intersection region, the excited state population is transferred to the ground state.
The excited state lifetime is obtained by fitting the excited state population to a single exponential decay function f(t) = exp(−(t − td)/tf) where td is the time delay before the population of the ground state starts to rise and tf is the time decay. The lifetime τ is computed by adding the time delay and decay (see Table S4 in the ESI† for overall lifetimes in all dynamics simulations).
3 Results and discussion
3.1 Excited state dynamics of TPE
The excited state dynamics of TPE has been investigated since the early 70s.27–29,33–37,61–68 Yet, the interpretation of the excited state decay is still somewhat controversial. The initial interpretations mainly considered the ethylenic twist to be the main deactivation pathway.35,37,61 Other studies pointed out the importance of the torsional motion of the phenyl rings.36,62,69 As the field of AIE advanced, since 2001, the torsional motion was considered the main decay channel in the framework of RIM.27,62,63,67 Recently, two computational groups (including our own) have shown the importance of photocyclization, which can be rationalized from Woodward–Hoffmann rules.33,34 Photocyclization indeed involves some torsional motion of the phenyl rings. Occasionally, proof of cyclization can also be found in the experimental literature.66,70–74 Still, the most recent work stated that the ethylenic twist plays the crucial role in the fluorescence quenching of TPE.64–66Although there is still no final consensus about the excited state dynamics of TPE, identifying the TD-DFTB approximation which could qualitatively reproduce DFT results (gas phase) would be extremely useful, as it would allow significant computational speedup. This opens the possibility to investigate longer timescales, which are important for dynamics in the condensed phase. On the other hand, the dynamics in solvent could be directly compared to available experiments, which will be an additional test for the proposed computational protocol.
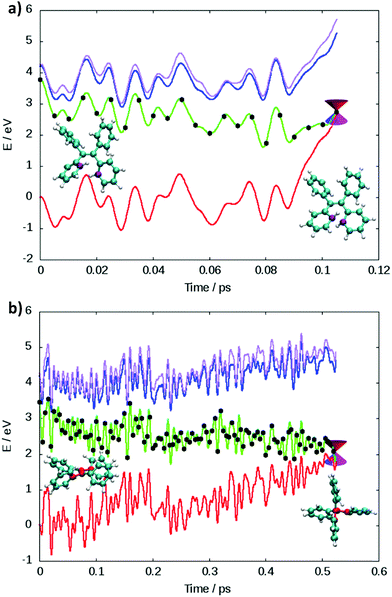
Two main deactivation mechanisms of TPE were identified, photocyclization and ethylenic twist (see Fig. 2). The shape of the excited state population decay (see Fig. S4(d) in the ESI†) indicates that the two mechanisms have a slightly different timescale. The “fast” deactivation mechanism corresponds to the photocyclization, which involves a small torsion of the phenyl rings. The “slow” deactivation mechanism is the ethylenic twist, where a more significant geometrical reorganization of the molecule is necessary in order to reach the conical intersection.
The presence of two mechanisms can be outlined by plotting the minimum distance between the carbon atoms involved in the cyclization and the twisting dihedral angle of TPE (see Fig. 3). The two major mechanisms are represented by the two regions of black dots, which correspond to the geometries at the S1/S0 crossing for the different trajectories. The black dots at 2 Å correspond to the photocyclization and the region with a high dihedral angle (close to 90°) represents the ethylenic twist. The red dots correspond to the nuclear geometries during the dynamics, thus the density of red dots represents the regions of configurational space where the molecule spends most of the time. Note that the TD-DFT dynamics is based on a smaller number of trajectories and slightly different sampling of initial conditions.33 For that reason we do not directly compare the population decay (Fig. S4, ESI†). The ratio between the two mechanisms critically depends on the electronic structure level employed. While LC1-TD-DFTB predicts that nonradiative decay almost entirely occurs via photocyclization, pure TD-DFTB (no long-range correction) clearly favors the ethylenic twist pathway. TD-DFTB and LC1-TD-DFTB represent the two extrema for the ratio of the deactivation mechanisms. While earlier theoretical work favored photocyclization, “pure” photocyclization as obtained with the LC1 approach is inconsistent with recent experimental work that emphasized the important role of the ethylenic twist.64,65 On the other hand, LC2-TD-DFTB predicts an important role of both mechanisms, with the preference towards photocyclization. This is in line with our earlier TD-DFT nonadiabatic dynamics computed at the PBE0/def2-SVP level.33 This conclusion is further supported by the CASPT2 computations by Thiel et al. in which the static profile of a TPE derivative shows that the photocyclization is as a barrierless process, while the photoisomerization is less favorable due to the presence of a barrier (8.4 kcal mol−1).34 Nevertheless, among all available TD-DFTB approximations, LC2-TD-DFTB appears as the closest substitute of the TD-DFT reference results.
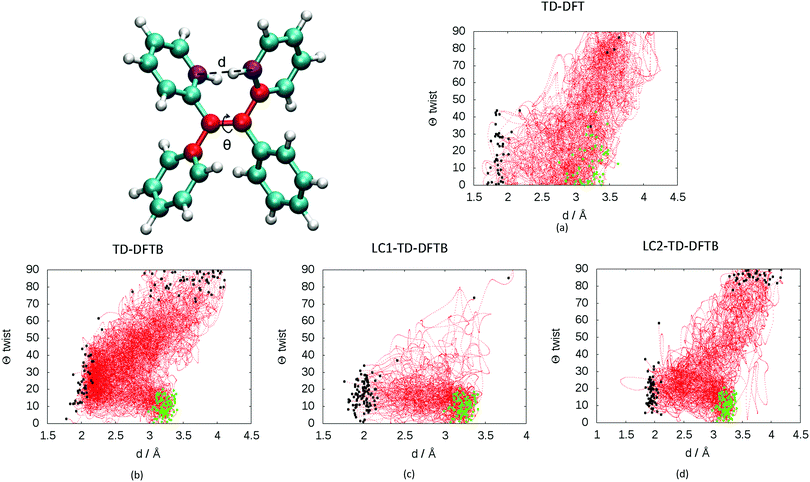 | ||
Fig. 3 Evolution of the distance d between the carbon atoms (in purple) involved in cyclization and the CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC (in red) dihedral angles Θ of in the dynamics at: (a) TD-DFT (60 trajectories taken from previous work on TPE computed with PBE0/def2-SVP, see ref. 33) and 100 trajectories at the (b) TD-DFTB, (c) LC1-TD-DFTB and (d) LC2-TD-DFTB levels. All dynamics were performed in the nonadiabatic regime except for standard TD-DFTB done within the adiabatic approximation. The C–C distance d corresponds to the minimum distance among the 8 possible C–C involved in cyclization at every step of the dynamics. The green dots represent the geometries of the initial condition for the different trajectories. The black dots represent the geometries corresponding to the S1/S0 crossing for the different trajectories. CC (in red) dihedral angles Θ of in the dynamics at: (a) TD-DFT (60 trajectories taken from previous work on TPE computed with PBE0/def2-SVP, see ref. 33) and 100 trajectories at the (b) TD-DFTB, (c) LC1-TD-DFTB and (d) LC2-TD-DFTB levels. All dynamics were performed in the nonadiabatic regime except for standard TD-DFTB done within the adiabatic approximation. The C–C distance d corresponds to the minimum distance among the 8 possible C–C involved in cyclization at every step of the dynamics. The green dots represent the geometries of the initial condition for the different trajectories. The black dots represent the geometries corresponding to the S1/S0 crossing for the different trajectories. | ||
In terms of vertical excitation energies (see Table S1 in the ESI†), pure TD-DFTB provides results similar to GGA functionals, i.e. underestimating the excitation energies of the valence ππ* states. Despite the TPE lowest lying singlet excited state not being a charge transfer state (see Table S2 and Fig. S1 in the ESI†), an improvement is observed upon usage of long-range correction for TD-DFTB. LC1 performs similarly to standard long-range corrected functionals with TD-DFT, upshifting the excitation energies. In contrast, the LC2 method provides results closer to standard hybrid functionals (such as B3LYP and PBE0), which is due to the different method employed for the implementation of long-range correction in the LC2 approach.
Overall, the dynamics in the framework of LC2-TD-DFTB is able to qualitatively reproduce the result obtained at higher levels of theory. For that reason, the results presented in the main text are mainly based on LC2-TD-DFTB, while the full comparison of different methods is given in the ESI.†
Since cyclization appears as the dominant mechanism in all recent theoretical contributions, we try to reconcile the theoretical predictions with the experiments. Greene35 measured a transient absorption spectrum of TPE in hexane with a broad peak at 620 nm decaying on an ultrafast timescale. The peak was explained in terms of excited state absorption. However, from the computed photoabsorption spectra (see Fig. 4), the broad peak centered around 600–650 nm observed by Greene could be attributed to the absorption of the cyclized form of TPE, biphenyl-dihydrophenanthrene (c-TPE). The disappearance of this peak within only several picoseconds, as observed by Greene, may be related to the degradation of c-TPE. However, c-TPE is expected to be stable following the Woodward–Hoffmann rules (the ground state energy barrier for the cycloconversion is 42.5 kcal mol−1 at the PBE0/def2-SVP level). Although, beyond the present investigation, different hypotheses can explain the possible disappearance of c-TPE on an ultrafast timescale: (1) upon irradiation with visible light, the ring opening of c-TPE may occur through a conical intersection leading to TPE.33 (2) The ring opening may occur in a “hot” ground state: after relaxation through the conical intersection, the system has high excess energy which may help to overcome the barrier for cycloreversion before being dissipated to the environment. (3) Upon formation of c-TPE, a side reaction may occur leading to the formation of side products which eventually convert to pristine TPE.74 The rapid degradation of c-TPE could also explain why photocyclization was not recognized in most earlier experimental work on TPE. The existence of a photocyclized intermediate is still under debate even in recent experimental work.65,66 In the spectroscopic results by Kayal et al.,65 a bi-exponential decay of TPE was observed with a “short” time constant of 0.29 ps and a longer time constant of 1.9 ps in hexane. While the latter was assigned to the ethylenic twist, the former was interpreted as a structural relaxation of the S1 Franck–Condon state to a torsionally relaxed state.
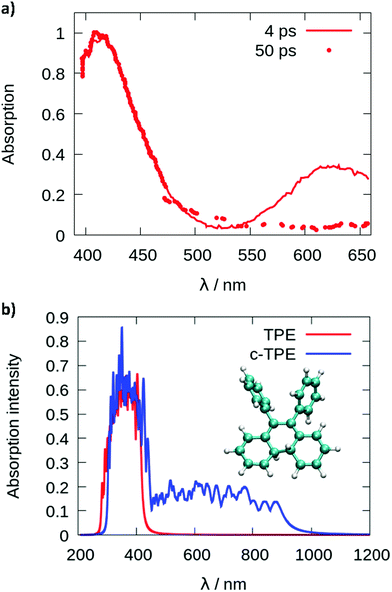 | ||
| Fig. 4 Photoabsorption spectra (a) reproduced from the paper of Greene35 and (b) computed from a Wigner distribution (ωB97XD/def2-SVP) for TPE in red and the cyclized form of TPE (c-TPE) in blue, at the LC2-TD-DFTB level for the isolated molecules. | ||
In light of our current result, we were able to qualitatively reproduce the experimental lifetime of the twisted state. There is a major disagreement about the interpretation of the short time constant. Experimentalists attribute this short time motion to the initial relaxation of the excited state initiated by the torsion of the phenyl ring.65,66 However, we note that the short time constant perfectly matches the photocyclization process observed in theoretical work. Another recent experimental study highlighted the existence of both deactivation mechanisms, demonstrating the limit of the RIM model to explain the AIE process in TPE and its derivatives.66 However, the photocyclization was not considered as the main deactivation pathway for pristine TPE and the photocyclized intermediates were detected as long-lived species (for derivatives of TPE). Thus, further investigation should be done to correctly quantify the main deactivation pathways in TPE and reach agreement between theory and experiment.
3.2 Excited state dynamics of DPDBF and DMTPS
The excited state decay of DPDBF and DMTPS in solution and aggregate states was recently investigated by Blancafort et al.,19,20 computing the energy profiles at CASPT2. The results demonstrated the key role of conical intersections in rationalizing the fluorescence quenching in solution. However, a static picture does not provide information about the excited state lifetime and may eventually lack information about the possible side mechanisms. Thus, our first goal is to compute the dynamics of these two model systems and to compare the observed deactivation mechanism to the results at CASPT2, in order to validate the accuracy of LC-TD-DFTB. The second aim is to investigate the effect of solvent on the nonradiative decay and the excited state lifetime.At the Franck–Condon point, the excitation from the S0 to the S2 state of DPDBF at LC2-TD-DFTB corresponds to the bright ππ* transition, while S1 has a very small oscillator strength (see Table S1 in the ESI†). By moving away from the Franck–Condon point, the S2 state can re-cross the potential energy surface of S1 and, thus, the ordering of the excited states may change. Following our protocol for sampling of initial conditions, some of the trajectories were initiated in S2, and some in S1, depending on which state carries more intensity.
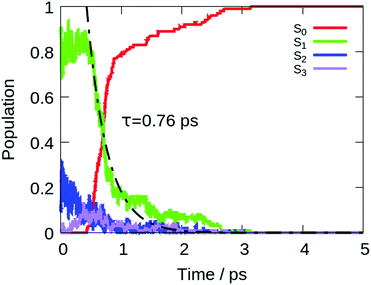
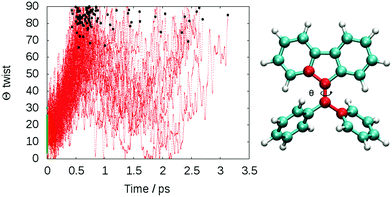
The computed lifetime of the excited states populated in the dynamics (S1 + S2 + S3) for the isolated DPDBF is 0.8 ps (Fig. 5). To monitor the evolution of the different trajectories, the dihedral angle Θ for the twisting is plotted with respect to time (Fig. 6). The different trajectories reached the crossing point with a dihedral angle Θ close to 90°, which corresponds to a twisted state. Thus, only a single mechanism is observed for the fluorescence quenching of DPDBF, which is the ethylenic twist. These results are consistent with the previous work of Blancafort et al.19 A nonadiabatic molecular dynamics study by Gao et al.31 which employed an approximate time dependent Kohn–Sham approach also provided similar results with respect to the deactivation mechanism.
The decay to the ground state through an ethylenic twist involves a large molecular motion and the presence of solvent greatly increases the excited state lifetime compared to the gas-phase. An excited state lifetime value of 8.15 ps was computed from nonadiabatic dynamics in hexane solvent (see Fig. S13 in the ESI†). 70% of the trajectories (21/30) proceed through an ethylenic twist characterized by a large dihedral angle θ (>45°). This angle for DPDBF close to the S1/S0 crossing point is not as pronounced as in the gas-phase dynamics due to the more distorted geometries observed in the presence of hexane. Moreover, due to the steric effect by the surrounding solvent molecules, additional deactivation pathways appear for DPDBF such as photocyclization (1/30) and the distortion of the benzene ring (3/30), which are not observed for the isolated molecule (note that 5 trajectories remain in the excited state during the simulation time). All three mechanisms appear in both TPE and DPDBF, which can be rationalized by their similar conjugation pattern. DPDBF has a more rigid structure than TPE and, thus, the photocyclization appears as a less favorable mechanism than the ethylenic twist. Further work with a higher level of theory should be considered for DPDBF to validate the existence of these side mechanisms.
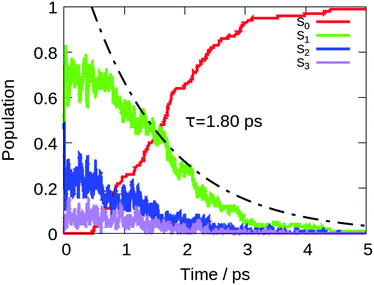
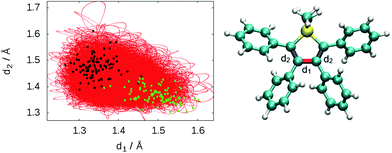
To describe the excited state dynamics of DMTPS with LC2-TD-DFTB, a nonadiabatic simulation is necessary, since the two lowest singlet excited states (S1 and S2) appear nearly degenerate at the Franck–Condon point. The computed gas phase excited state lifetime is 1.8 ps (Fig. 7). The evolution of C–C bond lengths in the silole ring (Fig. 8) shows an alternation of the three bond lengths near the crossing with the ground state (compared to the initial structures). The single bond d1 shrinks from an initial 1.4–1.6 Å to 1.25–1.45 Å, while the average length of the double bond d2 stretches from 1.3–1.4 Å to 1.4–1.6 Å.
The initial motion in the excited state dynamics is an in-plane vibration characterized by a bond length alternation of the single and double bonds of the silole ring. The deactivation mechanism of DMTPS can be related to cyclopentadiene.75 In cyclopentadiene derivatives, the conical intersection is reached by an in-plane motion conjugated with out-of-plane ring deformation. In DMTPS, out-of-plane silicon can be observed for all the trajectories. Thus, the strong deplanarization facilitates reaching the S1/S0 crossing. Overall, the results (i.e. mechanisms) agree qualitatively with the previous computational work of Blancafort et al.20
The presence of hexane solvent included via mechanical embedding does not change the deactivation mechanisms in DMTPS (see Fig. S16 in the ESI†) compared to the gas-phase dynamics. The computed excited state lifetime in hexane is 6 ps.
3.3 General discussion
The present results along with several previous computational studies demonstrate the importance of conical intersections for the fluorescence quenching of the most representative AIE systems. Thus, the RACI model proposed by Blancafort et al. appears more suitable to explain the fluorescence quenching mechanism for these systems than the RIM model. While the two models can be reconciled by stating that RACI is just a more specific variant of RIM,20 several remarks should be made. RIM, i.e. its most common submodel RIR (restriction of intramolecular rotations), assumes a full rotation of propeller-like moieties (such as phenyl rings). However, at the short timescales (i.e. femtoseconds to picoseconds) of the nonradiative decay, we do not observe rotations but rather limited torsions of rotatable groups. The short time does not allow for a full vibrational relaxation suggested by the RIM model, whereas nonadiabatic events such as deactivation through a conical intersection are more likely to happen on these timescales. Furthermore, the nonradiative deactivation does not comprise only photophysical, but also photochemical phenomena, such as cyclization. Likewise, the recent work of Tang et al. asserts that “the RIM paradigm needs to be revisited”.66 The central role of conical intersections in fluorescence quenching of AIE systems should not be surprising considering that their importance was already recognized for many other organic molecules such as BODIPY,76,77 oxazine dye,78 aminopurine,79 polycyclic aromatic hydrocarbons80etc. The role of conical intersections was also discussed for AIE-active ESIPT (excited state intramolecular proton transfer) materials.81,82While the present work focuses on prototypical (i.e. pristine) AIE systems, most of the experimental measurements refer to various derivatives. The effect of substituents cannot be neglected, as the functional groups can eventually alter the accessible decay pathways.34 Furthermore, the effect of solvent (polarity, viscosity) may be significant and should not be neglected when interpreting experimental results. For instance, changing the solvent may significantly extend the lifetime of the excited state.36 While the dynamics associated with the deactivation mechanism in hexane (low dielectric constant) resembles strongly that in the gas phase, this might not hold for other solvents.
4 Conclusions
We explore the mechanisms of the nonradiative decay in three prototypical AIE systems (TPE, DPDBF and DMTPS), both in the gas phase (reflecting the intrinsic molecular properties) and in hexane solution. The relaxation through the conical intersection plays a key role in the fluorescence quenching of these compounds. This favors the recently proposed RACI model, which exploits the concept of conical intersection accessibility to explain the fluorescence quenching in solution.TPE (both intrinsic and solvated) has two major excited state deactivation channels: photocyclization and ethylenic twist. DPDBF mainly decays through the ethylenic twist, while DMTPS decays via silole ring distortion. The hexane solvent does not significantly alter the photophysics and photochemistry of these compounds. The mechanisms which involve a sizable geometrical reorganization (ethylenic twist) and ring distortion occur on a longer timescale, while the photocyclization is only slightly slower in solution. The computational protocol we employ here, combining excited state molecular dynamics and a cheap electronic structure method (LC-TD-DFTB), provides a reliable picture of excited state phenomena at previously unprecedented computational speed. Thus, the same methodology will be further employed for rational design and screening of new AIE molecules.
TD-DFTB is an emerging and promising method for investigating excited state phenomena in large molecules. Earlier applications by Röhr et al. and Barbatti et al. outlined the strengths and weaknesses of this approach.83,84 Common AIE systems appear suitable for LC-TD-DFTB, since their photochemistry and photophysics are restricted to low-lying excited states (typically S1 and S2) of ππ* character. The present results are consistent with the earlier theoretical and available experimental data. In the cases where consensus is still not achieved, such as photocyclization of TPE, LC-TD-DFTB results still qualitatively agree with other theoretical methods (TD-DFT, CASPT2, semi-empirical). Yet, the precise quantitative measures (lifetimes, ratios) are still highly sensitive to the approximation employed (both for nuclear dynamics and electronic structure) and should serve only as a qualitative guideline to interpret experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
EPFL is acknowledged for funding support.Notes and references
- K. Kikuchi, Chem. Soc. Rev., 2010, 39, 2048–2053 RSC.
- N. Boens, V. Leen and W. Dehaen, Chem. Soc. Rev., 2012, 41, 1130–1172 RSC.
- L. Yuan, W. Lin, K. Zheng and S. Zhu, Acc. Chem. Res., 2013, 46, 1462–1473 CrossRef CAS.
- S. Kolemen, O. A. Bozdemir, Y. Cakmak, G. Barin, S. Erten-Ela, M. Marszalek, J.-H. Yum, S. M. Zakeeruddin, M. K. Nazeeruddin, M. Grätzel and E. U. Akkaya, Chem. Sci., 2011, 2, 949–954 RSC.
- Y. Ge and D. F. O’Shea, Chem. Soc. Rev., 2016, 45, 3846–3864 RSC.
- B. Gu, W. Wu, G. Xu, G. Feng, F. Yin, P. H. J. Chong, J. Qu, K. T. Yong and B. Liu, Adv. Mater., 2017, 29, 1701076 CrossRef.
- J. Luo, Z. Xie, J. W. Y. Lam, L. Cheng, H. Chen, C. Qiu, H. S. Kwok, X. Zhan, Y. Liu, D. Zhu and B. Z. Tang, Chem. Commun., 2001, 1740–1741 RSC.
- J. Mei, N. L. C. Leung, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Chem. Rev., 2015, 115, 11718–11940 CrossRef CAS.
- Y. Hong, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2011, 40, 5361–5388 RSC.
- Y. Hong, Methods Appl. Fluoresc., 2016, 4, 022003 CrossRef.
- S. Chen, H. Wang, Y. Hong and B. Z. Tang, Mater. Horiz., 2016, 3, 283–293 RSC.
- R. T. K. Kwok, C. W. T. Leung, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2015, 44, 4228–4238 RSC.
- M. Gao and B. Z. Tang, ACS Sens., 2017, 2, 1382–1399 CrossRef PubMed.
- D. Volyniuk, J. Sutaite, A. Tomkeviciene, N. Kostiv, G. Buika and J. V. Grazulevicius, J. Lumin., 2017, 192, 534–540 CrossRef CAS.
- Y. Hong, J. W. Y. Lam and B. Z. Tang, Chem. Commun., 2009, 4332–4353 RSC.
- Q. Zeng, Z. Li, Y. Dong, C. Di, A. Qin, Y. Hong, L. Ji, Z. Zhu, C. K. W. Jim, G. Yu, Q. Li, Z. Li, Y. Liu, J. Qin and B. Z. Tang, Chem. Commun., 2007, 70–72 RSC.
- J. Chen and B. Z. Tang, in Aggregation-Induced Emission: Fundamentals and Applications, ed. A. Qin and B. Z. Tang, John Wiley & Sons, Inc., New Jersey, 2013, ch. 14, vol. 1–2, pp. 307–322 Search PubMed.
- N. L. C. Leung, N. Xie, W. Yuan, Y. Liu, Q. Wu, Q. Peng, Q. Miao, J. W. Y. Lam and B. Z. Tang, Chem. – Eur. J., 2014, 20, 15349–15353 CrossRef CAS.
- Q. Li and L. Blancafort, Chem. Commun., 2013, 49, 5966–5968 RSC.
- X.-L. Peng, S. Ruiz-Barragan, Z.-S. Li, Q.-S. Li and L. Blancafort, J. Mater. Chem. C, 2016, 4, 2802–2810 RSC.
- R. Crespo-Otero, Q. Li and L. Blancafort, Chem. – Asian J., 2019 10.1039/asia.201801649.
- Y. Liu, X. Tao, F. Wang, J. Shi, J. Sun, W. Yu, Y. Ren, D. Zou and M. Jiang, J. Phys. Chem. C, 2007, 111, 6544–6549 CrossRef CAS.
- B. K. An, S. K. Kwon, S. D. Jung and S. Y. Park, J. Am. Chem. Soc., 2002, 124, 14410–14415 CrossRef CAS.
- B. K. An, D. S. Lee, J. S. Lee, Y. S. Park, H. S. Song and S. Y. Park, J. Am. Chem. Soc., 2004, 126, 10232–10233 CrossRef CAS PubMed.
- Y. Sonoda, S. Tsuzuki, M. Goto, N. Tohnai and M. Yoshida, J. Phys. Chem. A, 2010, 114, 172–182 CrossRef CAS PubMed.
- H. Wang, E. Zhao, J. W. Y. Lam and B. Z. Tang, Mater. Today, 2015, 18, 365–377 CrossRef CAS.
- J. Shi, N. Chang, C. Li, J. Mei, C. Deng, X. Luo, Z. Liu, Z. Bo, Y. Q. Dong and B. Z. Tang, Chem. Commun., 2012, 48, 10675–10677 RSC.
- E. P. J. Parrott, N. Y. Tan, R. Hu, J. A. Zeitler, B. Z. Tang and E. Pickwell-MacPherson, Mater. Horiz., 2014, 1, 251–258 RSC.
- G.-J. Zhao, K.-L. Han, Y.-B. Lei and Y.-S. Dou, J. Chem. Phys., 2007, 127, 94307 CrossRef.
- M.-C. Li, M. Hayashi and S.-H. Lin, J. Phys. Chem. A, 2011, 115, 14531–14538 CrossRef CAS.
- X. Gao, Q. Peng, Y. Niu, D. Wang and Z. Shuai, Phys. Chem. Chem. Phys., 2012, 14, 14207–14216 RSC.
- Z. Zhao, B. He and B. Z. Tang, Chem. Sci., 2015, 6, 5347–5365 RSC.
- A. Prlj, N. Došlić and C. Corminboeuf, Phys. Chem. Chem. Phys., 2016, 18, 11606–11609 RSC.
- Y. J. Gao, X. P. Chang, X. Y. Liu, Q. S. Li, G. Cui and W. Thiel, J. Phys. Chem. A, 2017, 121, 2572–2579 CrossRef CAS.
- B. I. Greene, Chem. Phys. Lett., 1981, 79, 51–53 CrossRef CAS.
- P. F. Barbara, S. D. Rand and P. M. Rentzepis, J. Am. Chem. Soc., 1981, 103, 2156–2162 CrossRef CAS.
- E. Lenderink, K. Duppen and D. A. Wiersma, J. Phys. Chem., 1995, 99, 8972–8977 CrossRef CAS.
- M. A. Robb, M. Garavelli, M. Olivucci and F. Bernardi, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, John Wiley & Sons, Inc., New Jersey, 2007, ch. 2, vol. 15, pp. 87–146 Search PubMed.
- T. Frauenheim, G. Seifert, M. Elstner, T. Nienhaus, C. Köhler, M. Amkreutz, M. Sternberg, Z. Hajnal, A. Di Carlo and S. Suhai, J. Phys.: Condens. Matter, 2002, 14, 3015–3047 CrossRef CAS.
- A. Domínguez, B. Aradi, T. Frauenheim, V. Lutsker and T. A. Niehaus, J. Chem. Theory Comput., 2013, 9, 4901–4914 CrossRef.
- A. Humeniuk and R. Mitrić, J. Chem. Phys., 2015, 143, 134120 CrossRef.
- A. Humeniuk and R. Mitrić, Comput. Phys. Commun., 2017, 221, 174–202 CrossRef CAS.
- E. Titov, A. Humeniuk and R. Mitrić, Phys. Chem. Chem. Phys., 2018, 20, 25995–26007 RSC.
- V. Lutsker, B. Aradi and T. A. Niehaus, J. Chem. Phys., 2015, 143, 184107 CrossRef CAS.
- J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, J. Chem. Theory Comput., 2017, 13, 1737–1747 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revis. D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. Van Der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- D. Hollas, J. Suchan, M. Ončák and P. Slavíček, ABIN, ZENODO, 2018, DOI:10.5281/zenodo.1228462.
- M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, J. Phys. Chem. A, 2010, 114, 6757–6765 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 14101 CrossRef.
- F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405 CrossRef CAS.
- M. Barbatti and R. Crespo-Otero, in Density-Functional Methods for Excited States, ed. N. Ferré, M. Filatov and M. Huix-Rotllant, Springer International Publishing, New York, 2016, ch. 10, vol. 368, pp. 415–444 Search PubMed.
- J. Ma, G. B. Dutt, D. H. Waldeck and M. B. Zimmt, J. Am. Chem. Soc., 1994, 116, 10619–10629 CrossRef CAS.
- N. B. Shustova, T. C. Ong, A. F. Cozzolino, V. K. Michaelis, R. G. Griffin and M. Dincǎ, J. Am. Chem. Soc., 2012, 134, 15061–15070 CrossRef CAS PubMed.
- Z. Yang, W. Qin, N. L. C. Leung, M. Arseneault, J. W. Y. Lam, G. Liang, H. H. Y. Sung, I. D. Williams and B. Z. Tang, J. Mater. Chem. C, 2016, 4, 99–107 RSC.
- K. Kokado, T. Machida, T. Iwasa, T. Taketsugu and K. Sada, J. Phys. Chem. C, 2018, 122, 245–251 CrossRef CAS.
- S. Kayal, K. Roy and S. Umapathy, J. Chem. Phys., 2018, 148, 024301 CrossRef.
- Y. Cai, L. Du, K. Samedov, X. Gu, F. Qi, H. H. Y. Sung, B. O. Patrick, Z. Yan, X. Jiang, H. Zhang, J. W. Y. Lam, I. D. Williams, D. L. Phillips, A. Qin and B. Z. Tang, Chem. Sci., 2018, 9, 4662–4670 RSC.
- N.-W. Tseng, J. Liu, J. C. Y. Ng, J. W. Y. Lam, H. H. Y. Sung, I. D. Williams and B. Z. Tang, Chem. Sci., 2012, 3, 493–497 RSC.
- H. H. Klingenberg, E. Lippert and W. Rapp, Chem. Phys. Lett., 1973, 18, 417–419 CrossRef CAS.
- D. A. Shultz and M. A. Fox, J. Am. Chem. Soc., 1989, 111, 6311–6320 CrossRef CAS.
- F. B. Mallory, C. S. Wood and J. T. Gordon, J. Am. Chem. Soc., 1964, 86, 3094–3102 CrossRef CAS.
- R. J. Olsen and R. E. Buckles, J. Photochem., 1979, 10, 215–220 CrossRef CAS.
- M. P. Aldred, C. Li and M. Q. Zhu, Chem. – Eur. J., 2012, 18, 16037–16045 CrossRef CAS PubMed.
- G. Huang, B. Ma, J. Chen, Q. Peng, G. Zhang, Q. Fan and D. Zhang, Chem. – Eur. J., 2012, 18, 3886–3892 CrossRef CAS.
- A. Jain, A. Achari, N. Mothi, M. Eswaramoorthy and S. J. George, Chem. Sci., 2015, 6, 6334–6340 RSC.
- T. S. Kuhlman, W. J. Glover, T. Mori, K. B. Møller and T. J. Martínez, Faraday Discuss., 2012, 157, 193–212 RSC.
- A. Prlj, A. Fabrizio and C. Corminboeuf, Phys. Chem. Chem. Phys., 2016, 18, 32668–32672 RSC.
- A. Prlj, L. Vannay and C. Corminboeuf, Helv. Chim. Acta, 2017, 100, e1700093 CrossRef.
- J. Brazard, L. A. Bizimana, T. Gellen, W. P. Carbery and D. B. Turner, J. Phys. Chem. Lett., 2016, 7, 14–19 CrossRef CAS PubMed.
- M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2015, 17, 15452–15459 RSC.
- Y. Harabuchi, T. Taketsugu and S. Maeda, Phys. Chem. Chem. Phys., 2015, 17, 22561–22565 RSC.
- M. Dommett, M. Rivera and R. Crespo-Otero, J. Phys. Chem. Lett., 2017, 8, 6148–6153 CrossRef CAS PubMed.
- M. Dommett and R. Crespo-Otero, Phys. Chem. Chem. Phys., 2017, 19, 2409–2416 RSC.
- J. Hoche, H.-C. Schmitt, A. Humeniuk, I. Fischer, R. Mitrić and M. I. S. Röhr, Phys. Chem. Chem. Phys., 2017, 19, 25002–25015 RSC.
- L. Stojanović, S. G. Aziz, R. H. Hilal, F. Plasser, T. A. Niehaus and M. Barbatti, J. Chem. Theory Comput., 2017, 13, 5846–5860 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Parameters for the nonadiabatic dynamics and additional analysis of the electronic population and mechanisms. See DOI: 10.1039/c9cp00691e |
| This journal is © the Owner Societies 2019 |