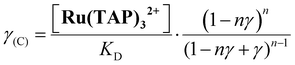Ru(TAP)32+ uses multivalent binding to accelerate and constrain photo-adduct formation on DNA†
Willem
Vanderlinden
 *ab,
Pauline J.
Kolbeck
a,
Wout
Frederickx
b,
Sebastian F.
Konrad
a,
Thomas
Nicolaus
a,
Carola
Lampe
a,
Alexander S.
Urban
*ab,
Pauline J.
Kolbeck
a,
Wout
Frederickx
b,
Sebastian F.
Konrad
a,
Thomas
Nicolaus
a,
Carola
Lampe
a,
Alexander S.
Urban
 a,
Cécile
Moucheron
c and
Jan
Lipfert
a,
Cécile
Moucheron
c and
Jan
Lipfert
 a
a
aDepartment of Physics, Nanosystems Initiative Munich, and Center for NanoScience, LMU Munich, Amalienstrasse 54, 80799 Munich, Germany
bDepartment of Chemistry, Division of Molecular Imaging and Photonics, KU Leuven-University of Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: willem.vanderlinden@kuleuven.be
cDepartment of Chemistry, Laboratory of Organic Chemistry and Photochemistry, Université Libre de Bruxelles, Avenue Franklin D. Roosevelt 50, 1050 Brussels, Belgium
First published on 17th May 2019
Abstract
Ru(II)-complexes with polyazaaromatic ligands can undergo direct electron transfer with guanine nucleobases on blue light excitation that results in DNA lesions with phototherapeutic potential. Here we use single molecule approaches to demonstrate DNA binding mode heterogeneity and evaluate how multivalent binding governs the photochemistry of [Ru(TAP)3]2+ (TAP = 1,4,5,8-tetraazaphenanthrene).
Ru(II)-polypyridyl complexes carry three bidentate ligands that can be designed to tune the DNA-binding and electronic properties of the complex.1,2 Complexes bearing DNA-intercalating moieties can exhibit light-switching properties in the presence of DNA,3,4 and targeted ligand design has enabled selective detection of mismatches and abasic sites in DNA duplexes.5,6 Further, π-deficient ligands such as polyazaaromatic TAP (1,4,5,8-tetraazapenanthrene) convey highly oxidizing properties to the complex in the triplet metal-to-ligand charge transfer (3MLCT) excited state: on excitation, the homoleptic complex Ru(TAP)32+ (Fig. 1) can extract an electron from guanine nucleobases.7 The oxidized guanine either undergoes a back-electron transfer with the reduced complex or results in DNA-lesions. While the formation of single-strand DNA breaks is easily detected via topological conversions of supercoiled DNA targets, recombination of the oxidized guanine with the reduced complex to form covalent photo-adducts8 is the dominant pathway. Recent work has demonstrated targeted photo-induced DNA damage by Ru–TAP complexes in live cells,9 suggesting that this class of compounds could be used in phototherapeutic applications.
To design Ru–TAP complexes for therapeutic applications, it is essential to understand how ground-state DNA-binding affects the photochemistry of Ru(TAP)32+ with DNA. However, the binding mode of Ru(TAP)32+ and the related Ru(phen)32+ (phen = 1,10-phenanthroline; Fig. 1) to DNA is controversial, with evidence for (hydrogen bond-mediated10) groove-binding as well as binding through intercalation11 or semi-intercalation, i.e. partial insertion between adjacent basepairs.12–15 Here, we use single-molecule approaches to unravel the binding modes of racemic Ru(TAP)32+ and show how they affect the photochemistry with DNA.
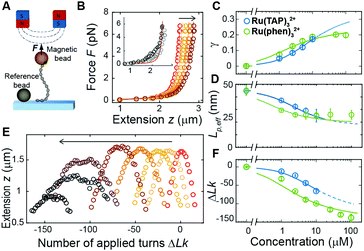
Previously, single-molecule manipulation assays have revealed the binding modes of small molecules interacting with DNA.16–20 We use magnetic tweezers (MT) to quantify the ground-state binding of racemic Ru(TAP)32+ and Ru(phen)32+ to DNA in 10 mM phosphate buffer (Fig. 2A). In MT, DNA molecules (7.95 kbp; crystallographic length 2.7 μm) were attached at one end to the bottom surface of a flow cell and at the other end to a paramagnetic bead. Using permanent magnets, we can controllably exert stretching forces and torques21 on the DNA molecules.
First, we performed force-extension measurements on nicked DNA tethers to evaluate the changes in DNA extension and elasticity on titration with racemic Ru(TAP)32+ (Fig. 2B). By fitting the worm-like chain (WLC) model,22 we determined the DNA contour length Lc and bending persistence length Lp. In the absence of Ru(TAP)32+ we find Lc = 2.68 ± 0.03 μm and Lp = 45 ± 3 nm, in excellent agreement with the crystallographic length of B-form DNA and with previous measurements of Lp, respectively.23 On addition of low to intermediate concentrations ([Ru(TAP)32+] ≤ 10 μM), Lc increases gradually, while Lp decreases (Fig. 2C and D). The increase of Lc is consistent with intercalative binding, and can be used to calculate the fractional occupancy γ of intercalated Ru(TAP)32+via γ = (LC(C) − Lc(0))/(Δl·N) with Lc(0) the contour length in the absence of Ru(TAP)32+, Δl the contour length increment per intercalation event, and N the number of basepairs (7.95 kbp).17 Assuming Δl = 0.34 nm, we fit the Ru(TAP)32+ data to the McGhee-von Hippel model:24
Fixing KD = 19.7 μM and n = 2.7 (determined from the contour length increase), we obtain a kink angle θ = 11° (Fig. 2D), far below the value suggested by crystallography.13 Conversely, fixing θ = 51°, we obtain a best fit with a kink frequency that is ≈10-fold smaller than the fractional occupancy of intercalated Ru(TAP)32+γ. Thus, our data are inconsistent with the view that TAP predominantly interacts with DNA via semi-intercalation that results in severe DNA kinking.
We note that at [Ru(TAP)32+] > 10 μM the WLC model does not provide a good fit to the force-extension data and that the DNA length decreases with increasing concentration, suggesting effects of Ru(TAP)32+ binding beyond intercalation. In contrast, the force-extension behaviour of DNA interacting with racemic Ru(phen)32+ is accurately described by the WLC model over the entire concentration range tested (0–100 μM) and we find KD = 4.9 ± 1 μM, n = 4.0 ± 0.2 fitting the McGhee-von Hippel equation (Fig. 2C). Similar to Ru(TAP)32+, Ru(phen)32+-binding decreases the DNA bending persistence length Lp,eff, and fitting the Popov model26 yields a kink density κ = 0.12·γ/0.34 nm (for θ = 51°) (Fig. 2D).
To obtain additional insights in the binding of Ru(TAP)32+ with DNA, we use the capability of MT to control the DNA linking number Lk in torsionally constrained DNA by rotating the external magnets. At low force (F = 0.3 pN) magnet rotation leads to a symmetrical response of the molecular extension for both under- and over-winding of bare DNA, due to the formation of plectonemic supercoils21 (Fig. 2E). Titration with Ru(TAP)32+ induces a shift of the midpoints of the rotation curves to more negative linking differences ΔLk, in line with DNA unwinding upon Ru(TAP)32+ intercalation16 (Fig. 2E). Using KD and n from the force-extension data (Fig. 2B and C), we determined the unwinding angle ϕ = 16 ± 4° per intercalation event from the dependence of ΔLk on [Ru(TAP)32+] (Fig. 2F). Notably, at [Ru(TAP)32+] > 10 μM the extension of the rotation curves rapidly decreases with increasing concentration, in contrast to the behaviour for classical intercalation, but in agreement with the observations from force-extension experiments. Notably, at these higher concentrations, the rotation curves become more erratic and feature sudden extension jumps.
In contrast, rotation curves with increasing concentrations of Ru(phen)32+ follow the behaviour of a classical intercalator (Fig. S1, ESI†). Analysis of the shift in ΔLk yields an unwinding angle ϕ = 26.3 ± 2° for Ru(phen)32+ (Fig. 2E and F), in reasonable agreement with the results of a topoisomerase assay.27 Together, our data indicate that Ru(phen)32+ is a stronger intercalator than Ru(TAP)32+, in agreement with a previous report.28 We note that for Ru(phen)32+ only at high [Ru(phen)32+] = 100 μM, and in few cases (∼10% of all beads), the maximal extension in rotation curves is reduced with respect to the expected values, in contrast to the anomalous behaviour observed for Ru(TAP)32+.
To dynamically probe the anomalous behaviour at [Ru(TAP)32+] > 10 μM we subjected nicked DNA tethers to rotation in the MT (Fig. S2A, ESI†). At low concentrations (<10 μM), tether extension remains unaffected on magnet rotation, as expected for a torsionally unconstrained DNA. However, at [Ru(TAP)32+] > 10 μM, the DNA extension occasionally decreases on magnet rotation until sudden extension jumps restore the original z-position. We interpret this result as the consequence of topological shielding of the nicking site via transient DNA looping by binding to multiple sites that bridge the nick. To further test the hypothesis of DNA looping by Ru(TAP)32+ we performed force-jump experiments wherein the DNA is first kept at a low force (0.1 pN) and then suddenly subjected to a high force (6 pN). In the presence of [Ru(TAP)32+] > 10 μM, our data demonstrate step-wise extension increments on application of high force, in line with forced dissociation of Ru(TAP)32+-mediated loops (Fig. S2B, ESI†). Consistent with our observations of classical intercalation (Fig. 2), no signatures for Ru(phen)32+-mediated loop formation were observed from force-jump experiments or rotation of nicked DNA.
To directly visualize the bending or kinking behaviour at short length scales, we performed atomic force microscopy (AFM) imaging. Linear DNA fragments (486 bp) were incubated with Ru(TAP)32+ under dimmed light conditions and subsequently deposited onto poly-L-lysine coated mica (Methods). We analysed the AFM images by tracing the DNA contour29 with a step length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 5 nm. Under the conditions used, we find that at the molecular length scale DNA adopts conformations corresponding to kinetic trapping on surface adsorption, as observed previously.25 Yet, at short length scales (
= 5 nm. Under the conditions used, we find that at the molecular length scale DNA adopts conformations corresponding to kinetic trapping on surface adsorption, as observed previously.25 Yet, at short length scales (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 5 nm) the bend angle distribution implies local chain equilibration that enables quantitative evaluation of DNA bending or kinking (if any) on incubation with Ru(TAP)32+. The bend angle distributions of DNA molecules incubated with varying amounts of Ru(TAP)32+ are, to first approximation, well described by a single folded Gaussian (Fig. 3B) with a variance 〈θ2〉 that relates to the DNA persistence length as 〈θ2〉 =
= 5 nm) the bend angle distribution implies local chain equilibration that enables quantitative evaluation of DNA bending or kinking (if any) on incubation with Ru(TAP)32+. The bend angle distributions of DNA molecules incubated with varying amounts of Ru(TAP)32+ are, to first approximation, well described by a single folded Gaussian (Fig. 3B) with a variance 〈θ2〉 that relates to the DNA persistence length as 〈θ2〉 = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /Lp. Based on this analysis, we only find a weak dependence of Lp on [Ru(TAP)32+]. On average Lp = 58 ± 3 nm in agreement with previous AFM analyses of DNA bending behaviour.29 However, the fit residuals feature a peak at angles of 40–50°, in a concentration-dependent fashion. The integrated peak accounts only for ≈1.5% of the total angle distribution at the highest concentrations tested in good agreement with our MT analysis that suggests infrequent kinks induced by Ru(TAP)32+.
/Lp. Based on this analysis, we only find a weak dependence of Lp on [Ru(TAP)32+]. On average Lp = 58 ± 3 nm in agreement with previous AFM analyses of DNA bending behaviour.29 However, the fit residuals feature a peak at angles of 40–50°, in a concentration-dependent fashion. The integrated peak accounts only for ≈1.5% of the total angle distribution at the highest concentrations tested in good agreement with our MT analysis that suggests infrequent kinks induced by Ru(TAP)32+.
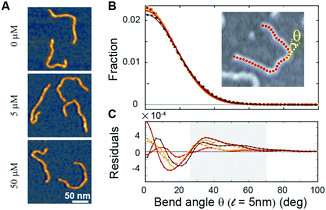 | ||
Fig. 3 Atomic force microscopy demonstrates Ru(TAP)32+-mediated DNA kinking with low yield. (A) AFM topographs of 486 bp linear DNA molecules incubated with increasing concentrations of Ru(TAP)32+. (B) Bend angle distributions (Kernel density estimate with bandwidth 4°) of DNA generated by automated tracing of the chain contours with a step length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 5 nm. For each condition ≈10 = 5 nm. For each condition ≈10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 angles are recorded. Solid lines are fits to a folded Gaussian. Colour code is the same as in Fig. 2. (C) Residuals of the folded Gaussian fits in (B) depicting a concentration-dependent increase of bend angles in the range of 30 deg < θ < 70 deg (grey area). 000 angles are recorded. Solid lines are fits to a folded Gaussian. Colour code is the same as in Fig. 2. (C) Residuals of the folded Gaussian fits in (B) depicting a concentration-dependent increase of bend angles in the range of 30 deg < θ < 70 deg (grey area). | ||
Taken together, our MT and AFM data suggest that Ru(TAP)32+ binds to DNA in an intercalative binding mode that occasionally forms kinks and that infers helix lengthening and unwinding. In addition, we observe clear evidence for binding-induced loop formation that implies multivalent binding to DNA, which in turn suggests that Ru(TAP)32+ can interact via (at least) two interfaces simultaneously. Interestingly, Ru(phen)32+ does not form DNA synapses to the extent observed for Ru(TAP)32+, despite the higher affinity for intercalation, suggesting that loop formation is mediated in part by the N1 and N8 atoms of TAP, potentially via hydrogen bonding.10
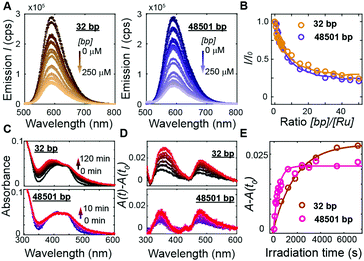
To address how multivalent binding by Ru(TAP)32+ might impact excited state processes, we carried out spectroscopic measurements with either short (32 bp; 50% GC; expected to behave as a rigid rod) or long (48501 bp; 49% GC; that will adopt a random coil conformation, which increases the local concentration of DNA segments) DNA to modulate the contact probability that would lead to Ru(TAP)32+-mediated synapse formation. First we tested whether DNA length affects luminescence by recording spectra upon titrating Ru(TAP)32+ (5 μM) with the different DNA substrates. Luminescence quenching was evaluated for both DNA substrates in the same concentration range ([bp] = 0–250 μM) and found to be approximately independent of DNA length (Fig. 4A and B). The quenching as a function of [bp] is well-described by the McGhee-von Hippel binding model with (KD,n) from the force-extension data and including an offset that takes into account non-productive binding at AT-sequences. The luminescence quenching follows the same concentration dependence as the lengthening observed in MT, which strongly suggests that intercalative binding governs quenching of the 3MLCT state.
To probe the effect of local DNA concentration on photo-adduct formation, we recorded the changes in absorption at the MLCT bands on irradiation of Ru(TAP)32+ (5 μM) at 465 nm, in the presence of either 32 bp or 48.5 kbp-long DNA ([bp] = 100 μM; Fig. 4C and D). Formation of covalent adducts leads to the appearance of an absorption peak at ≈350 nm whereas non-covalent adducts resulting from ligand-exchange with a nucleobase increase the absorption at ≈500 nm.30 We find that photo-adduct formation is faster for the long than for the short DNA (with first order reaction times of τ = 7 ± 2 min and τ = 33 ± 7 min, respectively; Fig. 4E), but achieves a lower final yield. In addition, the peak at 350 nm is much narrower for the long DNA construct as compared the short variant (Fig. 4D), implying a smaller range of photo-adduct species. The spectroscopic data demonstrate that photo-adduct formation, in contrast to luminescence quenching, is faster on long than on short DNA. The lower yield and better-defined photo-adducts suggest that binding to long DNA imposes geometrical constraints that prevent the formation of a broad range of products.
In conclusion, our work reconciles previous apparently contradicting reports on the DNA-binding modes of Ru(TAP)32+. Racemic Ru(TAP)32+ and Ru(phen)32+ can interact with DNA via (semi-)intercalation that occasionally occurs in a kinked state, consistent with a combination of the differential effects observed for enantiopure complexes.11–15Ru(TAP)32+ additionally can mediate DNA looping, presumably via combined (semi-)intercalation and hydrogen-bonding.10 This multivalent binding might explain the differential yield of photo-adduct formation on short versus long DNA. The dependence of photo-adduct formation on local DNA concentration is important towards applications of Ru–TAP complexes in vivo.
We thank the Deutsche Forschungsgemeinschaft (SFB 863, project A11) and F.R.S-F.N.R.S. (CDR J.0022.18) for funding, and Theo Lohmueller and Stefanie Pritzl for use of a LED.
Conflicts of interest
There are no conflicts to declare.References
- F. E. Poynton, S. A. Bright, S. Blasco, D. C. Williams, J. M. Kelly and T. Gunnlaugsson, Chem. Soc. Rev., 2017, 46, 7706–7756 RSC.
- F. Heinemann, J. Karges and G. Gasser, Acc. Chem. Res., 2017, 50, 2727–2736 CrossRef CAS PubMed.
- A. E. Friedman, J. C. Chambron, J. P. Sauvage, N. J. Turro and J. K. Barton, J. Am. Chem. Soc., 1990, 112, 4960–4962 CrossRef CAS.
- C. Moucheron, A. Kirsch-De Mesmaeker and S. Choua, Inorg. Chem., 1997, 36, 584–592 CrossRef CAS.
- A. N. Boynton, L. Marcélis and J. K. Barton, J. Am. Chem. Soc., 2016, 138, 5020–5023 CrossRef CAS.
- Q. Deraedt, L. Marcélis, F. Loiseau and B. Elias, Inorg. Chem. Front., 2017, 4, 91–103 RSC.
- J.-P. Lecomte, A. K.-D. Mesmaeker, J. M. Kelly, A. B. Tossi and H. Görner, Photochem. Photobiol., 1992, 55, 681–689 CrossRef CAS PubMed.
- L. Jacquet, R. J. H. Davies, A. Kirsch-De Mesmaeker and J. M. Kelly, J. Am. Chem. Soc., 1997, 119, 11763–11768 CrossRef CAS.
- C. S. Burke, A. Byrne and T. E. Keyes, J. Am. Chem. Soc., 2018, 140, 6945–6955 CrossRef CAS PubMed.
- W. Vanderlinden, M. Blunt, C. C. David, C. Moucheron, A. Kirsch-De Mesmaeker and S. De Feyter, J. Am. Chem. Soc., 2012, 134, 10214–10221 CrossRef CAS PubMed.
- J. K. Barton, A. Danishefsky and J. Goldberg, J. Am. Chem. Soc., 1984, 106, 2172–2176 CrossRef CAS.
- P. Lincoln and B. Nordén, J. Phys. Chem. B, 1998, 102, 9583–9594 CrossRef CAS.
- J. P. Hall, K. O’Sullivan, A. Naseer, J. A. Smith, J. M. Kelly and C. J. Cardin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17610 CrossRef CAS PubMed.
- S. Satyanarayana, J. C. Dabrowiak and J. B. Chaires, Biochemistry, 1992, 31, 9319–9324 CrossRef CAS PubMed.
- K. Gisselfält, P. Lincoln, B. Nordén and M. Jonsson, J. Phys. Chem. B, 2000, 104, 3651–3659 CrossRef.
- J. Lipfert, S. Klijnhout and N. H. Dekker, Nucleic Acids Res., 2010, 38, 7122–7132 CrossRef CAS PubMed.
- I. D. Vladescu, M. J. McCauley, M. E. Nuñez, I. Rouzina and M. C. Williams, Nat. Methods, 2007, 4, 517 CrossRef CAS PubMed.
- M. Manosas, J. Camunas-Soler, V. Croquette and F. Ritort, Nat. Commun., 2017, 8, 304 CrossRef PubMed.
- K. Günther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526–6532 CrossRef PubMed.
- A. Sischka, K. Toensing, R. Eckel, S. D. Wilking, N. Sewald, R. Ros and D. Anselmetti, Biophys. J., 2005, 88, 404–411 CrossRef CAS PubMed.
- T. R. Strick, J. F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, Science, 1996, 271, 1835 CrossRef CAS PubMed.
- C. Bouchiat, M. D. Wang, J. F. Allemand, T. Strick, S. M. Block and V. Croquette, Biophys. J., 1999, 76, 409–413 CrossRef CAS PubMed.
- F. Kriegel, N. Ermann and J. Lipfert, J. Struct. Biol., 2017, 197, 26–36 CrossRef CAS PubMed.
- J. D. McGhee and P. H. von Hippel, J. Mol. Biol., 1974, 86, 469–489 CrossRef CAS.
- T. Brouns, H. De Keersmaecker, S. F. Konrad, N. Kodera, T. Ando, J. Lipfert, S. De Feyter and W. Vanderlinden, ACS Nano, 2018, 12, 11907–11916 CrossRef CAS PubMed.
- Y. O. Popov and A. V. Tkachenko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051905 CrossRef PubMed.
- J. M. Kelly, A. B. Tossi, D. J. McConnell and C. OhUigin, Nucleic Acids Res., 1985, 13, 6017–6034 CrossRef CAS PubMed.
- A. B. Tossi and J. M. Kelly, Photochem. Photobiol., 1989, 49, 545–556 CrossRef CAS PubMed.
- P. A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Phillips, J. Widom, C. Dekker and P. C. Nelson, Nat. Nanotechnol., 2006, 1, 137 CrossRef CAS PubMed.
- M. M. Feeney, J. M. Kelly, A. B. Tossi, A. K.-d. Mesmaeker and J.-P. Lecomte, J. Photochem. Photobiol., B, 1994, 23, 69–78 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Methods section, supporting Fig. S1 and S2. See DOI: 10.1039/c9cc02838b |
| This journal is © The Royal Society of Chemistry 2019 |