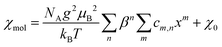Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic interactions in the S = 1/2 square-lattice antiferromagnets Ba2CuTeO6 and Ba2CuWO6: parent phases of a possible spin liquid†
Otto
Mustonen
 *ab,
Sami
Vasala
*ab,
Sami
Vasala
 cd,
Heather
Mutch
b,
Chris I.
Thomas
cd,
Heather
Mutch
b,
Chris I.
Thomas
 a,
Gavin B. G.
Stenning
e,
Elisa
Baggio-Saitovitch
c,
Edmund J.
Cussen
b and
Maarit
Karppinen
a,
Gavin B. G.
Stenning
e,
Elisa
Baggio-Saitovitch
c,
Edmund J.
Cussen
b and
Maarit
Karppinen
 *a
*a
aDepartment of Chemistry and Materials Science, Aalto University, FI-00076 Espoo, Finland. E-mail: maarit.karppinen@aalto.fi; ohj.mustonen@gmail.com
bDepartment of Materials Science and Engineering, University of Sheffield, Mappin Street, Sheffield S1 3JD, UK
cCentro Brasileiro de Pesquisas Físicas (CBPF), Rua Dr Xavier Sigaud 150, Urca, Rio de Janeiro 22290-180, Brazil
dTechnische Universität Darmstadt, Institut für Materialwissenschaft, Fachgebiet Materialdesign durch Synthese, Alarich-Weiss-Straße 2, 64287 Darmstadt, Germany
eISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Didcot, OX11 0QX, UK
First published on 2nd January 2019
Abstract
The isostructural double perovskites Ba2CuTeO6 and Ba2CuWO6 are shown by theory and experiment to be frustrated square-lattice antiferromagnets with opposing dominant magnetic interactions. This is driven by differences in orbital hybridisation of Te6+ and W6+. A spin-liquid-like ground state is predicted for Ba2Cu(Te1−xWx)O6 solid solution similar to recent observations in Sr2Cu(Te1−xWx)O6.
Magnetic frustration can stabilise novel quantum ground states such as quantum spin liquids or valence bond solids.1 Frustration occurs when not all of the magnetic interactions in a material can be satisfied simultaneously as a result of lattice geometry or competing interactions. We have recently shown that a quantum-spin-liquid-like state forms in the double perovskite solid solution Sr2Cu(Te1−xWx)O6 with a square lattice of Cu2+ (3d9, S = 1/2) cations.2,3 This was the first observation of a spin-liquid-like state in a square-lattice compound after 30 years of theoretical predictions.4–8
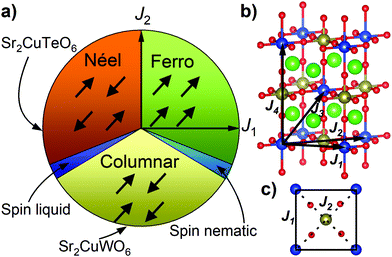
The parent compounds Sr2CuTeO6 and Sr2CuWO6 are frustrated square-lattice (FSL) antiferromagnets.9–13 The FSL model (Fig. 1) has two interactions: nearest-neighbour J1 interaction (side) and next-nearest-neighbour J2 interaction (diagonal). Dominant antiferromagnetic J1 leads to Néel type antiferromagnetic order and dominant J2 leads to columnar magnetic order. Magnetic frustration arises from the competition of J1 and J2, and a quantum spin liquid state has been predicted for J2/J1 = 0.5 where frustration is maximised.4–8
Sr2CuTeO6 and Sr2CuWO6 are the first known isostructural FSL systems with different dominant interactions and magnetic structures: dominant J1 and Néel order for Sr2CuTeO6 and dominant J2 and columnar order for Sr2CuWO6 respectively.9,10 The two compounds have a tetragonal I4/m double perovskite structure with nearly identical bond distances and angles.11,13 The magnetism becomes highly two-dimensional as a result of a Jahn–Teller distortion as the only unoccupied Cu orbital 3dx2−y2 is in the ab square plane. The major differences in dominant magnetic interactions are due to the diamagnetic Te6+ d10 and W6+ d0 cations located in the middle of the Cu2+ square (Fig. 1c), which hybridise differently with O 2p allowing different superexchange paths between the Cu2+ cations.14,15 The spin-liquid-like ground state forms when these two perovskites are mixed into a Sr2Cu(Te1−xWx)O6 solid solution.2,3,16 Muon spin relaxation experiments revealed the absence of magnetic order or static magnetism in a wide composition range of x = 0.1–0.6.2,3 The specific heat displays T-linear behaviour suggesting gapless excitations in a similar composition range.2,3,16 The ground state has been proposed to be a random-singlet state with a disordered arrangement of non-magnetic valence bond singlets.17,18
Motivated by these exciting findings in the Sr2Cu(Te1−xWx)O6 system, we have investigated the magnetic interactions of the isostructural barium analogues Ba2CuTeO6 and Ba2CuWO6. Ba2CuWO6 is known to have columnar magnetic order,19,20 but little is known about Ba2CuTeO6 as the perovskite phase requires high pressures to synthesise.21 Here we use density functional theory (DFT) calculations and high-temperature series expansion (HTSE) fitting of experimental susceptibility data to show that these compounds are FSL antiferromagnets with opposite dominant interactions similar to Sr2CuTeO6 and Sr2CuWO6. We predict a quantum-spin-liquid-like state in Ba2Cu(Te1−xWx)O6 with strong antiferromagnetic interactions.
Magnetic interactions and electronic structure in Ba2CuTeO6 and Ba2CuWO6 were calculated using the DFT+U framework, where an on-site Coulomb repulsion term U was used to model electron correlation effects of localised Cu 3d orbitals. Interactions up to the fourth-nearest neighbour were evaluated, see Fig. 1b. J1 and J2 are the square plane interactions of the FSL model, and J3 and J4 are additional out-of-plane interactions. Energies of different spin configurations were mapped onto a Heisenberg Hamiltonian to obtain J1–J4. We have previously shown this approach works well for Sr2CuWO6.10 The J1 and J2 interactions were also determined from experimental magnetic susceptibility data using high-temperature series expansion fitting. Ba2CuTeO6 was prepared by high-pressure synthesis and Ba2CuWO6 by conventional solid state synthesis. Details of the DFT calculations, sample synthesis and characterisation are available in the ESI.†
The calculated magnetic interactions of Ba2CuTeO6 and Ba2CuWO6 are presented in Table 1. The calculated values depend on the Coulomb U term as is typical with DFT+U, but the same trends are observed for reasonable values of U. Despite being isostructural, the magnetic interactions in Ba2CuTeO6 and Ba2CuWO6 are very different. Ba2CuTeO6 has a very dominant antiferromagnetic J1 interaction with weak J2, J3 and J4 interactions. It is a near-ideal FSL Néel antiferromagnet. Ba2CuWO6, in contrast, has a dominant antiferromagnetic J2 interaction slightly frustrated by an antiferromagnetic J1 interaction with negligible J3 and J4 interactions. The strong J2 interaction is consistent with the known columnar magnetic structure of this compound.20 Due to the weakness of the out-of-plane J3 and J4 interactions, magnetism in both compounds is highly two-dimensional and well described by the FSL model.
| U = 7 eV | U = 8 eV | U = 9 eV | HTSE | |
|---|---|---|---|---|
| a Significant uncertainty in this value due to error in J1. | ||||
| Ba2CuTeO6 | ||||
| J 1 (meV) | −23.65 | −20.22 | −17.22 | −16.54(3) |
| J 2 (meV) | 0.13 | 0.23 | 0.06 | −0.04(3) |
| J 3 (meV) | 1.28 | 0.83 | 0.67 | — |
| J 4 (meV) | −0.30 | 0.01 | 0.05 | — |
| J 2/J1 | −0.01 | −0.01 | −0.003 | 0.002 |
| Ba2CuWO6 | ||||
| J 1 (meV) | −1.25 | −1.17 | −1.27 | 0.2(9) |
| J 2 (meV) | −14.71 | −11.94 | −9.56 | −10.0(1) |
| J 3 (meV) | 0.05 | −0.01 | 0.01 | — |
| J 4 (meV) | 0.03 | 0.37 | 0.02 | — |
| J 2/J1 | 11.79 | 10.18 | 7.55 | −50a |
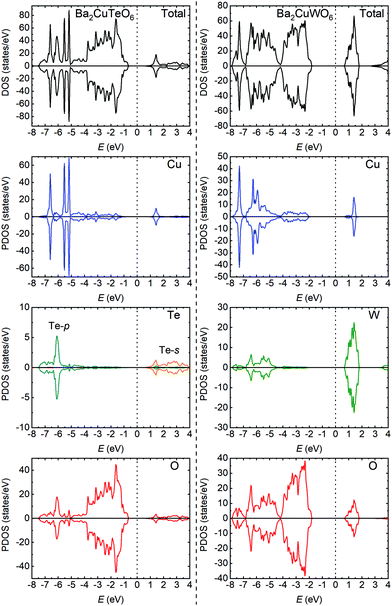
The significant differences in the magnetic interactions of Ba2CuTeO6 and Ba2CuWO6 can be explained by their electronic structures. We have plotted total and partial densities of states for both compounds in Fig. 2. Ba2CuTeO6 and Ba2CuWO6 are antiferromagnetic insulators: the band gaps open between the occupied Cu 3d states hybridised with O 2p (valence band) and the unoccupied Cu 3dx2−y2 states hybridised with O 2p (conduction band). In Ba2CuWO6 the conduction band is further hybridised with unoccupied W 5d states. The W 5d states also hybridise with the Cu 3d/O 2p states in the valence band, which allows a 180° Cu–O–W–O–Cu superexchange pathway resulting in a strong antiferromagnetic J2 interaction. This hybridisation does not occur in Ba2CuTeO6 and therefore J2 is negligible. In Ba2CuTeO6 the Te 5p states hybridise to a lesser degree with the Cu 3d/O 2p states in the conduction band, which could explain the strong antiferromagnetic J1 interaction. However, the role of Te in the J1 superexchange in Sr2CuTeO6 is under debate.9,14 Overall, the electronic structures of Ba2CuTeO6 and Ba2CuWO6 are similar to their strontium analogues Sr2CuTeO6 and Sr2CuWO6, and the differences in magnetic interactions are driven by the same orbital hybridisation mechanism.
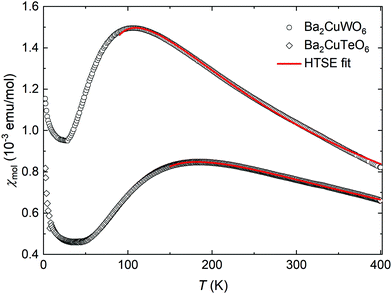
The experimental magnetic susceptibilities of synthesised Ba2CuTeO6 and Ba2CuWO6 samples are shown in Fig. 3. The broad maximum observed in the susceptibility is due to the two-dimensional nature of the magnetism in these materials. Our maximum temperature of 400 K was not enough for reliable Curie–Weiss fits. Previous measurements21 up to 800 K yielded the Curie–Weiss constants ΘCW = −400 K for Ba2CuTeO6 and ΘCW = −249 K for Ba2CuWO6 revealing strong antiferromagnetic interactions.
The magnetic susceptibilities were fitted to a high-temperature series expansion of the FSL model.22 The molar magnetic susceptibility χmol is given by:
The best fits were obtained with the parameters J1 = −16.54(3) meV, J2 = −0.04(3) meV, g = 2.20(1) for Ba2CuTeO6 and J1 = 0.2(9) meV, J2 = −10.0(1) meV, g = 2.26(5) for Ba2CuWO6 in the temperature ranges 150–400 K and 90–400 K, respectively. The fitted exchange constants depend slightly on the minimum temperature used. For both compounds the calculated dominant interaction remains stable in a wide fitting range, but the weaker interaction cannot be accurately quantified. In Ba2CuTeO6 the sign of J2 changes depending on the fitting range, whereas in Ba2CuWO6 the error of J1 is much larger than its value. We can conclude, however, that the dominant interaction is much stronger than the weak one in both Ba2CuTeO6 (|J2|/|J1| < 0.02) and Ba2CuWO6 (|J1|/|J2| < 0.12) and that the DFT and HTSE results are in good agreement.
The magnetic properties of Ba2CuTeO6, Ba2CuWO6, Sr2CuTeO6 and Sr2CuWO6 are summarised in Table 2. Magnetic interactions in Ba2CuTeO6 and Ba2CuWO6 are notably stronger than their strontium analogues. This is due to the smaller a0a0c− tilt of the CuO6 octahedra in the barium phases, which leads to stronger orbital overlap in the ab plane as the Cu–O–Te/W angle is closer to 180°,21 see ESI† for further details. As long-range magnetic order is driven by the weak out-of-plane interactions which are of the same order in all compounds, Ba2CuTeO6 and Ba2CuWO6 are even closer to ideal two-dimensional antiferromagnets than their strontium analogues. The transition temperature of Ba2CuTeO6 is not known, but we predict it to have the highest frustration index f = ΘCW/TN of these compounds and the Néel magnetic structure due to the very strong J1 interaction. Magnetic excitations in Sr2CuTeO6 and Sr2CuWO6 have been observed at temperatures higher than 2TN driven by the two-dimensional magnetic interactions.9,10 The stronger in-plane J1 and J2 interactions of the barium phases indicate the excitations survive to even higher temperatures.
| Ba2CuTeO6 | Sr2CuTeO6 | Ba2CuWO6 | Sr2CuWO6 | |
|---|---|---|---|---|
| a Predicted based on magnetic interactions. | ||||
| J 1 (meV) | −20.22 (DFT) | −7.18 (INS)9 | −1.17 (DFT) | −2.45 (DFT)10 |
| −16.54(3) (HTSE) | −0.2(9) (HTSE) | −1.2 (INS)10 | ||
| J 2 (meV) | 0.23 (DFT) | −0.21 (INS)9 | −11.94 (DFT) | −8.83 (DFT)10 |
| −0.04(3) (HTSE) | −10.0(1) (HTSE) | −9.5 (INS)10 | ||
| Θ CW (K) | −40021 | −802 | −24921 | −1652 |
| T N (K) | — | 2911 | 2820 | 2413 |
| f = ΘCW/TN | — | 2.8 | 8.9 | 6.9 |
| k | [1/2 1/2 kz]a | [1/2 1/2 0]11 | [0 1/2 1/2]20 | [0 1/2 1/2]12 |
| Magnetic order | Néela | Néel | Columnar | Columnar |
Since Ba2CuTeO6 has a dominant J1 interaction and Ba2CuWO6 has a dominant J2 interaction, we predict a spin-liquid-like state will form in the Ba2Cu(Te1−xWx)O6 solid solution similar to Sr2Cu(Te1−xWx)O6. In the Sr2Cu(Te1−xWx)O6 system the Néel order is destabilised already at x = 0.1, and spin-liquid-like state exist in the composition region x = 0.1–0.6. Columnar order is observed for x = 0.7–1. Since the J1 interaction of Ba2CuTeO6 is so strong even compared to J2 in Ba2CuWO6, we predict the Néel order remains more stable against W substitution. For the same reason, the columnar order near x = 1 is likely to be less stable in Ba2Cu(Te1−xWx)O6. The extent of the spin-liquid-like region depends also on disorder, and is difficult to predict just from the properties of the end phases. Finally, the stronger antiferromagnetic interactions in the barium phases indicate that the quantum disordered ground state will remain stable up to higher temperatures.
The previous discussion concerns a double perovskite Ba2Cu(Te1−xWx)O6 solid solution, which near x = 0 will require high-pressure synthesis to form. The ambient pressure form of Ba2CuTeO6 is triclinic with a tolerance factor higher than 1.03.24 Therefore, a Ba2Cu(Te1−xWx)O6 solid solution prepared in ambient pressure will have a triclinic to tetragonal structural change at some composition. Triclinic Ba2CuTeO6 is a spin ladder system close to a quantum critical point,25 and we propose Te-for-W substitution could drive the system from magnetic order to a spin singlet state.
In conclusion, we have investigated the magnetic interactions of the tetragonal double perovskites Ba2CuTeO6 and Ba2CuWO6 by DFT calculations and by HTSE fitting. Both compounds are well described by the frustrated square-lattice model as out-of-plane interactions are very weak. In Ba2CuTeO6 the antiferromagnetic nearest-neighbor J1 interaction dominates (|J2|/|J1| < 0.02), whereas in Ba2CuWO6 the antiferromagnetic next-nearest neighbor interaction J2 dominates (|J1|/|J2| < 0.12). The Ba2Cu(Te,W)O6 system is the second known FSL system where isostructural compounds have opposite magnetic interactions. This is driven by differences in orbital hybridisation of Te 5p/5s and W 5d with O 2p. A spin-liquid-like ground state is predicted for the Ba2Cu(Te1−xWx)O6 solid solution similar to the recent findings in the Sr2Cu(Te1−xWx)O6 system.
The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources. The authors are thankful for access to the MPMS3 instrument in the Materials Characterisation Laboratory at the ISIS Muon and Neutron Source. OM, HM and EJC are thankful for funding by the Leverhulme Trust Research Project Grant RPG-2017-109. SV is thankful for the support of the Brazilian funding agencies CNPq (grants no. 150503/2016-4 and 152331/2016-6) and FAPERJ (grant no. 202842/2016). In addition, EBS acknowledges support from FAPERJ through several grants including Emeritus Professor fellow and CNPq for BPA and corresponding grants.
Conflicts of interest
There are no conflicts to declare.Notes and references
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- O. Mustonen, S. Vasala, E. Sadrollahi, K. P. Schmidt, C. Baines, H. C. Walker, I. Terasaki, F. J. Litterst, E. Baggio-Saitovitch and M. Karppinen, Nat. Commun., 2018, 9, 1085 CrossRef CAS.
- O. Mustonen, S. Vasala, K. P. Schmidt, E. Sadrollahi, H. C. Walker, I. Terasaki, F. J. Litterst, E. Baggio-Saitovitch and M. Karppinen, Phys. Rev. B, 2018, 98, 064411 CrossRef.
- P. W. Anderson, Science, 1987, 235, 1196–1198 CrossRef CAS PubMed.
- F. Mezzacapo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045115 CrossRef.
- H.-C. Jiang, H. Yao and L. Balents, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 024424 CrossRef.
- W.-J. Hu, F. Becca, A. Parola and S. Sorella, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 060402 CrossRef.
- W.-Y. Liu, S. Dong, C. Wang, Y. Han, H. An, G.-C. Guo and L. He, Phys. Rev. B, 2018, 98, 241109 CrossRef.
- P. Babkevich, V. M. Katukuri, B. Fåk, S. Rols, T. Fennell, D. Pajić, H. Tanaka, T. Pardini, R. R. P. Singh, A. Mitrushchenkov, O. V. Yazyev and H. M. Rønnow, Phys. Rev. Lett., 2016, 117, 237203 CrossRef CAS PubMed.
- H. C. Walker, O. Mustonen, S. Vasala, D. J. Voneshen, M. D. Le, D. T. Adroja and M. Karppinen, Phys. Rev. B, 2016, 94, 064411 CrossRef.
- T. Koga, N. Kurita, M. Avdeev, S. Danilkin, T. J. Sato and H. Tanaka, Phys. Rev. B, 2016, 93, 054426 CrossRef.
- S. Vasala, M. Avdeev, S. Danilkin, O. Chmaissem and M. Karppinen, J. Phys.: Condens. Matter, 2014, 26, 496001 CrossRef CAS PubMed.
- S. Vasala, H. Saadaoui, E. Morenzoni, O. Chmaissem, T. Chan, J. Chen, Y. Hsu, H. Yamauchi and M. Karppinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 134419 CrossRef.
- Y. Xu, S. Liu, N. Qu, Y. Cui, Q. Gao, R. Chen, J. Wang, F. Gao and X. Hao, J. Phys.: Condens. Matter, 2017, 29, 105801 CrossRef PubMed.
- M. Zhu, D. Do, C. R. Dela Cruz, Z. Dun, H. D. Zhou, S. D. Mahanti and X. Ke, Phys. Rev. Lett., 2014, 113, 076406 CrossRef CAS PubMed.
- M. Watanabe, N. Kurita, H. Tanaka, W. Ueno, K. Matsui and T. Goto, Phys. Rev. B, 2018, 98, 054422 CrossRef.
- K. Uematsu and H. Kawamura, Phys. Rev. B, 2018, 98, 134427 CrossRef.
- L. Liu, H. Shao, Y.-C. Lin, W. Guo and A. W. Sandvik, Phys. Rev. X, 2018, 8, 041040 Search PubMed.
- Y. Todate, J. Phys. Soc. Jpn., 2001, 70, 337 CrossRef CAS.
- Y. Todate, W. Higemoto, K. Nishiyama and K. Hirota, J. Phys. Chem. Solids, 2007, 68, 2107–2110 CrossRef CAS.
- D. Iwanaga, Y. Inaguma and M. Itoh, J. Solid State Chem., 1999, 147, 291–295 CrossRef CAS.
- H. Rosner, R. R. P. Singh, W. H. Zheng, J. Oitmaa and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 014416 CrossRef.
- A. A. Tsirlin, R. Nath, A. M. Abakumov, Y. Furukawa, D. C. Johnston, M. Hemmida, H. A. Krug Von Nidda, A. Loidl, C. Geibel and H. Rosner, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014429 CrossRef.
- G. N. Rao, R. Sankar, A. Singh, I. P. Muthuselvam, W. T. Chen, V. N. Singh, G.-Y. Guo and F. C. Chou, Phys. Rev. B, 2016, 93, 104401 CrossRef.
- D. Macdougal, A. S. Gibbs, T. Ying, S. Wessel, H. C. Walker, D. Voneshen, F. Mila, H. Takagi and R. Coldea, Phys. Rev. B, 2018, 98, 174410 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting computational and experimental details, figures and tables. See DOI: 10.1039/c8cc09479a |
| This journal is © The Royal Society of Chemistry 2019 |