Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrically controlled mass transport into microfluidic droplets from nanodroplet carriers with application in controlled nanoparticle flow synthesis†
Tonghan
Gu
 a,
Cao
Zheng
a,
Fan
He
a,
Yunfei
Zhang
a,
Saif A.
Khan
a,
Cao
Zheng
a,
Fan
He
a,
Yunfei
Zhang
a,
Saif A.
Khan
 b and
T. Alan
Hatton
b and
T. Alan
Hatton
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: tahatton@mit.edu
bNational University of Singapore, Department of Chemical and Bimolecular Engineering, 4 Engineering Drive 4 E5-02-28, 117576 Singapore. E-mail: saifkhan@nus.edu.sg
First published on 28th March 2018
Abstract
Microfluidic droplets have been applied extensively as reaction vessels in a wide variety of chemical and biological applications. Typically, once the droplets are formed in a flow channel, it is a challenge to add new chemicals to the droplets for subsequent reactions in applications involving multiple processing steps. Here, we present a novel and versatile method that employs a high strength alternating electrical field to tunably transfer chemicals into microfluidic droplets using nanodroplets as chemical carriers. We show that the use of both continuous and cyclic burst square wave signals enables extremely sensitive control over the total amount of chemical added and, equally importantly, the rate of addition of the chemical from the nanodroplet carriers to the microfluidic droplets. An a priori theoretical model was developed to model the mass transport process under the convection-controlled scenario and compared with experimental results. We demonstrate an application of this method in the controlled preparation of gold nanoparticles by reducing chloroauric acid pre-loaded in microfluidic droplets with L-ascorbic acid supplied from miniemulsion nanodroplets. Under different field strengths, L-ascorbic acid is supplied in controllable quantities and addition rates, rendering the particle size and size distribution tunable. Finally, this method also enables multistep synthesis by the stepwise supply of miniemulsions containing different chemical species. We highlight this with a first report of a three-step Au–Pd core–shell nanoparticle synthesis under continuous flow conditions.
Introduction
Droplet microfluidics has been widely applied in the field of chemistry and biology for applications ranging from chemical reactions, material synthesis, to sensing and high throughput screening, to name a few.1–3 The ability to exquisitely generate highly monodisperse microdroplets makes droplet microfluidics an ideal tool to transform traditional batch processes, which typically require large sample volumes and suffer from spatial inhomogeneity and batch-to-batch variation issues, into continuous flow processes with microdroplets acting as individual process vessels.4 In addition to the large number of applications developed by leveraging the benefits of droplet microfluidic systems, there have also been extensive studies on the fundamentals of these systems, such as droplet breakup, actuation, merging, and sorting, etc.5–7 Mass transport within or between microdroplets under external stimuli, such as surface acoustic waves,8 magnetic fields,9 and hydrodynamic forces,10–12 has also received significant attention. One of the challenges in this area is to add/extract solutes to/from these microdroplets easily and flexibly. Due to the small dimensions of droplets and the closed environment of a pressure-driven flow system, it is typically difficult to control the delivery of chemicals across the continuous phase (often with an intervening surfactant layer) into the microdroplets. As a result, most applications involve only an initial mixing of all the chemicals prior to the generation of microdroplets.4,13Many chemical reaction systems, such as reactions generating solids14–16 or those requiring a rate-controlled addition of one or more chemicals, require the addition of chemicals into generated microdroplets. Multistep preparation in microdroplets has also only been achievable with such techniques.17 The most common addition strategy is to alternately generate microdroplets of similar sizes in pairs carrying two reactive species, and fuse them together by mechanical or electrical stimuli,18,19 which typically requires droplet synchronization.20 Another method is to directly inject chemicals into the droplets through a side channel, where the chemical solution to be added forms a pendant drop at the fluid junction and merges with the microdroplets passing by, building a pathway for mass transfer until the microdroplet leaves and disconnects from this side channel.21,22 Nightingale et al. reported an improvement to this method by introducing gas plugs, which help pinch off the pendent drop to achieve a more precise addition, and applied it to a multistep growth of CdSe quantum dots.23 To enable better control over the chemical infusion rate, Ismagilov et al. fabricated an array of side channels that links to the main reaction channel; the chemical can be added to microdroplets through these side channels at multiple locations along their flow path, and therefore at discrete time points.24 Later studies also showed strategies for improving pressure control as required in this method.25 However, the device still requires fabrication with polydimethylsiloxane (PDMS), which limits its application for many organic solvents.
To precisely control both the amount of chemical added and the rate of addition, we present here a novel method that enables highly controlled material transport into the microfluidic droplets. This work is based on a previous study in which we demonstrated that instead of using an inert oil as the carrier fluid, a W/O miniemulsion can be used as the continuous phase (CP) to generate aqueous monodisperse microdroplets as dispersed phase (DP).26 A W/O miniemulsion (or called nanoemulsion27) is a thermodynamically metastable system with aqueous nanodroplets, typically in the 50–500 nm range, dispersed in an immiscible organic solvent with a stabilizing surfactant. These nanodroplets serve as carriers for chemicals to be supplied to the aqueous microdroplets. In this paper, we enable the controllable transport of nanodroplets into the microdroplets via electrocoalescence, mediated by an applied alternating electrical field. Although electrocolaescence has been applied extensively in droplet microfluidic systems to merge droplets of similar sizes,7 we report here for the first time its application to merge droplets of dramatically different sizes, which requires a much higher electrical field strength (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1) to realize. Since the nanodroplets are three orders of magnitude smaller than the microdroplets, we can easily achieve a nanodroplet-to-microdroplet population ratio of greater than 1 million. Such a large population ratio makes it possible to control the chemical addition rate over a wide range, and the addition is in fact “quasi-continuous”, while a paired fusion of microdroplets of similar sizes or infusion through side channels can only achieve a “one-shot” or “multi-shot” discrete injection. Two different types of signal – continuous and cyclic burst square waves – are used. For the continuous signal, the addition rate is controlled by the field strength while the total quantity of chemical added is controlled by the residence time of the microdroplet under the electrical field. For cyclic burst square wave signals, the control over chemical addition is achieved with the number of cycles and the field-on/field-off periods in each cycle. In this method, the electrical field is applied between two parallel electrodes placed outside the flow channel without any physical contact with the droplet flow. Such non-invasiveness makes it easily implementable to many existing systems, such as in the much-explored area of flow synthesis of nanomaterials.15,18,28–32 Here, we demonstrate an application in the controlled nucleation and growth of gold nanoparticles. The addition of the reducing reagent, L-ascorbic acid, is well-controlled to produce gold nanoparticles of tunable size and size distributions. Finally, this method is extended to achieve a three-step continuous synthesis of Au–Pd core–shell nanoparticles with multiple additions of miniemulsions carrying different chemical species. Our work enhances the operational flexibility of microdroplets as reaction vessels, enabling precisely controlled mass transfer at the sub-millimeter scale.
000 V cm−1) to realize. Since the nanodroplets are three orders of magnitude smaller than the microdroplets, we can easily achieve a nanodroplet-to-microdroplet population ratio of greater than 1 million. Such a large population ratio makes it possible to control the chemical addition rate over a wide range, and the addition is in fact “quasi-continuous”, while a paired fusion of microdroplets of similar sizes or infusion through side channels can only achieve a “one-shot” or “multi-shot” discrete injection. Two different types of signal – continuous and cyclic burst square waves – are used. For the continuous signal, the addition rate is controlled by the field strength while the total quantity of chemical added is controlled by the residence time of the microdroplet under the electrical field. For cyclic burst square wave signals, the control over chemical addition is achieved with the number of cycles and the field-on/field-off periods in each cycle. In this method, the electrical field is applied between two parallel electrodes placed outside the flow channel without any physical contact with the droplet flow. Such non-invasiveness makes it easily implementable to many existing systems, such as in the much-explored area of flow synthesis of nanomaterials.15,18,28–32 Here, we demonstrate an application in the controlled nucleation and growth of gold nanoparticles. The addition of the reducing reagent, L-ascorbic acid, is well-controlled to produce gold nanoparticles of tunable size and size distributions. Finally, this method is extended to achieve a three-step continuous synthesis of Au–Pd core–shell nanoparticles with multiple additions of miniemulsions carrying different chemical species. Our work enhances the operational flexibility of microdroplets as reaction vessels, enabling precisely controlled mass transfer at the sub-millimeter scale.
This paper is organized as follows. First we discuss how chemical addition rate and dosage are controlled by a continuous or cyclic burst electrical signal in section II and III. In section IV, we show how such control capabilities can be leveraged for gold nanoparticle synthesis. Section V demonstrates how the multi-step synthesis of gold–palladium core–shell nanoparticles can be easily achieved with this method. In the last section, an a priori simulation based on the electrostatic theory and Navier–Stokes equation is presented to reveal the physical principles involved in this process.
Experimental
Materials
Dodecane, sorbitan monolaurate (Span 20), chloroauric acid trihydrate, L-ascorbic acid, palladium chloride, sodium chloride, and polyvinylpyrrolidone (PVP) were purchased from Sigma Aldrich. Hamilton glass syringes were used for organic samples and BD plastic syringes were used for aqueous samples to avoid corrosion. Harvard PHD Ultra syringe pumps were used for pumping all flow streams. 1.02 mm thru-hole PTFE T-fluid connectors, and fluoroethylene polymer (FEP) tubings with an outer diameter of 1.59 mm and an inner diameter of 0.76 mm were purchased from IDEX-Healthcare. Copper electrode plates and 1.59 mm inner diameter PVDF Y-connectors were purchased from Macmaster. Indium tin oxide (ITO) glass electrodes were purchased from SPI Supplies. Deionized water was prepared with a Millipore ultrafiltration system. Two BK Precision waveform generators (purchased from Cole-Parmer) and a high voltage amplifier (Model 2220, Trek Technologies) were used in combination to generate high strength, high frequency electrical fields.Methods
Continuous square wave signals were used for this experiment. Two different electrical field strengths, 4300 V cm−1 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1, were applied to control the electrocoalescence rate, and their influence on the final gold nanoparticle size and size distribution was investigated. For the low field strength condition, the miniemulsion prepared with 0.17 wt% L-ascorbic acid solution was used. After a residence time of 600 seconds, 75% of the total nanodroplets were consumed (calculated from microdroplet size expansion). This was equivalent to adding 0.0075 mmol of L-ascorbic acid per 1 mL of the HAuCl4 solution (0.01 mmol gold). For the high field condition, we still used a residence time of 600 seconds for consistency, although electrocoalescence was completed in less than 60 seconds. To keep the total amount of added L-ascorbic acid the same, we used the miniemulsion prepared with a 0.13 wt% (75% of 0.17 wt%) L-ascorbic acid solution instead, which was then fully consumed to achieve the same final reaction stoichiometry.
400 V cm−1, were applied to control the electrocoalescence rate, and their influence on the final gold nanoparticle size and size distribution was investigated. For the low field strength condition, the miniemulsion prepared with 0.17 wt% L-ascorbic acid solution was used. After a residence time of 600 seconds, 75% of the total nanodroplets were consumed (calculated from microdroplet size expansion). This was equivalent to adding 0.0075 mmol of L-ascorbic acid per 1 mL of the HAuCl4 solution (0.01 mmol gold). For the high field condition, we still used a residence time of 600 seconds for consistency, although electrocoalescence was completed in less than 60 seconds. To keep the total amount of added L-ascorbic acid the same, we used the miniemulsion prepared with a 0.13 wt% (75% of 0.17 wt%) L-ascorbic acid solution instead, which was then fully consumed to achieve the same final reaction stoichiometry.
To achieve variable residence times at fixed flow rates of the CP and DP, we fixed the applied electrical field strength at 11400 V cm−1, and varied the tube length under the electric field to achieve residence times of 3, 8, and 60 seconds. A miniemulsion prepared with a higher concentration 0.34 wt% L-ascorbic acid solution was used here, and these three residence times yielded 25%, 50%, and 100% microdroplet size expansion. Equivalently, they resulted in 25%, 50% and 100% nanodroplet consumption respectively, giving final reaction stoichiometries of 0.005, 0.01, and 0.02 mmol L-ascorbic acid per 1 mL of the HAuCl4 solution (containing 0.01 mmol gold).
After electrocoalescence, the reaction mixture was collected in a glass vial. The pink aqueous phase was decanted, washed with ethanol 3 times to remove all of the surfactant, and re-dispersed in deionized water. Due to aggregation, dynamic light scattering (NanoBrook 90Plus PALS) characterization did not give the primary particle information. Thus, UV-vis spectroscopy (Agilent Cary 60) and transmission electron microscopy (TEM, FEI Tecnai F20) were used to characterize the size and size distribution of the primary gold nanoparticles.
The 3-step synthesis of Au–Pd nanoparticles is shown in Fig. 1(b). HAuCl4 aqueous droplets were first generated by the ascorbic acid miniemulsion at the T-junction, with both syringe pumps operated at 30 μL min−1. The microdroplets and the miniemulsion were passed into an 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1 electrical field for electrocoalescence. Although electrocoalescence was fast at such a high field strength, we allowed an additional two-minute residence time for complete gold nanoparticle growth. Following this crystal growth process, the Pd-precursor emulsion was infused into the system at a rate of 30 μL min−1 through the PVDF Y-junction. This flow rate was low enough to allow the addition of nanodroplets of Na2PdCl4 without breakage of the elongated microdroplet plugs. The nanodroplets and microdroplets were routed under the same electrode couple for the transfer of all Na2PdCl4 into the microdroplet. After that, another stream of ascorbic acid miniemulsion was infused at a rate of 30 μL min−1 through another PVDF Y-junction, followed by another electrocoalescence process to reduce Na2PdCl4. The aqueous phase was then decanted and washed with ethanol three times to remove surfactants and dodecane residue, and re-dispersed in water for UV-Vis and TEM characterization.
400 V cm−1 electrical field for electrocoalescence. Although electrocoalescence was fast at such a high field strength, we allowed an additional two-minute residence time for complete gold nanoparticle growth. Following this crystal growth process, the Pd-precursor emulsion was infused into the system at a rate of 30 μL min−1 through the PVDF Y-junction. This flow rate was low enough to allow the addition of nanodroplets of Na2PdCl4 without breakage of the elongated microdroplet plugs. The nanodroplets and microdroplets were routed under the same electrode couple for the transfer of all Na2PdCl4 into the microdroplet. After that, another stream of ascorbic acid miniemulsion was infused at a rate of 30 μL min−1 through another PVDF Y-junction, followed by another electrocoalescence process to reduce Na2PdCl4. The aqueous phase was then decanted and washed with ethanol three times to remove surfactants and dodecane residue, and re-dispersed in water for UV-Vis and TEM characterization.
Results and discussion
I. Droplet flow pattern
With the experimental set-up depicted in Fig. 1(a), water-in-oil microdroplet flow was generated with deionized water (with dye) as the DP operated at 10 μL min−1, and a W/O miniemulsion as the CP at 50 μL min−1. The T-junction yielded monodisperse microdroplets generated at a period of 6.3 ± 0.3 seconds per droplet (1.05 μL per droplet). The microdroplets were elongated, moving at a constant speed of 2.2 mm s−1. The circulation in both microdroplets and the plugs between droplets created significant mixing. Although a smaller T-junction or a faster continuous phase flow rate could have resulted in much smaller droplets, we used the condition above to allow a detailed study of mass transport by imaging the size expansion of the large microdroplets with a digital camera.II. Addition dosage and rate control with continuous signals
Without an electrical field, microdroplet size expansion was not detected even after 10 minutes of flow. When a continuous square wave signal was applied to two electrodes placed in parallel to the tubing, the electrical field caused droplets to coalesce and the microdroplets expanded, as seen in Fig. 2(a). The rate of addition was controlled by field strength and the total quantity added (referred as dosage for the rest of paper) was controlled by the residence time under the electrical field. Fig. 2(b) shows the size expansion of the microdroplet as a function of residence time under different electrical fields. Microdroplet expansion was caused by the fusion with nanodroplets; thus, the rate of size expansion was a direct indication of the rate of addition of the nanodroplets. As shown in Fig. 2(b), a strong electrical field caused the microdroplet to expand more quickly than a weak electrical field for the same residence time, thus showing that a higher field strength enhances electrocoalescence to achieve a high rate of chemical addition. In our experiment, CP flowed at 50 μL min−1 and DP at 10 μL min−1. Since CP was an emulsion that contained 20% vol of water, the maximum size expansion of each microdroplet was 100% i.e. doubled its original size (if evaporation during ultrasonication-based preparation of the CP is neglected). Thus, all curves converge asymptotically to 100% at infinitely long time. Using Fig. 2(b) as a reference, one can choose the right field strength to achieve a rate-controlled chemical addition into the microdroplets. Note that as the field strength reaches 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1, further increase in field strength does not significantly change the size expansion rate, indicating that we have almost reached a limiting scenario, which will be discussed in detail later in section VI.
000 V cm−1, further increase in field strength does not significantly change the size expansion rate, indicating that we have almost reached a limiting scenario, which will be discussed in detail later in section VI.
Besides addition rate control, dosage control could also be achieved by controlling the residence time. By adjusting the length of the FEP tubing wound under the electrodes, we were able to control the residence time for a droplet to pass through, at constant flow velocity. For example, under 7100 V cm−1, we could allow a 7 second residence time for the passage of the microdroplet for a 20% size expansion, or a 17 second residence time to obtain a 50% size expansion by looking up the required size expansion-time relationship in Fig. 2(b).
In summary, both addition rate and dosage can be tuned with a continuous square wave signal by changing the field strength and residence time. For real-time digital control, however, continuous signals only work for modulation of the addition rate because field strength can be adjusted digitally, while changing the residence time for the modulation of the dosage requires the rearrangement of the tube length or changing electrode size, and is thus not suitable for online control.
III. Addition dosage and rate control with cyclic burst signals
An alternative option that enables a real-time digital control of the added material is to use a cyclic burst signal to modulate the time of exposure of the droplets to the electric field. The waveform of the cyclic burst signal used in this work is characterized by repeated on-and-off cycles, with each field-on duration containing five to sixty square wave periods, as shown in Fig. 3(a). The square wave frequency was maintained at 500 Hz for consistency and thus each period was 2 ms. The amplitude of the waveform generator was controlled at 7 V to yield a field strength of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1 after amplification.
000 V cm−1 after amplification.
Still using microdroplet size expansion as a characterization of the rate and dosage of chemical addition, we measured the size expansion of microdroplets as a function of the number of cycles. In these experiments, the tubing length was fixed to give a residence time of 66 seconds. As shown in Fig. 3(b), an increase in the number of cycles or the field-on time in each cycle (correlated to number of periods in each cycle) could increase the dosage. Interestingly, when these two variables were multiplied to form a new variable - the total field-on time, all curves overlapped, and a clear relationship between dosage and total field-on time can be visualized as in Fig. 3(c). Because of the replenishment of nanodroplets near microdroplets during the field-off time, the total field-on time required for microdroplet size expansion was shorter under these conditions than that required for a continuous 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1 square wave, which has been shown in Fig. 2(b).
000 V cm−1 square wave, which has been shown in Fig. 2(b).
Thus, with a fixed residence time, dosage can be tuned digitally by the control of the total field-on time using Fig. 3(c) as a reference without changes to the device geometry, which now provides real-time dosage control capability. In addition, we can tune the field-off time interval between bursts and maintain a fixed total field-on time, which correspondingly results in different total process times, to achieve different addition rates with a fixed dosage.
IV. Application: controlled nucleation and growth of gold nanoparticles
We used pure water in miniemulsion and microdroplets (with dye for visualization in the microdroplets) to demonstrate the ability to control addition rate and dosage, as measured by the growth of the microdroplets with applied signal. However, the goal of this study is to deliver chemicals into microdroplets for controlled chemical reactions where the rate of addition of chemicals influences the final outcome. Here we demonstrate an application of this method to the controlled nucleation and growth of gold nanoparticles following a synthesis protocol published by Jana et al.33 Briefly, a gold precursor – chloroauric acid (HAuCl4) – can be reduced by L-ascorbic acid with a stabilization agent, polyvinylpyrrolidone (PVP). Köhler et al.14,34 and Benyahia et al.15 adopted this chemistry in the continuous flow synthesis of gold nanoparticles in a single phase system. Pre-treatment of reaction tubing and careful reaction condition control are needed to avoid surface fouling due to gold nanoparticle deposition. In our experiment, HAuCl4 was enclosed in microdroplets while L-ascorbic acid was supplied from nanodroplets, and surface fouling could be prevented. The growth of gold nanoparticles follows a nucleation-growth mechanism: seed crystals of gold are first created by a sudden increase in supersaturation with L-ascorbic acid addition. Further addition of L-ascorbic acid reduces more HAuCl4, either creating new seeds or increasing the size of the formed seed crystals. Theoretically, a fast addition of L-ascorbic acid leads to a burst generation of gold seeds at the beginning, and relatively uniform growth on these seeds subsequently, with minimal generation of new seeds; therefore, fast addition should yield smaller particles with a narrower size distribution compared to particles obtained with a slower addition of the reducing agent.Under a continuous square wave signal, the field strength was controlled to achieve different rates of L-ascorbic acid addition, and the results follow the hypothesis above very well. By maintaining a reaction stoichiometry of 0.0075 mmol of ascorbic acid to 0.01 mmol of HAuCl4, and using a high field of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1 or a low field of 4300 V cm−1, we fused nanodroplets into the microdroplets to achieve fast or slow mass transfer respectively. In the low field case, a long residence time of 600 s was needed, while in the high field case, nanodroplets were completely consumed in less than 60 s (although we let the train of droplets flow in the tube for the entire 600 s for consistency). In both cases, the microdroplets turned pink, showing the formation of gold nanoparticles. A detailed characterization of the UV-vis spectrum of these two samples reveals key differences; as shown in Fig. 4(a), the slow addition sample gave a higher peak absorption wavelength at 560 nm compared to 535 nm for the fast addition sample. Previous research35 shows a positive correlation between the wavelength of the UV-vis absorption peak and the size of the primary particles. This indicates that the slow addition of the reducing agent resulted in a larger mean particle size, as discussed above. We confirmed this inference with TEM characterization, as shown in Fig. 4(c–f). The size of the gold nanoparticles prepared with a fast addition over 60 seconds was 44.6 ± 12.6 nm, while it was 81.2 ± 25.5 nm when L-ascorbic acid was added slowly over 600 seconds. Under an 11
400 V cm−1 or a low field of 4300 V cm−1, we fused nanodroplets into the microdroplets to achieve fast or slow mass transfer respectively. In the low field case, a long residence time of 600 s was needed, while in the high field case, nanodroplets were completely consumed in less than 60 s (although we let the train of droplets flow in the tube for the entire 600 s for consistency). In both cases, the microdroplets turned pink, showing the formation of gold nanoparticles. A detailed characterization of the UV-vis spectrum of these two samples reveals key differences; as shown in Fig. 4(a), the slow addition sample gave a higher peak absorption wavelength at 560 nm compared to 535 nm for the fast addition sample. Previous research35 shows a positive correlation between the wavelength of the UV-vis absorption peak and the size of the primary particles. This indicates that the slow addition of the reducing agent resulted in a larger mean particle size, as discussed above. We confirmed this inference with TEM characterization, as shown in Fig. 4(c–f). The size of the gold nanoparticles prepared with a fast addition over 60 seconds was 44.6 ± 12.6 nm, while it was 81.2 ± 25.5 nm when L-ascorbic acid was added slowly over 600 seconds. Under an 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1 continuous square wave signal, dosage of the L-ascorbic acid can be tuned by varying the residence time by changing the length of tubing between the two electrode plates. Under the same high field condition (11
400 V cm−1 continuous square wave signal, dosage of the L-ascorbic acid can be tuned by varying the residence time by changing the length of tubing between the two electrode plates. Under the same high field condition (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1), we investigated three different residence times 3 s, 8 s, and 60 s (at the same flow speed) to control the added ascorbic acid quantity. We also raised the concentration of L-ascorbic acid to more substantially differentiate these three conditions, resulting in different reaction stoichiometries of 0.005, 0.01, and 0.02 mmol ascorbic acid per 0.01 mmol of HAuCl4. As shown in Fig. 4(b), an increase in the amount of added ascorbic acid results in a higher absorption peak wavelength, due to contributions from different size and shaped nanoparticles in the samples (TEM images and size distribution histograms in the ESI†).
400 V cm−1), we investigated three different residence times 3 s, 8 s, and 60 s (at the same flow speed) to control the added ascorbic acid quantity. We also raised the concentration of L-ascorbic acid to more substantially differentiate these three conditions, resulting in different reaction stoichiometries of 0.005, 0.01, and 0.02 mmol ascorbic acid per 0.01 mmol of HAuCl4. As shown in Fig. 4(b), an increase in the amount of added ascorbic acid results in a higher absorption peak wavelength, due to contributions from different size and shaped nanoparticles in the samples (TEM images and size distribution histograms in the ESI†).
V. Application: multistep synthesis of gold–palladium core–shell nanoparticles
In addition to the application in a single step reaction, this miniemulsion-coalescence method could also be extended to multistep synthesis operations, which is where it enables decisive advantages compared to the more conventional droplet addition methods mentioned in the Introduction section. Further addition of different chemicals can be achieved easily by subsequent injections of additional miniemulsions carrying other chemicals, followed by the same electrocoalescence treatment. As a demonstration of this capability, we added two more steps to the preparation of PVP-stabilized gold nanoparticles – the addition of Na2PdCl4 followed by the addition of ascorbic acid to prepare Au–Pd core–shell nanoparticles. Au–Pd core–shell nanoparticles have been used in applications such as surface enhanced Raman spectroscopy36 and the catalytic conversion of formic acid37 and alcohol.38 While synthesizing other core–shell nanoparticles in continuous droplet flow has been achieved in literature,39 to the best of our knowledge, the continuous synthesis of Au–Pd core–shell nanoparticles has not yet been reported. Our detailed experimental procedures are presented in the experimental section and a schematic of the experimental set-up is shown in Fig. 1(b).As shown in Fig. 5(a), the prepared Au–Pd nanoparticles formed a black suspension when dispersed in water, which matches previous reports on Au–Pd nanoparticles prepared by batch methods.40Fig. 5(b) shows the UV-vis characterization of the Au nanoparticles collected before Na2PdCl4 addition, and the finally collected Au–Pd nanoparticles after three steps, both prepared with a gold concentration of 10−6 mol mL−1. Sánchez-Ramírez et al.41 and Hu et al.36 studied the difference in optical properties between Au–Pd bimetallic nanoparticles and a mixture of Pd and Au nanoparticles, showing that a complete disappearance of the surface plasmon resonance absorbance is an indication of effective coating. Ideally, the gold surface plasmon resonance peak should be completely eliminated if the coverage of Pd on Au is 100%, and a broad featureless absorption which contributes to the black color of the suspension, should be obtained.36 In our case, the residue peak indicated an insufficient coverage, although the absorbance had been significantly suppressed. The result is also in agreement with the report from Shim et al. that Pd nanoparticles do not have surface plasmon resonance absorption peaks.42 An increase in Na2PdCl4 concentration could result in a further increase in Pd coverage, but also result in more self-nucleated pure Pd nanoparticles.
TEM characterization of the Au–Pd nanoparticles gives a clearer view of the Au core–Pd shell structure. With different electron transmission rates, Pd shell and Au core can be easily distinguished for small particles, which had a shell thickness of about 10 nm, as shown in Fig. 5(d). The Pd-coating was non-uniform, indicating that it formed mostly through secondary nucleation on the gold surface. The morphology is also consistent with previous reports on two-step Au–Pd core–shell nanoparticle synthesis using batch methods.43 For larger particles, however, the relatively thin Pd shell was difficult to observe (Fig. 5(c)) that TEM-EDS (energy dispersive spectrum) was needed to visualize the surface coverage of palladium. Fig. 5(e) and (f) give evidence for effective palladium coating, and a clear Au core–Pd shell structure is seen. Defective edges without thick Pd coating were also observed, and probably contributed to the residual surface plasmon resonance peak in the UV-vis spectrum of the Au–Pd sample (Fig. 5(b)).
VI. Theory
To understand the physical principles governing the electrocoalescence between microdroplets and nanodroplets, and to predict the rate nanodroplets are consumed by microdroplets, here we present an a priori model based on the Navier–Stokes equation and dipole–dipole electrostatic interaction forces.| b = 0.643(3Ca)2/3r1 | (1) |
For an elongated microdroplet transported in a circular channel, r1 is the radius of the hemispherical droplet end. Since r1 + b = rtube = 381 μm, we calculate r1 = 368 μm and the lubrication layer had a thickness of only 13 μm. The microdroplet length and drop–drop distance can be calculated from the flow rates and the droplet generation frequency.
With the geometrical parameters determined above, nanodroplet motion can be simulated by numerically solving the Navier–Stokes equation. Under the 50 μL min−1 (CP)/10 μL min−1 (DP) flow condition, for droplets with a diameter smaller than 60 μm, the fluid drag force (calculated based on a characteristic velocity of 1 mm s−1) is stronger than the gravitational force, as calculated from the Stokes law. Thus for nanodroplets, gravitational settling of the nanodroplets can be neglected and the droplets are entrained by dodecane. Treating the miniemulsion as a pseudo-single phase, we determined the nominal viscosity (measured with a Ubbelohde viscometer) and density to be 4 cP and 800 kg m−3, respectively. Thus, the laminar flow field could be calculated numerically, with results shown in Fig. 6(a). Note that we fix the coordinate on the microdroplet, effectively making the wall move in the opposite direction at a speed of 2.2 mm s−1.
 | (2) |
 | (3) |
From the electrostatic force expressions, it can be inferred that the force is extremely sensitive to drop–drop distance and the nanodroplet size. Thus, a theoretical analysis is complicated by the fact that nanodroplet size and size distribution are not time-invariant since, under a high electrical field, nanodroplet self-coalescence is significant. Self-coalescence of nanodroplets under an alternating electrical field has been reported previously.46 To verify self-coalescence, when we flowed only the miniemulsion continuous phase through this field, the nanodroplets easily self-coalesced into naked eye-visible large droplets in 5–10 seconds. When microdroplets were present, we did not observe the formation of these large droplets due to the continuous consumption of the nanodroplets by the microdroplets, preventing them from growing too large. To in situ characterize the dynamic time-evolution of nanodroplet size and size distribution accurately was beyond our experimental capability, while analysis performed after the collection of self-coalesced droplets was inaccurate due to their easier subsequent coalescence in the collection well. Thus, self-coalescence complicates the theoretical prediction based solely on the electrostatic force expressions, as the actual miniemulsion droplet sizes are unknown and time-dependent.
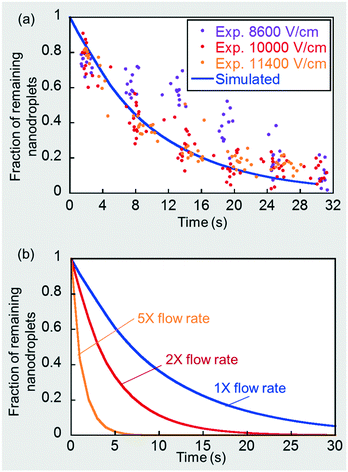
Details of the assumptions made and the numerical simulation set-up in a commercial finite element software, COMSOL Multiphysics®, are presented in the ESI.† The a priori simulated nanodroplet consumption rate under these physically limiting conditions is shown by the solid line in Fig. 7(a). Note that nanodroplet depletion leads to microdroplet expansion and, at a flow rate ratio of 5 (CP)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (DP), corresponds to microdroplet size expansion on a one-to-one basis. For example, a 50% nanodroplet depletion corresponds to a 50% microdroplet size expansion. The simulated curve is the theoretical convection-controlled limit of nanoemulsion consumption rate under a continuous signal. Recall that in section 3.2 and Fig. 2(b) we showed that the mass transport rate was barely enhanced when the field strength was sufficiently strong, which corresponds to this theoretical limit. We obtained additional microdroplet size expansion data points for the three highest field strengths, 8600, 10
1 (DP), corresponds to microdroplet size expansion on a one-to-one basis. For example, a 50% nanodroplet depletion corresponds to a 50% microdroplet size expansion. The simulated curve is the theoretical convection-controlled limit of nanoemulsion consumption rate under a continuous signal. Recall that in section 3.2 and Fig. 2(b) we showed that the mass transport rate was barely enhanced when the field strength was sufficiently strong, which corresponds to this theoretical limit. We obtained additional microdroplet size expansion data points for the three highest field strengths, 8600, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 11
000 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 V cm−1, and deduced the rate of nanodroplet depletion based on the one-to-one relationship mentioned before. As shown in Fig. 7(a), once the field was sufficiently high (∼10
400 V cm−1, and deduced the rate of nanodroplet depletion based on the one-to-one relationship mentioned before. As shown in Fig. 7(a), once the field was sufficiently high (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1), further increase in the field strength did not contribute to a faster consumption rate, indicating we had approached the convection-controlled limit. The close proximity between the predicted curve and experimental results also strengthens this conclusion and provides a good validation of the numerical model. We further simulated such convection-controlled cases for higher flow rates at a fixed DP-to-CP flow rate ratio of 1
000 V cm−1), further increase in the field strength did not contribute to a faster consumption rate, indicating we had approached the convection-controlled limit. The close proximity between the predicted curve and experimental results also strengthens this conclusion and provides a good validation of the numerical model. We further simulated such convection-controlled cases for higher flow rates at a fixed DP-to-CP flow rate ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. The droplet flow pattern, including droplet sizes and drop–drop distances, are different under different flow conditions. A higher total flow rate decreases droplet size and drop-drop distance using the same T-junction, which were measured experimentally and used to determine the simulation geometries for each case (see details in ESI†). These additional simulation results are plotted in Fig. 7(b), showing that increasing flow rates greatly enhanced nanodroplet depletion rate by a stronger convection and a shorter drop-drop distance.
5. The droplet flow pattern, including droplet sizes and drop–drop distances, are different under different flow conditions. A higher total flow rate decreases droplet size and drop-drop distance using the same T-junction, which were measured experimentally and used to determine the simulation geometries for each case (see details in ESI†). These additional simulation results are plotted in Fig. 7(b), showing that increasing flow rates greatly enhanced nanodroplet depletion rate by a stronger convection and a shorter drop-drop distance.
Conclusion
A novel and versatile electrocoalescence method to transport chemicals into microfluidic droplets from nanodroplet carriers has been developed successfully with the use of a miniemulsion as the continuous phase. Both the dosage and the rate of addition of the chemical can be tuned sensitively to meet experimental requirements under two different types of signals, continuous and cyclic burst square waves. Under very high field strengths, greater than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V cm−1, the electrocoalescence is so fast that the entire process is controlled by the convection of nanodroplets to the microdroplet surfaces as they are dragged by the circulating continuous phase flow, in agreement with theoretical predictions of the process rate under this convection-controlled scenario. This method was applied to a single step synthesis of gold nanoparticles and a multistep flow synthesis of Au–Pd core–shell nanoparticles, with the size and size distribution of the resulting nanoparticles well controlled. Our approach is advantageous for the post-addition of chemicals to microfluidic droplets since there is no requirement for droplet synchronization, as in the droplet pair-fusion method, or surface wettability control, as in the direct injection method, or complicated channel fabrication, as in the arrayed side-channel injection method. The electrical field is applied by external electrodes with no physical contact with the reagents, making this method well suited to many existing aqueous flow synthesis systems.
000 V cm−1, the electrocoalescence is so fast that the entire process is controlled by the convection of nanodroplets to the microdroplet surfaces as they are dragged by the circulating continuous phase flow, in agreement with theoretical predictions of the process rate under this convection-controlled scenario. This method was applied to a single step synthesis of gold nanoparticles and a multistep flow synthesis of Au–Pd core–shell nanoparticles, with the size and size distribution of the resulting nanoparticles well controlled. Our approach is advantageous for the post-addition of chemicals to microfluidic droplets since there is no requirement for droplet synchronization, as in the droplet pair-fusion method, or surface wettability control, as in the direct injection method, or complicated channel fabrication, as in the arrayed side-channel injection method. The electrical field is applied by external electrodes with no physical contact with the reagents, making this method well suited to many existing aqueous flow synthesis systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank MIT center for material science and engineering (CMSE) for the use of the TEM facility, Gina S.Y. Liu and Dallace J. Francis for participating in this research as undergraduate researchers, and Eunice W.Q. Yeap and Denise Z. Ng for the insightful discussions.Notes and references
- S.-Y. Teh, R. Lin, L. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- V. Trivedi, A. Doshi, G. K. Kurup, E. Ereifej, P. J. Vandevord and A. S. Basu, Lab Chip, 2010, 10, 2433–2442 RSC.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 CrossRef CAS PubMed.
- C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 RSC.
- Y.-C. Tan, J. S. Fisher, A. I. Lee, V. Cristini and A. P. Lee, Lab Chip, 2004, 4, 292–298 RSC.
- D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556–2560 CrossRef CAS PubMed.
- J. Friend, L. Yeo, M. Tan and R. Shilton, Proc. - IEEE Ultrason. Symp., 2008, 014910, 930–933 Search PubMed.
- U. Lehmann, S. Hadjidj, V. K. Parashar, C. Vandevyver, A. Rida and M. A. M. Gijs, Sens. Actuators, B, 2006, 117, 457–463 CrossRef CAS.
- F. Sarrazin, L. Prat, N. Di Miceli, G. Cristobal, D. R. Link and D. A. Weitz, Chem. Eng. Sci., 2007, 62, 1042–1048 CrossRef CAS.
- M. R. Bringer, C. J. Gerdts, H. Song, J. D. Tice and R. F. Ismagilov, Philos. Trans. R. Soc., A, 2004, 362, 1087–1104 CrossRef CAS PubMed.
- X. Wang, G. Liu, K. Wang and G. Luo, Microfluid. Nanofluid., 2015, 19, 757–766 CrossRef.
- A. B. Theberge, F. Courtois, Y. Schaerli, M. Fischlechner, C. Abell, F. Hollfelder and W. T. S. Huck, Angew. Chem., Int. Ed., 2010, 49, 5846–5868 CrossRef CAS PubMed.
- J. Wagner and J. M. Köhler, Nano Lett., 2005, 5, 685–691 CrossRef CAS PubMed.
- M. V. Bandulasena, G. T. Vladisavljević, O. G. Odunmbaku and B. Benyahia, Chem. Eng. Sci., 2017, 171, 233–243 CrossRef CAS.
- L. Capretto, S. Mazzitelli, C. Balestra, A. Tosi and C. Nastruzzi, Lab Chip, 2008, 8, 617–621 RSC.
- I. Shestopalov, J. D. Tice and R. F. Ismagilov, Lab Chip, 2004, 4, 316–321 RSC.
- L.-H. Hung, K. M. Choi, W.-Y. Tseng, Y.-C. Tan, K. J. Shea and A. P. Lee, Lab Chip, 2006, 6, 174–178 RSC.
- M. Chabert, K. D. Dorfman and J.-L. Viovy, Electrophoresis, 2005, 26, 3706–3715 CrossRef CAS PubMed.
- K. Wang, Y. Lu, C. P. Tostado, L. Yang and G. Luo, Chem. Eng. J., 2013, 227, 90–96 CrossRef CAS.
- Y. Wang, E. Tumarkin, D. Velasco, M. Abolhasani, W. Lau and E. Kumacheva, Lab Chip, 2013, 13, 2547–2553 RSC.
- A. R. Abate, T. Hung, P. Mary, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19163–19166 CrossRef CAS PubMed.
- A. M. Nightingale, T. W. Phillips, J. H. Bannock and J. C. de Mello, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- L. Li, J. Q. Boedicker and R. F. Ismagilov, Anal. Chem., 2007, 79, 2756–2761 CrossRef CAS PubMed.
- M. Rhee, Y. K. Light, S. Yilmaz, P. D. Adams, D. Saxena, R. J. Meagher and A. K. Singh, Lab Chip, 2014, 14, 4533–4539 RSC.
- T. Gu, E. W. Q. Yeap, A. Somasundar, R. Chen, T. A. Hatton and S. A. Khan, Lab Chip, 2016, 16, 2694–2700 RSC.
- A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841 RSC.
- J. B. Edel, R. Fortt, J. C. deMello and A. J. deMello, Chem. Commun., 2002,(10), 1136–1137 RSC.
- S. Duraiswamy and S. A. Khan, Small, 2009, 5, 2828–2834 CrossRef CAS PubMed.
- S. A. Khan, A. Günther, M. A. Schmidt and K. F. Jensen, Langmuir, 2004, 20, 8604–8611 CrossRef CAS PubMed.
- M. T. Rahman, P. G. Krishnamurthy, P. Parthiban, A. Jain, C. P. Park, D.-P. Kim and S. A. Khan, RSC Adv., 2013, 3, 2897–2900 RSC.
- W. K. Wong, S. K. Yap, Y. C. Lim, S. A. Khan, F. Pelletier and E. C. Corbos, React. Chem. Eng., 2017, 2, 636–641 CAS.
- N. R. Jana, L. Gearheart and C. J. Murphy, Chem. Mater., 2001, 13, 2313–2322 CrossRef CAS.
- J. Wagner, T. Kirner, G. Mayer, J. Albert and J. M. Köhler, Chem. Eng. J., 2004, 101, 251–260 CrossRef CAS.
- W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
- J.-W. Hu, Y. Zhang, J.-F. Li, Z. Liu, B. Ren, S.-G. Sun, Z.-Q. Tian and T. Lian, Chem. Phys. Lett., 2005, 408, 354–359 CrossRef CAS.
- X. Gu, Z.-H. Lu, H.-L. Jiang, T. Akita and Q. Xu, J. Am. Chem. Soc., 2011, 133, 11822–11825 CrossRef CAS PubMed.
- W. Hou, N. A. Dehm and R. W. J. Scott, J. Catal., 2008, 253, 22–27 CrossRef CAS.
- A. Knauer, A. Thete, S. Li, H. Romanus, A. Csáki, W. Fritzsche and J. M. Köhler, Chem. Eng. J., 2011, 166, 1164–1169 CrossRef CAS.
- C. Hsu, C. Huang, Y. Hao and F. Liu, Nanoscale Res. Lett., 2013, 8, 113 CrossRef PubMed.
- J. F. Sánchez-Ramírez and U. Pal, Superficies Vacio, 2001, 13, 114–116 Search PubMed.
- J. H. Shim, J. Kim, C. Lee and Y. Lee, Chem. Mater., 2011, 23, 4694–4700 CrossRef CAS.
- D. Varade and K. Haraguchi, Chem. Commun., 2014, 50, 3014–3017 RSC.
- A. Cherukumudi, E. Klaseboer, S. A. Khan and R. Manica, Microfluid. Nanofluid., 2015, 19, 1221–1233 CrossRef CAS.
- P. Parthiban and S. A. Khan, Lab Chip, 2012, 12, 582–588 RSC.
- S. Mhatre, V. Vivacqua, M. Ghadiri, A. M. Abdullah, M. J. Al-Marri, A. Hassanpour, B. Hewakandamby, B. Azzopardi and B. Kermani, Chem. Eng. Res. Des., 2015, 96, 177–195 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc00114f |
| This journal is © The Royal Society of Chemistry 2018 |